ニューラルネットワークが簡単に(第3回): コンボリューションネットワーク

MetaTrader 5 — 例 | 11 1月 2021, 07:48

727

Dmitriy Gizlyk

イントロダクション

ニューラルネットワークの話題の続きとして、畳み込み型ニューラルネットワークの考察を提案します。これらのニューラルネットワークは、通常、写真や動画像の物体認識に関連する問題に応用されています。畳み込みニューラルネットワークは、ズームや角度の変化などの空間画像の歪みに強いとされています。アーキテクチャは、シーンのどこにいても同じように物体を認識することを可能にします。トレードに応用する場合は、畳み込み型ニューラルネットワークを使って、価格チャート上の取引パターンの認識を改善したいと考えています。

1. 畳み込みニューラルネットワークの特徴

畳み込みネットワークは、完全パーセプトロンと比較して、畳み込み（フィルタ）とサブサンプリングの2つの新しいレイヤータイプを持っています。これらの層は、主成分の選択とソースデータのノイズの除去を目的とし、データ次元（体積）を小さくすることを交互に行っています。このデータは、意思決定のために完全に接続されたパーセプトロンに入力されます。畳み込み型ニューラルネットワークの構造を図示すると下図のようになります。タスクに応じて、コンボリューション層とサブサンプル層を交互に使用するいくつかのグループを順次使用することができます。

畳み込みニューラルネットワークのグラフィカルな表現

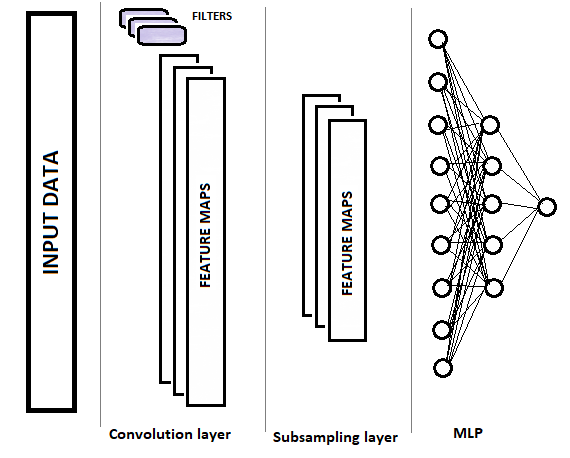
1.1. 畳み込み層

畳み込みレイヤは、ソースデータ配列内のオブジェクトを認識する役割を果たします。このレイヤは、元のデータの数学的畳み込みの逐次演算を、小さなパターン（フィルタ）を畳み込みカーネルとして実行します。

コンボリューションは、2つの関数（fとg）に対する関数分析操作で、相互相関関数f(x)とg(-x)に対応する第3の関数を生成します。畳み込み演算は、ある関数と別の関数のコピーを反転させてシフトさせたものとの「類似度」と解釈できます（Wikipedia）。

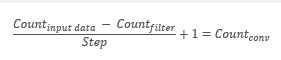
すなわち、畳み込み層は、元のサンプル全体の中からパターン要素を探索します。各イテレーションでは、テンプレートは初期データ配列に沿って所定のステップでシフトされ、そのサイズは "1 "からパターンサイズまでとすることができます。オフセットステップサイズがパターンサイズよりも小さい場合、このような畳み込みをオーバーラップと呼びます。

畳み込み演算では、各繰り返しで元のデータと必要なパターンとの「類似度」を示す特徴量の配列が生成されます。アクティベーション関数は、データの正規化に使用されます。結果として得られる配列のサイズは、元のデータ配列よりも小さくなります。このような配列の数は、フィルタの数に等しい。

フィーチャー配列のサイズ

重要なポイントは、ニューラルネットワークを設計する際にパターンを指定するのではなく、学習の過程でパターンを選択するということです。

1.2. サブサンプリング層

次のサブサンプリング層は、特徴配列の次元を縮小し、ノイズをフィルタリングするために使用されます。この繰り返しの使用は、元のデータとパターンの間の類似性の存在が第一であり、元のデータ配列内の特徴の正確な座標はそれほど重要ではないという仮定に由来しています。これにより、所望のオブジェクト間の距離にある程度のばらつきを持たせることができるので、スケーリング問題の解決策を提供することができます。

この段階では、与えられた「ウィンドウ」内で最大値または平均値を保持することにより、データを圧縮します。このように、データ「ウィンドウ」ごとに1つの値だけが保存されます。演算は反復的に実行され、ウィンドウは新しい反復のたびに所定のステップでシフトされます。データ圧縮は特徴配列ごとに個別に行われます。

ウィンドウと2に等しいステップを持つサブサンプルレイヤがよく使われます - これにより、特徴配列の次元を半分にすることができます。しかし、実際にはより大きなウィンドウを使用することができ、コンパクション反復は、オーバーラップ（ステップサイズがウィンドウサイズよりも小さい場合）またはアウトなしで実行することができます。

サブサンプル層は、より小さな次元の特徴配列を出力します。

問題の複雑さに応じて、サブサンプル層の後に、畳み込み層とサブサンプル層から１つ以上のグループを使用することも可能です。それらの構成原理および機能性は、上述した層に対応します。一般的なケースでは、1つまたは複数の畳み込み＋圧縮のグループの後、すべてのフィルタについて得られた特徴量の配列を1つのベクトルに集めて多層パーセプトロンに送り込み、ニューラルネットワークが判断するようにします (多層パーセプトロンの構築については、この記事シリーズの第1部で詳しく説明しています)。

2. 畳み込み層におけるニューロンの学習原理

畳み込み型ニューラルネットワークは、以前の記事で取り上げたバックプロパゲーション法で学習します。これは教師付き学習法の一つです。これは、ニューロンの出力層から隠れ層を経て、ニューロンの入力層まで誤差勾配を降下させ、反勾配に向かって重み補正を行うことで構成されています。

多層パーセプトロンの学習については、最初の記事で説明したので、ここでは説明を省略します。ここでは、サブサンプル層と畳み込み層のニューロンの訓練について考えてみましょう。

サブサンプル層では、完全に接続されたパーセプトロンのニューロンの勾配と同様に、各特徴配列要素に対して誤差勾配が計算されます。勾配を前の層に移すためのアルゴリズムは、適用される圧縮操作に依存します。最大値のみを使用する場合は、最大値を持つニューロンに全体のグラデーションが供給されます（圧縮ウィンドウ内の他のすべての要素にはゼロのグラデーションが設定されます）。ウィンドウ内の平均化の操作が使用されている場合、グラデーションはウィンドウ内のすべての要素に均等に分布します。

コンパクション操作では重みを使用しないので、学習過程では何も調整されません。

畳み込み層のニューロンを訓練する場合、計算はやや複雑になります。誤差勾配は、特徴配列の各要素について計算され、前の層の対応するニューロンに供給されます。畳み込み層の学習処理は、畳み込み演算と逆畳み込み演算に基づいて行われます。

サブサンプル層からの誤差勾配を畳み込みのものに渡すために、サブサンプル層から得られた誤差勾配の配列のエッジをまずゼロ要素で補い、得られた配列を畳み込みカーネルを１８０°回転させて畳み込みを行います。出力は、入力データ配列と等しい次元の誤差勾配の配列であり、勾配のインデックスは、コンボリュート層の前の対応するニューロンのインデックスに対応しています。

この層の誤差勾配の行列を１８０°回転させて入力値の行列を畳み込み、重みのデルタを求めます。これは、畳み込みカーネルと同じサイズのデルタの配列を出力します。結果として得られるデルタは、畳み込み層活性化関数の微分と学習因子に対して調整する必要があります。その後、調整されたデルタの値によって畳み込みカーネルの重みが変更されます。

これはかなりわかりにくいかもしれません。以下の詳細なコード解析の中で、いくつかの瞬間を明らかにしてみたいと思います。

3. 畳み込みニューラルネットワークの構築

畳み込み型ニューラルネットワークは、特徴的なクラスのニューロンを持つ3種類のニューラル層（畳み込み型、サブサンプル型、完全接続型）で構成され、フォワードパスとバックワードパスのために異なる機能を持つことになります。同時に、全てのニューロンを一つのネットワークにまとめ、処理されたニューロンに対応するデータ処理手段の呼び出しを整理する必要があります。一番整理しやすいのは、クラス継承と関数の仮想化だと思います。

まずは、クラスの継承構造を構築してみましょう。

ニューロンクラスの継承構造

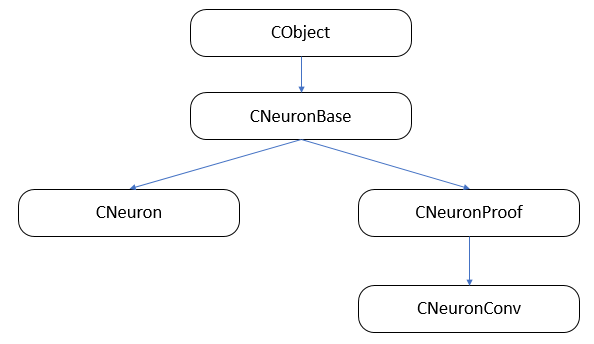
3.1. ニューロンの基底クラス。

最初の記事では、CObjectクラスのオブジェクトへのポインタを格納するための動的配列クラスであるCArrayObjの子孫としてCLayerレイヤークラスを作成しました。したがって、すべてのニューロンはこのクラスを継承しなければなりません。 CObjectクラスをベースにCNeuronBaseクラスを作成しました。クラス本体では、ニューロンのすべてのタイプに共通する変数を宣言し、メインメソッドのテンプレートを作成します。クラスのすべてのメソッドは、さらなる再定義を可能にするために仮想的に宣言されています。

class CNeuronBase    :  public CObject
  {
protected:
   double            eta;
   double            alpha;
   double            outputVal;
   uint              m_myIndex;
   double            gradient;
   CArrayCon        *Connections;
//--- 
   virtual bool      feedForward(CLayer *prevLayer)               {  return false;     }
   virtual bool      calcHiddenGradients( CLayer *&nextLayer)     {  return false;     }
   virtual bool      updateInputWeights(CLayer *&prevLayer)       {  return false;     }
   virtual double    activationFunction(double x)                 {  return 1.0;       }
   virtual double    activationFunctionDerivative(double x)       {  return 1.0;       }
   virtual CLayer    *getOutputLayer(void)                        {  return NULL;      }
public:
                     CNeuronBase(void);
                    ~CNeuronBase(void);
   virtual bool      Init(uint numOutputs, uint myIndex);
//---
   virtual void      setOutputVal(double val)                     {  outputVal=val;    }
   virtual double    getOutputVal()                               {  return outputVal; }
   virtual void      setGradient(double val)                      {  gradient=val;     }
   virtual double    getGradient()                                {  return gradient;  }
//---
   virtual bool      feedForward(CObject *&SourceObject);
   virtual bool      calcHiddenGradients( CObject *&TargetObject);
   virtual bool      updateInputWeights(CObject *&SourceObject);
//---
   virtual bool      Save( int const file_handle);
   virtual bool      Load( int const file_handle)                  {  return(Connections.Load(file_handle)); }
//---
   virtual int       Type(void)        const                       {  return defNeuronBase;                  }
  };

変数名やメソッド名は、先ほど説明したものと同じです。 Let us consider methods feedForward(CObject *&SourceObject), сalcHiddenGradients(CObject *&TargetObject) and updateInputWeights(CObject *&SourceObject), in which dispatching for working with fully connected and convolutional layers is performed.

3.1.1. フィードフォワード

feedForward(CObject *&SourceObject)メソッドは、フォワード・パス中に呼び出され、結果のニューロン値を計算します。フォワード・パスの間、完全に接続された層の各ニューロンは、前の層のすべてのニューロンの値を受け取り、前の層全体を入力として受け取る必要があります。畳み込み層とサブサンプリング層では、このフィルタに関連するデータの一部のみがニューロンに供給されます。考慮された方法では、パラメータで得られたクラスの種類に基づいてアルゴリズムが選択されます。

まず、メソッドのパラメータで取得したオブジェクトポインタの有効性を確認します。

bool CNeuronBase::feedForward(CObject *&SourceObject)
  {
   bool result=false;
//---
   if(CheckPointer(SourceObject)==POINTER_INVALID)
      return result;

クラスインスタンスは選択演算子の中で宣言できないので、あらかじめテンプレートを用意しておく必要があります。

   CLayer *temp_l;
   CNeuronProof *temp_n;

次に、選択演算子では、パラメータで受信したオブジェクトの種類を確認します。ニューロンの層へのポインタを受信した場合、前の層は完全に接続されていることになるので、完全に接続された層を扱うためのメソッドを呼び出す必要があります（第1回記事で詳しく説明しています）。それが畳み込み層やサブサンプル層のニューロンであれば、まずこのフィルタの出力ニューロンの層を取得して、完全に接続された層を処理する方法を使用して、現在のフィルタのニューロンの層を入力して、処理結果をresult変数に保存しなければなりません（畳み込み層やサブサンプル層のニューロンの構造についての詳細は後述します）。操作後、メソッドを終了し、操作結果を渡します。

   switch(SourceObject.Type())
     {
      case defLayer:
        temp_l=SourceObject;
        result=feedForward(temp_l);
        break;
      case defNeuronConv:
      case defNeuronProof:
        temp_n=SourceObject;
        result=feedForward(temp_n.getOutputLayer());
        break;
     }
//---
   return result;
  }

3.1.2. 誤差勾配計算。

フォワード・パスと同様に、ニューラル・ネットワークの隠れ層の誤差勾配を計算する関数を呼び出すためのディスパッチャが作成されました - сalcHiddenGradients(CObject*&TargetObject)。メソッドのロジックや構造は、上述したものと同様です。まず、受信したポインタの有効性を確認します。次に、対応するオブジェクトへのポインタを格納する変数を宣言します。そして、受信したオブジェクトの種類に応じて、選択機能で適切なメソッドを選択します。畳み込みレイヤまたはサブサンプルレイヤの要素へのポインタがパラメータに渡されている場合に違いが生じます。このようなニューロンを介した誤差勾配の計算は、異なるものであり、前の層のすべてのニューロンに適用されるのではなく、サンプリングウィンドウ内のニューロンにのみ適用されます。そのため、calcInputGradientsメソッドでは、これらのニューロンに勾配計算が転送されていました。また、層ごとの計算方法や特定のニューロンごとの計算方法にも違いがあります。そのため、必要なメソッドは、呼び出されるオブジェクトの種類に応じて呼び出されます。

bool CNeuronBase::calcHiddenGradients(CObject *&TargetObject)
  {
   bool result=false;
//---
   if(CheckPointer(TargetObject)==POINTER_INVALID)
      return result;
//---
   CLayer *temp_l;
   CNeuronProof *temp_n;
   switch(TargetObject.Type())
     {
      case defLayer:
        temp_l=TargetObject;
        result=calcHiddenGradients(temp_l);
        break;
      case defNeuronConv:
      case defNeuronProof:
        switch(Type())
          {
           case defNeuron:
             temp_n=TargetObject;
             result=temp_n.calcInputGradients(GetPointer(this),m_myIndex);
             break;
           default:
             temp_n=GetPointer(this);
             temp_l=temp_n.getOutputLayer();
             temp_n=TargetObject;
             result=temp_n.calcInputGradients(temp_l);
             break;
          }
        break;
     }
//---
   return result;
  }

すべてのウェイトを更新するupdateInputWeights(CObject *&SourceObject)ディスパッチャは、上記の原則に基づいています。フルコードは添付ファイルにあります。

3.2. サブサンプリング層要素。

サブサンプル・レイヤーの主な構成要素は CNeuronProof クラスで、これは先に説明した CNeuronBase 基底クラスを継承しています。このクラスの 1 つのインスタンスが、サブサンプル層の各フィルタに対して作成されます。そのため、コンパクションウィンドウのサイズとシフトステップを格納するために、追加の変数（iWindowとiStep）が導入されています．また、特徴配列、誤差勾配、必要に応じて完全に接続されたパーセプトロンに特徴を渡すための重みを格納するためのニューロンの内部層を追加します。また、要求に応じてニューロンの内層へのポインタを受信する方法を追加します。

class CNeuronProof : public CNeuronBase
  {
protected:
   CLayer            *OutputLayer;
   int               iWindow;
   int               iStep;
   
   virtual bool      feedForward(CLayer *prevLayer);
   virtual bool      calcHiddenGradients( CLayer *&nextLayer);
   
public:
                     CNeuronProof(void){};
                    ~CNeuronProof(void);
   virtual bool      Init(uint numOutputs,uint myIndex,int window, int step, int output_count);
//---
   virtual CLayer   *getOutputLayer(void)  { return OutputLayer;  }
   virtual bool      calcInputGradients( CLayer *prevLayer) ;
   virtual bool      calcInputGradients( CNeuronBase *prevNeuron, uint index) ;
   //--- methods for working with files
   virtual bool      Save( int const file_handle)                         { return(CNeuronBase::Save(file_handle) && OutputLayer.Save(file_handle));   }
   virtual bool      Load( int const file_handle)                         { return(CNeuronBase::Load(file_handle) && OutputLayer.Load(file_handle));   }
   virtual int       Type(void)   const   {  return defNeuronProof;   }
  };

基底クラスで宣言された仮想関数のロジックを再定義することを忘れないでください。

3.2.1. フィードフォワード

フィードフォワード法は、ノイズをフィルタリングし、特徴量配列の次元を小さくするために適用されます。記述された解決策では、データをコンパクトにするために算術平均関数が使用されます。メソッドのコードをもう少し詳しく考えてみましょう。メソッドの最初に、取得したポインタのニューロンの前の層への関連性を確認します。

bool CNeuronProof::feedForward(CLayer *prevLayer)
  {
   if(CheckPointer(prevLayer)==POINTER_INVALID)
      return false;

次に、パラメータで得られた層のすべてのニューロンを、所定のステップでループします。

   int total=prevLayer.Total()-iWindow+1;
   CNeuron *temp;
   for(int i=0;(i<=total && result);i+=iStep)
     {

ループ本体では、指定された圧縮ウィンドウ内で前のレイヤーのニューロンの出力値の合計を計算するための入れ子のループを作成します。

      double sum=0;
      for(int j=0;j<iWindow;j++)
        {
         temp=prevLayer.At(i+j);
         if(CheckPointer(temp)==POINTER_INVALID)
            continue;
         sum+=temp.getOutputVal();
        }

和を計算した後、結果データを格納している内層の対応するニューロンを使用して、得られた和のウィンドウサイズに対する比率を結果値に書き込む。この比率は、現在の圧縮ウィンドウの算術平均となります。

      temp=OutputLayer.At(i/iStep);
      if(CheckPointer(temp)==POINTER_INVALID)
         return false;
      temp.setOutputVal(sum/iWindow);
     }
//---
   return true;
  }

すべてのニューロンをパスした後、メソッドは完了します。

3.2.2. 誤差勾配計算。

このクラスでは、誤差勾配を計算するための2つのメソッドが作成されています。calcHiddenGradients と calcInputGradients です。最初のクラスは、後続のレイヤーの誤差勾配に関するデータを収集し、現在のレイヤー要素の勾配を計算します。第２のクラスは、第１の方法で得られたデータを用いて、前の層の要素間で誤差を分散させます。

ここでも、calcHiddenGradientsメソッドの先頭で、取得したポインタの妥当性を確認します。さらに、ニューロンの内層の状態を確認します。

bool CNeuronProof::calcHiddenGradients( CLayer *&nextLayer)
  {
   if(CheckPointer(nextLayer)==POINTER_INVALID || CheckPointer(OutputLayer)==POINTER_INVALID || OutputLayer.Total()<=0)
      return false;

次に、すべての内層ニューロンをループし、誤差勾配を計算するメソッドを呼び出します。

   gradient=0;
   int total=OutputLayer.Total();
   CNeuron *temp;
   for(int i=0;i<total;i++)
     {
      temp=OutputLayer.At(i);
      if(CheckPointer(temp)==POINTER_INVALID)
         return false;
      temp.setGradient(temp.sumDOW(nextLayer));
     }
//---
   return true;
  }

この方法は、ニューロンの完全に接続された層が続く場合に正しく動作することに注意してください。畳み込み層またはサブサンプリング層が続く場合は、次の層のニューロンのcalcInputGradientsメソッドを使用します。

calcInputGradientsメソッドは、パラメータで前のレイヤーへのポインタを受け取ります。メソッドの開始時にポインタの有効性を確認することを忘れないでください。

bool CNeuronProof::calcInputGradients(CLayer *prevLayer) 
  {
   if(CheckPointer(prevLayer)==POINTER_INVALID || CheckPointer(OutputLayer)==POINTER_INVALID)
      return false;

次に、レイヤパラメータで取得した第１の要素の種類を確認します。結果として得られる参照がサブサンプル層または畳み込み層を指している場合は、フィルタに対応するニューロンの内側の層への参照を要求します。

   if(prevLayer.At(0).Type()!=defNeuron)
     {
      CNeuronProof *temp=prevLayer.At(m_myIndex);
      if(CheckPointer(temp)==POINTER_INVALID)
         return false;
      prevLayer=temp.getOutputLayer();
      if(CheckPointer(prevLayer)==POINTER_INVALID)
         return false;
     }

次に、前のレイヤーのすべてのニューロンをループして、処理されたニューロンへの参照の有効性をチェックします。

   CNeuronBase *prevNeuron, *outputNeuron;
   int total=prevLayer.Total();
   for(int i=0;i<total;i++)
     {
      prevNeuron=prevLayer.At(i);
      if(CheckPointer(prevNeuron)==POINTER_INVALID)
         continue;

内層のどのニューロンが処理されたニューロンの影響を受けているかを判断します。

      double prev_gradient=0;
      int start=i-iWindow+iStep;
      start=(start-start%iStep)/iStep;
      double stop=(i-i%iStep)/iStep+1;

ループ内で、処理されたニューロンの誤差勾配を計算し、結果を保存します。この方法は、前の層のすべてのニューロンを処理した後に終了します。

      for(int out=(int)fmax(0,start);out<(int)fmin(OutputLayer.Total(),stop);out++)
        {
         outputNeuron=OutputLayer.At(out);
         if(CheckPointer(outputNeuron)==POINTER_INVALID)
            continue;
         prev_gradient+=outputNeuron.getGradient()/iWindow;
        }
      prevNeuron.setGradient(prev_gradient);
     }
//---
   return true;
  }

別々のニューロンの勾配を計算する同名のメソッドは、似たような構造をしています。この違いは、外部サイクルの反復ニューロンを除外している点です。その代わりに、ニューロンはインデックスによって呼び出されます。

サブサンプル層では重みを使用しないので、重みの更新方法を省略することができます。ニューロン・クラスの構造を保持したい場合は、空のメソッドを作成して、呼び出されたときに true を作成することができます。

すべてのメソッドと関数の完全なコードは添付ファイルにあります。

3.3. 畳み込みレイヤ要素。

畳み込み層は、CNeuronConvクラスのオブジェクトを使用して構築されますが、このオブジェクトはCNeuronProofクラスを継承します。今回はこのタイプのニューロンの活性化関数としてパラメトリックReLUを選択しました。この関数は完全に接続されたパーセプトロンニューロンで使用される双曲正接よりも計算が簡単です。関数を計算するための変数paramを追加で導入してみましょう。

class CNeuronConv  :  public CNeuronProof
  {
protected:
   double            param;   //PReLU param
   virtual bool      feedForward(CLayer *prevLayer);
   virtual bool      calcHiddenGradients(CLayer *&nextLayer);
   virtual double    activationFunction(double x);
   virtual bool      updateInputWeights(CLayer *&prevLayer);
public:
                     CNeuronConv() :   param(0.01) { };
                    ~CNeuronConv(void)             { };
//---
   virtual bool      calcInputGradients(CLayer *prevLayer) ;
   virtual bool      calcInputGradients(CNeuronBase *prevNeuron, uint index) ;
   virtual double    activationFunctionDerivative(double x);
   virtual int       Type(void)   const   {  return defNeuronConv;   }
  };

フォワードパス法とバックワードパス法は、CNeuronプルーフクラスと同様のアルゴリズムに基づいています。違いは活性化関数と重み係数の使い方にあります。なので、詳しくは書かないことにします。ここでは、重量調整方法updateInputWeightsについて考えてみましょう。

このメソッドは、ニューロンの前の層へのポインタを受け取ります。ここでも、メソッドの開始時にポインタの有効性と内層の状態をチェックします。

bool CNeuronConv::updateInputWeights(CLayer *&prevLayer)
  {
   if(CheckPointer(prevLayer)==POINTER_INVALID || CheckPointer(OutputLayer)==POINTER_INVALID)
      return false;

次に、すべてのウェイトを通るループを作成します。受信したオブジェクトポインタの有効性を確認することを忘れないでください。

   CConnection *con;
   for(int n=0; n<iWindow && !IsStopped(); n++)
     {
      con=Connections.At(n);
      if(CheckPointer(con)==POINTER_INVALID)
         continue;

その後、入力データの配列を１８０°回転させた内層誤差勾配の配列との畳み込みを計算します。これは、以下のスキームに従って入力データ配列の要素を乗算した内部層の全要素をループして行われます。

入力データ配列の最初の要素に誤差勾配配列の最後の要素を乗算したもの（重みの序数に等しいステップ数だけシフトしたもの）.
入力データ配列の2番目の要素に誤差勾配配列の2番目から最後の要素を乗算したもの（重みの序数に等しいステップ数だけシフトしたもの）。
重みの序数に等しいステップ数だけシフトした内層配列の要素数に等しいインデックスを持つ要素が、誤差勾配配列の最初の要素に乗算されるまで。

そして、得られた積の和を求めます。

      double delta=0;
      int total_i=OutputLayer.Total();
      CNeuron *prev, *out;
      for(int i=0;i<total_i;i++)
        {
         prev=prevLayer.At(n*iStep+i);
         out=OutputLayer.At(total_i-i-1);
         if(CheckPointer(prev)==POINTER_INVALID || CheckPointer(out)==POINTER_INVALID)
            continue;
         delta+=prev.getOutputVal()*out.getGradient();
        }

計算された製品の合計は、ウェイトを調整するための基礎となります。セットしたトレーニングスピードを考慮してウェイトを調整します。

      con.weight+=con.deltaWeight=(delta!=0 ? eta*delta : 0)+(con.deltaWeight!=0 ? alpha*con.deltaWeight : 0);
     }
//---
   return true;  
  }

すべてのウェイトを調整したら、メソッドを終了します。

CNeuronクラスについては、最初の記事で詳しく説明しています。あまり変わっていないので、ここでは説明を省略します。

3.4. 畳み込みニューラルネットワーククラスを作成します。

全てのレンガが出来上がったので、いよいよ家づくりに取り掛かります。あらゆる種類のニューロンを明確な構造にまとめる畳み込み型ニューラルネットワークのクラスを作成し、ニューラルネットワークの仕事を整理していきます。このクラスを作成する際に最初に出てくる問題は、必要なネットワーク構造をどのように設定するかということです。完全に接続されたパーセプトロンの場合、各層のニューロンの数の情報を持つ要素の配列を渡しました。さて、所望のネットワーク層を生成するためには、より多くの情報が必要です。レイヤーの構造を記述するための小さなクラス CLayerDescription を作成してみましょう。このクラスにはメソッドは含まれておらず（コンストラクタとデストラクタを除く）、層内のニューロンの種類、そのようなニューロンの数、ウィンドウサイズ、畳み込み層とサブサンプル層のニューロンのステップを指定するための変数のみが含まれています。畳み込みネットワーククラスのコンストラクタのパラメータには、レイヤーの記述を持つクラスの配列へのポインタが渡されます．

class CLayerDescription    :  public CObject
  {
public:
                     CLayerDescription(void);
                    ~CLayerDescription(void){};
//---
   int               type;
   int               count;
   int               window;
   int               step;
  };
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
CLayerDescription::CLayerDescription(void)   :  type(defNeuron),
                                                count(0),
                                                window(1),
                                                step(1)
  {}

CNetConvolution 畳み込みニューラルネットワーククラスの構造を考えてみましょう。クラスに含まれています。

layers - レイヤーの配列．
recentAverageError — カレントネットワークエラー;
recentAverageSmoothingFactor — エラー平均化係数;
CNetConvolution — クラスコンストラクタ;
~CNetConvolution — クラスデストラクタ;
feedForward — ダイレクトパス法;
backProp — バックワード通過法;
getResults - 最後のフォワードパスの結果を得るためのメソッド．
getRecentAverageError - 現在のネットワークエラーを取得するためのメソッド。
SaveおよびLoad - 以前に作成され、訓練されたメソッドを保存およびロードするためのメソッド。

class CNetConvolution
  {
public:
                     CNetConvolution(CArrayObj *Description);
                    ~CNetConvolution(void)                     {  delete layers; }
   bool              feedForward( CArrayDouble *inputVals);
   void              backProp( CArrayDouble *targetVals);
   void              getResults(CArrayDouble *&resultVals) ;
   double            getRecentAverageError()                   { return recentAverageError; }
   bool              Save( string file_name, double error, double undefine, double forecast, datetime time, bool common=true);
   bool              Load( string file_name, double &error, double &undefine, double &forecast, datetime &time, bool common=true);
   //---
   static double     recentAverageSmoothingFactor;
   virtual int       Type(void)   const   {  return defNetConv;   }

private:
   CArrayLayer       *layers;
   double            recentAverageError;
  };

メソッド名や構築アルゴリズムは、最初の記事で説明した完全に接続されたパーセプトロンのものと似ています。ここではクラスの主なメソッドだけを取り上げてみましょう。

3.4.1. 畳み込みニューラルネットワーククラスのコンストラクタ。

クラスのコンストラクタを考えてみましょう。コンストラクタは、ネットワークを構築するためのレイヤー記述の配列へのポインタをパラメータとして受け取ります。そこで、受信したポインタの有効性を確認し、レイヤの数を決定し、レイヤ配列の新しいインスタンスを作成する必要があります。

CNetConvolution::CNetConvolution(CArrayObj *Description)
  {
   if(CheckPointer(Description)==POINTER_INVALID)
      return;
//---
   int total=Description.Total();
   if(total<=0)
      return;
//---
   layers=new CArrayLayer();
   if(CheckPointer(layers)==POINTER_INVALID)
      return;

次に、内部変数を宣言します。

   CLayer *temp;
   CLayerDescription *desc=NULL, *next=NULL, *prev=NULL;
   CNeuronBase *neuron=NULL;
   CNeuronProof *neuron_p=NULL;
   int output_count=0;
   int temp_count=0;

これで準備作業は終了です。直接、ニューラルネットワーク層の周期的な生成に進んでみましょう。サイクルの最初に、現在の層と次の層の情報を読みます。

   for(int i=0;i<total;i++)
     {
      prev=desc;
      desc=Description.At(i);
      if((i+1)<total)
        {
         next=Description.At(i+1);
         if(CheckPointer(next)==POINTER_INVALID)
            return;
        }
      else
         next=NULL;

レイヤーの出力接続数を数え、ニューラルレイヤークラスの新しいインスタンスを作成します。レイヤー出力での接続数は、完全に接続されたレイヤーの前にのみ示すべきであり、そうでない場合はゼロを指定することに注意してください。これは、畳み込みニューロンが入力重み自体を保存するのに対し、サブサンプル層は入力重みを全く使用しないからです。

      int outputs=(next==NULL || next.type!=defNeuron ? 0 : next.count);
      temp=new CLayer(outputs);

そして、層内のニューロンの種類に応じてアルゴリズムを分割したニューロンを生成します。完全に接続された層では、新しいニューロン・インスタンスが作成され、初期化されます。完全に接続されたレイヤーでは、説明に記載されている数に加えて、さらに1つのニューロンが作成されることに注意してください。このニューロンをベイジアンバイアスとして使用します。

      for(int n=0;n<(desc.count+(i>0 && desc.type==defNeuron ? 1 : 0));n++)
        {
         switch(desc.type)
           {
            case defNeuron:
              neuron=new CNeuron();
              if(CheckPointer(neuron)==POINTER_INVALID)
                {
                 delete temp;
                 delete layers;
                 return;
                }
              neuron.Init(outputs,n);
              break;

畳み込み層用の新しいニューロン・インスタンスを作成します。前の層の情報に基づいて出力要素の数をカウントし、新たに作成したニューロンを初期化します。

            case defNeuronConv:
              neuron_p=new CNeuronConv();
              if(CheckPointer(neuron_p)==POINTER_INVALID)
                {
                 delete temp;
                 delete layers;
                 return;
                }
              if(CheckPointer(prev)!=POINTER_INVALID)
                {
                 if(prev.type==defNeuron)
                   {
                    temp_count=(int)((prev.count-desc.window)%desc.step);
                    output_count=(int)((prev.count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2));
                   }
                 else
                    if(n==0)
                      {
                       temp_count=(int)((output_count-desc.window)%desc.step);
                       output_count=(int)((output_count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2));
                      }
                }
              if(neuron_p.Init(outputs,n,desc.window,desc.step,output_count))
                 neuron=neuron_p;
              break;

同様のアルゴリズムがサブサンプル層のニューロンに適用されます。

            case defNeuronProof:
              neuron_p=new CNeuronProof();
              if(CheckPointer(neuron_p)==POINTER_INVALID)
                {
                 delete temp;
                 delete layers;
                 return;
                }
              if(CheckPointer(prev)!=POINTER_INVALID)
                {
                 if(prev.type==defNeuron)
                   {
                    temp_count=(int)((prev.count-desc.window)%desc.step);
                    output_count=(int)((prev.count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2));
                   }
                 else
                    if(n==0)
                      {
                       temp_count=(int)((output_count-desc.window)%desc.step);
                       output_count=(int)((output_count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2));
                      }
                }
              if(neuron_p.Init(outputs,n,desc.window,desc.step,output_count))
                 neuron=neuron_p;
              break;
           }

ニューロンを宣言して初期化したら、ニューラル層に追加します。

         if(!temp.Add(neuron))
           {
            delete temp;
            delete layers;
            return;
           }
         neuron=NULL;
        }

次のレイヤーのニューロンを生成するサイクルが完了したら、そのレイヤーをストレージに追加します。すべてのレイヤーを生成した後、メソッドを終了します。

      if(!layers.Add(temp))
        {
         delete temp;
         delete layers;
         return;
        }
     }
//---
   return;
  }

3.4.2. 畳み込みニューラルネットワークのフォワード伝播法。

ニューラルネットワークの全体の動作は、feedForwardフォワードパスメソッドで構成されています。このメソッドは、分析のためのオリジナルのデータ（私たちの場合、このデータは価格チャートと指標からの情報です）をパラメータとして受け取ります。まず、受信したデータ配列への参照の妥当性とニューラルネットワークの初期化状態を確認します。

bool CNetConvolution::feedForward(CArrayDouble *inputVals)
  {
   if(CheckPointer(layers)==POINTER_INVALID || CheckPointer(inputVals)==POINTER_INVALID || layers.Total()<=1)
      return false;

次に、補助変数を宣言し、受信した外部データをニューラルネットワーク入力層に転送します。

   CLayer *previous=NULL;
   CLayer *current=layers.At(0);
   int total=MathMin(current.Total(),inputVals.Total());
   CNeuronBase *neuron=NULL;
   for(int i=0;i<total;i++)
     {
      neuron=current.At(i);
      if(CheckPointer(neuron)==POINTER_INVALID)
         return false;
      neuron.setOutputVal(inputVals.At(i));
     }

ニューラルネットワークにソースデータをロードした後、ニューラルネットワークの入力からその出力まで、すべてのニューラル層を介してループを実行します。

   CObject *temp=NULL;
   for(int l=1;l<layers.Total();l++)
     {
      previous=current;
      current=layers.At(l);
      if(CheckPointer(current)==POINTER_INVALID)
         return false;

起動したループの中で、各レイヤーに対して入れ子になったループを実行して、レイヤー内のすべてのニューロンを反復処理し、その値を再計算します。完全に接続されたニューラル層では、最後のニューロンの値は再計算されないことに注意してください。前述したように、このニューロンはベイズバイアスとして使用されるため、その重みだけが使用されることになります。

      total=current.Total();
      if(current.At(0).Type()==defNeuron)
         total--;
//---
      for(int n=0;n<total;n++)
        {
         neuron=current.At(n);
         if(CheckPointer(neuron)==POINTER_INVALID)
            return false;

さらに、方法の選択は、前の層のニューロンの種類に依存します。完全に接続されたレイヤーの場合は、パラメータに前のレイヤーへの参照を指定して、フォワード伝播メソッドを呼び出します。

         if(previous.At(0).Type()==defNeuron)
           {
            temp=previous;
            if(!neuron.feedForward(temp))
               return false;
            continue;
           }

以前に畳み込み層またはサブサンプル層があった場合は、再計算されたニューロン・タイプを確認してください。完全に接続された層のニューロンについては、前の層のすべてのニューロンの内層を1つの層に集め、パラメータで指定されたニューロンの全層を参照して、現在のニューロンのフォワード伝播法を呼び出します。

         if(neuron.Type()==defNeuron)
           {
            if(n==0)
              {
               CLayer *temp_l=new CLayer(total);
               if(CheckPointer(temp_l)==POINTER_INVALID)
                  return false;
               CNeuronProof *proof=NULL;
               for(int p=0;p<previous.Total();p++)
                 {
                  proof=previous.At(p);
                  if(CheckPointer(proof)==POINTER_INVALID)
                     return false;
                  temp_l.AddArray(proof.getOutputLayer());
                 }
               temp=temp_l;
              }
            if(!neuron.feedForward(temp))
               return false;
            if(n==total-1)
              {
               CLayer *temp_l=temp;
               temp_l.FreeMode(false);
               temp_l.Shutdown();
               delete temp_l;
              }
            continue;
           }

このレイヤーのすべてのニューロンを対象としたループが完了したら、レイヤー全体のオブジェクトを削除します。ここでは、同じオブジェクトが我々の畳み込み層とサブサンプル化層で使用され続けるので、この層に含まれるニューロンのオブジェクトを削除せずに、層のオブジェクトを削除する必要があります。これは、m_free_m_modeフラグをfalseの状態にしてから、オブジェクトを削除することで行うべきです。

これが畳み込みレイヤまたはサブサンプル化レイヤの要素である場合は、適切なフィルタの前の要素へのポインタをパラメータとして渡して、フォワード伝播法を行う。

         temp=previous.At(n);
         if(CheckPointer(temp)==POINTER_INVALID)
            return false;
         if(!neuron.feedForward(temp))
            return false;
        }
     }
//---
   return true;
  }

すべてのニューロンとレイヤーを反復処理した後、このメソッドを終了します。

3.4.3. 畳み込みニューラルネットワークバックワード伝播法。

ニューラルネットワークは、backPropバックワード伝播法を用いて訓練されます。ニューラルネットワークの出力層から入力へのバックエラー伝搬の方法を実装しています。そのため、メソッドは実際のデータをパラメータで受け取ります。

メソッドの開始時に、ポインタ値オブジェクトへのポインタの有効性をチェックします。

void CNetConvolution::backProp(CArrayDouble *targetVals)
  {
   if(CheckPointer(targetVals)==POINTER_INVALID)
      return;

そして、実際のデータと比較したニューラルネットワークのフォワードパスの出力におけるルート-平均二乗誤差を算出し、出力層のニューロンの誤差勾配を算出します。

   CLayer *outputLayer=layers.At(layers.Total()-1);
   if(CheckPointer(outputLayer)==POINTER_INVALID)
      return;
//---
   double error=0.0;
   int total=outputLayer.Total()-1;
   for(int n=0; n<total && !IsStopped(); n++)
     {
      CNeuron *neuron=outputLayer.At(n);
      double target=targetVals.At(n);
      double delta=(target>1 ? 1 : target<-1 ? -1 : target)-neuron.getOutputVal();
      error+=delta*delta;
      neuron.calcOutputGradients(targetVals.At(n));
     }
   error/= total;
   error = sqrt(error);

   recentAverageError+=(error-recentAverageError)/recentAverageSmoothingFactor;

次のステップは、すべてのニューラルネットワーク層を介してバックワードループを整理することです。ここでは、対応する層のすべてのニューロンを通して入れ子になったループを実行して、隠れ層のニューロンの誤差勾配を再計算します。

   CNeuronBase *neuron=NULL;
   CObject *temp=NULL;
   for(int layerNum=layers.Total()-2; layerNum>0; layerNum--)
     {
      CLayer *hiddenLayer=layers.At(layerNum);
      CLayer *nextLayer=layers.At(layerNum+1);
      total=hiddenLayer.Total();
      for(int n=0; n<total && !IsStopped(); ++n)
        {

前進伝搬法と同様に、現在のニューロンと次の層のニューロンの種類に応じて、誤差勾配を更新するために必要な方法を選択します。次に完全に接続された層のニューロンが続く場合は、分析されたニューロンのcalcHiddenGradientsメソッドを呼び出し、パラメータにニューラルネットワークの次の層のオブジェクトへのポインタを渡します。

         neuron=hiddenLayer.At(n);
         if(nextLayer.At(0).Type()==defNeuron)
           {
            temp=nextLayer;
            neuron.calcHiddenGradients(temp);
            continue;
           }

この後に畳み込み層またはサブサンプル層が続く場合は、現在のニューロンのタイプを確認します。完全に接続されたニューロンの場合は、次の層のすべてのフィルタをループしながら、指定されたニューロンの各フィルタの誤差勾配再計算を開始します。そして、得られたグラデーションを合計します。現在のレイヤーも畳み込みまたはサブサンプル化されている場合は、対応するフィルタを用いて誤差勾配を決定します。

         if(neuron.Type()==defNeuron)
           {
            double g=0;
            for(int i=0;i<nextLayer.Total();i++)
              {
               temp=nextLayer.At(i);
               neuron.calcHiddenGradients(temp);
               g+=neuron.getGradient();
              }
            neuron.setGradient(g);
            continue;
           }
         temp=nextLayer.At(n);
         neuron.calcHiddenGradients(temp);
        }
     }

すべてのグラデーションを更新した後、同じ分岐ロジックで同様のループを実行してニューロンの重みを更新します。ウェイトを更新したらメソッドを終了します。

   for(int layerNum=layers.Total()-1; layerNum>0; layerNum--)
     {
      CLayer *layer=layers.At(layerNum);
      CLayer *prevLayer=layers.At(layerNum-1);
      total=layer.Total()-(layer.At(0).Type()==defNeuron ? 1 : 0);
      int n_conv=0;
      for(int n=0; n<total && !IsStopped(); n++)
        {
         neuron=layer.At(n);
         if(CheckPointer(neuron)==POINTER_INVALID)
            return;
         if(neuron.Type()==defNeuronProof)
            continue;
         switch(prevLayer.At(0).Type())
           {
            case defNeuron:
              temp=prevLayer;
              neuron.updateInputWeights(temp);
              break;
            case defNeuronConv:
            case defNeuronProof:
              if(neuron.Type()==defNeuron)
                {
                 for(n_conv=0;n_conv<prevLayer.Total();n_conv++)
                   {
                    temp=prevLayer.At(n_conv);
                    neuron.updateInputWeights(temp);
                   }
                }
              else
                {
                 temp=prevLayer.At(n);
                 neuron.updateInputWeights(temp);
                }
              break;
            default:
              temp=NULL;
              break;
           }
        }   
     }
  }

すべてのメソッドとクラスの完全なコードは、以下の添付ファイルにあります。

4. テスト

このシリーズの中の2回目の記事の分類エキスパートアドバイザーを使って、畳み込みニューラルネットワークの動作をテストしてみましょう。ニューラルネットワークの目的は、現在のローソク足のフラクタルを予測するために学習することです。この目的のために、最後のN個のローソク足の形成に関するニューラルネットワークの情報と、同じ期間の4つのオシレーターからのデータにフィードします。

ニューラルネットワークの畳み込み層では、分析されたローソク足の総ローソク足形成データとオシレーターの読み取り値のパターンを検索する4つのフィルターを作成します。フィルタウィンドウとステップは、ローソク足の記述あたりのデータ量に対応します。つまり、これは各ローソク足の情報を全て特定のパターンと比較し、収束値を返してくれます。このアプローチでは、大きなパフォーマンスの低下を招くことなく、ローソク足に関する新しい情報（分析のための指標の追加など）で初期データを補足することができます。

サブサンプリング層では特徴配列のサイズを小さくするとともに、結果を平均化して平滑化します。

EA自体は最低限の変更が必要でした。この変更はニューラルネットワーククラスに適用されます。

CNetConvolution     *Net;

その他の変更点は、OnInit関数の中でニューラルネットワークの構造を設定する部分です。試験は、1つの畳み込み層と1つのサブサンプリング層がそれぞれ4つのフィルタを有するネットワークを用いて行われました。完全に接続された層の構造は変わっていない（畳み込み層がネットワーク全体の動作に与える影響を評価するために意図的に行った）。

   Net=new CNetConvolution(NULL);
   ResetLastError();
   if(CheckPointer(Net)==POINTER_INVALID || !Net.Load(FileName+".nnw",dError,dUndefine,dForecast,dtStudied,false))
     {
      printf("%s - %d -> Error of read %s prev Net %d",__FUNCTION__,__LINE__,FileName+".nnw",GetLastError());
      CArrayObj *Topology=new CArrayObj();
      if(CheckPointer(Topology)==POINTER_INVALID)
         return INIT_FAILED;
//---
      CLayerDescription *desc=new CLayerDescription();
      if(CheckPointer(desc)==POINTER_INVALID)
         return INIT_FAILED;
      desc.count=(int)HistoryBars*12;
      desc.type=defNeuron;
      if(!Topology.Add(desc))
         return INIT_FAILED;
//---
      int filters=4;
      desc=new CLayerDescription();
      if(CheckPointer(desc)==POINTER_INVALID)
         return INIT_FAILED;
      desc.count=filters;
      desc.type=defNeuronConv;
      desc.window=12;
      desc.step=12;
      if(!Topology.Add(desc))
         return INIT_FAILED;
//---
      desc=new CLayerDescription();
      if(CheckPointer(desc)==POINTER_INVALID)
         return INIT_FAILED;
      desc.count=filters;
      desc.type=defNeuronProof;
      desc.window=3;
      desc.step=2;
      if(!Topology.Add(desc))
         return INIT_FAILED;
//---
      int n=1000;
      bool result=true;
      for(int i=0;(i<4 && result);i++)
        {
         desc=new CLayerDescription();
         if(CheckPointer(desc)==POINTER_INVALID)
            return INIT_FAILED;
         desc.count=n;
         desc.type=defNeuron;
         result=(Topology.Add(desc) && result);
         n=(int)MathMax(n*0.3,20);
        }
      if(!result)
        {
         delete Topology;
         return INIT_FAILED;
        }
//---
      desc=new CLayerDescription();
      if(CheckPointer(desc)==POINTER_INVALID)
         return INIT_FAILED;
      desc.count=3;
      desc.type=defNeuron;
      if(!Topology.Add(desc))
         return INIT_FAILED;
      delete Net;
      Net=new CNetConvolution(Topology);
      delete Topology;
      if(CheckPointer(Net)==POINTER_INVALID)
         return INIT_FAILED;
      dError=-1;
      dUndefine=0;
      dForecast=0;
      dtStudied=0;
     }

Expert Advisorの残りのコードは変更されませんでした。

テストは、H1タイムフレームのEURUSDペアを使用して行われました。畳み込み型ニューラルネットワークと完全に接続されたネットワークを用いた2つのエキスパートアドバイザーが、同じ端末で、同じシンボルの異なるチャート上に同時に立ち上がりました。畳み込みニューラルネットワークの完全に接続された層のパラメータは、第２のエキスパートアドバイザーの完全に接続されたネットワークのパラメータと一致します。つまり、以前に作成したネットワークに、単純に畳み込み層とサブサンプル化層を追加しただけです。

テストでは、畳み込みニューラルネットワークの性能がわずかに向上することが示されました。 2層を追加したにもかかわらず、畳み込みニューラルネットワークの1エポック（24エポックの結果に基づく）の平均学習時間は2時間4分、完全に接続されたネットワークの平均学習時間は2時間10分でした。

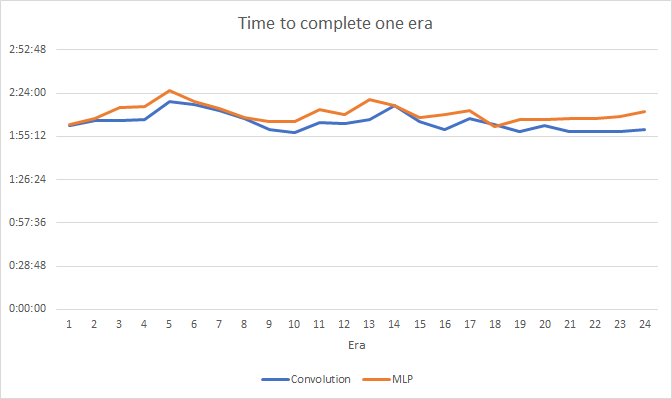
1つのEAのエポックトレーニングのタイムライン

畳み込みニューラルネットワークは、予測誤差と「的打ち」の点でやや良い結果を示しています。

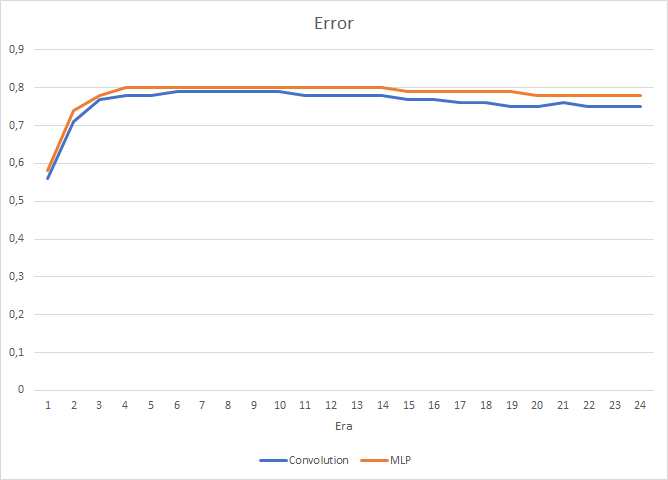
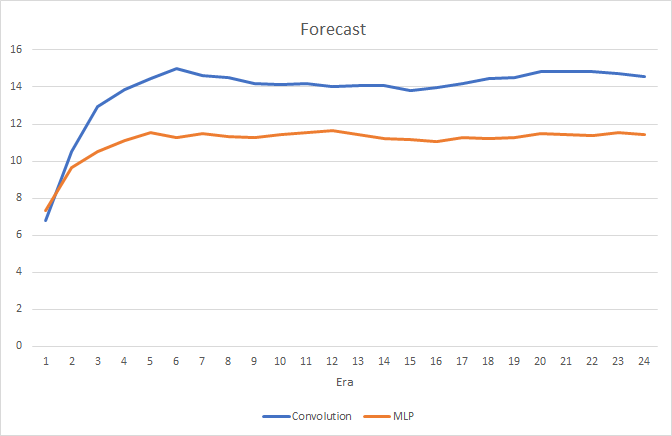
ニューラルネットワークの根平均二乗誤差正しく定義されたフラクタルの割合

視覚的には、畳み込みニューラルネットワークチャート上でのシグナルの出現頻度が低いことがわかりますが、ターゲットに近いことがわかります。

畳み込み型ニューラルネットワークのテスト。

完全に接続されたニューラルネットワークのテスト

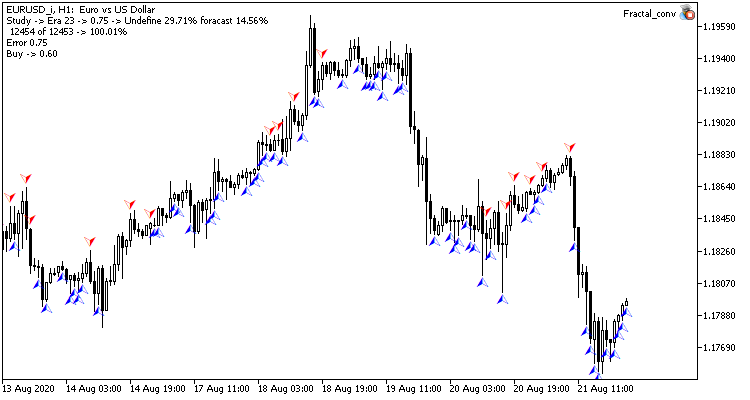
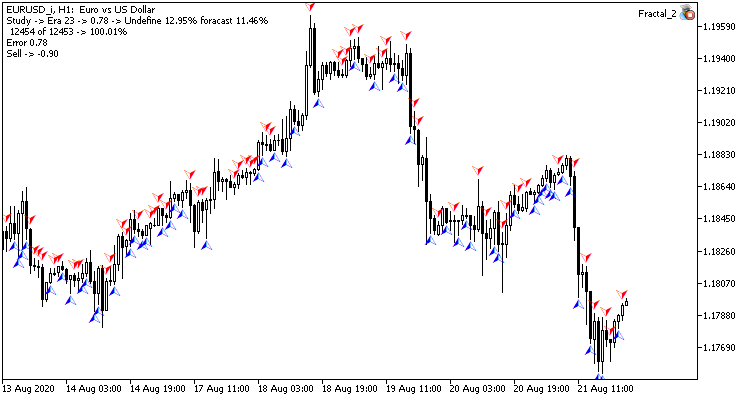
結論

今回は、金融市場における畳み込み型ニューラルネットワークの活用の可能性を検討しました。テストでは、それらを使用することで、完全に接続されたニューラルネットワークの結果を改善できることが示されています。これは、完全に接続されたパーセプトロンに供給するデータの前処理と接続することができます。元データは、畳み込み層とサブサンプリング層でフィルタリングしてノイズを除去することで、元データの品質とニューラルネットワークの品質を向上させます。さらに、次元数を減らすことで、元のデータとのパーセプトロンの接続数を減らすことができ、性能を向上させることができます．

参考文献一覧

記事内で使用しているプログラム

#	発行	タイプ	詳細
1	Fractal.mq5	エキスパートアドバイザー	回帰ニューラルネットワーク（出力層に1ニューロン）を持つエキスパートアドバイザー
2	Fractal_2.mq5	エキスパートアドバイザー	分類ニューラルネットワーク（出力層に3つのニューロン）を持つエキスパートアドバイザー
3	NeuroNet.mqh	クラスライブラリ	ニューラルネットワーク（パーセプトロン）を作成するためのクラスのライブラリ
4	Fractal_conv.mq5	エキスパートアドバイザー	畳み込みニューラルネットワーク（出力層に3つのニューロン）を用いたエキスパートアドバイザー