Ti stai perdendo delle opportunità di trading:
- App di trading gratuite
- Oltre 8.000 segnali per il copy trading
- Notizie economiche per esplorare i mercati finanziari
Registrazione
Accedi
Accetti la politica del sito e le condizioni d’uso
Se non hai un account, registrati
È tranquillo, o non ho tempo per questo :)
Ho aggiunto lì le condizioni del problema.
Risolviamo il problema da qui.
Proprio così. Il prossimo...
O il rapporto è negativo? - Aumentando i prelievi in tasca - diminuisce automaticamente la crescita del deposito.
nelle condizioni date -- esattamente positivo!
Ti stai confondendo... Purché si faccia l'analisi senza intascare - cioè cosa costituisce un tale sistema!
E per quanto riguarda la crescita esponenziale, ho dato per scontato che tu avessi posto questa condizione a priori.
Beh, non importa. Che sia negativo e severo - non è il punto.
Cosa c'è di nuovo nella sua dichiarazione? Abbiamo: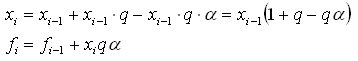
Sostituite qa con k e arriviamo alle stesse equazioni che ho io:
Con gli stessi problemi.
.
Nel nostro caso particolare G(s)=0
e le equazioni sono semplificate da
Ora, applicando la trasformata di Laplace inversa, otteniamo il risultato:
.
qui abbiamo l'esponente come risultato, non come destinazione.
.
Questo è tutto - è chiaro come si comporta il sistema.
Ora possiamo passare a considerare la seconda parte del problema: aprire la valvola e separare il flusso.
.
zy.
Ci arriverò oggi, ma un po' più tardi...
P.S. Nel caso qualcuno sia interessato, ecco i dati del censimento globale di Goskomstat per tutta la storia dell'umanità:
Anno milioni di persone.
Ho dovuto fare due logaritmi per ottenere questo grafico, ma anche così la crescita è più veloce di una linea retta. Questo significa che la relazione è ancora più veloce di exp(exp(t))
Ho dovuto fare il logaritmo due volte per ottenere questo grafico, ma anche così la crescita è più veloce che in una linea retta. Questo significa che la dipendenza è ancora più veloce di exp(exp(t))
Sì, la correlazione è interessante.
Negli anni 90 S.P. Kapitsa (colui che conduce lo show "Obvious incredible") venne da noi con un rapporto sulla popolazione della terra. È interessante che secondo il suo modello, che all'epoca si adattava bene ai dati storici, dN/dt=N^2 e prevedeva una crescita esplosiva della popolazione nel 2025 (la cosiddetta catastrofe malthusiana se non mi sbaglio). In generale, per adempiere alla condizione della difesa di cui sopra, è necessario che ogni donna in età riproduttiva dia alla luce un figlio da ogni uomo :-) È in queste condizioni che l'uguaglianza del tasso di crescita al quadrato della popolazione totale sarebbe soddisfatta. Il che sembra assurdo. Poi ho capito che era una conseguenza dell'adattamento del modello ai dati disponibili. E se non si prendono i dati prima del 1945. E se non si prendono i dati prima del 1945 (dove si vede un picco di natalità), ma si lavora su un periodo più o meno calmo dal 1945 a oggi, allora non c'è nessuna catastrofe:
Inoltre, si può vedere che la popolazione globale tende asintoticamente verso un livello di equilibrio di 11 miliardi e raggiungerà tale livello in circa 100 anni.
Deve essere equiparato a zero e risolto rispetto a k.