[Archives] Mathématiques pures, physique, chimie, etc. : problèmes d'entraînement cérébral sans rapport avec le commerce. - page 304
Vous manquez des opportunités de trading :
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Inscription
Se connecter
Vous acceptez la politique du site Web et les conditions d'utilisation
Si vous n'avez pas de compte, veuillez vous inscrire
F(1/y, 1/x) = min( 1/y, 1/x + y, x ) = F(x,y).
Par conséquent, si vous remplacez y par 1/x et x par 1/y, le minimum ne changera pas. Y = 1/x.
Donc F(x,1/x) = min( x, 2/x, x ) = min( x, 2/x ). Il est égal à x si x < sqrt(2), et 2/x sinon.
Tracez les deux courbes y=x et y=2/x. Évidemment, le maximum se trouve exactement au point de leur intersection et est égal à sqrt(2).
La solution dans le livre de problèmes est plutôt vague, je n'aime pas ça :
Suivant (8ème) :
Cette partie est construite de manière triviale. Laissons l'intrigue de côté.
La deuxième partie du problème (également 8ème) :
Simplification de la figure :
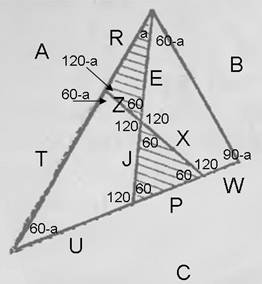
Richie, comment se fait-il qu'il y ait des angles égaux dans un triangle ombragé ?
D'ailleurs, l'énoncé du problème ne dit rien sur le fait que le triangle original soit équilatéral. Bien qu'il soit dessiné comme un équilatéral.
Allez. Prouvez-le.
-
Bref, l'idée était la suivante :
L'aire d'un triangle 4x est égale au tiers de la différence entre l'aire du grand triangle et celle des 4 petits triangles, soit 4 cm².
Pour trouver l'aire du grand triangle, vous devez trouver son côté (dans la figure - A).
Trouver le côté du triangle central par aire, savoir qu'il est équilatéral n'est pas un problème, il est égal à sqr(4*S/sqr(3)).
В центральном? Это очевидно.
Seulement si les trois triangles (à part celui du centre) sont identiques.Mais ce n'est pas un fait selon les conditions
Il doit y avoir quelque chose à quoi s'accrocher. Il y a une piste, mais je ne sais pas encore quoi en faire.
Seulement si les trois triangles (sauf celui du centre) sont identiques.
Mais ce n'est pas un fait.
Eh bien, tu m'as complètement embrouillé.
Je croyais que le grand triangle était équilatéral. Les 3 petits triangles sont équilatéraux, donc par conséquent ils sont similaires.