Vous manquez des opportunités de trading :
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Inscription
Se connecter
Vous acceptez la politique du site Web et les conditions d'utilisation
Si vous n'avez pas de compte, veuillez vous inscrire
OK. Voici les données.Il semble que nous nous soyons mal compris. Mes sentiments sur l'anormalité ne s'appliquent pas au générateur, mais au marché. Construisez une distribution des premiers incréments et voyez par vous-même.
Eh bien, pour le cheval sphérique dans le vide, c'est-à-dire pour une distribution normale garantie, oui, c'est peu probable. Eh bien, les vrais ne sont pas des chevaux dans un vide. Il y a 5 ou 6 s.c.e. et même 10.
Mon oncle, s'il vous plaît, voici une autre photo de la livre de 1971, les journaux intimes. Il peut y avoir une seule fente (et il n'y en a pas une seule d'ailleurs :), le plus important est que cela ne devienne pas un schéma. N'est-ce pas ?
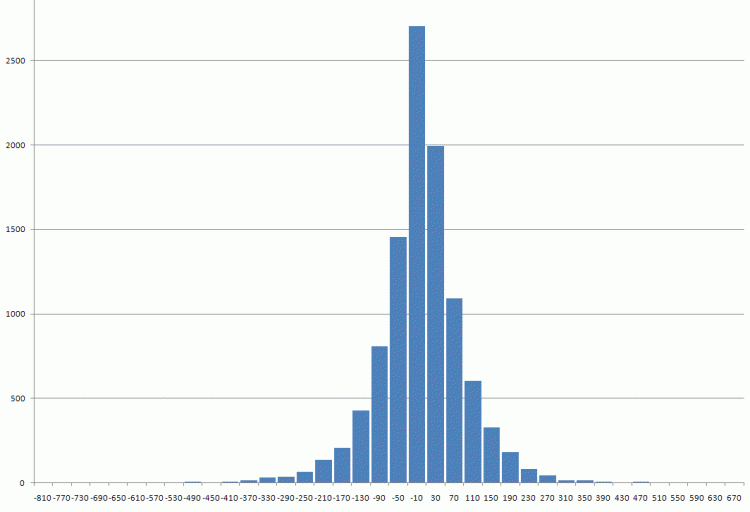
Les données à vérifier sont jointes.Premières différences de livres depuis 1971.
>>S. Il faudrait peut-être vérifier la stationnarité :)
Mon oncle, s'il vous plaît, voici une autre photo de la livre de 1971, les journaux intimes. Il peut y avoir une seule fente (et il n'y en a pas une seule d'ailleurs :), le plus important est que cela ne devienne pas un schéma. N'est-ce pas ?
Les données du contrôle sont jointes.Les premiers écarts de la livre depuis 1971
À vue de nez, je dirais que c'est une distribution de Laplace.
Je l'appellerais la distribution de Laplace à l'œil.
La clé est qu'il n'y a pas de sigmas 5-6-10. Sinon, oui, mais vous devez le tester. Et pourtant, ça pourrait être bien.Ilya, voici une suggestion : approximer cette distribution par une distribution normale. Et voyez ensuite à quel point l'histogramme réel et l'approximation de la courbe gaussienne sont différents l'un de l'autre. Ne vous limitez pas à trois sigmas, cherchez-en au moins dix.
Autre vérification triviale : calculer les premiers moments de cette distribution et les comparer avec les moments de la distribution normale.
Le phénomène des queues de poisson dans les séries financières est connu depuis longtemps. Que veux-tu me prouver ?
Ilya, voici une suggestion : approximer cette distribution par une distribution normale. Et voyez ensuite à quel point l'histogramme réel et l'approximation de la courbe gaussienne sont différents l'un de l'autre. Ne vous limitez pas à trois sigmas, cherchez-en au moins dix.
Autre vérification triviale : calculer les premiers moments de cette distribution et les comparer avec les moments de la distribution normale.
Le phénomène des queues de poisson dans les séries financières est connu depuis longtemps. Que veux-tu me prouver ?
La discussion a porté sur 5-6-10 RMS. Je ne vois pas de modèle dans leur apparence.
La clé est qu'il n'y a pas de sigmas 5-6-10. Tel qu'il est, oui, mais il doit être testé. Et pourtant, cela pourrait être normal.est hautement improbable. Les distributions normales se retrouvent généralement dans la nature, où une "grande" variable aléatoire est la somme d'un grand nombre de "petites" variables aléatoires distribuées d'une certaine manière (mais de manière égale). Un excellent exemple est le mouvement brownien, auquel de nombreuses pages ont déjà été consacrées dans le fil suivant. Dans le cas du marché, on est loin de la loi de formation des prix, car pour obtenir une loi normale, il faut un très grand nombre de "perturbations" extérieures - qui doivent être le principal facteur de formation de la distribution. Mais nous ne pensons pas que la fixation des prix sur le marché soit du bruit, n'est-ce pas ?
Sur un graphique, purement visuel, et vous ne verrez pas ce 5-6-10.
Quelque part, j'avais même un tableau montrant les différences. Si vous prenez les deux premiers moments de la distribution et que vous les considérez comme des moments d'approximation de la normale, la différence de fréquences de 3, 4, 5, etc. sigmas est facile à calculer.
Je ne me souviens pas des chiffres exacts, mais la fréquence réelle de l'écart à 3 sigmas est 3 à 4 fois plus élevée que la fréquence gaussienne (gaussienne 0,3 %, réelle plus de 1 %). Dans la réalité, l'écart à 4 sigma est environ 15 fois plus fréquent que l'écart gaussien. Pour 5 sigma, la différence est de plusieurs dizaines de fois, voire de centaines. Et ainsi de suite.
Tant que vous n'évaluez pas les risques, vous vous moquez de savoir si c'est gaussien ou non.
P.S. Au fait, il semble que, selon Taleb, LTCM se soit effondré précisément à cause de la sous-estimation des risques. Une déviation de 10 sigmas était considérée comme un événement rare négligeable. Et c'est exactement ce qui s'est passé.
Je ne me souviens pas des chiffres exacts, mais la fréquence réelle de l'écart à 3 sigmas est 3-4 fois supérieure à la fréquence gaussienne (gaussienne 0,3%, réelle plus de 1%). Dans la réalité, l'écart à 4 sigmas est environ 15 fois plus fréquent que l'écart gaussien. Pour les écarts à 5 sigmas, la différence est de plusieurs dizaines de fois. Et ainsi de suite.
...ce qui est encore une fois une preuve en faveur de Laplace.
Tant que vous n'évaluez pas les risques, vous ne vous souciez pas de savoir si c'est gaussien ou non.
Pouvez-vous me dire comment aborder l'évaluation des risques ?