
OpenCL : De la programmation naïve à une programmation plus perspicace
Introduction
Le premier article"OpenCL: Le Pont vers les Mondes Parallèles" était une introduction au sujet d’OpenCL. Il abordait les problèmes fondamentaux d'interaction entre le programme dans OpenCL (également appelé noyau bien que ce ne soit pas tout à fait correct) et le programme externe (hôte) dans MQL5. Certaines capacités de performance du langage (par exemple, l'utilisation de types de données vectorielles) ont été illustrées par le calcul de pi = 3,14159265...
L'optimisation des performances du programme a été dans certains cas considérable. Cependant, toutes ces optimisations étaient naïves car elles ne prenaient pas en compte les spécifications matérielles utilisées pour effectuer tous nos calculs. La connaissance de ces spécifications peut, dans la plupart des cas, nous permettre d'atteindre en connaissance de cause des accélérations qui dépassent largement les capacités du CPU.
Pour démontrer ces optimisations, l'auteur a dû recourir à un exemple qui n'est plus original et qui est probablement l'un des plus étudiés dans la littérature sur OpenCL. C'est la multiplication de deux grandes matrices.
Commençons par l'essentiel - le modèle de mémoire OpenCL avec les particularités de son implémentation sur l'architecture matérielle réelle.
1. Hiérarchie de la Mémoire dans les Appareils de Calcul Modernes
1.1. Le Modèle de Mémoire OpenCL
D'une manière générale, les systèmes de mémoire diffèrent largement les uns des autres selon les plates-formes informatiques. Par exemple, tous les CPU modernes prennent en charge la mise en cache automatique des données, contrairement aux GPU où ce n'est pas toujours le cas.
Pour assurer la portabilité du code, un modèle de mémoire abstrait est adopté dans OpenCL que les programmeurs ainsi que les fournisseurs qui doivent implémenter ce modèle sur du matériel réel peuvent utiliser. La mémoire telle que définie dans OpenCL peut être illustrée de manière théorique dans la figure ci-dessous :
Fig. 1. Le modèle de Mémoire OpenCL
Une fois les données transférées de l'hôte vers l'appareil, elles sont stockées dans la mémoire globale de l'appareil. Toutes les données transférées dans le sens opposé sont également stockées dans la mémoire globale (mais cette fois, dans la mémoire hôte globale). Le mot-clé __global (deux tirets-bas !) est un modificateur indiquant que les données associées à un certain pointeur sont stockées dans la mémoire globale :
__kernel void foo( __global float *A ) { /// kernel code }
Mémoire globaleest accessible à toutes les unités de informatiques au sein de l’appareil tel que RAM dans le système hôte.
La mémoire constante, contrairement à son nom, ne stocke pas nécessairement des données en lecture seule. Ce type de mémoire est conçu pour les données où chaque élément peut être simultanément accessible par toutes les unités de travail Les variables avec des valeurs constantes entrent bien sûr également dans cette catégorie. La mémoire constante dans le modèle OpenCL fait partie de la mémoire globale et les objets mémoire transférés vers la mémoire globale peuvent donc être indiqués comme __constant.
La mémoire locale est une mémoire de bloc-notes où l'espace d'adressage est unique à chaque appareil. Dans le matériel, il se présente souvent sous la forme de mémoire sur puce, mais il n'y a pas d'exigence particulière pour qu'elle soit exactement la même pour OpenCL.
L'accès à ce type de mémoire entraîne une latence beaucoup plus faible et la bande passante mémoire est donc bien supérieure à celle de la mémoire globale. Nous essaierons de profiter de sa latence plus faible pour l'optimisation des performances du noyau.
La spécification OpenCL dit qu'une variable en mémoire locale peut être déclarée à la fois dans l'en-tête du noyau :
__kernel void foo( __local float *sharedData ) { }et dans son corps :
__kernel void foo( __global float *A ) { __local float sharedData[ 64 ]; }Notez qu'un tableau dynamique ne peut pas être déclaré dans le corps du noyau ; vous devez toujours indiquer sa taille.
Ci-dessous, dans l'optimisation du noyau pour la multiplication de deux grandes matrices, vous verrez comment gérer les données locales et quelles spécificités d'implémentation cela implique dans MetaTrader 5 telles que vécues par l'auteur.
Les variables locales et les arguments du noyau qui ne comportent pas de pointeurs sont privés par défaut (si spécifiés sans le modificateur __local). En pratique, ces variables sont généralement localisées dans des registres. Et vice versa,les tableaux privés et tout registre renversé se trouve habituellement en dehors de la mémoire de puce c’est-à-dire une mémoire à latence plus élevée Permettez-moi de citer les informations pertinentes de Wikipédia :
Dans de nombreux langages de programmation, le programmeur a l'illusion d'allouer arbitrairement de nombreuses variables. Cependant, lors de la compilation, le compilateur doit décider comment allouer ces variables à un petit ensemble fini de registres. Toutes les variables ne sont pas utilisées (ou « actives ») en même temps, de sorte que certains registres puissent être affectés à plus d'une variable. Cependant, deux variables utilisées en même temps ne peuvent pas être affectées au même registre sans en altérer la valeur.
Les variables qui ne peuvent pas être affectées à un registre doivent être conservées dans la RAM et chargées en entrée/sortie pour chaque lecture/écriture, un processus appelé déversement. L'accès à la RAM est nettement plus lent que l'accès aux registres et ralentit la vitesse d'exécution du programme compilé, donc un compilateur d'optimisation vise à assigner autant de variables que possible aux registres. La pression du registre est le terme utilisé lorsqu'il y a moins de registres matériels disponibles que ce qui aurait été optimal ; une pression plus élevée indique généralement que plus de déversements et de recharges sont nécessaires.
Le modèle de mémoire OpenCL tel que décrit est très similaire à la structure de mémoire des GPU modernes. La figure ci-dessous indique une corrélation entre le modèle de mémoire OpenCL et le modèle de mémoire GPU AMD Radeon HD 6970.
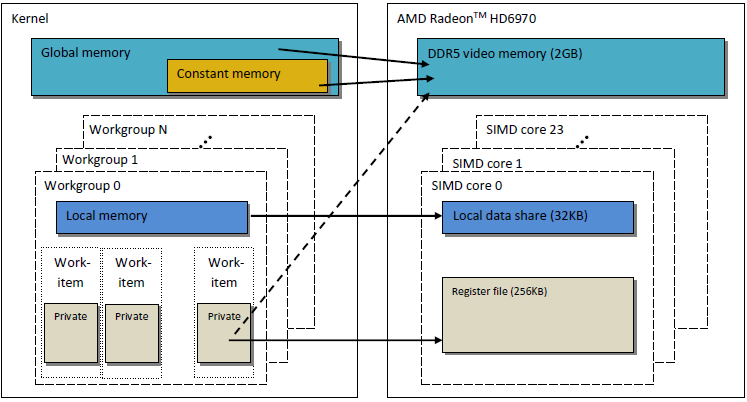
Fig. 2. La corrélation entre la structure de mémoire Radeon HD 6970 et le modèle abstrait de mémoire OpenCL
Passons à un examen plus détaillé des problèmes liés à une implémentation spécifique de la mémoire GPU.
1.2. Mémoire dans les GPU discrets modernes
1.2.1. Requêtes de Mémoire de Fusion
Ces informations sont également importantes pour l'optimisation des performances du noyau, car l'objectif principal est d'obtenir une bande passante mémoire élevée.
Jetez un œil à la figure ci-dessous pour mieux comprendre le processus d'adressage de la mémoire :
Fig. 3. Schéma d'adressage des données dans la mémoire globale de l'appareil
Admettons que le pointeur vers un tableau de variables entières int est l'adresse de Х = 0x00001232. Chaque entier prend 4 octets de mémoire. Admettons qu’un thread (qui est un logiciel analogue d’unité de travail qui exécute le code noyau) adresse les données à Х[ 0 ]:
int tmp = X[ 0 ];
Nous admettons que la largeur du bus mémoire est de 32 octets (256 bits). Cette largeur de bus est typique des GPU puissants, tels que Radeon HD 5870. Dans certains autres GPU, la largeur du bus de données peut être différente, par exemple 384 bits ou même 512 dans certains modèles NVidia.
L'adressage du bus mémoire doit correspondre à sa structure, c'est-à-dire avant tout sa largeur. En d'autres termes, les données en mémoire sont stockées par blocs de 32 octets (256 bits) chacun. Indépendamment de ce que nous adressons dans la plage de 0x00001220 à 0x0000123F (il y a exactement 32 octets dans cette plage, vous pouvez le constater par vous-même), nous obtiendrons toujours l'adresse 0x00001220 comme adresse de départ pour la lecture.
L'accès à l'adresse 0x00001232 renverra toutes les données aux adresses comprises entre 0x00001220 et 0x0000123F, c'est-à-dire 8 nombres entiers. Par conséquent, il n'y aura que 4 octets (un nombre int) de données utiles tandis que les 28 octets restants (7 nombres int) seront inutiles :
Fig. 4. Schéma d'obtention des données requises de la mémoire
Le numéro dont nous avons besoin situé à l'adresse spécifiée précédemment - 0x00001232 - est encerclé dans le schéma.
Pour maximiser l'utilisation du bus, le GPU essaie de fusionner les accès mémoire de différents threads en une seule requête mémoire ; moins il y a d'accès mémoire, mieux c'est. La raison en est que l'accès à la mémoire globale de l'appareil nous coûte du temps et nuit donc grandement à la vitesse d'exécution du programme. Considérez la ligne suivante du code du noyau :
int tmp = X[ get_global_id( 0 ) ];
Admettons que notre tableau Х soit le tableau de l'exemple précédent donné ci-dessus. Ensuite, les 16 premiers threads (noyaux) accéderont aux adresses de 0x00001232 à 0x00001272 (il y a 16 nombres entiers dans cette plage, soit 64 octets). Si chaque requête était envoyée par les noyaux indépendamment, sans avoir été préalablement fusionnée en une seule, chacune des 16 requêtes contiendrait 4 octets de données utiles et 28 octets de données inutiles, soit un total de 64 octets utilisés et 448 octets inutilisés.
Ce calcul est basé sur le fait que chaque accès à une adresse située dans un même bloc mémoire de 32 octets retournera des données absolument identiques. C'est le point clé. Il serait plus correct de fusionner plusieurs requêtes en une seule et cohérente pour économiser sur les requêtes inutiles. Cette opération sera ci-après dénommée coalescente et les requêtes coalisées en tant que telles seront qualifiées de cohérentes.
Fig. 5. Seules trois demandes de mémoire sont nécessaires pour obtenir les données requises
Chaque cellule de la figure ci-dessus est de 4 octets. Dans notre exemple, 3 requêtes suffiraient. Si le début du tableau était aligné sur l'adresse du début de chaque bloc de mémoire de 32 octets, même 2 requêtes suffiraient.
En AMD GPU 64, threads font partie d’unfront d’onde et doit par conséquent, exécuter la même instruction comme dans l’exécution SIMD. 16 threads arrangés par get_global_id( 0 ), représentant exactement un quart du front d'onde, sont fusionnés en une requête cohérente pour une utilisation efficace du bus.
Ci-dessous, une illustration de la bande passante mémoire requise pour les requêtes cohérentes par rapport aux requêtes incohérentes, c'est-à-dire "spontanées". Il s'agit de Radeon HD 5870. Un résultat similaire peut être constaté pour les cartes NVidia.
Fig. 6. Analyse comparative de la bande passante mémoire requise pour les requêtes cohérentes et incohérentes
Nous voyons clairement qu'une requête mémoire cohérente permet d'augmenter la bande passante mémoire d'environ un ordre de magnitude.
1.2.2. Banques de Mémoire
La mémoire consiste enbanques où les données sont réellement stockées. Dans les GPU modernes, il s'agit généralement de mots de 32 bits (4 octets). Les données sérielles sont stockées dans des banques de mémoire adjacentes. Un groupe de threads accédant à des éléments sériels ne produira aucun conflit bancaire.
L'effet négatif maximal des conflits bancaires est généralement observé dans la mémoire GPU locale. Il est donc conseillé que les accès locaux aux données depuis les threads voisins ciblent des banques mémoire différentes.
Sur le matériel AMD, le front d'onde qui génère des conflits de banques se bloque jusqu'à ce que toutes les opérations de mémoire locale soient terminées. .Cela mène à la sérialisation dans laquelle les blocs de code qui doivent être exécutés en parallèle sont séquentiellement exécutés. Cela a un effet extrêmement négatif sur les performances du noyau.
Fig. 7. Schémas d'accès mémoire sans conflits bancaires
La figure ci-dessus montre l'accès à la mémoire sans conflits de banque car tous les threads accèdent à des données différentes.
Illustrons l'accès mémoire avec des conflits de banque :
Fig. 8. Accès mémoire avec conflits bancaires
Cependant,cette situation présente une exception: si tous les accès sont d’adresse identique, la banque peut effectuer une diffusionpour éviter un retard:
Fig. 9. Tous les threads accèdent à la même adresse
Des événements similaires se produisent également lors de l'accès à la mémoire globale, mais l'impact de tels conflits est considérablement plus faible.
- La mémoire GPU est différente de la mémoire CPU. L'objectif principal de l'optimisation des performances du programme à l'aide d'OpenCL est d'assurer la bande passante maximale au lieu de réduire la latence, comme ce serait le cas sur le processeur.
- La nature de l'accès à la mémoire a un grand impact sur l'efficacité de l'utilisation du bus. Une faible efficacité d'utilisation du bus indique une faible vitesse de fonctionnement.
- Pour améliorer les performances du code, il est souhaitable que l'accès mémoire soit cohérent. De plus, il est fortement préférable d'éviter les conflits bancaires.
- Les spécifications matérielles (largeur du bus, nombre de banques de mémoire, ainsi que le nombre de threads pouvant être fusionnés pour un seul accès cohérent) peuvent être trouvées dans la documentation fournie par le fournisseur.
Les spécifications de certaines cartes vidéo de la série Radeon 5xxx sont présentées ci-dessous à titre d'exemple :
Fig. 10. Spécifications techniques des cartes vidéo Radeon HD 58xx moyen et haut de gamme
Passons maintenant à la programmation.
2. Multiplication de Grandes Matrices Carrées : Du code CPU série au code GPU parallèle
2.1. MQL5 Code
La tâche à accomplir, contrairement à l'articleprécédent "OpenCL : The Bridge to Parallel Worlds", est standard, c'est-à-dire multiplier deux matrices. Il est choisi principalement en raison du fait que de nombreuses informations sur le sujet peuvent être trouvées dans différentes sources. La plupart d'entre eux, d'une manière ou d'une autre, proposent des solutions plus ou moins coordonnées. C'est la voie que nous allons emprunter, en clarifiant pas à pas le sens des structures de modèles tout en gardant à l'esprit que nous travaillons sur du vrai matériel.
Vous trouverez ci-dessous une formule de multiplication matricielle bien connue en algèbre linéaire, modifiée pour les calculs informatiques. Le premier index est le numéro de ligne de la matrice, le second index est le numéro de colonne. Chaque élément de matrice de sortie est calculé en ajoutant séquentiellement chaque produit successif d'éléments dans les première et seconde matrices à la somme accumulée. Finalement, cette somme accumulée est l'élément calculé de matrice de sortie :
Fig. 11. Formule de multiplication matricielle
Elle peut être schématiquement représentée comme suit :
Fig. 12. Algorithme de multiplication matricielle (exemplifié par le calcul d'un élément de matrice de sortie) représenté schématiquement
Nous pouvons facilement constater que lorsque les deux matrices ont les mêmes dimensions égales à N, le nombre d'additions et de multiplications peut être estimé par la fonction O(N^3) : pour calculer chaque élément de matrice de sortie, vous devez obtenir le produit scalaire d'une ligne dans la première matrice et d'une colonne dans la seconde matrice. Il nécessite environ 2*N additions et multiplications. Une estimation nécessaire est obtenue en multipliant par le nombre d'éléments de matrice N^2. Ainsi, le temps d'exécution approximatif du code dépend assez largement de N au cube.
Le nombre de lignes et de colonnes pour les matrices est fixé ci-après à 2000 pour des raisons de commodité uniquement ; ils peuvent être arbitraires mais pas trop importants.
Le code en MQL5 n'est pas très compliqué :
//+------------------------------------------------------------------+ //| matr_mul_2dim.mq5 | //+------------------------------------------------------------------+ #define ROWS1 1000 // rows in the first matrix #define COLSROWS 1000 // columns in the first matrix = rows in the second matrix #define COLS2 1000 // columns in the second matrix float first[ ROWS1 ][ COLSROWS ]; // first matrix float second[ COLSROWS ][ COLS2 ]; // second matrix float third[ ROWS1 ][ COLS2 ]; // product //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { MathSrand(GetTickCount()); Print("======================================="); Print("ROWS1 = "+i2s(ROWS1)+"; COLSROWS = "+i2s(COLSROWS)+"; COLS2 = "+i2s(COLS2)); genMatrices(); ArrayInitialize(third,0.0f); //--- execution on the CPU uint st1=GetTickCount(); mul(); double time1=(double)(GetTickCount()-st1)/1000.; Print("CPU: time = "+DoubleToString(time1,3)+" s."); return; } //+------------------------------------------------------------------+ //| i2s | //+------------------------------------------------------------------+ string i2s(int arg) { return IntegerToString(arg); } //+------------------------------------------------------------------+ //| genMatrices | //| generate initial matrices; this generation is not reflected | //| in the final runtime calculation | //+------------------------------------------------------------------+ void genMatrices() { for(int r=0; r<ROWS1; r++) for(int c=0; c<COLSROWS; c++) first[r][c]=genVal(); for(int r=0; r<COLSROWS; r++) for(int c=0; c<COLS2; c++) second[r][c]=genVal(); return; } //+------------------------------------------------------------------+ //| genVal | //| generate one value of the matrix element: | //| uniformly distributed value lying in the range [-0.5; 0.5] | //+------------------------------------------------------------------+ float genVal() { return(float)(( MathRand()-16383.5)/32767.); } //+------------------------------------------------------------------+ //| mul | //| Main matrix multiplication function | //+------------------------------------------------------------------+ void mul() { // r-cr-c: 10.530 s for(int r=0; r<ROWS1; r++) for(int cr=0; cr<COLSROWS; cr++) for(int c=0; c<COLS2; c++) third[r][c]+=first[r][cr]*second[cr][c]; return; }
Liste 1. Programme séquentiel initial sur l'hôte
Résultats de performance utilisant différents paramètres :
2012.05.19 09:39:11 matr_mul_2dim (EURUSD,H1) CPU: time = 10.530 s. 2012.05.19 09:39:00 matr_mul_2dim (EURUSD,H1) ROWS1 = 1000; COLSROWS = 1000; COLS2 = 1000 2012.05.19 09:39:00 matr_mul_2dim (EURUSD,H1) ======================================= 2012.05.19 09:41:04 matr_mul_2dim (EURUSD,H1) CPU: time = 83.663 s. 2012.05.19 09:39:40 matr_mul_2dim (EURUSD,H1) ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.19 09:39:40 matr_mul_2dim (EURUSD,H1) =======================================
Comme nous pouvons le constater, notre dépendance estimée du temps d'exécution sur les tailles de matrices linéaires s'est avérée vraie : une multiplication par deux de toutes les dimensions de la matrice a entraîné une augmentation d'environ 8 fois du temps d'exécution.
Quelques mots sur l'algorithme : l'ordre des boucles peut être modifié arbitrairement dans la fonction de multiplication mul(). Il s'avère que cela a un impact considérable sur le temps d'exécution : le rapport de la variante d'exécution la plus lente à la variante la plus rapide est d'environ 1,73.
L'article ne montre que la variante la plus rapide ; les variantes testées restantes se trouvent dans le code joint à la fin de l'article (fichier matr_mul_2dim.mq5). À ce propos, le guide de programmation OpenCL (Aaftab Munshi, Benedict R. Gaster, Timothy G. Mattson, James Fung, Dan Ginsburg) dit ce qui suit (p. 512) :
Ce ne sont évidemment pas toutes des optimisations du code "non parallèle" initial que nous pouvons implémenter. Certains d’eux sont liés par les instructions du matériel ((S)SSEx instructions) tandis que els autres sont purement algorithmiques, e.g. Algorithme Strassen, Algorithme Coppersmith–Winograd, etc. Notez que la taille des matrices multipliées pour l'algorithme de Strassen conduisant à une accélération considérable par rapport à l'algorithme classique est assez petite, n'étant que de 64х64. Dans cet article, nous allons apprendre à multiplier rapidement des matrices dont la taille linéaire va jusqu'à quelques milliers (environ jusqu'à 5000).
2.2. La première Implémentation de l'Algorithme dans OpenCL
Portons maintenant cet algorithme sur OpenCL, en créant des threads ROWS1 * COLS2, c'est-à-dire en supprimant les deux boucles externes du noyau. Chaque thread exécutera des itérations COLSROWS afin que la boucle interne demeure une partie du noyau.
Comme nous devrons créer trois tampons linéaires pour le noyau OpenCL, il serait raisonnable de retravailler l'algorithme initial pour qu'il soit aussi similaire que possible à l'algorithme du noyau. Le code du programme « non parallèle » sur un « processeur à un seul noyau » avec des tampons linéaires sera fourni avec le code du noyau. L'optimalité du code avec des tableaux à deux dimensions n’indique pas que son analogue sera également optimal pour les tampons linéaires : tous les tests devront être répétés. Par conséquent, nous optons à nouveau pour cr-cr comme variante initiale qui correspond à la logique standard de la multiplication matricielle en algèbre linéaire.
Cela dit, pour éviter une éventuelle confusion entre les éléments matrice/tampon, répondez à la question principale : si une matrice Matr( M lignes par N colonnes ) est disposée dans la mémoire globale du GPU en tant que tampon linéaire, comment pouvons-nous calculer un décalage linéaire d’un élément Matr[ ligne ][ colonne ] ?
Il n'y a en effet pas d'ordre fixe de disposition d'une matrice dans la mémoire GPU puisqu'il est déterminé par la seule logique du problème. Par exemple, des éléments des deux matrices pourraient être disposés différemment dans des tampons car en ce qui concerne l'algorithme de multiplication matricielle, les matrices sont asymétriques, c'est-à-dire que les lignes de la première matrice sont multipliées par les colonnes de la deuxième matrice. Un tel réarrangement peut grandement affecter les performances de calcul dans la lecture séquentielle des éléments de la matrice à partir de la mémoire globale du GPU à chaque itération du noyau.
La première implémentation de l'algorithme comportera des matrices disposées de la même manière - dans l'ordre des lignes principales. Les premiers éléments de ligne seront en premier lieu placés dans le tampon suivis par tous les éléments de la seconde ligne et ainsi de suite. La formule d'aplatissement d'une représentation à 2 dimensions d'une matrice Matr[ M (lignes) ][ N (colonnes) ] sur une mémoire linéaire est la suivante :
Fig. 13. Algorithme pour convertir un espace d'index bidimensionnel en linéaire pour disposer la matrice dans le tampon GPU
La Figure ci-dessus donne également un exemple de la façon dont une représentation matricielle à 2 dimensions est aplatie sur une mémoire linéaire dans l'ordre des colonnes principales.
Vous trouverez ci-dessous un code légèrement réduit de notre première implémentation de programme exécutée sur l’appareil OpenCL :
//+------------------------------------------------------------------+ //| matr_mul_1dim.mq5 | //+------------------------------------------------------------------+ #property script_show_inputs #define ROWS1 2000 // rows in the first matrix #define COLSROWS 2000 // columns in the first matrix = rows in the second matrix #define COLS2 2000 // columns in the second matrix #define REALTYPE float REALTYPE first[]; // first linear buffer (matrix) rows1 * colsrows REALTYPE second[]; // second buffer colsrows * cols2 REALTYPE thirdGPU[ ]; // product - also a buffer rows1 * cols2 REALTYPE thirdCPU[ ]; // product - also a buffer rows1 * cols2 input int _device=1; // here is the device; it can be changed (now 4870) string d2s(double arg,int dig) { return DoubleToString(arg,dig); } string i2s(long arg) { return IntegerToString(arg); } //+------------------------------------------------------------------+ const string clSrc= "#define COLS2 "+i2s(COLS2)+" \r\n" "#define COLSROWS "+i2s(COLSROWS)+" \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " int c = get_global_id( 1 ); \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " out[ r * COLS2 + c ] += \r\n" " in1[ r * COLSROWS + cr ] * in2[ cr * COLS2 + c ]; \r\n" "} \r\n"; //+------------------------------------------------------------------+ //| Main matrix multiplication function; | //| Input matrices are already generated, | //| the output matrix is initialized to zeros | //+------------------------------------------------------------------+ void mulCPUOneCore() { //--- c-r-cr: 11.544 s //st = GetTickCount( ); for(int c=0; c<COLS2; c++) for(int r=0; r<ROWS1; r++) for(int cr=0; cr<COLSROWS; cr++) thirdCPU[r*COLS2+c]+=first[r*COLSROWS+cr]*second[cr*COLS2+c]; return; } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { initAllDataCPU(); //--- start working with non-parallel version ("bare" CPU, single core) //--- calculate the output matrix on a single core CPU uint st=GetTickCount(); mulCPUOneCore(); //--- output total calculation time double timeCPU=(GetTickCount()-st)/1000.; Print("CPUTime = "+d2s(timeCPU,3)); //--- start working with OCL int clCtx; // context handle int clPrg; // handle to the program on the device int clKrn; // kernel handle int clMemIn1; // first (input) buffer handle int clMemIn2; // second (input) buffer handle int clMemOut; // third (output) buffer handle //--- start calculating the program runtime on GPU //st = GetTickCount( ); initAllDataGPU(clCtx,clPrg,clKrn,clMemIn1,clMemIn2,clMemOut); //--- start calculating total OCL code runtime st=GetTickCount(); executeGPU(clKrn); //--- create a buffer for reading and read the result; we will need it later REALTYPE buf[]; readOutBuf(clMemOut,buf); //--- stop calculating the total program runtime //--- together with the time required for retrieval of data from GPU and transferring it back to RAM double timeGPUTotal=(GetTickCount()-st)/1000.; Print("OpenCL total: time = "+d2s(timeGPUTotal,3)+" sec."); destroyOpenCL(clCtx,clPrg,clKrn,clMemIn1,clMemIn2,clMemOut); //--- calculate the time elapsed Print("CPUTime / GPUTotalTime = "+d2s(timeCPU/timeGPUTotal,3)); //--- debugging: random checks. Multiplication accuracy is checked directly //--- on the initial and output matrices using a few dozen examples for(int i=0; i<10; i++) checkRandom(buf,ROWS1,COLS2); Print("________________________"); return; } //+------------------------------------------------------------------+ //| initAllDataCPU | //+------------------------------------------------------------------+ void initAllDataCPU() { //--- initialize random number generator MathSrand(( int) TimeLocal()); Print("======================================="); Print("1st OCL martices mul: device = "+i2s(_device)+"; ROWS1 = " +i2s(ROWS1)+ "; COLSROWS = "+i2s(COLSROWS)+"; COLS2 = "+i2s(COLS2)); //--- set the required sizes of linear representations of the input and output matrices ArrayResize(first,ROWS1*COLSROWS); ArrayResize(second,COLSROWS*COLS2); ArrayResize(thirdGPU,ROWS1*COLS2); ArrayResize(thirdCPU,ROWS1*COLS2); //--- generate both input matrices and initialize the output to zeros genMatrices(); ArrayInitialize( thirdCPU, 0.0 ); ArrayInitialize( thirdGPU, 0.0 ); return; } //+------------------------------------------------------------------+ //| initAllDataCPU | //| lay out in row-major order, Matr[ M (rows) ][ N (columns) ]: | //| Matr[row][column] = buff[row * N(columns in the matrix) + column]| //| generate initial matrices; this generation is not reflected | //| in the final runtime calculation | //| buffers are filled in row-major order! | //+------------------------------------------------------------------+ void genMatrices() { for(int r=0; r<ROWS1; r++) for(int c=0; c<COLSROWS; c++) first[r*COLSROWS+c]=genVal(); for(int r=0; r<COLSROWS; r++) for(int c=0; c<COLS2; c++) second[r*COLS2+c]=genVal(); return; } //+------------------------------------------------------------------+ //| genVal | //| generate one value of the matrix element: | //| uniformly distributed value lying in the range [-0.5; 0.5] | //+------------------------------------------------------------------+ REALTYPE genVal() { return(REALTYPE)((MathRand()-16383.5)/32767.); } //+------------------------------------------------------------------+ //| initAllDataGPU | //+------------------------------------------------------------------+ void initAllDataGPU(int &clCtx, // context int& clPrg, // program on the device int& clKrn, // kernel int& clMemIn1, // first (input) buffer int& clMemIn2, // second (input) buffer int& clMemOut) // third (output) buffer { //--- write the kernel code to a file WriteCLProgram(); //--- create context, program and kernel clCtx = CLContextCreate( _device ); clPrg = CLProgramCreate( clCtx, clSrc ); clKrn = CLKernelCreate( clPrg, "matricesMul" ); //--- create all three buffers for the three matrices //--- first matrix - input clMemIn1=CLBufferCreate(clCtx,ROWS1 *COLSROWS*sizeof(REALTYPE),CL_MEM_READ_WRITE); //--- second matrix - input clMemIn2=CLBufferCreate(clCtx,COLSROWS*COLS2 *sizeof(REALTYPE),CL_MEM_READ_WRITE); //--- third matrix - output clMemOut=CLBufferCreate(clCtx,ROWS1 *COLS2 *sizeof(REALTYPE),CL_MEM_READ_WRITE); //--- set arguments to the kernel CLSetKernelArgMem(clKrn,0,clMemIn1); CLSetKernelArgMem(clKrn,1,clMemIn2); CLSetKernelArgMem(clKrn,2,clMemOut); //--- write the generated matrices to the device buffers CLBufferWrite(clMemIn1,first); CLBufferWrite(clMemIn2,second); CLBufferWrite(clMemOut,thirdGPU); // 0.0 everywhere return; } //+------------------------------------------------------------------+ //| WriteCLProgram | //+------------------------------------------------------------------+ void WriteCLProgram() { int h=FileOpen("matr_mul_OCL_1st.cl",FILE_WRITE|FILE_TXT|FILE_ANSI); FileWrite(h,clSrc); FileClose(h); } //+------------------------------------------------------------------+ //| executeGPU | //+------------------------------------------------------------------+ void executeGPU(int clKrn) { //--- set the workspace parameters for the task and execute the OpenCL program uint offs[ 2 ] = { 0, 0 }; uint works[ 2 ] = { ROWS1, COLS2 }; bool ex=CLExecute(clKrn,2,offs,works); return; } //+------------------------------------------------------------------+ //| readOutBuf | //+------------------------------------------------------------------+ void readOutBuf(int clMemOut,REALTYPE &buf[]) { ArrayResize(buf,COLS2*ROWS1); //--- buf - a copy of what is written to the buffer thirdGPU[] uint read=CLBufferRead(clMemOut,buf); Print("read = "+i2s(read)+" elements"); return; } //+------------------------------------------------------------------+ //| destroyOpenCL | //+------------------------------------------------------------------+ void destroyOpenCL(int clCtx,int clPrg,int clKrn,int clMemIn1,int clMemIn2,int clMemOut) { //--- destroy all that was created for calculations on the OpenCL device in reverse order CLBufferFree(clMemIn1); CLBufferFree(clMemIn2); CLBufferFree(clMemOut); CLKernelFree(clKrn); CLProgramFree(clPrg); CLContextFree(clCtx); return; } //+------------------------------------------------------------------+ //| checkRandom | //| random check of calculation accuracy | //+------------------------------------------------------------------+ void checkRandom(REALTYPE &buf[],int rows,int cols) { int r0 = genRnd( rows ); int c0 = genRnd( cols ); REALTYPE sum=0.0; for(int runningIdx=0; runningIdx<COLSROWS; runningIdx++) sum+=first[r0*COLSROWS+runningIdx]* second[runningIdx*COLS2+c0]; //--- element of the buffer m[] REALTYPE bufElement=buf[r0*COLS2+c0]; //--- element of the matrix not calculated in OpenCL REALTYPE CPUElement=thirdCPU[r0*COLS2+c0]; Print("sum( "+i2s(r0)+","+i2s(c0)+" ) = "+d2s(sum,8)+ "; thirdCPU[ "+i2s(r0)+","+i2s(c0)+" ] = "+d2s(CPUElement,8)+ "; buf[ "+i2s(r0)+","+i2s(c0)+" ] = "+d2s(bufElement,8)); return; } //+------------------------------------------------------------------+ //| genRnd | //+------------------------------------------------------------------+ int genRnd(int max) { return(int)(MathRand()/32767.*max); }
Liste 2. La première implémentation du programme en OpenCL
Les deux dernières fonctions sont utiles pour vérifier l'exactitude des calculs. Le code complet se trouve en pièce jointe à la fin de l'article (matr_mul_1dim.mq5). Notez que les dimensions ne doivent pas nécessairement correspondre uniquement à des matrices carrées.
D'autres modifications concerneront presque toujours uniquement le code du noyau, par conséquent, seuls les codes de modification du noyau seront présentés ci-après.
Le type REALTYPE est introduit pour faciliter la modification de la précision de calcul de float à double. Il convient de mentionner que le type REALTYPE est déclaré non seulement dans le programme hôte mais également dans le noyau. Si nécessaire, toute modification concernant ce type devra être effectuée à deux endroits en même temps, à la fois dans #define du programme hôte et dans le code du noyau.
Les résultats des performances du code (ci-après, type de données float partout) :
CPU (OpenCL, _device = 0) :
2012.05.20 22:14:57 matr_mul_1dim (EURUSD,H1) CPUTime / GPUTotalTime = 12.479 2012.05.20 22:14:57 matr_mul_1dim (EURUSD,H1) OpenCL total: time = 9.266 sec. 2012.05.20 22:14:57 matr_mul_1dim (EURUSD,H1) read = 4000000 elements 2012.05.20 22:14:48 matr_mul_1dim (EURUSD,H1) CPUTime = 115.628 2012.05.20 22:12:52 matr_mul_1dim (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.20 22:12:52 matr_mul_1dim (EURUSD,H1) =======================================
Lorsqu'il est exécuté sur Radeon HD 4870 (_device = 1) :
2012.05.27 01:40:50 matr_mul_1dim (EURUSD,H1) CPUTime / GPUTotalTime = 9.002 2012.05.27 01:40:50 matr_mul_1dim (EURUSD,H1) OpenCL total: time = 12.729 sec. 2012.05.27 01:40:50 matr_mul_1dim (EURUSD,H1) read = 4000000 elements 2012.05.27 01:40:37 matr_mul_1dim (EURUSD,H1) CPUTime = 114.583 2012.05.27 01:38:42 matr_mul_1dim (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 01:38:42 matr_mul_1dim (EURUSD,H1) =======================================
Comme nous pouvons le constater, l'exécution du noyau sur le GPU est beaucoup plus lente. Cependant, nous n'avons pas encore abordé l'optimisation spécialement pour le GPU.
Quelques conclusions :
- Le changement de représentation matricielle de deux dimensions à linéaire (correspondant à la représentation dans le programme exécuté sur l'appareil) n'a pas eu d'impact considérable sur le temps d'exécution total de la version séquentielle du programme.
- L'algorithme de calcul le plus intuitif correspondant à la définition de la multiplication matricielle en algèbre linéaire a été sélectionné comme variante initiale pour une optimisation ultérieure. Il est un peu plus lent que le plus rapide mais compte tenu de l'accélération future du GPU, ce facteur n'est pas essentiel.
- Le temps d'exécution doit être calculé uniquement après la lecture des tampons dans la RAM plutôt qu'après la commandeCLExecute() . La raison derrière cela, soulignée par MetaDriver à l'auteur, est probablement la suivante :MetaDriver: Avant de lire depuis le tampon, CLBufferRead() attend simplement l’accomplissement réel du programme. CLExecute() est en fait une fonction de mise en file d'attente asynchrone. Il renvoie le résultat immédiatement, bien avant la fin de l'opération de code cl.
- Les guides informatiques GPU ne calculent généralement pas le temps d’exécution du noyau mais plutôt ledébiten rapport avec les divers objets-mémoire, arithmétique, etc. Nous pouvons et ferons de même ci-après.
On sait que le calcul d'une matrice de la taille de 2000 nécessite environ 2 * 2000 additions/multiplications pour chaque élément. En multipliant par le nombre d'éléments de la matrice (2000 * 2000),nous trouvons que le nombre total d'opérations sur les données de type float est de 16 milliards. Cela dit, l'exécution sur le processeur prend 115,628 secondes, ce qui correspond à une vitesse de flux de données égale à
D'un autre côté, rappelez-vous que le calcul le plus rapide à ce jour sur un "processeur à noyau unique" avec une taille de matrice de 2000 n'a pris que 83,663 secondes (voir notre premier code sans OpenCL). D'où
Prenons cette figure comme référence, point de départ de nos optimisations.
De même, le calcul utilisant OpenCL sur le CPU donne :
Enfin, calculez le débit sur le GPU :
2.3. Éliminer les Accès aux Données Incohérents
En examinant le code du noyau, vous pouvez facilement constater quelques non-optimalités.
Jetez un œil au corps de la boucle dans le noyau :
for( int cr = 0; cr < COLSROWS; cr ++ ) out[ r * COLS2 + c ] += in1[ r * COLSROWS + cr ] * in2[ cr * COLS2 + c ];
Il est facile de voir que lorsque le compteur de boucle (cr++) est en cours d'exécution, les données contiguës sont extraites du premier tampon in1[]. Alors que les données du deuxième tampon in2[] sont prises avec des "lacunes" égales à COLS2. En d’autres termes, la partie majeure des données prises du deuxième tampon sont inutiles car les demandes en mémoire sont incohérentes (voir12.1. Requêtes de Mémoire de Fusions). Pour remédier à cette situation, il suffit de modifier le code à trois endroits en modifiant la formule de calcul de l'indice du tableau in2[], ainsi que son schéma de génération :
for( int cr = 0; cr < COLSROWS; cr ++ ) out[ r * COLS2 + c ] += in1[ r * COLSROWS + cr ] * in2[ cr + c * COLSROWS ];Désormais, lorsque les valeurs du compteur de boucle (cr++) changent, les données des deux tableaux seront prises de manière séquentielle, sans aucune "lacune".
- Code de remplissage de tampon dans genMatrices(). Il devrait maintenant être rempli dans l'ordre des colonnes principales au lieu de l'ordre des lignes principales utilisé au début :
for( int r = 0; r < COLSROWS; r ++ ) for( int c = 0; c < COLS2; c ++ ) /// second[ r * COLS2 + c ] = genVal( ); second[ r + c * COLSROWS ] = genVal( );- Code de vérification dans la fonction checkRandom() :
for( int runningIdx = 0; runningIdx < COLSROWS; runningIdx ++ ) ///sum += first[ r0 * COLSROWS + runningIdx ] * second[ runningIdx * COLS2 + c0 ]; sum += first[ r0 * COLSROWS + runningIdx ] * second[ runningIdx + c0 * COLSROWS ];Résultats de performances sur le CPU :
2012.05.24 02:59:22 matr_mul_1dim_coalesced (EURUSD,H1) CPUTime / GPUTotalTime = 16.207 2012.05.24 02:59:22 matr_mul_1dim_coalesced (EURUSD,H1) OpenCL total: time = 5.756 sec. 2012.05.24 02:59:22 matr_mul_1dim_coalesced (EURUSD,H1) read = 4000000 elements 2012.05.24 02:59:16 matr_mul_1dim_coalesced (EURUSD,H1) CPUTime = 93.289 2012.05.24 02:57:43 matr_mul_1dim_coalesced (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.24 02:57:43 matr_mul_1dim_coalesced (EURUSD,H1) =======================================Radeon HD 4870 :
2012.05.27 01:50:43 matr_mul_1dim_coalesced (EURUSD,H1) CPUTime / GPUTotalTime = 7.176 2012.05.27 01:50:43 matr_mul_1dim_coalesced (EURUSD,H1) OpenCL total: time = 12.979 sec. 2012.05.27 01:50:43 matr_mul_1dim_coalesced (EURUSD,H1) read = 4000000 elements 2012.05.27 01:50:30 matr_mul_1dim_coalesced (EURUSD,H1) CPUTime = 93.133 2012.05.27 01:48:57 matr_mul_1dim_coalesced (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 01:48:57 matr_mul_1dim_coalesced (EURUSD,H1) =======================================
Comme vous pouvez le constater, l'accès cohérent aux données n'a pratiquement aucun effet sur le temps d'exécution sur le GPU ; Cependant, cela a clairement amélioré le temps d'exécution sur le processeur. Il est fort probable qu'il s'agisse de facteurs qui seront optimisés par la suite, notamment avec une latence très élevée d'accès aux variables globales dont nous devrions nous débarrasser au plus vite.
throughput_arithmetic_CPU_OCL = 16 000000000 / 5.756 ~ 2.780 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 12.979 ~ 1.233 GFlops.
Le nouveau code du noyau se trouve dans matr_mul_1dim_coalesced.mq5 à la fin de l'article.
Le code du noyau est présenté ci-dessous :
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " int c = get_global_id( 1 ); \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " out[ r * COLS2 + c ] += \r\n" " in1[ r * COLSROWS + cr ] * in2[ cr + c * COLSROWS ]; \r\n" "} \r\n";
Liste 3. Noyau avec accès aux données de la mémoire globale fusionnée
Passons à d'autres optimisations.
2.4. Suppression de l'accès « coûteux » de la mémoire GPU globale de la matrice de sortie
Il est connu que la latence de l'accès global à la mémoire GPU est extrêmement élevée (environ 600-800 cycles). Par exemple, la latence d’ effectuer une addition de deux nombres est d'environ 20 cycles. L'objectif principal des optimisations lors du calcul sur GPU est de masquer la latence en augmentant le débit des calculs. Dans la boucle du noyau précédemment élaborée, nous accédons en permanence à des éléments de mémoire globale ce qui nous coûte du temps.
Introduisons maintenant la somme de la variable locale dans le noyau (qui est accessible plusieurs fois plus rapidement car il s'agit d'une variable privée du noyau située dans le registre de l'unité de travail) et à la fin de la boucle,attribuonsindividuellementla valeur somme obtenue à l’ élément du tableau de sortie:
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " int c = get_global_id( 1 ); \r\n" " REALTYPE sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " sum += in1[ r * COLSROWS + cr ] * in2[ cr + c * COLSROWS ]; \r\n" " out[ r * COLS2 + c ] = sum; \r\n" "} \r\n" ;
Liste 4. Présentation de la variable privée pour calculer la somme cumulée dans la boucle de calcul du produit scalaire
Le fichier de code source complet, matr_mul_sum_local.mq5, est joint à la fin de l'article.
CPU
2012.05.24 03:28:17 matr_mul_sum_local (EURUSD,H1) CPUTime / GPUTotalTime = 24.863 2012.05.24 03:28:16 matr_mul_sum_local (EURUSD,H1) OpenCL total: time = 3.759 sec. 2012.05.24 03:28:16 matr_mul_sum_local (EURUSD,H1) read = 4000000 elements 2012.05.24 03:28:12 matr_mul_sum_local (EURUSD,H1) CPUTime = 93.460 2012.05.24 03:26:39 matr_mul_sum_local (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000CARTE GRAPHIQUE HD 4870 :
2012.05.27 01:57:30 matr_mul_sum_local (EURUSD,H1) CPUTime / GPUTotalTime = 69.541 2012.05.27 01:57:30 matr_mul_sum_local (EURUSD,H1) OpenCL total: time = 1.326 sec. 2012.05.27 01:57:30 matr_mul_sum_local (EURUSD,H1) read = 4000000 elements 2012.05.27 01:57:28 matr_mul_sum_local (EURUSD,H1) CPUTime = 92.212 2012.05.27 01:55:56 matr_mul_sum_local (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 01:55:56 matr_mul_sum_local (EURUSD,H1) =======================================C'est un vrai boost de productivité !
throughput_arithmetic_CPU_OCL = 16 000000000 / 3.759 ~ 4.257 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 1.326 ~ 12.066 GFlops.
Le principe de base que nous essayons de respecter dans les optimisations séquentielles est le suivant : vous devez d'abord réorganiser la structure de données de la manière la plus complète possible afin qu'elle soit appropriée pour une tâche donnée et en particulier le matériel sous-jacent et ensuite seulement procéder à des optimisations fines utilisant des algorithmes de calcul rapides, tels que mad() ou fma(). Gardez à l'esprit que les optimisations séquentielles n'entraînent toujours pas nécessairement une augmentation des performances - cela ne peut pas être garanti.
2.5. Augmenter les Opérations Exécutées par le Noyau
En programmation parallèle, il est important d’organiser les calculs afin de minimisersurcharge (temps passé) sur l’organisation d’opération parallèle. Dans les matrices de dimension 2000, une unité de travail calculant un élément de matrice de sortie effectue le volume de travail égale à 1/4000000 de la tâche totale.
C'est évidemment trop et trop loin du nombre réel d'unités effectuant des calculs sur le matériel. Maintenant, dans la nouvelle version du noyau, nous allons calculer la ligne entière de la matrice au lieu d'un élément.
Il est important que l'espace des tâches passe maintenant de 2 dimensions à une dimension car la dimension entière - la ligne entière, plutôt qu'un seul élément de la matrice, est maintenant calculée dans chaque tâche du noyau. Par conséquent, l'espace des tâches se transforme en nombre de lignes de la matrice.
Fig. 14. Schéma de calcul de la ligne entière de la matrice de sortie
Le code du noyau devient plus compliqué :
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE sum; \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " sum += in1[ r * COLSROWS + cr ] * in2[ cr + c * COLSROWS ]; \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
Liste 5. Le noyau pour le calcul de la ligne entière de la matrice de sortie
void executeGPU( int clKrn ) { //--- set parameters of the task workspace and execute the OpenCL program uint offs[ 1 ] = { 0 }; uint works[ 1 ] = { ROWS1 }; bool ex = CLExecute( clKrn, 1, offs, works ); return; }
Résultats de performance (le code source complet se trouve dans matr_mul_row_calc.mq5) :
CPU
2012.05.24 15:56:24 matr_mul_row_calc (EURUSD,H1) CPUTime / GPUTotalTime = 17.385 2012.05.24 15:56:24 matr_mul_row_calc (EURUSD,H1) OpenCL total: time = 5.366 sec. 2012.05.24 15:56:24 matr_mul_row_calc (EURUSD,H1) read = 4000000 elements 2012.05.24 15:56:19 matr_mul_row_calc (EURUSD,H1) CPUTime = 93.288 2012.05.24 15:54:45 matr_mul_row_calc (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.24 15:54:45 matr_mul_row_calc (EURUSD,H1) =======================================
GPU 4870 :
2012.05.27 02:24:10 matr_mul_row_calc (EURUSD,H1) CPUTime / GPUTotalTime = 55.119 2012.05.27 02:24:10 matr_mul_row_calc (EURUSD,H1) OpenCL total: time = 1.669 sec. 2012.05.27 02:24:10 matr_mul_row_calc (EURUSD,H1) read = 4000000 elements 2012.05.27 02:24:08 matr_mul_row_calc (EURUSD,H1) CPUTime = 91.994 2012.05.27 02:22:35 matr_mul_row_calc (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 02:22:35 matr_mul_row_calc (EURUSD,H1) =======================================
Nous pouvons constater que le temps d'exécution sur le CPU s'est clairement empiré et s'est légèrement, mais pas beaucoup pire que sur le GPU. Tout n'est pas si mal : ce changement stratégique qui aggrave temporairement la situation au niveau local n'est là que pour augmenter encore considérablement la performance.
throughput_arithmetic_CPU_OCL = 16 000000000 / 5.366 ~ 2.982 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 1.669 ~ 9.587 GFlops.
2.6. Transfert de la ligne du premier tableau vers la mémoire privée
La particularité principale de l'algorithme de multiplication matricielle est un grand nombre de multiplications avec accumulation concomitante des résultats. Une optimisation appropriée et de haute qualité de cet algorithme devrait impliquer la minimisation des transferts de données. Mais jusqu'à présent, dans les calculs au sein de la boucle principale d'accumulation de produits scalaires, toutes nos modifications de noyau ont stocké deux des trois matrices dans la mémoire globale.
Cela indique que toutes les données d'entrée pour chaque produit scalaire (étant en fait chaque élément de matrice de sortie) sont constamment diffusées dans toute la hiérarchie de la mémoire - du global au privé - avec les latences associées. Ce trafic peut être réduit en s'assurant que chaque unité de travail réutilise une même ligne de la première matrice pour chaque ligne calculée de la matrice de sortie.
Fig. 15. Transfert de la ligne de la première matrice dans la mémoire privée de l'unité de travail
Cela n'entraîne aucune modification du code du programme hôte. Et les changements dans le noyau sont minimes. Du fait qu'un tableau privé unidimensionnel intermédiaire est généré dans le noyau, le GPU essaie de le placer dans la mémoire privée de l'unité qui exécute le noyau. La ligne requise de la première matrice est simplement copiée de la mémoire globale vers la mémoire privée. Cela dit, il convient de noter que même cette copie sera relativement rapide. L'astuce réside dans le fait que la copie la plus "coûteuse" des éléments de ligne du premier tableau de la mémoire globale vers la mémoire privée est effectuée de manière cohérente et la surcharge de la copie est assez modeste par rapport au temps d'exécution de la double boucle principale calculant la ligne de la matrice de sortie .
Le code du noyau (le code commenté dans la boucle principale est ce qu'il y avait dans la version précédente) :
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE rowbuf[ COLSROWS ]; \r\n" " for( int col = 0; col < COLSROWS; col ++ ) \r\n" " rowbuf[ col ] = in1[ r * COLSROWS + col ]; \r\n" " REALTYPE sum; \r\n" " \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " ///sum += in1[ r * COLSROWS + cr ] * in2[ cr + c * COLSROWS ]; \r\n" " sum += rowbuf[ cr ] * in2[ cr + c * COLSROWS ]; \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
Liste 6. Noyau comportant la ligne de la première matrice en mémoire privée de l'unité de travail.
CPU2012.05.27 00:51:46 matr_mul_row_in_private (EURUSD,H1) CPUTime / GPUTotalTime = 18.587 2012.05.27 00:51:46 matr_mul_row_in_private (EURUSD,H1) OpenCL total: time = 4.961 sec. 2012.05.27 00:51:46 matr_mul_row_in_private (EURUSD,H1) read = 4000000 elements 2012.05.27 00:51:41 matr_mul_row_in_private (EURUSD,H1) CPUTime = 92.212 2012.05.27 00:50:08 matr_mul_row_in_private (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 00:50:08 matr_mul_row_in_private (EURUSD,H1) =======================================GPU :
2012.05.27 02:28:49 matr_mul_row_in_private (EURUSD,H1) CPUTime / GPUTotalTime = 69.242 2012.05.27 02:28:49 matr_mul_row_in_private (EURUSD,H1) OpenCL total: time = 1.327 sec. 2012.05.27 02:28:49 matr_mul_row_in_private (EURUSD,H1) read = 4000000 elements 2012.05.27 02:28:47 matr_mul_row_in_private (EURUSD,H1) CPUTime = 91.884 2012.05.27 02:27:15 matr_mul_row_in_private (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 02:27:15 matr_mul_row_in_private (EURUSD,H1) =======================================
throughput_arithmetic_CPU_OCL = 16 000000000 / 4.961 ~ 3.225 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 1.327 ~ 12.057 GFlops.
Le débit du CPU est resté à peu près au même niveau que la dernière fois, tandis que le débit du GPU est revenu au plus haut niveau atteint, mais dans la nouvelle capacité. Notez que le débit du CPU est comme s'il s'était figé sur place, n'étant que légèrement instable, tandis que le débit du GPU augmente (pas toujours, cependant) par des sauts assez importants.
Précisons que le débit arithmétique réel devrait être un peu plus élevé car, en raison de la copie de la ligne de la première matrice dans la mémoire privée, plus d'opérations sont exécutées maintenant qu'avant. Cependant, il a peu d'effet sur l'estimation finale du débit.
Le code source se trouve dans matr_mul_row_in_private.mq5.
2.7. Transfert de la colonne du deuxième tableau vers la mémoire locale
Maintenant, il est facile de deviner quelle sera la prochaine étape. Nous avons déjà pris des mesures pour masquer les latences associées à la sortie et aux premières matrices d'entrée. Il reste la deuxième matrice.
Une étude plus approfondie des produits scalaires utilisés dans la multiplication matricielle indique qu'au cours du calcul de la ligne de la matrice de sortie, toutes les unités de travail du groupe retransmettent les données des mêmes colonnes de la deuxième matrice multipliée à travers le dispositif. Ceci est illustré dans le schéma ci-dessous :
Fig. 16. Le transfert de la colonne de la deuxième matrice vers le partage local de donnéesdu groupe de travail
La surcharge de transfert de données depuis la mémoire globale peut être réduite si les unités de travail formant le groupe de travail copient les colonnes de la seconde matrice dans la mémoire du groupe de travail avantque le calcul de la matrice de sortie des lignes commence.
Cela nécessitera des modifications dans le noyau, ainsi que dans le programme hôte. Le changement le plus important est la configuration de la mémoire locale pour chaque noyau. Il doit être explicite car l'allocation dynamique de mémoire n'est pas prise en charge dans OpenCL. Par conséquent, un objet mémoire de taille adéquate doit d'abord être placé dans l'hôte pour être traité ultérieurement dans le noyau.
Et alors seulement, lors de l'exécution du noyau, les unités de travail copient la colonne de la deuxième matrice dans la mémoire locale. Cela se fait en parallèle en utilisant une distribution cyclique des itérations de boucle sur toutes les unités de travail du groupe de travail. Cependant, toutes les copies doivent être terminées avant que l'unité de travail ne commence son opération principale (calcul de la ligne de la matrice de sortie).
C'est pourquoi la commande suivante est insérée après la boucle en charge de la copie :
barrier(CLK_LOCAL_MEM_FENCE);
Il s'agit d'une « barrière de mémoire locale » assurant que chaque unité de travail au sein du groupe peut « voir » la mémoire locale dans un certain état coordonné avec d'autres unités. Toutes les unités de travail dans le groupe de travail doivent exécuter des commandes jusqu'à la barrière avant qu'aucune d'entre elles ne puisse procéder à l'exécution du noyau. En d'autres termes, la barrière est un mécanisme de synchronisation spécial entre les unités de travail au sein du groupe de travail.
Les mécanismes de synchronisation entre groupes de travail ne sont pas prévus dans OpenCL.
Ci-dessous, l'illustration de la barrière en action :
Fig. 17. Illustration de la barrière en action
En fait, il semble seulement que les unités de travail au sein du groupe de travail exécutent le code de manière strictement concurrente. Il s'agit simplement d'une abstraction du modèle de programmation OpenCL.
Jusqu'à présent, nos codes de noyau exécutés sur différentes unités de travail n'ont pas nécessité de synchronisation des opérations car il n'y avait pas de communication explicite entre eux qui serait définie par programme dans le noyau ; d'ailleurs, ce n'était même pas nécessaire. Cependant, la synchronisation est nécessaire dans le noyau puisque le processus de remplissage dans le tableau local est distribuéparallèlement entre toutes les unités du groupe de travail.
En d'autres termes, chaque unité de travail écrit ses valeurs dans le partage local de données (ici, le tableau) sans savoir jusqu'où en sont les autres unités de travail dans ce processus d'écriture. La barrière est là pour qu'une certaine unité de travail ne procède pas à l'exécution du noyau avant que cela ne soit nécessaire, c'est-à-dire avant qu'un tableau local n'ait été complètement créé.
Il faut comprendre que cette optimisation ne sera guère bénéfique aux performances sur le CPU : Le guide d'optimisation OpenCL d'Intel indique que lors de l'exécution d'un noyau sur le processeur, tous les objets de mémoire OpenCL sont mis en cache par le matériel, de sorte que la mise en cache explicite à l'aide de la mémoire locale introduise simplement une surcharge inutile (modérée).
Il y a un autre point important à noter ici qui a coûté beaucoup de temps à l'auteur de l'article. Cela tient au fait qu'une variable locale ne peut pas être passée dans l'en-tête de la fonction noyau, c'est-à-dire au stade de la compilation, dans l'implémentation actuelle construite par les développeurs du terminal. La raison derrière est que pour allouer la mémoire à un objet de mémoire comme argument de la fonction noyau, nous devrions en premier lieu,explicitement créer un tel objet dans la mémoire CPU à l’aide de la fonctionCLBufferCreate()et explicitement indiquer sa taille en tant que paramètre de fonction. Cette fonction renvoie un descripteur d'objet mémoire qui sera ensuite stocké dans la mémoire globale du GPU car c'est le seul endroit où il peut être.
La mémoire locale est cependant la mémoire différente de la mémoire globale et, par conséquent, un objet mémoire créé ne peut pas être placé dans la mémoire locale du groupe de travail.
L'API OpenCL complète permet d'attribuer explicitement la mémoire de la taille requise avec le pointeur NULL à l'argument du noyau, même sans créer l'objet mémoire en tant que tel (fonctionCLSetKernelArg()).. Cependant, la syntaxe de la fonction CLSetKernelArgMem() étant analogue de MQL5 de la fonction entièrement fonctionnelle API ne nous permet pas de passer dans la taille de la mémoire allouée à l’argument sans créer l’objet de mémoire lui-même. ce que nous pouvons transmettre à la fonctionCLSetKernelArgMem()est seulement le descripteur du tampondéjà créedans la mémoire globale du CPU destinée à transférer vers la mémoire globale GPU. Voici le paradoxe.
Heureusement, il existe une manière équivalente de travailler avec les tampons locaux dans le noyau. Vous déclarez simplement ce tampon avec le modificateur __local dans le corps du noyau. La mémoire locale allouée au groupe de travail sera ainsi déterminée lors de l'exécution au lieu de la phase de compilation.
Les commandes venant après la barrière dans le noyau (la ligne de barrière dans le code est marquée en rouge) sont, en substance, les mêmes que dans l'optimisation précédente. Le code du programme hôte est resté le même (le code source se trouve dans matr_mul_col_local.mq5).
Voici donc le nouveau code du noyau :
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE rowbuf[ COLSROWS ]; \r\n" " for( int col = 0; col < COLSROWS; col ++ ) \r\n" " rowbuf[ col ] = in1[ r * COLSROWS + col ]; \r\n" " \r\n" " int idlocal = get_local_id( 0 ); \r\n" " int nlocal = get_local_size( 0 ); \r\n" " __local REALTYPE colbuf[ COLSROWS ] ; \r\n" " \r\n" " REALTYPE sum; \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " for( int cr = idlocal; cr < COLSROWS; cr = cr + nlocal ) \r\n" " colbuf[ cr ] = in2[ cr + c * COLSROWS ]; \r\n" " barrier( CLK_LOCAL_MEM_FENCE ); \r\n" " \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " sum += rowbuf[ cr ] * colbuf[ cr ]; \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
Liste 7. La colonne du deuxième tableau transférée dans la mémoire locale du groupe de travail
2012.05.27 06:31:46 matr_mul_col_local (EURUSD,H1) CPUTime / GPUTotalTime = 17.630 2012.05.27 06:31:46 matr_mul_col_local (EURUSD,H1) OpenCL total: time = 5.227 sec. 2012.05.27 06:31:46 matr_mul_col_local (EURUSD,H1) read = 4000000 elements 2012.05.27 06:31:40 matr_mul_col_local (EURUSD,H1) CPUTime = 92.150 2012.05.27 06:30:08 matr_mul_col_local (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 06:30:08 matr_mul_col_local (EURUSD,H1) =======================================GPU :
2012.05.27 06:21:36 matr_mul_col_local (EURUSD,H1) CPUTime / GPUTotalTime = 58.069 2012.05.27 06:21:36 matr_mul_col_local (EURUSD,H1) OpenCL total: time = 1.592 sec. 2012.05.27 06:21:36 matr_mul_col_local (EURUSD,H1) read = 4000000 elements 2012.05.27 06:21:34 matr_mul_col_local (EURUSD,H1) CPUTime = 92.446 2012.05.27 06:20:01 matr_mul_col_local (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 06:20:01 matr_mul_col_local (EURUSD,H1) =======================================
Les deux cas démontrent une dégradation des performances qui ne peut cependant pas être qualifiée de majeure. Il se peut fort bien que la performance puisse être améliorée plutôt que dégradée en modifiant la taille du groupe de travail. L'exemple ci-dessus servirait plutôt un objectif différent - montrer comment utiliser les objets de mémoire locale.
Il existe une hypothèse qui explique une diminution de performance lorsque la mémoire locale est utilisée. L’articleComparant OpenCL avec CUDA, GLSL et OpenMP (en russe) publié y a 2 ans sur habrahabr.ru dit que:
Autrement dit, cela signifie-t-il que la mémoire locale des produits sortis il y a 2 ans n'est pas plus rapide que la mémoire globale ? Le moment où ce qui précède a été publié suggère qu'il y a deux ans, les cartes vidéo de la série Radeon HD 58xx étaient déjà sorties, mais la situation, selon l'auteur, était loin d'être optimiste. Je trouve cela difficile à croire, surtout compte tenu de la série sensationnelle Evergreen d'AMD. Il serait intéressant de le vérifier en utilisant des cartes plus modernes, par exemple la série HD 69xx.
Ajout : démarrez GPU Caps Viewer et vous verrez ce qui suit dans l'onglet OpenCL :
Fig. 18. Principaux paramètres OpenCL pris en charge par HD 4870
CL_DEVICE_LOCAL_MEM_TYPE: Global
L'explication de ce paramètre fournie dans la spécification du langage (Tableau 4.3, p. 41) est la suivante :
Type de mémoire locale pris en charge. Cela peut être défini sur CL_LOCAL,impliquant un stockage de mémoire local dédié tel que SRAM ou CL_GLOBAL.
Ainsi, la mémoire locale du HD 4870 fait vraiment partie de la mémoire globale et toute manipulation de la mémoire locale dans cette carte vidéo est donc inutile et n'entraînera rien de plus rapide que la mémoire globale. Ici est un autre lien où un spécialiste en AMD clarifie le point des séries HD 4xxx. Cela ne signifie pas nécessairement que ce sera aussi mauvais pour la carte vidéo que vous avez ; c'était juste pour montrer où ces informations concernant le matériel peuvent être trouvées - dans ce cas, dans GPU Caps Viewer.
throughput_arithmetic_CPU_OCL = 16 000000000 / 5.227 ~ 3.061 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 1.592 ~ 10.050 GFlops.
Enfin, ajoutons quelques touches finales en vectorisant explicitement le noyau. Le noyau dérivé au stade du transfert de la ligne du premier tableau vers la mémoire privée (matr_mul_row_in_private.mq5) servira de noyau initial puisqu'il s'est avéré être le plus rapide.
2.8. Vectorisation du noyau
Cette opération devrait mieux être décomposée en plusieurs étapes, pour éviter toute confusion. Dans la modification initiale, nous ne changeons pas les types de données des paramètres externes du noyau et vectorisons uniquement les calculs dans la boucle interne :
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" "#define REALTYPE4 float4 \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE rowbuf[ COLSROWS ]; \r\n" " for( int col = 0; col < COLSROWS; col ++ ) \r\n" " { \r\n" " rowbuf[ col ] = in1[r * COLSROWS + col ]; \r\n" " } \r\n" " \r\n" " REALTYPE sum; \r\n" " \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS; cr += 4 ) \r\n" " sum += dot( ( REALTYPE4 ) ( rowbuf[ cr ], \r\n" " rowbuf[ cr + 1 ], \r\n" " rowbuf[ cr + 2 ], \r\n" " rowbuf[ cr + 3 ] ), \r\n" " ( REALTYPE4 ) ( in2[c * COLSROWS + cr ], \r\n" " in2[c * COLSROWS + cr + 1 ], \r\n" " in2[c * COLSROWS + cr + 2 ], \r\n" " in2[c * COLSROWS + cr + 3 ] ) ); \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
Liste 8. Vectorisation partielle du noyau à l'aide de float4 (seulement boucle interne)
CPU
2012.05.27 21:28:16 matr_mul_vect (EURUSD,H1) CPUTime / GPUTotalTime = 18.657 2012.05.27 21:28:16 matr_mul_vect (EURUSD,H1) OpenCL total: time = 4.945 sec. 2012.05.27 21:28:16 matr_mul_vect (EURUSD,H1) read = 4000000 elements 2012.05.27 21:28:11 matr_mul_vect (EURUSD,H1) CPUTime = 92.259 2012.05.27 21:26:38 matr_mul_vect (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 21:26:38 matr_mul_vect (EURUSD,H1) =======================================
GPU :
2012.05.27 21:21:30 matr_mul_vect (EURUSD,H1) CPUTime / GPUTotalTime = 78.079 2012.05.27 21:21:30 matr_mul_vect (EURUSD,H1) OpenCL total: time = 1.186 sec. 2012.05.27 21:21:30 matr_mul_vect (EURUSD,H1) read = 4000000 elements 2012.05.27 21:21:28 matr_mul_vect (EURUSD,H1) CPUTime = 92.602 2012.05.27 21:19:55 matr_mul_vect (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 21:19:55 matr_mul_vect (EURUSD,H1) =======================================
Étonnamment, même une vectorisation aussi primitive a donné de bons résultats sur le GPU ; bien que peu significatif, le gain semble être d'environ 10 %.
Continuez à vectoriser à l'intérieur du noyau : transférez les opérations de conversion de type vectoriel REALTYPE4 « coûteuses » ainsi que la spécification des composants vectoriels explicites vers la boucle auxiliaire externe remplissant la variable privée rowbuf[]. Il n'y a toujours pas de changements dans le noyau.
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" "#define REALTYPE4 float4 \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE4 rowbuf[ COLSROWS / 4 ]; \r\n" " for( int col = 0; col < COLSROWS / 4; col ++ ) \r\n" " { \r\n" " rowbuf[ col ] = ( REALTYPE4 ) ( in1[r * COLSROWS + 4 * col ], \r\n" " in1[r * COLSROWS + 4 * col + 1 ], \r\n" " in1[r * COLSROWS + 4 * col + 2 ], \r\n" " in1[r * COLSROWS + 4 * col + 3 ] ); \r\n" " } \r\n" " \r\n" " REALTYPE sum; \r\n" " \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS / 4; cr ++ ) \r\n" " sum += dot( rowbuf[ cr ], \r\n" " ( REALTYPE4 ) ( in2[c * COLSROWS + 4 * cr ], \r\n" " in2[c * COLSROWS + 4 * cr + 1 ], \r\n" " in2[c * COLSROWS + 4 * cr + 2 ], \r\n" " in2[c * COLSROWS + 4 * cr + 3 ] ) ); \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
Liste 9. Se débarrasser des opérations 'coûteuses' de conversion de type dans la boucle principale du noyau
Notez que la valeur de comptage maximale du compteur de boucle interne (ainsi qu'auxiliaire) est devenue 4 fois inférieure car les opérations de lecture qui sont maintenant requises pour le premier tableau sont 4 fois inférieures à ce qu'elles étaient auparavant - la lecture est clairement devenue une opération vectorielle.
2012.05.27 22:41:43 matr_mul_vect_v2 (EURUSD,H1) CPUTime / GPUTotalTime = 24.480 2012.05.27 22:41:43 matr_mul_vect_v2 (EURUSD,H1) OpenCL total: time = 3.791 sec. 2012.05.27 22:41:43 matr_mul_vect_v2 (EURUSD,H1) read = 4000000 elements 2012.05.27 22:41:39 matr_mul_vect_v2 (EURUSD,H1) CPUTime = 92.805 2012.05.27 22:40:06 matr_mul_vect_v2 (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 22:40:06 matr_mul_vect_v2 (EURUSD,H1) =======================================GPU :
2012.05.27 22:35:28 matr_mul_vect_v2 (EURUSD,H1) CPUTime / GPUTotalTime = 185.605 2012.05.27 22:35:28 matr_mul_vect_v2 (EURUSD,H1) OpenCL total: time = 0.499 sec. 2012.05.27 22:35:28 matr_mul_vect_v2 (EURUSD,H1) read = 4000000 elements 2012.05.27 22:35:27 matr_mul_vect_v2 (EURUSD,H1) CPUTime = 92.617 2012.05.27 22:33:54 matr_mul_vect_v2 (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 22:33:54 matr_mul_vect_v2 (EURUSD,H1) =======================================Débit arithmétique :
throughput_arithmetic_CPU_OCL = 16 000000000 / 3.791 ~ 4.221 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 0.499 ~ 32.064 GFlops.
Comme nous pouvons le constater, les changements de performance pour le CPU sont considérables, tout en étant presque révolutionnaires pour le GPU. Le code source se trouve dans matr_mul_vect_v2.mq5.
Effectuons les mêmes opérations par rapport à la dernière variante du noyau, en utilisant uniquement une largeur de vecteur de 8. La décision de l'auteur s'explique par le fait que la bande passante mémoire du GPU est de 256 bits, soit 32 octets ou 8 nombres de type float ; par conséquent, le traitement simultané de 8 floats, qui équivaut à l'utilisation simultanée de float8, semble tout à fait naturel.
Gardez à l'esprit que dans ce cas, la valeur COLSROWS doit être intégralement divisible par 8. Il s'agit d'une exigence naturelle car des optimisations plus fines définissent des exigences plus spécifiques pour les données.
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" "#define REALTYPE4 float4 \r\n" "#define REALTYPE8 float8 \r\n" " \r\n" "inline REALTYPE dot8( REALTYPE8 a, REALTYPE8 b ) \r\n" "{ \r\n" " REALTYPE8 c = a * b; \r\n" " REALTYPE4 _1 = ( REALTYPE4 ) 1.; \r\n" " return( dot( c.lo + c.hi, _1 ) ); \r\n" "} \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE8 rowbuf[ COLSROWS / 8 ]; \r\n" " for( int col = 0; col < COLSROWS / 8; col ++ ) \r\n" " { \r\n" " rowbuf[ col ] = ( REALTYPE8 ) ( in1[r * COLSROWS + 8 * col ], \r\n" " in1[r * COLSROWS + 8 * col + 1 ], \r\n" " in1[r * COLSROWS + 8 * col + 2 ], \r\n" " in1[r * COLSROWS + 8 * col + 3 ], \r\n" " in1[r * COLSROWS + 8 * col + 4 ], \r\n" " in1[r * COLSROWS + 8 * col + 5 ], \r\n" " in1[r * COLSROWS + 8 * col + 6 ], \r\n" " in1[r * COLSROWS + 8 * col + 7 ] ); \r\n" " } \r\n" " \r\n" " REALTYPE sum; \r\n" " \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS / 8; cr ++ ) \r\n" " sum += dot8( rowbuf[ cr ], \r\n" " ( REALTYPE8 ) ( in2[c * COLSROWS + 8 * cr ], \r\n" " in2[c * COLSROWS + 8 * cr + 1 ], \r\n" " in2[c * COLSROWS + 8 * cr + 2 ], \r\n" " in2[c * COLSROWS + 8 * cr + 3 ], \r\n" " in2[c * COLSROWS + 8 * cr + 4 ], \r\n" " in2[c * COLSROWS + 8 * cr + 5 ], \r\n" " in2[c * COLSROWS + 8 * cr + 6 ], \r\n" " in2[c * COLSROWS + 8 * cr + 7 ] ) ); \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
Liste 10. Vectorisation du noyau utilisant une largeur de vecteur de 8
Nous avons dû insérer dans le code du noyau la fonction en ligne dot8() qui permet de calculer le produit scalaire pour les vecteurs de largeur 8. Dans OpenCL, la fonction standard dot() ne peut calculer le produit scalaire que pour les vecteurs jusqu'à la largeur 4. Le code source se trouve dans matr_mul_vect_v3.mq5.
2012.05.27 23:11:47 matr_mul_vect_v3 (EURUSD,H1) CPUTime / GPUTotalTime = 45.226 2012.05.27 23:11:47 matr_mul_vect_v3 (EURUSD,H1) OpenCL total: time = 2.200 sec. 2012.05.27 23:11:47 matr_mul_vect_v3 (EURUSD,H1) read = 4000000 elements 2012.05.27 23:11:45 matr_mul_vect_v3 (EURUSD,H1) CPUTime = 99.497 2012.05.27 23:10:05 matr_mul_vect_v3 (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 23:10:05 matr_mul_vect_v3 (EURUSD,H1) =======================================GPU :
2012.05.27 23:20:05 matr_mul_vect_v3 (EURUSD,H1) CPUTime / GPUTotalTime = 170.115 2012.05.27 23:20:05 matr_mul_vect_v3 (EURUSD,H1) OpenCL total: time = 0.546 sec. 2012.05.27 23:20:05 matr_mul_vect_v3 (EURUSD,H1) read = 4000000 elements 2012.05.27 23:20:04 matr_mul_vect_v3 (EURUSD,H1) CPUTime = 92.883 2012.05.27 23:18:31 matr_mul_vect_v3 (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 23:18:31 matr_mul_vect_v3 (EURUSD,H1) =======================================
Les résultats sont inattendus : le temps d'exécution sur le CPU est presque deux fois plus faible qu'avant, alors qu'il a légèrement augmenté pour le GPU, malgré le fait que float8 soit d’une largeur de bus adéquate pour HD 4870 (étant égale à 256 bits). Et ici, nous recourons à nouveau à GPU Caps Viewer.
L'explication se trouve sur la figure 18, à l'avant-dernière ligne de la liste des paramètres :
CL_DEVICE_PREFERRED_VECTOR_WIDTH_FLOAT: 4
Consultez la spécification OpenCL et vous verrez le texte suivant concernant ce paramètre dans la dernière colonne du tableau 4.3 en page 37 :
Taille native de largeur de vecteur préférée pour les types scalaires intégrés pouvant être placés dans des vecteurs. La largeur du vecteur est définie comme le nombre d'éléments scalaires pouvant être stockés dans le vecteur.
Ainsi, pour HD 4870, la largeur de vecteur préférée du vecteur floatN est float4 au lieu de float8.
Terminons ici le cycle d'optimisation du noyau. Nous pourrions aller plus loin, mais la longueur de cet article ne permet pas une discussion aussi approfondie.
Conclusion
L'article a démontré certaines capacités d'optimisation qui s'ouvrent lorsqu'au moins une certaine considération est accordée au matériel sous-jacent sur lequel le noyau est exécuté.
Les chiffres obtenus sont loin d'être des valeurs plafond mais même ils suggèrent que disposer des ressources existantes disponibles ici et maintenant (l'API OpenCL telle qu'implémentée par les développeurs du terminal ne permet pas de contrôler certains paramètres importants pour l'optimisation - - notamment, la taille du groupe de travail), le gain en performance sur l'exécution du programme hôte est très important : le gain en exécution sur le GPU par rapport au programme séquentiel sur le CPU (bien que peu optimisé) est d'environ 200:1.
Ma sincère gratitude va àMetaDriver pour ses précieux conseils et la possibilité d'utiliser le GPU discret alors que le mien n'était pas disponible.
Contenu des fichiers joints :
- matr_mul_2dim.mq5 - Programme initial séquentiel sur le hôte avec une présentation de données à deux dimensions;
- matr_mul_1dim.mq5 - le première implémentation du noyau avec une représentation de données linéaire et une liaison pertinent pour MQL5 OpenCL API;
- matr_mul_1dim_coalesced - le noyau représentant un accès de mémoire global de fusion;
- matr_mul_sum_local- une variable privée introduite pour le calcul du produit scalaire, au lieu d'accéder à une cellule calculée du tableau de sortie stocké dans la mémoire globale ;
- matr_mul_row_calc- le calcul de toute la ligne de la matrice de sortie dans le noyau ;
- matr_mul_row_in_private- la ligne du premier tableau transféré dans la mémoire privée ;
- matr_mul_col_local.mq5-la colonne du deuxième tableau transférée dans la mémoire locale ;
- matr_mul_vect.mq5 - la première vectorisation du noyau (en utilisant float4, seule la sous-boucle interne de la boucle principale) ;
- matr_mul_vect_v2.mq5 - se débarrasser des opérations "coûteuses" de conversion de données dans la boucle principale ;
- matr_mul_vect_v3.mq5 - vectorisation utilisant une largeur de vecteur de 8.
Traduit du russe par MetaQuotes Ltd.
Article original : https://www.mql5.com/ru/articles/407
 La Programmation Basée sur des Automates comme Nouvelle Approche pour créer des Systèmes de Trading Automatisés
La Programmation Basée sur des Automates comme Nouvelle Approche pour créer des Systèmes de Trading Automatisés
 OpenCL : Le Pont vers les Mondes Parallèles
OpenCL : Le Pont vers les Mondes Parallèles
 Les membres de la MQL5.community les plus actifs ont reçu des iPhones !
Les membres de la MQL5.community les plus actifs ont reçu des iPhones !
 Pourquoi le Marché MQL5 est-il le Meilleur Endroit pour Vendre des Stratégies de Trading et des Indicateurs Techniques
Pourquoi le Marché MQL5 est-il le Meilleur Endroit pour Vendre des Stratégies de Trading et des Indicateurs Techniques
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Vous acceptez la politique du site Web et les conditions d'utilisation