Modèle de Régression Universel pour la Prévision des Prix du Marché

Introduction

Le prix du marché est formé à partir d’un équilibre stable entre l’offre et la demande qui, à son tour, dépendent d’une variété de facteurs économiques, politiques et psychologiques qui sont difficiles à traiter directement en raison des différences de nature ainsi que des causes de leur influence.

Il est toutefois nécessaire d’être en mesure d’anticiper et de prédire le comportement futur des prix du marché avec un certain degré de précision afin d’être en mesure de prendre les bonnes décisions concernant l’achat ou la vente de biens, y compris la monnaie ou les actions, dans la situation actuelle. Ce problème peut être résolu en utilisant une quantité considérable d’informations de nature différente provenant de toutes sortes de sources qui sont traitées d’une manière ou d’une autre.

Il existe 4 types d’analyse /1/ qui sont utilisés pour l’élaboration d’une stratégie et d’une tactique efficaces du comportement du marché en fonction de l’objectif, de la qualification ou de la prédisposition du chercheur:

1. Analyse technique axée sur l’affirmation que le prix du marché prend en compte tout ce qui peut l’affecter. Elle utilise des techniques mathématiques avancées /2/;
2. Analyse fondamentale traitant de l’impact de différents facteurs économiques sur le prix du marché. Elle utilise essentiellement des modèles macroéconomiques /3-5/;
3. Analyse intuitive étayée par la connaissance des principaux indices et indicateurs du marché, méthode de prédiction de leur comportement futur dont les résultats ne peuvent être prouvés en appliquant directement des règles logiques et des mathématiques aux prémisses initiales, mais qui s’avèrent néanmoins inexplicablement très souvent vrais;
4. Psychanalyse axée sur une analyse psychologique des conditions du marché par chaque client individuellement et collectivement dans son ensemble, ce qui se traduit par un succès divers.

État des Connaissances Concernant le Problème

Toute technique, y compris une nouvelle méthode proposée pour la prévision des prix du marché, devrait à notre avis considérer et, dans une combinaison chanceuse de circonstances, expliquer les lois objectivement existantes basées sur trois axiomes connus sous le nom de théorie de Dow /6,7/ qui peuvent être brièvement formulés, comme suit:

1. Le prix du marché tient compte de tous les facteurs affectant la loi de l’offre et de la demande et il suffit de disposer de données sur les variations du prix du marché au cours du temps pour le prévoir;
2. La dépendance du prix du marché au temps est soumise à des tendances (tendances) qui sont principalement en forme de S, dont les hauts et les bas sont reliés par des lignes horizontales (plates) appelées tendance latérale, ou sans aucune;
3. Il existe objectivement des modèles de variation des prix du marché qui demeurent inchangés au cours du temps, connus sous le nom de principes « l’histoire se répète » ou « ils ont fonctionné dans le passé, fonctionnent maintenant et fonctionneront à l’avenir ».

Cependant, les étapes de repos dynamiques de la série chronologique des prix du marché, par exemple les taux de change, sont suivies d’étapes si complexes que l’on a l’impression d’un chaos imprévisible complet qui, dans le processus d’auto-organisation, donne à nouveau naissance à l’ordre.

Mais à un moment donné, le système dynamique affaibli par la stabilité produit à nouveau le chaos qui nous donne des raisons de croire que la nature des séries chronologiques d’indicateurs économiques est mitigée. Cela indique que les séries chronologiques de prix du marché sont déterministes et analysables à un moment donné, mais ne peuvent pas être prédites de manière fiable à un autre point et suivent la loi de distribution normale /8/ et agissent comme une variable aléatoire à un autre point.

Ainsi, le monde scientifique manque encore d’une opinion commune sur la nature des variations du prix du marché qui nous empêche de trouver les dépendances qui les définiraient de manière adéquate et qui seraient applicables dans la pratique.

Fonctions Transitoires pour un Modèle à Cellule Unique de Boîte Noire

En raison du flou du processus, je suggère que nous examinions d’abord un modèle à cellule unique en boîte noire qui est parfois attribué au problème en question /1/ et que nous appliquons l’équation du bilan matière.

En développant les axiomes ci-dessus, admettons que le prix d’équilibre du marché ne peut changer que lorsqu’il est affecté par une force externe D(t) dont la quantité et la valeur seront mesurées dans la même dimension que le prix.

Nous admettons également que la variation du prix du marché P(t) au cours du temps t depuis le début de l’impact de la force spécifiée augmente en continu à partir de la valeur nulle conformément à une loi qui est encore inconnue en tentant d’atteindre une valeur de P(∞) = D0 à l’infini. En d’autres termes, D0 indiquera un incrément fini ou une décrément du prix du marché en fonction de la nature et du signe de la force pesante.

Il est également sous-entendu que D(t=0) = D0. Nous admettons en outre qu’au cours de la période infinitésimale de temps dt, la force pesante diminuera de la valeur de dD(t) proportionnellement à la force D(t) restant par le temps t:

d’où nous obtenons la dépendance exponentielle D(t) sur le temps t, comme suit:

                                                                                                                  (1)

Où                                                                                                                                   

t est le temps entre le début de l’impact de la force déstabilisatrice en unités de la série chronologique, sec. (min, hrs, jours, semaines, décennies, mois, années);

τ (tau) est le facteur de proportionnalité numériquement égal à la constante de temps de traitement, sec. (min, hrs, jours, semaines, décennies, mois, années).

Admettons maintenant que le prix du marché P(t) change de vitesse V(t) est proportionnel à la fois à la valeur de D(t) et au temps t:

Où :                                                                                                                                    (2)

k est le facteur de proportionnalité qui dispose d’une dimension 1/(temps)^2 ;

β = k*τ*D0 est le facteur de proportionnalité qui dispose de la dimension de la vitesse de variation du prix du marché.

L’incrément absolu ou la décrémentation du prix par unité de temps par le temps donné t qui est exprimé en H(t) est numériquement égal à V(t):

H(t) = V(t) = β*m

Sans aucun doute, en intégrant H(t) dans toute la gamme du temps t change, nous obtiendrons une valeur totale de la variation du prix du marché P(t) par le temps t depuis le début de sa déstabilisation:   

Où :                                                                                                                    (3)

Puisque sur la base de (3), il apparaît que lorsque t = ∞ s = 1, nous tirons une conclusion que:

P(∞) = β*τ = D0;

ou : β = D0/τ ;

En comparant la notation précédente de β avec le résultat que nous avons reçu, nous concluons que :

   k = 1/τ^2;

Maintenant, les rapports suivants sont vraies: 

         H(t) = D0*m;

         P(t) = D0*s.

Par conséquent, si des coefficients τ et β sont déterminés, il est possible d’estimer et de prévoir la valeur limite de variation de prix D0 à n’importe quel stade de la variation de prix, y compris au stade précoce. Toutefois, ces affirmations ne seront vraies que lorsque la condition du bilan matières sera remplie :

D(t) + H(t) + P(t) = D0                                                                                                                                     (4)

ou

   Par conséquent, l’exigence de normalisation doit être remplie:

      l + m + s = 1;                                                                                                                                          (5)

   Vérifions ce fait en utilisant des rapports (1-3):

     

Le respect précis de la condition de bilan matières (4) et la satisfaction de l’exigence de normalisation (5) indiquent que les hypothèses que nous avons formulées et les rapports proposés sont vraies.

Fonctions Transitoires pour un Modèle à Cellules Multiples 

En raisonnant de la même manière en ce qui concerne un modèle à cellules multiples de boîte noire composé de n cellules, nous obtenons les rapports suivants pour les fonctions D(t), H(t) et P(t) :

• D(t) = D0 * L;
• H(t) = D0 * M;
• P(t) = D0 * S;

Où :

                                                                                                         (6)

que j’ai appelé une « fonction de distribution exponentielle cumulative à deux paramètres » pour l’instant

                                                                                                 (7)

est une sorte de fonction de densité de probabilité de la distribution gamma ou de densité de probabilité de la distribution d’Erlang;

                                                                                                       (8)

est une sorte de fonction de distribution cumulative de la distribution Gamma ou fonction de distribution cumulative de la distribution d’Erlang,

•  t/τ, n sont des paramètres de distribution;
• 1 est une expression booléenne évaluée à « vrai » ;
• 0 est une expression booléenne évaluée à « false » ;

L’intégration (8) peut prouver que :

ou         

Par conséquent, selon (6-8), l’exigence de normalisation est remplie précisément dans ce cas également:

                                    L+M+S = 1;                                                                                                              (9)

J’ai appelé la fonction L une « fonction des périodes futures » puisque le prix du marché futur dépend de sa valeur, la fonction M une « fonction du présent » puisqu’elle détermine la variation du prix du marché par unité de la période donnée, et la fonction S une « fonction du passé » car le niveau de prix du marché atteint sur toute la période de temps depuis la déstabilisation des prix dépend de la valeur de cette fonction ce qui ne contredit pas la notion transitoire et élargit considérablement notre idée de ce qui se passe en termes de philosophie du problème.

En substituant n = 1 en (6-8), nous pouvons constater que les fonctions L, M et S deviennent respectivement des fonctions ℓ, m et s, nous examinerons donc uniquement les fonctions L, M et S comme les cas les plus généraux des fonctions de cette classe à des fins de prédiction.

Développement d’un Modèle de Régression Universel pour la Prévision des Prix du Marché sur la Base des Fonctions Transitoires Révélées

La dépendance du niveau de prix du marché P(h) sur le temps t depuis le début des observations sera exprimée comme suit:

Dans un modèle à cellule unique :

  (10a)

Dans un modèle à plusieurs cellules : 

  (10b)

Où :     P0 est le niveau de prix juste avant sa déstabilisation, c’est-à-dire au moment t = 0.

Les paramètres n et τ ainsi que le coefficient β sont déterminés en utilisant les valeurs réelles des prix du marché depuis le début de sa déstabilisation sur le marché, par laquelle nous analysons les variations du prix du marché f par unité de temps t qui peuvent être considérées comme la valeur de la dérivée de (10b). Nous pouvons constater que l’erreur d’accepter cette hypothèse est négligeable étant de quelques centièmes de pour cent de la valeur de change du prix. L’acceptation de cette hypothèse facilite considérablement le processus de détermination des paramètres ci-dessus et β coefficient.

De l’analyse de la fonction S, nous pouvons maintenant procéder à l’analyse de la fonction M:

                                                        (11)

En divisant les deux parties de (11) par t^n et en prenant le logarithme du rapport obtenu, on obtient une équation d’une droite en coordonnées semi-logarithmiques :

Maintenant, si les valeurs de la fonction f aux points de temps t correspondants sont connues, les paramètres n et τ ainsi que β coefficient peuvent être déterminés, comme suit:

                                                       (12)

                                                                                                        (13)

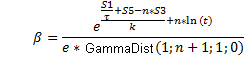                                                                                                                          (14)

Où :

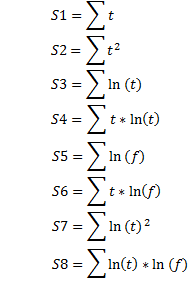
Les valeurs de la fonction f aux points de temps t correspondants ainsi que le temps t sont déterminés sur la base des valeurs réelles des prix du marché Р0, Р1,..., Рк par les points de temps һ0, һ1,..., һк à partir du début de la déstabilisation des prix du marché au moyen de la différenciation numérique et de l’intégration au milieu de l’intervalle:

f1 = (P1 - P0)/(һ1 – һ0);

f2 = (P2 – P1)/( һ2– һ1);

f3 = (P3 – P2)/( һ3– һ2); et ainsi de suite;

t1 = (һ0 + һ1)/2;

t2 = (һ1 + һ2)/2;

t3 = (һ3 + һ2)/2; et ainsi de suite.

Correction et Ajustement du Modèle 

L’essai pratique des équations (10a) et (10b) en tant que modèle de régression lors de l’utilisation des données réelles a montré que les valeursР(0) et D 0 doivent être corrigées, comme suit:

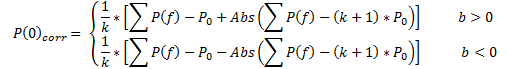                                                         (15)

                                                                                                     (16)

Où : Sf et Sr sont respectivement des aires de courbes réelles et théoriques;

∑Pf = P0+ P1 + P2 + ...+ Pk est la somme des valeurs réelles de prix;

                                                                                                      (17)

i = 0, 1,2,......k; 

k>2 est le nombre d’intervalles de temps pour lesquels l’écart de prix est déterminé;

b est le coefficient de l’équation de régression linéaire  qui détermine la direction de la tendance des données réelles.

Maintenant, l’équation de régression (10b) pour la prédiction du prix du marché P(t) prend la forme finale, comme suit:

                                                                                           (18) 

Test de modèle

Il s’est avéré que les valeurs de prix du marché P (t) calculées de cette manière et les valeurs de prix réelles Pf telles que fournies dans l’exemple de marché Forex ci-dessous, remplissent toujours entièrement et précisément la condition de bilan matières:

∑ P(t) = ∑ Pf.                                                                                                                                                                    (19)

Le fait que les sommes des valeurs réelles et théoriques du paramètre étudié, en particulier le prix du marché, correspondent absolument et exactement à n’importe quelle valeur d’argument, en particulier le temps, prouve que les calculs, les transformations et les hypothèses acceptés à la sortie de la fonction sont corrects et indique l’universalité du modèle de régression proposé.

L’image ci-dessous montre les résultats du traitement réel des données du marché Forex (période de 1 minute) d’une manière spécifiée en utilisant l’équation (18) où l’on peut noter une correspondance satisfaisante entre les valeurs réelles (Pf) (ligne jaune avec points rouges), les valeurs théoriques et de prédiction (P1) (ligne bleue) et les valeurs futures réelles qui n’ont pas été prises en compte à des fins de calcul (Pff) (ligne bleue avec points rouges) des cotations EUR / USD.

                                                                      
     

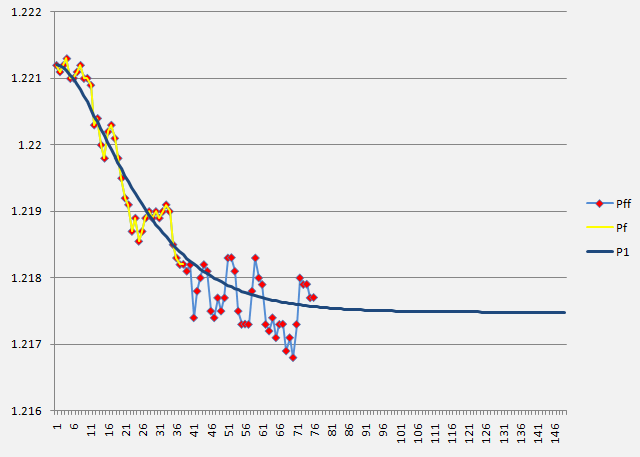
Conclusions

Nous avons identifié et proposé trois fonctions qui décrivent respectivement trois transitoires dynamiques, qui sont définis comme diverses modifications de la fonction de distribution Gamma déterminant le comportement du paramètre en cours d’ étude, en particulier le prix du marché, en fonction du temps dans le futur, le présent et le passé depuis le début de sa déstabilisation.

À la suite de l’analyse des processus spécifiés, le modèle de régression universel pour la prévision des prix du marché a été présenté; il peut servir de base pour le développement, par exemple, d’indicateurs de marché à des fins diverses, d’Expert Advisors optimisant l’activité des traders, de systèmes de trading automatisés et peut même donner lieu au développement d’un robot de trading - ROBOTRADER trading seul au profit d’une personne.

P.S. Tous les rapports et formules ainsi que les principales hypothèses et conclusions de cet article ont été vérifiés, élaborés, introduits et rendus publics dans la presse ouverte pour la première fois.

Références

1. A. E. Kotenko. Sur les Méthodes d’Analyse Technique et Fondamentale dans l’Etude de Marché Forex. Revue électronique « ENQUÊTÉ EN RUSSIE », http://zhurnal.ape.relarn.ru/articles/2003/151.pdf
2. V. N. Yakimkin. Forex Market – Your Way to Success, М., « Akmos-Media », 2001.
3. V. N. Likhovidov. Analyse Fondamentale des Marchés des Devises : Méthodes de Prédiction et de Prise de Décision. Vladivostok, 1999.
4. M. K. Bunkina. A. M. Semenov. Principes des Rapports Monétaires, М., Urait, 2000.
5. Jeffrey D. Sachs, Felipe B. Larrain. Macroéconomie dans l’Économie Mondiale. М., Delo, 1996.
6. Rhea, Robert. Dow Theory,- New York; Barrons, 1932.
7. Greiner, P. et H.C. Whitcomb: Dow Theory, New York: Investor’s Intelligence, 1969.
8. O. S. Gulyaeva. Gestion du Risque de Change sur la Base d’une Analyse de Pré-Prédiction des Taux de Change à l’Aide de Méthodes Fractales. Thèse de doctorat, Moscou-Tver, TvGU, 2008.