Comprobación estadística del sistema de gestión de dinero de Labouchere

Hay tres tipos de mentiras: las mentiras, las grandes mentiras y las estadísticas.

Introducción

Navegando por Internet durante el fin de semana, me he topado con un sistema de gestión de dinero del que nunca había oído hablar. Se llama el sistema de Labouchere o de cancelación (Forex Vacuum Cleaner System using the Labouchere, está en ruso). Puede encontrar la descripción en inglés aquí. Este sistema es una variación de la Martingala, ya que exige subir la apuesta después de perder y bajarla después de ganar. No obstante, es una versión menos agresiva, ya que en lugar de duplicar las apuestas se incrementan en cierta cantidad.

Estos son algunos extractos que describen las propiedades del sistema y que me han realmente intrigado:

• "Por lo tanto, tenga en cuenta que la cantidad de operaciones rentables tiene que ser superior al 33-40% para que el sistema funcione correctamente y que hayan ganancias".  Es una afirmación muy contundente. Sin embargo, no está claro por qué el rango del porcentaje inicial es tan amplio; de 33% a 40%.

• "Tenga en cuenta que este método puede ser considerado fraudulento en las salas de juego".  ¿De verdad? Entonces, ¡puede que funcione de verdad!

• "Pero el principio sigue siendo el mismo; el 33% de las ganancias compensa el 66% de las pérdidas. Así que si quiere utilizar este sistema de gestión de dinero en el trading Forex real, necesita un sistema de trading con una probabilidad de ganar del 50% y un factor de beneficio >=1".

De hecho, el artículo que he encontrado afirma que necesitamos un sistema de trading donde las ganancias son iguales a las pérdidas y que la probabilidad de ganar es del 50% (o incluso "superior al 33%"). Si dispone de este sistema, ¡el método de Labouchere puede hacer que sea rentable fácilmente! Entonces, ¿por qué tenemos que buscar un sistema con una previsión matemática positiva si existe la posibilidad de trasladarlo a una zona positiva? Después de todo, no es demasiado difícil desarrollar un sistema de trading con el 47% de ganancias...

Veamos cómo nos afecta el sistema Labouchere.

En general, se supone que la apuesta mínima es igual a una unidad. Si ganamos, el tamaño de la apuesta no cambia, mientras que nuestro balance aumenta ligeramente.

Si perdemos, se incrementa nuestra apuesta de una unidad; hasta 2, y añadimos el tamaño de la apuesta perdedora a la línea:

-1

Si ganamos en este punto, añadimos 2 a nuestra línea:

-1 2

Después eliminamos estos números, ya que hemos recuperado lo que hemos perdido (en otras palabras, hemos incrementado nuestro balance de 1 en una serie de dos apuestas).

Veamos ahora una serie perdedora más prolongada.

-1

Apostamos 2. Perdemos:

-1 -2

Apostamos 3. Perdemos:

-1 -2 -3

Apostamos 4. Perdemos:

-1 -2 -3 -4

Apostamos 5. Perdemos:

-1 -2 -3 -4 -5

Apostamos 6. perdemos otra vez:

-1 -2 -3 -4 -5 -6

Apostamos 7. Al final ganamos:

-1 -2 -3 -4 -5 -6 +7

Así que eliminamos "-1", "-6" y "+7", ya que nuestra apuesta ganadora ha compensado dos apuestas perdedora. La siguiente apuesta es la suma del primer y último de los valores que quedan en la línea, es decir, 7 otra vez. Si ganamos:

-2 -3 -4 -5 +7

Eliminamos "-2", "-5" y "+7". El tamaño de la siguiente apuesta es de nuevo la suma del primer y último de los valores que quedan en la línea. Sí, es 7 otra vez (algunos seguidores del método recomiendan añadir 1 a esta apuesta para obtener el mínimo de beneficio en lugar de 0, si tiene un poco de suerte). Si ganamos:

-3 -4 +7

Eliminamos todos los números que quedan en la línea puesto que hemos recuperado todas nuestras pérdidas.

Si se produce una pérdida en alguna etapa intermedia, se añade el tamaño de esta pérdida a la línea, y la siguiente apuesta será igual a la suma del primer y último valor de la línea.

¿Cuáles son las primeras conclusiones?

1. Una serie de 6 pérdidas se compensa, de hecho, por una serie de 3 ganancias (pero en realidad tienen que ser series; comentaremos esto más adelante). A primera vista, el sistema hace que sea realmente fácil evitar pérdidas en el mercado.

2. El tamaño de la apuesta se incrementa mucho más despacio en comparación con la Martingala. Si hubiéramos utilizado estas series con el sistema Martingala original, el tamaño de la última apuesta sería 64 veces superior al tamaño de la apuesta inicial.

3. La pérdida total de depósito (la suma de las apuestas perdedoras) en el ejemplo anterior es igual a 21 unidades sólo, mientras que en la Martingala sería de 63.

4. Unos cálculos sencillos muestran que en el caso de una apuesta inicial igual al 1% del depósito tenemos que sufrir 13 pérdidas seguidas para perder todo nuestro fondo y 44 pérdidas seguidas si es igual al 0,1% del depósito. Y puede pensar: "¿44 pérdidas seguidas con una probabilidad de ganancias del 50%? ¡La probabilidad es muy pequeña! ¡Es más probable que me caiga encima un meteorito! ¡Esta probabilidad me conviene!", etc).

5. Puede encontrar fácilmente varios estudios dedicados a las pérdidas y los riesgos del sistema de Martingala. De hecho, puede comprobar estas pérdidas por sí mismo haciendo unos sencillos cálculos con un papel y un bolígrafo. No obstante, no he sido capaz de encontrar estudios similares para el sistema de Labouchere.

6. El sistema de apuestas parece muy complicado, lo que dificulta el cálculo matemático de sus previsiones.

Pero volvamos a nuestras series de apuestas perdedoras. Supongamos que nuestras 6 pérdidas en una línea fueron seguidas de 2 ganancias en lugar de 3. Entonces nuestra línea se quedaría así:

-3 -4

Apostamos 7 y perdemos:

-3 -4 -7

Apostamos 10 (tenga en cuenta que mientras perdemos, el tamaño de la apuesta se incrementa de 3 unidades en lugar de 1 unidad, haciendo peligrar nuestro depósito). Perdemos otra vez:

-3 -4 -7 -10

Tenemos que apostar 13 ahora.

Por lo tanto, el sistema hace que incrementemos nuestras apuestas con más de 1 unidad en caso de pérdidas repetidas. Parece que es el único modo de compensar por completo las pérdidas. Nuestro depósito puede estar realmente en peligro en este punto, ya que necesitamos unas series de ganancias para compensar las pérdidas. El cálculo de la previsión sobre el papel puede parecer demasiado complicado o al menos demasiado aburrido...

¿Le interesa saber de qué es capaz este sistema? Si la respuesta es sí, vamos entonces a profundizar en la materia.

Planteamiento de la tarea: El qué y el cómo

La cuestión más importante es si el sistema de gestión de dinero de Labouchere es realmente capaz de trasladar una previsión matemática (en particular a una zona positiva). Por supuesto, el texto mencionado sobre el 33% de ganancias y donde las pérdidas son iguales a las ganancias suena un poco raro. Pero, ¿tal vez el 49% o el 50% de ganancias sea suficiente? Si no es así, ¿qué otras ventajas puede tener el sistema de Labouchere?

Usaremos las estadísticas, lo que significa que tenemos que desarrollar un programa en MQL (en MQL4, ya que aún no controlo muy bien MQL5). Dejaremos que el programa lleve a cabo millones de transacciones y que "funda" miles de depósito sin preocuparnos por nuestros fondos. Si el resultado del programa es satisfactorio, sería posible implementar el algoritmo en el trading real.

Se ha desarrollado el sistema de Labouchere suponiendo que pérdida = ganancia. Se puede adaptar a otras proporciones, pero esto no sería apropiado. Si el sistema influye en la previsión matemática con pérdida = ganancia, también lo puede hacer con otras proporciones. Si no puede hacerlo, entonces estamos simplemente perdiendo el tiempo con una posible adaptación.

Por otra parte, podemos imaginar más fácilmente un sistema con pérdida = ganancia y una condición de equilibrio de las apuestas ganadoras del 50%, ya que estamos todos familiarizados con el lanzamiento de una moneda. Por lo tanto, llamaremos a nuestro programa CoinTest.

En primer lugar, tenemos que describir las principales características de nuestro programa:

1. Tenemos que poder modificar la probabilidad de ganancia. La proporción 50/50 es sólo un caso particular de la condición de equilibrio.

2. Tenemos que poder establecer el nivel de riesgo. El sistema Labouchere funciona con un tamaño de apuesta fijo. Si ajustamos nuestra apuesta inicial al tamaño de nuestro depósito, el sistema ya no funciona puesto que nuestro depósito no volverá nunca a su estado inicial después de eliminar todos los valores de la línea. Podemos volver a calcular el tamaño de la apuesta después de producirse una pérdida, pero obtendremos valores fraccionarios que van a dificultar el trabajo. Así que vamos a utilizar dos variables para establecer el riesgo; el depósito inicial y la apuesta inicial.

3. Hay que establecer el número máximo de transacciones por depósito. Tiene que ser lo suficientemente grande para poder averiguar si vamos a perder el depósito, incluso con un riesgo inicial muy bajo. Después de todo, si el depósito sigue creciendo, puede ser infinito y nunca sabremos el resultado.

4. Tenemos que ser capaces de analizar los resultados de una serie de transacciones en un sólo depósito, tanto para la depuración del programa como para replantear nuestra lógica de trading. Nos puede venir muy bien enviar los resultados a un archivo.

5. Después de escribir con éxito el código para una sola ejecución en un depósito, tenemos que recoger las estadísticas de las series de ejecuciones en los depósitos individuales y (lo ideal) con distintos parámetros. Como puede imaginar, el resultado de una sola prueba no significa nada en este contexto. Los resultados estadísticos se envían también al archivo. Ya no nos hace falta analizar el historial de los depósitos individuales.

Se puede utilizar nuestro sistema de selección del tamaño de la apuesta en el trading real, por lo que debemos hacer que sea una clase.

La apertura real de las transacciones en MetaTrader no es útil para nosotros en este momento y es muy costosa en términos de recursos computacionales. Sólo tenemos que arreglar los resultados de las transacciones aleatorias mediante un tamaño de lote requerido y una probabilidad de ganancia predeterminada. En base a esto, vamos a desarrollar un script, ya que este tipo de programas en MQL es perfecto para una sola ejecución en comparación con los Asesores Expertos y los indicadores.

Comprobación estadística de la calidad del generador del número pseudoaleatorio

La calidad del generador del número pseudoaleatorio (GNPA) es de extrema importancia para nosotros, ya que se va a utilizar para determinar el resultado de cada transacción (pérdidas/ganancias). La precisión de la distribución de una serie de pérdidas/ganancias larga es aún más crítica. Trataremos de evaluar la distribución sin recurrir a las complicadas teorías de las estadísticas matemáticas.

Este artículo no pretende ser un estudio detallado de la calidad del GNPA (de lo contrario, tendríamos que realizar 15 pruebas). Lo que más nos interesa son las propiedades del GNPA que afectan a los resultados de la prueba del sistema Labouchere y que no exigen procedimientos de comprobación muy complejos.

MetaTrader dispone de la función GNPA estándar MathRand(). Se inicializa la secuencia del GNPA mediante la función MathSrand().

Vamos a escribir un pequeño script (RandFile) para comprobar la calidad del GNPA estándar. El script tiene 2 parámetros:

• El número (en millones) de palabras aleatorias de 32 bits que debe generar (una palabra de 32 bits por 3 llamadas de la función MathRand() proporciona 15 bits significativos). La unidad de medida habitual es el millón decimal en lugar de 2 elevado a 20, ya que vamos a analizar los resultados visualmente también.

• El parámetro lógico CalcSeries (si hay que calcular la distribución de las longitudes de las series de bits similares).

El cálculo de la distribución de las longitudes de las series de bits requiere muchos recursos (multiplica el tiempo de ejecución del script por 10). Por lo tanto, se ha puesto como una opción separada.

El script genera los siguientes resultados:

• el tiempo (time) de cálculo (aparece en el diario);
• la cantidad de bits "1" detectados entre todos los bits generados (aparece en el diario);
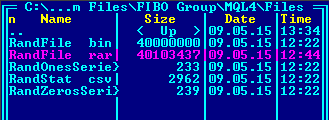
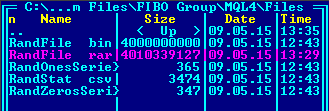
• el archivo RandFile.bin — archivo binario con el resultado del GNPA;
• el archivo RandStat.csv — archivo de registro que contiene las tasas de aparición de ciertos bytes;
• el archivo RandOnesSeries.csv — archivo de registro que contiene las longitudes de las series de bits "1";
• el archivo RandZerosSeries.csv — archivo de registro que contiene las longitudes de las series de bits "0";

Vamos a generar 3 conjuntos de pruebas de longitudes diferentes:

• 10 millones de palabras de prueba de 4 bytes cada una (40 millones de bytes en total);
  
• 100 millones de palabras de prueba de 4 bytes cada una (400 millones de bytes en total);
• 1000 millones de palabras de prueba de 4 bytes cada una (4000 millones de bytes en total);

Vamos a comprobar ahora los siguientes parámetros:

1. Capacidad de compresión de los archivos que contienen los datos aleatorios mediante WinRAR con las opciones de compresión más altas. Los datos aleatorios de alta calidad no se comprimen. Que los archivos no se puedan comprimir no quiere decir necesariamente que contienen datos aleatorios de alta calidad. Pero si se pueden comprimir, esto quiere decir que los datos tienen regularidad estadística.

   

   

   

2. Cantidad de bits "1":
   

   	Equilibrio	Real	Desviación absoluta	Desviación, %
   10М	160 000 000	160 004 431	4 431	0,0027694
   100М	1 600 000 000	1 599 978 338	21 662	0,0013539
   1000М	16 000 000 000	15 999 996 180	3 820	0,0000239

3. Tasa de aparición de los valores de ciertos bytes in archivos aleatorios:

   
   

   
   

   
   

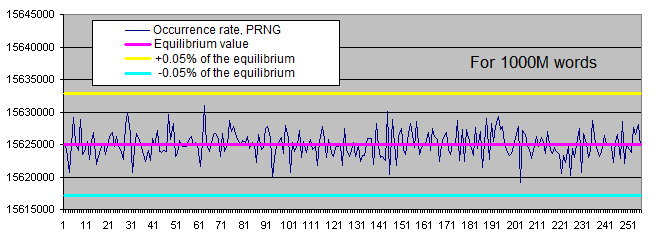
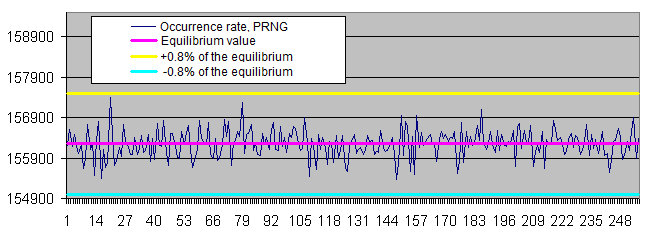
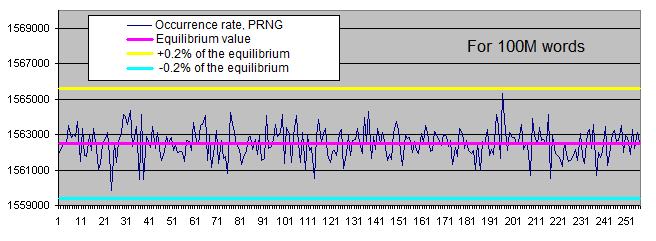
4. Longitudes de series de bits idénticos. Vamos a generar dos gráficos para cada tamaño:

   • el primero muestra la cantidad real de series de bits idénticos detectados de una longitud concreta, así como el valor de equilibrio de la cantidad de series de esta longitud (en la escala logarítmica);
   • el segundo muestra el porcentaje de la desviación de la cantidad real de las series de bits idénticos detectados desde el valor de equilibrio (en escala logarítmica).

   La escala lineal del gráfico no nos conviene debido a la gran dispersión de los valores (hay valores que van desde 1 hasta 4 000 000 000 o desde 0,00001 hasta 6000 en el mismo gráfico). Por otra parte, el gráfico muestra el valor de equilibrio del número de series largas en una escala logarítmica en forma de línea recta, es decir, mientras la longitud de las series se aumenta de 1, la probabilidad de que aparezca se reduce a la mitad.

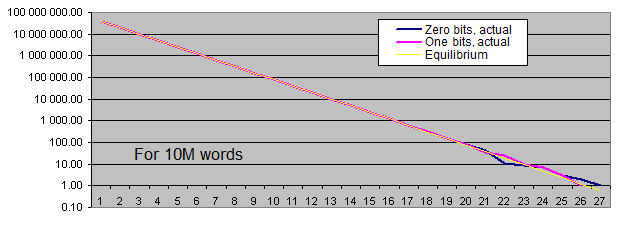
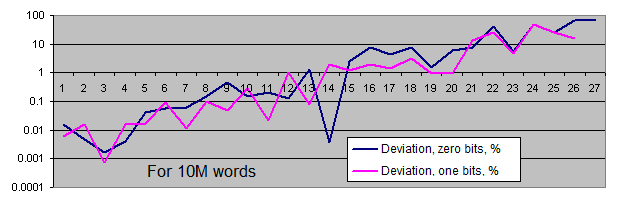
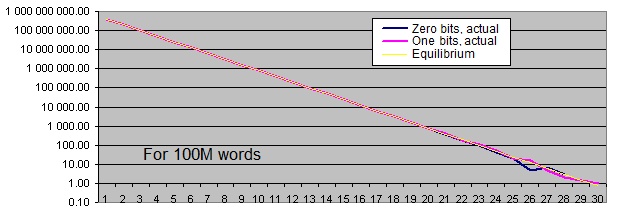
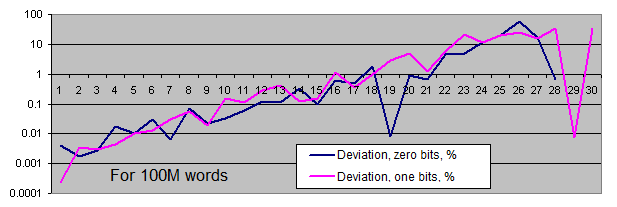
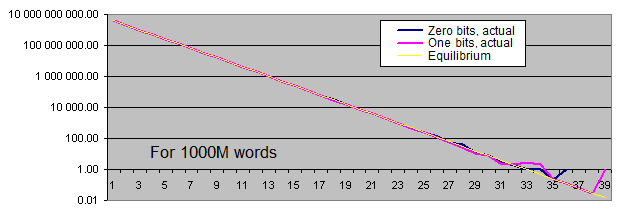
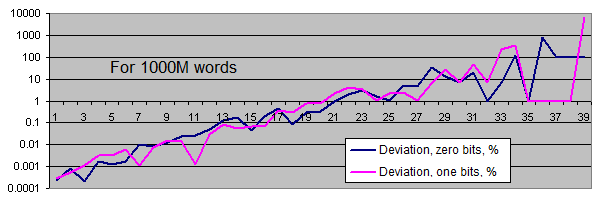
¿Qué conclusiones se pueden sacar de estas pruebas?

• La eficiencia del GNPA es aceptable para nuestra tarea.

• Copiar los archivos que contienen los resultados de funcionamiento del GNPA no conduce a su compresión.

• El número de bits "0" y "1" correspondientes al valor equidistante. La desviación desde el equilibrio (en porcentaje) disminuye a medida que aumenta el tamaño de la muestra.

• La distribución de la tasa de aparición de ciertos bytes en los resultados de funcionamiento del GNPA fluctúa dentro de un intervalo estrecho alrededor del equilibrio. La dispersión de la tasa de aparición disminuye a medida que aumenta el tamaño de la muestra.

• Se desvía la tasa de aparición de las series de bits idénticos del equilibrio sólo si las series son bastante largas (es muy raro). Con el incremento de la longitud de la muestra, la tasa de aparición real del "punto de desviación" se aleja del punto de equilibrio en el sentido del incremento de la longitud de las series y siempre alrededor de 100 inclusiones para toda la secuencia.

Por lo tanto, no hemos encontrado ningún fallo estadístico importante en el GNPA estándar que pueda distorsionar los resultados de las pruebas, incluso con secuencias de aproximadamente 3000 millones de generaciones (una palabra de 32 bits requiere 3 generaciones).

Escribir la clase CLabouchere para gestionar el tamaño de la posición

La clase CLabouchere ha resultado ser muy pequeña. Su interfaz se compone de dos funciones contenedoras para ajustar/recibir el tamaño del lote inicial y dos funciones de trabajo; para ajustar el resultado de una transacción y recibir el tamaño de la posición actual, así como para reiniciar el estado inicial:

// Labouchere money management.
// Take/stop is assumed = 1/1.
class CLabouchere
{
        private:
        protected:
                // Initial lot. By default - 0.1.
                double p_dStartLot;

                // The string where numbers are stored according to Labouchere
                double p_dLotsString[];
        public:
                void CLabouchere();
                void ~CLabouchere();

                double GetStartLot() {return p_dStartLot;};
                void SetStartLot(double a_dStartLot) {p_dStartLot = a_dStartLot;};

                // Return a lot that is to be used during the next market entry
                double GetCurrentLot();

                // Write the current trade result - take (true) or stop (false)
                void SetResult(bool a_bResult);

                // Reset to the initial state except for the initial lot
                void Init() {ArrayResize(p_dLotsString, 0);};
};

Escritura del script. Evaluación preliminar

Es el momento de escribir un script con un centenar de cadenas. Los parámetros de entrada son los siguientes:

//--- input parameters
input int RepeatsCount=100000;
input int StartBalance = 10000;
input int Take = 50;
input double SuccessPercent = 50.0;
// If true, SuccessPercent is ignored
input bool FiftyFifty = true;

El script realiza una serie de transacciones hasta que se pierda depósito o se alcance RepeatsCount.

Para el caso de la proporción pérdida/ganancia = 50/50 se establece un parámetro independiente. En este último caso, se usan los bits "1" del número pseudoaleatorio como resultados del lanzamiento de una moneda. De lo contrario, se calcula el valor límite de ganancia/pérdida y se compara con el número aleatorio. Se ha implementado el parámetro independiente para el caso con la proporción 50/50 debido a que el ciclo de trabajo de los bits "1" del GNPA nos conviene, aunque no hemos evaluado el ciclo de aparición de los valores que exceden el valor límite.

Los ajustes por defecto son los siguientes:

• depósito inicial: 10 000;
• apuesta inicial: 50 (0.5% del depósito inicial).

Aproximadamente, en la décima ejecución del script obtenemos un resultado impresionante; el depósito en el paso 2335 es igual a 46 300. Sin embargo, a partir del paso 2372 empiezan las pérdidas.

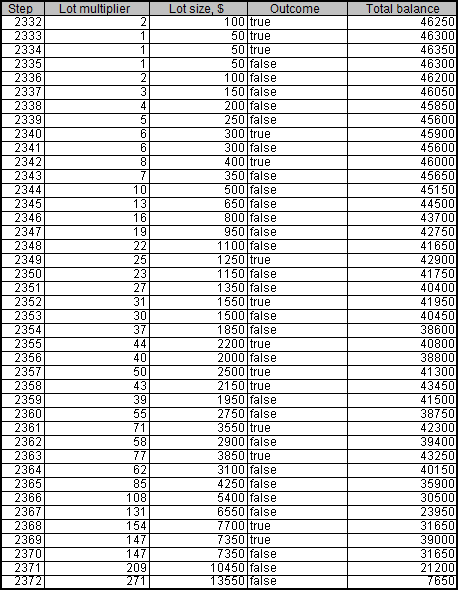
Es así como se ve en el gráfico:

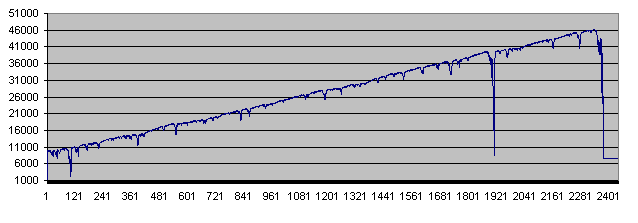
Como podemos observar, el balance cae a niveles críticos dos veces antes de que desaparezca el depósito del todo.

En algunos casos, se ha liquidado el depósito dentro de las primeras docenas de transacciones, y no hubo ningún máxima vida útil de 100 000 transacciones.

Mientras estaba probando varios parámetros se me ocurrieron las siguientes modificaciones:

• Sería razonable añadir un parámetro que determina la cantidad de fondos que se retiran de la cuenta de trading. Si tratamos de retirar fondos que superan el depósito inicial antes de su desaparición, nuestro depósito inicial se convierte simplemente en una pérdida predecible. Así que se ha implementado el nuevo parámetro llamado PocketPercent. Define el porcentaje de las transacciones rentables que retiramos de la cuenta de trading y metemos en el "bolsillo". Está prohibido sacar dinero del "bolsillo", sólo los fondos que están en la cuenta de trading están expuestos al riesgo. Después de todo, es así en la vida real.

• Por supuesto, hay que ejecutar el depósito varias veces en un bucle (sería muy aburrido ejecutar un tarea cientos de veces manualmente). También tenemos que modificar un par de parámetros – PocketPercent y Take (el tamaño de la apuesta inicial), así como calcular los resultados promedios (fondos del "bolsillo" y fondos del depósito, ya que el depósito nunca al cero, sólo baja a un punto en el cual es imposible realizar la siguiente transacción).

• Debemos tener dos versiones del script: la primera lleva a cabo las ejecuciones repetidas sin la necesidad de escribir los detalles del trading en un archivo, mientras que la segunda funciona de manera inversa. Las ejecuciones repetidas implican la necesidad de utilizar el código objeto. Para ello, desarrollamos el "código de funcionamiento" como clase CCoinTest, mientras simplificamos los scripts al máximo.

El código del script para una pasada es muy sencillo y está completo a continuación (todo el trabajo, incluso la escritura de los detalles de la transacción en un archivo, lo hace la clase CCoinTest):

#include <CCoinTest.mqh>

//--- input parameters
input int RepeatsCount=100000;
input int StartBalance = 10000;
input int Take = 50;
input int PocketPercent = 10;
input double SuccessPercent = 50.0;
input string S2 = "If true, SuccessPercent is ignored";
input bool FiftyFifty = true;
input string S3 = "If true, use a fixed lot instead of Labouchere";
input bool FixedLot = false;

void OnStart()
{
        MathSrand(GetTickCount());

        CCoinTest Coin;

        Coin.SetRepeatsCount(RepeatsCount);
        Coin.SetStartBalance(StartBalance);
        Coin.SetTake(Take);
        Coin.SetPocketPercent(PocketPercent);
        Coin.SetSuccessPercent(SuccessPercent);
        Coin.SetFiftyFifty(FiftyFifty);
        Coin.SetFileName("Coin.csv");
        Coin.SetFixedLot(FixedLot);

        Coin.Go();
}

Después de añadir el "bolsillo", el gráfico del funcionamiento del sistema ha cambiado un poco (en el siguiente ejemplo, se retira el 40% del beneficio):

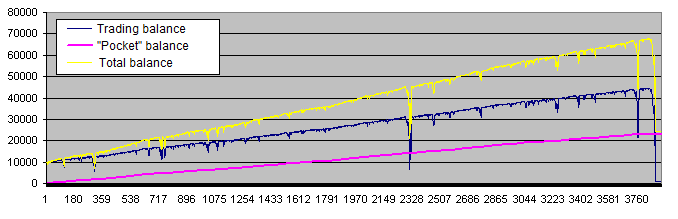
La línea morada (balance del "bolsillo") es muy parecida al gráfico de la cuenta de trading perfecta con la que sueñan todos los traders. Pero en realidad, tenemos que fijarnos más en la línea amarilla (balance total de la cuenta de trading y del "bolsillo"), que no es tan perfecta. Por otra parte, los siguientes gráficos son más habituales:

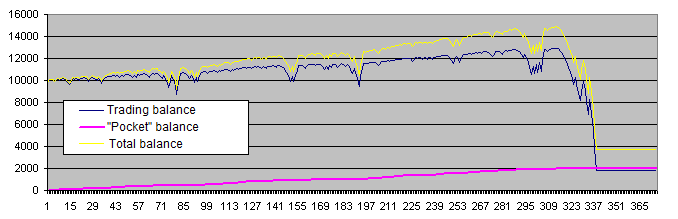
Estas son las conclusiones que hemos sacado en esta etapa:

• El sistema muestra realmente el comportamiento pensado por el autor: las pérdidas se compensan a menudo y el depósito es cada vez mayor.

• A veces, este intento acaba en un fracaso total. De hecho, el sistema sólo dispone de dos opciones después de producirse una pérdida; se puede compensar la pérdida o perder todo el depósito.

• Cuanto más tiempo dura el depósito, mayores son los máximos que puede alcanzar.

• La apuesta inicial de este ejemplo es el 0,5% del depósito inicial (50 de 10 000). En el primer ejemplo, el nivel básico de riesgo ha disminuido de 0,1% aproximadamente (se ha incrementado el depósito 4,5 veces y la apuesta inicial sigue siendo la misma). Sin embrago, esto no ha permitido evitar la desaparición del depósito.

Evaluación final para distintos valores de probabilidad. Comparación de los resultados del sistema de Labouchere y del sistema de apuesta fija

Hemos llegado a la parte más emocionante; recoger los resultados de varios experimentos. Estamos a punto de averiguar si las operaciones con ganancias pueden compensar las pérdidas. ¿Es posible que el algoritmo sea más eficiente si se disminuye (ya que costará más perder el depósito) el tamaño de la apuesta inicial o se incrementa? ¿Qué porcentaje de ganancias debe derivarse de la cuenta de trading? ¿Cuál es la diferencia entre el sistema de Labouchere y el sistema de apuesta fija? ¿Y qué pasaría si el sistema original tiene una previsión matemática positiva (hay más ganancias con la "moneda")? Como puede ver, hay muchas preguntas a las que debemos responder de manera adecuada.

El script para la ejecución de los depósitos en el bucle con distintos parámetros está compuesto por cerca de 100 cadenas. Sólo voy a mostrar algunos fragmentos.

Los parámetros de entrada:

//--- input parameters
input int RepeatsCount=100000;
input int StartBalance = 10000;
input string S1 = "Amount of deposits lost";
input int Deposits = 100;
input double SuccessPercent = 50.0;
input string S2 = "If true, SuccessPercent is ignored";
input bool FiftyFifty = true;
input string S3 = "If true, use a fixed lot instead of Labouchere";
input bool FixedLot = false;

Las matrices que contienen el valor de la apuesta inicial y el porcentaje de ganancias colocadas en el bolsillo":

// PocketPercent array
int iPocketPercents[24] = {1, 2, 3, 5, 7, 10, 15, 20, 25, 30, 35, 40, 45, 50, 60, 70, 75, 80, 85, 90, 95, 97, 98, 99};

// Initial bet array
int iTakes[15] = {5, 10, 15, 20, 50, 75, 100, 150, 200, 300, 400, 500, 1000, 2000, 3000};

Como se puede observar, el tamaño de la apuesta inicial oscila entre 5 (0,05% del depósito inicial) y 3000 (30% del depósito inicial). Los fondos colocados en el "bolsillo" varían del 1% al 99%. Se establecen los parámetros con un margen de seguridad que se solapa con los límites razonables en ambas direcciones.

Por lo tanto, el espacio de búsqueda es bidimensional. Hay 360 puntos discretos (24 * 15) en este espacio. Se calcula el balance total promedio (fondos del "bolsillo" + fondos de la cuenta de trading) y el número medio de transacciones antes de la pérdida del depósito (vida útil del depósito) para cada punto en base a los resultados de las series. Se establece el número de depósitos por series mediante el parámetro Deposits.

Los resultados del cálculo del espacio bidimensional son tridimensionales, es decir que es difícil visualizarlos con herramientas bidimensionales. Para solucionar este problema, vamos a dibujar simplemente los gráficos bidimensionales con el eje X para representar los números de serie de los puntos que se encuentran en el espacio de búsqueda (del 0 al 359). Si es necesario, vamos a proporcionar por separado algunos valores de Takes y PocketPercent.

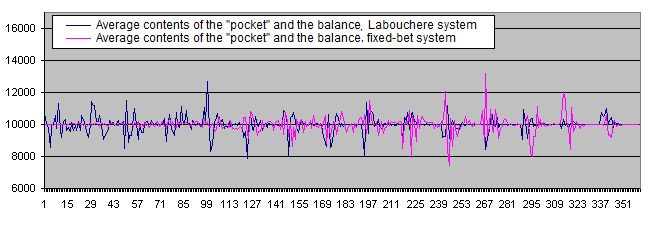
Después de ejecutar 100 depósitos, el balance promedio es el siguiente:

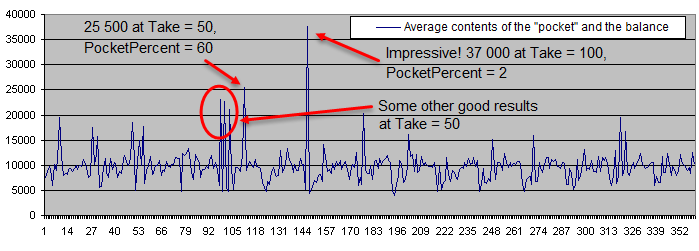
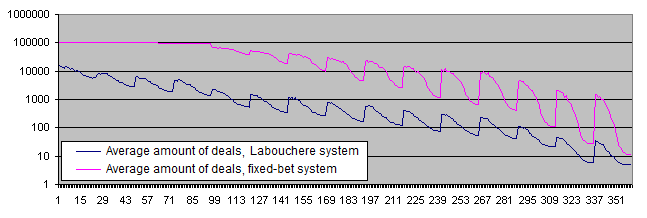
El siguiente gráfico representa el vida útil del depósito (en la escala logarítmica):

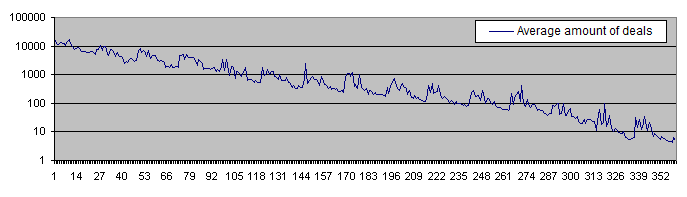
La vida útil del depósito supera 10 000 transacciones con un riesgo inicial del 0,05% y disminuye progresivamente hasta llegar a menos de 10 transacciones con un riesgo inicial del 30%. El elevado valor de PocketPercent reduce también la cantidad media de las transacciones antes de la pérdida del depósito. Esto era de esperar.

Podemos seleccionar algunos puntos clave en el gráfico que muestra el promedio de la cantidad del "bolsillo" y del balance. Cuatro de estos puntos se ubican muy cerca los unos de los otros, así que espero que podamos encontrar la zona óptima. Ahora vamos a calcular los resultados para Deposits = 1 000 y superponerlos en el mismo gráfico:

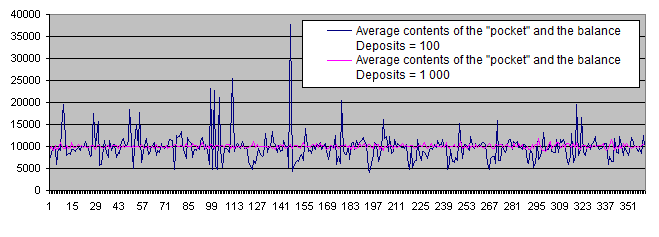
Como podemos ver, la supuesta zona óptima se ha simplemente desvanecido bajo la presión de una cantidad suficientemente grande de datos estadísticos. Independientemente de cualquier parámetro, el gráfico fluctúa de manera aleatoria cerca del balance inicial de 10 000.

Por lo tanto, Deposits = 100 no es suficiente. Se realizarán todos los experimentos posteriores con Deposits = 1 000.

Vamos a mostrar los resultados del sistema de Labouchere y el sistema de apuesta fija en el mismo gráfico:

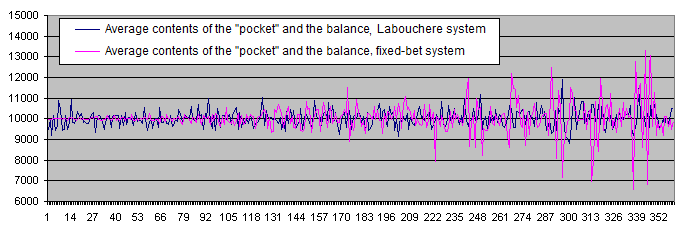
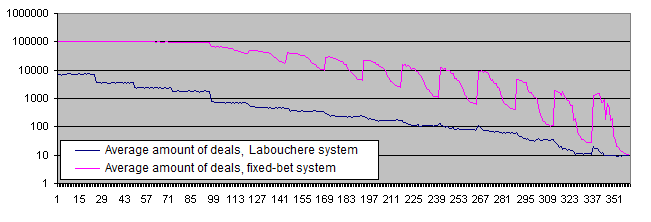
Gráfico de la vida útil del sistema de Labouchere y del sistema de apuesta fija:

Conclusiones:

• Los resultados financieros del sistema de Labouchere y del sistema de apuesta fija no coinciden.

• A diferencia del sistema de Labouchere, el sistema de apuesta fija presenta una mayor dispersión de datos alrededor de la media. Parece que los valores fijos de Deposits no se están en armonía con el comportamiento estadístico del sistema con apuesta fija.

• La vida útil del depósito es mucho más corta con el sistema de Labouchere (10 veces y más con la mayoría de los parámetros y hasta más de 100 veces con algunos parámetros). En el caso de un nivel de riesgo bajo, podemos ver que el gráfico alcance el límite establecido mediante el parámetro RepeatsCount (el valor por defecto es 100 000). Estos resultados confirman parcialmente la opinión generalizada que dice que los sistemas capaces de aumentar el riesgo son peligrosos para el depósito. Estos sistemas reducen la vida útil del depósito, aunque todavía no hemos detectado ningún riesgo en los resultados financieros (por lo menos en el promedio y siempre y cuando se retira algún porcentaje de las ganancias).

Vamos a añadir al script un nuevo parámetro que nos permite recoger datos estadísticos suficientes para evaluar el comportamiento de las zonas de alto riesgo:

input string S2 = "Minimum amount of deals per each pair of parameters";
input int MinDeals = 10000000;

Si tenemos menos de 10 millones de transacciones por 1000 depósitos perdidos, debemos continuar.

En consecuencia, los datos del gráfico son menos dispersos:

Ahora vamos a comprobar el funcionamiento de los sistemas con una probabilidad inicial distinta a 50/50.

Vida útil del depósito:

¿Qué podemos observar en estos gráficos?

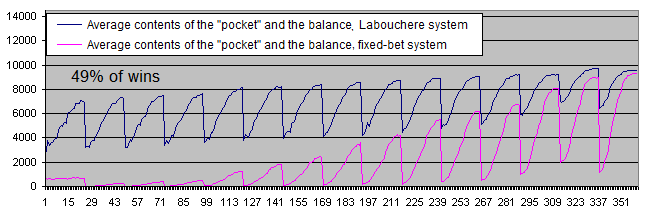
• En el caso del 49% de transacciones rentables, ninguno de los sistemas es rentable.

• Los resultados financieros del sistema de apuesta fija son muy bajos, lo que demuestra que la retirada de las ganancias al "bolsillo" es mucho más práctica con el sistema de Labouchere en el caso de un porcentaje de ganancias inferior al 50%. Se transfieren los fondos al "bolsillo" sólo después de salir de la zona de pérdidas.

  A diferencia del sistema de apuesta fija, el sistema de Labouchere es capaz de establecer nuevos registros una y otra vez (siempre y cuando haya suficiente dinero para hacer otra apuesta) incluso con un porcentaje inferior al 49%. Si el depósito cae rápidamente, los traders humanos no van a llevar a cabo 100 000 o ni siquiera 10 000 transacciones hasta la pérdida total de su depósito. Seguro que detienen el trading mucho antes. El algoritmo del sistema de apuesta fija no permite esto. En este sentido, el algoritmo del sistema de Labouchere es mucho más parecido al razonamiento humano, puesto que se comportaría igual que un trader estimulado por nuevos registros y operando así hasta la pérdida total del depósito.

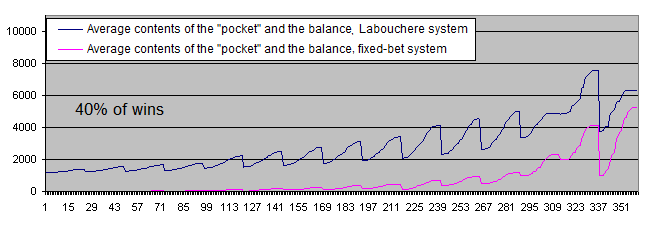
¿Recuerda el artículo que mencioné en la introducción? Decía que el sistema funcionará incluso con un porcentaje del "33-40%" de ganancias. Vamos a comprobar el límite superior (40%) de este rango por diversión sólo:

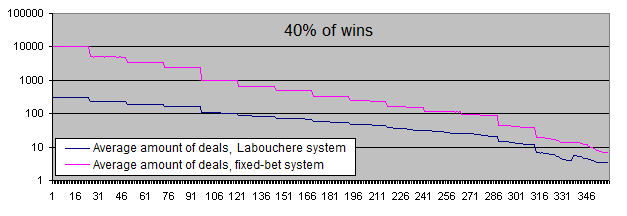
Vamos a considerar ahora la previsión matemática positiva del sistema inicial (más del 50% de ganancias).

Tenemos que mostrar los gráficos del balance en una escala logarítmica incluso con un porcentaje del 51%.

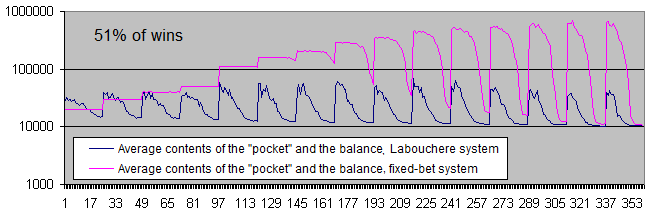
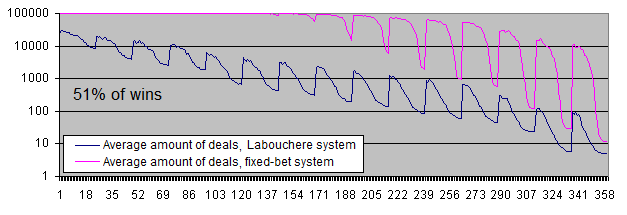
Conclusiones:

• Ambos sistemas se han desplazado a unas previsiones positivas.

• En el caso de un nivel de riesgo bajo, el sistema de apuesta fija tiene una "persistencia" ilimitada. En otras palabras, es casi imposible perder el depósito.

• Sin embargo, el sistema de Labouchere si que puede perder todo el depósito (pero no hay que olvidar el "bolsillo").

• El sistema de apuesta fija genera 10 veces más de beneficio que el e Labouchere con la mayoría de los parámetros (y a veces hasta 17 veces con algunos parámetros).

La mayoría de los lectores puede pensar que el sistema de apuesta fija es superior al sistema de Labouchere. ¡No sólo protege el depósito mucho mejor, sino que logra un beneficio 10 veces mayor! Por desgracia, las estadísticas les han engañado las estadísticas.

El sistema de apuesta fija está sometido a una limitación de 100 000 transacciones por depósito. Si el parámetro RepeatsCount fuera 200 000, el sistema hubiera generado 2 veces más de beneficio. "¡Pero esto es maravilloso!" dirían los lectores engañados por las estadísticas. Y una vez más estarán equivocados.

Eche un vistazo al gráfico del beneficio promedio que han generado los sistemas por transacción (en la escala logarítmica):

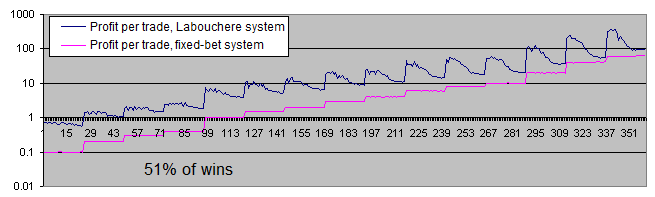
El gráfico del beneficio por transacción expresado en porcentaje de la apuesta inicial ofrece una imagen aún más clara:

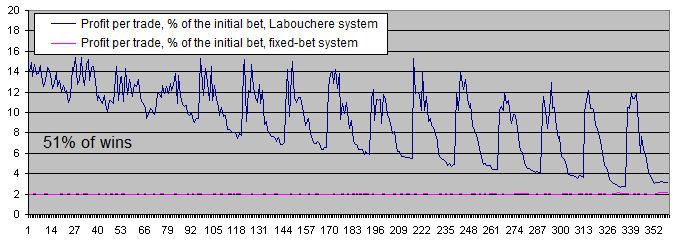
Conclusiones:

• El sistema e apuesta fija alcanza el 2% de la apuesta inicial por transacción. Esto es totalmente coherente con la teoría, ya que la proporción ganancia/pérdida es igual a 51/49. En otras palabras, las ganancias superan las pérdidas por 2.

• El sistema de Labouchere genera más beneficio incluso con los parámetros menos favorables. Y si se establecen los parámetros correctamente, puede llegar a generar un beneficio de 6 o 7 veces mayor.

Por lo tanto, si dispone de un tiempo ilimitado, puede que tenga éxito con el sistema de Labouchere.

Puede argumentar que quizá podemos sustituir el sistema de apuesta fija por el sistema de porcentaje de riesgo fijo de modo que aumente el beneficio por transacción (en realidad, el beneficio seguirá creciendo, pero tenemos que utilizar distancias similares para la comparación). Sin embargo, también hay que cambiar el volumen de la posición para el sistema de Labouchere en este caso.

Así que parece que el sistema de Labouchere es más rentable, ¿verdad?

Si es así, entonces le han engañado las estadísticas otra vez.

Eche un vistazo a la siguiente tabla:

Tamaño apuesta	Porcentaje enviado al "bolsillo"	Promedio del "bolsillo" y balance, sistema de Labouchere	Número de transacciones, sistema de Labouchere	Promedio del "bolsillo" y balance, sistema de apuesta fija	Número de transacciones, sistema de apuesta fija	Beneficio por transacción, sistema de Labouchere	Beneficio por transacción, sistema de apuesta fija	Beneficio por transacción, % de la apuesta inicial, sistema de Labouchere	Beneficio por transacción, % de la apuesta inicial, sistema de apuesta fija
75	10	51 177,34	3 728,62	160 489,6	99 530,41	11,04	1,51	14,72	2,02
500	45	14 016,36	127,27	349 479	33 771,46	31,56	10,05	6,31	2,01

De hecho, podemos obtener fácilmente el mismo beneficio mediante el sistema de apuesta fija. Simplemente aumentamos la apuesta 7 veces (del 0,75% hasta el 5% en este caso). Por supuesto, el 5% es un nivel de riesgo muy elevado. Pero en este caso, el sistema de apuesta fija todavía tiene 10 veces más de "persistencia".

Así que parece que el sistema de apuesta fija es más rentable, ¿verdad?

Creo que las estadísticas le han engañado otra vez.

De hecho, no importa a cuántas transacciones puede aguantar tu depósito (en promedio, por supuesto), ya que hemos retirado parte de nuestras ganancias al "bolsillo". Si el total de los fondos del "bolsillo" supera el balance inicial de la cuenta varias veces, la pérdida del depósito no es muy importante.

Quizá, la conclusión más evidente que se puede sacar de estos cálculos es la siguiente: "Si la probabilidad de ganancias es del 51%, los beneficios generados por el sistema de Labouchere y de apuesta fija son prácticamente los mismos, con la condición de que el primero tenga una apuesta inicial del 0,75% del depósito y que se retire el 10% de la cuenta, mientras que el segunda tenga una apuesta fija del 5% del depósito inicial y se retira el 45% de la cuenta. El sistema de Labouchere alcanza el mismo nivel de rentabilidad incrementando el tamaño de la posición durante su funcionamiento".

Además, hay que tener en cuenta que las conclusiones estadísticas se consideran válidas sólo si se lleva a cabo un gran número de experimentos. Se puede dividir una sola cuenta virtual en varios depósitos, Por lo cual la pérdida de un depósito virtual supondría la pérdida de una parte de la cuenta de trading y después vuelve la tamaño de la apuesta inicial al alcanzar un determinado nivel de riesgo. Sin embargo, el artículo muestra que la simulación de incluso 100 depósitos sigue dando unos resultados muy dispersos. Y si dividimos un depósito promedio de un trader en 100 partes, un trading normal sería imposible.

¿Cuál es el mejor sistema? Es difícil decirlo. La elección depende de las preferencias del trader, y la previsión matemática del sistema inicial es sumamente importante aquí. El código que se muestra en el artículo permite a cualquiera simular el sistema de Labouchere en su propio sistema de trading.

Veamos los gráficos de ambos sistemas con una probabilidad de ganancias del 55%:

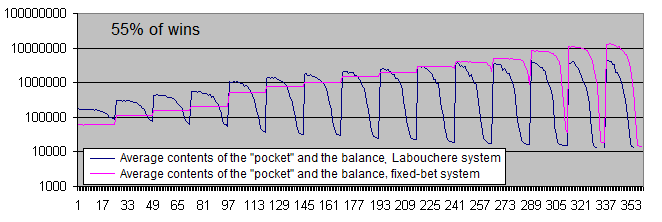
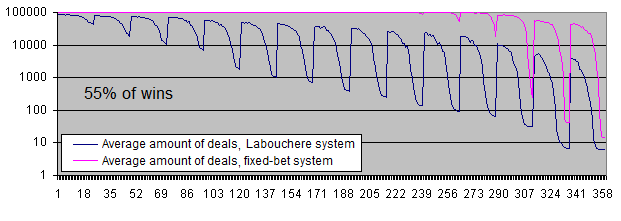
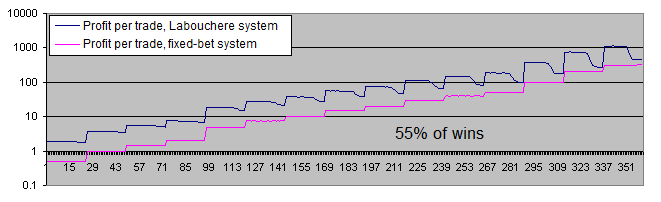
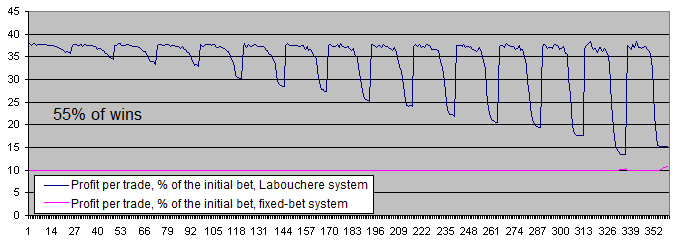
Con una probabilidad de ganancias del 55%, ambos sistemas son rentables.

La diferencia entre el beneficio promedio por transacción ha disminuido desde 6-7 veces (51% de probabilidad de ganancias) hasta 3,7 (55% de probabilidad de ganancias). Esto se debe a la elevada previsión matemática del sistema inicial, el sistema de Labouchere requiere menos tiempo para los retiros y por lo tanto no tiene que operar con un lote elevado muy a menudo.

Conclusión

No se ha producido ningún milagro. El sistema de gestión de dinero de Labouchere no puede convertir un sistema con pérdidas en un sistema rentable o incluso neutral.

Además, hemos visto con claridad algunos mitos y conceptos erróneos sobre el sistema de Labouchere:

• La complejidad que dificulta el cálculo de los resultados del sistema.
• La falta de datos estadísticos durante las pruebas manuales.
  
• La capacidad del sistema de establecer nuevos registros de beneficio una y otra vez, incluso si el sistema inicial tiene una previsión negativa, haciendo que los traders confíen en su eficacia.
  

¿Vale la pena probar el sistema de Labouchere con un sistema cuyas previsiones son positivas? La elección es suya. El sistema de Labouchere es muy complejo, y su rentabilidad no es digna de mencionar. En cualquier caso, le puedo dar dos consejos: no superar nunca el nivel de riesgo aceptable si le preocupa su depósito y tratar de mejorar la previsión matemática de su sistema de trading.