ラブシェール資産運用法の統計的検証

三つの嘘　－　嘘、図々しい嘘、そして統計

概論

休日にふらふらとネットサーフィンをしていると、今まで聞いたことがない資産運用法を見つけた。ラブシェール法、または削除メソッドという。(ラブシェール法を利用したForex Vacuum Cleaner System). 実際、このシステムはマーチンゲールの変わり種で、つまり負けの後にはかけ金をあげ、勝ちの後には最小限のかけ金にする。しかし、これはオリジナルのマーチンゲールよりも攻撃的な変わり種ではない、というのもかけ金は2倍にアップするのではなく、一定の額だからだ。

では、ここから非常に僕の興味を引いたこのシステムの性能の記述に、コメントを加えていくことにする。

• 「さて、皆さんご注目!システムが機能し勝つためには、33％～40％以上の利益のある取引を持っていなければだめだ！！！」とても強烈な声明だ。本当に、なんで助走がこんな大きい33％～40％なんてわからないね？

• 「こういうゲームのメソッドはもしかしたら不運なカジノのように見えるかもしれないということを念頭においておいてほしい」  — まさかね？もしかしたら、このメソッドは本当に使えないのか？！

• 「しかし、原則は変わることはない。33％の勝ちが66％の負けを相殺するのだ。このように、こういったマネーマネジメントをFXの実際の取引に採用しつつも、我々には50％の勝ちが見込める、そして予想される損失に対し、予想できる利益の相関が大きい、または1と同等、つまりProfit factor >=1という取引システムが必要なのだ。」

実際、僕が見つけたソースでも、もし負けに対して勝ちが同等で、50％の勝ちが見込める（もしくは「33％以上」でさえも）システムを採用するなら、ラブシェール法は簡単にそこから利益を生み出すと断言している。もし僕たちに代わってプラス領域に引き寄せてくれる方法が考えられているなら、何の為にプラスの期待値を持つシステムを探すのか？だって、例えば47％の勝率のシステムを作るなんて簡単だし・・・

ではラブシェール法がどのようにかけ金を変えることを提案しているのか見てみよう。

最少のかけ金、ということで1にする。勝ちの場合には、特に面白いことは起こらない。かけ金はそのまま残って、取引残高が少し成長するだけだ。

しかし、負けの場合、かけ金は2まで1つ大きくなる。そして、リストに負けたかけ金をメモしていく。

-1

上げたかけ金の勝ちの場合、リストにメモする。

-1 2

それから、2つの数字を消す、というのは僕たちは自分の負けを戻したからだ。（つまり、2つのかけ金からのパターンの結果においては、残高は1増えたのだ）

もっと長い期間の負けパターンを見てみよう。

-1

かけ金を2にする。また負け。

-1 -2

かけ金を3にする。また負け。

-1 -2 -3

かけ金を4にする。また負け。

-1 -2 -3 -4

かけ金を5にする。また負け。

-1 -2 -3 -4 -5

かけ金を6にする。また負け。

-1 -2 -3 -4 -5 -6

かけ金を7にする、するとやっと勝つ。

-1 -2 -3 -4 -5 -6 +7

この後で「-1」、「-6」そして「+7」を消す。なぜなら、この勝ちで二つの負けを相殺するからだ。次のかけ金は表に残った初めと最後の額と同じにする、つまり前回と同じ7だ。勝ちの場合

-2 -3 -4 -5 +7

「-2」、「-5」そして「+7」を消す。もう一度掛け金を表に残った最初と最後の額と同等にする、つまり前回の7だ。（他のソースでは、勝ちの場合にただの『ゼロ』にならないように、さらにこれに1を加えると書かれていることもあるが、とはいっても最小限の利益だろう）勝ちの場合

-3 -4 +7

表から全ての数字をけす、なぜなら僕たちは負けを取り返したからだ。

中間段階で負けを被る場合、またこの負けの割合を同様に表に書き込んで、表の端の２つの数字と同等の金額をかける必要がある。

さて、では僕たちに何が起こったか見てみよう。

1. 本当に、6つの負けの回を、全部で３つの勝ちので相殺することができた。（本当に回で相殺したわけだが、このことについては後ほど）一見、システムは簡単に乾いたところから水を出せるもののように思える。

2. 掛け金の増大は、このような回で初掛金の64倍になったであろうオリジナルのマーチンゲールよりもかなりゆっくりだ。

3. デポジットの失敗の合計は（かけ金の額）引用した例では全部で21で、同じ時期にオリジナルのマーチンゲールでは63だった。

4. 簡単な計算だと、初掛金の額がデポジットの1％の場合にデポジットを失うのは、続けて13回負けた場合で、また初掛金の額がデポジットの0.1％の場合は、続けて44回負けた場合だ。（ここでは手をこすって、「どこでこんなのお目にかかれる－50：50のチャンスのなかで44の損失とか？！これは数兆分の1だ!僕の頭の上に隕石が落ちてくることの方が確立が高いだろう！こんな負けの確率なら絶対に使わなければ！」などなどと言いたくなる）

5. 公開資料にはオリジナルのマーチンゲール法の『奇跡の効果』は無いというたくさんの根拠があって、確かにこれを確認するのは、紙のリストとペンがあればさほど難しくはない。でもラブシェール法については、僕は一つの検証も見つけることはできなかった。

6. かけ金のシステムは、『紙の上の』最終期待値の計算がとても難しくて、すごくこんがらがって見える。

しかしながら、僕たちの失敗パターンからの脱出プロセスに戻ってみよう。6回連続の負けの後で、僕たちは全部で、3ではなく、2の勝ちを得たとしよう。では、紙の上には次のことが書かれる。

-3 -4

かけ金7、そしてここで待ち望む勝ちの代わりに、負けを得たとする。

-3 -4 -7

かけ金10（負けから負けへとかけ金はすでに1増えて、3に増えるよりも十分賢明で安全なように見えることに気づいてもらいたい）そしてまた負け。

-3 -4 -7 -10

もうかけ金は13だ。

ということは、完全な相殺までに繰り返し負けを被る場合、システムはかけ金を１よりも多いかけ金に増やすよう指示してくるのだ。そして、ほら、ここで僕たちのデポジットには本当の危険が待ち伏せているかもしれなく、つまり失敗からの脱出の為には、僕たちには正に勝ちのパターンが必要なのだ。前と同じように紙の上で期待値を計算するアイディアはとても難しく、少なくともとても退屈に見えるけど・・・。

みんなはこのシステムで何ができるか興味があるかな？僕はとても興味があるよ。

課題の提起、それは何をどんな方法で確かめるかだ

一番の主要な問題、そして僕たちが探す答えは、それはラブシェール資産運用法が期待値を、特にプラスの方向に動かす能力（もしくは無能力）だ。勿論、勝ちの際の勝率33％は十分だと言える＝負けにはファンタジーに聞こえる、しかし、せめて49％もしくは50％の勝率なら十分か？もしそうでないなら、何かしらの強みがラブシェール法にはあるのだろうか？

検証は統計でもって行う、つまりMQLのプログラムに書く必要がある。（ここではMQL4を使う。MQL5はまだマスターしていないので）そしてプログラムに数百万の取引をさせて、数千のデポジットを出させる。僕たちはお財布に害なく結果を見て、分析するのだ。万が一プログラムが稼いでいることがわかったら、実際の取引にこれを全部導入したっていい。

ラブシェール法は勝ちを想定して開発されていて、つまり負けに対してやその他の相互関係にも適応させることはできるが、こういった複雑化は妥当ではないように思える。だってこの方法はゲームの勝ちの期待値に影響を与えることが可能なら＝負けやその他の相互関係に影響を与えることはとても簡単であろうから。もしそうでないとしたら、これは変種の正当性の検証に無駄な時間を浪費することになる。

その他に、勝ちを伴うシステム＝負けや50％の勝率と同等の数値を持つ取引は、もっと簡単に人々に受け入れられる。というのも、僕たちはみんな資金の増加することを知っているから。なのでプログラムをこう名付けよう―CoinTestと。

さて、プラグラムに要望を書き込もう。

1. 勝ちの確率が変わることは必須だ。50：50のゲームになるのは、平衡的に特殊なケースでしかない。

2. リスクレベルのセッティングの可能性を持つことは必須だ。ラブシェール法では1のかけ金が固定額になっている。もし僕たちがデポジットの額に応じて初掛金を大きくすると、この方法の要が失われてしまう。というのは、表から全ての数字を消した後、デポジットは初期の額には戻らないからだ。マイナスからの脱却後に掛け金の額を計算しなおすことはできるが、その場合理解（比較、検査）が難しい細かい数字がでてくることになる。というわけで、リスクレベルは2つの可変のもの－初期デポジットの額と、初掛金の額でセッティングする。

3. 1つのデポジットに最大数の取引を指示する必要がある。最も低い初期リスクの時にも僕たちはデポジットを失うかどうか知ることができるほど十分に多くだ。もしデポジットが伸びたら、これは終わりなく続いて、僕たちは結果を知ることができないかもしれない。

4. １セット分のデポジットの検査結果は、プログラムの調整やビジネスロジックの変更の為にも持っておきたいものだ。ファイルへの出力はこの目的の為には十分適している。

5. 1つのデポジットのコードランの記入に成功したら、それぞれのデポジットと回ごとに統計を取る必要がある。この時できれば変更を伴ったパラメータがあるといい。だって1つの実験では、全く統計とは言えないから。統計の出力は同じようにファイルに行う。この時デポジットごとの履歴詳細は興味を引かなくなる。

かけ額の選択のシステムコードは、実際の取引にも使ってもいいので、作成するときはクラスの形態で。

MetaTraderでの実際の取引の開始は、この場合、演算リソースの観点で見ると、とても消費的で無益だ。予め決めた勝率のロット額でのランダムな取引の結果を確定できればそれで十分だ。ここから書くのはアドバイザーでもなく、インディケーターでもなく、スクリプトだけだ。というのは、MQLプログラムの多様性は1回の起動にもよく適しているからだ。

標準擬似乱数生成器の性質の統計的検証

僕たちのもくろみにとって、擬似乱数生成器は大きな意味を持つ、というのは、それこそが僕たちに勝ちと負け、どちらをもたらしてくれるか教えてくれるからだ。　その際、勝ち、または負けの長いパターンの分類の『正直さ』がとても重要だ。長いパターンの分類の正確性を難しい数学的統計論無しに、『目分量』で評価してみよう。

この記事は、擬似乱数生成器の性質を真面目な検査で追及するものではない。（15の様々なテストを行う必要がある）確かめるのはラブシェール法の検証結果に影響を与える擬似乱数生成器の性能だけで、その際に検証のプロセスはあまり難しくないものにする。

MetaTraderでは、僕たちはMathRand()で擬似乱数生成器のスタンダードな機能を利用することができる。. 擬似乱数生成器の一貫性MathSrand()の機能によって初期化される。

スタンダードな擬似乱数生成器の性質を確かめる為に、2つのパラメータを持つ小さいRandFileのスクリプトを書いてみよう。

• 生成される数百万の32ビットのランダムワード（1つの32ビットのワード―15の有効ビットを与える3つのMathRand()呼出機能）測定単位は、通常の10進法の100万で、2^20ではない、というのは結果は目で審査することになるからだ。

• ロジックパラメーター　CalcSeries（同じビットの長いパターン分類の計算をするか）

長いビットパターンの分類計算プロセスはとてもリソースを消費するものだ。（スクリプトの実行時間が10倍になる）その為、このプロセスは別箇のオプションへ移した。

スクリプトは次の結果を出す。

• 時間の記録欄には計算にかかった時間
• 単位の記録欄には、全ての生成されたビットの中でいくつの単位が見出されたか
• RandFile.binファイル―擬似乱数生成器の動作結果を持つバイナリファイル
• RandStat.csvファイル―特定バイトの頻度の統計ファイル
• RandOnesSeries.csvファイル―「1」ビットパターンの長さの統計ファイル
• RandZerosSeries.csvファイル―「0」ビットパターンの長さの統計ファイル

長さの違う３つのテストセットを生成しよう。

• 1000万各々に4バイトごとのテストワード（全部で4000万バイト）
  
• 1億各々に４バイトごとのテストワード（全部で4億バイト）
• 10億各々に4バイトごとのテストワード（全部で40億バイト）

それから、テストしてみよう。

1. 最大圧縮設定でアーカイバWinRarによるランダムデータのファイルの圧縮率定性ランダムデータは圧縮されない。勿論、ファイルが圧縮されないということは、その中にあるランダムデータの高い質を意味しているわけではないが、もし圧縮されるなら、それは確かにデータには統計的規則性があることを意味する。

   

   

   

2. 「1」ビットの数
   

   	均衡数	実数	絶対偏差	偏差　％
   1000万	160 000 000	160 004 431	4 431	0,0027694
   1億	1 600 000 000	1 599 978 338	21 662	0,0013539
   10億	16 000 000 000	15 999 996 180	3 820	0,0000239

3. ランダムファイルの中の特定のバイトの値の頻度:

   
   

   
   

   
   

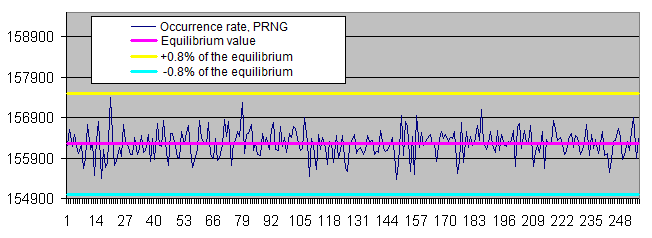
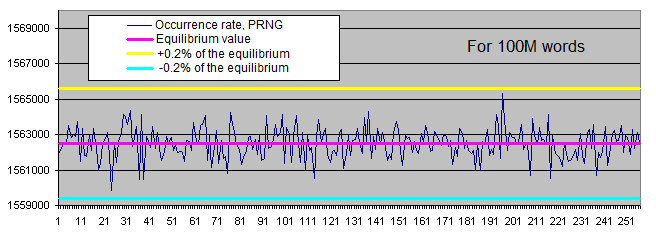
4. 同じビットパターンの長さそれぞれのサンプルサイズを2つのグラフで見てみよう。

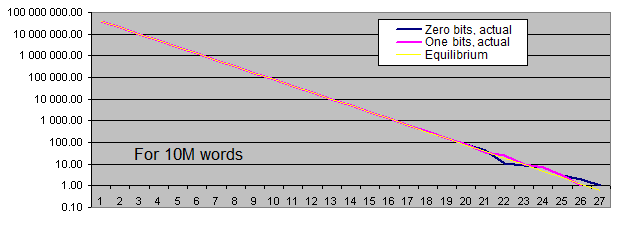
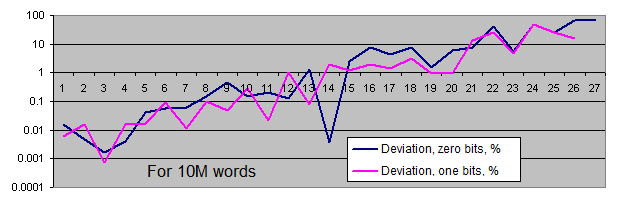
   • 事実上規定された特定の長さの同じビットパターン数のグラフ、また同様にこのような長さの平均ビット数のグラフ（対数目盛）
   • 平均ビット数からの事実上規定された同ビットパターン数の偏差率グラフ（同様に対数目盛）

   グラフの縮尺は数値に極端に高いばらつきがあるという理由で適さない。（一方、また他方のグラフでは1から40億まで、または0.00001から6000までの数値が必要）その他に対数目盛での長いパターンの平均数値は、そのものが直線を描く、というのはパターンの長さの1つの増長は、その降下の確率が２倍下がるからだ。

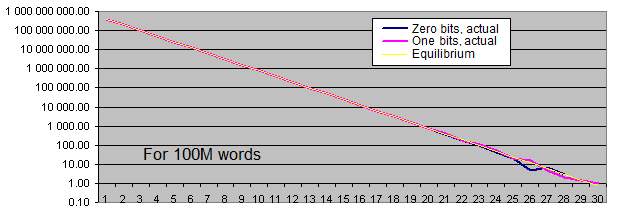
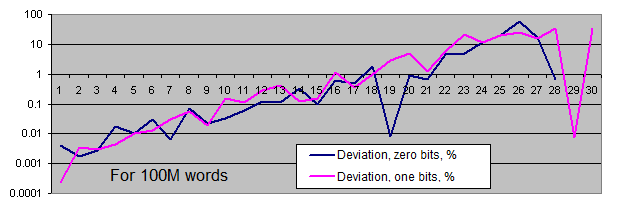
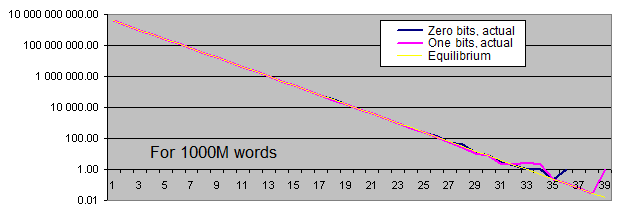
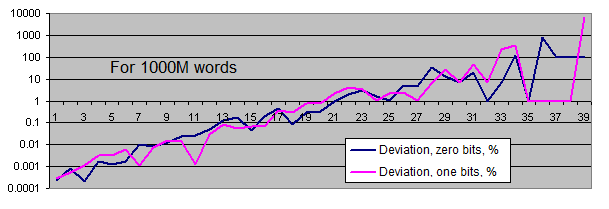
これらの検証からどんな結論を出せるか？

• 標準的な擬似乱数生成器の吐き出し量は、僕たちの課題にとっては妥当なものだ。

• 擬似乱数生成器の動作結果のファイルのアーカイブは、それらの圧縮には至らない。

• 0と1のバイトの数は等確率に一致し、均衡からの偏差（％）はサンプルサイズが大きくなるにつれ下がっていく。

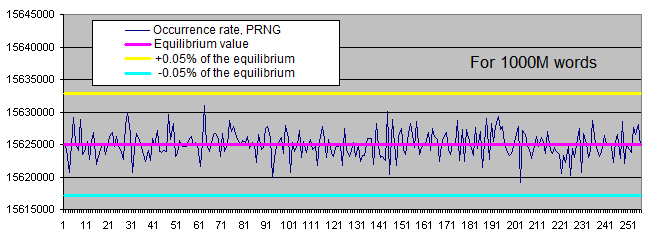
• 擬似乱数生成器の動作結果の中の特定のバイトの頻度の分類は、平均線の回りの狭い範囲で変動する。頻度のばらつきはサンプルの増大と共に低下する。

• 同じビットパターンの頻度は、十分に大きく長いパターンの時（稀な事例）のみ、平均値と共に行ったり来たりする。サンプルの長さの増大と共に、平均値からの事実頻度の「点の発散」はパターンの長さの増長の方向へ混ざり、また全ての数列が常に100の数値あたりにある。

このようにして、僕たちの検証結果を歪める重大な統計的バグは、30億の数列の生成時にさえ標準擬似乱数生成器ではでてこなかった。（一つの32ビットのワードに対して3つの生成が利用される）

ポジションサイズのコントロールを実行するラブシェール法のクラスの表記

ラブシェール法のクラスは極めてコンパクトだ。そのインターフェイスは全部で初期ロットのサイズの設定と取得の為の２つのラップ機能と、２つの実際に働く機能から成っている。現行ポジションサイズの取得と取引結果の設定、同様に初期状態へのリセット機能だ。

// ラブシェール・マネーマネジメントの実行
// テイク/ストップの提案 = 1/1.
class CLabouchere
{
        private:
        protected:
                // スタートロット初期設定―0.1
                double p_dStartLot;

                // ラブシェール法に従って保存される列
                double p_dLotsString[];
        public:
                void CLabouchere();
                void ~CLabouchere();

                double GetStartLot() {return p_dStartLot;};
                void SetStartLot(double a_dStartLot) {p_dStartLot = a_dStartLot;};

                // 今入る必要があるロットを戻す
                double GetCurrentLot();

                // 現行トレードの結果を記録する―テイク（true）またはストップ（false）
                void SetResult(bool a_bResult);

                // 初期ロット以外を初期状態へリセットする
                void Init() {ArrayResize(p_dLotsString, 0);};
};

動作スクリプトコードの表記結果の事前評価

難しくないスクリプトを次の入力パラメータを持つ百数列に書く。

//--- input parameters
input int RepeatsCount=100000;
input int StartBalance = 10000;
input int Take = 50;
input double SuccessPercent = 50.0;
// もしここでtureならば、SuccessPercentは無視される
input bool FiftyFifty = true;

スクリプトはかけ金のパターンを、デポジットがなくなるまで、またはRepeatsCountに到達するまで作成する。

50：50の勝率が必要な例は、個別の設定へ。この場合、浪費結果の性質には、擬似乱数の1のビットが現れる。他の場合には勝ちと負けの境目を意味する数が算出され、ランダムナンバーはこの境界線と比較される。擬似乱数生成器の個別のビット系列は設定されたが、それ以上の他の境界線数値降下の系列は査定されなかった為、50：50の勝率の場合の為に、個別の設定が実行された。

初期設定：

• デポジットの額―1万
• 初掛金の額―50（つまり、初期デポジットの0.5％）

およそ10回目のスクリプトの起動で印象的な結果が得られる―2335点目でデポジットは46300になる。しかしながら、2372点目から降下していく。

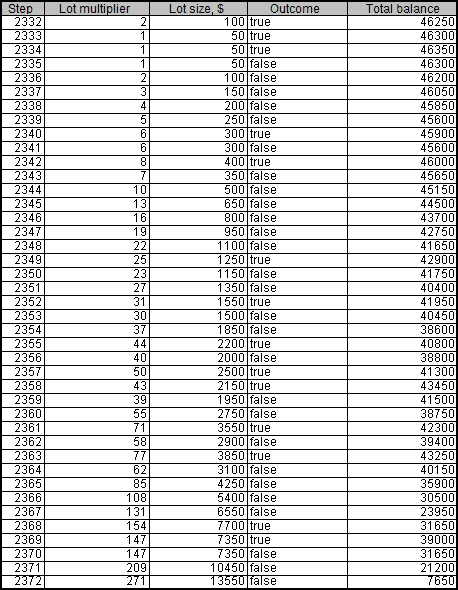
チャート内ではこのデポジットはこう見える。

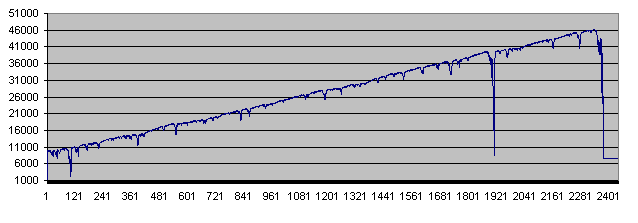
デポジットを失うまで残高は２回危機的数値まで低下したのがわかる。

いくつかの場面において、デポジットは初めの数十回の取引で無くなっていき、最大の10万回の取引を終えることはなかった。

パラメーターと多数の負けの観測の検証の結果、僕の頭には次のことが浮かんだ。

• 取引アカウントから引き出される金額のパラメータを追加する。だって、もしデポジットの存続時間内に、その初期の金額よりも多くを引き出してしまうなら、初期のデポジットは完全に予定損失になってしまうからだ。結果、取引アカウントから『ポケット』へ移せる勝ちのパーセント―PocketPercentのパラメータが出現した。この時、ポケットから現金を出すことは禁止だ。リスクを被るのは取引アカウントだけだ。だって、人生では全てが大体こういう風に起こるものだろう。

• 勿論、サイクルごとにデポジットのランを実行する必要がある。（これは優雅なことでもなく、数百回と手動で行う）この時、いくつかのパラメータを変更する必要がある。PocketPercentと初掛金の額Takeだ。また同様に平均スコアを計算する（ポケットの中の金額とデポジットの中の残金―なぜならそれは0までではなく、次の取引ができない時点まで消費されるからだ。）

• 2つのスクリプトのバージョンが必要だ。一つは周期的な実行の為の、しかしファイルへの具体的な取引の詳細の出力のない物。もう一つは反対の物。どこで再利用するかというと、オブジェクトコードだ。結果、主な『有効コード』はCCoinTestのクラスで構成される必要があり、スクリプトを作成するのは全く簡単なものだ。

一つの実行の為のスクリプトコードは、記事に全部を移すことができるほどに短くできた。（デポジット存続期間内の詳細事項を含むCCoinTestのクラスに載ったファイル記録を含む）

#include <CCoinTest.mqh>

//--- input parameters
input int RepeatsCount=100000;
input int StartBalance = 10000;
input int Take = 50;
input int PocketPercent = 10;
input double SuccessPercent = 50.0;
input string S2 = 「もしここでtrueなら、SuccessPercentは無視される」;
input bool FiftyFifty = true;
input string S3 = 「もしtrueだったら、ラブシェールの代わりに固定ロットに行ってみよう。」
input bool FixedLot = false;

void OnStart()
{
        MathSrand(GetTickCount());

        CCoinTest Coin;

        Coin.SetRepeatsCount(RepeatsCount);
        Coin.SetStartBalance(StartBalance);
        Coin.SetTake(Take);
        Coin.SetPocketPercent(PocketPercent);
        Coin.SetSuccessPercent(SuccessPercent);
        Coin.SetFiftyFifty(FiftyFifty);
        Coin.SetFileName("Coin.csv");
        Coin.SetFixedLot(FixedLot);

        Coin.Go();
}

ポケットが追加された後でシステム動作のチャートは、少し違った風に見えてくる。（この例ではポケットへ40％の利益が示されている）

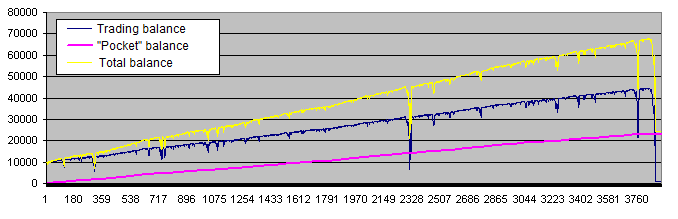
紫色の線（ポケット残高）は取引アカウントのあらゆるトレーダーが夢みる理想的なチャートにとても似ている。しかしながら、実際には僕たちは黄色の線に興味を持つ必要がある。『取引アカウントとポケットの合計残高』、これはもうすでにそんなに良くはないが。その他に、遥かに頻繁にこういうパラメータに出会う。

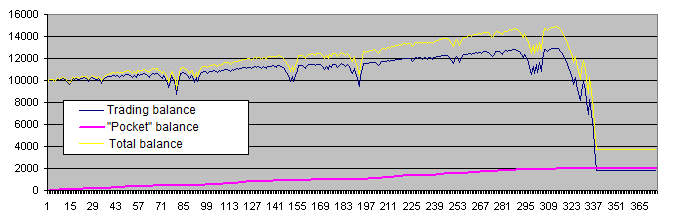
チャートから分かることは、

• システムは実際、作成者が入力した行動を行う。とても頻繁に沈下を相殺でき、その後でデポジットは勢いよく新しい頂点へと向かう。

• 時々、負けを相殺する試みは完全な破綻に終わる。事実上沈下に陥った場合、2つの種類がある。そこから抜け出すか、完全にデポジットを失うかだ。

• より長くデポジットがもつほど、より高みに到達する。

• これらの例では初掛金の額は、初めのデポジットの0.5％だ（初めのデポジットが1万の場合、50ということ）初めの例では主要なリスクの額は大体0.1％まで下がった。（デポジットは4.5倍に達し、初掛金の額は以前のまま残った）そして、このような低リスクの時でさえ破産を免れることはできなかった。

様々な確率にとっての最終的な評価結果ラブシェール法と固定かけ法の結果の比較

さて、一番面白いことへ進んでいこう。多数の実験結果の収集で、うまくいったデポジットの勝ちで、うまく行かなかった方の損失をカバーできるかようやくはっきりしてくる。もしかしたら、アルゴリズムは自身にとても低い初掛金の額を現すかもしれない。（なぜなら、そうした方がデポジットを失うことがより難しくなるからだ）もしくは、反対の場合もある。つまりとても高い額のかけ金？勝ちの何％を取引アカウントから引き出す必要があるか？ラブシェール法は固定かけの方法とは違う結果を表せるのか？主要なシステムの期待値がプラスの時何が起こるのか？（もし『コイン』が頻繁に勝ちを与えたら？）疑問は山のようにある、そしてそれらを一つずつ解消していく必要がある。

パラメータの変更を伴うサイクルごとのデポジットの実行の為のスクリプトは、およそ100の列を使用するので、その一部を引用する。

入力パラメータ

//--- input parameters
input int RepeatsCount=100000;
input int StartBalance = 10000;
input string S1 = "Столько депозитов будем сливать";
input int Deposits = 100;
input double SuccessPercent = 50.0;
input string S2 = 「もしここでtrueなら、SuccessPercentは無視される」;
input bool FiftyFifty = true;
input string S3 = 「もしtrueだったら、ラブシェールの代わりに固定ロットに行ってみよう。」
input bool FixedLot = false;

初掛金の額とポケットに入る勝率の値を持つ配列

// PocketPercentのバージョンの配列
int iPocketPercents[24] = {1, 2, 3, 5, 7, 10, 15, 20, 25, 30, 35, 40, 45, 50, 60, 70, 75, 80, 85, 90, 95, 97, 98, 99};

// 初掛金の額の配列
int iTakes[15] = {5, 10, 15, 20, 50, 75, 100, 150, 200, 300, 400, 500, 1000, 2000, 3000};

初掛金の額は5から（初めのデポジットの0.05％）3000まで（初めのデポジットの30％）までに変わったことがわかる。取引アカウントからポケットへ移るパーセンテージは、1％から99％までだ。予め予備とともに選択されたパラメータは、双方の理に適った範囲をカバーする為だ。

このようにして、検索域は2次元のものであり、360の離散点（24×15）が現れ、パターンの結果の一つずつに（パターン内のデポジット量はDepositsパラメータで設定されている）個別のデポジットの平均合計残高が計算される（ポケット内と取引アカウント内の額として）またデポジットの損失までの平均取引数（デポジットの存続期間）

2次元空間における計算結果は3次元であり、つまりそれらを平面媒体で具象化するのは困難だ。その為、横座標によって検索域から点の原子番号を差し引いた2次元のグラフを描くことにする。（0から359まで）必要に応じて、別箇に具体的なTakesとPocketPercentの数値を表示する。

100デポジットの実行結果はこのような平均残高になる。

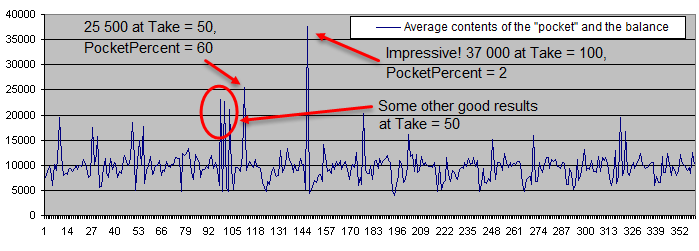
そしてこのようなデポジット存続期間のグラフだ（対数目盛で）

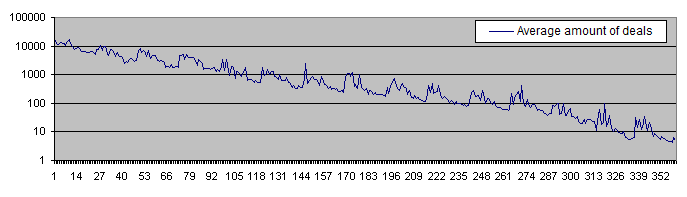
0.05％の初期リスクのデポジットの存続期間は1万取引以上で、30％の初期リスクの際は連続的に10取引以下まで下がる。PocketPercentの高い数値は同様にデポジットがなくなるまで平均取引数を下げている。十分予期できる結果だ。

ポケットと取引残高の平均グラフはいくつかの点が分離し、そのうちの4つは近くに分布している。これは最適領域を発見したという希望を起こさせる。ここで、Deposits = 1 000の為の結果を計算し、このグラフに載せよう。

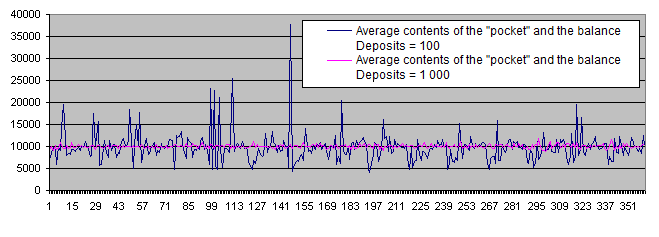
条件に最も適すると仮定する領域は、十分多い数の統計データの急襲のもとに消え去ってしまった。あらゆるパラメータによる、ランダムな方法でのグラフは初期残高数である1万近辺にとても近いところで変動している。

このようにして、Deposits = 100の数値は十分なものではない。全てのこれからの実験はDeposits = 1 000をもって行う。

1つのグラフにラブシェール法の結果と固定かけ法の結果を反映させる。

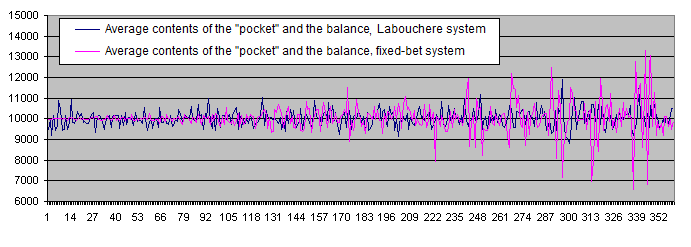
また、ラブシェール法と固定かけ法のデポジット存続期間のグラフ

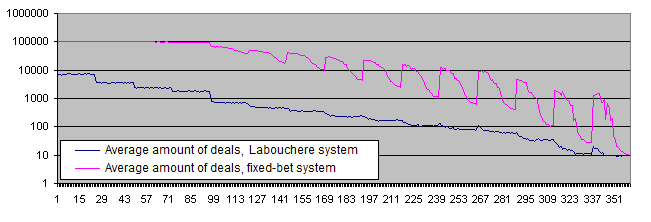
グラフから何が見えるか。

• ラブシェール法の会計結果は0で、固定賭け法の会計結果と一致する。

• 固定かけ法は、ラブシェール法とは違い、平均から結果のばらつきが広がる動きをしている。Depositsの固定数が、固定かけ法の統計行動に適していないとわかる。

• ラブシェール法のデポジットの存続期間は固定かけ法のものよりもずっと低い。（多数のパラメータによる場合10またはそれ以上の回数、いくつかのパラメータによる場合は100回以上）低リスクの為に、上の局限に届いたRepeatsCountのパラメータによるグラフを見よう。これらの結果は部分的に、リスクレベルの高いシステムはデポジットにとって危険であるという、普遍的なトレーダー間の意見を肯定するものだ。これらのシステムはデポジットの存続期間にとって危険なものであるが、会計結果にとっては危険なものであるかどうか、僕たちはまだ見つけ出していない。（平均は勿論、稼ぎの一部を引き出す条件下でも）

リスクレベルの高い部分の挙動の十分な統計を集める為に、もう一つスクリプトを設定しよう。

input string S2 = 『それぞれのパラメータのペアに対する取引最小値』;
input int MinDeals = 10000000;

もし1000の負けのデポジットの間に、1000万取引があったとしたら、続ける必要がある。

結果、グラフのばらつきは少なくなる。

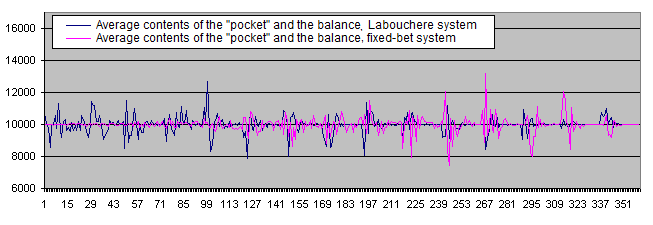
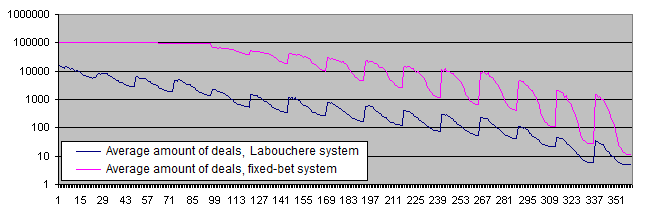
ここで50：50と違う初期システムの確率でのシステムの働きを確かめてみよう。

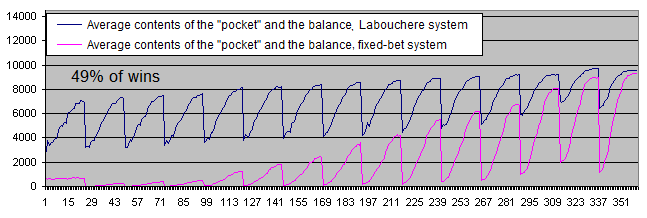
デポジットの存続期間

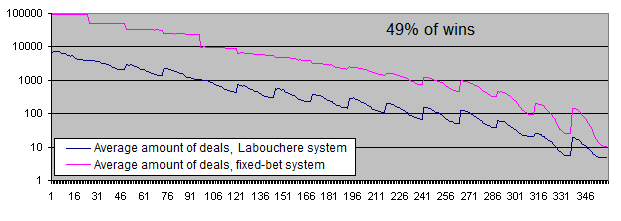
これらのグラフから何が見えるか？

• 49％の勝率の下では両方のシステムは明確に不利なものとなる。

• 固定かけ法のとても低い会計結果が目に飛び込んでくる。実際、これは稼いだお金を『財布』に引き出すラブシェール法にとってとても適した方法の表明なのだが、50以下の勝率下では固定かけ法にとっては適さないのだ。さて、取引アカウントから資金の一部を『財布』に移すのは、沈下からの脱出が出来てからだけだ。

  ラブシェール法は49％の勝率下でさえ、何度でも新しい記録をたてることができ（当面の掛け額の資金が足りている間）固定かけ法はそうではない。人間であるトレーダーは残高の急速な減少の時に、10万または1万取引を行ってデポジットを失うまで持っていかないだろう。まずトレーダーは僕たちのアルゴリズムとは違い、もっと早くに取引をやめるだろう。ラブシェール法を見ると、人は僕たちのアルゴリズムと同じことをする。常に全ての新記録に興味を引かれつつ完全なデポジットの損失まで取引をするのだ。

概論部で引用した賛美記事を覚えているだろうか？そこには33～40％の勝率下でもこのシステムは働くとあった。スポーツ的興味の為に上部の踏切板、40％を検証してみよう。

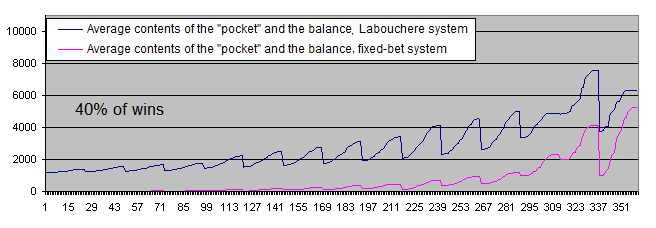
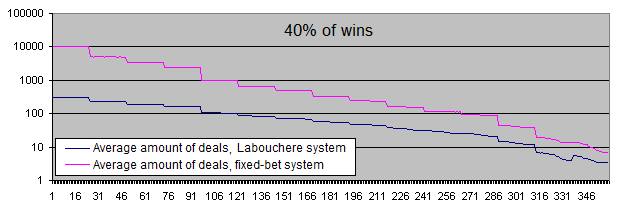
ここで初期システムの期待値のプラス値へ移る、つまり50以上の勝率へ移る。

取引の51％の勝率下の残高グラフも対数目盛で描くことになる。

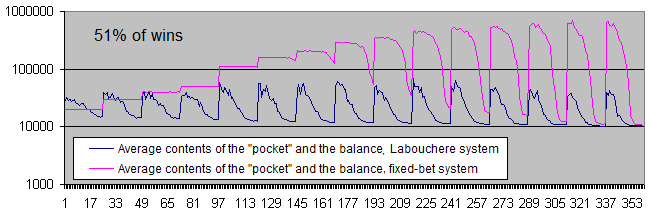
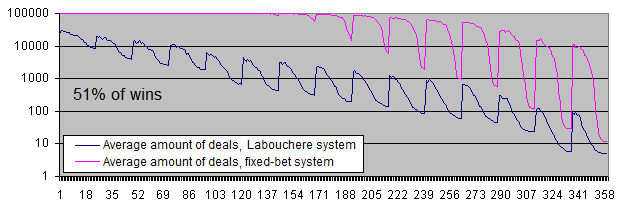
グラフから何が見えるか。

• 両方のシステムはプラスの期待値の領域へと移った。

• 低リスクの際には固定かけ法は無限の『持続力』を見せ、デポジットを失うことは実際上不可能だ。

• ラブシェール法はとても低いリスクの時でさえ、デポジットを失う可能性がある。（しかし『お財布』のことは忘れないでほしい）

• 固定かけ法は多数のパラメータの下では、ラブシェール法よりも10倍のお金をもたらし、いくつかのパラメータの下では17倍以上だ。

多くの読者がここで、固定かけ法が全てのパラメータにおいてラブシェールに勝ると結論するだろう。ましてやデポジットを失わないし、その上、10倍ものお金をもたらしてくれるのだから！そして統計に騙されるのだ。

固定かけ法は一つのデポジットに対し、10万取引の局限にぶつかった。もしRepeatsCountのパラメータが20万だったら、システムは２倍の利益をもたらしただろう。「ただただ素晴らしいじゃないか！」そう騙された読者は言うだろう。そしてまた間違うのだ。

1つの取引のシステムによってもたらされる平均利益をグラフで見てもらいたい（対数目盛で）。

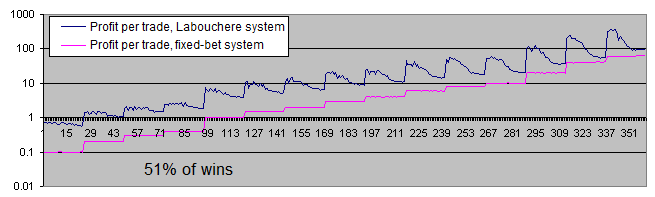
もっと分かり易くするために、１つの取引に対する利益を初掛金の％で表したグラフを引用する。

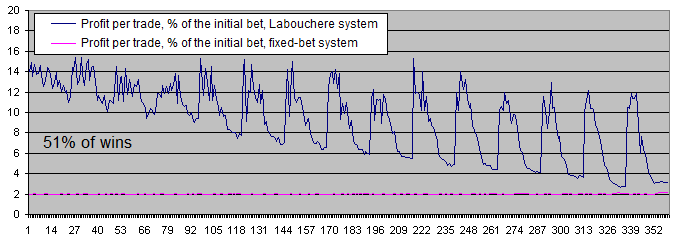
ほら、これらのグラフでわかるのは、

• 固定かけ法は1取引で初掛金の丁度2％をもたらす。これはまさに理論と一致するものだ。だって僕たちの場合は51の勝ちに対して、49の負けになるわけで、つまり勝ちは丁度２つ多いということだ。

• ラブシェール法は一番うまく行かない場合の設定であってももっと多く利益をもたらすし、正確な設定の下では6～7倍も多いのだ。

もしあなた達に無制限の時間量があるとしたら、あなた達はラブシェール法抜きにやっていけるだろう。

注意深い読者は、もし固定ロットのシステムを固定リスクパーセンテージに変えれば、１取引あたりの利益は伸びると反発するかもしれない。（実際、利益は絶え間なく伸びるが、比較の為には同じ期間を採用しなければいけない）しかしながら、このような場合、ラブシェール法に同様のポジションサイズの変更を行う必要がある。

さて、ラブシェール法の長所を確信しましたか？

もしそうなら、またまた統計はあなた達を騙したということだ。

表を見てほしい。

かけ金の額	ポケットへの 送金%	ラブシェール法の ポケットと 残高の中身の 平均	ラブシェール法の 平均取引数	固定かけ法の ポケットと 残高の中身の平均	固定かけ法の 平均取引数	1取引あたりの利益, ラブシェール法	1取引あたりの利益， 固定かけ法	1取引あたりの利益, 初掛金からの％ ラブシェール法	1取引あたりの利益, 初掛金からの％ 固定かけ法
75	10	51 177.34	3 728.62	160 489.6	99 530.41	11.04	1.51	14.72	2.02
500	45	14 016.36	127.27	349 479	33 771.46	31.56	10.05	6.31	2.01

実際、固定かけ法からこのような取引にたいする平均利益数を得る単純な方法がある。それはラブシェール法が見せてくれる。かけ金を７倍にするだけだ（この例では0.75％から5％まで）勿論、5％というのはとても高いレベルのリスクだが、このようなリスクの下でさえ、固定かけ法は10回以上の『持続力』を持つ。

さて、固定かけ法の長所を確信しましたか？

僕が思うに、統計はまたまたあなた達を騙したようだ。

実際デポジットがいくつの取引を生き延びるかは重要ではない（平均は勿論）、だって稼いだ資金の一部をポケットに移す計算で、僕たちの利益は見積もられているのだから。金額の引出しに成功した場合、取引アカウントの初期額を数倍上回り、デポジットの損失は重要な問題ではない。

そして、これらの計算から出せる最も正しい結論は、大体こんな感じになる。初掛金がデポジットの0.75％でラブシェール法の勝率51％、そして10％の利益を引き出す場合、45％の利益を引き出す初期デポジット5％の固定かけ法と同じ収入額が予想される。ラブシェール法はその過程で一時的にポジションサイズを増やすことでこれくらいの収入額に達する。

同様に、どんな統計的な結論も、多数の実験の下でのみ意義を見出すことができるということを忘れてはいけない。一つの取引アカウントはもしかしたら仮想的にいくつかのデポジットにおいて成長するかもしれない。こうして、一つの仮想デポジットの損失は取引アカウントの一部の損失、またいくらかのリスクレベルに達した時に初掛金に移ることを意味する。しかしながら、記事で見たように、動作のシュミレーションは100のデポジットでさえ、とてもばらつきの多い結果を出したし、もし平凡なトレーダーのデポジットの100分の1だったら、取引なんてまったく実行できないだろう。

どのシステムの方がいいか？難しい問題だ。選択はトレーダーの好みによるし、決定値は初期システムの期待値が持つ。その他に、記事に引用されたコードで、どんな希望者も自分の取引システムにラブシェール法のシュミレーションを実行できる。

比較の為に2つのシステムの勝率55％のグラフを引用する。

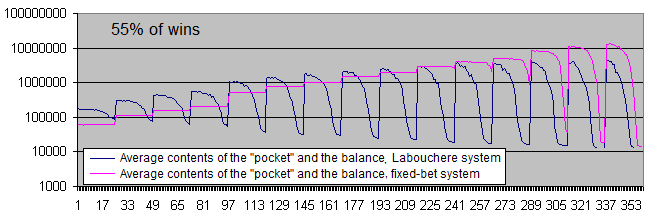
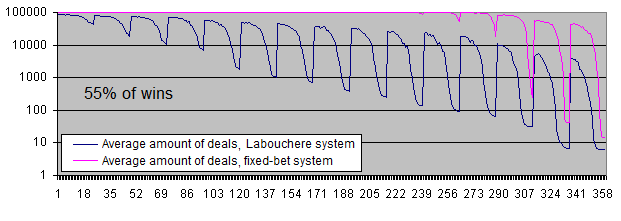
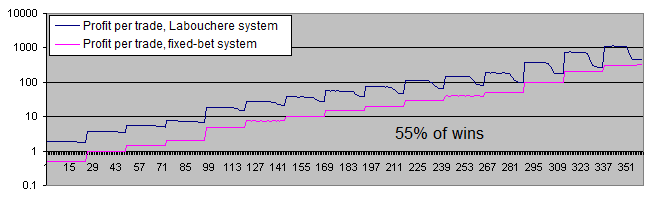
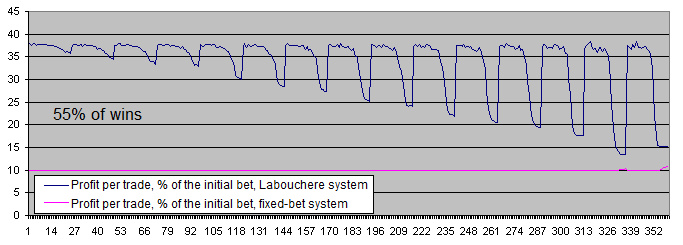
見てわかるように、55％の勝率下ではどちらのシステムからも、あなた達に利益をもたらすのを邪魔するのは難しくなる。

1取引あたりの平均利益の違いは、勝率51％の際の6～7倍から、勝率55％の際の大体3.7倍まで下がった。これは初期システムの期待値が高いほど、ラブシェール法は沈下時間は短く、またそれゆえ、高いロットでの取引時間も短い。

おわりに

勿論、奇跡は起きなかった。ラブシェール資産運用法は損失から、また中立のシステムからでさえ利益を生み出せない。

それに加え、概論に引用したラブシェール法についての作り話が出てきた理由がわかってきた。

• システム適用からの効果の計算が難しいこと。
• 手作業での統計データの十分な数がない。
  
• システムの性能が、初期システムの良くない期待値の場合ですら、トレーダーにその性能の効果を確信させるほど、何度でも新しいレコードを打ち立てる。
  

プラスの期待値がある取引にラブシェール法を用いることは有益だろうか？選択は、トレーダー次第だ。ラブシェール法の運用は十分難しいが、収益性への影響は、優れていると言えなくもない。しかしながら、どんな場合においても、僕は２つのアドバイスを与えることができる。もしデポジットを大切にするのなら、陥り易いリスクレベルを上げないこと、そしてあなたの取引システムの期待値が高まった上で用いることだ。