
Build Self Optmising Expert Advisors in MQL5
Introduction
Self-optimizing automated systems are essential in today's dynamic financial markets. In the digital age markets have become notably more volatile due to the widespread adoption of algorithmic trading, especially by high-frequency traders. According to this working paper by the SEC, SEC High-Frequency Trading Paper, high-frequency traders account for nearly half of all trades in Europe and the USA.
MQL5 is ideally suited for this task, contrary to some beliefs. Its API provides extensive matrix and vector functions, allowing for the creation of compact machine learning models. This introduction emphasizes using MQL5 for building self-optimizing bots. An Object-Oriented Programming approach reduces repetitive coding and enhances adaptability across different time frames and market conditions.
Opting for MQL5's matrix and vector capabilities over alternatives like ONNX and Python has considerable benefits. Using an ONNX model would require separate model instances for each trading symbol and new models for any minor parameter changes, such as time frame adjustments. MQL5, however, offers adaptability without the need to manage numerous models for varying conditions.
Synopsis: To develop self-optimizing Expert Advisors
We need a framework to evaluate how effectively our expert advisor is performing. Once a definitive performance metric is defined, we can then maximize or minimize our chosen metric accordingly. When building supervised machine learning models for price prediction, our objective is to minimize the error between predicted values and actual observations. On the other hand, for reinforcement learning problems, the goal is to maximize total discounted expected rewards.
In this article we will minimize the difference between the expected future price predicted by our expert advisor and the actual observed price in the future. This can be achieved by computing the absolute differences between these prices.
This article explores the fundamental aspects of constructing a self-optimizing expert advisor. Future articles will delve into more advanced methodologies for creating self-optimizing expert advisors using more advanced features from the MQL5 API.
After reading this article, the reader will understand:
- A selection of useful matrix and vector functions
- Foundational concepts of Object Oriented Programming in MQL5
- A framework for building dynamic and self-adapting expert advisors in MQL5
Self Optimization With Gradient Descent
Our goal is to design an expert advisor capable of consistently realigning itself with current market conditions. To achieve this we will implement the gradient descent algorithm in MQL5. For readers who are unfamiliar with the gradient descent algorithm, it might be helpful to compare the algorithm to the process by which a DJ sets up his sound equipment. Imagine you are a DJ getting ready to perform a set. You turn on your equipment and the volume is far too loud. What would you do next? You would most likely reduce the volume. However, now the volume is too soft, and therefore you will increase it. This jostle between increasing and decreasing happens until you find a balanced level.
The gradient descent algorithm works in a similar fashion. We start off with random coefficients in the model of the market we are in. Then we measure the error produced by our current coefficients. Similar to what the DJ does, we iteratively adjust the coefficients of our model in the opposite direction of increasing error. We take derivatives with respect to inputs, such as coefficients in a linear model, to deduce which direction the error is increasing.
Furthermore, alongside coefficients, another crucial parameter in gradient descent is the learning rate.The learning rate is analogous to how big of change in volume the DJ makes with each adjustment of the volume control. The learning rate governs the size of the step we will take each time we adjust the parameters of our model. If our learning rate is too large or too small, our model will fail to learn optimally.
Each market might have a different optimal learning rate.The ideal approach is to design our expert advisor to dynamically optimize learning rates and coefficients for each market scenario, even if we change time-frames and data scopes. This adaptability will hopefully empower us to effectively be on the right side of the market, leveraging the full potential of native solutions to trade without limitations.
Trading Strategy
Our trading strategy will be a hybrid approach of employing technical analysis and machine learning. We will use a moving average to help us determine the dominant market trend. If price is above the moving average we assume the dominant trend is bullish, otherwise if price is beneath the moving average we will assume the market trend is bearish. Once we have deduced the market trend, we will then seek for confirmation from 2 supporting indicators. The Relative Strength Index (RSI) and the William's Percent Range (WPR).
The RSI indicator gives readings between 0 and 100. Typically when the RSI reading is above 70 the security is considered overbought and should be sold, and if the RSI reading is below 30 the security is considered oversold and should be bought.This strategy works well when trading securities that exist in limited numbers, like shares or commodities, however when trading currency pairs this strategy doesn't make intuitive sense. Currencies cannot be oversold or overbought, central banks can create as much or as little as they deem necessary, therefore in our strategy when the RSI reading is above 50 we will want to buy instead of sell, likewise when the RSI reading is below 50 we will sell instead of buying.
The WPR indicator gives readings between 0 and -100. Like the RSI, the WPR indicator identifies overbought and oversold zones. However currencies cannot be overbought or oversold, the supply of currency is unlimited, therefore in our strategy we will interpret the WPR slightly different. In our strategy, when the WPR indicator is above -20, we will register that as a buy signal and if the WPR indicator is beneath -80 we will register that as a sell signal.
If all 3 indicators are aligned on the same side of the market we will then finally call upon our model to forecast the expected price in future. If our model's forecast aligns with our sentiment from analyzing our indicators we will open the position, otherwise if our model and our indicators are giving contradictory signals, we will wait until they align.
Our take profit and stop loss levels will also be dynamically set using the current market volatility levels, we will take the absolute value of the difference between price and the moving average. Our stop loss and take profit will be 2 times the absolute value of the height between the moving average and the close price. Our rationale is that under lethargic market conditions, our stop loss and take profit will be tight and on volatile market days our stop loss and take profit will be adequately wide enough. In short, our entire system will dynamically adjust itself without any intervention from us.
Implementation In MQL5
To get started we first need to define a class for our machine learning model. Using Objected Oriented Programming (OOP) has many advantages, especially for data science projects. Imagine if you had built a machine learning model, and then just manually copied that code and inserted it into every expert advisor you have. Days later, you realize a mistake you made in one of the functions in your code. If you were not using OOP design principles, then you would have to manually go through each instance of the code you copied and make the corrections one by one. However if you were employing OOP design principles then you only need to correct the class and then compile the the other programs again. In short OOP design principles can give you definite and precise control over thousands of different instances of your code.
We start by building a new class in our MetaTrader 5 Editor.
Fig 1: Building a new class in MQL5.
From there we set the name of the class. Be sure that your class is being saved in the "Include" folder, furthermore I'd recommend that you assign each class its own folder, and give the folder the same name as the class.By doing so, it will be easier to find these classes in future.
Fig 2: Building our linear regression class.
If you followed the steps above,the MQL5 wizard will help you produce code similar to this.
class LinearRegegression { private: public: LinearRegegression(); ~LinearRegegression(); }; LinearRegegression::LinearRegegression() { } LinearRegegression::~LinearRegegression() { }
If this is your first time dealing will OOP in MQL5, then let's walk through the above code together. At the very top we have the class definition. The class keyword defines this entire code as a class, after the class keyword is the name of the class. From there we enter the body of the class. The keyword "private" defines variables and functions that cannot be accessed outside the class whereas the "public" keyword defines variables and functions that can be accessed from outside the class. Notice that we have 2 functions already in our class definitions.
The first function "LinearRegression()" is called the constructor. This is the first function called whenever we launch a new instance of our class, and the last function "~LinearRegression()" is called the destructor. The destructor is the last function called whenever we are remove the class of our chart.
We can now progress to defining variables we will use to calculate our linear regression model.
- The max learning rate power defines how high we will search for a good learning rate.
- Fetch is simply the number of candles we want to analyze from the market.
- Start and predict define when we will start fetching data and the point from which we make our forecast.
- Look ahead defines how many steps into the future we wish to forecast.
- mae_array is the array that will store our error metric.
- Trained is a flag that tells us if our model has been trained and is ready to use.
- Epochs power defines the number of epochs that we will use to train our model.
- We have 2 vectors mae_train and mae_validation that store our error metrics from training and validation.
- We have 4 vectors x and y validation, x and y train. These vectors contain our training and validation data.
- The m and b vectors contain estimates for the appropriate m and b coefficients for our model.
- The 'double forecast' is simply our model's prediction.
- Learning rate power is the power to which we will raise 0.1 to define our learning rate.
- Epochs is the number of times we will train the model.
- n is the number of rows in our data, it is always equal to fetch.
- "output_end,output_start,input_end,input_start" define our train/test split.
private: //This is the highest power that we will raise ten to, as we are searching for coefficients ulong max_learning_rate_power; //This is how many bars we should fetch int fetch; //This is where we will start collecting data, it is the end of our validation data set. datetime start,predict; //This is how many steps into the future we want to forecast int look_ahead; //This is the array that will contain our MAE readings from testing different learning rates on the validation data double mae_array[30]; //Trained flag to inform us if the model has been fit and optimised succesfuly and is ready for use bool trained; //The number to raise the power of 10 buy when calculating the number of epochs int epochs_power; //Our error metrics vector mae_train,mae_validation; //This vector contains our inputs validation and training set vector x_validation,x_train; //This vector contains our outputs validation and training set vector y_validation,y_train; //This vector contains our predictions on the validation set vector y_hat_validation,y_hat_train; //This vector contains our gradient coefficient vector m; //This vector contains our model bias vector b; //This is our model's forecast double forecast; //This is our current learning rate power ulong learning_rate_power; //This is the learning rate power we are currently evaluating int lr_error_index; //This is our current learning rate double learning_rate; //This is the number of rounds we will allow whilst training our model double epochs; //This is used in calculations, it is the number of rows in our data, or the fetch size. ulong n; //These are the times for our input and output data datetime output_end,output_start,input_end,input_start; //These are the index times for our input and output data int index_output_end,index_output_start,index_input_end,index_input_start; //This is the value we will use to scale our data double first_reading; bool allowed_to_evaluate; //Update the learning rate bool UpdateLearningRate(void); //Update the number of epochs bool UpdateEpochs(void); //Set the number of epochs bool SetEpochs(int _epochs_power); //Reset the number of epochs bool ResetEpochs(void); //Reset the learning rate bool ResetLearningRate(void); //This function will fit the coeffeicients bool Fit(void); //This function evaluates the current settings bool Evaluate(ulong _index,int _epochs_power); //This function will scale the input data bool ScaleInputs(void); //This function sets the learning rate bool SetLearningRate(ulong _learning_rate_power);
Now we move on to public definitions in our class.
public: //Constructor LinearRegression(); //Fetch Current Validation Data bool GetCurrentValidationData(void); //Initialise the LinearRegressor Model void Init(int _fetch,int _look_ahead); //Function to determine if the model has been trained and is ready for use. bool Trained(void); //A function to train the model using the best learning rate and the most recent prices bool Train(void); //A function to predict future price using the current price. double Predict(void); //Destructor ~LinearRegression();
The above code defined the functions we have in our class and the signature of each function, however we are yet to implement each function. Let's start by implementing the constructor.
Notice that our constructor takes no inputs, this is called a default or non-parametric constructor. Furthermore, notice the constructor has no return type, not even void
LinearRegression::LinearRegression()
{
Print("Current Symbol: ",_Symbol);
}
Our constructor, by design, performs no actions apart from displaying the current trading symbol. This intentional design choice enables us to retrieve inputs from our expert advisor's inputs, and use them to initialize our linear regression object based on these inputs. Notably, the constructor refrains from setting any variables or default values, a task reserved for a separate method defined the "Init()" function. In short separating the constructor from the Init() function proves highly advantageous as it allows us to dynamically gather inputs from the expert advisor's settings. Had the constructor been responsible for variable initialization, this dynamic input gathering would have been constrained.
Let's now define the Init() function responsible for initializing our variables to their default values. After initializing our variables, the Init method will automatically attempt to scale the inputs and train the model for us.
void LinearRegression::Init(int _fetch,int _look_ahead) { //Clear The Chart ObjectsDeleteAll(0); //Allow evaluations allowed_to_evaluate = true; //Epochs power epochs_power =4; //Set the number of epochs epochs = 5 * MathPow(10,epochs_power); //Has the model been trained? trained = false; //Set the maximum learning rate power max_learning_rate_power = 30; //Set the end of our validation data start = iTime(_Symbol,PERIOD_CURRENT,1); //This is how much data we're going to fetch this.fetch = _fetch - 1; //This is how far into the future we want to forecast this.look_ahead = _look_ahead + 1; //Set the gradient coefficient to a random value m = vector::Zeros(1); //Set the bias to a random value b = vector::Zeros(1); //Set the forecast to 0 forecast = 0; //Our model's learning rate will start at 0 learning_rate_power = 0; //This is the learning rate we are evaluting lr_error_index = 0; mae_train = vector::Full(1,MathPow(10,100)); mae_validation = vector::Full(30,MathPow(10,10000)); //Set the initial learning rate learning_rate = MathPow(0.1,(learning_rate_power)); //Set the number of rows n = fetch; if(GetCurrentValidationData()) { //Scale the data ScaleInputs(); //Fit the model Fit(); } }
The predict function is designed to return a double data type without any parameters, that's why it has void input. It's noteworthy that to designate a function as a class member, we prefix it with the class name followed by two colons and the function name.
The predict function will first check whether the model has undergone training,by calling the "Trained()" function. Once the model's training status has been confirmed, we proceed to gather real-time data, specifically the current price and closing price, alongside timestamp data for the prediction context. We calculate the predicted price by multiplying the current price by m and adding b. We then return the forecast or return 0 if the model isn't trained.
double LinearRegression::Predict(void) { if(Trained()) { double _current_reading = iClose(_Symbol,PERIOD_CURRENT,0); predict = iTime(_Symbol,PERIOD_CURRENT,0); double prediction = (m[0]*_current_reading)+b[0]; if(prediction > _current_reading) { Comment("Buy, forecast: ",prediction); } else if(prediction < _current_reading) { Comment("Sell, forecast: ",prediction); } ObjectCreate(0,"prediction point",OBJ_VLINE,0,predict,0); ObjectCreate(0,"forecast",OBJ_HLINE,0,predict,prediction); return(prediction); } return(0); }
Our next function is tasked with gathering training and validation data, always fetching the latest market data available. This process is accomplished through the copy_rates vector function, specifically designed to transfer historical price data to a vector.
After fetching the data,we have to ensure the vectors are the same size, by using the vector size function.
bool LinearRegression::GetCurrentValidationData(void) { //Indexes index_output_end = 1; index_output_start = index_output_end + fetch; index_input_end = index_output_end + look_ahead; index_input_start = index_output_start + look_ahead; //Assigning time stamps output_end = iTime(Symbol(),PERIOD_CURRENT,index_output_end); output_start = iTime(Symbol(),PERIOD_CURRENT,index_output_start); input_end = iTime(Symbol(),PERIOD_CURRENT,index_input_end); input_start = iTime(Symbol(),PERIOD_CURRENT,index_input_start); //Get the output data if(!y_validation.CopyRates(_Symbol,PERIOD_CURRENT,COPY_RATES_CLOSE,output_end,fetch)) { Print("Failed to get market data: ",GetLastError()); return(false); } //Get the input data if(!x_validation.CopyRates(_Symbol,PERIOD_CURRENT,COPY_RATES_CLOSE,input_end,fetch)) { Print("Failed to get market data: ",GetLastError()); return(false); } //Print the vectors we have if(x_validation.Size() != y_validation.Size()) { Print("Failed to get market data: Our vectors aren't the same length."); return(false); } //Print the vectors and plot the data points Print("X validation: ",x_validation); ObjectCreate(0,"X validation end",OBJ_VLINE,0,input_end,0); ObjectCreate(0,"X validation start",OBJ_VLINE,0,input_start,0); //Print the vectors and plot the data points Print("y validation: ",y_validation); ObjectCreate(0,"y validation end",OBJ_VLINE,0,output_end,0); ObjectCreate(0,"y validation start",OBJ_VLINE,0,output_start,0); //Set the training data index_output_end = index_input_start + (look_ahead * 2); index_output_start = index_output_end + fetch; index_input_end = index_output_end + look_ahead; index_input_start = index_output_start + look_ahead; //Assigning time stamps output_end = iTime(Symbol(),PERIOD_CURRENT,index_output_end); output_start = iTime(Symbol(),PERIOD_CURRENT,index_output_start); input_end = iTime(Symbol(),PERIOD_CURRENT,index_input_end); input_start = iTime(Symbol(),PERIOD_CURRENT,index_input_start); //Copy the training data if(!y_train.CopyRates(_Symbol,PERIOD_CURRENT,COPY_RATES_CLOSE,output_end,fetch)) { Print("Error fetching training data ",GetLastError()); } //Copy the training data if(!x_train.CopyRates(_Symbol,PERIOD_CURRENT,COPY_RATES_CLOSE,input_end,fetch)) { Print("Error fetching training data ",GetLastError()); } //Check if the data matches if(x_train.Size() != y_train.Size()) { Print("Error fetching training dataL: The x and y vectors are not the same size"); } //Print the vectors and plot the data points Print("X training: ",x_train); ObjectCreate(0,"X training end",OBJ_VLINE,0,input_end,0); ObjectCreate(0,"X training start",OBJ_VLINE,0,input_start,0); Print("y training: ",y_train); ObjectCreate(0,"y training end",OBJ_VLINE,0,output_end,0); ObjectCreate(0,"y training start",OBJ_VLINE,0,output_start,0); return(true); }
We now define our fit function. The function begins by using the current values of m and b to generate predictions on the training data. Subsequently, it evaluates the error within the training data by computing the absolute differences between the actual Y observations and our predicted Y observations.
Once the error is determined, we calculate the mean error utilizing another efficient vector function, 'Mean,' to compute the arithmetic mean of the error vector.
Following this, we are now implementing the gradient descent algorithm by approximating the derivatives of our error concerning m and b. These derivative approximations guide us in updating our coefficients by a fraction of the derived derivatives.
Upon coefficient update, it is imperative to validate the new coefficients, as certain scenarios may yield invalid coefficients such as NaN or infinity. This validation step is crucial to ensure the integrity and usability of the updated coefficients.
bool LinearRegression::Fit() { Print("Fitting a linear regression on the training set with learning rate ",learning_rate_power); Print("Evalutaions: ",allowed_to_evaluate); for(int i =0; i < epochs;i++) { //Measure error y_hat_train = (m[0]*x_train) + b[0]; vector y_minus_y_hat = (y_train - y_hat_train); vector y_minus_y_hat_sqaured = MathAbs((y_train - y_hat_train)); mae_train.Set(0,( y_minus_y_hat_sqaured.Mean())); vector x_times_y_minus_y_hat = (x_train*(y_train -y_hat_train)); //Aproximate the derivatives double derivative_m = (-2.0/n) * x_times_y_minus_y_hat.Sum(); double derivative_b = (-2.0/n) * y_minus_y_hat.Sum(); //Update the linear parameters m[0] = m[0] - (learning_rate * derivative_m); b[0] = b[0] - (learning_rate * derivative_b); } //Finished fitting the coefficients Print("Fit on training data complete.\nm: ",m[0]," b: ",b[0]," mae ",mae_train[0],"\nlearning rate: ",learning_rate); if(allowed_to_evaluate) { Evaluate(learning_rate_power,epochs_power); } //Return true return(true); }
Let's move on to defining our evaluate function. The function is responsible for selecting the best learning rate for each symbol we trade. We start of by verifying the validity of our coefficients. If the coefficients are zero or contain NaN values, they are reset.
The rationale behind this validation process is to meticulously select coefficients that yield the lowest validation error across varying learning rates. Invalid coefficients, marked by high validation errors, are excluded from consideration during the coefficient selection phase. Conversely, valid coefficients are stored for further analysis.
Subsequently, we use these stored coefficients to generate predictions on our validation data and evaluate the error. This iterative process involves updating learning rates, fitting the model, and assessing errors. The maximum iteration limit set at 30,which corresponds to the maximum learning rate power.
Throughout the evaluate function, a continuous check ensures the index remains within the bounds of the maximum learning rate power. We collect the absolute error data into a vector for efficient processing, employing vector functions like vector.Min() and Argmin() to pinpoint the learning rate power associated with the lowest validation error.
//This function evaluates the current coefficient settings and learning rate bool LinearRegression::Evaluate(ulong _index) { Print("Evaluating the coefficients m:",m[0]," b: ",b[0]," at learning rate: ",learning_rate); //First check if the coefficient and learning rate are valid if((m.HasNan() > 0 || b.HasNan() > 0 || m[0] == 0 || b[0] == 0 || _index > max_learning_rate_power) && (_index < max_learning_rate_power)) { Print("Coefficients are invalid"); m[0] = 0; b[0] = 0 ; mae_array[_index] = MathPow(10,100000); //Update the learning rate UpdateLearningRate(); //Fit the model again Fit(); } else { //Validation predictions if(_index < max_learning_rate_power) { Print("Coefficients are valid, solution at index ",_index); y_hat_validation = (m[0] * x_validation) + b[0]; vector y_minus_y_hat_squared = MathAbs(y_validation - y_hat_validation); //If everything is fine, let's assess the validation mae mae_array[_index] = (1.0/n) * y_minus_y_hat_squared.Sum(); //What was the validation error? Print("Validation error: ",(1.0/n) * y_minus_y_hat_squared.Sum()); //Update the learning rate UpdateLearningRate(); //Fit the model again Fit(); } } if(_index == max_learning_rate_power) { for(int i = 0; i < max_learning_rate_power;i++) { mae_validation[i] = mae_array[i]; } allowed_to_evaluate = false; trained = true; Print("Validation mae: \n",mae_validation); Print("Lowest validation mae: ",mae_validation.Min()); ulong chosen_learning_rate = mae_validation.ArgMin(); Print("Chosen learning rate ",MathPow(0.1,(chosen_learning_rate))); SetLearningRate(chosen_learning_rate); Fit(); } return(true); }
We will also define a function for scaling our inputs. This function is easy to understand, it divides all our inputs by the first entry in our training vector.
//This function will scale our inputs bool LinearRegression::ScaleInputs(void) { //Set the first reading first_reading = x_train[0]; x_train = x_train / first_reading; x_validation = x_validation / first_reading; return(true); }
From there we define the destrcutor, the destrcutor resets all the coefficients we just optimized.
LinearRegression::~LinearRegression()
{
ResetLearningRate();
ResetLastError();
} The functions being called by the destructor are defined as follows
bool LinearRegression::ResetLearningRate(void) { learning_rate_power = 0; learning_rate = MathPow(0.1,learning_rate_power); return(true); }
When we put it all together, this becomes our class definition:
#property copyright "Gamuchirai Ndawana" #property link "https://www.mql5.com" #property version "1.00" class LinearRegression { private: //This is the highest power that we will raise ten to, as we are searching for coefficients ulong max_learning_rate_power; //This is how many bars we should fetch int fetch; //This is where we will start collecting data, it is the end of our validation data set. datetime start,predict; //This is how many steps into the future we want to forecast int look_ahead; //This is the array that will contain our MAE readings from testing different learning rates on the validation data double mae_array[30]; //Trained flag to inform us if the model has been fit and optimised succesfuly and is ready for use bool trained; //The number to raise the power of 10 buy when calculating the number of epochs int epochs_power; //Our error metrics vector mae_train,mae_validation; //This vector contains our inputs validation and training set vector x_validation,x_train; //This vector contains our outputs validation and training set vector y_validation,y_train; //This vector contains our predictions on the validation set vector y_hat_validation,y_hat_train; //This vector contains our gradient coefficient vector m; //This vector contains our model bias vector b; //This is our model's forecast double forecast; //This is our current learning rate power ulong learning_rate_power; //This is the learning rate power we are currently evaluating int lr_error_index; //This is our current learning rate double learning_rate; //This is the number of rounds we will allow whilst training our model double epochs; //This is used in calculations, it is the number of rows in our data, or the fetch size. ulong n; //These are the times for our input and output data datetime output_end,output_start,input_end,input_start; //These are the index times for our input and output data int index_output_end,index_output_start,index_input_end,index_input_start; //This is the value we will use to scale our data double first_reading; bool allowed_to_evaluate; //Update the learning rate bool UpdateLearningRate(void); //Update the number of epochs bool UpdateEpochs(void); //Set the number of epochs bool SetEpochs(int _epochs_power); //Reset the number of epochs bool ResetEpochs(void); //Reset the learning rate bool ResetLearningRate(void); //This function will fit the coeffeicients bool Fit(void); //This function evaluates the current settings bool Evaluate(ulong _index); //This function will scale the input data bool ScaleInputs(void); //This function sets the learning rate bool SetLearningRate(ulong _learning_rate_power); public: //Constructor LinearRegression(); //Fetch Current Validation Data bool GetCurrentValidationData(void); //Initialise the LinearRegressor Model void Init(int _fetch,int _look_ahead); //Function to determine if the model has been trained and is ready for use. bool Trained(void); //A function to train the model using the best learning rate and the most recent prices bool Train(void); //A function to predict future price using the current price. double Predict(void); //Destructor ~LinearRegression(); }; bool LinearRegression::UpdateEpochs(void) { epochs_power = epochs_power + 1; epochs = MathPow(10,epochs_power); return(true); } bool LinearRegression::ResetEpochs(void) { epochs_power = 0 ; epochs = MathPow(10,epochs_power); return(true); } bool LinearRegression::SetEpochs(int _epochs_power) { epochs_power = _epochs_power; epochs = MathPow(10,epochs_power); return(true); } double LinearRegression::Predict(void) { if(Trained()) { double _current_reading = iClose(_Symbol,PERIOD_CURRENT,0); predict = iTime(_Symbol,PERIOD_CURRENT,0); double prediction = (m[0]*_current_reading)+b[0]; if(prediction > _current_reading) { Comment("Buy, forecast: ",prediction); } else if(prediction < _current_reading) { Comment("Sell, forecast: ",prediction); } ObjectCreate(0,"prediction point",OBJ_VLINE,0,predict,0); ObjectCreate(0,"forecast",OBJ_HLINE,0,predict,prediction); return(prediction); } return(0); } bool LinearRegression::GetCurrentValidationData(void) { //Indexes index_output_end = 1; index_output_start = index_output_end + fetch; index_input_end = index_output_end + look_ahead; index_input_start = index_output_start + look_ahead; //Assigning time stamps output_end = iTime(Symbol(),PERIOD_CURRENT,index_output_end); output_start = iTime(Symbol(),PERIOD_CURRENT,index_output_start); input_end = iTime(Symbol(),PERIOD_CURRENT,index_input_end); input_start = iTime(Symbol(),PERIOD_CURRENT,index_input_start); //Get the output data if(!y_validation.CopyRates(_Symbol,PERIOD_CURRENT,COPY_RATES_CLOSE,output_end,fetch)) { Print("Failed to get market data: ",GetLastError()); return(false); } //Get the input data if(!x_validation.CopyRates(_Symbol,PERIOD_CURRENT,COPY_RATES_CLOSE,input_end,fetch)) { Print("Failed to get market data: ",GetLastError()); return(false); } //Print the vectors we have if(x_validation.Size() != y_validation.Size()) { Print("Failed to get market data: Our vectors aren't the same length."); return(false); } //Print the vectors and plot the data points Print("X validation: ",x_validation); ObjectCreate(0,"X validation end",OBJ_VLINE,0,input_end,0); ObjectCreate(0,"X validation start",OBJ_VLINE,0,input_start,0); //Print the vectors and plot the data points Print("y validation: ",y_validation); ObjectCreate(0,"y validation end",OBJ_VLINE,0,output_end,0); ObjectCreate(0,"y validation start",OBJ_VLINE,0,output_start,0); //Set the training data index_output_end = index_input_start + (look_ahead * 2); index_output_start = index_output_end + fetch; index_input_end = index_output_end + look_ahead; index_input_start = index_output_start + look_ahead; //Assigning time stamps output_end = iTime(Symbol(),PERIOD_CURRENT,index_output_end); output_start = iTime(Symbol(),PERIOD_CURRENT,index_output_start); input_end = iTime(Symbol(),PERIOD_CURRENT,index_input_end); input_start = iTime(Symbol(),PERIOD_CURRENT,index_input_start); //Copy the training data if(!y_train.CopyRates(_Symbol,PERIOD_CURRENT,COPY_RATES_CLOSE,output_end,fetch)) { Print("Error fetching training data ",GetLastError()); } //Copy the training data if(!x_train.CopyRates(_Symbol,PERIOD_CURRENT,COPY_RATES_CLOSE,input_end,fetch)) { Print("Error fetching training data ",GetLastError()); } //Check if the data matches if(x_train.Size() != y_train.Size()) { Print("Error fetching training dataL: The x and y vectors are not the same size"); } //Print the vectors and plot the data points Print("X training: ",x_train); ObjectCreate(0,"X training end",OBJ_VLINE,0,input_end,0); ObjectCreate(0,"X training start",OBJ_VLINE,0,input_start,0); Print("y training: ",y_train); ObjectCreate(0,"y training end",OBJ_VLINE,0,output_end,0); ObjectCreate(0,"y training start",OBJ_VLINE,0,output_start,0); return(true); } bool LinearRegression::Train(void) { m = vector::Zeros(1); //Set the bias to a random value b = vector::Zeros(1); forecast = 0; if(GetCurrentValidationData()) { if(Fit()) { Print("Model last updated: ",iTime(_Symbol,PERIOD_CURRENT,0)); return(true); } } return(false); } void LinearRegression::Init(int _fetch,int _look_ahead) { //Clear The Chart ObjectsDeleteAll(0); //Allow evaluations allowed_to_evaluate = true; //Epochs power epochs_power =4; //Set the number of epochs epochs = 5 * MathPow(10,epochs_power); //Has the model been trained? trained = false; //Set the maximum learning rate power max_learning_rate_power = 30; //Set the end of our validation data start = iTime(_Symbol,PERIOD_CURRENT,1); //This is how much data we're going to fetch this.fetch = _fetch - 1; //This is how far into the future we want to forecast this.look_ahead = _look_ahead + 1; //Set the gradient coefficient to a random value m = vector::Zeros(1); //Set the bias to a random value b = vector::Zeros(1); //Set the forecast to 0 forecast = 0; //Our model's learning rate will start at 0 learning_rate_power = 0; //This is the learning rate we are evaluting lr_error_index = 0; mae_train = vector::Full(1,MathPow(10,100)); mae_validation = vector::Full(30,MathPow(10,10000)); //Set the initial learning rate learning_rate = MathPow(0.1,(learning_rate_power)); //Set the number of rows n = fetch; if(GetCurrentValidationData()) { //Scale the data ScaleInputs(); //Fit the model Fit(); } } bool LinearRegression::Trained(void) { return(trained); } bool LinearRegression::SetLearningRate(ulong _learning_rate_power) { learning_rate_power = _learning_rate_power; learning_rate = MathPow(0.1,(learning_rate_power)); return(true); } bool LinearRegression::UpdateLearningRate(void) { learning_rate_power = learning_rate_power + 1; learning_rate = MathPow(0.1,(learning_rate_power)); Print("New learning rate: ",learning_rate," learning rate power: ",learning_rate_power); return(true); } bool LinearRegression::ResetLearningRate(void) { learning_rate_power = 0; learning_rate = MathPow(0.1,learning_rate_power); return(true); } LinearRegression::LinearRegression() { Print("Current Symbol: ",_Symbol); } bool LinearRegression::Fit() { Print("Fitting a linear regression on the training set with learning rate ",learning_rate_power); Print("Evalutaions: ",allowed_to_evaluate); for(int i =0; i < epochs;i++) { //Measure error y_hat_train = (m[0]*x_train) + b[0]; vector y_minus_y_hat = (y_train - y_hat_train); vector y_minus_y_hat_sqaured = MathAbs((y_train - y_hat_train)); mae_train.Set(0,( y_minus_y_hat_sqaured.Mean())); vector x_times_y_minus_y_hat = (x_train*(y_train -y_hat_train)); //Aproximate the derivatives double derivative_m = (-2.0/n) * x_times_y_minus_y_hat.Sum(); double derivative_b = (-2.0/n) * y_minus_y_hat.Sum(); //Update the linear parameters m[0] = m[0] - (learning_rate * derivative_m); b[0] = b[0] - (learning_rate * derivative_b); } //Finished fitting the coefficients Print("Fit on training data complete.\nm: ",m[0]," b: ",b[0]," mae ",mae_train[0],"\nlearning rate: ",learning_rate); if(allowed_to_evaluate) { Evaluate(learning_rate_power); } //Return true return(true); } //This function evaluates the current coefficient settings and learning rate bool LinearRegression::Evaluate(ulong _index) { Print("Evaluating the coefficients m:",m[0]," b: ",b[0]," at learning rate: ",learning_rate); //First check if the coefficient and learning rate are valid if((m.HasNan() > 0 || b.HasNan() > 0 || m[0] == 0 || b[0] == 0 || _index > max_learning_rate_power) && (_index < max_learning_rate_power)) { Print("Coefficients are invalid"); m[0] = 0; b[0] = 0 ; mae_array[_index] = MathPow(10,100000); //Update the learning rate UpdateLearningRate(); //Fit the model again Fit(); } else { //Validation predictions if(_index < max_learning_rate_power) { Print("Coefficients are valid, solution at index ",_index); y_hat_validation = (m[0] * x_validation) + b[0]; vector y_minus_y_hat_squared = MathAbs(y_validation - y_hat_validation); //If everything is fine, let's assess the validation mae mae_array[_index] = (1.0/n) * y_minus_y_hat_squared.Sum(); //What was the validation error? Print("Validation error: ",(1.0/n) * y_minus_y_hat_squared.Sum()); //Update the learning rate UpdateLearningRate(); //Fit the model again Fit(); } } if(_index == max_learning_rate_power) { for(int i = 0; i < max_learning_rate_power;i++) { mae_validation[i] = mae_array[i]; } allowed_to_evaluate = false; trained = true; Print("Validation mae: \n",mae_validation); Print("Lowest validation mae: ",mae_validation.Min()); ulong chosen_learning_rate = mae_validation.ArgMin(); Print("Chosen learning rate ",MathPow(0.1,(chosen_learning_rate))); SetLearningRate(chosen_learning_rate); Fit(); } return(true); } //This function will scale our inputs bool LinearRegression::ScaleInputs(void) { //Set the first reading first_reading = x_train[0]; x_train = x_train / first_reading; x_validation = x_validation / first_reading; return(true); } LinearRegression::~LinearRegression() { ResetLearningRate(); ResetEpochs(); ResetLastError(); }
Now that we have defined our LinearRegression class we are ready to use it in our expert advisor.
We begin by creating a new expert advisor and including the class in our expert advisor.
#property copyright "Gamuchirai Zororo Ndawana" #property link "https://www.mql5.com" #property version "1.00" //Include our linear regression class #include <LinearRegression/LinearRegression.mqh> LinearRegression ExtLinearRegression;
The above code calls the default constructor of our LinearRegression class.
From there we also include other useful classes.
//Include the trade class #include <Trade/Trade.mqh> CTrade Trade;
We define the inputs needed by our expert advisor.
//Inputs int input look_ahead = 10; //How many steps into the future should we forecast? int input fetch_data = 100; //How much data should we fetch? int input ma_period = 10; //Moving Average Period int input rsi_period = 10; //RSI Period int input wr_period = 10; //Williams Percent R Period
We will also define other variables useful for technical analysis, such as the minimum trading volume allowed and vectors to store our indicator buffers.
//Technical Analysis double min_volume =SymbolInfoDouble(_Symbol,SYMBOL_VOLUME_MIN); //Indicator Handlers int ma_handler,rsi_handler,wr_handler,total_time; vector ma_vector,rsi_vector,wr_vector; double _price; ulong _ticket;
Once complete we are now ready to define the OnInit() handler for our expert advisor, our handler initialises our linear regression object using the parameters the user passed to the expert advisor, and then it set's up our technical indicators.
int OnInit() { //Setup our model ExtLinearRegression.Init(fetch_data,look_ahead); //Keep Track Of Time total_time = 0; //Set up our technical indicators ma_handler = iMA(_Symbol,PERIOD_CURRENT,ma_period,0,MODE_EMA,PRICE_CLOSE); rsi_handler = iRSI(_Symbol,PERIOD_CURRENT,rsi_period,PRICE_CLOSE); wr_handler = iWPR(_Symbol,PERIOD_CURRENT,wr_period); return(INIT_SUCCEEDED); }
We now arrive at the on tick function. The on tick function keeps track of time, allowing us to perform certain actions after every new candle and some actions after every tick. On each new candle, if the total number of candles that have elapsed are greater than the forecast horizon the user selected, we need to train our model again using the Train funciton we implemented. Furthermore we would like to update the indicator values we have on record using another useful vector function CopyIndicatorBuffer. We have created a function responsible for this. Laslty if we have an open position, we have created a function responsible for managing open positions.
void OnTick() { //--- static datetime time_stamp; datetime current_time = iTime(_Symbol,PERIOD_CURRENT,0); if(time_stamp != current_time) { //Update the values of the indicators update_vectors(); total_time += 1; if(total_time > look_ahead) { total_time = 0; //Let the model adapt to the market dynamically ExtLinearRegression.Train(); } //If our model is ready then let's start trading if(ExtLinearRegression.Trained()) { if(PositionsTotal() == 0) { analyse_indicators(); } } if(PositionsTotal() == 1) { //Get position ticket _ticket = PositionGetTicket(0); //Manage the position manage_position(_ticket); } time_stamp = current_time; } }
This function is responible for fetching the most uptodate bars avaialble from our broker.
void update_vectors(void) { //Get the current reading of our indicators ma_vector.CopyIndicatorBuffer(ma_handler,0,1,1); rsi_vector.CopyIndicatorBuffer(rsi_handler,0,1,1); wr_vector.CopyIndicatorBuffer(wr_handler,0,1,1); _price = iClose(_Symbol,PERIOD_CURRENT,1); }
This function is responsible for intepreting our indicators and our model's forecast. If all of them are alligned then we can open a trade otherwise, we will wait for them to allign.
void analyse_indicators(void) { double forecast = ExtLinearRegression.Predict(); Comment("Forecast: ",forecast," Price: ",_price); //If price is above the moving average, check if the other indicators also confirm the buy signal if(_price - ma_vector[0] > 0) { if(rsi_vector[0] > 50) { if(wr_vector[0] > -20) { if(forecast > _price) { Trade.Buy(min_volume,_Symbol,SymbolInfoDouble(_Symbol,SYMBOL_ASK),0,0); } } } } //If price is below the moving average, check if the other indicators also confirm the sell signal if(_price - ma_vector[0] < 0) { if(rsi_vector[0] < 50) { if(wr_vector[0] < -80) { if( forecast < _price) { Trade.Sell(min_volume,_Symbol,SymbolInfoDouble(_Symbol,SYMBOL_BID),0,0); } } } }
This function is responsible for managing any open positions we have and setting up the stop loss and take profit dynamically based on current volatility levels in the market. Notice that it will only modify the position if the position has no stop loss or take profit.
void manage_position(ulong m_ticket) { if(PositionSelectByTicket(m_ticket)) { double volatility = 2 * MathAbs(ma_vector[0] - _price); double entry = PositionGetDouble(POSITION_PRICE_OPEN); double current_sl = PositionGetDouble(POSITION_SL); double current_tp = PositionGetDouble(POSITION_TP); if(PositionGetInteger(POSITION_TYPE) == POSITION_TYPE_BUY) { double new_sl = _price - volatility; double new_tp = _price + volatility; if(current_sl == 0 || current_tp == 0) { Trade.PositionModify(m_ticket,new_sl,new_tp); } } if(PositionGetInteger(POSITION_TYPE) == POSITION_TYPE_SELL) { double new_sl = _price + volatility; double new_tp = _price - volatility; if(current_sl == 0 || current_tp == 0) { Trade.PositionModify(m_ticket,new_sl,new_tp); } } } }
Our expert advisor now looks like this
Fig 3: Self optimizing expert EA.
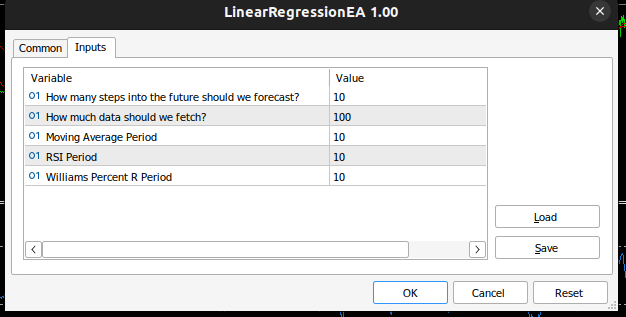
Fig 4: Inputs for our self optimizing EA.
Whenever you apply the Expert on any Symbol you can see the calculations its performing on your behalf in the experts tab
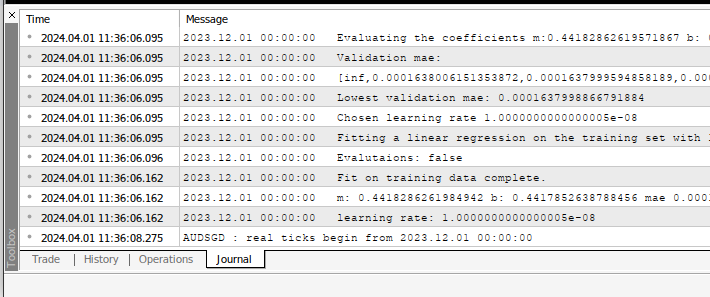
Fig 5: The calculations performed by our expert advisor.
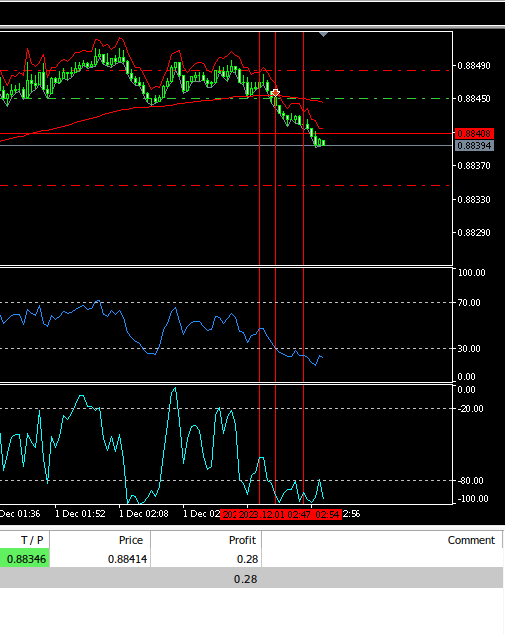
FIg 6: Backtesting our EA.
Recommendations
This article taught the simplest method possible for building self optimisng EA's. However this is not the best approach possible,this is a manual search for optmial coefficients. The ideal solution would employ more advanced matrix and vector calculations to automatically find the optimal coefficients. In fact, when we use matrix and vector functions, we can build our linear regression model without ever using a single for loop. Our code will be more compact and our coefficients will be more numerically stable. Manual searches do not always gaurentee solutions.
Conclusion
Building self adapting expert advisors in MQL5 is easy thanks to the powerfull matrix and vector functions in the MQL5 API. In truth what we can build in MQL5 is only limited by our understanding of the API.
 Neural networks made easy (Part 67): Using past experience to solve new tasks
Neural networks made easy (Part 67): Using past experience to solve new tasks
 Neural networks made easy (Part 66): Exploration problems in offline learning
Neural networks made easy (Part 66): Exploration problems in offline learning
 MQL5 Wizard Techniques You Should Know (Part 15): Support Vector Machines with Newton's Polynomial
MQL5 Wizard Techniques You Should Know (Part 15): Support Vector Machines with Newton's Polynomial
 Introduction to MQL5 (Part 6): A Beginner's Guide to Array Functions in MQL5 (II)
Introduction to MQL5 (Part 6): A Beginner's Guide to Array Functions in MQL5 (II)
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
I love your proactive approach. You're right, there are several exceptions that may get raised when trying to fetch historical data. For example, if you try to change time frames in the middle of a trading session, the "-nan" issue may be observed yet again.
There was an inherent tradeoff between keeping the message easy to follow and fixing all the bugs I observed. If I went for the latter, the code may have been necessarily more complex and not as easy to follow as it is. So I decided to keep it easy to follow, with the intentions that you would be able to rapidly extend it.
Your solution sounds very promising, how is it turning out?
I have tried running the LinearRegressionEA and find it an exciting concept. I trade mostly GOLD CFDs and established a liking for the WPR indicator in this example.
Sometimes I get incorrect Prediction prices that are way out of range with a factor 100, but sometimes correct !
If someone figure that issue out I would appreciate that a lot. Debugging linear regression code is not my expertise.
I did not see if you wrote anything about preferred Period for trading, I have it set at 30 Minutes.
In that scenario,
if there is not yet a trade
and the EA runs its 'analyse_indicators()' function,
this is done once per bar, so in my case once every 30 minutes.
So it means if the indicators does not line up for a trade decision this is not attempted again until next bar, in my case 30 minutes later.
IMO this is too far between for establishing the initial trade,
so I added a Timer task that runs the analyse step every 10 seconds until indicators are in favor for a trade;
I establish the Buy or Sell order and then return to the regular per bar processing of the manage_position() function.
Thank you for your valuable commitment, especially for the opportunity to open our minds to new horizons - which is the most important thing I think.
I have practical and maybe naive questions
thank you
have a great time
Hey Giulio.
To setup a magic number and a custom comment, you would simply extend the code by calling the appropriate function instead.
I think the PositionOpen may be what you're looking for, you can check the documentation with this link.
If that doesn't satisfy what you need, try this YouTube tutorial using this link.
If none of these resources are able to help you, then I have a channel where I post more helpful articles like these. You can find it using this link.
Hello again I had to create my account again to login. Anyway,
I have tried running the LinearRegressionEA and find it an exciting concept. I trade mostly GOLD CFDs and established a liking for the WPR indicator in this example.
Sometimes I get incorrect Prediction prices that are way out of range with a factor 100, but sometimes correct !
If someone figure that issue out I would appreciate that a lot. Debugging linear regression code is not my expertise.
I did not see if you wrote anything about preferred Period for trading, I have it set at 30 Minutes.
In that scenario,
if there is not yet a trade
and the EA runs its 'analyse_indicators()' function,
this is done once per bar, so in my case once every 30 minutes.
So it means if the indicators does not line up for a trade decision this is not attempted again until next bar, in my case 30 minutes later.
IMO this is too far between for establishing the initial trade,
so I added a Timer task that runs the analyse step every 10 seconds until indicators are in favor for a trade;
I establish the Buy or Sell order and then return to the regular per bar processing of the manage_position() function.
I'm sorry to hear you were experiencing difficulties logging in, I trust you've gotten that fixed by now.
You are correct, the predictions given by our current model may at times be out of the acceptable range by a wide margin, but there is no bug in the code.
Let me explain why we can expect this to happen.
We are using a simple implementation of the Gradient Descent algorithm to optimise our model coefficients. Unfortunately, Gradient Descent can be sensitive to the starting positions of our coefficients. To remedy this, the Stochastic Gradient Descent (SGD) algorithm was developed. SGD performs optimisations by changing the starting coefficients each time to maximise the probability of finding optimal coefficients. For simplicity, we kept our coeffiecients fixed and this may cause the model to get stuck in dismal states. This youtube video may be helpful, use this link.
Yes you are right, I intentionally called for calculations to be performed on every candle. This was done to speed up backtests, to turn this feature off simply delete the condition check "if(timestamp != current_time)".
Furthermore, there are ways we can build our model such that it customises itself to the data we have at hand, you can find that information using this link.
Hi, it's amazing! Thanks!
I get this lines:
How can I fix this?
does any one have also this problem?
Hi, it's amazing! Thanks!
I get this lines:
How can I fix this?
does any one have also this problem?
Hey Javier, Could you upload more of the output from the terminal?
Because what you shared seems normal, I would expect output like that.
However, the problem I'm noticing with your output is the "0.0" at the end. Getting an error of 0.0 implies the model is perfect, which isn't realistically possible.