Sie verpassen Handelsmöglichkeiten:
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Registrierung
Einloggen
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Wenn Sie kein Benutzerkonto haben, registrieren Sie sich
Interessant. Erstens ist sie ungenau, denn es sind nicht die "Quadrate", sondern die "Summe der Quadrate", die minimiert werden soll. Zweitens, wenn man den letzten Punkten einen größeren Wert geben will, ist es einfach, in der minimierten Summe nicht nur Quadrate, sondern gewichtete Quadrate zu nehmen, die mit einigen positiven Gewichtungskoeffizienten multipliziert werden. Ihre Werte am Ende des Arrays sollten größer sein, die am Anfang kleiner. Für eine Anzahl von Punkten i von 1 bis n ergeben beispielsweise Gewichte gleich q^(n-i) mit q < 1 Quadrate von Abweichungsmultiplikatoren, die den Gewichten von Kursen in einem exponentiellen gleitenden Durchschnitt ähneln. Oft wird ihre Summe auch gleich eins gemacht, wenn wir verschiedene Annäherungen anhand des Wertes der minimalen gewichteten Summe der Quadrate der Abweichung vergleichen wollen.
Und was ist der "Mittelpunkt" eines gekrümmten Kanals, dessen Grenzen durch verschiedene Formeln beschrieben werden? Oder zumindest für die erste Variante, durch Exponentialfunktionen?
Wenn es sich einfach um den Mittelpunkt des Abschnitts zwischen dem vorletzten und dem letzten Wert der Reihe handelt, reicht es aus, die Abweichungsgewichte in den letzten beiden Punkten der Reihe sehr groß zu machen. Man braucht andere Voraussetzungen für die Abweichungen, sonst ist das Problem untertrieben.
Sie sehen doch die Mitte im horizontalen Kanal, oder?
ist hier dasselbe. Sie sollten die Funktion so auswählen, dass ihr letzter Punkt nach Augenmaß in der Mitte des Preiskanals liegt.
Und was ist der "Mittelpunkt" eines gekrümmten Kanals, dessen Grenzen durch verschiedene Formeln beschrieben werden? Oder zumindest bei der ersten Variante durch indikative Funktionen?
Wenn Sie es so genau brauchen: Nehmen Sie den oberen Teil des Kreises, wenden Sie ein bestimmtes Rauschen darauf an. Das wird die Zeitreihe sein. Dann regressieren Sie die Funktion auf diese Zeitreihe.
Wenn das Ende des Funktionsgraphen mit dem Ende des Kreisgraphen zusammenfällt, den Sie für die Konstruktion Ihrer Zeitreihe verwendet haben, wird das der "Mittelpunkt des Kanals" sein.
Was nützt es, den "Mittelpunkt" am letzten Punkt zu berechnen?
Der Indikator ist ein gleitender Indikator. Es wird nur der äußerste Punkt genommen.
ist dasselbe wie der Bindestrich. Es ist die mittlere Linie, von der nur der letzte Punkt genommen wurde.
Bei mir ist ein Kanal ein Rauschen, das eine bestimmte Flugbahn überlagert.
Ein Handelskanal kann eine Trajektorie sein:
Mash kann nur mit einem horizontalen Handelskanal umgehen.
Es ist wichtig, eine Funktion zu finden, die alle diese Arten von Flugbahnen verarbeiten kann.
Nun, in einem horizontalen Kanal sehen Sie die Mitte, nicht wahr?
Auch hier müssen Sie die Funktion so wählen, dass ihr letzter Punkt in der Mitte des Preiskanals liegt.
Wenn Sie es so genau brauchen: Nehmen Sie den oberen Teil des Kreises, wenden Sie ein bestimmtes Rauschen darauf an. das wird die Zeitreihe sein.
Wenn das Ende des Funktionsgraphen mit dem Ende des Kreisgraphen übereinstimmt, den Sie für die Darstellung Ihrer Zeitreihe verwendet haben, ist dies der "Mittelpunkt des Kanals".
Wozu? Es ist ein beweglicher Indikator. Nur der äußerste Punkt wird erfasst.
Es ist dasselbe wie bei einer sich bewegenden Welle. Es ist die mittlere Linie, von der Sie nur den letzten Punkt genommen haben.
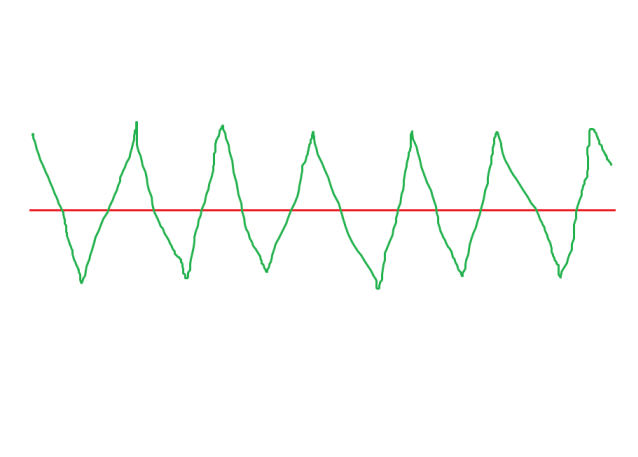
Wie die rote Linie konstruiert ist, verstehe ich nicht. Wenn Sie die Kurspunkte (grün in der Abbildung) mit denselben Excel-Tools glätten (Erstellung eines Trends durch lineares Filtern über 5 Punkte), erhalten Sie eine Kurve, die viel näher am Verlauf liegt als die (rote) horizontale Linie, und es gibt keine einfache Mittellinie mehr.
Wenn Sie bereits eine Möglichkeit haben, die Verlaufskurven zu klassifizieren und nur die Enden der Mittellinien finden müssen, dann bestimmt die Klassifizierung selbst (Kreis, horizontale Gerade, schräge Gerade usw.) die Wahl der Näherungsfunktion. Allerdings ist es sehr seltsam, dass sie auch durch einen einzigen Endpunkt des Kurses führen muss. Entweder Sie approximieren die Punkte über das gesamte betrachtete Intervall oder Sie nehmen nur den letzten Punkt - das sind unterschiedliche Aufgaben.
Die Art und Weise, wie Sie über den Kreis und das Rauschen berichtet haben, ist nicht nur eine Funktionsannäherung, sondern eine Rekonstruktion der Abhängigkeit (die im Gegensatz zum Kreis im Voraus nicht bekannt ist), was viel komplizierter ist. Bei Interesse suchen Sie bitte hier im Wapnick-Forum.
P.S. Zu "Der Verlauf des Handelskanals kann sein:". Ich habe gelesen, dass ein berühmter Philosoph des frühen 20. Jahrhunderts gesagt hat, dass es am schwierigsten ist, herauszufinden, was sich hinter dem Wort "dies" verbirgt. Glauben Sie, dass Ihre Klassifizierung der Flugbahnen bei allen Lesern denselben Eindruck erweckt? Man kann die Eigenschaften jeder der von Ihnen in der Abbildung gezeigten Flugbahnen auf sehr unterschiedliche Weise charakterisieren..."Extrapolationen durch Polynom- und Fourier-Methoden sind von völlig anderer Natur. Die Fourier-Extrapolation kann nur auf einen flachen Markt angewandt werden, da dieser periodisch ist (die Linie ist die Summe von Sinuskurven mit unterschiedlicher Frequenz, Phase und Amplitude) und immer wiederkehrt.
Die Polynomextrapolation ist dagegen gut für einen Trend geeignet, da sie aufgrund ihres Grades immer wieder versucht, nach unten oder oben zu "fliegen". "Nikolai Semko
Es gibt noch mehr:
Es ist also sehr sinnvoll, die beiden Methoden zu kombinieren. Eine einfache Aufzählung reicht hier natürlich nicht aus. Aber ich habe eine klare Vorstellung davon, wie man sie am besten kombiniert
Entweder Sie approximieren die Punkte über das gesamte betrachtete Intervall oder Sie nehmen nur den letzten Punkt - das sind unterschiedliche Aufgaben.
Nähern Sie sich den Punkten auf dem gesamten betrachteten Intervall und sehen Sie, wohin der letzte Punkt fallen wird.
Wie die rote Linie konstruiert ist, verstehe ich nicht. Wenn man die Punkte des Verlaufs (grün in der Abbildung) mit denselben Excel-Tools glättet (um einen Trend durch lineares Filtern nach 5 Punkten zu erstellen), erhält man keine (rote) horizontale Linie, sondern eine Kurve, die viel näher am Verlauf liegt, und eine so einfache Mitte wird es nicht mehr geben.
es ist nur eine durchschnittliche Zeile. Summe der Preise / durch ihre Anzahl. nicht stören)
Glauben Sie, dass Ihre Klassifizierung der Flugbahnen bei allen Lesern denselben Eindruck erweckt? Man kann die Eigenschaften jeder der von Ihnen in der Abbildung gezeigten Flugbahnen auf sehr unterschiedliche Weise charakterisieren...
Nun, ich verwende Polynomial, also sind es "verschiedene Teile einer Parabel".

Sie könnten auch versuchen, einen Bogen zu verwenden, aber ich weiß nicht, wie man damit eine Regression durchführt.
Können Sie von hier aus die Bogengleichung ableiten, um sie in Excel zu bewerten?
http://sci.sernam.ru/book_geom.php?id=39
es gibt noch eine Fortsetzung:
DasProblem bleibt dasselbe, wir müssen eine Funktion finden, deren letzter Punkt in der Mitte des Preiskanals liegt.
Es gibt keine solche Funktion, Sie brauchen nichtparametrische Methoden, die einfachste ist SMA, die komplizierteste ist hier
https://www.mql5.com/ru/forum/221552/page523#comment_8560475
Die Flugbahn des Handelskanals kann sein:
Der Trick dabei ist, dass sich die Flugbahn plötzlich ändern kann und dann alle Näherungen zum Teufel gehen.
Sie können die Mitte in einem horizontalen Kanal sehen, richtig?
Auch hier können Sie die Funktion so wählen, dass ihr letzter Punkt in der Mitte des Preiskanals liegt.
Wenn Sie es so genau brauchen: Nehmen Sie den oberen Teil des Kreises, wenden Sie ein bestimmtes Rauschen darauf an. das wird die Zeitreihe sein. dann regressieren Sie die Funktion auf diese Zeitreihe.
Wenn das Ende des Funktionsgraphen mit dem Ende des Kreisgraphen übereinstimmt, den Sie zur Erstellung Ihrer Zeitreihe verwendet haben, ist dies der "Mittelpunkt des Kanals".
Wozu? Es ist ein beweglicher Indikator. Nur der äußerste Punkt wird erfasst.
Es ist dasselbe wie bei einer sich bewegenden Welle. Es ist die Mittellinie, von der man nur den letzten Punkt nimmt.
Ich verstehe nicht ganz, warum Sie die ANC-Methode und die Polynome nicht mögen, der Kanal ist doch einfach zu bauen...
Hier ist ein weiteres Diagramm für Sie. Parabolische Interpolation, Kanalbreite - 0,9 der maximalen Hüllkurve