Sie verpassen Handelsmöglichkeiten:
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Registrierung
Einloggen
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Wenn Sie kein Benutzerkonto haben, registrieren Sie sich
Was ist mit dem Armaturenbrett los?


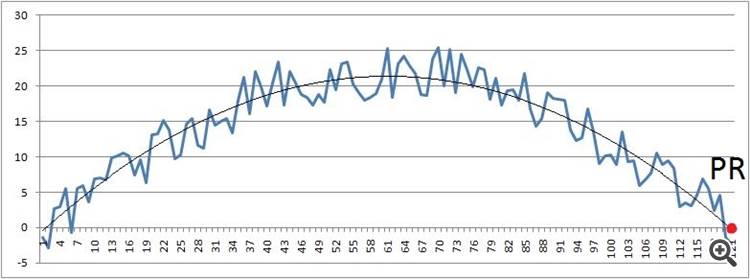
Sie zeigt den Durchschnittswert des Diagramms an. Was wäre der Durchschnittswert eines Graphen, der von Punkt 0 bis Punkt 10 ansteigt?
5.
Die Skala steht jetzt also bei 5. Auch wenn die Grafik bereits bei 10.
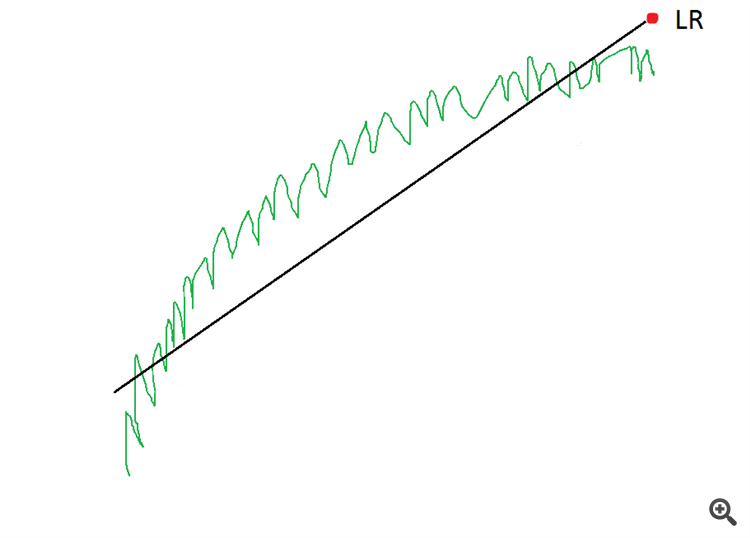
Eine lineare Regression ist hilfreich.
Die Linie einer linearen Regression wird durch die Mitte des Preiskanals verlaufen, und der letzte Punkt dieser Linie wird bei 10 liegen.
Aber Kanäle sind nicht immer gerade. Einige Kanäle sind bogenförmig. In diesem Fall wird die LR nicht gut funktionieren.
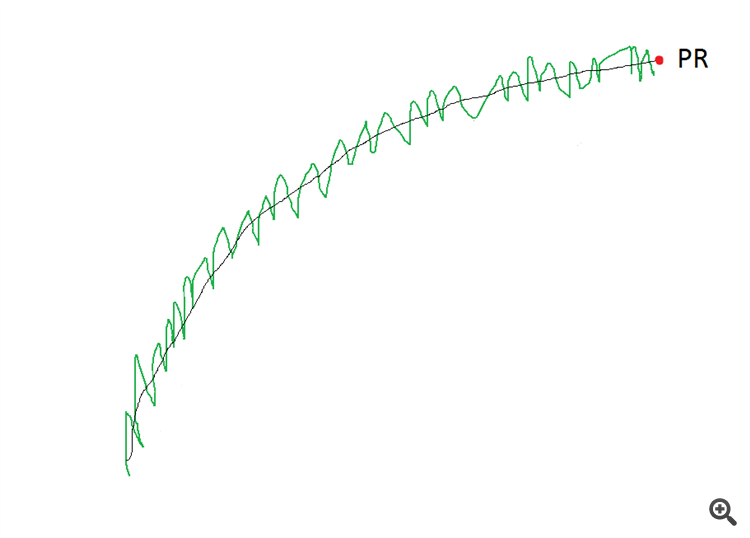
Hier kommt die polynomiale Regression zum Einsatz.
Der OR-Plot verläuft gerade in der Mitte des Kanals, und sein letzter Punkt liegt ebenfalls in der Mitte des Kanals.
Und so wird die PR entlang eines solchen Bogens verlaufen (wenn sie genau ist - es ist ein Ausschnitt einer Sinuswelle)
man muss auch die Nachteile bedenken...
Was ist mit dem Armaturenbrett los?
Sie zeigt den Durchschnittswert des Diagramms an. Was wäre der Durchschnittswert eines Graphen, der von Punkt 0 bis Punkt 10 ansteigt?
5.
Die Skala steht jetzt also bei 5. Auch wenn die Grafik bereits bei 10.
Eine lineare Regression ist hilfreich.
Die Linie einer linearen Regression wird durch die Mitte des Preiskanals verlaufen, und der letzte Punkt dieser Linie wird bei 10 liegen.
Aber Kanäle sind nicht immer gerade. Einige Kanäle sind bogenförmig. In diesem Fall wird die LR nicht gut funktionieren.
Hier kommt die polynomiale Regression zum Einsatz.
Die PR-Kurve verläuft gerade in der Mitte des Kanals und ihr letzter Punkt liegt ebenfalls in der Mitte des Kanals.
Hier, ein weiterer Bogen. (d. h. ein Ausschnitt der Sinuswelle).
wir müssen auch die Nachteile bedenken...
Aber die Grundlage ist dieselbe - Rekonstruktion von Abhängigkeiten durch Einführung von Mappings in neue Dimensionen unter Verwendung von Kernel-Transformationen, und es gibt noch mehr
auf diese Weise noch besser:
herausfinden, wie man das Problem lösen kann.
Maxim Dmitrievsky:
Wie sieht es mit Prognosen aus? ))
Defekt?)))
herausfinden, wie man das Problem lösen kann.
in der gegenwärtigen Dimension - es gibt keine Möglichkeit, das Problem zu lösen, das ist das Problem. Ihre Regression weiß nichts von der Möglichkeit, dass ein solches Ereignis eintritt
Übrigens, Victor hat einen Artikel über Kernwahrscheinlichkeitsdichten, hier
Ich glaube nicht, dass es um Kernel-Tricks geht - die Abbildung von Merkmalsvektoren auf andere Räume
zumindest meiner Meinung nach nicht... ich habe es nicht gelesen.
in der gegenwärtigen Dimension - es gibt keine Möglichkeit, das Problem zu lösen, das ist das Problem. Ihre Regression weiß nichts von der Möglichkeit, dass ein solches Ereignis eintritt
Nachteil?)))
noch besser so:
herausfinden, wie man das Problem lösen kann.
normalerweise so.
in der gegenwärtigen Dimension - es gibt keine Möglichkeit, das Problem zu lösen, das ist das Problem. Ihre Regression weiß nichts von der Möglichkeit, dass ein solches Ereignis eintritt