[Archiv!] Reine Mathematik, Physik, Chemie usw.: Gehirntrainingsprobleme, die in keiner Weise mit dem Handel zusammenhängen - Seite 313
Sie verpassen Handelsmöglichkeiten:
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Registrierung
Einloggen
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Wenn Sie kein Benutzerkonto haben, registrieren Sie sich
P.S. Вероятно, предполагается, что гири можно ставить только на одну чашку весов. На другой - груз.
Одно решение очевидно: 1, 2, 4, 8, 16, 32.
1,2,4,8,16,32 - einfache Antwort
Wenn ein Gewicht kleiner als 2^n ist, ist das Gesamtgewicht kleiner als 63,
Wenn mehr, gibt es Lücken in der Reihenfolge der Gewichte, die mit diesen Kettlebells erreicht werden können.
Interessanterweise wird das Problem wesentlich schwieriger und interessanter, wenn die Gewichte gleichzeitig auf beide Schalen gelegt werden können. Das ist der, den ich gerne quälen würde. Aber ich kenne die Lösung nicht.
Auf jeden Fall stellt sich heraus, dass das Mindestgewicht der Gewichte 1 ist. Dies bedeutet jedoch nicht automatisch, dass sie den Grad 2 erreichen.
Next (10.):
Интересно, что задача становится существенно сложнее и интереснее, если гирьки можно ставить на обе чашки одновременно. Вот ее бы помучить. Но известного мне решения нет.
Хотя в любом случае получается, что гирька минимального веса - это 1. Но это не означает автоматически, что они идут степенью двойки.
Ich bin mir nicht sicher, ob die Mindestanzahl der Kettlebells 1
vielleicht würden auch zwei Kettlebells 2 und 3 funktionieren.
Интересно, что задача становится существенно сложнее и интереснее, если гирьки можно ставить на обе чашки одновременно. Вот ее бы помучить. Но известного мне решения нет.
Хотя в любом случае получается, что гирька минимального веса - это 1. Но это не означает автоматически, что они идут степенью двойки.
Der Computer hat die Berechnungen durchgeführt :)
Wenn die Gewichte gleichzeitig auf beide Tassen gelegt werden können, hat das Problem 2136 Lösungen (genau 63 Gewichte können ausgeglichen werden).
In der Tat enthalten alle Lösungen ein Gewicht von 1.
Компьютер подсчитал :)
Если гирьки можно ставить на обе чашки одновременно, то задача имеет 2136 решений (можно уравновесить ровно 63 груза).
Действительно все решения содержат гирьку с весом 1.
Werden Sie das Programm veröffentlichen? Bitte, bitte!
Ja, fragen Sie unter Tränen nach einem Programm.
Доказательство того, что минимальная - 1, несложно: максимально возможный вес равен сумме всех шести чисел, а тот, что ближайший к нему, равен сумме пяти (шесть без минимальной гирьки). Разница между максимальным и ближайшим к нему весом должна быть равна 1. Следовательно, минимальная равна 1. ihor, доказано, надеюсь?
Ага, слезно просим программку.
Ich habe mich bei 1. geirrt.
Das Programm ist uninteressant, eine einfache Überschreitung.
#include <stdio.h>
#define COUNT 63
bool isOK(int v0,int v1,int v2,int v3,int v4,int v5){
bool arr[COUNT];
for(int i=0;i<COUNT;i++) arr[i]=false;
// 1 - auf einem Becher, 0 - Gewicht ist nicht beteiligt -1 - auf dem zweiten Becher
for(int i0=-1;i0<=1;i0++)
for(int i1=-1;i1<=1;i1++)
for(int i2=-1;i2<=1;i2++)
for(int i3=-1;i3<=1;i3++)
for(int i4=-1;i4<=1;i4++)
for(int i5=-1;i5<=1;i5++) {
int ves=v0*i0+v1*i1+v2*i2+v3*i3+v4*i4+v5*i5;
if(ves > COUNT) return false;
if(ves>0) arr[ves-1]=true;
}
for(int i=0;i<COUNT;i++)
if(!arr[i]) return false;
true zurückgeben;
}
main(){
for(int i0=1;i0<COUNT;i0++)
for(int i1=i0;i1<=COUNT-i0;i1++)
for(int i2=i1;i2<=COUNT-i0-i1;i2++)
for(int i3=i2;i3<=COUNT-i0-i1-i2;i3++)
for(int i4=i3;i4<=COUNT-i0-i1-i2-i3;i4++)
for(int i5=i4;i5<=COUNT-i0-i1-i2-i3-i4;i5++)
if(isOK(i0,i1,i2,i3,i4,i5))
printf("%d %d %d %d %d %d\n",i0,i1,i2,i3,i4,i5);
}
Следующая (10-й):
Der Beweis ist nicht sehr streng, aber korrekt.
Führen wir die Notation der Scheitelpunktkoordinaten ein, wie in der Abbildung gezeigt. Damit Blau ein Quadrat ist
x1-x2=y1-y4 ;
y1-y2=x1-x2;
wie auch
x3-x4=y2-y3;
y4-y3=x2-x3.
Aus den ersten beiden Gleichungen ergibt sich, wenn wir uns an die Graphengleichung erinnern, folgendes
x4-x2=A(sinx2-sinx4),
aus dem dritten und vierten
x3-x1=A(sinx1-sinx3).
Da es außer der Mindestanzahl der Quadrate keine weiteren Beschränkungen für die Quadrate gibt, werden wir nur die Fälle betrachten, in denen die Quadrate symmetrisch zum Ursprung sind. Aber dann ist x4=-x2, x3=-x1 und dasselbe mit Sinus. Unsere Gleichungen werden die Form haben:
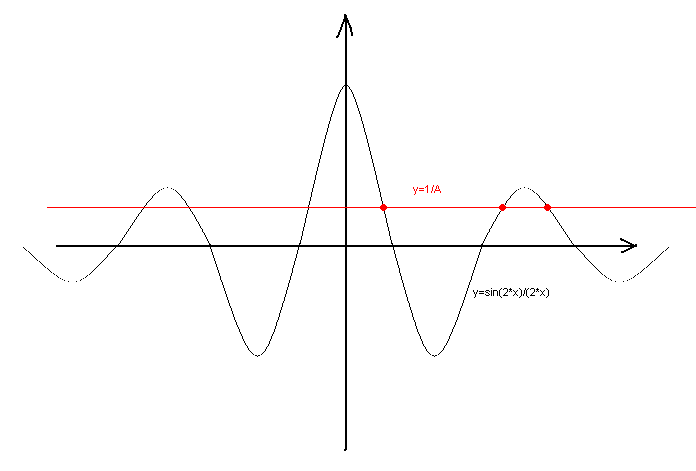
sin(2*x2)/(2*x2)=1/A
sin(2*x1)/(2*x1)=1/A
Erinnern Sie sich an den Graphen der Funktionen von x2 und x1, die auf den linken Seiten stehen. Schauen Sie sich dazu die Abbildung an: Das Diagramm hat abnehmende Extrema sowohl bei positivem als auch bei negativem x. Es liegt auf der Hand, dass wir durch schrittweises Verringern der Zahl A so viele Wurzeln erhalten können, wie wir brauchen, einschließlich 1978 und mehr.
Die erhaltenen Wurzeln sind unterschiedlich und stehen in einer rein irrationalen Beziehung zueinander. Ich brauche nicht im Detail zu beweisen, dass die Quadrate in diesem Fall nicht paarweise gleich sind.