[Archiv!] Reine Mathematik, Physik, Chemie usw.: Gehirntrainingsprobleme, die in keiner Weise mit dem Handel zusammenhängen - Seite 14
Sie verpassen Handelsmöglichkeiten:
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Registrierung
Einloggen
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Wenn Sie kein Benutzerkonto haben, registrieren Sie sich
Какие это такие запросы? Вы свой запрос перечитайте, запрос так запрос, - я на первом предложении то застрял, а развитие мысли "какие после каких бывают" добил меня окончательно.
PS: Жаль, что у Вас нет компаса. Хорошая штука - стороны света разные там показывает, направления всякие ...
Nun, ich habe leider nichts zu sagen. :(
Ну мне сказать тут нечего, увы. :(
über den Kompass? - Das war ein Witz, ich dachte, er würde zu Ihrem "Psychotyp" passen. :о)
Алексей, тебя мое решение устраивает ?
Думаешь для 7-го это слишком круто (не общий, а частный случай 25 одноклассников) ?
Ja, das ist ein bisschen viel für eine 7. Aber es ist elementar, und das ist gut so.
Yurixx schrieb(a) >> Zwei Elemente müssen die gleichen Werte haben.
Es ist nicht schwer zu überprüfen, dass bei N=26 (d.h. es gibt keinen Schüler mit null Verbindungen in der Klasse), diese wiederholte Zahl = 13 ist.
Das einzige, was ich nicht verstehe, ist, warum 13 und nicht 14 oder 2. Sie und Ihr sequenzielles Partitionierungsverfahren haben mein Gehirn erweichen lassen - aber vielleicht sollten Sie dort nach einer Erklärung suchen, warum es 13 ist :)
Sie haben übrigens das Dirichletsche Prinzip verwendet, ohne es zu nennen.
А почему так?
gute Frage)
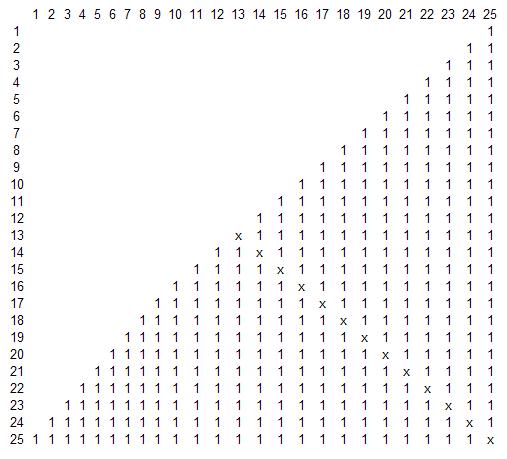
das Bild ist (von 1 bis 25)
diagonal xxx, niemand ist Freunde mit sich selbst, ist es notwendig, es zu tun Petya und so ist es sichtbar dreizehn Mal)))
im Fall von Null bis 24 kann man einen Mitschüler ignorieren und erhält ein Quadrat von 24*24 und 12 X.
Bei einem Quadrat ungerader Größe ist die Diagonale = (N+1)/2, bei einem geraden Quadrat N/2.
Sie können sich das als den Unterschied zwischen den Freundschaften in der Klasse mit und ohne Petya vorstellen.
Das klingt nicht nach einem strengen Beweis. Es handelt sich eher um eine Illustration mit dem Fingerzeig, ohne dass klar ist, warum genau 12 oder 13. OK, lassen Sie uns darüber nachdenken.
Das einzige, was ich nicht verstehe, ist, warum 13 und nicht 14 oder 2. Sie und Ihr sequentielles Partitionierungsverfahren haben mich erweicht - aber vielleicht sollten Sie dort nach einer Erklärung suchen, warum es 13 ist :)
Sie haben übrigens das Dirichlet-Prinzip verwendet, ohne es zu nennen.
Der Punkt ist, dass Petya bei dieser Aufteilung (die nur einem Prinzip gehorcht - jeder hat eine unterschiedliche Anzahl von Freunden und ist daher recht allgemein) überhaupt nicht teilnimmt. Er ist einer von 26 Studenten und den anderen absolut gleichgestellt. Als Ergebnis stellt sich heraus, dass jeder nicht eine unterschiedliche Anzahl von Freunden haben kann - die Reihe von 1 bis N-1 kann nicht fortlaufend mit N verschiedenen Zahlen nummeriert werden (das steht im letzten Beweis). Daher müssen zwei Schüler die gleiche Anzahl von Freunden haben. Und diese beiden Schüler stehen nebeneinander in der Mitte der Reihe. Es stellt sich also heraus, dass Petya einer dieser beiden sein muss. Nur hat in diesem Fall jeder andere eine andere Anzahl von Freunden. Alle anderen Kennzeichnungen können diese Bedingung nicht erfüllen.
Versuchen Sie einmal, mit der Hand in der Mitte aufzuteilen, dann werden Sie es selbst sehen.
Die Tabelle von Swan veranschaulicht dies.
Ich hoffe, ich habe Ihre Frage richtig verstanden.
Ich glaube, ich habe nicht das Dirichlet-Prinzip verwendet, sondern einen elementaren Beweis für seinen Spezialfall angeboten.
Mir persönlich hat es gefallen.
Es ist elegant.
Das erinnerte mich an die Fabel über den kleinen, flinken Gauß und den Lehrer, der der Klasse die Aufgabe gab, die Zahlen von 1 bis 99 zu addieren, und dann für eine Weile wegging - während die Kinder addierten.
Das Einmaleins kannten sie schon, aber Wiederholung ist die Mutter des Lernens...
Gauß täuschte den Lehrer - die Antwort kam auf Anhieb.
;)
Swetten у нас самая дружелюбная.
:)
В коллективе из N сотрудников не может быть ситуации когда у каждого разное количество друзей
А вот если добавить - "у двух возможно одинаковое количество друзей" тогда нет проблем
Остается обозвать Петей одного из этих двух
Ja, das ist fast richtig.
Wenn man die Aufgabe richtig liest, dann KANN Peter die gleiche Anzahl von Freunden haben wie einer der anderen.
Ich habe Ihnen gesagt, dass dieses Problem bei JEDER Auslegung der Bedingungen falsch ist. Ich kann es wahrscheinlich beweisen, und zwar auf verschiedene Weise. Aber ich werde noch nicht......