Programmierung eines Tiefen Neuronalen Netzes von Grund auf mit der Sprache MQL

Einführung

Da maschinelles Lernen in letzter Zeit an Popularität gewonnen hat, haben viele von Deep Learning gehört und möchten wissen, wie man es in der MQL-Sprache anwenden kann. Ich habe einfache Implementierungen von künstlichen Neuronen mit Aktivierungsfunktionen gesehen, aber nichts, was ein echtes Deep Neural Network (Tiefes Neuronales Netz) implementiert. In diesem Artikel werde ich Ihnen ein Tiefes Neuronales Netz vorstellen, das in der MQL-Sprache mit seinen verschiedenen Aktivierungsfunktionen implementiert ist, wie die hyperbolische Tangens-Funktion für die versteckten Schichten und die Softmax-Funktion für die Ausgabeschicht. Wir werden uns vom ersten Schritt bis zum Ende bewegen, um das Tiefe Neuronale Netz vollständig zu bilden.

1. Erstellen eines künstlichen Neurons

Es beginnt mit der Grundeinheit eines Neuronalen Netzes: einem einzelnen Neuron. In diesem Artikel werde ich mich auf die verschiedenen Teile des Neuronentyps konzentrieren, den wir in unserem Tiefen Neuronalen Netz verwenden werden, obwohl der größte Unterschied zwischen den Neuronentypen normalerweise die Aktivierungsfunktion ist.

1.1. Teile eines einzelnen Neurons

Das künstliche Neuron, das in etwa einem Neuron im menschlichen Gehirn nachempfunden ist, beinhaltet einfach die mathematischen Berechnungen. Wie unsere Neuronen wird es ausgelöst, wenn es auf ausreichende Reize trifft. Das Neuron kombiniert die Eingaben aus den Daten mit einer Reihe von Koeffizienten oder Gewichten, die diese Eingaben entweder verstärken oder abschwächen, wodurch den Eingaben eine Bedeutung für die Aufgabe zugewiesen wird, die der Algorithmus zu lernen versucht. In der nächsten Abbildung sehen Sie jeden Teil des Neurons in Aktion:

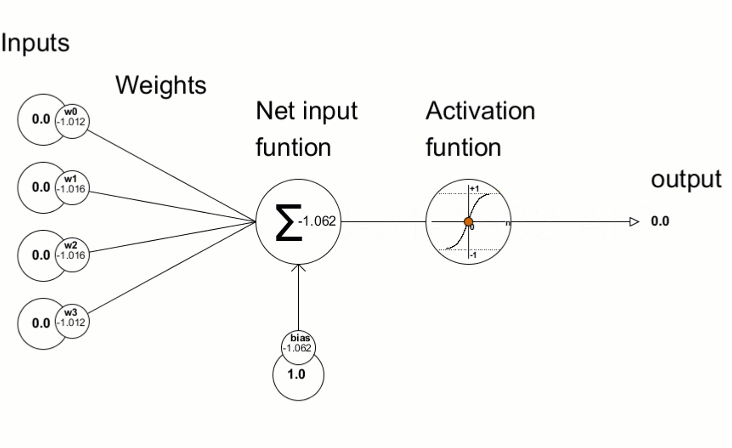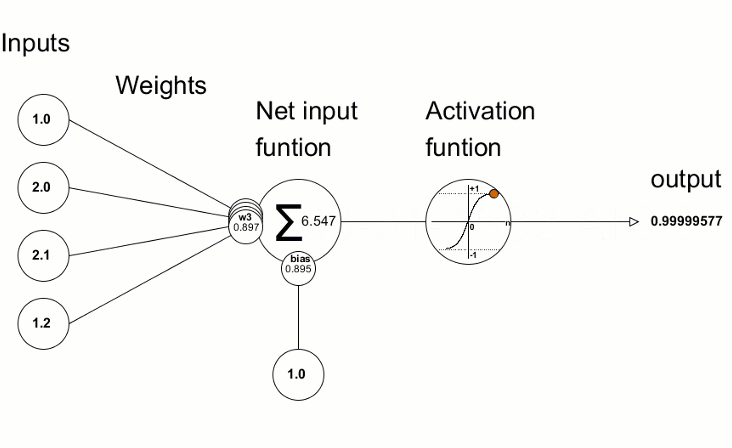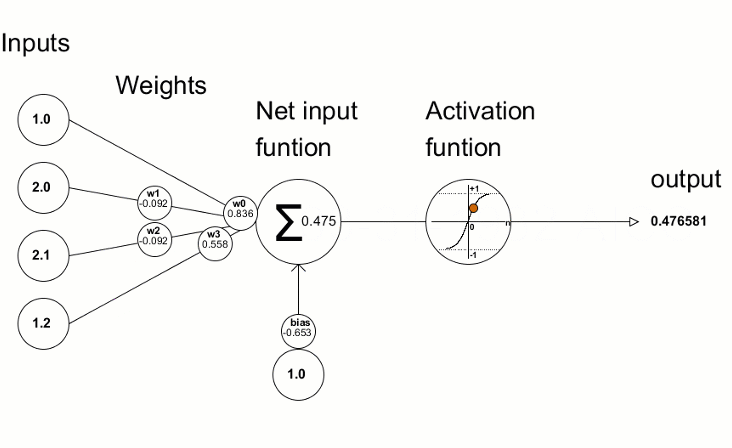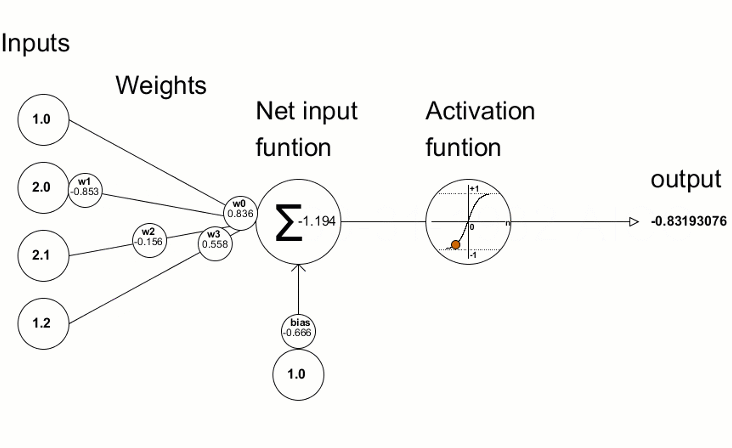
1.1.1. Eingaben

Die Eingabe ist entweder ein externer Auslöser aus der Umwelt oder stammt von der Ausgabe eines anderen künstlichen Neuronen; er soll vom Netz ausgewertet werden. Das dient als "Nahrung" für das Neuron, durchläuft es und wird so zu einer Ausgabe, die wir aufgrund des Trainings, das wir dem Neuron gegeben haben, interpretieren können. Sie können diskrete Werte oder reelle Zahlen sein.

1.1.2. Gewichte

Gewichte sind Faktoren, die mit den Eingaben, die ihnen entsprechen, multipliziert werden, wodurch ihr Wert erhöht oder verringert wird und der Eingabe, die in das Neuron geht, und damit der Ausgabe, die herauskommt, eine größere oder geringere Bedeutung verliehen wird. Ziel der Trainingsalgorithmen für Neuronale Netze ist es, den "bestmöglichen" Satz von Gewichtungswerten für das zu lösende Problem zu bestimmen.

1.1.3. Die Eingabefunktion des Netzes

In diesem Neuronenteil konvergieren die Eingaben und Gewichte in einem Einzelergebnisprodukt als Summe der Multiplikation jeder Eingabe mit ihrem Gewicht. Dieses Ergebnis oder dieser Wert wird durch die Aktivierungsfunktion geleitet, die uns dann das Maß des Einflusses liefert, den das Eingangsneuron auf den Ausgang des Neuronalen Netzes hat.

1.1.4. Aktivierungsfunktion

Die Aktivierungsfunktion führt zu der Ausgabe. Es kann mehrere Arten von Aktivierungsfunktionen geben (Sigmoid, Tan-h, Softmax, ReLU, u.a.). Sie entscheidet, ob ein Neuron aktiviert werden soll oder nicht. Dieser Artikel konzentriert sich auf die Funktionstypen Tan-h und Softmax.

1.1.5. Ausgang

Schließlich haben wir den Ausgang. Er kann an ein anderes Neuron weitergegeben oder von der äußeren Umgebung abgetastet werden. Dieser Wert kann diskret oder reell sein, je nach verwendeter Aktivierungsfunktion.

2. Aufbau des Neuronalen Netzes

Das Neuronale Netz ist inspiriert von den Informationsverarbeitungsmethoden biologischer Nervensysteme, wie z. B. des Gehirns. Es besteht aus Schichten von künstlichen Neuronen, wobei jede Schicht mit der nächsten verbunden ist. Daher dient die vorherige Schicht als Eingabe für die nächste Schicht und so weiter bis zur Ausgabeschicht. Der Zweck eines Neuronalen Netzes kann das Clustering durch unüberwachtes Lernen, die Klassifizierung durch überwachtes Lernen oder die Regression sein. In diesem Artikel konzentrieren wir uns auf die Fähigkeit, in drei Zustände zu klassifizieren: KAUFEN, VERKAUFEN oder HALTEN. Nachfolgend sehen Sie ein Neuronales Netzwerk mit einer versteckten Schicht:

3. Skalierung von einem Neuronalen Netz zu einem Tiefen Neuronalen Netz, dem Deep Neural Network

Ein Tiefes Neuronales Netz unterscheidet sich von den üblichen einschichtigen Neuronalen Netzen durch die Anzahl der Schichten, die seine Tiefe ausmachen. Bei mehr als drei Schichten (einschließlich Eingabe und Ausgabe) spricht man von "tiefem" Lernen. Tief" ist also ein streng definierter technischer Begriff, der mehr als eine verborgene Schicht bedeutet. Je weiter man in das Neuronale Netz vordringt, desto komplexere Merkmale können von den Neuronen erkannt werden, da sie Merkmale aus der vorherigen Schicht zusammenfassen und neu kombinieren. Dadurch sind Deep-Learning-Netze in der Lage, sehr große, hochdimensionale Datensätze mit Milliarden von Parametern zu verarbeiten, die nichtlineare Funktionen durchlaufen. In der Abbildung unten sehen Sie ein Deep Neural Network mit 3 versteckten Schichten:

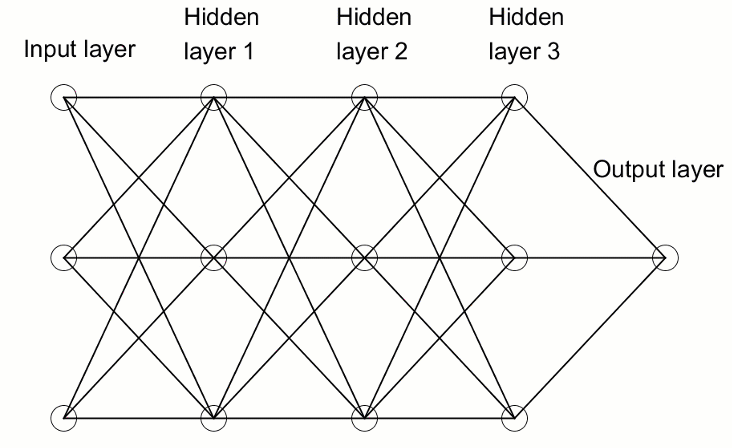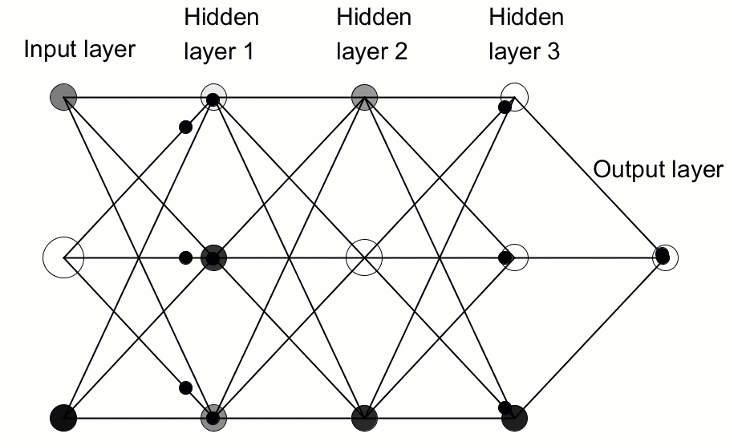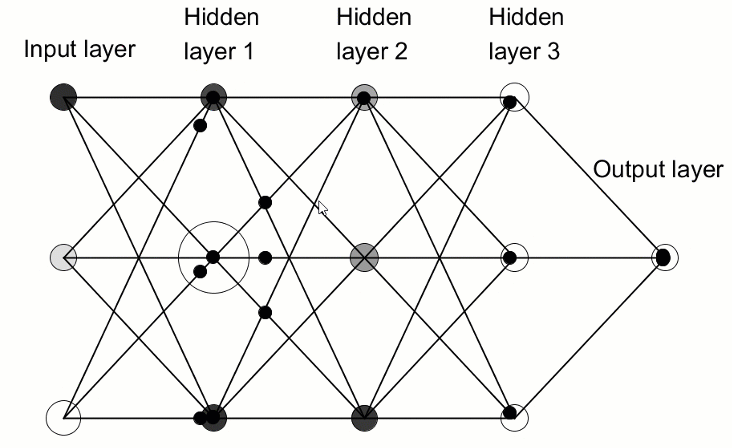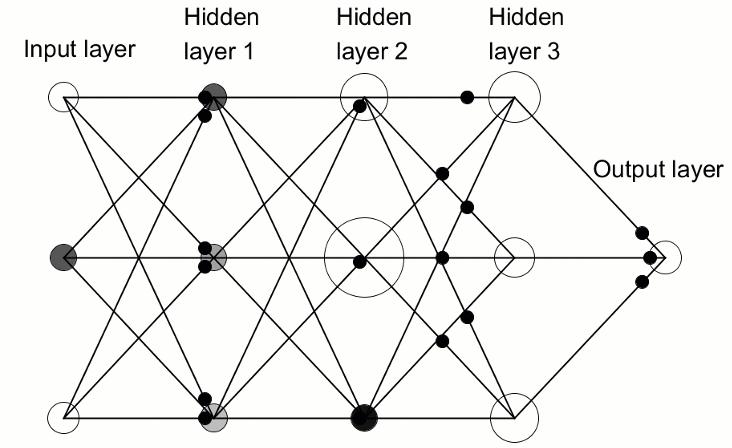
3.1. Die Klasse des Tiefen Neuronalen Netzwerks

Sehen wir uns nun die Klasse an, mit der wir unser Neuronales Netzwerk erstellen werden. Das Tiefe Neuronale Netzwerk ist in einer programmdefinierten Klasse namens DeepNeuralNetwork gekapselt. Die Hauptmethode instanziiert ein 3-4-5-3 vollständig verbundenes Neuronales Feed-Forward-Netzwerk. Später, in einer Trainingssitzung des Tiefen Neuronalen Netzes in diesem Artikel, werde ich einige Beispiele für Eingaben zeigen, mit denen unser Netz gefüttert werden kann, aber jetzt konzentrieren wir uns erst einmal auf die Erstellung des Netzes. Das Netzwerk ist für zwei versteckte Schichten fest programmiert. Neuronale Netze mit drei oder mehr Schichten sind sehr selten, aber wenn Sie ein Netz mit mehr Schichten erstellen möchten, können Sie dies leicht tun, indem Sie die in diesem Artikel vorgestellte Struktur verwenden. Die Gewichte der Eingaben zu Schicht A werden in der Matrix iaWeights gespeichert, die Gewichte von Schicht A zu Schicht B in der Matrix abWeights, und die Gewichte von Schicht B zu Ausgabe in der Matrix boWeights. Da ein mehrdimensionales Array nur in der ersten Dimension statisch oder dynamisch sein kann und alle weiteren Dimensionen statisch sind, wird die Größe der Matrix mit der Anweisung "#define" als konstante Variable deklariert. Um Platz zu sparen, habe ich alle using-Anweisungen mit Ausnahme derjenigen entfernt, die auf den System-Namensraum der obersten Ebene verweist. Den vollständigen Quellcode finden Sie in den Anhängen des Artikels.

Struktur des Programms:

#define SIZEI 4
#define SIZEA 5
#define SIZEB 3
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class DeepNeuralNetwork
  {
private:

   int               numInput;
   int               numHiddenA;
   int               numHiddenB;
   int               numOutput;

   double            inputs[];

   double            iaWeights[][SIZEI];
   double            abWeights[][SIZEA];
   double            boWeights[][SIZEB];

   double            aBiases[];
   double            bBiases[];
   double            oBiases[];

   double            aOutputs[];
   double            bOutputs[];
   double            outputs[];

public:

                     DeepNeuralNetwork(int _numInput,int _numHiddenA,int _numHiddenB,int _numOutput)
     {...}
     

   void SetWeights(double &weights[])
     {...}      
    

   void ComputeOutputs(double &xValues[],double &yValues[])
     {...}     
          

   double HyperTanFunction(double x)
     {...}      
     

   void Softmax(double &oSums[],double &_softOut[])
     {...}
      

  };
//+------------------------------------------------------------------+

Die beiden versteckten Schichten und die einzelne Ausgabeschicht haben jeweils ein Array mit zugehörigen Bias-Werten, die aBiases, bBiases bzw. oBiases heißen. Die lokalen Ausgaben für die versteckten Schichten werden in klassenübergreifenden Arrays mit den Namen aOutputs und bOutputs gespeichert.

3.2. Die Berechnung der Ausgaben des Tiefen Neuronalen Netzes

Die Methode ComputeOutputs beginnt mit der Einrichtung von Scratch-Arrays, die vorläufige Summen (vor der Aktivierung) enthalten. Als Nächstes wird die vorläufige Summe der Gewichte mal den Eingaben für die Knoten der Schicht A berechnet, die Bias-Werte addiert und dann die Aktivierungsfunktion angewendet. Dann werden die lokalen Ausgaben der Schicht B berechnet, wobei die soeben berechneten Ausgaben der Schicht A als lokale Eingaben verwendet werden, und schließlich werden die endgültigen Ausgaben berechnet.

void ComputeOutputs(double &xValues[],double &yValues[])
     {
      double aSums[]; // hidden A nodes sums scratch array
      double bSums[]; // hidden B nodes sums scratch array
      double oSums[]; // output nodes sums

      ArrayResize(aSums,numHiddenA);
      ArrayFill(aSums,0,numHiddenA,0);
      ArrayResize(bSums,numHiddenB);
      ArrayFill(bSums,0,numHiddenB,0);
      ArrayResize(oSums,numOutput);
      ArrayFill(oSums,0,numOutput,0);

      int size=ArraySize(xValues);

      for(int i=0; i<size;++i) // copy x-values to inputs
         this.inputs[i]=xValues[i];

      for(int j=0; j<numHiddenA;++j) // compute sum of (ia) weights * inputs
         for(int i=0; i<numInput;++i)
            aSums[j]+=this.inputs[i]*this.iaWeights[i][j]; // note +=

      for(int i=0; i<numHiddenA;++i) // add biases to a sums
         aSums[i]+=this.aBiases[i];

      for(int i=0; i<numHiddenA;++i) // apply activation
         this.aOutputs[i]=HyperTanFunction(aSums[i]); // hard-coded

      for(int j=0; j<numHiddenB;++j) // compute sum of (ab) weights * a outputs = local inputs
         for(int i=0; i<numHiddenA;++i)
            bSums[j]+=aOutputs[i]*this.abWeights[i][j]; // note +=

      for(int i=0; i<numHiddenB;++i) // add biases to b sums
         bSums[i]+=this.bBiases[i];

      for(int i=0; i<numHiddenB;++i) // apply activation
         this.bOutputs[i]=HyperTanFunction(bSums[i]); // hard-coded

      for(int j=0; j<numOutput;++j) // compute sum of (bo) weights * b outputs = local inputs
         for(int i=0; i<numHiddenB;++i)
            oSums[j]+=bOutputs[i]*boWeights[i][j];

      for(int i=0; i<numOutput;++i) // add biases to input-to-hidden sums
         oSums[i]+=oBiases[i];

      double softOut[];
      Softmax(oSums,softOut); // softmax activation does all outputs at once for efficiency
      ArrayCopy(outputs,softOut);

      ArrayCopy(yValues,this.outputs);

     }

Unter der Oberfläche verwendet das Neuronale Netz die Aktivierungsfunktion hyperbolischer Tangens (Tan-h) bei der Berechnung der Ausgänge der beiden versteckten Schichten und die Aktivierungsfunktion Softmax bei der Berechnung der endgültigen Ausgangswerte.

• Hyperbolischer Tangens (Tan-h): Wie das logistische Sigmoid ist auch die Tan-h-Funktion sigmoidal, gibt aber stattdessen Werte im Bereich (-1, 1) aus. Daher führen stark negative Eingaben in die Tan-h-Funktion zu negativen Ausgaben. Außerdem werden nur Eingaben mit dem Wert Null auf Ausgaben nahe Null abgebildet. In diesem Fall zeige ich nicht nur die mathematische Formel, sondern auch ihre Implementierung im MQL-Quellcode.

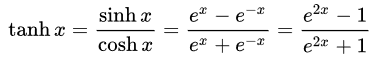
   double HyperTanFunction(double x)
     {
      if(x<-20.0) return -1.0; // approximation is correct to 30 decimals
      else if(x > 20.0) return 1.0;
      else return MathTanh(x); //Use explicit formula for MQL4 (1-exp(-2*x))/(1+exp(-2*x))
     }

• Softmax: weist jeder Klasse dezimale Wahrscheinlichkeiten zu, wenn es mehrere Klassen gibt. Diese dezimalen Wahrscheinlichkeiten müssen sich zu 1,0 addieren. Diese zusätzliche Einschränkung ermöglicht eine schnellere Konvergenz des Trainings.

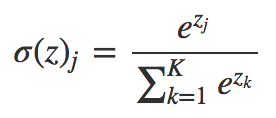
   void Softmax(double &oSums[],double &_softOut[])
     {
      // determine max output sum
      // does all output nodes at once so scale doesn't have to be re-computed each time
      int size=ArraySize(oSums);
      double max= oSums[0];
      for(int i = 0; i<size;++i)
         if(oSums[i]>max) max=oSums[i];

      // determine scaling factor -- sum of exp(each val - max)
      double scale=0.0;
      for(int i= 0; i<size;++i)
         scale+= MathExp(oSums[i]-max);

      ArrayResize(_softOut,size);
      for(int i=0; i<size;++i)
         _softOut[i]=MathExp(oSums[i]-max)/scale;

     }

4. Demo Expert Advisor unter Verwendung der Klasse DeepNeuralNetwork

Bevor wir mit der Entwicklung des Expert Advisors beginnen, müssen wir die Daten definieren, mit denen unser Deep Neural Network gefüttert werden soll. Da ein Neuronales Netzwerk gut im Klassifizieren von Mustern ist, werden wir die relativen Werte einer japanischen Kerze als Eingabe verwenden. Diese Werte wären die Größe des oberen Schattens, des Körpers, des unteren Schattens und die Richtung der Kerze (auf- oder abwärts). Die Anzahl der Eingaben muss nicht unbedingt klein sein, aber in diesem Fall reicht sie als Testprogramm aus.

Der Demo-Expert Advisor:

Ein Neuronales Netz der Struktur 4-4-5-3 benötigt insgesamt (4 * 4) + 4 + (4 * 5) + 5 + (5 * 3) + 3 = 63 Gewichte und Bias-Werte.

#include <DeepNeuralNetwork.mqh> 

int numInput=4;
int numHiddenA = 4;
int numHiddenB = 5;
int numOutput=3;

DeepNeuralNetwork dnn(numInput,numHiddenA,numHiddenB,numOutput);


//--- weight & bias values
input double w0=1.0;
input double w1=1.0;
input double w2=1.0;
input double w3=1.0;
input double w4=1.0;
input double w5=1.0;
input double w6=1.0;
input double w7=1.0;
input double w8=1.0;
input double w9=1.0;
input double w10=1.0;
input double w11=1.0;
input double w12=1.0;
input double w13=1.0;
input double w14=1.0;
input double w15=1.0;
input double b0=1.0;
input double b1=1.0;
input double b2=1.0;
input double b3=1.0;
input double w40=1.0;
input double w41=1.0;
input double w42=1.0;
input double w43=1.0;
input double w44=1.0;
input double w45=1.0;
input double w46=1.0;
input double w47=1.0;
input double w48=1.0;
input double w49=1.0;
input double w50=1.0;
input double w51=1.0;
input double w52=1.0;
input double w53=1.0;
input double w54=1.0;
input double w55=1.0;
input double w56=1.0;
input double w57=1.0;
input double w58=1.0;
input double w59=1.0;
input double b4=1.0;
input double b5=1.0;
input double b6=1.0;
input double b7=1.0;
input double b8=1.0;
input double w60=1.0;
input double w61=1.0;
input double w62=1.0;
input double w63=1.0;
input double w64=1.0;
input double w65=1.0;
input double w66=1.0;
input double w67=1.0;
input double w68=1.0;
input double w69=1.0;
input double w70=1.0;
input double w71=1.0;
input double w72=1.0;
input double w73=1.0;
input double w74=1.0;
input double b9=1.0;
input double b10=1.0;
input double b11=1.0;

Für die Eingaben in unser Neuronales Netz werden wir die folgende Formel verwenden, um zu bestimmen, welcher Prozentsatz jeden Teil der Kerze unter Berücksichtigung der Gesamtgröße repräsentiert.

//+------------------------------------------------------------------+
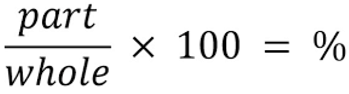
//|percentage of each part of the candle respecting total size       |
//+------------------------------------------------------------------+
int CandlePatterns(double high,double low,double open,double close,double uod,double &xInputs[])
  {
   double p100=high-low;//Total candle size   
   double highPer=0;
   double lowPer=0;
   double bodyPer=0;
   double trend=0;

   if(uod>0)
     {
      highPer=high-close;
      lowPer=open-low;
      bodyPer=close-open;
      trend=1;

     }
   else
     {
      highPer=high-open;
      lowPer=close-low;
      bodyPer=open-close;
      trend=0;
     }
   if(p100==0)return(-1);
   xInputs[0]=highPer/p100;
   xInputs[1]=lowPer/p100;
   xInputs[2]=bodyPer/p100;
   xInputs[3]=trend;

   return(1);

  }

Jetzt können wir die Eingaben durch unser Neuronales Netz verarbeiten:

   MqlRates rates[];
   ArraySetAsSeries(rates,true);
   int copied=CopyRates(_Symbol,0,1,5,rates);

   //Compute the percent of the upper shadow, lower shadow and body in base of sum 100%
   int error=CandlePatterns(rates[0].high,rates[0].low,rates[0].open,rates[0].close,rates[0].close-rates[0].open,_xValues);

   if(error<0)return;
   
   dnn.SetWeights(weight);

   double yValues[];
   dnn.ComputeOutputs(_xValues,yValues);

Jetzt wird die Handelsmöglichkeit auf der Grundlage der Berechnung des Neuronalen Netzes verarbeitet. Denken Sie daran, dass die Softmax-Funktion 3 Ausgänge auf der Grundlage der Summe von 100 % erzeugt. Die Werte werden im Array "yValues" gespeichert, und der Wert mit einer Zahl größer als 60 % wird ausgeführt.

//--- if the output value of the neuron is mare than 60%
   if(yValues[0]>0.6)
     {
      if(m_Position.Select(my_symbol))//check if there is an open position
        {
         if(m_Position.PositionType()==POSITION_TYPE_SELL) m_Trade.PositionClose(my_symbol);//Close the opposite position if exists
         if(m_Position.PositionType()==POSITION_TYPE_BUY) return;
        }
      m_Trade.Buy(lot_size,my_symbol);//open a Long position
     }
//--- if the output value of the neuron is mare than 60%
   if(yValues[1]>0.6)
     {
      if(m_Position.Select(my_symbol))//check if there is an open position
        {
         if(m_Position.PositionType()==POSITION_TYPE_BUY) m_Trade.PositionClose(my_symbol);//Close the opposite position if exists
         if(m_Position.PositionType()==POSITION_TYPE_SELL) return;
        }
      m_Trade.Sell(lot_size,my_symbol);//open a Short position
     }

   if(yValues[2]>0.6)
     {
      m_Trade.PositionClose(my_symbol);//close any position

     }

5. Trainieren eines Tiefen Neuronalen Netzes mithilfe der Strategieoptimierung

Wie Sie vielleicht bemerkt haben, wurde nur der Feed-Forward-Mechanismus des Tiefen Neuronalen Netzes implementiert, und es wird kein Training durchgeführt. Diese Aufgabe ist für den Strategietester reserviert. Nachfolgend zeige ich Ihnen, wie Sie das Neuronale Netz trainieren können. Beachten Sie, dass es aufgrund der großen Anzahl von Eingaben und der Bandbreite der Trainingsparameter nur in Metatrader 5 trainiert werden kann, aber sobald die Werte für die Optimierung ermittelt wurden, kann es leicht in Metatrader 4 kopiert werden.

Die Konfiguration des Strategietesters:

Für die Gewichte und den Bias kann ein Zahlenbereich von -1 bis 1 und eine Schrittweite von 0,1, 0,01 oder 0,001 für das Training verwendet werden. Sie können diese Werte ausprobieren und sehen, welcher Wert das beste Ergebnis liefert. In meinem Fall habe ich 0,001 für den Schritt verwendet, wie in der Abbildung unten gezeigt:

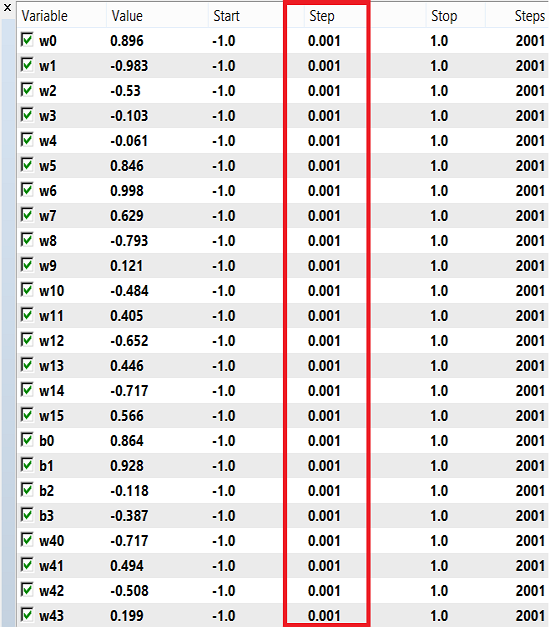
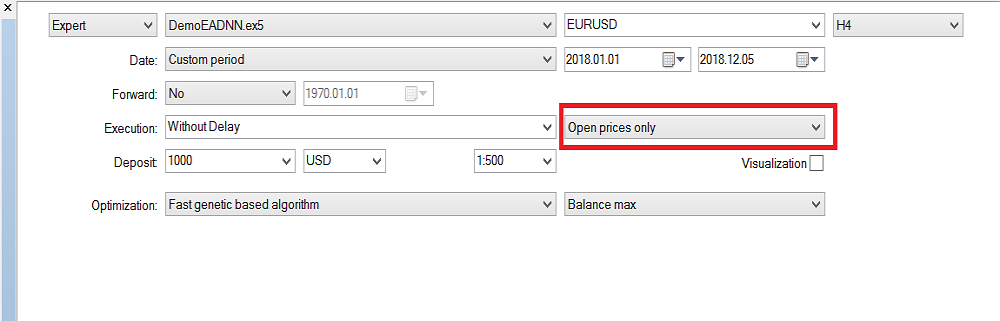
Bitte beachten Sie, dass ich "Open Prices Only" (Nur Öffnungspreise) verwendet habe, weil ich die letzte geschlossene Kerze verwende, so dass es sich nicht lohnt, die Optimierung für jeden Tick auszuführen. Jetzt habe ich die Optimierung auf dem H4-Zeitrahmen ausgeführt und im letzten Jahr habe ich dieses Ergebnis im Backtest erhalten:

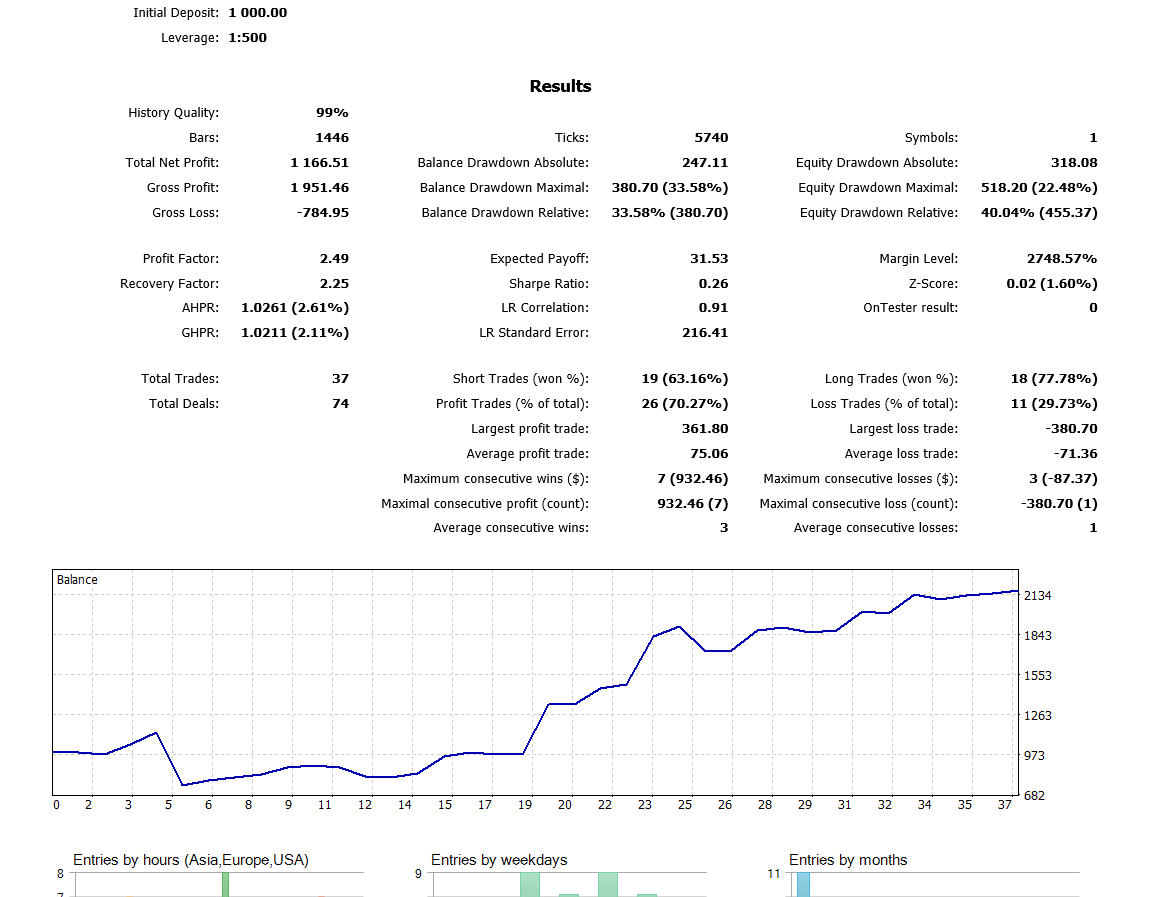
Schlussfolgerung

Der in diesem Artikel vorgestellte Code und die Erläuterungen sollten Ihnen eine gute Grundlage für das Verständnis Neuronaler Netze mit zwei versteckten Schichten bieten. Was ist mit drei oder mehr versteckten Schichten? In der Forschungsliteratur herrscht Einigkeit darüber, dass zwei verborgene Schichten für fast alle praktischen Probleme ausreichend sind. In diesem Artikel wird ein Ansatz zur Entwicklung verbesserter Modelle für die Wechselkursprognose mit Hilfe von Tiefen Neuronalen Netzen vorgestellt, der durch die Fähigkeit Tiefer Netze motiviert ist, abstrakte Merkmale aus Rohdaten zu lernen. Vorläufige Ergebnisse bestätigen, dass unser Tiefes Netzwerk eine deutlich höhere Vorhersagegenauigkeit als die Basismodelle für entwickelte Währungsmärkte liefert.