
Erweiterung des StrategieTesters um ausschließlich Indikatoren zu optimieren am Beispiel von Seitwärts- und Trend-Märkten
Problem
Es gibt zu viele Parameter zu optimieren.Ein Handels-EA mit vielen Indikatoren, die mehrere Parameter haben, benötigt mit unter eine lange Zeit für eine Optimierung, weil viel zu viele Kombinationen auszutesten wären. Was, wenn wir in der Lage waren, diese Menge von Kombinationen zu senken, bevor wir mit der Optimierung der Handels-EA beginnen? In anderen Worten, vor der Kodierung eines Handels-EA programmieren wir einen Pseudo-EA, der nur ganz spezifische Fragen an den Markt stellt. Wir unterteilen ein großes Problem in kleinere und lösen sie einzeln. Dieser Pseudo-EA handelt nicht! Als Beispiel wählen wir den ADX und prüfen, ob dieser Indikator in der Lage ist, zwischen Seitwärts- und Trend-Märkten zu unterscheiden, und vielleicht gewinnen wir sogar zusätzliche Informationen.
Stellen Sie sich für den Handels-EA eine kurzfristige Handelsidee vor, die wissen muss, ob der Markt sich seitwärts bewegt für die "swing-trades" (Handel hin zu einem gleitenden Durchschnitt), oder, ob es sich um einen Trend-Markt handelt für eine Trendfolge-Strategie (Handel weg vom gleitenden Durchschnitt). Um das zu unterscheiden soll unserer Handels-EA (nur) den ADX auf einem höheren Zeitrahmen verwenden - hier 1h-Bars. Neben dem ADX würde der Handels-EA weitere 5 Indikatoren verwenden (für seine kurzfristigen Handelsentscheidungen). Für jeden müssten 4 Parameter bestimmt werden, die wegen ihrer kleinen Schrittweite jeweils über 2000 unterschiedliche Werte annehmen könnten. Das ergibt insgesamt 2000*5*4 = 40 000. Ergänzen wir nun den ADX. Für jede Kombination der Parameter des ADX müssten wir theoretisch 40 000 zusätzliche Testläufe durchführen.
Hier in diesem Beispiel bestimmen wird für den ADX die Periode (PER) und einen Schwellenwert (LIM), so dass ein beginnender Trend dadurch definiert wird, dass der ADX (MODE_MAIN) über LIM steigt, und ein Seitwärts-Markt dadurch, dass er unter LIM fällt. Für die Periode (PER) versuchen wir die Werte 2,..,90 (Schritt 1 => 89 verschiedene Werte), für den Kalkulationspreis wählen wir 0,..,6 (=Close,..,Weighted, Schritt 1 => 7) und für LIM versuchen wir 4,..,90 (Schritt 1 => 87). Das ergibt insgesamt 89*7*87 = 54 201. Hier ist das Setup des Strategie-Testers:
Wenn Sie diese Optimierung wiederholen, vergessen Sie nicht, jedes Mal vorher die cache-Datei im Verzeichnis \tester\cache\ zu löschen! Andernfalls finden Sie die Ergebnisse zwar unter "Ergebnisse der Optimierung" und "Optimierungsdiagramm" des Strategie-Testers, aber NICHT in der csv-Datei, da OnTester() in einem solchen Fall nicht immer ausgeführt wird.
Natürlich würde man solche Spannen nicht für die Optimierung verwenden, aber erstens wollen wir sinnlose Ergebnisse finden, um zu sehen, ob wir diese feststellen und ausschließen können und zweitens gibt es pädagogisch Gründe die Spanne auszuweiten. Aufgrund der Tatsache, dass unsere Pseudo-EA nicht handelt (keine Notwendigkeit für jeden Tick!) und wir nur einen Indikator mit 54 201 Kombinationen testen, können wir den Genetischen Algorithmus abschalten und lassen den Tester alle Kombinationen berechnen.
Würden wir diese Vorab-Optimierung des ADX nicht machen, könnten wir die Anzahl der Kombinationen des ADX nicht reduzieren, wir müssten die 40 000 Kombinationen der anderen Variablen der Handels-EA mit den 54 201 Kombinationen des ADX multiplizieren und kämen auf 2 168 040 000 Kombinationen für die Optimierung - eine ganz Menge zu tun und wir müssten den Genetischen Algorithmus verwenden.
Am Ende werden wir nicht nur in der Lage sein, die Spanne der Parameter des ADX drastisch zu reduzieren - das ist in Ordnung, das ist zu erwarten! Wir erhalten auch ein besseres Verständnis des ADX, weil wir sehen werden, dass der ADX in der Tat zwischen einem Seitwärts- und einem Trend-Markt unterscheiden kann - auch wenn das Erkennen eines Seitwärts-Marktes ein wenig mehr hinterher hinkt als das des Trend-Marktes (Raum für Verbesserung?)! Darüber hinaus erhalten wir eine Vorstellung, wie die Stopp-Loss' und die Profit-Targets des Handels-EA zu bestimmen wären, auf Grund der sich ergebenden Spannen der Seitwärts- und der Trend-Märkte. Die Periodenlänge des ADX wird getestet von PER: 11..20 (Schritt 1=> 10), PRC: 0,6 (Schritt 6=>2) und LIM: 17,..,23 (Schritt 1=> 7) - insgesamt verbleiben nur 140 maßgebende Kombinationen. Das bedeutet, statt 2 168 040 000 muss der Handels-EA nur 4 680 000 Kombinationen testen, das wäre ~460 mal schneller ohne den Genetischen Algorithmus oder ~460 mal besser mit dem Genetischen Algorithmus. Der Genetische Algorithmus veranlasst in etwa 10.000 Testläufe, aber jetzt können viel mehr Werte anderer Parameter des Handels-EA getestet werden!
Anmerkung zum Genetischen Algorithmus: Seine Ergebnisse variieren erheblich in Abhängigkeit von der Gesamtzahl möglicher Kombinationen und den tatsächlich durchgeführten Testläufen. Je schlechter die Ergebnisse während der Optimierung, desto kleiner ist die Zahl guter Ergebnisse, aus denen die nächsten Einstellungen der nächsten Testläufe ausgewählt werden.
Die Idee
Wir bauen eine Pseudo-EA, der nicht handelt. Es hat nur drei wichtige Funktionen. OnTick(), dort holen wir uns die Werte des Indikators und bestimmen den Status des Marktes, OnTester(), dort schreiben wir das Endresultat in unsere csv-Datei, und calcOptVal(), dort berechnen wir den Wert von OptVal, der von OnTester() an den Strategie-Tester übergeben wird für die Reihung und den Genetischen Algorithmus. Die Funktion OnTester(), die am Ende jedes Testlaufs aufgerufen wird, gibt einen bestimmten Wert zurück und fügt eine neue Zeile einer csv-Datei hinzu, für eine Analyse nach der ganzen Optimierung.
Die Pseudo-EA, Erster Versuch
Wir müssen jetzt die Kriterien bestimmen für die Berechnung des zurückgegebene Wertes: OptVal. Wir wählen die Spanne der Seitwärts- und der Trend-Märkte, es ist die Differenz zwischen dem höchsten Hoch und dem tiefsten Tief der jeweiligen Märkte, und teilen "TrndRange" durch "FlatRange", so dass der Optimierer dies maximieren kann:
double TrndRangHL, // Summe von höchsten Hoch - tiefstem Tief der Trend-Märkte TrndNum, // Anzahl der Trend-Märkte FlatRangHL, // Summe von höchsten Hoch - tiefstem Tief der Seitwärts-Märkte FlatNum, // Anzahl der Seitwärts-Märkte RangesRaw, // Spanne der Trend-Märkte dividiert durch die Spanne der Seitwärts-Märkte (je größer, desto besser) // ... siehe unten double calcOptVal() // Erster Ansatz!! { FlatRange = FlatRangHL / FlatNum; TrndRange = TrndRangHL / TrndNum; RangesRaw = FlatRange>0 ? TrndRange/FlatRange : 0.0; return(RangesRaw); } ... double OnTester() { OptVal = calcOptVal(); return( OptVal ); }
Wir lassen die Optimierung mit den oben genannten Einstellungen laufen und OptVal = RangesRaw, das Ergebnis im Optimierungsdiagramm schaut so aus:
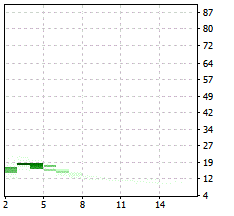
Wenn wir uns die besten Werte in den "Ergebnisse der Optimierungen" anschauen und die Spalte "OnTester Resultat" von oben nach unten sortieren, sehen wir:
Absurd hohe Verhältnisse! Schauen wir in die csv-Datei, erkennen wir, dass die durchschnittliche Länge des Seitwärts-Marktes 1 Bar beträgt und die Zahl der Wechsel (Zahl der Seitwärts-Märkte + Zahl der Trend-Märkte) ist auch zu klein für eine sinnvolle Verwendung. (Die seltsame Zahl für PRC=1994719249 statt 0,..,6 sollte uns nicht beunruhigen, da die korrekte Zahl für den Preis des ADX in der csv-Datei steht!).
Dieses unbefriedigende Ergebnis bedeutet, dass wir weitere Kriterien einführen müssen, um solche sinnlosen Ergebnisse zu verhindern.
Pseudo-EA, Verbesserungen
Als erstes ergänzen ganz einfach ein Minimum von Bars für Seitwärts- oder Trend-Märkte:
FlatBarsAvg = FlatBars/FlatNum; // Summe aller 'Seitwärts-Bars' / Anzahl der Seitwärts-Märkte TrndBarsAvg = TrndBars/TrndNum; // Summe aller 'Trend-Bars' / Anzahl der Trend-Märkte BrRaw = fmin(FlatBarsAvg,TrndBarsAvg);
Als zweites bestimmen wir ein Minimum der Wechsel zwischen Seitwärts- und Trend-Märkte:
SwitchesRaw = TrndNum+FlatNum; // Anzahl von Trend- und Seitwärts-MärkteJetzt stehen wir vor dem nächsten Problem! RangesRaw schwankt zwischen 0 und 100.000,0, BrRaw zwischen 0 und 0,5 und SwitchesRaw zwischen 0 und ~8000 (=Bars()) - theoretisch, wenn jede neue Bar zum anderen Markt wechselt.
Wir müssen diese drei Kriterien angleichen! Für alle verwenden wir dieselbe Funktion: Arcus Tangens - oder in mq4 - atan(..)! Anders als z.B. sqrt() oder log() haben wir keine Probleme mit 0 oder negativen Werten. atan() überschreitet niemals einen Grenzwert, so dass, zum Beispiel für RangesRaw, die Differenz zwischen atan(100,000) and atan(20) gegen 0 geht und damit praktisch gleich gewichtet werden, so dass die anderen Ergebnisse mehr Einfluss erhalten. Darüber hinaus erzeugt atan() einen weichen Anstieg hin zum Grenzwert, während ein hartes Limit wie if(x>limit) alle Werte über dem Limit gleich gewichtet und wieder würde es beste Ergebnisse nahe des Limits geben, aber das ist nicht das, was wir suchen. Sie werden das später erkennen!
Sehen wir mal, wie atan() arbeitet (für die grafische Darstellung von atan() verwende ich dies):
Die blaue Version ist nur beschränkt auf +1 und -1 (durch die Division mit pi/2).
Die rote Linie (und ihre Funktion) zeigt, wie wir den Schnittpunkt mit der x-Achse weg von x=0 auf x=4 verschieben können.
Die grüne Linie zeigt, wie wir die Steilheit ändern. Damit kontrollieren wir, wie schnell atan() sich dem Grenzwert nähert, wie schnell die Unterschiede immer kleiner werden.
Was wir hier nicht benötigen, ist eine Veränderung des Grenzwertes, dem sich atan() nähert. Aber zu Ihrer Information, wenn Sie z.B. das erste 1*atan(..) in 2*atan(..) ändern, werden die Grenzwerte auf +2 und -2 verschoben.
Was wir auch nicht benötigen, ist, den oberen und den unteren Grenzwert zu vertauschen, in dem wir 1*atan() durch -1*atan() ersetzen. Nun würde sich unsere Funktion für große x der -1 annähern.
Jetzt haben wir alles für unseren Pseudo-EA. Beginnen wir die Dinge zusammen zu setzen.
Der Pseudo-EA, Finale Version
Unser Pseudo-EA handelt nicht! Er ruft iADX(..) nur auf, wenn einen neue Bar eröffnet wird. Das bedeutet, wir benötigen nicht "Jeder Tick" oder die "Kontrollpunkte"! Wir können das schnellste Modell "Open Preis" verwenden, da wir den Status des Marktes auf Grunde der 2 vorangegangenen Bars des ADX bestimmen:
extern int PER = 22; // Adx Periodlänge extern ENUM_APPLIED_PRICE PRC = PRICE_TYPICAL; // Adx Kalkulationspreis extern double LIM = 14.0; // Grenzwert für die Hauptlinie des Adx' extern string fName = ""; // Dateiname in \tester\files, "" => KEINE csv-Datei! //+------------------------------------------------------------------+ //| Global variable definition | //+------------------------------------------------------------------+ double OptVal, // dieser Wert wird von OnTester() zurückgegeben und er kann in der Spalte "OnTester Resultat" der "Ergebnisse der Optimierung" gefunden werden TrndHi, // höchste Hoch des aktuellen Trend-Marktes TrndLo, // tiefstes Tief des aktuellen Trend-Marktes TrndBeg, // Preis zu Beginn des Trend-Marktes TrndRangHL, // Summe von höchstes Hoch - tiefstes Tief des Trend-Marktes TrndRangCl, // letztes Close - erstem Close des Trend-Marktes (noch 'übrig', aber nicht verwendet) TrndNum, // Anzahl von Trend-Märkten TrndBars=0.0, // Anzahl von Bars in den Trend-Märkten TrndBarsAvg=0.0, // Durchschnitts-Bar der Trend-Märkte FlatBarsAvg=0.0, // Durchschnitts-Bar der Seitwärts-Märkte FlatHi, // höchstes Hoch des aktuellen Seitwärts-Marktes FlatLo, // tiefstes Tief des aktuellen Seitwärts-Marktes FlatBeg, // Preis zu Beginn eines Seitwärts-Marktes FlatRangHL, // Summe von höchstem Hoch - tiefstem Tief eines Seitwärts-Marktes FlatRangCl, // letztes Close - erstem Close eines Seitwärts-Marktes (noch 'übrig', aber nicht verwendet) FlatNum, // Anzahl von Seitwärts-Märkten FlatBars=0.0, // Anzahl von Bars der Seitwärts-Märkte FlatRange, // tmp FlatRangHL / FlatNum TrndRange, // tmp TrndRangHL / TrndNum SwitchesRaw, // Anzahl von Markt-Wechsel SwitchesAtan, // Atan der Anzahl von Markt-Wechsel BrRaw, // Minimum der Stunden von entweder Seitwärts- oder Trend-Märkten (mehr ist besser) BrAtan, // Atan von BrRaw RangesRaw, // Spanne des Trend-Markts dividiert durch die Spanne des Seitwärts-Marktes (je größer, desto besser) RangesAtan; // Atan von (TrndRange/FlatRange) enum __Mkt // 3 Zustände des Marktes { UNDEF, FLAT, TREND }; __Mkt MARKET = UNDEF; // Anfangszustand des Marktes. string iName; // Indikatorname double main1,main2; // Werte der Hauptlinie des ADX' //+------------------------------------------------------------------+ //| OnTick Kalk. des Indik., Bestimmung des Marktes | //+------------------------------------------------------------------+ void OnTick() { //--- static datetime tNewBar=0; if ( tNewBar < Time[0] ) { tNewBar = Time[0]; main1 = iADX(_Symbol,_Period,PER,PRC, MODE_MAIN, 1); // ADX main2 = iADX(_Symbol,_Period,PER,PRC, MODE_MAIN, 2); // ADX) iName = "ADX"; // setzen der Vars. auf den entsprechenden Marktzustand if ( MARKET == UNDEF ) { if ( main1 < LIM ) main2 = LIM+10.0*_Point; // MARKET wird FLAT else if ( main1 > LIM ) main2 = LIM-10.0*_Point; // MARKET wird TREND FlatHi = High[0]; FlatLo = Low[0]; FlatBeg = Close[2];// TrndHi = High[0]; TrndLo = Low[0]; TrndBeg = Close[2];// } // ist es jetzt ein Seitwärts-Markt? if ( MARKET != FLAT && main2>LIM && main1<LIM) // ADX { //beende den Trend-Markt TrndRangCl += fabs(Close[2] - TrndBeg)/_Point; TrndRangHL += fabs(TrndHi - TrndLo)/_Point; // erneuere die maßgeblichen Werte OptVal = calcOptVal(); //stelle den neuen Seitwärts-Markt ein MARKET = FLAT; FlatHi = High[0]; FlatLo = Low[0]; FlatBeg = Close[1];// ++FlatNum; if ( IsVisualMode() ) { if (!drawArrow("Flat "+TimeToStr(Time[0]), Time[0], Open[0]-(High[1]-Low[1]), 243, clrDarkBlue) ) // 39:Kerze, Markt schläft Print("Error drawError ",__LINE__," ",_LastError); } } else if ( MARKET == TREND ) // aktualisiere den aktuellen Trend-Markt { TrndHi = fmax(TrndHi,High[0]); TrndLo = fmin(TrndLo,Low[0]); TrndBars++; } // ist es jetzt ein Trend-Markt? if ( MARKET != TREND && main2<LIM && main1>LIM) { // beende den Seitwärts-Markt FlatRangCl += fabs(Close[2] - FlatBeg)/_Point; FlatRangHL += fabs(FlatHi - FlatLo)/_Point; // erneuere die maßgeblichen Werte OptVal = calcOptVal(); // stelle den neuen Trend-Markt ein MARKET = TREND; TrndHi = High[0]; TrndLo = Low[0]; TrndBeg = Close[1];// ++TrndNum; TrndBars++; if ( IsVisualMode() ) { if(!drawArrow("Trend "+TimeToStr(Time[0]), Time[0], Open[0]-(High[1]-Low[1]), 244, clrRed)) // 119:kl Diamant Print("Error drawError ",__LINE__," ",_LastError); } } else if ( MARKET == FLAT ) // aktualisiere den aktuellen Seitwärts-Markt { FlatHi = fmax(FlatHi,High[0]); FlatLo = fmin(FlatLo,Low[0]); FlatBars++; } } if ( IsVisualMode() ) // im "Visuellen Modus" zeige die aktuelle Situation { string lne = StringFormat("%s PER: %i PRC: %s LIM: %.2f\nMarket # BarsAvg RangeAvg"+ "\nFlat: %03.f %06.2f %.1f\nTrend: %03.f %06.2f %.1f => %.2f", iName,PER,EnumToString(PRC),LIM,FlatNum,FlatBarsAvg,FlatRange, TrndNum,TrndBarsAvg,TrndRange,(FlatRange>Point?TrndRange/FlatRange:0.0) ); Comment(TimeToString(tNewBar)," ",EnumToString(MARKET)," Adx: ",DoubleToString(main1,3), " Adx-Lim:",DoubleToString(main1-LIM,3),"\n",lne); } }Wenn der ADX LIM kreuzt, beenden wir den vorherigen Marktstatus und bereiten den den neuen vor. Der Pseudo-EA berechnet alle Preisdifferenzen in Points!
Schauen wir nun, was wir erreichen wollen und was wir dazu benötigen. Wir benötigen eine Zahl, die OnTester() zurück liefert. Der Optimierer des Strategie Testers rechnet nach dem Motto je größer je besser. Der Wert, den OnTester() (OptVal) zurück gibt, muss daher ansteigen, wenn die Unterscheidung zwischen einem Seitwärts- und einem Trend-Markt besser wird für unseren Zweck!
Wir bestimmen drei Variablen zur Berechnung von OptVal. Für zwei von ihnen können wir begründbare Minima festlegen:
- RangesRaw = TrndRage/FlatRange muss größer sein als 1! Der Trend-Markt soll eine größere durchschnittliche Spanne haben als der Seitwärts-Markt. TrndRage und FlatRange werden bestimmt durch höchstes Hoch - tiefstes Tief des aktuellen Marktes. Setzen wird den Schnittpunkt mit der x-Aches auf x=1.
- BrRaw soll größer sein als 3 Bars (= 3 Stunden). BrRaw = fmin(FlatBarsAvg,TrndBarsAvg). FlatBarsAvg und TrndBarsAvg ist durchschnittliche Anzahl der Bars im jeweiligen Markt. Wir brauchen das, um die oben erwähnten absurden Werte an den Grenzen zu vermeiden. Wir setzen diese Schnittstelle mit der x-Achse auf x=3.
- SwitchesRaw. Wir werden über mehr als 8000 Bars optimieren. Ein Ergebnis von z. B. nur 20 Wechsel (10 Seitwärts- und 10 Trend-Märkte) würde keinen Sinn machen. Es würde durchschnittlich 400 Stunden oder 16 Tage je Markt bedeuten?
Das Problem ist einen guten Grenzwert für SwitchesRaw zu finden, hängt er doch stark vom Zeitrahmen und von der Gesamtzahl der Bars ab. Anders als für 1) und 2), wo wie durch Plausibilitätsüberlegungen zu den Grenzwerten kamen, müssen wir uns die ersten Ergebnisse noch einmal anschauen (das Tabelle: Opti ADX ALL der beigefügten csv-Datei) um einen Grenzwert abzuleiten:
Statt die ~2500 Wechsel zu einzeln zu klassifizieren, verwenden wir nur sqrt(2500) = 50 Klassen, womit viel leichter zu arbeiten ist. Für jede Klasse berechnen und zeichnen wir den Durchschnitt. Wir sehen, das lokale Minimum ist bei 172. Nehmen wir einmal 100, um zu sehen wie unser Pseudo-EA mit dieser Grenze umgeht. Wir verwenden einen kleine Koeffizienten von 0,01 für einen langsamen Anstieg hin zum Grenzwert von 100. Noch einmal, normalerweise würden man eine höheres Limit setzen, vielleicht 200 - aber aus pädagogischen Gründen...
Um einen anderen Koeffizienten abzuleiten, schauen wir auf den Funktionsplotter. Wir ändern den so, dass die Kurve dort nicht zu flach ist, wo wir interessante Ergebnisse erwarten. (Blau ist die Funktion für SwitchesRaw):
Schauen wir jetzt auf die beiden anderen Auswertungsfunktionen.
Rot ist die Funktion für BrRaw: Akzeptiertes Minimum für jedwede Dauer eines Marktes ist 3 Bars und ein Koeffizient von 0,5 garantiert, dass auch 8 Bars (Stunden) noch einen Unterschied machen.
Grün für RangesRaw: Akzeptiertes Minimum hier ist 1 und, weil es keine Wunder gibt, mehr als 8 kein seriöses Ergebnis sein kann.
Jetzt können wir die Funktion bilden, die OptVal berechnet, den OnTester() zurück geben wird.
- Da für alle drei Variablen gilt, je größer, desto besser, können wir sie miteinander multiplizieren!
- Wir haben drei Variablen und für alle könnte atan(..) negativ werden, daher rechnen wir so: fmax(0.0,atan(..)). Sonst könnten z. B. zwei negative Resultate von atan() zu einem falschen positiven Wert für OptVal führen.
//+------------------------------------------------------------------+ //| calcOptVal kalk. OptVal zur Rückgabe an den Strategie Tester | //| und den Koeffizienten für die Auswertung | //+------------------------------------------------------------------+ // Koeff. für SwitchesAtan, Anzahl der Wechsel: double SwHigh = 1.0, SwCoeff=0.01, SwMin = 100; // Koeff. for BrAtan, Anzahl der Bars: double BrHigh = 1.0, BrCoeff=0.5, BrMin = 3.0; // Koeff. für RangesAtan, TrendRange/FlatRange: double RgHigh = 1.0, RgCoeff=0.7, RgMin = 1.0; double calcOptVal() { if ( FlatNum*TrndNum>0 ) { SwitchesRaw = TrndNum+FlatNum; SwitchesAtan = SwHigh*atan( SwCoeff*(SwitchesRaw-SwMin))/M_PI_2; FlatBarsAvg = FlatBars/FlatNum; TrndBarsAvg = TrndBars/TrndNum; BrRaw = fmin(FlatBarsAvg,TrndBarsAvg); BrAtan = BrHigh*atan( BrCoeff*(BrRaw-BrMin))/M_PI_2; FlatRange = FlatRangHL / FlatNum; TrndRange = TrndRangHL / TrndNum; RangesRaw = FlatRange>0 ? TrndRange/FlatRange : 0.0; RangesAtan = FlatRange>0 ? RgHigh*atan( RgCoeff*(RangesRaw-RgMin))/M_PI_2 : 0.0; return(fmax(0.0,SwitchesAtan) * fmax(0.0,BrAtan) * fmax(0.0,RangesAtan)); } return(0.0); }
Die anderen Teile des Pseudo-EA sind: OnInit(), in dem die Spaltenköpfe der csv-Datei geschrieben werden:
//+------------------------------------------------------------------+ //| Initialisierungs-Funktion des Experten | //+------------------------------------------------------------------+ int OnInit() { //--- // schreibe die Kopfzeile des Kalkulationsblattes if ( StringLen(fName)>0 ) { if ( StringFind(fName,".csv", StringLen(fName)-5) < 0 ) fName = fName+".csv"; // prüfe den Dateinamen if ( !FileIsExist(fName) ) { // schreibe die Spaltenköpfe einer neuen Datei int fH = FileOpen(fName,FILE_WRITE); if ( fH == INVALID_HANDLE ) Print("ERROR open ",fName,": ",_LastError); string hdr = StringFormat("Name;OptVal;RangesRaw;PER;PRC;LIM;FlatNum;FlatBars;FlatBarsAvg;FlatRgHL;FlatRgCls;FlatRange;"+ "TrendNum;TrendBars;TrendBarsAvg;TrendRgHL;TrendRgCl;TrendRange;"+ "SwitchesRaw;SwitchesAtan;BrRaw;BrAtan;RangesRaw;RangesAtan;FlatHoursAvg;TrendHoursAvg;Bars;"+ "Switches: %.1f %.1f %.f, Hours: %.1f %.1f %.1f, Range: %.1f %.1f %.1f\n", SwHigh,SwCoeff,SwMin,BrHigh,BrCoeff,BrMin,RgHigh,RgCoeff,RgMin); FileWriteString(fH, hdr, StringLen(hdr)); FileClose(fH); } } //--- return(INIT_SUCCEEDED); }
und OnTester(), der den offenen Marktstatus finalisiert und die Ergebnisse der Optimierung an das Ende der csv-Datei schreibt:
double OnTester() { // prüfe das K.o.-Kriterium: mindestens 1 Wechsel if ( FlatNum*TrndNum<=1 ) return(0.0); // eines ist 0 => ignoriere sinnlose Ergebnisse // jetzt finalisiere den letzten Marktstatus: seitwärts if ( MARKET == FLAT ) { TrndRangCl += fabs(Close[2] - TrndBeg)/_Point; TrndRangHL += fabs(TrndHi - TrndLo)/_Point; // erneuere die maßgeblichen Werte OptVal = calcOptVal(); } else if ( MARKET == TREND ) // .. und Trend { FlatRangCl += fabs(Close[2] - FlatBeg)/_Point; FlatRangHL += fabs(FlatHi - FlatLo)/_Point; // aktualisiere OptVal OptVal = calcOptVal(); } // schreibe die Werte in die csv-Datei if ( StringLen(fName)>0 ) { string row = StringFormat("%s;%.5f;%.3f;%i;%i;%.2f;%.0f;%.0f;%.1f;%.0f;%.0f;%.2f;%.2f;%.0f;%.0f;%.1f;%.0f;%.0f;%.2f;%.2f;%.0f;%.5f;%.6f;%.5f;%.6f;%.5f;%.2f;%.2f;%.0f\n", iName,OptVal,RangesRaw,PER,PRC,LIM, FlatNum,FlatBars,FlatBarsAvg,FlatRangHL,FlatRangCl,FlatRange, TrndNum,TrndBars,TrndBarsAvg,TrndRangHL,TrndRangCl,TrndRange, SwitchesRaw,SwitchesAtan,BrRaw,BrAtan,RangesRaw,RangesAtan, FlatBarsAvg*_Period/60.0,TrndBarsAvg*_Period/60.0, (FlatBars+TrndBars) ); int fH = FileOpen(fName,FILE_READ|FILE_WRITE); if ( fH == INVALID_HANDLE ) Print("ERROR open ",fName,": ",_LastError); FileSeek(fH,0,SEEK_END); FileWriteString(fH, row, StringLen(row) ); FileClose(fH); } // Rückgabe von 0.0 statt neg. Werte! Die bringen unser Optimierungsdiagramm durcheinander. return( fmax(0.0,OptVal) ); }
Jetzt ist unser Pseudo-EA fertig und wir bereiten den Strategie-Tester für die Optimierung vor:
- Schalten Sie den "Genetischen Algorithmus" aus, um jede Kombination zu testen.
- Setzen die "Optimierte Parameter" auf "Custom". Das zeigt uns interessantere Bilder im Optimierungsdiagramm.
- Stellen Sie sicher, dass die cache-Datei in ..\tester\caches gelöscht wurde.
- Für eine csv-Datei stellen Sie sicher, dass fName nicht leer ist und ein u.U. existierende Datei dieses Namens in \tester\files gelöscht wurde.
- Wenn Sie einen Dateinamen stehen lassen, wird der Optimierer Zeile um Zeile ergänzen und die Datei so lange vergrößern, bis Sie wegen der Größe Probleme bekommen!
- Wir wählen das Symbol EURUSD.
- Period ist auf H1 gesetzt (hier von 2015. 08. 13 to 2015.11.20).
- Modell ist auf "Open Preis" eingestellt.
- Nicht vergessen aktivieren Sie "Optimierung".
Nach 25 Minuten auf meinem Laptop von 2007 ist der Strategie Tester fertig mit der Optimierung und wir finden die Ergebnisse in der csv-Datei in ..\tester\files\.
Im Optimierungsdiagramm können wir zum Beispiel sehen (unten=LIM, rechts=PER):
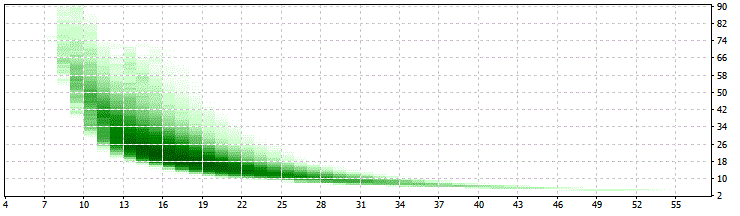
Das schaut viel besser aus als unsere erste Optimierung. Wir sehen ein klares Feld mit erhöhter Dichte bei 34>PER>10 and 25>LIM>13, das viel besser ist als 2,..,90 und 4,..,90!
Überprüfen wir jetzt, ob die Ergebnisse mit anderen Minima für die Wechsel ähnlich aussehen (= Zeichen stabiler Ergebnisse) oder nicht:
SwMin = 50:
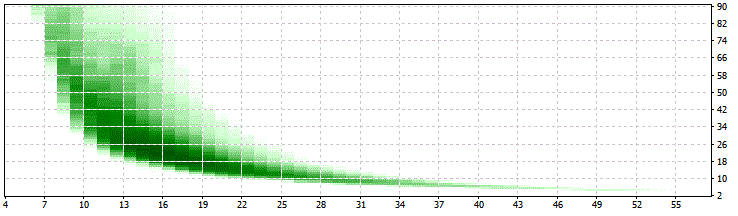
SwMin = 150
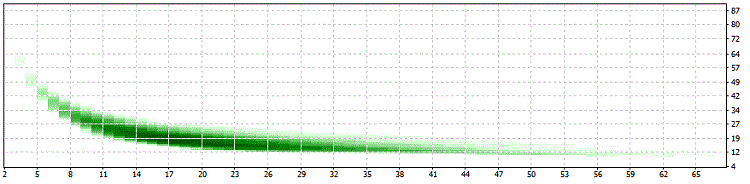
SwMin = 200:
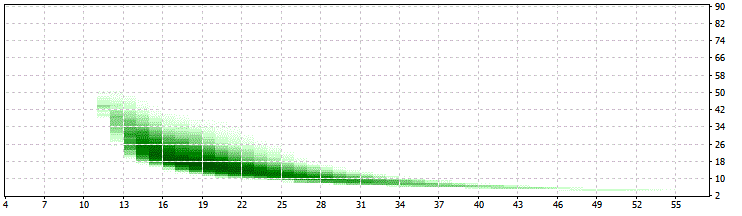
Für alle Optimierungen gelten diese Limits: 34>PER>10 und 25>LIM>13, das ist ein gutes Zeichen für die Robustheit dieses Ansatzes!
- Wir müssen die Funktion atan(..) verwenden, um OptVal gleich sensitiv für unsere drei Variablen machen.
- Die Verwendung der atan-Funktion mit unterschiedlichen Koeffizienten ist mehr oder weniger willkürlich! Ich probierte so lange, bis ich zufriedenstellende Resultate erhielt. Es könnte eine bessere Lösung geben, versuchen Sie es selber!
- Sie könnten denke, ich habe so lange etwas geändert, bis ich erhielt, was ich wollte - so, wie man einen EA überadaptiert. Richtig, deshalb müssen wir die Ergebnisse sorgfältig überprüfen!
- Dieser Pseudo-EA ist nicht gedacht, um eine beste, einzelne Lösung zu finden, sondern nur um vernünftige, kleinere Limits für jeden Parameter zu finden! Am Ende wird der Erfolg allein durch den Handels-EA bestimmt!
Analyse der Ergebnisse in EXCEL, Plausibilitätsprüfung
Jeder Testlauf fügt eine Zeile der csv-Datei hinzu mit weit aus mehr Information als der Strategie Tester anbietet und ignoriert dabei Kategorien, die wir nicht brauchen wie Gewinn, Anzahl an Trades, Profitfaktor, ... Diese Datei laden wir in Excel (in meinem Fall LibreOffice).
Wir müssen alles sortieren erstens nach OptVal, zweitens nach RangesRaw, und dann erhalten wir dies (Tabelle: "Optimizing ADX SwLim 100 raw"):
Wir schauen auf die 'besten' 50 von OptVal. Die verschiedenen Parameter PER, PRC und LIM sind farbig hervorgehoben, für eine leichtere Erkennung.
- RangesRaw schwankt von 2.9 bis 4.5. Das bedeutet der Trend-Markt hat eine 3 bis 4,5 fache größere Spanne als der Seitwärts-Markt.
- Der Seitwärts-Markt dauert zwischen 6 bis 9 Bars (Stunden).
- Der Seitwärts-Markt umfasst zwischen 357 bis 220 Points - genug Raum für ein "Range-Trading".
- Der Trend dauert zwischen 30 und 53 Stunden.
- Der Trend-Markt umfasst zwischen 1,250 und 882 Points.
- Wenn man nicht nur auf die obersten 50 sondern 200 schaut, die Spannen sind fast gleich RangesRaw: 2.5 bis 5.4, Seitwärts-Markt zwischen 221 und 372, Trend-Markt: 1,276 bis 783.
- PER der obersten 200: 14 bis 20 und LIM: 14 bis 20, aber wir sollten uns das im Detail anschauen!
- Wir schauen auf den Teil, wenn OptVal 0.0 wird, wir sehen sehr hohe Werte für RangesRaw, aber andere Werte sagen uns, es wäre nicht gut zu handeln (Tabelle: "skipped OptVal=0"):
RangesRaw ist irrwitzig hoch, aber FlatBarsAvg ist einfach zu kurz zum Handeln und/oder TrndBarsAvg ist zu hoch mit mehr als 1000 Stunden.
Prüfen wir jetzt RangeRaw dort, wo OptVal>0 und sortieren nach RangesRaw (Tabelle: "OptVal>0 sort RangesRaw"):
Die höchsten 50 Werte von RangesRaw reicht von 20 bis 11. Aber schauen Sie auf TrendBarsAvg: Im Durchschnitt etwa 100, das wären mehr als 4 Tage.
Insgesamt können wir sagen OptVal hat ziemlich gut alle ADX Ergebnisse abgewertet, die ziemlich schwierig zu handeln wären. Auf der anderen Seite, die höchsten RangesRaw der oberen 200 (5.4) oder oberen 500 (7.1) sehen sehr vielversprechend aus.
Parameter Prüfung
Nun, nach der notwendigen Plausibilitätsüberprüfung schauen wir uns unsere Parameter des ADX an PER und PRC und seine LIM Grenzen.
Wegen der vielen Zeilen (=29 106) beschränken wir uns auf jene mit OptVal größer 0. In der unbearbeiteten Tabelle sind das die ersten 4085 Zeilen (nachdem wir nach OptVal sortiert haben!). Wir kopieren sie in eine neue Tabelle. Dort ergänzen wir drei Spalten neben PER wie im Bild dargestellt. Alle Formeln finden Sie in der beigefügten csv-Datei.
Ab Zeile 5 tragen sie in die Spalten D,E,F ein: AVERAGE(D$2:D5), STDEV(D$2:D5), SKEW(D$2:D5). Die Zelle in Zeile 2 zeigt nur den Wert der letzten Zeile mit den Statistik-Ergebnissen der ganzen Spalte von RangesRaw. Warum? Da die Tabelle von den besten zu den schlechtesten Werten sortiert ist, sehen wir in Zeile n den Durchschnitt, die Standardabweichung und Schiefe der besten n. Der Vergleich der besten n Werte mit allen Ergebnissen sagt uns, wo wir möglicherweise finden, was wir suchen (tab: "OptVal>0 Check PER, PRC, LIM"):
Welche Informationen sehen wir hier? In der zweiten Zeile (unter last) sehen wir, der Durchschnitt (Avg) für alle PER ist 33.55, die Standardabweichung (StdDev) 21.60. Wenn PER wie eine Gauß-Verteilung verteilt ist, finden wir 68% aller Werte von PER innerhalb Durchschnitt +/- StdDev und 95% innerhalb +/-2*StdDev. Hier wäre das zwischen 33.55 - 21.60 = 11.95 und 33.55 + 21.60 = 55,15. Schauen wir jetzt auf die Zeilen der Besten. Der Durchschnitt beginnt bei 19 in der Zeile 5 und wächst langsam auf 20. StdDev steigt von 2.0 auf 2.6. Jetzt überdecken die 68% 18 bis 23. Zum Schluss zur Schiefe. Sie ist 0.61 in Zeile 2 für alle PER. Das heißt, die linke Seite (kleiner als der Mittelwert) hat mehr Werte als die rechte Seite, obwohl es immer noch eine Gauß-Verteilung ist. Erst wenn die Schiefe +/- 1,96 überschreitet, können wir nicht mehr von einer Gauß-Verteilung ausgehen, und wir müssten sehr vorsichtig mit den Werten von Durchschnitt und Standardabweichung umgehen, da eine Seite stark 'übergewichtet', die andere Seite praktisch 'leer' ist. Ist die Schiefe größer 0 heißt das, die rechte Seite (>Durchschnitt) hat weniger Werte als die linke Seite. Also, PER ist normalverteilt (Gauß-Verteilung) und wir können Durchschnitt und Standardabweichung verwenden. Wenn wir die Entwicklung der obersten Ergebnisse (nach OptVal) vergleichen, sehen wir, dass der Durchschnitt langsam von 19 auf 20 steigt (Zeile 487!). Die Standardabweichung wächst währenddessen von ~2.0 auf 5.36 (Zeile 487). Die Schiefe steigt niemals über 0.4, wenn wir die ersten 10 Ergebnisse ignorieren, und ist im Wesentlichen positiv und das bedeutet, das wir einen (oder zwei) Werte 'auf der linken Seite' des Durchschnitts ergänzen.
Die Ergebnisse von PRC müssen anders behandelt werden! Im Gegensatz zu PER und LIM sind die Werte von PRC die einer Nominalskala, jede Berechnung mit ihnen macht keinen Sinn. Daher zählen wir nur, wie oft sie erscheinen, und berechnen davon den Mittelwert von RangesRaw für jeden PRC 0,..,6. Nich vergessen, wir wollten auch absurde Einstellungen prüfen. Normalerweise würden wir PRC=Open (1), PRC=High (2) or PRC=Low (3) nicht verwenden. Trotzdem müssen wir aber erkennen, Open ist der häufigste Wert unter den besten 50. Das ist wahrscheinlich der Tatsache geschuldet, dass wir nur ganze Bars verwenden, der ADX das Hoch und Tief der Bar verwendet und daher das Hoch und Tief 'dem Open bekannt' ist - eine Art unmoralischer Vorteil, wenn der ADX das verwendet. Der Erfolg von Hoch und Tief? Schwer zu erklären! Die Tatsache, dass der Preis von 1,33 im Aug. 2014 auf 1.08 im Dez. 2015 fällt, könnte der Erfolg des Low erklären, aber nicht das High. Vielleicht ist es das Ergebnis einer stärkeren Marktdynamik. Jedenfalls blenden wir sie aus. Vergleichen wir PER = Close, Typical, Median und Weighted erkennen wir, es gibt keine großen Unterschiede, wenn wir die Spalten Q, R, und S betrachten. Unter den oberen 100 PRC=Typical(4) wäre die beste Wahl, sogar besser als PRC=High(2). Aber unter den oberen 500 PRC=Close ist das Beste.
Für LIM verwenden wir die selben Formeln wie für PER. Interessant ist, dass die 'letzte' Schiefe (für alle) weit über +1.96 ist, aber nicht für die oberen 100 (=0.38) oder für die Top 500 (=0.46). Verwenden wir also nur die besten 500. Der Durchschnitt der obersten 500 ist 16.65 und die Standardabweichung 3.03. Natürlich, LIM hängt stark von PER ab: je kleiner PER desto höher LIM und vice versa. Die Spannen von LIM und von PER korrespondieren.
Wählen wir also die besten Spannen für unsere drei Variablen PER, PRC und LIM die Ergebnisse der besten 500:
- PER Avg=20.18 +/- StdDev=5.51 Skew=0.35 (-2) => (20.18-5.41-2=) 14,..,(20.18+5.52=) 26 (Schritt 1 => 13).
- PRC according to row 500 we can decide for only close (Schritt 0 => 1).
- LIM Avg=16.64 +/- StdDev=3.03 Skew=0.46 (-2) => (16.64-3.03-2=) 12,..,(16.64+3.03=) 20 (Schritt 1 => 9)
Insgesamt haben wir jetzt nur noch 13*1*9 = 117 Kombinationen für den Handels-EA für seine Optimierung.
Betrachten wir die Ergebnisse einmal genauer (Es ist die Tabelle mit Namen: "OPT Top 500 Best PER's Average"):
Wir sehen, dass PER=18 am häufigsten unter den oberen 500 auftritt und PER=22 den höchsten Durchschnitt hat. Beide sind Teil unserer Auswahl ebenso wie ihre jeweiligen LIM.
Visueller Mode
Überprüfen wir als letztes PER mit den besten Durchschnitten der oberen 500: PER=22. Ohne PRC=Open,Low,High ist diese Einstellung mit einem Verhältnis der Spanne von 4.48 in der Zeile 38, mit gelbem Hintergrund im vorherigen Bild der Tabelle.
Wie lassen nun den Pseudo-EA im "Visuellen Modus" laufen und ergänzen den ADX mit dem selben Einstellungen.
(Nur) Im Visuellen Modus platziert unser Pseudo-EA einen blauen rechts-links Pfeil auf der nächsten Bar, wenn ein Seitwärts-Markt erkannt wurde und einen roten auf-ab Pfeil im Falle einer Trend-Bar (hier von : Mi. 2015.07.30 05:00 bis Di. 2015.08.04 12:00):
Deutlich können wir die Probleme des ADX erkennen, die Sie vielleicht ermutigen diese Idee zu verbessern!
- Der ADX ist zu spät, speziell, wenn er den Seitwärts-Markt erkennen soll nach dem eine große Kursbewegung den ADX nach oben geschleudert hat. Er braucht ziemlich lange, um sich wieder 'abzukühlen'. Es wäre schön, wenn der Seitwärts-Markt bereits um den Zeitpunkt 2015.08.03 00:00 entdeckt worden wäre und nicht erst am 2015.08.3 09:00.
- Wenn der ADX LIM zu nahe kommt, erkennen wir ein störendes Hin-und-Her. Es wäre zum Beispiel besser, wenn zum Zeitpunkt 2015.08.03 14:00 der Trend-Markt nicht signalisiert worden wäre.
- Wenn die Hoch-Tief-Spanne der Bars immer kleiner wird, genügen bereits ein paar 'kleine' Bars der selben Richtung, um einen neuer Trend zu erkennen. Statt des neuen Trends um 2015.08.03 20.00 wäre es besser, wenn der Trend erst später als solcher erkannt worden wäre, vielleicht gegen 2015.08.04 07:00.
- Der Pseudo-EA unterscheidet nicht zwischen Aufwärts- und Abwärts-Trend. Es bleibt Ihnen überlassen, dafür z.B. DI+ und DI- des ADX oder andere Indikatoren zu verwenden.
- Vielleicht ist die durchschnittlich Länge der Trend-Märkte (46.76), das sind fast 4 Tage(!), zu lang. In diesem Fall könnte entweder ein höherer Wert für SwMin (statt 100) oder ein kleinerer SwCoeff (statt 0.01) oder beides zu Ergebnissen führen, die der Idee näher kommen könnten.
Schlussfolgerung
Ein Handels-EA, der den ADX verwendet, müsste 54 201 Kombinationen testen, nur um einen einzelnen Indikator zu optimieren - in der Hoffnung, dass der ADX auch tatsächlich leistet, was er tun soll! Wenn der Handels-EA nicht so gut ist wie erhofft, könnte es schwierig werden, das eigentliche Problem zu erkennen, um dort mit Verbesserungen anzusetzen. Nach dieser Optimierung, die nur ein paar Minuten für die gesamten 54 201 Kombinationen benötigt, haben wir herausgefunden:
- Der ADX ist in der Lage zwischen Seitwärts- und Trend-Märkten zu unterscheiden und
- Wir konnten die 54 201 auf 117 (= 13 (PER) * 1 (PRC) * 9 (LIM)) reduzieren.
- Die Spanne des Seitwärts-Marktes bewegt sich zwischen 372 und 220 Points (Top 100).
- Die Spanne des Trend-Marktes bewegt sich zwischen 1277 und 782 Points.
Daher können die eigentlichen 2 168 040 000 Kombinationen des Handels-EA auf (117*40 000=) 4 680 000 reduzieren. Das sind nur 0,21%, und das bedeutet entweder 99.7% schneller oder um sehr viel besser im Falle einer genetischen Optimierung, weil einfach viel mehr Werte der Nicht-Adx-Parameter getestet werden. Dies sind die verringerten Einstellungen für unseren Pseudo-EA:
Darüber hinaus erhalten wir (das hängt natürlich von der Handelsidee ab) wertvolle Informationen für Kriterien eine Position zu eröffnen, zu schließen und Stopp-Loss und Take-Profit zu setzen.
Der Pseudo-EA und die Excel-Datei sind beide beigefügt. Wir haben jeden Schritt erklärt, warum wir so vorgingen, und die Fallen aufgezeigt, die auftreten könnten. All das sollte es Ihnen ermöglichen, jetzt eigene optimierte Indikatoren zu entwickeln, bevor Sie sie in einem Handels-EA verwenden. Wenn Sie jetzt einen eigenen Version entwickeln wollen, Seitwärts- und Trend-Märkte zu ermitteln, können diese Ergebnisse verwenden, um die eigenen Ergebnisse damit zu vergleichen, um herauszufinden, welche Indikatorkombinationen besser sind!
Wenn Sie das verwenden wollen, einen besseren Indikator oder eine Reihe von Indikatoren für die Bestimmung von Seitwärts- und Trend-Märkte zu finden, müssen Sie sehr wahrscheinlich die Koeffizienten für calcOptVal() anpassen. Z.B. wenn Sie eine längere Testperiode verwenden wollen, müssen Sie zumindest SwMin erhöhen. Bedenken Sie, ein guter OptVal ermöglicht es dem Genetischen Algorithmus die besten Einstellungen aus vielen möglichen zu finden!! Aber Sie können die Idee auch für eine vollkommen andere Optimierung allein von Indikatoren ohne einen Handels-EA verwenden. In diesem Fall könnte es nötig sein, die Funktion calcOptVal() komplett neu zu schreiben.
Wenn Sie mit diesem EA arbeiten wollen, vergessen Sie nicht:
- Stellen Sie sicher, dass die cache-Datei in ..\tester\caches gelöscht wurde.
- Wenn Sie die csv-Datei in ..\tester\files\ benötigen, tragen Sie den Dateinamen für fName ein und löschen Sie eine existierende csv-Datei gleichen Namens.
- Wenn Sie keine csv-Datei wollen, lassen Sie den Eintrag für fName des Pseudo-EAs leer.
- Wenn Sie einen Dateinamen für eine csv-Datei stehen lassen, wird der Optimierer Zeile und Zeile ergänzen und die Datei so lange vergrößern, bis Sie wegen der Größe Probleme bekommen!
- Setzen Sie den "Optimierte Parameter" auf "Custom" im "Test" Tab.
- Der einfachste Weg, OptVal und die Ergebnisse des Genetischen Algorithmus zu beeinflussen, ist die Minima der drei Koeffizienten: SwMin, BrMin, RgMin zu verändern.
- Setzen Sie das "Model" auf "Open Preis", es ist schneller.
- Wenn Sie anderen Zeitpunkte ("Use Date" : From..To) verwenden, müssen Sie die Koeffizienten im Code genau über der Funktion calcOptVal() im Pseudo-EA anpassen.
- Nach der Optimierung wählen Sie eine Einstellung aus "Ergebnisse der Optimierung" und starten Sie einen neuen Testlauf im "Visuellen Modus" , um zu sehen, ob die Optimierung das gewünschte Ziel erreicht hat.
- Die blauen rechts-links Pfeile zeigen den Beginn eines Seitwärts-Marktes, die roten auf-ab Pfeile den eines Trend-Marktes.
- Wenn Sie eine bessere Alternative zum ADX entwickeln wollen, brauchen Sie nicht unbedingt die csv-Datei: Einfach nur optimieren, die besten Ergebnisse im "Visuellen Modus" anschauen, etwas ändern, erneut optimieren, ...
- Für andere Fragen an den Markt als Seitwärts- oder Trend-Markt benötigen Sie wahrscheinlich die Analysen in der csv-Datei und wahrscheinlich eine andere Art OptVal zu kalkulieren.
Aber nicht vergessen, es gibt keine Garantie für einen schnellen noch für einen Erfolg überhaupt.
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/2118
 Graphische Interfaces III: Einfache und multifunktionale Buttons (Kapitel 1)
Graphische Interfaces III: Einfache und multifunktionale Buttons (Kapitel 1)
 Grafische Interfaces II: Das Hauptmenü Element (Kapitel 4)
Grafische Interfaces II: Das Hauptmenü Element (Kapitel 4)
 Graphische Interfaces III: Gruppen von einfachen und multifunktionalen Buttons (Kapitel 2)
Graphische Interfaces III: Gruppen von einfachen und multifunktionalen Buttons (Kapitel 2)
 Grafische Interfaces II: Einrichtung des Eventhandlers für die Bibliothek (Kapitel 3)
Grafische Interfaces II: Einrichtung des Eventhandlers für die Bibliothek (Kapitel 3)
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Vielen Dank für die Arbeit, Carl.