Risikomodell für ein Portfolio unter Verwendung des Kelly-Kriteriums und der Monte-Carlo-Simulation

Einführung

Seit Jahrzehnten verwenden Händler die Kelly-Formel, um den optimalen Anteil des Kapitals zu bestimmen, der einer Investition oder Wette zugewiesen werden sollte, um das langfristige Wachstum zu maximieren und gleichzeitig das Risiko des Ruins zu minimieren. Das blinde Befolgen des Kelly-Kriteriums auf der Grundlage der Ergebnisse eines einzigen Backtests ist jedoch für einzelne Händler oft gefährlich, da beim Live-Handel der Handelsvorsprung im Laufe der Zeit abnimmt und die vergangene Leistung keine Vorhersage für das zukünftige Ergebnis ist. In diesem Artikel werde ich einen realistischen Ansatz für die Anwendung des Kelly-Kriteriums für die Risikoallokation eines oder mehrerer EAs in MetaTrader 5 vorstellen und dabei die Ergebnisse der Monte-Carlo-Simulation von Python einbeziehen.

Die Theorie des Leverage Space Trading Model

Das Leverage Space Trading Model (LSTM) ist ein theoretischer Rahmen, der vor allem im Zusammenhang mit Finanzmärkten und Vermögensverwaltung verwendet wird. Es integriert das Konzept der Hebelwirkung, das sich auf den Einsatz von Fremdkapital zur Steigerung potenzieller Erträge bezieht, mit einem dynamischeren und raumorientierten Ansatz zur Modellierung des Marktverhaltens. 

LSTM verwenden das Kelly-Kriterium, um den prozentualen Anteil des Portfolios am Risiko pro Handel für eine einzelne Strategie zu berechnen

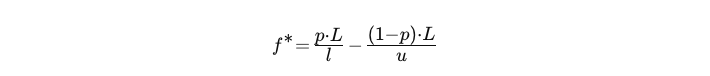
• L: Hebelfaktor
• p: Erfolgswahrscheinlichkeit
• u: gehebelte Gewinnquote
• l: gehebelte Verlustquote

Ausgehend von einem Backtest-Ergebnis können wir den Variablenwert mit den folgenden Formeln ermitteln.

Nehmen wir an, Sie handeln mit einer Hebelwirkung von 2:1. Nehmen Sie Folgendes an:

• Die Wahrscheinlichkeit eines erfolgreichen Handels (p) = 0,6 (60% Gewinnchance).
• Die erwartete Rendite (u) = 0,1 (10% Gewinn ohne Hebelwirkung, also gehebelt 2:1 = 20% Gewinn).
• Der erwartete Verlust (l) = 0,05 (5% Verlust ohne Hebelwirkung, also gehebelt 2:1 = 10% Verlust).

Wir setzen das in die Kelly-Formel ein:

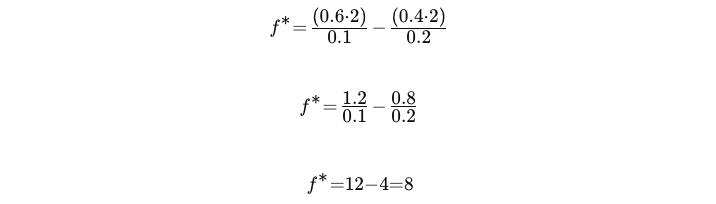
Der optimale Anteil Ihres Kapitals, den Sie bei diesem Handel riskieren sollten, wäre also 8 % Ihres Gesamtkapitals.

Nachdem Sie diese Formel auf einen Ihrer eigenen EAs angewendet haben, werden Sie unweigerlich ein Gefühl des Unbehagens verspüren, wenn Sie sehen, wie viel Risiko Sie pro Handelsgeschäft hätten eingehen müssen. Diese Formel geht nämlich davon aus, dass Ihre künftigen Ergebnisse genauso gut sein werden wie Ihr Backtest, was unrealistisch ist. Deshalb wendet man in der Branche in der Regel einen Bruchteil von Kelly auf das Risiko an, d. h., man teilt den Wert durch eine ganze Zahl, um das Risiko zu verringern und Spielraum für künftige Widrigkeiten zu schaffen.

Jetzt müssen wir die Frage beantworten: Welcher Anteil sollte so gewählt werden, dass sich die Händler mit dem Risiko wohlfühlen und trotzdem ihren erwarteten Ertrag pro Handel maximieren?

In dem Buch The Leverage Space Trading Model von Ralph Vince wurde durch einen stochastischen Optimierungsprozess festgestellt, dass die Renditeerwartungsfunktion unabhängig von der Dimension konvex ist. Das bedeutet, dass es für die optimale erwartete Rendite nur eine einzige Lösung gibt und der Erwartungswert kontinuierlich abnimmt, wenn sich der Wert von f* von der optimalen Lösung entfernt.

Da der Live-Handel nicht so ideal ist wie das Backtesting, erwarten wir, dass das reale f*, das unsere Rendite maximiert, kleiner ist als das mit der Kelly-Formel berechnete f*. Alles, was wir also tun müssen, ist, unser zugewiesenes Risiko auf das höchste Niveau zu erhöhen, das wir tolerieren können, wobei wir sicherstellen müssen, dass es immer noch kleiner ist als das Kelly-Risiko.

In der Regel wird die Toleranzgrenze eines Händlers an dem maximalen Drawdown gemessen, den er ertragen kann. Für den Rest des Artikels gehe ich davon aus, dass ein maximaler Drawdown von 30 % eine angemessene Toleranzgrenze darstellt.

Anwendung des gehebelten Risikos in MQL5

Um das gehebelte Risiko in MQL5 anzuwenden, deklarieren wir zunächst den Risikoprozentsatz als globale Variable. In diesem Fall riskieren wir 2 % pro Handel.

input double risk = 2.0;

Als Nächstes schreiben wir eine Funktion zur Berechnung des Lot-Volumens auf der Grundlage des Stop Loss in der aktuellen Preiseinheit. Wenn der Stop-Loss beispielsweise bei einem Kurs von 0 gesetzt wird, entsprechen die Stop-Loss-Punkte direkt dem aktuellen Kurs, und das Ergebnis des Handels spiegelt die exakte Bewegung des Basiswerts wider.

//+------------------------------------------------------------------+
//| Calculate the corresponding lot size given the risk              |
//+------------------------------------------------------------------+
double calclots(double slpoints)
{
   double riskAmount = AccountInfoDouble(ACCOUNT_BALANCE) * risk / 100;

   double ticksize = SymbolInfoDouble(_Symbol, SYMBOL_TRADE_TICK_SIZE);
   double tickvalue = SymbolInfoDouble(_Symbol, SYMBOL_TRADE_TICK_VALUE);
   double lotstep = SymbolInfoDouble(_Symbol, SYMBOL_VOLUME_STEP);

   double moneyperlotstep = slpoints / ticksize * tickvalue * lotstep;
   double lots = MathFloor(riskAmount / moneyperlotstep) * lotstep;
   lots = MathMin(lots, SymbolInfoDouble(_Symbol, SYMBOL_VOLUME_MAX));
   lots = MathMax(lots, SymbolInfoDouble(_Symbol, SYMBOL_VOLUME_MIN));
   return lots;
}

Der obige Code bestimmt zunächst den Risikobetrag, indem er den Kontostand mit dem Risikoprozentsatz multipliziert.

Anschließend werden die Tick-Größe, der Tick-Wert und der Lot-Schrittweite des Symbols abgerufen und der Geldwert jedes Lot-Schrittes auf der Grundlage des Stop-Loss-Abstandes berechnet.

Die Losgröße wird ermittelt, indem der Risikobetrag durch den Geldbetrag pro Losgrößenstufe geteilt und auf die nächste Losgrößenstufe gerundet wird.

Schließlich wird sichergestellt, dass die berechnete Losgröße innerhalb der zulässigen Mindest- und Höchstgrenzen für das Symbol liegt, bevor das Ergebnis zurückgegeben wird.

Beachten Sie, dass nicht jede Handelsstrategie einen festen Stop-Loss und Take-Profit beinhaltet. Im Bereich des Hebelhandels gehen wir jedoch davon aus, dass wir einen festen Stop-Loss verwenden, da wir beim Kelly-Kriterium wissen müssen, wie viel wir riskieren wollen, bevor wir ein Handelsgeschäft platzieren.

Wir rufen diese Funktion auf, bevor wir eine Ausführung vornehmen. Ein Beispiel könnte so lauten.

//+------------------------------------------------------------------+
//| Execute buy trade function                                       |
//+------------------------------------------------------------------+
void executeBuy(double price) {
       double sl = price- slp*_Point;
       sl = NormalizeDouble(sl, _Digits);
       double lots = lotpoint;
       if (risk > 0) lots = calclots(slp*_Point);
       trade.BuyStop(lots,price,_Symbol,sl,0,ORDER_TIME_DAY,1);
       buypos = trade.ResultOrder();
       }

Normalerweise sollte das Backtest-Ergebnis eines konsistent profitablen EAs einer Exponentialfunktion wie dieser ähneln:

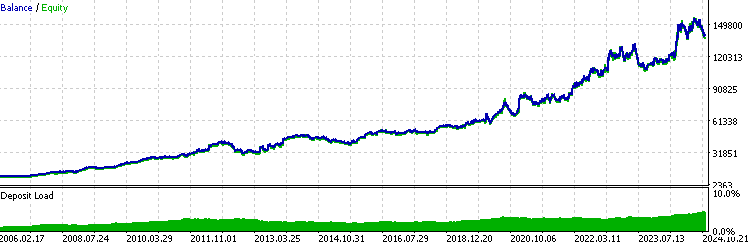
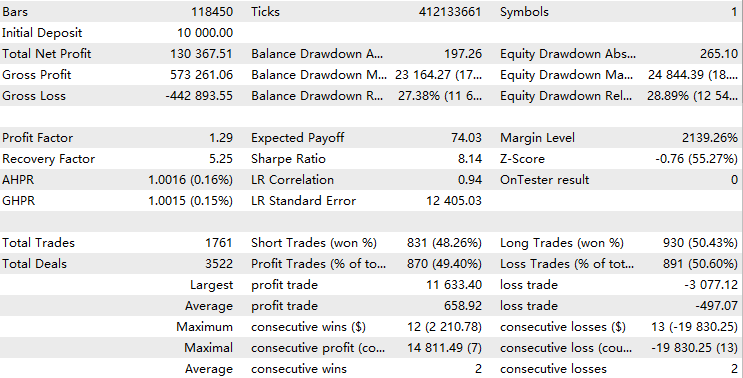
Bei der Analyse von Backtest-Statistiken sind bei der Verwendung dieses Leverage-Handelsmodells einige Dinge zu beachten:

• Wenn Ihr Expert Advisor konstant profitabel ist, haben die jüngsten Ergebnisse einen größeren Einfluss auf die Gesamtleistung des Backtests als frühere. Im Wesentlichen gewichten Sie die Bedeutung der jüngsten Leistungen stärker.
• Die LR-Korrelation ist nicht sinnvoll, da der Graph eine Exponentialkurve ist.
• Die Sharpe Ratio ist unrealistisch, weil sie von einem linearen Verhältnis zwischen Risiko und Rendite ausgeht. Die Hebelwirkung erhöht sowohl die potenziellen Renditen als auch die Risiken, was zu einer Verzerrung der risikobereinigten Performance-Metriken führt.

Wenn Sie die oben genannten Kennzahlen dennoch auswerten möchten, legen Sie einfach die Losgröße fest und führen einen weiteren Test durch.

Die Monte-Carlo-Simulation zur Maximierung des Drawdowns

Wir betrachten eine Kapitalkurve als eine Reihe von prozentualen Veränderungen unseres Kontostandes, und der maximale Drawdown kann als das Segment dieser Reihe mit dem kleinsten kumulierten Prozentsatz angesehen werden. Ein einziger Backtest repräsentiert nur eine mögliche Anordnung dieser Reihe, was ihre statistische Robustheit einschränkt. Ziel dieses Abschnitts ist es, die potenziellen Drawdowns zu verstehen und das 95. Perzentil als Referenz für die maximale Toleranz zu wählen.

Die Monte-Carlo-Simulation kann zur Simulation einer möglichen Kapitalkurve auf verschiedene Weise eingesetzt werden:

1. Zufallsstichproben von Ergebnissen: Durch die Generierung von Zufallsrenditen auf der Grundlage historischer Wertentwicklungen oder angenommener statistischer Verteilungen (z. B. normal) simulieren Sie potenzielle Kapitalkurven, indem Sie die Renditen im Laufe der Zeit aufzinsen.

2. Bootstrapping: Resampling historischer Renditen mit Ersetzung, um mehrere simulierte Kapitalentwicklungen zu erstellen, die die in der Vergangenheit beobachtete Variabilität der Performance widerspiegeln.

3. Umsortieren: Die Reihenfolge der historischen Renditen wird zufällig umsortiert (reshuffled) und die neu sortierten Reihen werden verwendet, um verschiedene Kapitalkurse zu generieren, was eine Vielzahl von Szenarien ermöglicht.

4. Risiko/Ertrags-Anpassungen: Modifizierung der Eingabeparameter (z. B. Volatilitäts- oder Drawdown-Grenzen) auf der Grundlage bestimmter Risikokriterien, um realistische Kapitalkurven unter verschiedenen Marktbedingungen zu erzeugen.

In diesem Artikel konzentrieren wir uns auf die Methode des Umsortierens, des „Shufflens“.

Zunächst rufen wir den Geschäftsbericht des Backtests auf, indem wir mit der rechten Maustaste wie folgt klicken.

Dann öffnen wir Python und extrahieren die nützlichen Zeilen, die Kontostand und Gewinn/Verlust von jedem Handel mit diesem Code haben.

import pandas as pd
# Replace 'your_file.xlsx' with the path to your file
input_file = 'DBG-XAU.xlsx'
# Load the Excel file and skip the first {skiprows} rows
data = pd.read_excel(input_file, skiprows=10757)

# Select the 'profit' column (assumed to be 'Unnamed: 10') and filter rows as per your instructions
profit_data = data[['Profit','Balance']][1:-1] 
profit_data = profit_data[profit_data.index % 2 == 0]  # Filter for rows with odd indices
profit_data = profit_data.reset_index(drop=True)  # Reset index
# Convert to float, then apply the condition to set values to 1 if > 0, otherwise to 0
profit_data = profit_data.apply(pd.to_numeric, errors='coerce').fillna(0)  # Convert to float, replacing NaN with 0
# Save the processed data to a new CSV file with index
output_csv_path = 'processed-DBG-XAU.csv'
profit_data.to_csv(output_csv_path, index=True, header=['profit_loss','account_balance'])
print(f"Processed data saved to {output_csv_path}")

Die zu überspringenden Zeilen sind grundsätzlich die Zeilen über diesem Index -1.

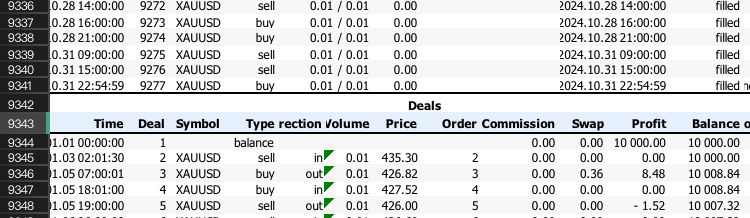
Als Nächstes müssen wir den Gewinn in eine prozentuale Veränderung für jeden Handel umrechnen, um sicherzustellen, dass die neu umsortierten Reihen zu demselben Endsaldo führen. Dazu wird die Kontosaldo-Spalte um eine Zeile verschoben und der Gewinn oder Verlust als Prozentsatz des Saldos vor jedem Handel berechnet.

initial_balance = account_balance.iloc[0] - profit_loss.iloc[0]

# Calculate the account balance before each trade
account_balance_before_trade = account_balance.shift(1)
account_balance_before_trade.iloc[0] = initial_balance

# Compute the percentage change made to the account balance for each trade
percentage_change = profit_loss / account_balance_before_trade

# Fill any NaN values that might have occurred
percentage_change.fillna(0, inplace=True)

Zum Schluss simulieren wir 1000 zufällige Serien und zeichnen die Top 10 mit dem höchsten Drawdown auf. Beachten Sie, dass die endgültigen Werte aufgrund der Kommutativ-Eigenschaft der Multiplikation alle gleich sein sollten. Die Multiplikation der prozentualen Veränderungsreihen ergibt das gleiche Ergebnis, unabhängig von der Reihenfolge, in der die Werte neu sortiert werden.

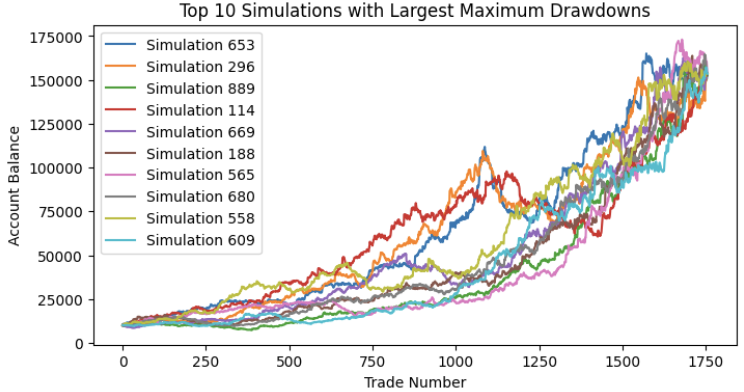
Die Verteilung des maximalen Drawdowns sollte einer Normalverteilung ähneln, und wir sehen hier, dass das 95 %-Perzentil (etwa zwei Standardabweichungen) bei etwa 30 % des maximalen Drawdowns liegt.

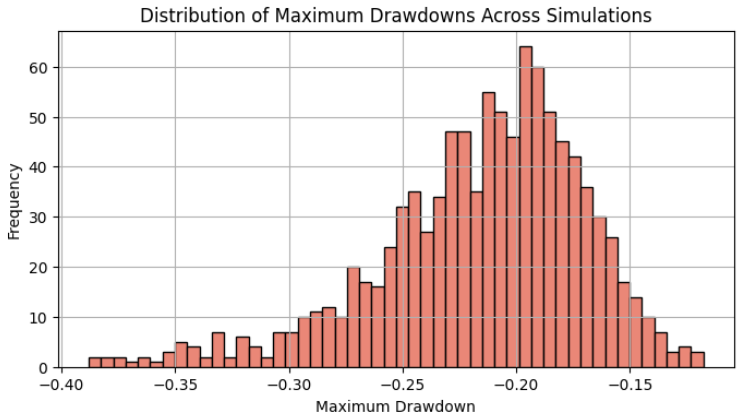
Der maximale Drawdown unseres ersten Backtests lag bei nur 17 % und damit unter dem Mittelwert dieser Verteilung. Hätten wir diesen Wert als den von uns erwarteten maximalen Drawdown angenommen, hätten wir unser Risiko um den Faktor 2 erhöht, verglichen mit dem Risiko, das wir nach den Ergebnissen der Monte-Carlo-Simulation nun einzugehen bereit sind. Wir haben uns für das 95 %-Perzentil entschieden, weil dies ein allgemeines Ergebnis ist, das nach Ansicht der Gelehrten der tatsächlichen Handelsleistung am nächsten kommt. Hier haben wir das Glück, dass das 95 %-Perzentil genau mit unserer maximalen Toleranz von 30 % übereinstimmt, die wir zu Beginn festgelegt hatten. Das bedeutet, dass wir mit einem Risiko von 2 % pro Handel unseren Gewinn maximieren und gleichzeitig unsere maximale Toleranzgrenze einhalten können, wenn wir diesen einzelnen EA in unserem Portfolio handeln. Wenn das Ergebnis abweicht, sollten wir das obige Verfahren wiederholen, bis wir die optimale Lösung gefunden haben.

Kelly-Kriterium für die Portfolio-Optimierung

Wenn wir mehrere EAs auf einem einzigen Konto einsetzen, müssen wir zunächst das oben beschriebene Verfahren für jeden EA durchführen, um sein optimales Risiko zu bestimmen. Dann wenden wir dieses Risiko auf das zugewiesene Kapital für jeden EA innerhalb des Gesamtportfolios an. Aus der Perspektive des gesamten Kontos entspricht der Risikobetrag für jeden EA dem ursprünglichen Risiko multipliziert mit dem zugewiesenen Anteil.

Der Kelly-Allokationsanteil für jeden EA wird durch seine Renditekorrelationen mit anderen EAs und seine gesamte Backtest-Performance bestimmt. Unser primäres Ziel ist es, sicherzustellen, dass sich die EAs gegenseitig so weit wie möglich ausgleichen, was zu einer gleichmäßigeren Kapitalkurve für das gesamte Portfolio führt. Es ist wichtig zu beachten, dass das Hinzufügen weiterer EAs und Strategien die Diversität des Portfolios nur dann erhöht, wenn sie nicht korreliert sind; andernfalls kann sich das Gesamtrisiko erhöhen, ähnlich wie bei der Verstärkung des Risikos eines einzelnen EAs.

Im Einzelnen berechnen wir den Kelly-Allokationsanteil für jede Strategie auf der Grundlage der erwarteten Renditen und der Kovarianzmatrix der Renditen mit Hilfe der folgenden Formeln:

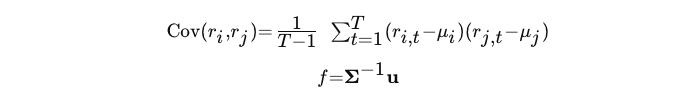
• r: die Rendite von EAi oder EAj zum Zeitpunkt t
• μ: die mittlere Rendite von EAi oder EAj
  
• f: Kelly-Zuweisung für jeden EA
• Σ-1: die Inverse der Kovarianzmatrix
  
• u: der Vektor der erwarteten Rendite für jeden EA

Um die Werte für die oben genannten Variablen zu extrahieren, müssen wir für jede Strategie einen Backtest durchführen und die prozentualen Renditereihen jeder Strategie in einem einzigen Datenrahmen speichern. Anschließend wählen wir auf der Grundlage der Häufigkeit aller EAs das geeignete Zeitintervall für die Aufzeichnung aus, da die Kovarianz auf der Grundlage der Korrelationen der Renditen innerhalb desselben Zeitraums berechnet wird. Wir führen solche Operationen mit diesem Python-Code durch:

# Read returns for each strategy
    for file in strategy_files:
        try:
            data = pd.read_csv(file, index_col='Time')
            # Ensure 'Time' is parsed correctly as datetime
            data.index = pd.to_datetime(data.index, errors='coerce')
            
            # Drop rows where 'Time' or 'return' is invalid
            data.dropna(subset=['return'], inplace=True)
            
            # Aggregate duplicate time indices by mean (or could use 'sum', but here mean can ignore the trade frequency significance)
            data = data.groupby(data.index).agg({'return': 'mean'})
            
            # Append results
            returns_list.append(data['return'])
            strategy_names.append(file)
        except Exception as e:
            print(f"Error processing {file}: {e}")
            continue 
    # Check if any data was successfully loaded
    if not returns_list:
        print("No valid data found in files.")
        return  
    # Combine returns into a single DataFrame, aligning by date
    returns_df = pd.concat(returns_list, axis=1, keys=strategy_names) 
    # Uncomment the below line if u wanna drop rows with missing values across strategies
    #returns_df.dropna(inplace=True)
    #Uncomment the below line if u wanna just fill unaligned rows with 0( I think this is best for backtest that may have years differences)
    returns_df.fillna(0, inplace=True)

Stellen Sie sicher, dass alle Backtest-Ergebnisse zur gleichen Zeit beginnen und enden. Wählen Sie außerdem ein geeignetes Zeitintervall für die Aggregation der Ergebnisse, sodass kein Intervall eine übermäßige Anzahl von Abschlüssen aufweist und auch kein Intervall, in dem überhaupt keine Abschlüsse getätigt werden. Wenn die Zeitintervalle zu diskret sind, gibt es möglicherweise nicht genügend Datenpunkte innerhalb derselben Zeitspannen, um die Kovarianz genau zu berechnen. In unserem Fall wählen wir ein einmonatiges Intervall und verwenden die durchschnittliche Rendite für jeden Monat als Renditemerkmal.

Jetzt machen wir die Berechnungen:

    # Calculate expected returns (mean returns)
    expected_returns = returns_df.mean()
    
    # Calculate the covariance matrix of returns
    cov_matrix = returns_df.cov()
    
    # Compute the inverse of the covariance matrix
    try:
        inv_cov_matrix = np.linalg.inv(cov_matrix.values)
    except np.linalg.LinAlgError:
        # Use pseudo-inverse if covariance matrix is singular
        inv_cov_matrix = np.linalg.pinv(cov_matrix.values)
    
    # Calculate Kelly optimal fractions
    kelly_fractions = inv_cov_matrix @ expected_returns.values
    kelly_fractions = kelly_fractions / np.sum(kelly_fractions)

Am Ende wird das Ergebnis etwa so aussehen:

         Strategy  Kelly Fraction
0  A1-DBG-XAU.csv        0.211095
1   A1-DBG-SP.csv        0.682924
2   A1-DBG-EU.csv        0.105981

Wir können dieses Risiko direkt in unseren ursprünglichen MQL5-Code implementieren, da die ursprüngliche Risikoberechnung bereits auf dem Gesamtkontostand basierte. Wenn sich der Kontostand ändert, wird das zugewiesene Kapital automatisch neu berechnet und auf den nächsten Handel angewendet.

double riskAmount = AccountInfoDouble(ACCOUNT_BALANCE) * risk / 100;

Um zum Beispiel die berechnete Kelly-Anteile auf unseren Beispiel-EA anzuwenden, ändern wir einfach diesen Teil des ursprünglichen Codes, und die Aufgabe ist erledigt.

input double risk = 2.0*0.211095;

Ich bin mir durchaus bewusst, dass wir alternativ das Risiko auf der Grundlage der Veränderung des zugewiesenen Kapitals für jeden EA neu berechnen könnten, aber die Berechnung auf der Grundlage des gesamten Portfolios ist aus folgenden Gründen vorzuziehen:

1. Den Überblick über die Veränderungen in den verschiedenen zugewiesenen Hauptstädten zu behalten, ist meiner Meinung nach schwierig. Unter Umständen muss man mehrere Konten eröffnen oder ein Programm schreiben, das die Änderungen nach jedem Handel aktualisiert.
2. Das Kelly-Kriterium wird verwendet, um das langfristige Wachstum des gesamten Portfolios zu maximieren. Die Performance einzelner EAs beeinflusst das Risiko der anderen EAs und erleichtert so das effiziente Wachstum eines kleinen Portfolios, wenn es sich vergrößert.
3. Wenn wir das Risiko auf die Veränderung des zugewiesenen Kapitals für jede EA stützen, werden die gut abschneidenden EAs im Laufe der Zeit einen Anstieg ihres zugewiesenen Kapitals erleben, was zu einer größeren Risikoexposition für diese EAs führt. Dies untergräbt unsere ursprüngliche Absicht, die Risikoallokation auf der Grundlage von Korrelationen zu berechnen.

Unser Ansatz weist jedoch gewisse Einschränkungen auf:

1. Das Risiko der einzelnen EAs schwankt mit der Gesamtperformance des Portfolios, was es schwierig macht, die Performance der einzelnen EAs zu verfolgen. Das gesamte Portfolio kann als ein Index wie der S&P 500 betrachtet werden. Um die individuelle Leistung zu bewerten, müsste man eher die prozentuale Veränderung als den absoluten Gewinn berechnen.
2. Unsere Berechnung der Risikoallokation berücksichtigt nicht die Handelshäufigkeit der einzelnen EAs. Das heißt, wenn die EAs auf ein und demselben Konto sehr unterschiedliche Handelsfrequenzen haben, könnte dies trotz der Zuteilung zu einer ungleichen Risikoexposition führen.

In Anbetracht des Potenzials zur Maximierung des Wachstums für einzelne Händler lohnt sich dieser Ansatz insgesamt.

Schlussfolgerung

In diesem Artikel haben wir das Kelly-Kriterium im Zusammenhang mit dem Leverage-Space-Handelsmodell und seiner Anwendung auf den Handel vorgestellt. Wir haben dann den Implementierungscode in MQL5 bereitgestellt. Anschließend haben wir mit Hilfe der Monte-Carlo-Simulation den optimalen maximalen Drawdown auf der Grundlage eines einzigen Backtests ermittelt, der dann zur Bewertung des Risikos für die einzelnen EAs herangezogen wurde. Schließlich haben wir einen Ansatz für die Kapitalallokation für jeden EA auf der Grundlage seiner Backtest-Performance und Korrelationen vorgestellt.

Datei-Tabelle

Name	Verwendung
KellyMultiFactors.ipynb	Berechnen der Kelly-Anteile für die Kapitalallokation
MonteCarloDrawdown.ipynb	Durchführung der Monte-Carlo-Simulationen