Kategorientheorie in MQL5 (Teil 22): Ein anderer Blick auf gleitende Durchschnitte

Einführung

Die Anwendung der Kategorientheorie auf das Finanzwesen war die Hauptstütze der Artikel in dieser Reihe. Wir haben uns viel mit Zeitreihenprognosen beschäftigt, weil sie für die meisten Händler relevant sind und sie die Mehrheit der Mitglieder auf dieser Plattform ausmachen. Darüber hinaus gibt es jedoch auch andere relevante Anwendungen wie Bewertung, Risiko, Portfolioallokation und viele andere. Und vielleicht noch ein kurzes Beispiel zur Bewertung: Es gibt eine Fülle von Möglichkeiten, wie die Kategorientheorie bei der Bewertung einer Aktie angewendet werden kann. Wenn wir beispielsweise die wichtigsten Aktienkennzahlen jeweils als Objekt einer Kategorie betrachten, können die Morphismen (oder Wege (Graphentheorie)), die diese verschiedenen Kennzahlen (wie Einnahmen, Schulden usw.) miteinander verbinden, verschiedenen Bewertungsklassen (z. B. A+, A, B usw.) zugeordnet werden. Sobald wir die Kennzahlen einer bestimmten Aktie kennen, können wir damit quantifizieren, inwieweit sie zu einer bestimmten Klasse gehört. Dies ist ein vereinfachter Ansatz, der nur als Anhaltspunkt dafür dienen soll, was in diesem Bereich getan werden könnte.

Bleibt man jedoch bei den Zeitreihen, so sind die Durchschnitte, auch wenn sie von einigen als zu simpel angesehen werden, in der technischen Analyse von großer Bedeutung, vor allem weil ihr Konzept die Grundlage für viele andere Indikatoren bildet, z. B. Bollinger-Bänder, MACD usw. Man könnte sie als eine weniger volatile Sichtweise des Preisgeschehens betrachten, und die Betonung auf „weniger volatil“ ist angesichts der Menge an Weißes Rauschen auf den Märkten wichtig.

In diesem Artikel setzen wir das Thema der natürlichen Transformationen fort, das wir im letzten Artikel vorgestellt haben, indem wir die Fähigkeit natürlicher Transformationen untersuchen, die Kluft zwischen verwandten Datensätzen unterschiedlicher Dimensionen zu überbrücken. „Dimensionen“ wird hier verwendet, um die Anzahl der Spalten innerhalb eines Datensatzes darzustellen. Wir haben es also nach wie vor mit zwei Kategorien zu tun, einer „einfachen“ Reihe von Rohpreisen und einer „zusammengesetzten“ Reihe von gleitenden Durchschnittspreisen. Unser Ziel ist es, Anwendungen in der Zeitreihenprognose mit einem Umfang von nur drei Funktoren zu zeigen.

Hintergrund

Lassen Sie uns also zunächst einige grundlegende Definitionen dessen, was wir hier betrachten, durchgehen. Ein Funktor (Mathematik) ist eine Funktion, die zwei Kategorien abbildet. Wir befassen uns hier mit drei davon, die in der nachstehenden Abbildung dargestellt sind:

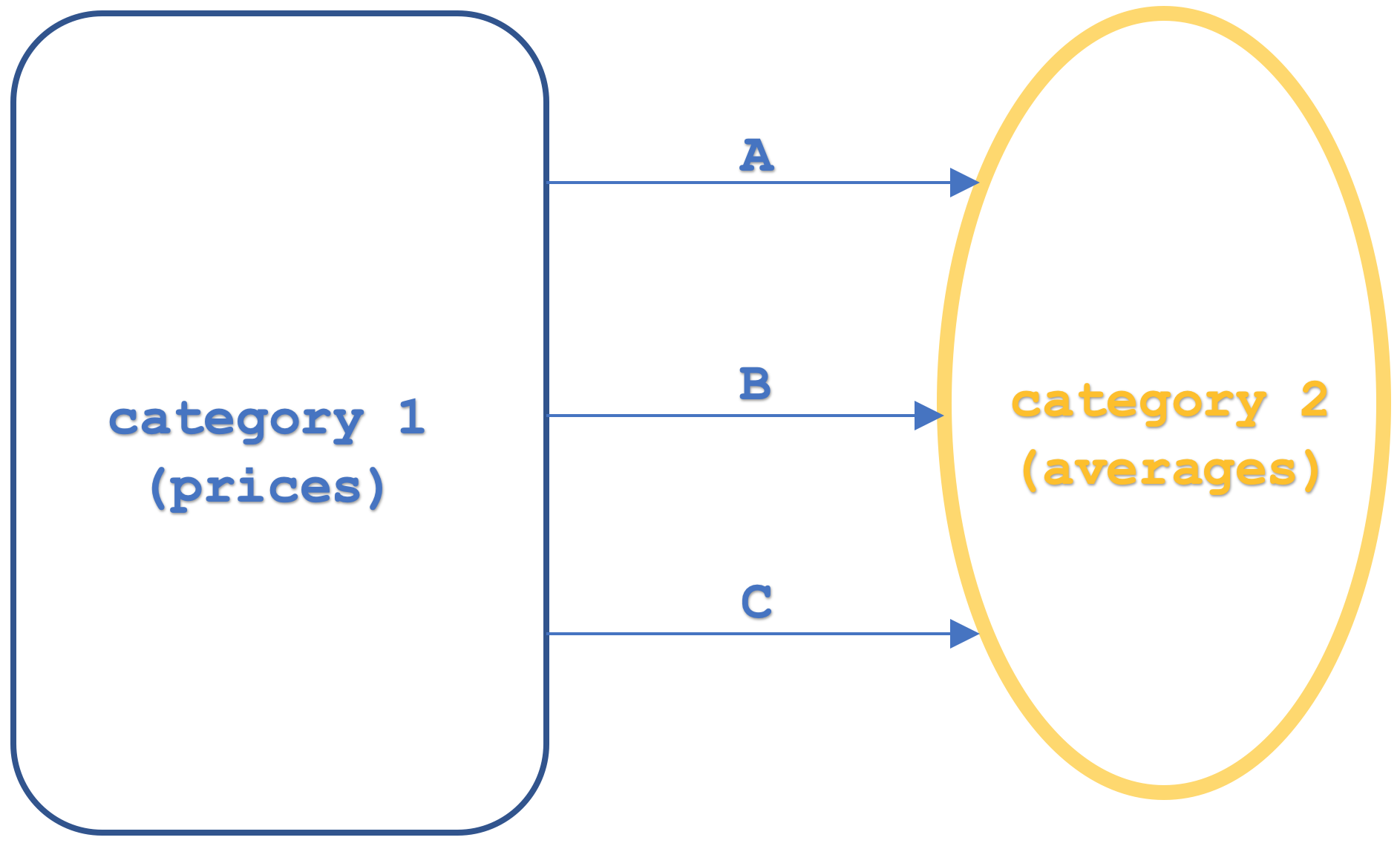
Unsere Domänenkategorie hat Objekte mit Preiswerten in bestimmten Zeitintervallen, während die Objekte der Codomäne der gleitenden Durchschnittspreiswerte ebenfalls in ähnlichen Zeitintervallen liegen. Wir haben drei Funktoren hervorgehoben, nämlich A, B und C. Wir haben in den letzten Artikeln Funktoren dargestellt, die Kategorien verknüpfen, was hier neu ist, ist der Zusatz eines dritten Funktors. Dies ist für unsere Zwecke nützlich, weil es Natürliche Transformation in einer „vertikalen“ Anordnung zeigt. Der „vertikale“ Aufbau ist im Diagramm angegeben, aber um zukünftige Unklarheiten zu vermeiden, bezieht sich „vertikal“auf natürliche Transformationen zwischen Funktoren, die dieselbe Domänen- und Kodomänenkategorie haben. Das heißt, wenn die Kategorien in einem Diagramm vertikal angeordnet wären und unsere natürlichen Transformationen in die horizontale Richtung zeigen würden, wären die natürlichen Transformationen immer noch in einer „vertikalen“ Anordnung.

Im weiteren Verlauf werden gleitende Durchschnitte in der Regel als Handelsindikatoren verwendet, indem man auf ihre Kreuzungspunkte achtet. Ein Kreuz nach oben ist bearish, da es eine Widerstandsbarriere darstellt, während ein Kreuz nach unten bullish ist, da es eine Unterstützung anzeigt. Häufiger jedoch liegen diese Kreuzungspunkte zwischen zwei gleitenden Durchschnitten unterschiedlicher Zeiträume. Wenn also der Durchschnitt der kürzeren Periode den Durchschnitt der längeren Periode übersteigt, haben wir in der Regel ein Aufwärts-Setup, da der längere und daher weniger volatile gleitende Durchschnitt eine Unterstützung anzeigt, während umgekehrt ein Durchbruch des Durchschnitts der kürzeren Periode unter den längeren Durchschnitt eine Abwärts-Entwicklung bedeuten würde. Zu diesem Zweck steht in diesem Modell jeder Funktor für eine bestimmte Glättungslänge. Funktor A ist also der kürzeste der drei Funktoren, während Funktor B dazwischen liegt und Funktor C die längste Glättungslänge hat.

Wenn wir die Kategorien betrachten, die wir in Betracht ziehen, kann es hilfreich sein, darzulegen, warum diese beiden Zeitreihen die Kategorieaxiome erfüllen. Wir haben bereits besprochen, wie Reihungen (order) (auf die sich Zeitreihen besser beziehen lassen) als Kategorien konstruiert werden kann, obwohl die Axiome für eine Kategorie Objekte, Morphismen, Identitätsmorphismen und Assoziation sind. Sowohl die Domänen- als auch die Co-Domänen-Kategorien sind Preiszeitreihen, sodass Illustrationen mit der einen Kategorie leicht auf die andere übertragen werden können. Wenn wir uns also auf die Kategorie „Rohpreise“ (den Bereich) konzentrieren, ist jeder Preispunkt ein Objekt, das aus zwei Elementen besteht. Zeit und Preis. Die Morphismen sind die sequentiellen Zuordnungen zwischen den Preispunkten, da jeder Preispunkt auf einen anderen Preispunkt folgt. Der Identitätsmorphismus zu jedem Preispunkt kann als gleitender Durchschnitt mit einer Periode von eins betrachtet werden. Dies ist dasselbe wie die Preisreihe, aber der Durchschnitt mit einer Periode liefert die Identitätsbeziehung. Schließlich ist die Zusammensetzung mit der Assoziation leicht nachzuvollziehen, da die drei aufeinanderfolgenden Preispunkte L, M und N gegeben sind:

L o (M o N) = (L o M) o N

Der Preis nach dem Morphismus von M nach N, wenn er sich auf den Morphismus von L bezieht, ist der gleiche wie der Preis bei N, wenn er sich auf das Ergebnis des Morphismus von L nach M bezieht.

Kategorien und Funktoren

Unsere Kategorie 1, die die Domänenkategorie für alle Funktoren sein wird, wird, wie erwähnt, eine rohe Preiszeitreihe enthalten, aus der die Funktoren ihre Durchschnittswerte abbilden.

Diese Kategorie wird also insgesamt 4 Funktoren haben, von denen nur 3 für uns von Interesse sind. Der erste, der nur erwähnt werden sollte, ist der Identitätsfunktor. Das liegt daran, dass sich Kategorien und Funktoren ziemlich ähnlich wie Objekte und Morphismen verhalten, sodass die Identität vorhanden sein muss. Für die anderen drei Funktoren, die, wie bereits erwähnt, verschiedene Implementierungen des gleitenden Durchschnitts darstellen, wird jede ihrer Perioden durch ganzzahlige Eingabeparameter festgelegt, nämlich 'm_functor_a', 'm_functor_b' und 'm_functor_c' für die Funktoren A, B bzw. C.

Die zweite Kategorie, die die Kodomäne für unsere drei Funktoren bildet, enthält drei Objekte mit gleitenden Durchschnittspreisen in einer Zeitreihe. Jeder Funktor aus den Rohpreisreihen in Kategorie 1 wird also auf ein eigenes Objekt in Kategorie 2 abgebildet.

Die Kategorie 2 hat einen einzigen Ursprungsfunktor, der, wie erwähnt, der Identitätsfunktor ist. Die Morphismen zwischen diesen Objekten wären äquivalent zu natürlichen Transformationen gemäß den Definitionen, die wir in unseren letzten Artikeln betrachtet haben. Dies alles lässt sich mit dem nachstehenden, etwas detaillierteren Diagramm zusammenfassen:

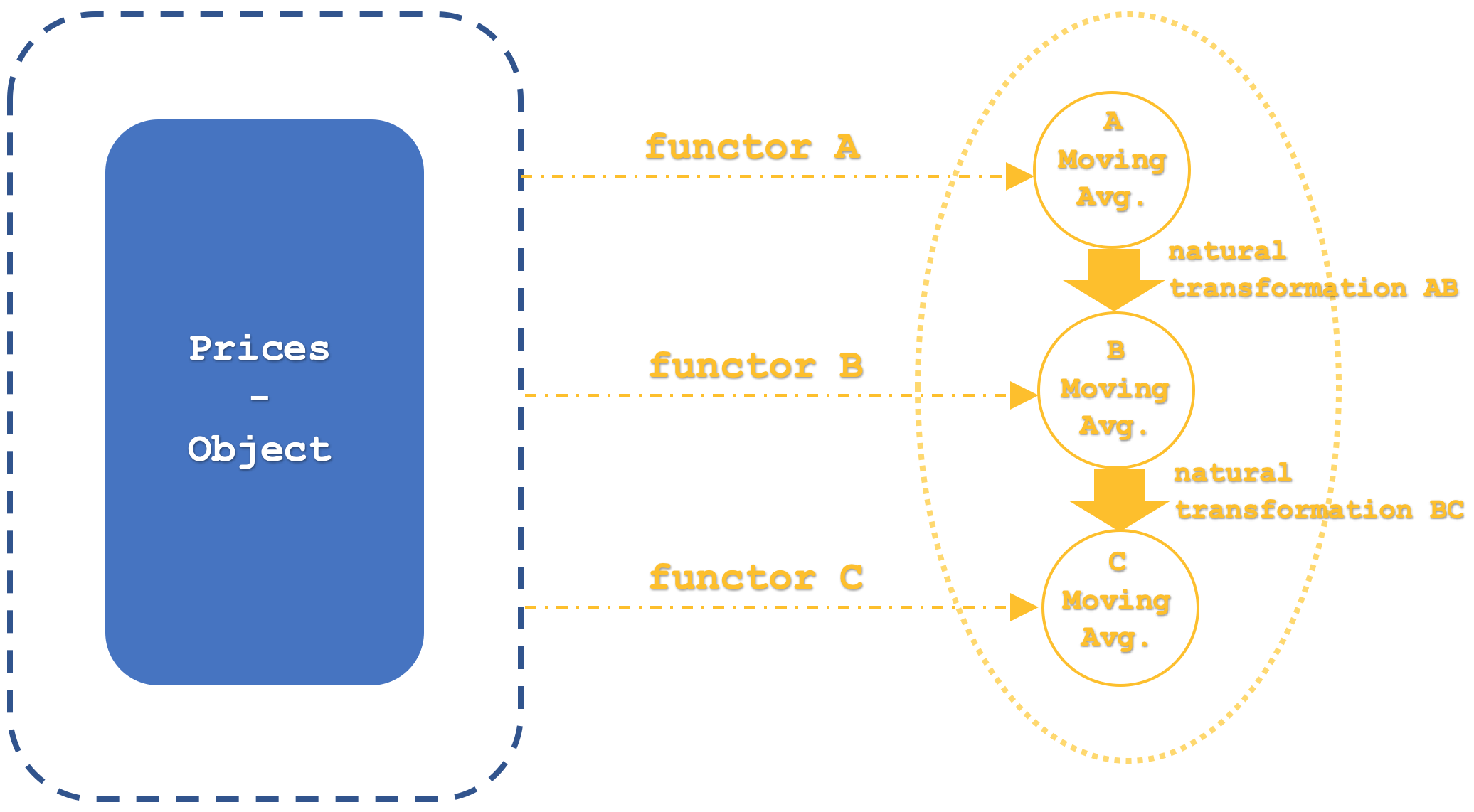
Unser Funktor-Mapping für diesen Artikel verwendet keine Algorithmen von Drittanbietern wie Multi-Layer-Perceptron, Random Distribution Forest oder lineare Diskriminanzanalyse, wie wir sie in den letzten Artikeln verwendet haben. Vielmehr handelt es sich um den Algorithmus des gleitenden Durchschnitts, und die natürlichen Transformationen werden sogar noch einfacher sein, da sie die arithmetische Differenz zwischen den Endwerten der beiden betrachteten Funktoren darstellen.

Natürliche Verwandlungen

Natürliche Transformationen im Zusammenhang mit Finanzen zu definieren, ist wie ein Ausflug ins Niemandsland. Es gibt nicht viel Material oder Referenzen, die das belegen könnten. Häufig werden andere Methoden wie die Korrelation verwendet oder in Betracht gezogen, für die es zwei Hauptimplementierungen gibt: Korrelationskoeffizient nach Bravais-Pearson und Spearman. Es gibt auch andere Methoden, die zum Vergleich herangezogen werden könnten, aber für diesen Artikel werden wir die Spearman-Korrelation als Teil unseres Algorithmus zur Signalerzeugung verwenden.

Eine natürliche Transformation zwischen zwei Funktoren ist also die Nettodifferenz der Zielobjekte der Funktoren. In unserem Fall haben wir 3 Funktoren, was 3 mögliche natürliche Transformationen impliziert. Wir werden uns jedoch nur auf zwei Transformationen konzentrieren, nämlich die zwischen Funktor A und Funktor B, die wir als AB bezeichnen können, und die zwischen Funktor B und Funktor C, die wir BC nennen werden. Wenn wir diese beiden Funktoren verwenden, wollen wir zwei Datenpuffer für jeden erstellen. Wir verfolgen also die jeweilige Differenz der gleitenden Durchschnitte und protokollieren sie in ihren jeweiligen Arrays, wodurch zwei Datenpuffer entstehen. Mit diesen Puffern verfolgen wir dann ihren Korrelationskoeffizienten. Die Verfolgung dieses Wertes stellt die These unseres Handelssignals dar. Ein positiver Wert deutet darauf hin, dass sich die Märkte in einem Trend befinden, während ein negativer Wert auf peitschende Märkte hindeutet.

Konkret bedeutet dies, dass unser Signal darauf abzielt, die Summe aller inkrementellen Veränderungen der gleitenden Durchschnitte mit dem angegebenen Signal abzugleichen. Wenn dieser Wert also positiv ist, deutet dies auf eine Aufwärtsbewegung hin, wenn er negativ ist, auf eine Abwärtsbewegung. Dieses Signal, das zwangsläufig bei jedem Balken einen Wert ergibt, wird, wie oben erwähnt, durch die Korrelation zwischen den beiden natürlichen Transformationspuffern gefiltert. Anders ausgedrückt: Unser System stellt die Frage, ob es einen zusätzlichen Nutzen bringt, natürliche Veränderungen zu verfolgen, da wir mit jedem gleitenden Durchschnitt bereits Trends festgelegt haben.

Vertikale Zusammensetzung der natürlichen Transformationen

Innerhalb der Kategorientheorie können die Ausdrücke „vertikale Komposition“ und ihre Antithese „horizontale Komposition“ natürlicher Transformationen je nach Kontext und Konvention der Autoren gelegentlich unterschiedliche Bedeutungen haben. Es wäre nicht verwunderlich, wenn in der Literatur natürliche Transformationen zwischen Funktoren, die sich Domänen- und Kodomänenkategorien teilen, als „horizontale Kompositionen“ bezeichnet werden. Dies ist nicht die Definition, die wir verwenden werden. In diesem Artikel und wahrscheinlich auch in den folgenden Artikeln wird sich die vertikale Komposition auf natürliche Transformationen zwischen Funktoren beziehen, die sich Domänen- und Kodomänenkategorien teilen.

Welche Bedeutung hat also die vertikale Komposition? Von den Konventionen, die wir angenommen haben, ist es die einfachere von beiden. Es bietet eine Möglichkeit, zwei relativ einfache Datensätze (die als Kategorien abgeleitet werden könnten) zu betrachten und spezielle Beziehungen zwischen ihnen abzuleiten, die bei der Arbeit mit mehreren Kategorien in komplexeren Zusammenhängen leicht übersehen werden könnten.

Eine gute Veranschaulichung hierfür ist die Wahl eines Preisreihen-Datensatzes und eines gleitenden Durchschnitts-Datensatzes für diesen Artikel. Außerhalb des Handels könnte ein weiteres aufschlussreiches Beispiel aus dem kulinarischen Bereich stammen. Betrachten Sie eine Liste von Ingredienzen (Domänenkategorie) und eine Sammlung von Menüs (Codomänenkategorie). Unsere Funktoren würden die Zutaten einfach mit ihren jeweiligen Menüs verbinden. Natürliche Transformationen wie Funktoren und Morphismen bewahren die Definitionen und die Struktur ihrer Ursprünge. Dies mag trivial erscheinen, ist aber ein Grundpfeiler der Kategorientheorie. Mit den Elementen und der Struktur des Objekts (d. h. den Menüs und ihren Bestandteilen) können natürliche Transformationen zwischen den Menüs helfen, die relative Zeit, die für die Zubereitung jedes Gerichts benötigt wird, oder die Kosten jedes Gerichts und eine Vielzahl anderer Bereiche von Interesse zu messen und zu bewerten, je nach dem Schwerpunkt eines Kochs/Restaurants. Mit diesen Informationen kann man die Isomorphie von Kategorien nutzen und erforschen, wie man aus einer Reihe von verschiedenen Menüs Zutaten ableiten kann. Während dies auch mit anderen Methoden und Systemen möglich ist, bietet die Kategorientheorie einen strukturerhaltenden und quantifizierbaren Ansatz.

Vorhersage von Preisänderungen

Die Nutzung dieser vertikalen Zusammensetzung bei der Vorhersage von Preisänderungen erfolgt durch die Aufzeichnung und Analyse der Korrelationskoeffizienten unserer beiden natürlichen Transformationspuffer. Diese Arrays müssen initialisiert werden, da beim ersten Start des Experten noch nicht genügend Daten geladen sind, um eine Korrelation durchzuführen. Dies wird so gehandhabt, wie in dieser Auflistung gezeigt:

//+------------------------------------------------------------------+
//| Get Direction function from Natural Transformations.             |
//+------------------------------------------------------------------+
void CSignalCT::Init(void)
   {
      if(!m_init)
      {
         m_close.Refresh(-1);
         
         int _x=StartIndex();
         
         m_o_prices.Cardinality(m_functor_c+m_functor_c);
         for(int i=0;i<m_functor_c+m_functor_c;i++)
         {
            m_e_price.Let();m_e_price.Cardinality(1);m_e_price.Set(0,m_close.GetData(_x+i));m_o_prices.Set(i,m_e_price);
         }
         
         m_o_average_a.Cardinality(m_transformations+1);
         m_o_average_b.Cardinality(m_transformations+1);
         m_o_average_c.Cardinality(m_transformations+1);
         
         for(int i=0;i<m_transformations+1;i++)
         {
            double _a=0.0;
            for(int ii=i;ii<m_functor_a+i;ii++)
            {
               _a+=m_close.GetData(_x+ii);
            }
            _a/=m_functor_a;
            m_e_price.Let();m_e_price.Cardinality(1);m_e_price.Set(0,_a);m_o_average_a.Set(i,m_e_price);
            //
            double _b=0.0;
            for(int ii=i;ii<m_functor_b+i;ii++)
            {
               _b+=m_close.GetData(_x+ii);
            }
            _b/=m_functor_b;
            m_e_price.Let();m_e_price.Cardinality(1);m_e_price.Set(0,_b);m_o_average_b.Set(i,m_e_price);
            //
            double _c=0.0;
            for(int ii=i;ii<m_functor_c+i;ii++)
            {
               _c+=m_close.GetData(_x+ii);
            }
            _c/=m_functor_c;
            m_e_price.Let();m_e_price.Cardinality(1);m_e_price.Set(0,_c);m_o_average_c.Set(i,m_e_price);
         }
         //
         ArrayResize(m_natural_transformations_ab,m_transformations);ArrayInitialize(m_natural_transformations_ab,0.0);
         ArrayResize(m_natural_transformations_bc,m_transformations);ArrayInitialize(m_natural_transformations_bc,0.0);
         
         for(int i=m_transformations-1;i>=0;i--)
         {
            double _a=0.0;
            m_e_price.Let();m_e_price.Cardinality(1);m_o_average_a.Get(i,m_e_price);m_e_price.Get(0,_a);
            double _b=0.0;
            m_e_price.Let();m_e_price.Cardinality(1);m_o_average_b.Get(i,m_e_price);m_e_price.Get(0,_b);
            double _c=0.0;
            m_e_price.Let();m_e_price.Cardinality(1);m_o_average_c.Get(i,m_e_price);m_e_price.Get(0,_c);
            
            m_natural_transformations_ab[i]=_a-_b;
            m_natural_transformations_bc[i]=_b-_c;
         }
         
         m_init=true;
      }
   }

Wir haben drei Handles für den gleitenden Durchschnitt für jeden Funktor deklariert und müssen diese aktualisieren, bevor wir irgendwelche Werte aus ihnen lesen. Die Periode jedes gleitenden Durchschnitts ist ein Eingabeparameter, sodass wir 'm_functor_a', 'm_functor_b' und 'm_functor_c' für die Handles 'm_ma_a', 'm_ma_b' bzw. 'm_ma_c' haben. Wir haben auch zwei Puffer für jede natürliche Transformation, nämlich 'm_natural_transformations_ab' und 'm_natural_transformations_bc'. Die Größe dieser Arrays wird durch den Eingabeparameter "m_transformations" festgelegt, sodass zu Beginn beide Arrays auf den entsprechenden Wert eingestellt werden müssen. Die Objekte der Kategorie "Codomain", nämlich: m_o_average_a", "m_o_average_b" und "m_o_average_c", müssen ebenfalls auf diesen Wert plus eins skaliert werden, um alle Änderungsinkremente zu erhalten.

So wird der Einfluss verschiedener gleitender Durchschnittsperioden auf die Fähigkeit zur Vorhersage mit diesem System bewertet, wenn Signale, die aus übereinstimmenden Änderungen im gleitenden Durchschnitt erzeugt werden, wenn die Korrelation der natürlichen Transformationspuffer größer als Null ist. Dies wird mit der unten aufgeführten einfachen Funktion "GetDirection" erfasst:

//+------------------------------------------------------------------+
//| Get Direction function from Natural Transformations.             |
//+------------------------------------------------------------------+
double CSignalCT::GetDirection()
   {
      double _r=0.0;
      
      Refresh();
      
      MathCorrelationSpearman(m_natural_transformations_ab,m_natural_transformations_bc,_r);
      
      return(_r);
   }

Und jede der Funktionen "CheckOpenLong" und "CheckOpenShort", die unseren "Trend" berechnen. Dieser Trend gibt die Signalrichtung vor, wobei die "Richtung" als Filter für Whipsaw-Märkte dient. Die Umsetzung ist hier aufgeführt:

      m_ma_a.Refresh(-1);
      m_ma_b.Refresh(-1);
      m_ma_c.Refresh(-1);
      
      int _x=StartIndex();
      
      double _trend= (m_ma_a.GetData(0,_x)-m_ma_a.GetData(0,_x+1))+
                     (m_ma_b.GetData(0,_x)-m_ma_b.GetData(0,_x+1))+
                     (m_ma_c.GetData(0,_x)-m_ma_c.GetData(0,_x+1));

Wir brauchen auch eine Funktion zur Aktualisierung dieser Werte, die der Funktion „Init“ sehr ähnlich ist. Der vollständige Quellcode ist am Ende des Artikels beigefügt.

Beim Backtesting des Devisenpaares USDJPY vom 1999.01.01 bis 2020.01.01 auf dem täglichen Zeitrahmen erhalten wir den folgenden Bericht mit einigen unserer idealen Einstellungen:

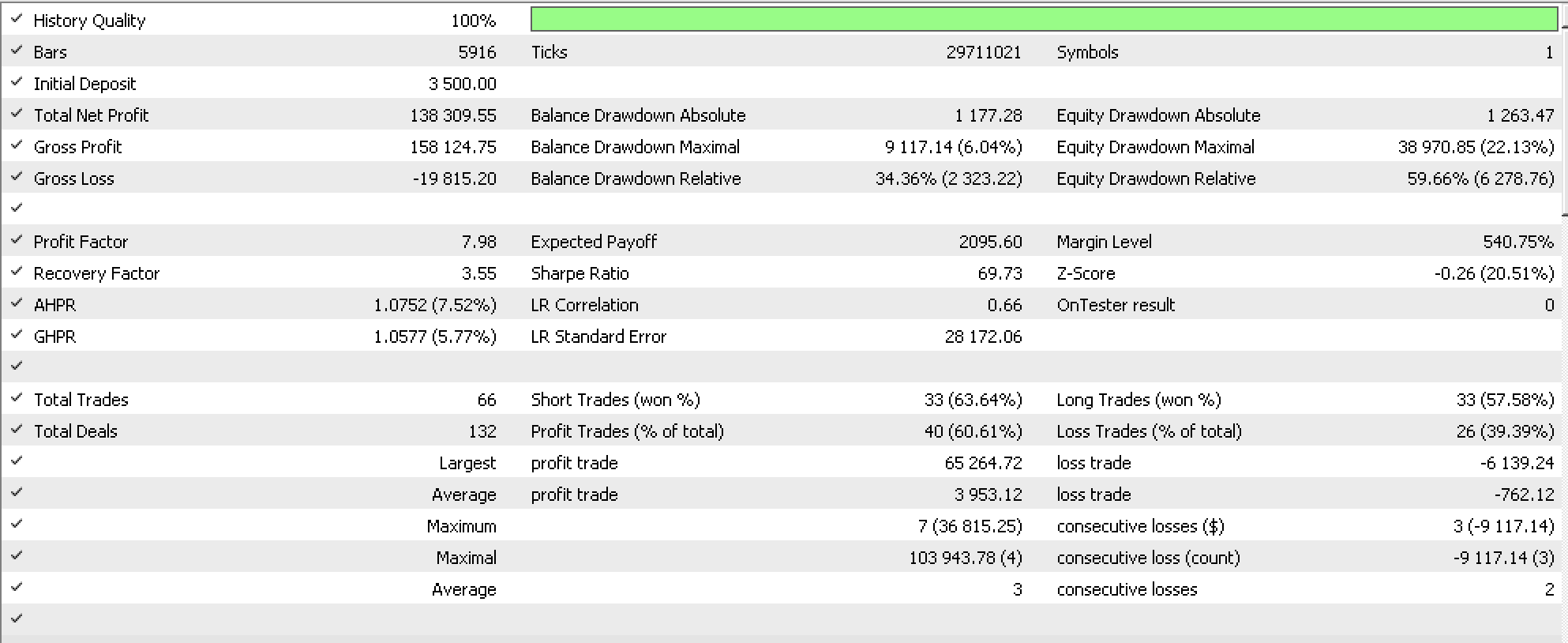
Wenn wir versuchen, mit diesen Einstellungen vom 01.01.2020 bis zum 08.08.2023 weiterzugehen, erhalten wir den folgenden Bericht:

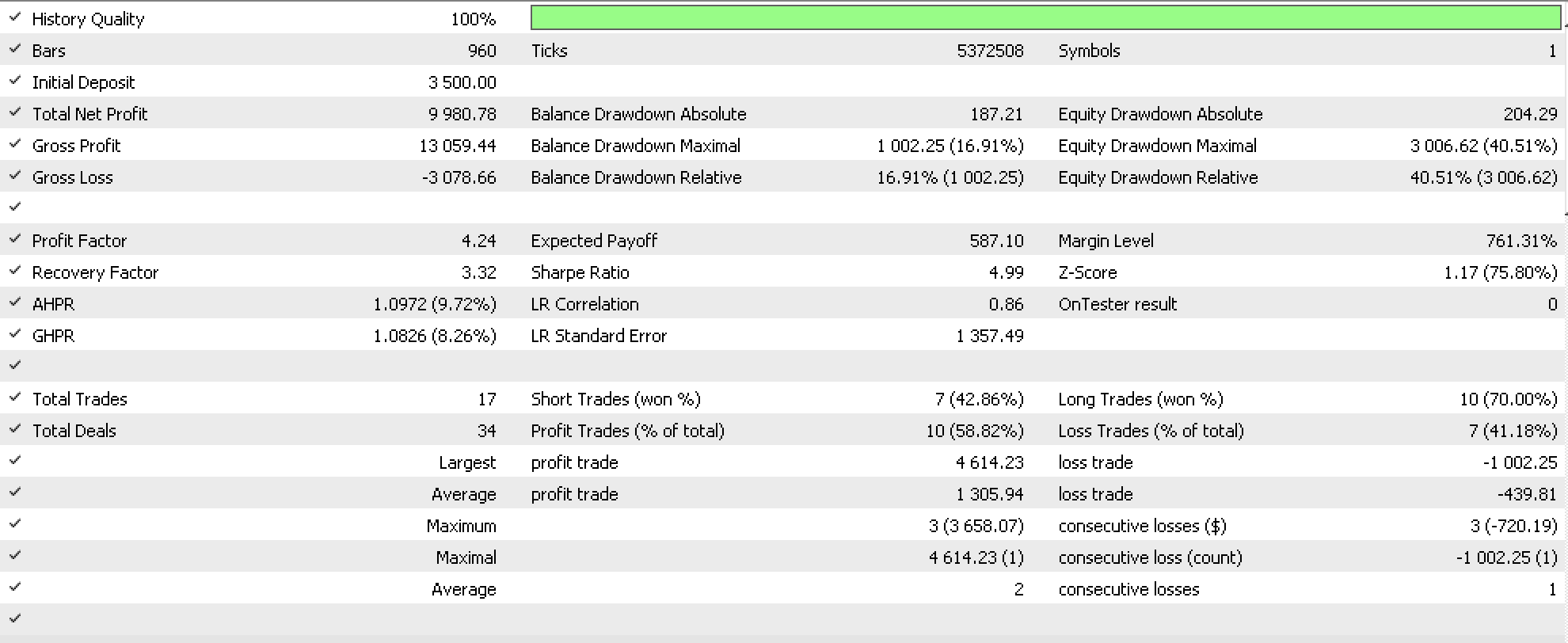
Es wird ein positiver Verlauf angezeigt, was wie immer nicht bedeutet, dass wir ein funktionierendes System haben, sondern eher, dass wir etwas haben könnten, das über längere Zeiträume getestet werden kann, um unsere ersten Erkenntnisse zu bestätigen.

Prüfstand für die Entwicklung von Handelssystemen

Die Integration dieser Signalklasse in ein neues oder bestehendes Handelssystem kann dank des MQL5-Assistenten nahtlos erfolgen. Alles, was wir tun müssen, ist, einen neuen Experten mit dieser Signalklasse als eines der anderen Signale zusammenzustellen, die ein Händler entweder immer verwendet oder ausprobieren möchte. Der typische Eingabeparameter „Signal_XXX_Weight“ (wobei XXX der Name der Signalklasse ist), dessen Wert normalerweise zwischen 0,0 und 1,0 liegt, kann für alle Signale optimiert werden, um die geeignete Gewichtung für jedes Signal zu bestimmen.

Die Bewertung eines solchen Handelssystems sollte auf der Grundlage der Bedürfnisse des Händlers erfolgen. In der Regel geht es um ein Hin und Her zwischen Wachstum und Kapitalerhalt. Aus dem Stegreif würde ich sagen, dass AHPR die beste Kennzahl für Wachstum ist, während der Recovery Factor für Sicherheit steht. Dies sind alles grobe Schätzungen, sodass der Leser und der ernsthafte Händler etwas mehr Sorgfalt walten lassen müssen, um herauszufinden, was für sie funktioniert.

Wenn ein System zur Leistungsbewertung vorhanden ist, muss als Nächstes - und vielleicht ebenso wichtig - eine Methode zur schrittweisen Verbesserung der Strategie entwickelt werden, ohne ihre Prämisse und ihre Fähigkeit, vorwärts zu gehen, zu gefährden. Dabei gibt es kein Patentrezept, sondern eine ständige Überprüfung der Backtest- und Walk-Forward-Leistung bei jeder Iteration oder Änderung des Systems.

Es besteht auch die Möglichkeit, wie immer eine Instanz einer nachgeschalteten Klasse zu haben, die auf diesem Modell basiert. Wir müssten ein paar Änderungen vornehmen, aber der Grundgedanke wäre derselbe. Für den Anfang würden unsere gleitenden Durchschnitte statt des Schlusskurses als angewandten Kurs etwas verwenden, das zur Volatilität tendiert - das könnte der typische Kurs oder vielleicht noch besser der Mediankurs sein. Zweitens würde die Vorhersagerichtung immer noch auf Korrelationen zwischen den beiden natürlichen Transformationspuffern hindeuten, aber in diesem Fall würden wir die aktuelle Veränderung im Balkenbereich als unseren „Trend“ verfolgen. Eine Verringerung der Badbreite müsste also durch positive Korrelationen (Werte über Null) untermauert werden. Das Gleiche gilt für die zunehmende Volatilität. Wenn die Korrelation null oder negativ ist, würde dies bedeuten, dass unser Modell darauf hindeutet, dass alle aktuellen Veränderungen der Volatilität ignoriert werden können. Eine entsprechende Implementierung ist ebenfalls am Ende dieses Artikels beigefügt.

Schlussfolgerung

Zusammenfassend lässt sich sagen, dass die Auswirkungen natürlicher Transformationen in einer vertikalen Komposition zu akademisch und archaisch klingen, um bei den meisten Menschen Interesse zu wecken. Und doch ist es wohl aufschlussreich, denn durch die Betrachtung von Abbildungen mit gängigen Indikatoren, wie z. B. dem gleitenden Durchschnitt für diesen Artikel, haben wir einige Muster aufgedeckt, aus denen wir Bestätigungssignale für die Prognose einer Zeitreihe ablesen konnten.

Die Verwendung dieser Daten zur Entwicklung eines robusten Handelssystems ist immer der springende Punkt und erfordert ein wenig mehr Arbeit seitens des Händlers, um sie zu verwirklichen. Nichtsdestotrotz gibt es für den entschlossenen Händler wohl genug Unterstützungsmaterial im Internet, um dies durchzuziehen.

Ich empfehle dringend, diese Konzepte außerhalb der Zeitreihenprognose und in anderen Bereichen des Handels und der Finanzen wie der Bewertung oder dem Risiko weiter zu erforschen, damit die Leser sich mit dem, was hier vermittelt wird, besser zurechtfinden.

Referenzen

Die meisten Zitate für diesen Artikel stammen von Wikipedia.

Ressourcen für die Umsetzung der Konzepte der Kategorientheorie in diesem Artikel sind unten angefügt. Es handelt sich um die Klassendatei zur Kategorientheorie mit dem Namen „ct_22.mq5“ und die Trailling-Datei „TraillingCT_22_r1.mqh“. Die Klassendatei sollte im Ordner „include“ abgelegt werden, während die Trailling-Datei im Ordner „Include\Expert\Trailling“ abgelegt werden sollte. Leser, die mit dem MQL5-Assistenten nicht vertraut sind, sollten sich diesen Artikel über die Zusammenstellung von Expert Advisors mit dem Assistenten ansehen, da diese Signaldatei für die Zusammenstellung im Assistenten gedacht ist.