用于预测波动性的计量经济学工具：GARCH模型

引言

波动性是衡量金融资产价格变动性的一个重要指标。在分析报价时，人们早已注意到，大幅度的价格变动往往会导致更大的变动，尤其是在金融危机期间。相反，小幅度的变动之后通常跟随着小幅度的价格变动。因此，平稳期之后往往会出现相对不稳定的时期。

首个尝试解释该现象的模型是ARCH，由Engle提出— 即自回归条件异方差（异质性）模型。除了集群效应（将收益分为大值和小值的群组）外，该模型还解释了重尾和正峰度的出现，这是所有价格增量分布的共同特征。ARCH条件高斯模型的成功催生了一系列其推广模型。这些推广模型的目的是为金融时间序列分析中观察到的其他多种现象提供解释。从历史上看，ARCH模型最早的推广之一便是ARCH的广义形式，即GARCH（Generalized ARCH）模型。

与ARCH相比，GARCH模型的主要优势在于它更为简洁，且在拟合样本数据时无需长滞后结构。在本文中，我想描述GARCH模型，并且最重要的是，提供一个基于该模型的现成的波动率预测工具，因为预测是分析金融数据时的主要目标之一。

非参数波动率估计方法

利用波动率来评估风险在交易者中是一个相当热门的话题。衡量波动率最常见的方法是简单地计算给定时间段内的标准差。

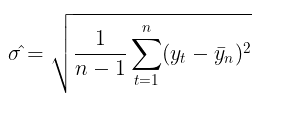
这就是所谓的非参数波动率估计方法。通过这种方式计算得到的波动率被称为历史波动率或经验波动率。在高斯随机游走模型中，这是衡量不确定性和可变性的主要指标，因为它假设波动率会随时间保持不变。

参数波动率估计方法

反过来，在GARCH模型中，假设波动率是一个随机变量（波动率本身具有波动性）。这更接近于现实情况。GARCH过程通过以下方程进行设置：

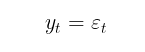
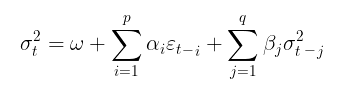
其中：

• Yt – 对数价格增量，
• εt - 模型残差
• σt^² 条件方差
• zt = i.i.d. N(0,1) – 标准正态分布
• zt = i.i.d. t-Student(v) – 自由度为v的标准t分布
• (omega,alpha,beta,v) – 应从数据样本中估计的模型参数

对模型参数施加以下限制：

• omega > 0，方差正性条件，
• alpha≥0,
• beta≥0,
• ∑alphai + ∑betaj < 1，平稳性，
• v>2

如果beta= 0，GARCH模型就变成了ARCH模型。

通常，GARCH模型会补充一个条件或无条件的数学期望模型。-例如，可以使用一阶自回归过程AR(1)作为条件数学期望的模型：

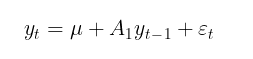
其中：

• u – 偏移参数
• A1 – 自回归模型参数

条件均值建模的目标是确定一系列平方残差(εt^²) ，这些残差将用于寻找条件方差。如果收益序列中没有自相关（这通常是情况），那么我们可以转向无条件数学期望模型：

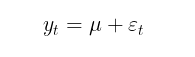
在这篇文章中，为了简化计算，我将使用一个不估计收益自相关的模型。因此，在GARCH模型中估计波动率的问题就简化为寻找模型比率（μ, ω, alpha, beta, v）的参数问题。

使用最大似然法估计GARCH模型参数

最大似然法通常用于寻找未知参数。假设et 残差服从高斯分布，对数 似然函数具有以下形式：

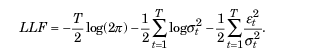
如果检测到偏离正态性的情况，可以使用标准化的t分布作为合适的分布。对于较小的v（自由度）参数值，它表现出比正态分布更高的峰度和更厚的尾部。在这种情况下，似然函数具有以下形式：

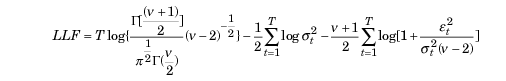
其中，

• Г — gamma 函数
• T – 数据样本量

ALGLIB MinBLEIC 优化器

为了找到GARCH模型参数的值，我们需要最大化似然函数。这需要使用优化方法。ALGLIB数值分析库可以帮助我们实现这一点。为了最大化目标函数，我选择了MinBLEIC（带边界线性等式不等式约束的最小化）算法。

//+------------------------------------------------------------------+
//|  Objective Function: Gaussian loglikelihood                      |
//+------------------------------------------------------------------+
void CNDimensional_GaussianFunc::Func(CRowDouble &x,double &func,CObject &obj)
  {
//x[0] - mu;
//x[1] - omega;
//x[2] - alpha;
//x[3] - beta;
   double returns[];
   ArrayResize(returns,N1);
   for(int i=0;i<N1;i++)
     {
      returns[i] = MathLog(close[i+1]/close[i]);
     }

   double residuals[];
   ArrayResize(residuals,N1);
   for(int i = 0; i<N1; i++)
     {
      residuals[i] = (returns[i] - x[0]);
     }

   double condVar[];
   ArrayResize(condVar,N1);
   condVar[0] = x[1]/(1-x[2]-x[3]);  // Unconditional Variance

   for(int i=1; i<N1; i++)
     {
      condVar[i] = x[1] + x[2]*MathPow(residuals[i-1],2) + x[3]*condVar[i-1]; // Conditional Variance
     }

   double LLF[],a[],b[];
   ArrayResize(LLF,N1);
   ArrayResize(a,N1);
   ArrayResize(b,N1);
   for(int i=0; i<N1; i++)
     {

      a[i]= 1/sqrt(2*M_PI*condVar[i]);
      if(!MathIsValidNumber(a[i]))
        {
         break;
        }

      b[i]= MathExp(- MathPow(residuals[i],2)/(2 * condVar[i]));
      if(!MathIsValidNumber(b[i]))
        {
         break;
        }

      LLF[i]=MathLog(a[i]*b[i]);
      if(!MathIsValidNumber(LLF[i]))
        {
         break;
        }
     }

   func = -MathSum(LLF); // Loglikelihood
  }

在GARCH函数中，该函数直接针对目标函数并寻找参数的最优值，为此需要：

• 指定参数的初始值，
• 设置数据尺度（优化成功与否的一个非常重要的因素），
• 指定参数可能变化的范围界限，
• 设置线性不等式约束（我们只有一个，即alpha+beta <1的平稳性条件），
• 指定优化算法的停止条件，
• 指定微分步长。

//+------------------------------------------------------------------+
//|  Function GARCH  Gaussian                                        |
//+------------------------------------------------------------------+
vector GARCH()
  {
   double              x[],s[];
   int                 ct[];
   CMatrixDouble       c;
   CObject Obj;
   CNDimensional_GaussianFunc ffunc;
   CNDimensional_Rep frep;

   double returns[];
   ArrayResize(returns,N1);
   for(int i=0;i<N1;i++)
     {
      returns[i] = MathLog(close[i+1]/close[i]);
     }
   double returns_mean  = MathMean(returns);
   double returns_var = MathVariance(returns);
   double KurtosisReturns = MathKurtosis(returns);
// Print("KurtosisReturns= ",KurtosisReturns);

// Initial parameters ---------------------------
   ArrayResize(x,4);
   x[0]=returns_mean;  //  Mu
   x[1]=returns_var;  // Omega
   x[2]=0.0;         // alpha
   x[3]=0.0;        // beta
//------------------------------------------------------------
   double mu;
   if(NormalizeDouble(returns_mean,10)==0)
     {
      mu = 0.0000001;
     }
   else
      mu = NormalizeDouble(returns_mean,10);
// Set Scale-----------------------------------------------
   ArrayResize(s,4);
   s[0] = NormalizeDouble(returns_mean,10);  //  Mu
   s[1] = NormalizeDouble(returns_var,10); // omega
   s[2] =1;
   s[3] =1;
//---------------------------------------------------------------
// Linearly inequality constrained: --------------------------------
   c.Resize(1,5);
   c.Set(0,0,0);
   c.Set(0,1,0);
   c.Set(0,2,1);
   c.Set(0,3,1);
   c.Set(0,4,0.999); // alpha + beta <= 0.999
   ArrayResize(ct,1);
   ct[0]=-1; // {-1:<=},{+1:>=},{0:=}
//--------------------------------------------------------------
// Box constraints ------------------------------------------------
   double bndl[4];
   double bndu[4];

   bndl[0] = -0.01;  // mu
   bndl[1] = NormalizeDouble(returns_var/20,10);  // omega
   bndl[2] = 0.0;  // alpha
   bndl[3] = 0.0;  // beta

   bndu[0] = 0.01;  // mu
   bndu[1] = NormalizeDouble(returns_var,10);  // omega
   bndu[2] = 0.999;  // alpha
   bndu[3] = 0.999;  // beta
//--------------------------------------------------------------
   CMinBLEICStateShell state;
   CMinBLEICReportShell rep;
   double epsg=0;
   double epsf=0;
   double epsx=0.00001;
   double diffstep=0.0001;
//--- These variables define stopping conditions for the outer iterations:
//--- * epso controls convergence of outer iterations;algorithm will stop
//---   when difference between solutions of subsequent unconstrained problems
//---   will be less than 0.0001
//--- * epsi controls amount of infeasibility allowed in the final solution
   double epso=0.00001;
   double epsi=0.00001;

   CAlglib::MinBLEICCreateF(x,diffstep,state); //---  create optimizer
   CAlglib::MinBLEICSetBC(state,bndl,bndu);  //--- add boundary constraints
   CAlglib::MinBLEICSetLC(state,c,ct);
   CAlglib::MinBLEICSetScale(state,s);
   CAlglib::MinBLEICSetPrecScale(state); // Preconditioner
   CAlglib::MinBLEICSetInnerCond(state,epsg,epsf,epsx);
   CAlglib::MinBLEICSetOuterCond(state,epso,epsi);
   CAlglib::MinBLEICOptimize(state,ffunc,frep,0,Obj);
   CAlglib::MinBLEICResults(state,x,rep);   // Get parameters
//---------------------------------------------------------

   double residuals[],resSquared[],Realised[];
   ArrayResize(residuals,N1);
   for(int i = 0; i<N1; i++)
     {
      residuals[i] = (returns[i] - x[0]);
     }

   MathPow(residuals,2,resSquared);
   ArrayCopy(resSquared_,resSquared,0,0,WHOLE_ARRAY);
   MathSqrt(resSquared,Realised);

   double condVar[],condStDev[];
   double ForecastCondVar,PriceConf_Upper,PriceConf_Lower;
   ArrayResize(condVar,N1);
   condVar[0] = x[1]/(1-x[2]-x[3]);
   for(int i = 1; i<N1; i++)
     {
      condVar[i] = x[1] + x[2]*MathPow(residuals[i-1],2) + x[3]*condVar[i-1];
     }

   double PlotUncondStDev[];
   ArrayResize(PlotUncondStDev,N1);
   ArrayFill(PlotUncondStDev,0,N1,sqrt(condVar[0])); // for Plot
   ArrayCopy(PlotUncondStDev_,PlotUncondStDev,0,0,WHOLE_ARRAY);
   MathSqrt(condVar,condStDev);
// Print("math expectation of conditional standard deviation = "," ",MathMean(condStDev));

   ArrayCopy(Real,Realised,0,0,WHOLE_ARRAY);
   ArrayCopy(GARCH_,condStDev,0,0,WHOLE_ARRAY);

   vector v_Realised, v_condStDev;
   v_Realised.Assign(Realised);
   v_condStDev.Assign(condStDev);
   double MSE=v_condStDev.Loss(v_Realised,LOSS_MSE); // Mean Squared Error
//-----------------------------------------------------------------------------
//-------- Standardize Residuals--------------------------------------
   double z[];
   ArrayResize(z,N1);
   for(int i = 0; i<N1; i++)
     {
      z[i] = residuals[i]/sqrt(condVar[i]);
     }
   ArrayCopy(Z,z,0,0,WHOLE_ARRAY);
//----------------------------------------------------------------------------------

//-------------- JarqueBeraTest for Normality  ----------------------------------
   double pValueJB;
   int JBTestH;
   CAlglib::JarqueBeraTest(z,N1,pValueJB);
   if(pValueJB <0.05)
      JBTestH =1;
   else
      JBTestH=0; // H=0 - data Normal, H=1 data are not Normal
   double Kurtosis = MathKurtosis(z); // Kurosis = 0 for Normal distribution
//---------------------------------------------------------------------------------

//-------------------------------------------------------------------------------------
//-------- Forecast Conditional Variance for m bars
   double FCV[];
   ArrayResize(FCV,forecast_m);
   for(int i = 0; i<forecast_m; i++)
     {
      FCV[i] = sqrt(x[1]*((1-MathPow(x[2]+x[3],i+1))/(1-x[2]-x[3])) + MathPow(x[2]+x[3],i)*(x[2]*MathPow(residuals[N1-1],2) + x[3]*condVar[N1-1])) ;
     }
   ArrayCopy(FCV_,FCV,0,0,WHOLE_ARRAY);
//-----------------------------------------------------------------------------------
   double LLF[];
   double Loglikelihood;
   ArrayResize(LLF,N1);
   for(int i = 0; i<N1; i++)
     {
      LLF[i] = MathLog(1/sqrt(2*M_PI*condVar[i])*MathExp(- MathPow(residuals[i],2)/(2*condVar[i])));
     }
   Loglikelihood = MathSum(LLF);
//--------------------------------------------------------------------------

   ForecastCondVar= x[1] + x[2]*MathPow(residuals[N1-1],2) + x[3]*condVar[N1-1];
   int err1;
   PriceConf_Lower = close[N1]*MathExp(-MathAbs(MathQuantileNormal((1-pci)/2,0,1,err1))*sqrt(x[1] + x[2]*MathPow(residuals[N1-1],2) + x[3]*condVar[N1-1])); // confidence interval pci%
   PriceConf_Upper = close[N1]*MathExp(MathAbs(MathQuantileNormal((1-pci)/2,0,1,err1))*sqrt(x[1] + x[2]*MathPow(residuals[N1-1],2) + x[3]*condVar[N1-1]));  // confidence interval pci%

//--------------------------------------------------------------------------------------
   vector result= {x[0],x[1],x[2],x[3],rep.GetTerminationType(),ForecastCondVar,PriceConf_Lower,PriceConf_Upper,MSE,Loglikelihood,condVar[0],returns_var,JBTestH,Kurtosis};
   return (result);
  }
//+------------------------------------------------------------------+

使用GARCH(1,1)模型进行波动率预测

波动率值预测

一旦找到模型参数，我们就可以进入主要任务——预测波动率。GARCH(1,1)模型向前m步的波动率预测是使用以下方程计算的：

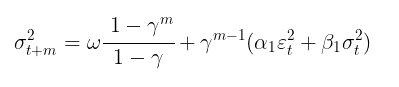
其中：

• γ = α1 + β 1.

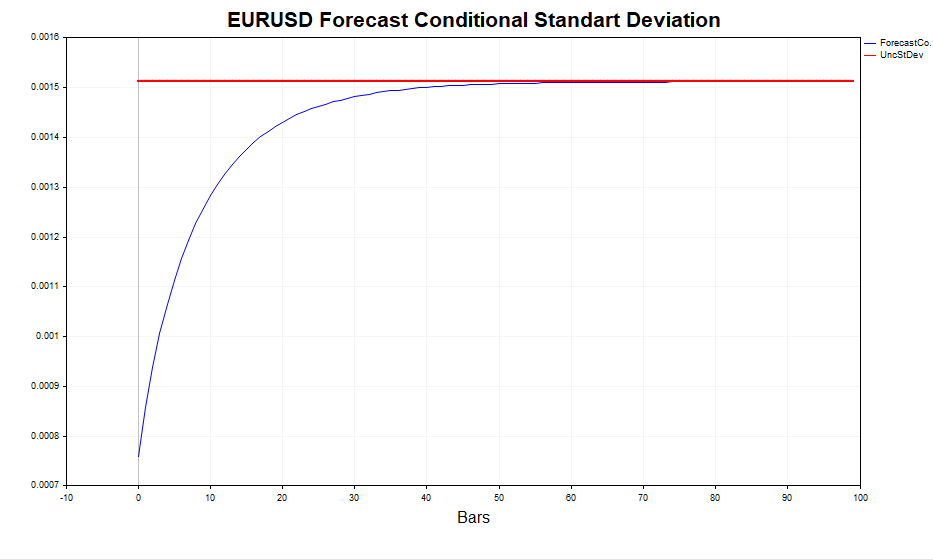
在m趋向于无穷大→∞的情况下，预测值会收敛到理论上的无条件GARCH方差（如果满足模型平稳性条件α1+β1 < 1）。

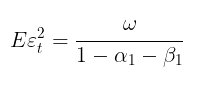
换句话说，预测的时间跨度越远，其预测值就越接近无条件方差的平稳值。GARCH脚本使得我们可以计算向前m步的波动率预测值，并将这些预测值与Eεt ²（即误差项的平方的期望值，通常表示为σ²或方差）进行比较，从而验证这一点。

区间预测

预测波动率的值是有用的，但更重要的是获得未来价格波动范围的概率估计，即获得具有一定显著性水平的置信区间。

假设正态性 zt = i.i.d. N(0,1)，置信区间可以使用以下方程来计算：

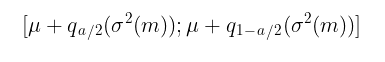
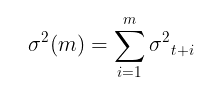
其中：

• q – 标准正态分布分位数

例如，对于一个可靠性水平为90%（a = 1-0.9）的置信区间，它将是以下区间：

[ u – 1,65σ ; u + 1,65σ ]

当假设zt = i.i.d. t-Student(v)时，情况就复杂得多了。 在这种情况下，没有逆分布函数的解析方程。因此，为了构造置信区间，需要使用蒙特卡洛模拟。

//+-------------------------------------------------------------------------+
//|Function calculate Forecast Confidence intervals using Monte-Carlo method|
//+-------------------------------------------------------------------------+
bool MCForecastStandardized_t(const double DoF,const double CondStDevForecast,const double prob, double & F_lower[],double & F_upper[])
  {

   double alpha = 1-prob;
   double qlower[1] = {alpha/2};       // q (a/2)
   double qupper[1] = {1-alpha/2};  // q (1-a/2)

   int N = 10000; //number Monte-Carlo simulates
   double h_St[];
   ArrayResize(h_St,N);
   for(int i=0;i<N;i++)
     {
      h_St[i] = CondStDevForecast * Standardized_t(DoF);   // GARCH-Student(1,1)
     }
   MathQuantile(h_St,qlower,F_lower);
   MathQuantile(h_St,qupper,F_upper);
   return(true);
  }

//+--------------------------------------------------------------------------+
//| Function calculate i.i.d. standardized t-distributed variable            |
//+--------------------------------------------------------------------------+
double  Standardized_t(const double DoF)
  {
   double randStandStudent;
   int err;
   randStandStudent = MathRandomNormal(0,1,err) * sqrt(DoF/((MathRandomGamma(DoF/2.0,1)*2.0)));
   randStandStudent = randStandStudent/sqrt(DoF/(DoF-2.0));
   return(randStandStudent);
  }
//+------------------------------------------------------------------+

很明显，模拟的次数越多（默认是10,000次），预测的结果就越准确，但所需的计算时间也会相应增加。最可接受的模拟次数是100,000次。在这种情况下，置信区间会看起来更加对称。

检验条件高斯GARCH模型的充分性

为了检查GARCH模型捕捉波动率异方差性的能力， 需要检验标准化残差是否存在自相关，以及是否符合标准正态分布。标准化残差简单来说，就是价格增量减去条件（或无条件）数学期望，再除以GARCH模型计算出的条件标准差。

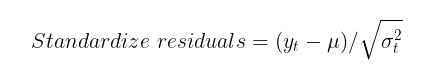
如果GARCH模型能够很好地拟合实际数据，那么标准化残差将是独立且同分布的标准正态值。

作为残差分析的一个例子，让我们采用过去四年间的EURUSD（欧元兑美元汇率）日数据，并计算模型的参数。

让我们检查残差平方的自相关性。

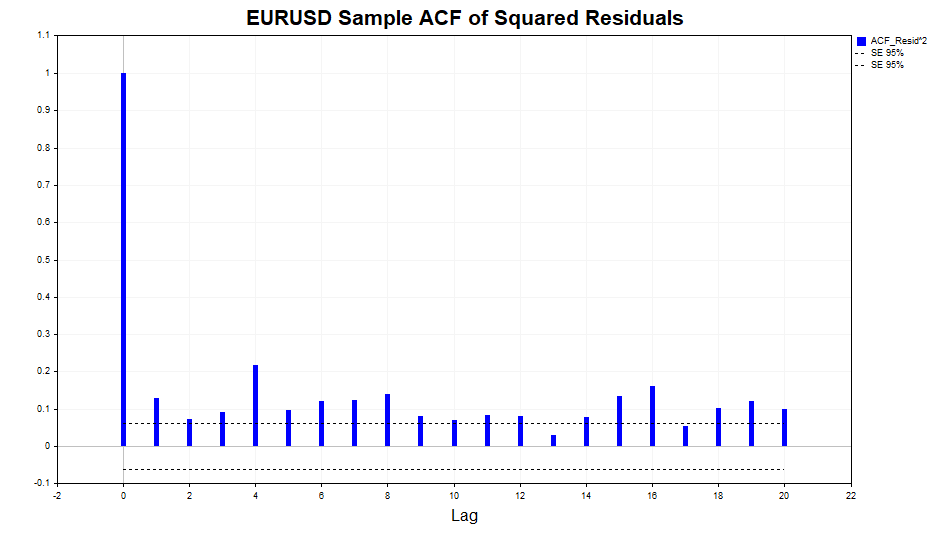
如我们所见，数据中存在轻微的依赖性，这种依赖性一直持续到滞后的20期。现在，让我们检查标准化残差平方的自相关性，并看看GARCH(1,1)模型是否能够充分描述这种依赖性。

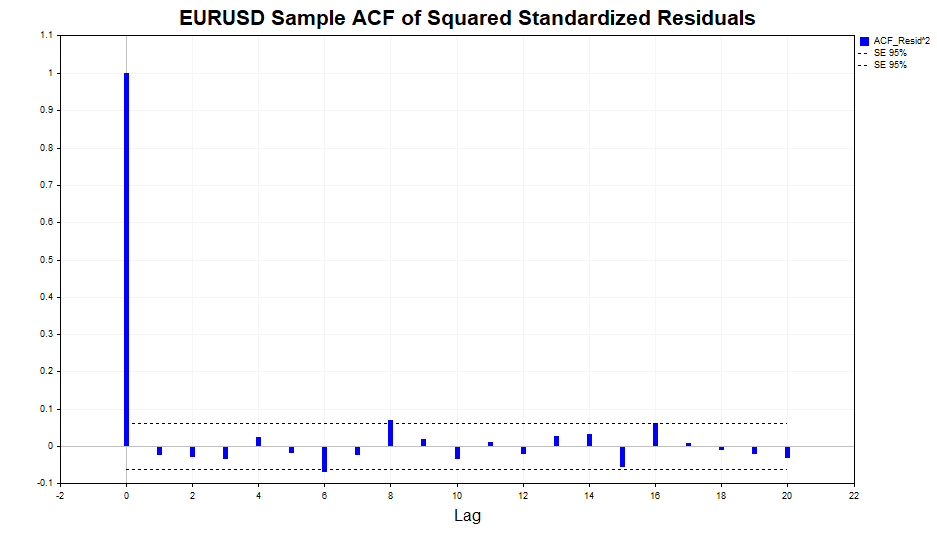
如我们所见，模型表现得非常出色。数据中不存在显著的相关性。

让我们来看看计算得到的实现波动率（对数价格增量的平方）和条件标准差（GARCH）。 模型对波动性的变化做出了相当成功的响应。无条件标准差作为GARCH波动率波动的均值。

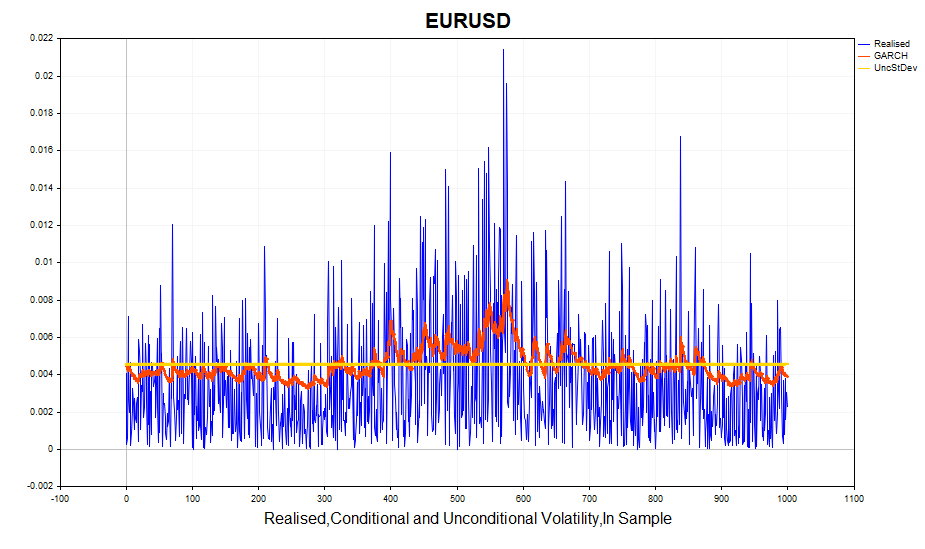
让我们检查标准化残差的正态性。

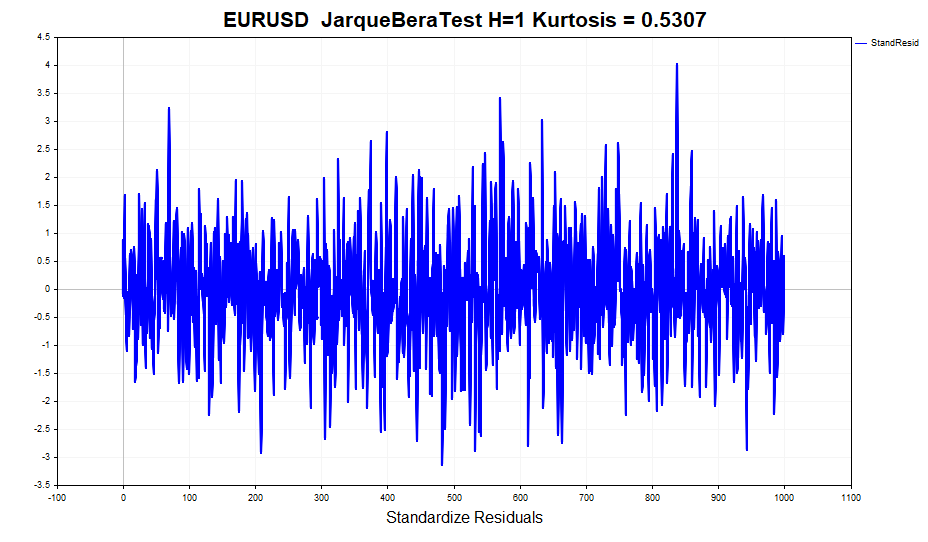
乍一看，数据似乎相当正常。没有明显的肥尾现象。但是，正式的正态性检验，如Jarque-Bera检验，拒绝了原假设。原因在于其过量值为0.5307，这与正态分布的值略有不同。同时，利润的额外值为1.2904。换句话说，GARCH模型虽然并未完全考虑，但部分引入了尖峰分布的影响。你可能还记得，无条件GARCH过程的分布具有肥尾特性。这是因为不同方差的高斯分布的混合会导致具有重尾和正峰度的分布。

因此，GARCH模型的一个假设——标准化残差具有条件正态分布——被违反了。因此，使用最大似然方法获得的模型参数估计值失去了一些有用性质，即它们不再具有渐近有效性(换句话说，随着样本量的增加，无法找到更准确的参数估计值)。

在这种情况下，作为正态分布的替代，我们可以选择t分布（学生分布），因为当自由度较小时，它具有正超额和重尾特性。在这种情况下，自由度数量成为一个额外的未知参数，应使用样本进行估计。

我们刚才简要讨论过的与各种统计量的可视化显示相关的所有操作，都已在GARCH脚本中设置，以便于分析。

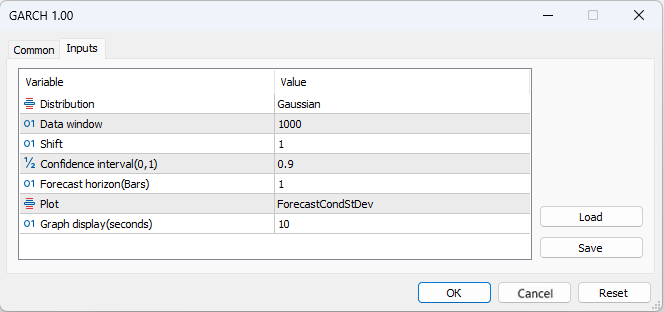
• Distribution – 标准正态分布或标准学生t-分布
• Data window - 用于计算模型参数的数据窗口
• Shift – 数据窗口位移（1 - 图表上的倒数第二个K线）
• Confidence interval – 置信区间的显著性水平（显著性水平越高，置信区间越宽）
• Forecast horizon –对未来一定数量的K线进行波动率预测
• Plot – 显示：波动率预测、标准化残差、实现波动率与GARCH波动率的比较、残差平方的自相关函数和标准化残差平方的自相关函数在图表上。

iGARCH指标

为了初步了解模型和我们将要应用此模型的数据，GARCH脚本就足够了。 但是，为了实时评估和预测波动率，我们需要一个算法，该算法将在每个新K线上重新计算模型参数，从而快速适应不断变化的市场。iGARCH自适应指标就是解决这个问题的方案。

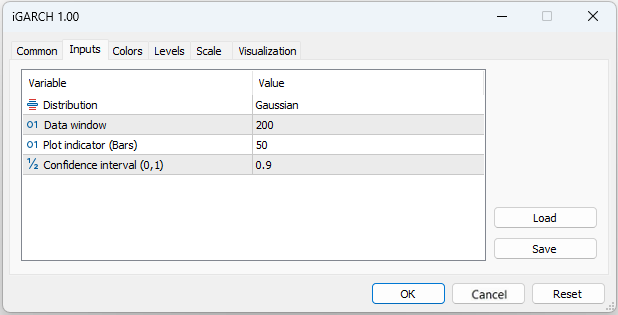
• Plot indicator – 指标将为其计算的K线数量

该指标预测波动率（条件标准差）和未来价格增量的置信区间，具有一定的一步预测可靠性水平。预测显示在当前K线上，用于计算参数的数据（数据窗口）从第一个K线开始获取。由于模型参数在每个K线上都会进行优化，因此不建议设置过大的绘图指标（K线数）值，因为计算可能需要很长时间(特别是对于具有学生分布的模型）。

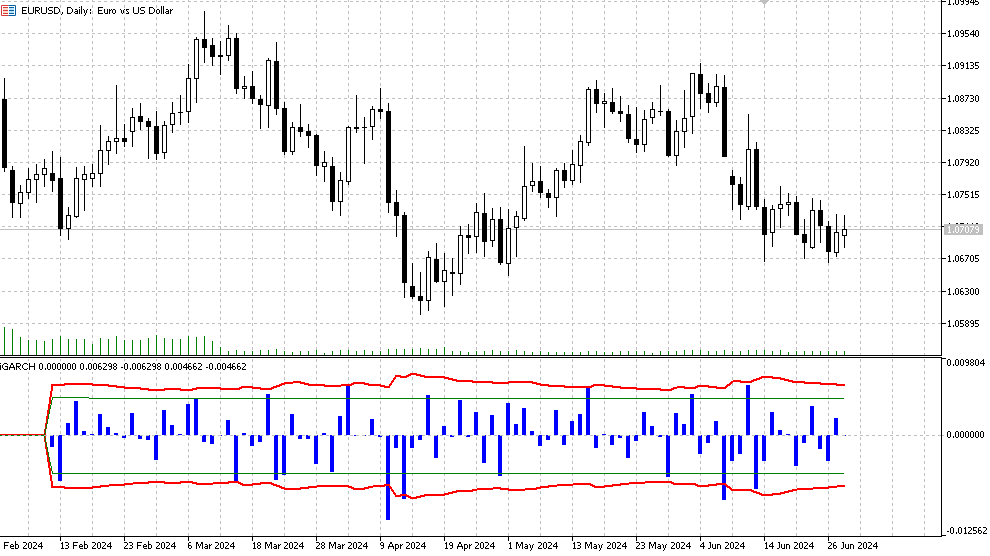
• 直方图 - 对数利润值 LN(Yt/Yt-1)，
• 红线表示根据置信区间显著性水平（默认为90%）确定的条件标准差预测的上限和下限。这意味着在大约90%的情况下，对数价格增量将位于这些限制之内，
• 绿线分别表示正常的历史波动率的下限和上限。

此外，以下信息将在日志中显示，该日志会在每个新K线出现时更新：

• 优化参数(mu, omega, alpha, beta, v)的最新值，
• 似然函数(LLF)值，
• 选定显著性水平下的预测价格水平，
• 成功完成优化的报告
• 预测的条件标准差值，
• GARCH理论无条件标准差值，
• 历史标准差值。

结论

我考虑了条件异方差性最受欢迎的模型之一——GARCH模型。事实证明，假设波动率随时间保持恒定的标准波动率估计方法并不能反映真实情况。相比之下，GARCH模型考虑了波动率随时间的变化，这使其在分析市场条件时更为恰当。

使用GARCH(1,1)模型作为示例，开发了一个自适应指标，该指标可以预测对数价格增量的一步提前波动率和置信区间。这提供了对未来价格变化进行概率评估的机会，从而更有效地管理开仓风险。
此指标不仅允许我们选择经典的高斯残差模型，还允许选择假设残差遵循学生分布的模型。同时，模型参数的优化在每个新K线上进行，这使我们能够快速响应当前市场情况。
为了使用最大似然法估计模型参数，我们使用了ALGLIB数值分析库中的MinBLEIC优化算法。GARCH脚本计算了与模型相关的所有必要统计量，并提供了用于评估数据中依赖性的可视化工具。
因此，在经济计量研究和金融分析中应用GARCH模型可以提供更准确的波动率预测，从而显著改善风险管理和投资决策。