
神经网络变得轻松(第四十部分):在大数据上运用 Go-Explore
概述
在上一篇文章 “神经网络变得轻松(第三十九部分):Go-Explore,一种不同的探索方式” 中,我们领略了 Go-Explore 算法,及其探索环境的能力。 您也许还记得,该算法包括 2 个阶段:
- 第 1 阶段 — 探索
- 第 2 阶段 — 依据样本训练策略
在第 1 阶段,我们使用随机动作选择来获得尽可能完整的环境全景。 这种方式令我们能够收集足够的样本数据库,令其能在一个日历月内基于历史数据成功训练代理者。 我们构建的模型能够依据训练集找到一种可盈利的策略。
但一个日历月的时间周期,对于总结数据,并制定在可预见的未来都能盈利的策略,无疑太短暂。 由此,为了寻找我们的策略,我们被迫增加训练周期。 当我们将训练周期延长到三个月时,我们发现使用随机动作选择无法产生一次可盈利的验算。
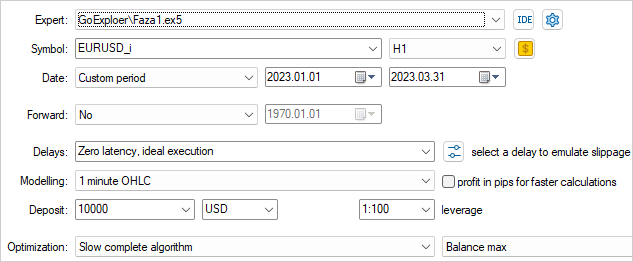
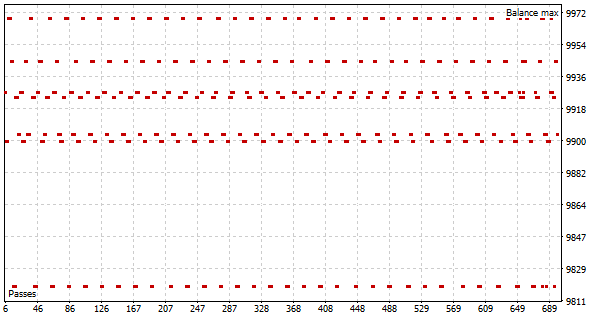
根据概率论,这是一个完全可预期的结果。 毕竟,一个总体事件的概率等于其所有组成部分的概率乘积。 但由于每个单独事件的概率小于 1,因此随着步数的增加,获得可盈利验算的概率就会降低。
此外,随着训练周期的增加,环境可能会发生变化,从而影响代理者的学习结果。 故此,定期监控代理者的性能,并在中间阶段分析其性能非常重要。
为了改进覆盖长周期训练结果,可以应用 Go-Explore 算法的各种优化方法,例如,使用改进的动作选择方法。 这种方式应考虑到任务的更广泛背景,并允许代理者做出更明智的决策。
在本文中,我们将仔细研究 Go-Explore 算法的可能优化方法,以提高其在覆盖长周期训练的绩效。
1. 随着训练周期的增加,运用 Go-Explore 的困难
Go-Explore 算法随着训练周期的增加,浮现出一定的困难。 其中一些包括:
-
维度诅咒:随着训练周期的增加,代理者可以访问的状态数量呈指数级增长,这令查找最优策略变得更加困难。
-
环境变化:随着训练周期的增加,环境也许会发生变化,而这也许会影响代理者的学习成果。 这会导致以前成功的策略变得无效,甚至不可能。
-
选择动作困难:随着训练周期的增加,代理者也许需要考虑任务的更广泛背景,以便做出明智的决定。 这会令选择最佳行的任务复杂化,并且需要更复杂的方法来优化算法。
-
训练时间增加:随着训练周期的增加,收集足够数据和训练模型所需时间也会增加。 这会降低代理者训练的效率和速度。
随着训练周期的增加,需要探索的状态空间维度也许会出现增加的问题。 这也许会导致 “维度诅咒” 问题,其中可能状态的数量随着维度的增加呈指数增长。 这令状态空间探索变得困难,并可能导致算法花费太多时间探索不相关的状态。
为了解决这个问题,可以使用降维技术,例如 PCA。 它们能够降低状态空间的维数,同时维护有关数据结构的信息。 我们还可以利用重要特征选择技术来降低状态空间的维数,并专注于问题最关切的方面。
此外,我们还可以运用其它方法,例如基于进化或遗传算法的优化,这令我们能够在大状态空间中寻找最优解。 这些方法令我们能够探索代理者行为的各种选项,并为给定任务选择最优解。
还可以采用各种行动选择方式,例如基于置信度的探索方法,它允许代理者探索状态空间的新区域,不仅考虑到获得奖励的概率,还考虑到有关任务知识的信心。 这有助于避免陷入局部最优的问题,并允许更有效地探索状态空间。
强化学习(RL)典型范例是计算机游戏或其它人工模拟的环境,其是固定的,这意味着它们不会随时间而变化。 不过,在现实世界的应用中,环境也许会随时间而变化,从而影响代理者的学习成果。
当运用 Go-Explore 算法,其中包括获取历史数据的环境探索步骤之时,若随后依据历史数据进行代理者训练时,环境的变化可能会导致意外结果。
例如,如果代理者已经接受了若干个月的数据训练,而在这期间环境发生了变化,诸如游戏规则的变化,或新物体的出现,那么代理者也许无法应对新环境,其以前成功的策略可能会变得无效,甚至不可能。
为了降低环境变化对代理者训练结果的影响,有必要在贯穿整个代理者训练过程中定期监测环境,并分析其变化。 如果检测到环境中的重大变化,则必须依据更新后的数据和算法重启代理者训练过程。
我们还可以采用在训练过程中考虑环境变化的训练方法,诸如基于模型的强化学习(RL)方法,该方法构建环境模型,并用它来预测未来的状态和奖励。 这令代理者能够适应环境的变化,并做出更明智的决策。
也可以采用其它优化技术,诸如更改算法的超参数,或更改算法本身,使之训练更有效。
通常,运用 Go-Explore 算法基于较长周期来训练代理者可能非常复杂,并且需要许多技术方案和改进。
结果就是,运用 Go-Explore 算法可能非常复杂,需要许多技术方案和改进。 Go-Explore 算法是一个强力的工具,适合探索复杂环境,以及含有大量状态和动作的训练代理者任务。 但其有效性可能会随着训练周期的增加,和任务条件的变化而降低。 故此,需要采用各种优化方法和参数调优,来达成最佳效果。这可能是一个非常实用,和有前途的研究方向。
2. 优化方式的选项
考虑到上面所说的,延长训练周期需要一种更谨慎的方式,而不是简单地在策略测试器中指定新日期,并加载额外的历史数据。 为了创建真实的交易策略,必须依据尽可能多的历史数据训练模型。 只有这种方式才能让我们创建一个有能力在未来产生盈利的模型。
在本文中,我们不会让模型复杂化。 取而代之的是,我们将采用几种简单的方式,这将有助于扩展历史数据的深度,以便运用 Go-Explore 算法进行模型训练。
在优化先前创建的算法之前,有必要分析其瓶颈。
第一步是更改 Cell 结构中的常量。 该结构存储系统的单独状态,和所采取的路径。 由于技术原因,我们被迫在此结构中仅使用静态数组。 随着模型训练周期的增加,达成所述状态的路径规模也会增加。 我们已经创建了一个常量,指示数组的大小。 现在我们应更改这个常量的值,以便有足够的空间来记录代理者从训练期开始到结束的整体路径。
为了判定常量的值,我们要用到简单的数学。 平均而言,一个日历月份包含 21-22 个工作日。 为避免出错,我们取工作日的最大值 — 22。 4 个月内将有 88 个工作日。
在测试模型时,我们将取用 H1 时间帧。 一个工作日有 24 小时。 因此,为了训练模型,我们需要一个包含 2112 个元素(88 * 24)的缓冲区。 这些计算考虑到可能的最大值,并略微超过实际的柱线数量,这令我们不必担心遭遇数组大小超界的严重错误。 不过,若依据包括周末在内的报价(例如,加密货币)上进行训练时,应采用日历日期来计算缓冲区大小,同时考虑到整个训练周期,和金融产品报价的特征。
#define Buffer_Size 2112
第二个瓶颈是在保存样本之前进行的排序。 实践表明,数据排序要比遍历历史数据和收集这些状态花费更多时间。 随着训练周期的增加,需要排序的数据量也会有所增加。 故此,我们决定放弃数据排序。 最终结果,Faza1.mq5 智能程序中的 OnTesterDeinit 函数得以改成以下形式:
//+------------------------------------------------------------------+ //| TesterDeinit function | //+------------------------------------------------------------------+ void OnTesterDeinit() { //--- int total = ArraySize(Total); printf("total %d", total); Print("Saving..."); SaveTotalBase(); Print("Saved"); }
在测试过程中,发现 EA 经常开立多笔仓位,并长期持仓。 我们希望通过采取整体方式来解决这个问题,并对样本收集 EA 进行一些更改。
其中一项变化涉及薪酬的定义。 以前,我们曾用净值变化作为奖励。 这种方式允许模型参考累计变化和未记录利润、惩罚性回撤、以及盈利仓位的利润积累的鼓励。 然而,这种方式限制了获利的可能性。 我们不想放弃采用净值的益处,但我们也想增加获利回吐奖励。
我们找到了一个折衷的方案,涉及采用净值和账户余额变化的算术平均值。 当持一笔持仓积累了利润或亏损时,净值会发生变化,但账户余额保持不变。 代理者获得的奖励或惩罚等于净值变化的一半。 当利润或损失被记录时,净值不会改变,但累计金额会在账户余额上反映出来。 代理者收到待结算的另一半奖励或惩罚。 因此,代理者对获利了结更感兴趣,而不太倾向于捂仓。
Base[action_count - 1].value = ( Base[action_count - 1].state[241] - state[241] + Base[action_count - 1].state[240] - state[240] ) / 2.0f;
我们还决定限制开仓的最大交易量,以减少其数量。 在创建样本和测试模型时,我们为每笔交易采用了固定的最小交易量。 因此,对开仓的交易量进行限制,与限制开仓的数量完全雷同。 不过,当描述系统的当前状态时,我们会收集有关持仓数量,和累计盈亏的信息。 为了避免额外的计算,我们采用开仓交易量来限制最大交易量。 我们将开仓的最大可能交易量的数值移到外部变量之中,这令我们能够取不同的数值进行实验。
input double MaxPosition = 0.1;
我们限制最大开仓交易量的最终目标是减少账户中的开仓数量,避免盈亏锁定时积累交易。 为此,我们分别检查多头和空头交易的限额,而并不考虑它们的差别。
要注意的重点是,我们并未明确指定模型的约束。 取而代之,我们在创建训练模型的样本阶段,会针对最大开仓交易量施加限制。 接下来,我们用这些样本来训练模型,且基于得到的样本自行构建其策略。 这种方式令模型能够适应不断变化的市场情况,并选择最有效的行动。
不过,值得考虑的是,在我们生成一个开仓动作的情况下,若由于施加的限制而无法执行时,系统的后续状态和奖励将与生成的动作不对应。 为了解决这个问题,我们在样本数据库中保存了一个与期望(无交易)相对应的动作,以防生成的动作未能执行。 这就确保了行动和奖励之间的对应关系,并确保正确训练模型。
switch(act) { case 0: if(buy_value >= MaxPosition || !Trade.Buy(Symb.LotsMin(), Symb.Name())) act = 3; break; case 1: if(sell_value >= MaxPosition || !Trade.Sell(Symb.LotsMin(), Symb.Name())) act = 3; break; case 2: for(int i = PositionsTotal() - 1; i >= 0; i--) if(PositionGetSymbol(i) == Symb.Name()) if(!Trade.PositionClose(PositionGetInteger(POSITION_IDENTIFIER))) { act = 3; break; } break; }
由于我们是在高风险的市场交易条件下运作,我们的任务不仅是赚取利润,而且还要尽量减少可能的损失。 为此,我们在模型中添加了持仓最长时间的限制。
此限制是一个整数型外部变量,以最大柱线数量为单位指定持仓时限。
input int MaxLifeTime = 48;
我们判定最久持仓的生存期,当达到边界值时,我们创建一个动作强制将所有持仓了结。
这是必要的,如此我们就不会持仓超期,否则可能导致巨大的损失。 在收集有关当前账户状态和持仓的信息时,我们会参考该限制,以免超过最长持有时间。
int total = PositionsTotal(); datetime time_current = TimeCurrent(); int first_order = 0; for(int i = 0; i < total; i++) { if(PositionGetSymbol(i) != Symb.Name()) continue; switch((int)PositionGetInteger(POSITION_TYPE)) { case POSITION_TYPE_BUY: buy_value += PositionGetDouble(POSITION_VOLUME); buy_profit += PositionGetDouble(POSITION_PROFIT); break; case POSITION_TYPE_SELL: sell_value += PositionGetDouble(POSITION_VOLUME); sell_profit += PositionGetDouble(POSITION_PROFIT); break; } first_order = MathMax((int)(PositionGetInteger(POSITION_TIME) - time_current) / PeriodSeconds(TimeFrame), first_order); }
不过,如果我们允许超过此限制,则应采取适当的措施。 在这种情况下,我们不是简单地在时间到期后平仓一笔,而是特指动作会将所有持仓了结。 这令我们能够在完成的动作、新状态和奖励之间保持对应关系,这对于模型的正确操作很重要。
int act = (first_order < MaxLifeTime ? SampleAction(4) : 2);
因此,使用持仓最长时间限制是我们模型中的另一种机制,可以帮助我们在不确定的市场条件下控制风险,并取得更稳定的结果。
我们讲述了在模型测试过程中,根据辨别出的缺点优化算法的方式。 现在,我们转移到基于扩展历史数据来训练模型。 我们研究一下将大型训练集合拆分为较小的部分,并依据每个部分来训练代理者的可能性。 我们可以假设,如果一个算法在很短的周期内运行良好,那么它也可以在较长的时间内运行良好。 因此,我们可以采用这种方式来改进大数据的模型训练。
这种方式令模型能够更有效地捕捉市场趋势,并增加其对外部因素变化的抵抗力。 当利用该模型在真实市场交易时,这一点尤其重要,因为在真实市场中,预测趋势方向的变化至关重要。 此外,这种方法令模型能够更有效地利用所有可用数据,而不仅仅是最新的观测结果,这反过来又提高了预测的品质。
需注意的重点是,将训练集合划分为更小的时间周期时,应考虑到数据的时间顺序,以避免数据重叠和预测偏差。 还必须考虑到,当将数据划分为更小的片段时,每个片段中可用于训练的数据量会更少,这可能会导致模型的预测精度降低。
因此,将训练集合拆分为更小的时间片段是优化算法的有效方式,可以显著提高模型的预测品质。
当将训练集合划分为更小的子集时,我们面对的是开发一个通体策略,以便我们能够成功地遍历整个训练集合。 为此,我们可以把随机动作抽样和定向分步训练结合使用,这将有助于我们找到最成功和最有利可图的策略。
这个思路是按顺序遍历小子集,在每个子集中使用动作随机抽样。 然后,我们选择最有利可图的验算,并将它们用作下一子集的起点。 如此,我们按顺序遍历整个训练集合,积累有利可图的策略样本。
这种方式结合了看似互逆的思路:随机抽样和定向训练。 使用随机抽样,我们是在探索环境;训练样本的定向推进则有助于我们找到最成功的策略。 结果就是,我们能为我们的代理者获得更普遍和更有利可图的策略。
一般来说,将随机抽样和定向训练相结合,可以让我们尽享随机性和已经积累的成功行动的经验,依据所传递的训练样本获得最优策略。
为了实现这种方式,我们需引入 3 个外部变量:
- MinStartSteps — 采样开始前的最小步数
- MaxSteps - 最大采样步数(序列大小)
- MinProfit - 保存到样本数据库的最低利润。
input int MinStartSteps = 96; input int MaxSteps = 120; input double MinProfit = 10;
在讨论算法优化时,我们发现在保存之前进行样本排序效率低下。 取而代之,我们决定采用 MinProfit 变量作为最低利润,判定是否将样本包含在数据库。 这令我们能够为后续抽样的起点优选样本。 此外,我们利用 MinStartSteps 变量来设置样本中起点所需的最小步骤。 这令我们能够避免在采样过程中陷入中间步骤,并继续下一子集。
我们还用到 MaxSteps 变量,其判定了最大子集长度。 一旦超过此数值,采样将不再有效,且我们需要保存行进的路径。 以这种方式,我们可以更有效地利用资源,并加快训练速度。
在 Faza1.mq5 EA 的 OnInit 方法中,加载以前创建的样本数据库后,我们首先选择满足完成步骤所需的样本。
if(LoadTotalBase()) { int total = ArraySize(Total); Cell temp[]; ArrayResize(temp, total); int count = 0; for(int i = 0; i < total; i++) if(Total[i].total_actions >= MinStartSteps) { temp[count] = Total[i]; count++; }
之后,从所选样本中随机抽样选择一个样本。 我们将用这个随机选择的样本作为起始采样点。
if(count > 0) { count = (int)(((double)(MathRand() * MathRand()) / MathPow(32768.0, 2.0)) * (count - 1)); StartCell = temp[count]; } else { count = (int)(((double)(MathRand() * MathRand()) / MathPow(32768.0, 2.0)) * (total - 1)); StartCell = Total[count]; } }
在 EA 的 OnTick 方法中,我们首先无条件地执行整条路径,直到我们到达子集的起点。
void OnTick() { //--- if(!IsNewBar()) return; bar++; if(bar < StartCell.total_actions) { switch(StartCell.actions[bar]) { case 0: Trade.Buy(Symb.LotsMin(), Symb.Name()); break; case 1: Trade.Sell(Symb.LotsMin(), Symb.Name()); break; case 2: for(int i = PositionsTotal() - 1; i >= 0; i--) if(PositionGetSymbol(i) == Symb.Name()) Trade.PositionClose(PositionGetInteger(POSITION_IDENTIFIER)); break; } return; }
只有在到达我们的子集开头后,我们才会转进到动作采样操作。 与此同时,我们控制随机操作执行的数量。 它们的数量不应超过最大子集长度。
如果达到最大步数,我们首先生成一个操作来把所有仓位平仓。
int act = (action_count < MaxSteps || first_order < MaxLifeTime ? SampleAction(4) : 2);
这次转进之后,我们着手结束 EA 的工作。
if(action_count > MaxSteps) ExpertRemove();
在策略测试器中完成验算后,我们检查验算后获得的利润规模。 如果满足达到最小盈利阈值的条件,我们将数据添加到样本数据库之中。
//+------------------------------------------------------------------+ //| Tester function | //+------------------------------------------------------------------+ double OnTester() { //--- double ret = 0.0; //--- double profit = TesterStatistics(STAT_PROFIT); action_count--; if(profit >= MinProfit) FrameAdd(MQLInfoString(MQL_PROGRAM_NAME), action_count, profit, Base); //--- return(ret); }
在此,我们仅提供并解释 EA 代码的微小更改,大部分在上一篇文章中已有详述。 完整的 EA 代码可在附件中找到。
3. 测试
如同上一篇文章,我们为训练模型来收集 EURUSD H1 上的历史数据样本。 不过,这次我们将取 2023 年 4 个月的历史数据。
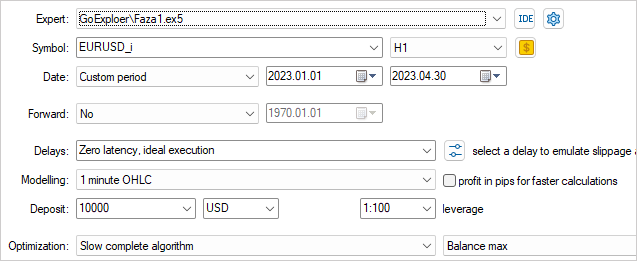
为了最有效地探索环境,必须在样本采集过程中采用各种外部参数值。 在这种情况下,我们将把这些参数作为优化参数,这样能令我们在每次验算时更改它们的数值。
为了开始优化过程,我们将选择两个参数:MaxSteps 和 MaxLifeTime。 第一个参数确定子集的最大长度,超距后,所收集样本无效。 第二个参数指示在一个子集中持仓的最长期限。 在收集样本的过程中采用这些参数的不同数值,我们可以尽可能全面地研究环境。
例如,通过采用 MaxSteps 和 MaxLifeTime 的不同数值,我们能够收集到不同持仓持续时间和期限的样本。 这令我们能够获得环境中也许会浮现的更广泛状况的样本。 以这种方式,我们能创建一个更通用、更有效的训练模型,该模型将参考许多不同的场景。
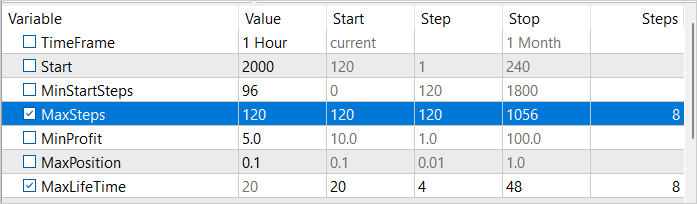
我们设置利润值的阈值接近 0。 毕竟,这是首次验算,我们只需要赚取微薄的利润。
作为优化过程的首次验算,我们看到在 2023 年 1 月的前 2 周内,有若干次成功的验算,达到 46 美元的利润。 此类验算的利润系数达到 1.55
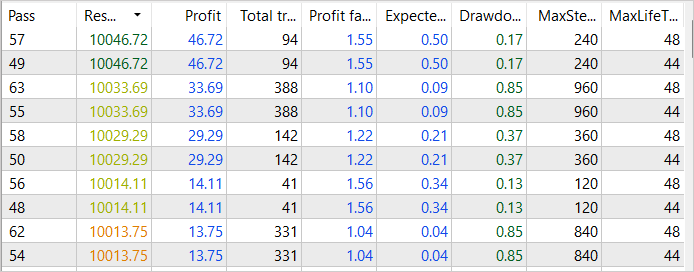
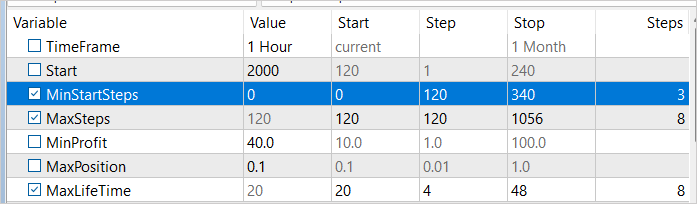
在运行优化之前,我们将对参数进行一些更改。 为确保按不同的时间间隔收集样本,我们将在采样开始之前往优化变量里加上最小步数。 此变量的值将在 1 到 3 周之间变化,增量按周为单位。 此外,我们把利润阈值提高到 40 美元,来提升所获得的结果。
根据第二次优化的结果,我们看到 2023 年 1 月的利润增加到 84 美元。 尽管利润因子下降到 1.38。
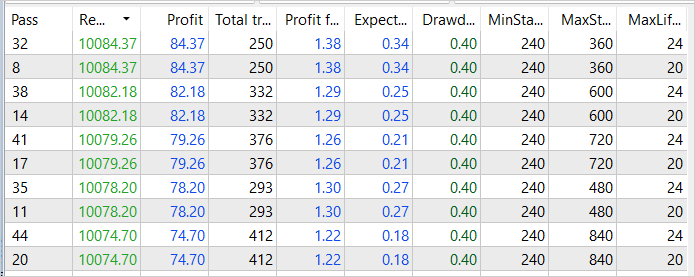
尽管如此,我们看到为优化样本采集过程付出的努力开始取得成果。 尽管我们还没有达成最终的成功,然事件的大趋势与我们的目标和期望是一致的。
我们在 2023 年 1 月的第二周开始采样之前增加最小步骤数,并执行另一次优化过程。 这一次,我们把最低盈利能力提高到 80 美元。 毕竟,我们努力寻找最有利可图的策略。
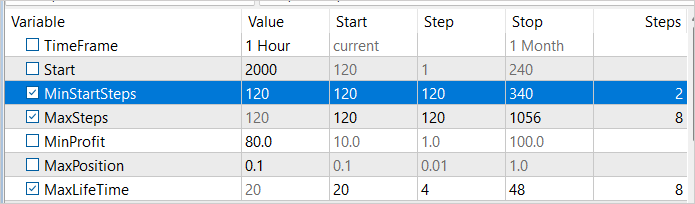
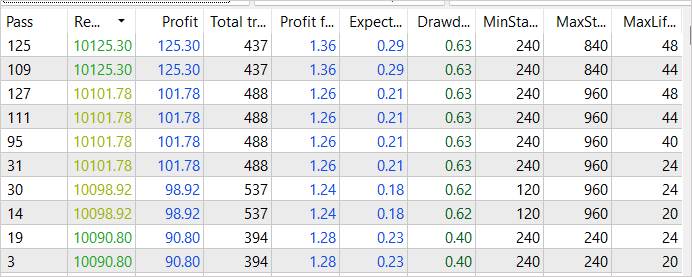
正如我们预期的那样,由于随后对样本收集过程的优化,我们达成更高的盈利能力。 最成功的验算总收入已增加到 125 美元。 同时,盈利因子略有下降,为 1.36,这仍然意味着盈利超过成本。 重点注意的是,这种盈利能力的提高是通过改进样本采集过程达成的,我们可以对其效率充满信心。 不过,请记住,训练尚未完成,我们将继续进行。
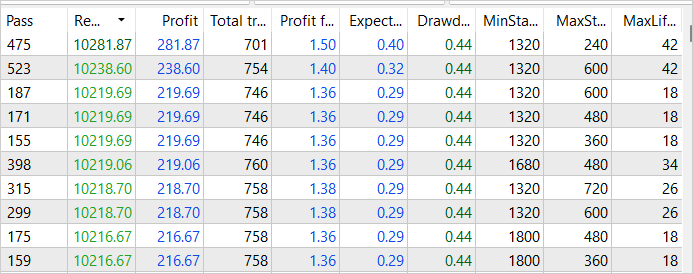
我们继续迭代在策略测试器的优化模式下收集样本,依次改变抽样起点,和利润阈值。 这种方式令我们能够在遍历整个训练集获得若干次成功验算的样本。 其中最有利可图的产生了 281 美元的收入,盈利系数为 1.5。 这些结果确认了我们优化案例收集流程的策略具有积极效果,有助于达成更高的利润门槛。 不过,我们明白这个过程并不完整,需要进一步优化和改进。
一旦收集样本的过程完成后,我们转进到依据所获数据运用 Go-Explore 算法训练模型。 然后,我们利用强化训练方法重新训练模型,以进一步提升其性能。
为了检查训练模型的品质和成效,我们依据训练和测试样本对其进行了测试。 重点注意的是,我们的模型能够自 2023 年 5 月第一周的历史数据中获利,这些数据不包括在训练集之中,而是训练集的直接延续。
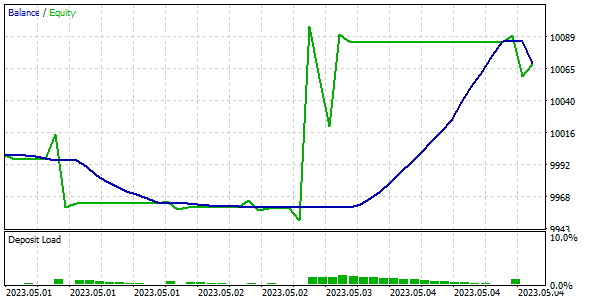
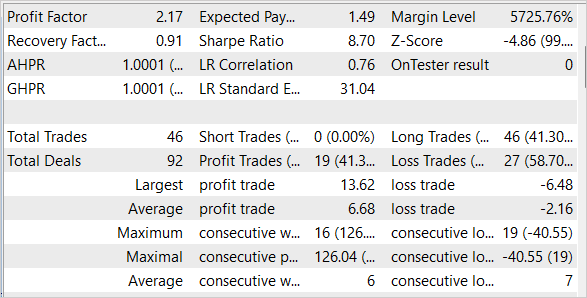
结束语
在本文中,我们研究了优化 Go-Explore 算法的简单但有效的方法,令其能够基于大数据训练模型。 我们的模型是依据 4 个月的历史数据上训练的,但感谢采用的优化方法,Go-Explore 算法可在更长的时间周期内训练模型。 我们还依据训练和测试样本进行了模型测试,确认了其高效率和高品质。
总体而言,Go-Explore 算法为基于大数据训练模型开辟了新的可能性,对于人工智能领域额各种应用,其已成为有力工具。
然而,重点是要记住,金融市场是极具动态的,且易受突发变化影响,因此即使是最优质的模型也不能保证 100% 的成功。 因此,我们必须不断监测市场的变化,并相应地调整我们的模型。
链接
- Go-Explore:解决艰难探索难题的新途径
- 神经网络变得轻松(第三十五部分):内在好奇心模块
- 神经网络变得轻松(第三十六部分):关系强化学习
- 神经网络变得轻松(第三十七部分):分散关注度
- 神经网络变得轻松(第三十八部分):凭借分歧进行自我监督探索
- 神经网络变得轻松(第三十九部分):Go-Explore,一种不同的探索方式
本文中用到的程序
| # | 名称 | 类型 | 说明 |
|---|---|---|---|
| 1 | Faza1.mq5 | 智能交易系统 | 第一阶段 EA |
| 2 | Faza2.mql5 | 智能交易系统 | 第二阶段 EA |
| 3 | GE-lerning.mq5 | 智能交易系统 | 优调 EA 的政策 |
| 4 | Cell.mqh | 类库 | 系统状态定义结构 |
| 5 | FQF.mqh | 类库 | 完全参数化模型的工作安排类库 |
| 6 | NeuroNet.mqh | 类库 | 用于创建神经网络的类库 |
| 7 | NeuroNet.cl | 代码库 | OpenCL 程序代码库 |
本文由MetaQuotes Ltd译自俄文
原文地址: https://www.mql5.com/ru/articles/12584
