Swaplar (Bölüm I): Kilitleme ve sentetik pozisyonlar
İçindekiler
- Giriş
- Swaplar hakkında
- İki işlem hesabı kullanarak kilitleme
- Döviz kurları hakkında
- Sentetik pozisyonlar kullanarak kilitleme
- Swap çokgenlerini kullanmak için bir yardımcı program yazma
- İlk testlerden elde edilen sonuçlar
- Sonuç
Giriş
Bu makalenin konusunu uzun zamandır düşünüyordum ancak detaylı bir araştırma yapmaya vaktim olmadı. Swap konusu web üzerinde oldukça yaygındır, özellikle de her pipi sayan alım-satım profesyonelleri arasında, ki bu aslında alım-satım için en iyi yaklaşımdır. Bu makaleden, swapların nasıl iyi bir şekilde kullanılacağını öğrenecek ve swapların her zaman dikkate alınması gerektiğini göreceksiniz. Ayrıca, makalede swap alım-satım yöntemlerinin nasıl modernize edileceğine dair çok karmaşık ama ilginç bir fikir de yer alıyor. Bu tür yöntemler (uygun şekilde hazırlandığında) tek bir hesap içinde veya iki hesap kullanan klasik kilitleme için bir kâr artırma aracı olarak kullanılabilir.
Swaplar hakkında
Swap fikrini ve teorisini açıklamayacağım. Ben sadece swapların pratik uygulamasıyla ilgileniyorum. En önemli soru, swap yoluyla kâr elde etmenin mümkün olup olmadığıdır. Bir yatırımcının bakış açısına göre, swap bir kâr veya zarardır. Dahası, birçok yatırımcı gün içi alım-satıma bağlı kaldıkları için bunu görmezden gelir. Diğerleri ise alım-satımı etkileyemeyecek kadar önemsiz olduğunu düşünerek dikkat etmez. Aslında, makasın neredeyse yarısı swapta gizlenebilir. Bu makas, alış veya satış sırasında değil, sunucuda gün değiştiğinde tahsis edilir.
Swap, açık pozisyon hacmine göre ücretlendirilir. Bu, aşağıdaki anlarda gerçekleşir:
- Pazartesiden salıya
- Salıdan çarşambaya
- Çarşambadan perşembeye (neredeyse tüm brokerlar bu gece üçlü swap ücreti tahsis eder)
- Perşembeden cumaya
Genellikle, swap değeri alım-satım enstrümanı özelliklerinde puan veya yüzde olarak belirtilir. Başka hesaplama yöntemleri de olabilir, ancak ben bunlardan sadece ikisini anlamayı başardım ki bu da oldukça yeterli. Swaplar hakkında çok az yapılandırılmış bilgi bulunmaktadır. Bununla birlikte, meseleyi incelerseniz, bazı verimli swap tabanlı stratejiler bile bulabilirsiniz. Minimum kâr yüzdesi üretirler, ancak büyük bir avantajları vardır - kâr kesinlikle garantilidir. Bu yaklaşımın temel zorluğu, en popüler brokerların pozitif swaplı çok az enstrümana sahip olmasıdır, bu nedenle bu fikirden para kazanmak gerçekten zordur. Olası potansiyel kâr bile son derece düşüktür. Yine de bu, bakiyeyi tamamen kaybetmekten daha iyidir. Ve başka bir alım-satım sistemi kullanıyorsanız, büyük olasılıkla kaybedeceksiniz.
Forex alım-satımıyla ilgili vardığım sonuç şu: pozitif swaplar dışında hiçbir şey kârı garanti etmez. Elbette, kâr elde edebilen bazı sistemler de vardır. Ancak, bunları kullanırken, herhangi bir alım-satım işlemi için paramızı brokera ödemeyi kabul ediyoruz ve fiyatın doğru yönde gideceğini umuyoruz. Pozitif swap ise bunun tersi bir süreçtir. Aşağıdaki ifadeleri pozitif swap yönünde işlem yapmanın işaretleri olarak görüyorum:
- Pozitif swap, açık pozisyonumuza doğru kısmi bir fiyat hareketine eşdeğerdir (her gün kâr)
- Bir süre sonra swap, makas ve komisyonlardaki kayıpları karşılayabilir; bir süre sonra swap para ekleyecektir
- Swapın işe yaraması için pozisyonun mümkün olduğunca uzun süre tutulması gerekir, böylece bu pozisyonların kâr faktörü maksimum olacaktır
- İyice geliştirilirse, kâr kesinlikle öngörülebilir ve garantili olacaktır
Elbette, bu yaklaşımın en büyük dezavantajı bakiye büyüklüğüne bağımlılıktır, ancak başka hiçbir kavram forexte kârı bu kadar güvenle garanti edemez. Bu bağımlılık, açık pozisyonların hacmini veya riski (ki bu aynı şeydir) düşürerek azaltılabilir. Risk, pozisyon hacminin bakiyeye oranıdır: pozisyon hacmindeki artış, fiyatın kaybedilen yöne gitme riskimizi artırır. Bakiye; makas ve komisyonlardan kaynaklanan kayıpları telafi etmek için swaplardan elde edilen kârı beklememiz için yeterli olmayabilir. Olası tüm olumsuz etkilerin etkisini en aza indirmek için bir kilitleme mekanizması keşfedildi.
İki işlem hesabı kullanarak kilitleme
Bu swap alım-satım yöntemi, yatırımcılar arasında en popüler olanıdır. Bu stratejiyi uygulamak için, aynı döviz çiftleri veya diğer varlıklar için farklı swaplara sahip iki hesaba ihtiyacınız olacaktır. Aynı hesapta iki zıt pozisyon açmak anlamsızdır - bu sadece bakiyeyi kaybetmekle eşdeğerdir. Bir sembol pozitif bir swapa sahip olsa bile, ters yönde işlem yapıldığında bu swap negatif olacaktır. Aşağıdaki diyagram bu yöntemin konseptini yansıtmaktadır:
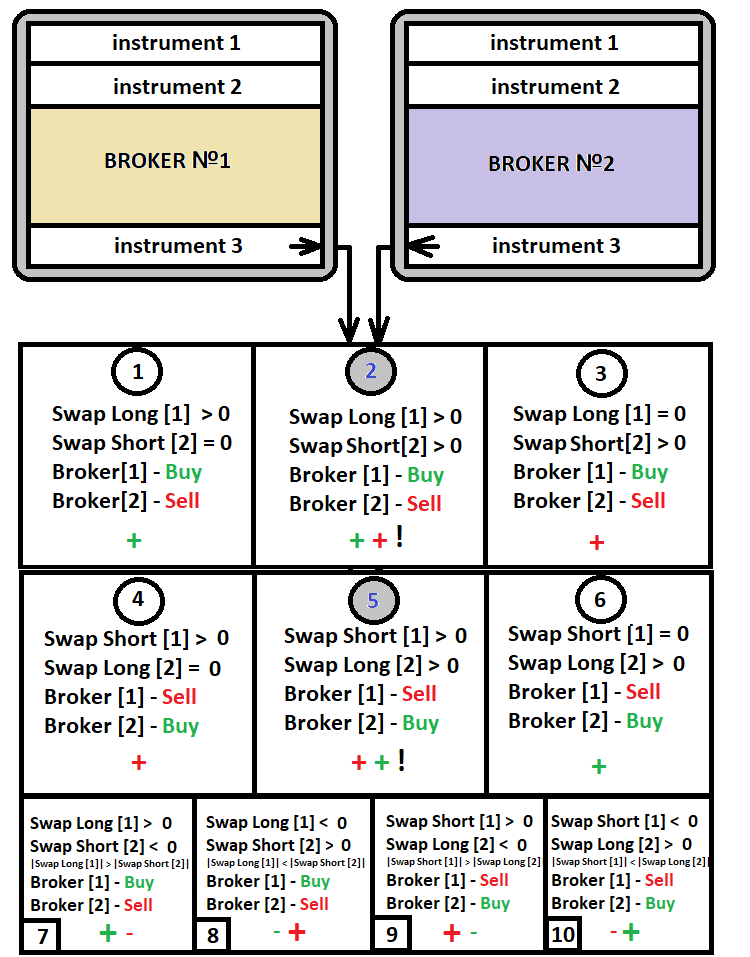
Diyagramdan da görebileceğiniz gibi, swap alım-satımı yapmak istediğimiz özel olarak seçilmiş bir enstrüman için yalnızca 10 işlem senaryosu vardır ve bunların 6'sı aktif olarak kullanılmaktadır. Son dört seçenek, "1-6" koşullarına uyan bir döviz çifti bulmak imkansızsa, son çare olarak seçilebilir, çünkü buradaki swaplardan biri negatiftir. Negatif olandan daha büyük olan pozitif swaptan kâr elde etmek mümkündür. Farklı brokerları ve bunların swap tablolarını analiz ederseniz yukarıda belirtilen tüm durumları bulabilirsiniz. Ancak bu strateji için en iyi seçenekler "2" ve "5"tir. Bu seçeneklerin her iki ucunda da pozitif swap vardır. Böylece her iki brokerdan da kâr elde edilir. Ayrıca, hesaplar arasında sık sık para taşımak zorunda kalmazsınız.
Bu stratejinin ana dezavantajı, hesaplar arasında hala para taşımanız gerektiğidir, çünkü zıt pozisyonlar açarken bir broker ile zararınız ve başka bir broker ile kârınız olacaktır. Bununla birlikte, mevcut bakiyeyle ilgili olarak işlem hacimlerini doğru bir şekilde hesaplarsanız, çok sık para taşımanız gerekmeyecektir. Ancak tartışılmaz bir avantajı vardır: her durumda kâr olacaktır ve bu kârın tam büyüklüğü tahmin edilebilir. Bence birçok kullanıcı bu rutinden kaçınmayı ve bir şekilde bu manipülasyonları tek bir hesap içinde gerçekleştirmeyi tercih eder (ki bu imkansızdır). Ancak, tek bir hesapta işlem yapılmasına izin vermese de, klasik swap alım-satım yönteminin kârının nasıl artırılacağına dair bir yöntem vardır. Bu yöntemin temel özelliklerini tartışalım.
Döviz kurları hakkında
Tüm mantığın üzerine inşa edildiği temel ile başlayalım. Matematiksel denklemler bu temel üzerine inşa edilebilir. Örneğin, EURUSD, USDJPY, EURJPY'yi düşünelim. Tüm bu 3 çift birbiriyle ilişkilidir. İlişkiyi anlamak için bu sembolleri biraz daha farklı bir biçimde sunalım:
- 1/P = EUR/USD
- 1/P = USD/JPY
- 1/P = EUR/JPY
- P, seçilen para biriminin kurudur
Herhangi bir alım-satım enstrümanında edindiğimiz bir para birimi (veya eşdeğer bir varlık) ve karşılığında verdiğimiz başka bir para birimi vardır. Örneğin, ilk pariteye (EURUSD çifti) bakalım, 1 lotluk bir alış pozisyonu açarken, 100,000 birim baz para birimi elde edersiniz. Bunlar forex alım-satım kurallarıdır: bir lot her zaman baz para biriminin 100,000 birimine eşittir. Bu çiftin baz para birimi EUR'dur ve bu nedenle USD karşılığında EUR satın alırız. Bu durumda "P" döviz kuru, 1 EUR'da kaç birim USD bulunduğu anlamına gelir. Aynı şey diğer tüm semboller için de geçerlidir: baz para birimi payda yer alırken, "ana para birimi" paydada bulunur (bu adlandırmayı kabul etmiyorsanız, lütfen aşağıya bir yorum ekleyin). Ana para biriminin miktarı, basitçe fiyatın EUR değeri ile çarpılmasıyla hesaplanır:
- 1/P = EUR/USD ---> USD/P = EUR ---> USD = P*EUR
- EUR = Lots*100000
Bir satış pozisyonu açarken, para birimleri yer değiştirir. Baz para birimi ana para birimi olarak hareket etmeye başlar ve ana para birimi baz para birimi haline gelir. Başka bir deyişle, EUR karşılığında USD satın alırız, ancak her iki para biriminin para miktarı aynı şekilde hesaplanır - EUR'ya göre. Bu doğru, çünkü aksi takdirde çok fazla kafa karışıklığı olurdu. Hesaplamalar diğer para birimleri için de aynıdır. Bu nedenle, daha sonraki hesaplamalarda baz para birimi için "+" işaretini ve ana para birimi için "-" işaretini kullanalım. Sonuç olarak, herhangi bir işlemde neyi ne için satın aldığımızı sembolize eden iki karşılık gelen sayı kümesi vardır. Bunun bir başka yorumu da, her zaman ürün olarak işlev gören bir para birimi ve para birimi olarak işlev gören ve ürünü satın almak için ödediğimiz başka bir para birimi olduğudur.
Birkaç enstrüman için birkaç pozisyon açarsak, daha fazla ana ve ek para birimi olacaktır ve böylece bir tür sentetik pozisyonumuz olur. Swap kullanımı açısından bakıldığında, böyle bir sentetik pozisyon kesinlikle işe yaramaz. Ancak çok faydalı olacak böyle bir sentetik pozisyon yaratabiliriz. Biraz sonra göstereceğim. İki para birimi ile ifade edilen hacim hesaplamasını belirledim. Buradan yola çıkarak, daha basit bir pozisyona eşdeğer olacak karmaşık bir sentetik pozisyon yaratabileceğimiz sonucuna varabiliriz:
- EUR/JPY = EUR/USD * USD/JPY - iki türevden oluşan döviz kuru
Gerçekte, çeşitli para birimlerinden oluşan sonsuz sayıda bu tür pariteler vardır. Para birimlerine örnek olarak:
- EUR - Euro
- USD - ABD doları
- JPY - Japon yeni
- GBP - İngiliz poundu
- CHF - İsviçre frankı
- CAD - Kanada doları
- NZD - Yeni Zelanda doları
- AUD - Avustralya doları
- CNY - Çin yuanı
- SGD - Singapur doları
- NOK - Norveç kronu
- SEK - İsveç kronu
Bu, para birimlerinin tam listesi değildir. Bilmemiz gereken şey, rastgele bir alım-satım enstrümanının bu listedeki herhangi bir para biriminden oluşabileceğidir. Bu alım-satım enstrümanından bazıları brokerlar tarafından sunulurken, diğerleri diğer enstrümanların pozisyonlarının bir kombinasyonu olarak elde edilebilir. Tipik bir örnek EURJPY çiftidir. Bu, türev döviz kurlarının oluşturulmasına ilişkin en basit örnektir, ancak bu fikirlere dayanarak herhangi bir pozisyonun diğer enstrümanlar için bir dizi pozisyon olarak sunulabileceği sonucuna varabiliriz. Yukarıdakilere göre, şu ortaya çıkıyor:
- Value1 - mutlak değerle ifade edilen baz sembol para birimi
- Value2 - mutlak değerle ifade edilen ek sembol para birimi
- A - pozisyonun baz para biriminin lot hacmi
- B - pozisyonun ana para biriminin lot hacmi
- Contract - mutlak değer olarak satın alınan veya satılan para birimi miktarı (1 lota karşılık gelir)
- A = 1/P = Value1/Value2 - herhangi bir alım-satım enstrümanının denklemidir (Piyasa Gözlemi penceresinde sunulmayanlar dahil)
- Value1 = Contract*A
- Value2 = Contract*B
Bu değerlere daha sonra lotları hesaplamak için ihtiyacımız olacak. Şimdilik lütfen onları aklınızda tutun. Bu değerler, alınan veya satılan para birimlerinin sayısının oranını tanımlar. Bu temel üzerine daha ciddi kod mantığı inşa edilebilir.
Sentetik pozisyonlar kullanarak kilitleme
Bu makalede, sentetik bir pozisyon, diğer birkaç pozisyondan oluşabilen bir pozisyondur, ancak bu diğer pozisyonlar mutlaka başka enstrümanlardan oluşmalıdır. Bu pozisyon herhangi bir enstrüman için bir açık pozisyona eşdeğer olmalıdır. Karmaşık mı görünüyor? Aslında her şey çok basit. Böyle bir pozisyona aşağıdakiler için ihtiyaç duyulabilir:
- Simüle edilen bir alım-satım enstrümanındaki orijinal pozisyonu kilitleme
- Tamamen farklı swap oranlarına sahip bir pozisyonun eşdeğerini oluşturmaya çalışma
- Diğer amaçlar
İşte bu yöntemin genel şeması:
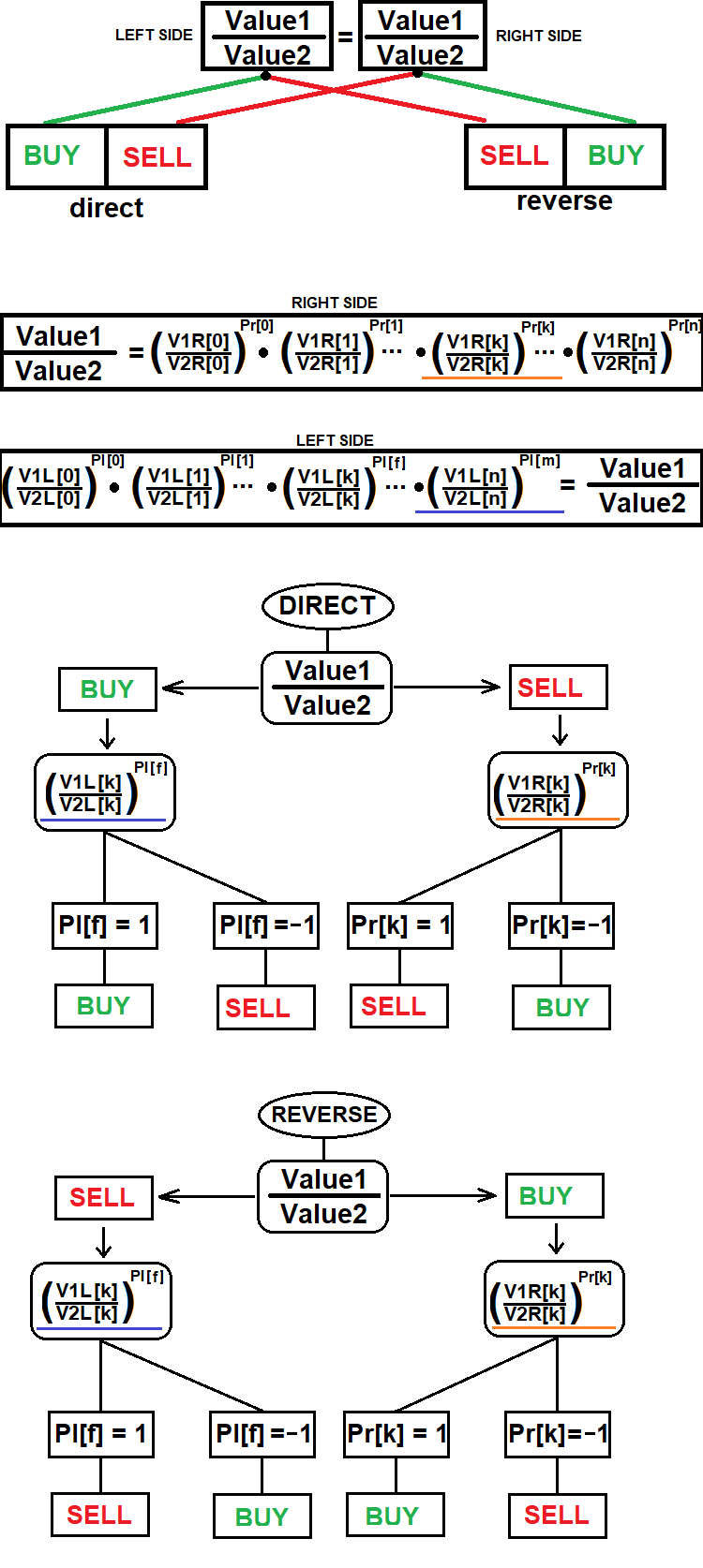
Bu şema bile sentetik bir pozisyonun nasıl açılacağına ilişkin tüm verileri kapsamamaktadır. Bu şema yalnızca sentetik bir pozisyonun belirli bir bileşeni için işlem yönünün nasıl belirleneceğini gösterir; bu bileşen mutlaka seçilen brokerın mevcut enstrümanlarından biri tarafından temsil edilmelidir.
Şimdi, bu pozisyonların hacimlerini nasıl hesaplayacağımızı belirlememiz gerekiyor. Mantıksal olarak, hacimler, pozisyonun, denklemin seçilen varyantının indirgendiği sonuç enstrümanı için 1 lotluk pozisyona eşdeğer olması gerektiği düşüncesine dayanarak hesaplanmalıdır. Hacim hesaplaması için aşağıdaki değerler gereklidir:
- ContractB - denklemin indirgendiği çiftin sözleşme büyüklüğü (çoğu durumda baz para biriminin 100,000 birimine eşittir)
- Contract[1] - lotunu belirlemek istediğimiz çiftin sözleşme büyüklüğü
- A[1] - önceki dengeli çiftin (veya zincirdeki ilk çiftin) lotları cinsinden ifade edilen baz para birimi miktarı
- B[1] - önceki dengeli çiftin (veya zincirdeki ilk çiftin) lotları cinsinden ifade edilen ana para birimi miktarı
- A[2] - dengelenmekte olan mevcut çiftin lotları cinsinden ifade edilen baz para birimi miktarı
- B[2] - dengelenmekte olan mevcut çiftin lotları cinsinden ifade edilen ana para birimi miktarı
- C[1] - önceki dengeli çiftin (veya zincirdeki ilk çiftin) sözleşme büyüklüğü
- C[2] - dengelenmekte olan mevcut çiftin sözleşme büyüklüğü
Kombinasyon sonucu ortaya çıkan enstrüman broker tarafından sağlanamayabileceğinden, "ContractB"yi belirlemenin her zaman mümkün olmadığına lütfen dikkat edin. Bu durumda sözleşme rastgele olarak, örneğin "100000" temel sabitine eşit olarak ayarlanabilir.
İlk olarak, zincirdeki ilk çift belirlenir ve bu çift, istenen pozisyonda sonuç enstrümanının baz para birimini içerir. Ardından, ortaya çıkan eşdeğere dahil edilmeyen ekstra para birimlerini dengeleyen diğer çiftler aranır. Dengeleme, ana para birimi mevcut paritede doğru pozisyonda olduğunda sona erer. Bunun nasıl yapıldığını göstermek için bir diyagram oluşturdum:
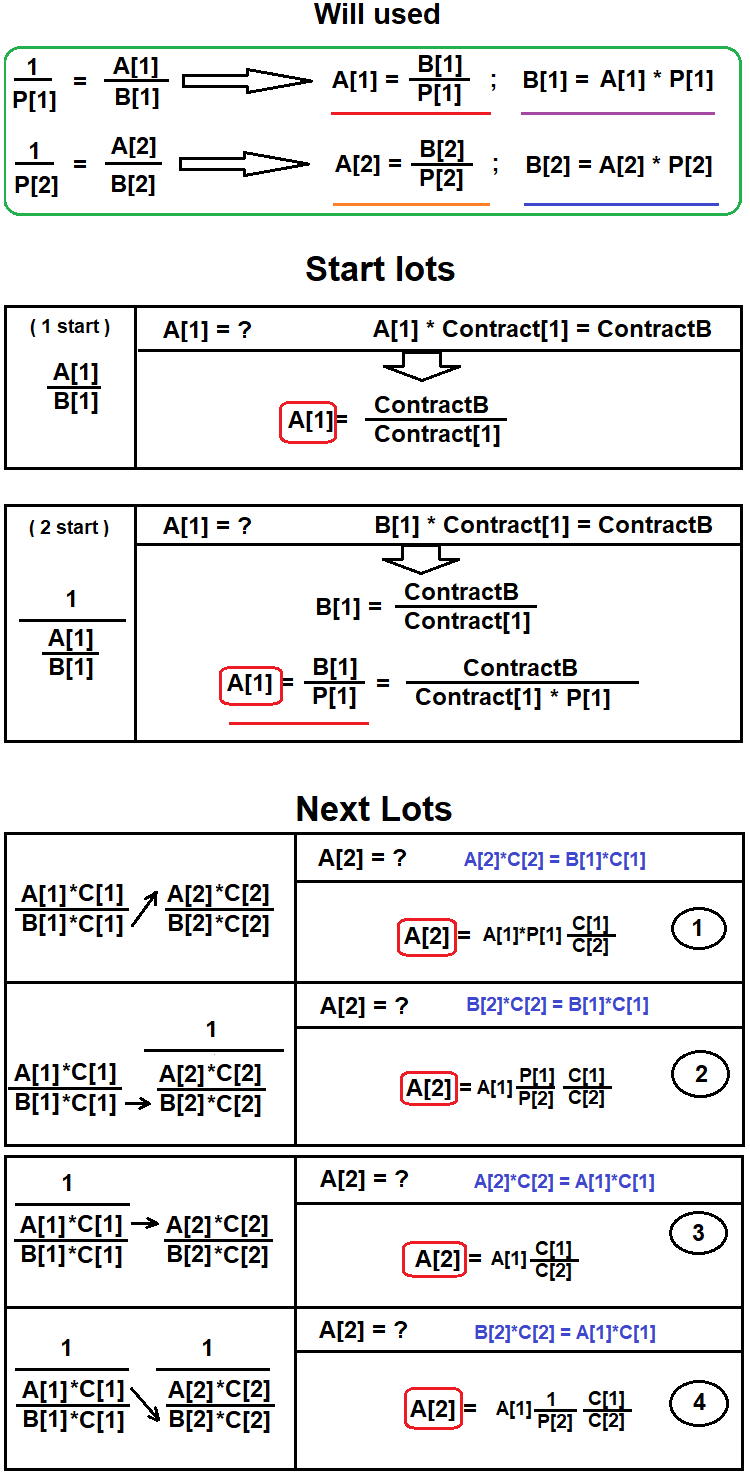
Şimdi bu teknikleri kodda uygulayalım ve sonuçları analiz edelim. İlk prototip çok basit olacaktır, çünkü tek amacı fikirlerin doğruluğunu değerlendirmektir. Umarım yukarıdaki diyagramlar fikrin tüm ayrıntılarını anlamanıza yardımcı olur.
Swap çokgenlerini kullanmak için bir yardımcı program yazma
Piyasa Gözlemini sıralama ve verileri hazırlama:
Bu tekniği kullanmak için, sadece adları tam olarak 6 karakter uzunluğunda olan ve sadece büyük harflerden oluşan çiftleri seçmek gerekir. Sanırım tüm brokerlar bu adlandırma kuralına uyuyor. Bazı brokerlar, dizge verilerle çalışacak şekilde algoritmalar yazarken de dikkate alınması gereken ön ekler veya son ekler ekler. Sembol bilgilerini uygun bir formatta saklamak için iki yapı oluşturdum (ikincisi daha sonra kullanılacaktır):
struct Pair// required symbol information { string Name;// currency pair double SwapBuy;// buy swap double SwapSell;// sell swap double TickValue;// profit from 1 movement tick of a 1-lot position double TickSize;// tick size in the price double PointX;// point size in the price double ContractSize;// contract size in the base deposit currency double Margin;// margin for opening 1 lot }; struct PairAdvanced : Pair// extended container { string Side;// in numerator or denominator double LotK;// lot coefficient double Lot;// lot };
Çiftleri sıralarken bazı alanlar kullanılmayacaktır. Gereksiz depo (container) üretmemek için yapının başka amaçlarla da kullanılabilmesi amacıyla biraz genişlettim. Benzer bir algoritmanın prototipine sahiptim, ancak çok sınırlı yeteneklere sahipti: yalnızca ana terminal penceresinde bulunan çiftleri dikkate alabiliyordu. Şimdi her şey daha basit. Daha da önemlisi, tüm süreç algoritmada otomatikleştirilmiştir. Enstrümanları içeren dizinin büyüklüğünü ayarlamak için aşağıdaki fonksiyona ihtiyaç vardır:
Pair Pairs[];// data of currency pairs void SetSizePairsArray()// set size of the array of pairs { ArrayResize(Pairs,MaxSymbols); ArrayResize(BasicPairsLeft,MaxPairs*2); // since each pair has 2 currencies, there can be a maximum of 2 times more base currencies ArrayResize(BasicPairsRight,MaxPairs*2);// since each pair has 2 currencies, there can be a maximum of 2 times more base currencies }
İlk satır, Piyasa Gözlemi penceresinden kullanabileceğimiz maksimum çift sayısını belirler. Diğer iki satır kullanılacak dizilerin büyüklüğünü belirler. Kalan 2 dizi yardımcı bir rol oynar - bir döviz çiftini 2 parçaya bölmeye izin verirler (2 bileşik para birimi). Sarı renkle vurgulanan değişkenler Uzman Danışmanın girdi parametreleridir.
- MaxSymbols - maksimum çift depolama büyüklüğü (manuel belirtme uyguladım)
- MaxPairs - oluşturduğumuz formülün her iki bölümündeki maksimum çift sayısı (bu sayıdan daha uzun formüller Uzman Danışman tarafından aranmayacaktır)
Bir alım-satım enstrümanının kriterleri karşılayıp karşılamadığını kontrol etmek için (diğer enstrümanlarda potansiyel olarak mevcut olabilecek iki farklı para biriminin işaretleri), aşağıdaki dayanak fonksiyonunu oluşturdum:
bool IsValid(string s)// checking the instrument validity (its name must consist of upper-case letters) { string Mask="abcdefghijklmnopqrstuvwxyz1234567890";// mask of unsupported characters (lowercase letters and numbers) for ( int i=0; i<StringLen(s); i++ )// reset symbols { for ( int j=0; j<StringLen(Mask); j++ ) { if ( s[i] == Mask[j] ) return false; } } return true; }
Bu fonksiyon, enstrümanların gelecekteki kontrolleri için tek koşul değildir. Ancak bu koşul bir mantıksal ifadenin içine yazılamaz, bu nedenle bunu bir dayanak olarak uygulamak daha kolaydır. Şimdi, diziyi gerekli verilerle dolduran ana fonksiyona geçelim:
void FillPairsArray()// fill the array with required information about the instruments { int iterator=0; double correction; int TempSwapMode; for ( int i=0; i<ArraySize(Pairs); i++ )// reset symbols { Pairs[iterator].Name=""; } for ( int i=0; i<SymbolsTotal(false); i++ )// check symbols from the MarketWatch window { TempSwapMode=int(SymbolInfoInteger(Pairs[iterator].Name,SYMBOL_SWAP_MODE)); if ( StringLen(SymbolName(i,false)) == 6+PrefixE+PostfixE && IsValid(SymbolName(i,false)) && SymbolInfoInteger(SymbolName(i,false),SYMBOL_TRADE_MODE) == SYMBOL_TRADE_MODE_FULL && ( ( TempSwapMode == 1 ) || ( ( TempSwapMode == 5 || TempSwapMode == 6 ) && CorrectedValue(Pairs[iterator].Name,correction) )) ) { if ( iterator >= ArraySize(Pairs) ) break; Pairs[iterator].Name=SymbolName(i,false); Pairs[iterator].TickSize=SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_TRADE_TICK_SIZE); Pairs[iterator].PointX=SymbolInfoDouble(Pairs[iterator].Name, SYMBOL_POINT); Pairs[iterator].ContractSize=SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_TRADE_CONTRACT_SIZE); switch(TempSwapMode) { case 1:// in points Pairs[iterator].SwapBuy=SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_SWAP_LONG)*Pairs[iterator].TickValue*(Pairs[iterator].PointX/Pairs[iterator].TickSize); Pairs[iterator].SwapSell=SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_SWAP_SHORT)*Pairs[iterator].TickValue*(Pairs[iterator].PointX/Pairs[iterator].TickSize); break; case 5:// in percent Pairs[iterator].SwapBuy=correction*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_SWAP_LONG)*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_BID)*Pairs[iterator].ContractSize/(360.0*100.0); Pairs[iterator].SwapSell=correction*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_SWAP_SHORT)*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_BID)*Pairs[iterator].ContractSize/(360.0*100.0); break; case 6:// in percent Pairs[iterator].SwapBuy=correction*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_SWAP_LONG)*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_BID)*Pairs[iterator].ContractSize/(360.0*100.0); Pairs[iterator].SwapSell=correction*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_SWAP_SHORT)*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_BID)*Pairs[iterator].ContractSize/(360.0*100.0); break; } Pairs[iterator].Margin=SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_MARGIN_INITIAL); Pairs[iterator].TickValue=SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_TRADE_TICK_VALUE); iterator++; } } }
Bu fonksiyon, tüm sembollerin basit bir şekilde yinelenmesini ve karmaşık bir bileşik koşulla filtrelenmesini sağlar; bu, hem dizge adı uzunluğu gerekliliğine uygunluğu hem de bu sembolün alım-satım olanağını ve ayrıca swap hesaplama yönteminin en yaygın kullanılandan (puan cinsinden) farklı olduğu sembollerle ilgili diğer parametreleri kontrol eder. "switch" bloğunda swap hesaplama yöntemlerinden biri seçilir. Şu anda iki yöntem uygulanmaktadır: puan ve yüzde cinsinden. Gereksiz hesaplamalardan kaçınmak için uygun sıralama öncelikle önemlidir. Ayrıca, lütfen kırmızı ile vurgulanan fonksiyona dikkat edin. Ana para birimi (baz para birimi değil) mevduat para birimiyle eşleşmeyen bir para birimiyle temsil edildiğinde, swapı mevduat para birimine dönüştürmek için belirli bir ayarlama katsayısı eklenmelidir. Bu fonksiyon ilgili değerleri hesaplar. İşte kodu:
bool CorrectedValue(string Pair0,double &rez)// adjustment factor to convert to deposit currency for the percentage swap calculation method { string OurValue=AccountInfoString(ACCOUNT_CURRENCY);// deposit currency string Half2Source=StringSubstr(Pair0,PrefixE+3,3);// lower currency of the pair to be adjusted if ( Half2Source == OurValue ) { rez=1.0; return true; } for ( int i=0; i<SymbolsTotal(false); i++ )// check symbols from the MarketWatch window { if ( StringLen(SymbolName(i,false)) == 6+PrefixE+PostfixE && IsValid(SymbolName(i,false)) )//find the currency rate to convert to the account currency { string Half1=StringSubstr(SymbolName(i,false),PrefixE,3); string Half2=StringSubstr(SymbolName(i,false),PrefixE+3,3); if ( Half2 == OurValue && Half1 == Half2Source ) { rez=SymbolInfoDouble(SymbolName(i,false),SYMBOL_BID); return true; } if ( Half1 == OurValue && Half2 == Half2Source ) { rez=1.0/SymbolInfoDouble(SymbolName(i,false),SYMBOL_BID); return true; } } } return false; }
Bu fonksiyon hem bir dayanak görevi görür hem de dışarıdan referans olarak aktarılan değişkene ayarlama katsayısı değerini geri döndürür. Ayarlama katsayısı, mevduat para birimimizi de içeren istenen para biriminin kuruna göre hesaplanır.
Rastgele oluşturulan formüller
Dizinin gerekli verilerle doldurulduğunu varsayalım. Şimdi, bir şekilde bu semboller üzerinde yineleme yapmamız ve bu çiftlerden oluşturulabilecek tüm olası formül kombinasyonlarını oluşturmaya çalışmamız gerekiyor. Öncelikle formülün hangi formda saklanacağına karar vermek gerekir. Bu formülün tüm öğelerini saklayan yapı, günlüğü görüntüleme ihtiyacı olması durumunda kullanıcılar için çok basit ve net olmalıdır (kesinlikle böyle bir ihtiyaç olacaktır, aksi takdirde hataları tespit etmek imkansız olacaktır).
Formülümüz, "=" işaretinin hem solunda hem de sağında yer alan bir dizi çarpandan oluşmaktadır. Çarpan, 1 veya -1 kuvvetindeki döviz kuru olabilir (bu, ters çevrilmiş bir kesre veya mevcut enstrüman kuruna atıfta bulunulan bir birime eşdeğerdir). Aşağıdaki yapıyı kullanmaya karar verdim:
struct EquationBasic // structure containing the basic formula { string LeftSide;// currency pairs participating in the formula on the left side of the "=" sign string LeftSideStructure;// structure of the left side of the formula string RightSide;// currency pairs participating in the right side of the formula string RightSideStructure;// structure of the right side of the formula };
Tüm veriler dizge biçiminde saklanacaktır. Formül üzerinde çalışmak için, bu dizgeler ihtiyacımız olan tüm gerekli bilgileri çıkarmak üzere ayrıştırılacaktır. Ayrıca, ihtiyaç duyulduğunda yazdırılabilirler. Oluşturulan formüller aşağıdaki biçimde yazdırılacaktır:
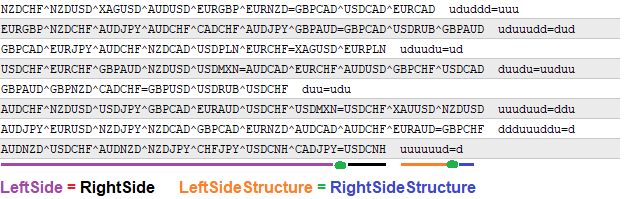
Şahsen benim için böyle bir kayıt kesinlikle net ve okunabilir. "^" karakteri çiftler arasında ayırıcı olarak kullanılır. Çarpanın derecesini gösteren "u" ve "d" karakterlerinden oluştuğu için formül yapısında ayırıcılara gerek yoktur:
- "u" - döviz kuru
- "d" - 1/döviz kuru
Gördüğünüz gibi, ortaya çıkan formüllerde denklemin her iki tarafının değişken uzunluğu ve büyüklüğü vardır, ancak bu büyüklüğün sınırlamaları mevcuttur. Bu yaklaşım, üretilen formüllerin maksimum değişkenliğini sağlar. Bu da, seçilen brokerın işlem koşulları dahilinde bulunan varyantların mümkün olan en yüksek kalitede olmasını sağlar. Brokerlar tamamen farklı koşullar sağlar. Bu formüllerin başarılı bir şekilde oluşturulmasını sağlamak için, gerekli aralıkta sayılar üretebilen ek rastgele fonksiyonlara ihtiyacımız var. Bu amaçla, yerleşik MathRand fonksiyonunun yeteneklerini kullanarak ilgili fonksiyonu oluşturalım:
int GenerateRandomQuantityLeftSide()// generate a random number of pairs on the left side of the formula { int RandomQuantityLeftSide=1+int(MathFloor((double(MathRand())/32767.0)*(MaxPairs-1))); if ( RandomQuantityLeftSide >= MaxPairs ) return MaxPairs-1; return RandomQuantityLeftSide; } int GenerateRandomQuantityRightSide(int LeftLenght)// generate a random number of pairs on the right side of the formula (taking into account the number of pairs on the left side) { int RandomQuantityRightSide=1+int(MathFloor((double(MathRand())/32767.0)*(MaxPairs-LeftLenght))); if ( RandomQuantityRightSide < 2 && LeftLenght == 1 ) return 2;// there must be at least 2 pairs in one of the sides, otherwise it will be equivalent to opening two opposite positions if ( RandomQuantityRightSide > (MaxPairs-LeftLenght) ) return (MaxPairs-LeftLenght); return RandomQuantityRightSide; } int GenerateRandomIndex()// generate a random index of a symbol from the MarketWatch window { int RandomIndex=0; while(true) { RandomIndex=int(MathFloor((double(MathRand())/32767.0) * double(MaxSymbols)) ); if ( RandomIndex >= MaxSymbols ) RandomIndex=MaxSymbols-1; if ( StringLen(Pairs[RandomIndex].Name) > 0 ) return RandomIndex; } return RandomIndex; }
Belirli bir aşamada her üç fonksiyona da ihtiyaç duyulacaktır. Şimdi, bu formülleri oluşturacak fonksiyonu yazabiliriz. Kod gittikçe daha karmaşık hale gelecektir, ancak görev standart olmadığı için nesne yönelimli bir yaklaşım kullanmayacağım. Prosedürel bir yaklaşım kullanmaya karar verdim. Ortaya çıkan prosedürler oldukça büyük ve hantaldır, ancak ekstra işlevsellik yoktur ve kod tekrarını önlemek için her fonksiyon herhangi bir ara fonksiyon kullanmadan belirli bir görevi yerine getirir. Aksi takdirde, görev özellikleri nedeniyle kodun anlaşılması daha da zor olacaktır. Fonksiyon aşağıdaki gibi görünecektir:
EquationBasic GenerateBasicEquation()// generate both parts of the random equation { int RandomQuantityLeft=GenerateRandomQuantityLeftSide(); int RandomQuantityRight=GenerateRandomQuantityRightSide(RandomQuantityLeft); string TempLeft=""; string TempRight=""; string TempLeftStructure=""; string TempRightStructure=""; for ( int i=0; i<RandomQuantityLeft; i++ ) { int RandomIndex=GenerateRandomIndex(); if ( i == 0 && RandomQuantityLeft > 1 ) TempLeft+=Pairs[RandomIndex].Name+"^"; if ( i != 0 && (RandomQuantityLeft-i) > 1 ) TempLeft+=Pairs[RandomIndex].Name+"^"; if ( i == RandomQuantityLeft-1 ) TempLeft+=Pairs[RandomIndex].Name; if ( double(MathRand())/32767.0 > 0.5 ) TempLeftStructure+="u"; else TempLeftStructure+="d"; } for ( int i=RandomQuantityLeft; i<RandomQuantityLeft+RandomQuantityRight; i++ ) { int RandomIndex=GenerateRandomIndex(); if ( i == RandomQuantityLeft && RandomQuantityRight > 1 ) TempRight+=Pairs[RandomIndex].Name+"^"; if ( i != RandomQuantityLeft && (RandomQuantityLeft+RandomQuantityRight-i) > 1 ) TempRight+=Pairs[RandomIndex].Name+"^"; if ( i == RandomQuantityLeft+RandomQuantityRight-1 ) TempRight+=Pairs[RandomIndex].Name; if ( double(MathRand())/32767.0 > 0.5 ) TempRightStructure+="u"; else TempRightStructure+="d"; } EquationBasic result; result.LeftSide=TempLeft; result.LeftSideStructure=TempLeftStructure; result.RightSide=TempRight; result.RightSideStructure=TempRightStructure; return result; }
Gördüğünüz gibi, daha önce ele alınan üç fonksiyon da burada rastgele bir formül oluşturmak için kullanılmaktadır. Bu fonksiyonlar kodun başka hiçbir yerinde kullanılmaz. Formül hazır olur olmaz, bu formülün adım adım analizine geçebiliriz. Tüm yanlış formüller bir sonraki son derece önemli karmaşık filtre tarafından atılacaktır. Her şeyden önce, eşitliği kontrol ederiz. Parçalar eşit değilse, bu formül yanlıştır. Uyumlu tüm formüller bir sonraki analiz adımına geçer.
Formül dengeleme
Bu adım aynı anda birkaç analiz kriterini gerçekleştirir:
- Pay ve paydadaki tüm ekstra çarpanların sayılması ve çıkarılması
- Payda 1 para birimi ve paydada 1 para birimi olup olmadığının kontrol edilmesi
- Elde edilen kesirlerin sol ve sağ taraftaki karşılıklarının kontrol edilmesi
- Eğer sağ taraf sol tarafın tersi ise, formülün sağ yapısını basitçe tersine çeviririz (bu, "-1" kuvvetine yükseltmeye benzer)
- Tüm aşamalar başarıyla tamamlanırsa, sonuç yeni bir değişkene yazılır
Bu adımlar kodda bu şekilde görünür:
BasicValue BasicPairsLeft[];// array of base pairs to the left BasicValue BasicPairsRight[];// array of base pairs to the right bool bBalanced(EquationBasic &CheckedPair,EquationCorrected &r)// if the current formula is balanced (if yes, return the corrected version to the "r" variable) { bool bEnd=false; string SubPair;// the full name of the currency pair string Half1;// the first currency of the pair string Half2;// the second currency of the pair string SubSide;// the currency pair in the numerator or denominator string Divider;// separator int ReadStartIterator=0;// reading start index int quantityiterator=0;// quantity bool bNew; BasicValue b0; for ( int i=0; i<ArraySize(BasicPairsLeft); i++ )//reset the array of base pairs { BasicPairsLeft[i].Value = ""; BasicPairsLeft[i].Quantity = 0; } for ( int i=0; i<ArraySize(BasicPairsRight); i++ )// resetting the array of base pairs { BasicPairsRight[i].Value = ""; BasicPairsRight[i].Quantity = 0; } //// Calculate balance values for the left side quantityiterator=0; ReadStartIterator=0; for ( int i=ReadStartIterator; i<StringLen(CheckedPair.LeftSide); i++ )// extract base currencies from the left side of the equation { Divider=StringSubstr(CheckedPair.LeftSide,i,1); if ( Divider == "^" || i == StringLen(CheckedPair.LeftSide) - 1 ) { SubPair=StringSubstr(CheckedPair.LeftSide,ReadStartIterator+PrefixE,6); SubSide=StringSubstr(CheckedPair.LeftSideStructure,quantityiterator,1); Half1=StringSubstr(CheckedPair.LeftSide,ReadStartIterator+PrefixE,3); Half2=StringSubstr(CheckedPair.LeftSide,ReadStartIterator+PrefixE+3,3); bNew=true; for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it { if ( BasicPairsLeft[j].Value == Half1 ) { if ( SubSide == "u" ) BasicPairsLeft[j].Quantity++; if ( SubSide == "d" ) BasicPairsLeft[j].Quantity--; bNew = false; break; } } if ( bNew ) { for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it { if ( StringLen(BasicPairsLeft[j].Value) == 0 ) { if ( SubSide == "u" ) BasicPairsLeft[j].Quantity++; if ( SubSide == "d" ) BasicPairsLeft[j].Quantity--; BasicPairsLeft[j].Value=Half1; break; } } } bNew=true; for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it { if ( BasicPairsLeft[j].Value == Half2 ) { if ( SubSide == "u" ) BasicPairsLeft[j].Quantity--; if ( SubSide == "d" ) BasicPairsLeft[j].Quantity++; bNew = false; break; } } if ( bNew ) { for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it { if ( StringLen(BasicPairsLeft[j].Value) == 0 ) { if ( SubSide == "u" ) BasicPairsLeft[j].Quantity--; if ( SubSide == "d" ) BasicPairsLeft[j].Quantity++; BasicPairsLeft[j].Value=Half2; break; } } } ReadStartIterator=i+1; quantityiterator++; } } /// end of left-side balance calculation //// Calculate balance values for the right side quantityiterator=0; ReadStartIterator=0; for ( int i=ReadStartIterator; i<StringLen(CheckedPair.RightSide); i++ )// extract base currencies from the right side of the equation { Divider=StringSubstr(CheckedPair.RightSide,i,1); if ( Divider == "^"|| i == StringLen(CheckedPair.RightSide) - 1 ) { SubPair=StringSubstr(CheckedPair.RightSide,ReadStartIterator+PrefixE,6); SubSide=StringSubstr(CheckedPair.RightSideStructure,quantityiterator,1); Half1=StringSubstr(CheckedPair.RightSide,ReadStartIterator+PrefixE,3); Half2=StringSubstr(CheckedPair.RightSide,ReadStartIterator+PrefixE+3,3); bNew=true; for ( int j=0; j<ArraySize(BasicPairsRight); j++ )// if the currency is not found in the list, add it { if ( BasicPairsRight[j].Value == Half1 ) { if ( SubSide == "u" ) BasicPairsRight[j].Quantity++; if ( SubSide == "d" ) BasicPairsRight[j].Quantity--; bNew = false; break; } } if ( bNew ) { for ( int j=0; j<ArraySize(BasicPairsRight); j++ )// if the currency is not found in the list, add it { if ( StringLen(BasicPairsRight[j].Value) == 0 ) { if ( SubSide == "u" ) BasicPairsRight[j].Quantity++; if ( SubSide == "d" ) BasicPairsRight[j].Quantity--; BasicPairsRight[j].Value=Half1; break; } } } bNew=true; for ( int j=0; j<ArraySize(BasicPairsRight); j++ )// if the currency is not found in the list, add it { if ( BasicPairsRight[j].Value == Half2 ) { if ( SubSide == "u" ) BasicPairsRight[j].Quantity--; if ( SubSide == "d" ) BasicPairsRight[j].Quantity++; bNew = false; break; } } if ( bNew ) { for ( int j=0; j<ArraySize(BasicPairsRight); j++ )// if the currency is not found in the list, add it { if ( StringLen(BasicPairsRight[j].Value) == 0 ) { if ( SubSide == "u" ) BasicPairsRight[j].Quantity--; if ( SubSide == "d" ) BasicPairsRight[j].Quantity++; BasicPairsRight[j].Value=Half2; break; } } } ReadStartIterator=i+1; quantityiterator++; } } /// end of right-side balance calculation /// calculate the number of lower and upper currencies based on the received data from the previous block int LeftUpTotal=0;// the number of upper elements in the left part int LeftDownTotal=0;// the number of lower elements in the left part int RightUpTotal=0;// the number of upper elements in the right part int RightDownTotal=0;// the number of lower elements in the right part string LastUpLeft; string LastDownLeft; string LastUpRight; string LastDownRight; for ( int i=0; i<ArraySize(BasicPairsLeft); i++ ) { if ( BasicPairsLeft[i].Quantity > 0 && StringLen(BasicPairsLeft[i].Value) > 0 ) LeftUpTotal+=BasicPairsLeft[i].Quantity; if ( BasicPairsLeft[i].Quantity < 0 && StringLen(BasicPairsLeft[i].Value) > 0 ) LeftDownTotal-=BasicPairsLeft[i].Quantity; } for ( int i=0; i<ArraySize(BasicPairsRight); i++ ) { if ( BasicPairsRight[i].Quantity > 0 && StringLen(BasicPairsRight[i].Value) > 0 ) RightUpTotal+=BasicPairsRight[i].Quantity; if ( BasicPairsRight[i].Quantity < 0 && StringLen(BasicPairsRight[i].Value) > 0 ) RightDownTotal-=BasicPairsRight[i].Quantity; } /// /// check if both sides are equal if ( LeftUpTotal == 1 && LeftDownTotal == 1 && RightUpTotal == 1 && RightDownTotal == 1 )// there must be one pair in the upper and in the lower part of both sides of the equality, otherwise the formula is invalid { for ( int i=0; i<ArraySize(BasicPairsLeft); i++ ) { if ( BasicPairsLeft[i].Quantity == 1 && StringLen(BasicPairsLeft[i].Value) > 0 ) LastUpLeft=BasicPairsLeft[i].Value; if ( BasicPairsLeft[i].Quantity == -1 && StringLen(BasicPairsLeft[i].Value) > 0 ) LastDownLeft=BasicPairsLeft[i].Value; } for ( int i=0; i<ArraySize(BasicPairsRight); i++ ) { if ( BasicPairsRight[i].Quantity == 1 && StringLen(BasicPairsRight[i].Value) > 0 ) LastUpRight=BasicPairsRight[i].Value; if ( BasicPairsRight[i].Quantity == -1 && StringLen(BasicPairsRight[i].Value) > 0 ) LastDownRight=BasicPairsRight[i].Value; } } else return false; if ( (LastUpLeft == LastUpRight && LastDownLeft == LastDownRight) || (LastUpLeft == LastDownRight && LastDownLeft == LastUpRight) ) { if ( LastUpLeft == LastDownRight && LastDownLeft == LastUpRight )// If the formula is cross-equivalent, then invert the structure of the right part of the equation (it is the same as raising to the power of -1) { string NewStructure;// the new structure that will be built from the previous one for ( int i=0; i<StringLen(CheckedPair.RightSideStructure); i++ ) { if ( CheckedPair.RightSideStructure[i] == 'u' ) NewStructure+="d"; if ( CheckedPair.RightSideStructure[i] == 'd' ) NewStructure+="u"; } CheckedPair.RightSideStructure=NewStructure; } } else return false;// if the resulting fractions on both sides are not equivalent, then the formula is invalid if ( LastUpLeft == LastDownLeft ) return false;// if result in one, then the formula is invalid /// Now it is necessary to write all the above into a corrected and more convenient structure string TempResult=CorrectedResultInstrument(LastUpLeft+LastDownLeft,r.IsResultInstrument); if ( r.IsResultInstrument && LastUpLeft+LastDownLeft != TempResult ) { string NewStructure="";// the new structure that will be built from the previous one for ( int i=0; i<StringLen(CheckedPair.RightSideStructure); i++ ) { if ( CheckedPair.RightSideStructure[i] == 'u' ) NewStructure+="d"; if ( CheckedPair.RightSideStructure[i] == 'd' ) NewStructure+="u"; } CheckedPair.RightSideStructure=NewStructure; NewStructure="";// the new structure that will be built from the previous one for ( int i=0; i<StringLen(CheckedPair.LeftSideStructure); i++ ) { if ( CheckedPair.LeftSideStructure[i] == 'u' ) NewStructure+="d"; if ( CheckedPair.LeftSideStructure[i] == 'd' ) NewStructure+="u"; } CheckedPair.LeftSideStructure=NewStructure; r.ResultInstrument=LastDownLeft+LastUpLeft; r.UpPair=LastDownLeft; r.DownPair=LastUpLeft; } else { r.ResultInstrument=LastUpLeft+LastDownLeft; r.UpPair=LastUpLeft; r.DownPair=LastDownLeft; } r.LeftSide=CheckedPair.LeftSide; r.RightSide=CheckedPair.RightSide; r.LeftSideStructure=CheckedPair.LeftSideStructure; r.RightSideStructure=CheckedPair.RightSideStructure; /// /// if code has reached this point, it is considered that we have found the formula meeting the criteria, and the next step is normalization return true; }
Yeşil renkle vurgulanan fonksiyon, sembol listesinin formülün indirgendiği sembolü içerip içermediğini belirlemek için gereklidir. Formülün, örneğin "USDJPY" değil, "JPYUSD" olarak indirgendiği ortaya çıkabilir. Oluşturulabilse bile böyle bir sembolün var olmadığı açıktır. Ancak bizim görevimiz formülü doğru bir alım-satım enstrümanı üretecek şekilde değiştirmektir. Bu durumda, formülün her iki kısmı da -1 kuvvetine yükseltilmelidir, bu da formülün yapısını tersine çevirmeye eşdeğerdir ("d"yi "u" olarak değiştirme veya tersini yapma). Piyasa Gözlemi penceresinde böyle bir sembol yoksa, olduğu gibi bırakırız:
string CorrectedResultInstrument(string instrument, bool &bResult)// if any equivalent symbol corresponds to the generated formula, return this symbol (or leave as is) { string Half1=""; string Half2=""; string Half1input=StringSubstr(instrument,0,3);//input upper currency string Half2input=StringSubstr(instrument,3,3);//input lower currency bResult=false; for ( int j=0; j<ArraySize(Pairs); j++ ) { Half1=StringSubstr(Pairs[j].Name,PrefixE,3); Half2=StringSubstr(Pairs[j].Name,PrefixE+3,3); if ( (Half1==Half1input && Half2==Half2input) || (Half1==Half2input && Half2==Half1input) )// direct match or crossed match { bResult=true; return Pairs[j].Name; } } return instrument; }
Filtreden geçen formülleri saklamak için aşağıdaki yapıyı hazırladım. Yapı, bir öncekinden bazı alanlara ve bazı yeni alanlara sahiptir:
struct EquationCorrected // corrected structure of the basic formula { string LeftSide;// currency pairs participating in the formula on the left side of the "=" sign string LeftSideStructure;// structure of the left side of the formula string RightSide;// currency pairs participating in the right side of the formula string RightSideStructure;// structure of the right side of the formula string ResultInstrument;// the resulting instrument to which both parts of the formula come after transformation bool IsResultInstrument;// has the suitable equivalent symbol been found string UpPair;// the upper currency of the resulting instrument string DownPair;// the lower currency of the resulting instrument };
Formülleri normalleştirme
Bu prosedür, sonuçları filtrelemenin bir sonraki adımıdır. Birbirini takip eden aşağıdaki sıralı işlemlerden oluşur:
- Eşitliğin her iki tarafından elde edilen sonuç sembolüne dayanarak, eşitliğin her iki tarafı için listeden bir başlangıç çifti seçeriz
- Her iki çift de, denklemdeki kuvvetlerine göre, kesir payında baz para birimini sağlamalıdır
- Böyle bir çift bulunduğunda ve kesrin alt para birimi, sonuç enstrümanının baz para birimini içermiyorsa, devam ederiz
- Bir sonraki çiftin üst para birimi bir öncekinin alt para birimini karşılayacak şekilde ilerleriz
- İstenen sonuç çifti bulunana kadar bu adımları tekrarlarız
- Sonuç çifti bulunduğunda, formülün kullanılmayan tüm bileşenleri atılır (çarpımları bir olduğu için)
- Bu sürece paralel olarak, "lot çarpanları" çiftten çifte sırayla hesaplanır (sonuç enstrümanımızı sağlaması amacıyla belirli çiftler için hangi lotta pozisyon açmamız gerektiğini gösterirler)
- Sonuç, bir sonraki analiz aşamasında kullanılacak olan yeni bir değişkene yazılır
Fonksiyon kodu aşağıdaki gibidir:
bool bNormalized(EquationCorrected &d,EquationNormalized &v)// formula normalization attempt (the normalized formula is returned in "v" ) { double PreviousContract;// previous contract bool bWasPairs;// if any pairs have been found double BaseContract;// contract of the pair to which the equation is reduced double PreviousLotK=0.0;// previous LotK double LotK;// current LotK string PreviousSubSide;// in numerator or denominator (previous factor) string PreviousPair;// previous pair string PreviousHalf1;// upper currency of the previous pair string PreviousHalf2;// lower currency of the previous pair string SubPair;// the full name of the currency pair string Half1;// the first currency of the pair string Half2;// the second currency of the pair string SubSide;// the currency pair in the numerator or denominator string Divider;// separator int ReadStartIterator=0;// reading start index int quantityiterator=0;// quantity int tryiterator=0;// the number of balancing attempts int quantityleft=0;// the number of pairs on the left after normalization int quantityright=0;//the number of pairs on the right after normalization bool bNew; BasicValue b0; for ( int i=0; i<ArraySize(BasicPairsLeft); i++ )//reset the array of base pairs { BasicPairsLeft[i].Value = ""; BasicPairsLeft[i].Quantity = 0; } for ( int i=0; i<ArraySize(BasicPairsRight); i++ )// resetting the array of base pairs { BasicPairsRight[i].Value = ""; BasicPairsRight[i].Quantity = 0; } if ( d.IsResultInstrument ) BaseContract=SymbolInfoDouble(d.ResultInstrument, SYMBOL_TRADE_CONTRACT_SIZE);// define the contract of the equivalent pair based on the instrument else BaseContract=100000.0; //// Calculate the number of pairs for the left side tryiterator=0; ReadStartIterator=0; for ( int i=ReadStartIterator; i<StringLen(d.LeftSide); i++ )// extract base currencies from the left side of the equation { Divider=StringSubstr(d.LeftSide,i,1); if ( Divider == "^" ) { ReadStartIterator=i+1; tryiterator++; } if ( i == StringLen(d.LeftSide) - 1 ) { ReadStartIterator=i+1; tryiterator++; } } /// end of quantity calculation for the left part ArrayResize(v.PairLeft,tryiterator); /// calculate the lot coefficients for the left side bool bBalanced=false;// is the formula balanced bool bUsed[]; ArrayResize(bUsed,tryiterator); ArrayFill(bUsed,0,tryiterator,false); int balancediterator=0; PreviousHalf1=""; PreviousHalf2=""; PreviousLotK=0.0; PreviousSubSide=""; PreviousPair=""; PreviousContract=0.0; bWasPairs=false;// have there been pairs for ( int k=0; k<tryiterator; k++ )// try to normalize the left side { if( !bBalanced ) { quantityiterator=0; ReadStartIterator=0; for ( int i=ReadStartIterator; i<StringLen(d.LeftSide); i++ )// extract base currencies from the left side of the equation { Divider=StringSubstr(d.LeftSide,i,1); if ( Divider == "^" || i == StringLen(d.LeftSide) - 1 ) { SubPair=StringSubstr(d.LeftSide,ReadStartIterator+PrefixE,6); SubSide=StringSubstr(d.LeftSideStructure,quantityiterator,1); Half1=StringSubstr(d.LeftSide,ReadStartIterator+PrefixE,3); Half2=StringSubstr(d.LeftSide,ReadStartIterator+PrefixE+3,3); if ( ! bUsed[quantityiterator] && (( PreviousHalf1 == "" && ((Half1 == d.UpPair && SubSide == "u") || (Half2 == d.UpPair && SubSide == "d")) ) // if it is the first pair in the list || ( (( PreviousHalf2 == Half1 && PreviousSubSide == "u" ) || ( PreviousHalf1 == Half1 && PreviousSubSide == "d" )) && SubSide == "u" ) // if the current pair is in the numerator || ( (( PreviousHalf2 == Half2 && PreviousSubSide == "u" ) || ( PreviousHalf1 == Half2 && PreviousSubSide == "d" )) && SubSide == "d" )) )// if the current pair is in the denominator {// find the entry point(pair) of the chain if( PreviousHalf1 == "" )// define the lot coefficient of the first pair { if ( SubSide == "u" ) { LotK=BaseContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE);// (1 start) v.PairLeft[balancediterator].LotK=LotK; PreviousLotK=LotK; bWasPairs=true; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } if ( SubSide == "d" ) { double Pt=SymbolInfoDouble(SubPair,SYMBOL_BID); if ( Pt == 0.0 ) return false; LotK=(BaseContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE))/Pt;// (2 start) v.PairLeft[balancediterator].LotK=LotK; PreviousLotK=LotK; bWasPairs=true; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } } else { if( PreviousSubSide == "u" )// define the lot coefficient of further pairs { if ( SubSide == "u" ) { double Pp=SymbolInfoDouble(PreviousPair,SYMBOL_BID); if ( Pp == 0.0 ) return false; if ( PreviousContract <= 0.0 ) return false; LotK=PreviousLotK*Pp*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// ( 1 ) v.PairLeft[balancediterator].LotK=LotK; PreviousLotK=LotK; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } if ( SubSide == "d" ) { double Pt=SymbolInfoDouble(SubPair,SYMBOL_BID); double Pp=SymbolInfoDouble(PreviousPair,SYMBOL_BID); if ( Pt == 0.0 ) return false; if ( Pp == 0.0 ) return false; if ( PreviousContract <= 0.0 ) return false; LotK=PreviousLotK*(Pp/Pt)*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// ( 2 ) v.PairLeft[balancediterator].LotK=LotK; PreviousLotK=LotK; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } } if( PreviousSubSide == "d" )// define the lot coefficient of further pairs { if ( SubSide == "u" ) { if ( PreviousContract <= 0.0 ) return false; LotK=PreviousLotK*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// ( 3 ) v.PairLeft[balancediterator].LotK=LotK; PreviousLotK=LotK; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } if ( SubSide == "d" ) { double Pt=SymbolInfoDouble(SubPair,SYMBOL_BID); if ( Pt == 0.0 ) return false; if ( PreviousContract <= 0.0 ) return false; LotK=(PreviousLotK/Pt)*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// ( 4 ) v.PairLeft[balancediterator].LotK=LotK; PreviousLotK=LotK; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } } } bNew=true; for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it { if ( BasicPairsLeft[j].Value == Half1 ) { if ( SubSide == "u" ) BasicPairsLeft[j].Quantity++; if ( SubSide == "d" ) BasicPairsLeft[j].Quantity--; bNew = false; break; } } if ( bNew ) { for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it { if ( StringLen(BasicPairsLeft[j].Value) == 0 ) { if ( SubSide == "u" ) BasicPairsLeft[j].Quantity++; if ( SubSide == "d" ) BasicPairsLeft[j].Quantity--; BasicPairsLeft[j].Value=Half1; break; } } } bNew=true; for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it { if ( BasicPairsLeft[j].Value == Half2 ) { if ( SubSide == "u" ) BasicPairsLeft[j].Quantity--; if ( SubSide == "d" ) BasicPairsLeft[j].Quantity++; bNew = false; break; } } if ( bNew ) { for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it { if ( StringLen(BasicPairsLeft[j].Value) == 0 ) { if ( SubSide == "u" ) BasicPairsLeft[j].Quantity--; if ( SubSide == "d" ) BasicPairsLeft[j].Quantity++; BasicPairsLeft[j].Value=Half2; break; } } } v.PairLeft[balancediterator].Name=SubPair; v.PairLeft[balancediterator].Side=SubSide; v.PairLeft[balancediterator].ContractSize=SymbolInfoDouble(v.PairLeft[balancediterator].Name, SYMBOL_TRADE_CONTRACT_SIZE); balancediterator++; PreviousHalf1=Half1; PreviousHalf2=Half2; PreviousSubSide=SubSide; PreviousPair=SubPair; quantityleft++; if ( SubSide == "u" && Half2 == d.DownPair )// if the fraction is not inverted { bBalanced=true;// if the missing part is in the denominator, then we have balanced the formula break;// since the formula is balanced, we don't need the rest } if ( SubSide == "d" && Half1 == d.DownPair )// if the fraction is inverted { bBalanced=true;// if the missing part is in the numerator, then we have balanced the formula break;// since the formula is balanced, we don't need the rest } int LeftUpTotal=0;// the number of upper elements in the left part int LeftDownTotal=0;// the number of lower elements in the left part string LastUpLeft; string LastDownLeft; for ( int z=0; z<ArraySize(BasicPairsLeft); z++ ) { if ( BasicPairsLeft[z].Quantity > 0 && StringLen(BasicPairsLeft[z].Value) > 0 ) LeftUpTotal+=BasicPairsLeft[z].Quantity; if ( BasicPairsLeft[z].Quantity < 0 && StringLen(BasicPairsLeft[z].Value) > 0 ) LeftDownTotal-=BasicPairsLeft[z].Quantity; } if ( bWasPairs && LeftUpTotal == 0 && LeftDownTotal == 0 ) return false; } ReadStartIterator=i+1; bUsed[quantityiterator]=true; quantityiterator++; } } } else break; } /// end of coefficient calculation for the left part if ( !bBalanced ) return false;// if the left side is not balanced, then there is no point in balancing the right side //// Calculate the number of pairs for the right side tryiterator=0; ReadStartIterator=0; for ( int i=ReadStartIterator; i<StringLen(d.RightSide); i++ )// extract base currencies from the right side of the equation { Divider=StringSubstr(d.RightSide,i,1); if ( Divider == "^" ) { ReadStartIterator=i+1; tryiterator++; } if ( i == StringLen(d.RightSide) - 1 ) { ReadStartIterator=i+1; tryiterator++; } } ArrayResize(v.PairRight,tryiterator); /// end of calculation of the number of pairs for the right side bBalanced=false;// is the formula balanced ArrayResize(bUsed,tryiterator); ArrayFill(bUsed,0,tryiterator,false); balancediterator=0; PreviousHalf1=""; PreviousHalf2=""; PreviousLotK=0.0; PreviousSubSide=""; PreviousPair=""; PreviousContract=0.0; bWasPairs=false; for ( int k=0; k<tryiterator; k++ )// try to normalize the right side { if ( !bBalanced ) { quantityiterator=0; ReadStartIterator=0; for ( int i=ReadStartIterator; i<StringLen(d.RightSide); i++ )// extract base currencies from the right side of the equation { Divider=StringSubstr(d.RightSide,i,1); if ( Divider == "^" || i == StringLen(d.RightSide) - 1 ) { SubPair=StringSubstr(d.RightSide,ReadStartIterator+PrefixE,6); SubSide=StringSubstr(d.RightSideStructure,quantityiterator,1); Half1=StringSubstr(d.RightSide,ReadStartIterator+PrefixE,3); Half2=StringSubstr(d.RightSide,ReadStartIterator+PrefixE+3,3); if ( ! bUsed[quantityiterator] && (( PreviousHalf1 == "" && ((Half1 == d.UpPair && SubSide == "u") || (Half2 == d.UpPair && SubSide == "d")) ) // if it is the first pair in the list || ( (( PreviousHalf2 == Half1 && PreviousSubSide == "u" ) || ( PreviousHalf1 == Half1 && PreviousSubSide == "d" )) && SubSide == "u" ) // if the current pair is in the numerator || ( (( PreviousHalf2 == Half2 && PreviousSubSide == "u" ) || ( PreviousHalf1 == Half2 && PreviousSubSide == "d" )) && SubSide == "d" )) )// if the current pair is in the denominator {// find the entry point(pair) of the chain if( PreviousHalf1 == "" )// define the lot coefficient of the first pair { if ( SubSide == "u" ) { LotK=BaseContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE);// (1 start) v.PairRight[balancediterator].LotK=LotK; PreviousLotK=LotK; bWasPairs=true; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } if ( SubSide == "d" ) { double Pt=SymbolInfoDouble(SubPair,SYMBOL_BID); if ( Pt == 0.0 ) return false; LotK=(BaseContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE))/Pt;// (2 start) v.PairRight[balancediterator].LotK=LotK; PreviousLotK=LotK; bWasPairs=true; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } } else { if( PreviousSubSide == "u" )// define the lot coefficient of further pairs { if ( SubSide == "u" ) { double Pp=SymbolInfoDouble(PreviousPair,SYMBOL_BID); if ( Pp == 0.0 ) return false; if ( PreviousContract <= 0.0 ) return false; LotK=PreviousLotK*Pp*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// (1) v.PairRight[balancediterator].LotK=LotK; PreviousLotK=LotK; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } if ( SubSide == "d" ) { double Pt=SymbolInfoDouble(SubPair,SYMBOL_BID); double Pp=SymbolInfoDouble(PreviousPair,SYMBOL_BID); if ( Pt == 0.0 ) return false; if ( Pp == 0.0 ) return false; if ( PreviousContract <= 0.0 ) return false; LotK=PreviousLotK*(Pp/Pt)*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// (2) v.PairRight[balancediterator].LotK=LotK; PreviousLotK=LotK; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } } if( PreviousSubSide == "d" )// define the lot coefficient of further pairs { if ( SubSide == "u" ) { if ( PreviousContract <= 0.0 ) return false; LotK=PreviousLotK*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// (3) v.PairRight[balancediterator].LotK=LotK; PreviousLotK=LotK; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } if ( SubSide == "d" ) { double Pt=SymbolInfoDouble(SubPair,SYMBOL_BID); if ( Pt == 0.0 ) return false; if ( PreviousContract <= 0.0 ) return false; LotK=(PreviousLotK/Pt)*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// (4) v.PairRight[balancediterator].LotK=LotK; PreviousLotK=LotK; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } } } bNew=true; for ( int j=0; j<ArraySize(BasicPairsRight); j++ )// if the currency is not found in the list, add it { if ( BasicPairsRight[j].Value == Half1 ) { if ( SubSide == "u" ) BasicPairsRight[j].Quantity++; if ( SubSide == "d" ) BasicPairsRight[j].Quantity--; bNew = false; break; } } if ( bNew ) { for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it { if ( StringLen(BasicPairsLeft[j].Value) == 0 ) { if ( SubSide == "u" ) BasicPairsRight[j].Quantity++; if ( SubSide == "d" ) BasicPairsRight[j].Quantity--; BasicPairsRight[j].Value=Half1; break; } } } bNew=true; for ( int j=0; j<ArraySize(BasicPairsRight); j++ )// if the currency is not found in the list, add it { if ( BasicPairsRight[j].Value == Half2 ) { if ( SubSide == "u" ) BasicPairsRight[j].Quantity--; if ( SubSide == "d" ) BasicPairsRight[j].Quantity++; bNew = false; break; } } if ( bNew ) { for ( int j=0; j<ArraySize(BasicPairsRight); j++ )// if the currency is not found in the list, add it { if ( StringLen(BasicPairsRight[j].Value) == 0 ) { if ( SubSide == "u" ) BasicPairsRight[j].Quantity--; if ( SubSide == "d" ) BasicPairsRight[j].Quantity++; BasicPairsRight[j].Value=Half2; break; } } } v.PairRight[balancediterator].Name=SubPair; v.PairRight[balancediterator].Side=SubSide; v.PairRight[balancediterator].ContractSize=SymbolInfoDouble(v.PairRight[balancediterator].Name, SYMBOL_TRADE_CONTRACT_SIZE); balancediterator++; PreviousHalf1=Half1; PreviousHalf2=Half2; PreviousSubSide=SubSide; PreviousPair=SubPair; quantityright++; if ( SubSide == "u" && Half2 == d.DownPair )// if the fraction is not inverted { bBalanced=true;// if the missing part is in the denominator, then we have balanced the formula break;// since the formula is balanced, we don't need the rest } if ( SubSide == "d" && Half1 == d.DownPair )// if the fraction is inverted { bBalanced=true;// if the missing part is in the numerator, then we have balanced the formula break;// since the formula is balanced, we don't need the rest } int RightUpTotal=0;// the number of upper elements in the right part int RightDownTotal=0;// the number of lower elements in the right part string LastUpRight; string LastDownRight; for ( int z=0; z<ArraySize(BasicPairsRight); z++ ) { if ( BasicPairsRight[z].Quantity > 0 && StringLen(BasicPairsRight[z].Value) > 0 ) RightUpTotal+=BasicPairsRight[z].Quantity; if ( BasicPairsRight[z].Quantity < 0 && StringLen(BasicPairsRight[z].Value) > 0 ) RightDownTotal-=BasicPairsRight[z].Quantity; } if ( bWasPairs && RightUpTotal == 0 && RightDownTotal == 0 ) return false; } ReadStartIterator=i+1; bUsed[quantityiterator]=true; quantityiterator++; } } } else break; } if ( quantityleft == 1 && quantityright == 1 ) return false;// if the equation has been normalized to only 2 pairs, it is not valid (at least 3 pairs are required) return bBalanced; }
Bu çok sağlıklı ve karmaşık bir prosedürdür, ancak bana öyle geliyor ki bu tür uygulamalarda ara durumlar üretmemek daha iyidir, çünkü bu önemli bir kod tekrarına yol açacaktır. Ayrıca, tüm aşamalar çok kompakttır ve mantıksal olarak bloklara ayrılmıştır. Bu fonksiyonlar kümesi bize, tüm dönüşümleri el yazısıyla gerçekleştirerek elde edebileceğimiz sonuçlarla karşılaştırılabilir tamamen aynı sonuçları verir. Burada, tüm bu matematiksel manipülasyonlar bir dizi karmaşık ama gerekli yöntemle gerçekleştirilir.
Bulunan formülün ne kadar kârlı olduğunu anlamak için özel bir analiz yapmamız gerekiyor. Her çift için hem yukarı hem de aşağı pozisyon açmanın mümkün olduğunu unutmayın. Buna göre, her formül için iki ara devre varyantı olabilir - doğrudan ve ters. Daha yüksek kârlılığa sahip olan sonuç olarak kabul edilecektir.
Kârlılığı değerlendirmek için, swaplardan kaynaklanan kâr ve zararlardan oluşan kâr faktörüne benzer bir metrik oluşturdum. Mevcut devrenin tahakkuk eden pozitif swapı mutlak negatif swaptan daha büyükse, böyle bir devre kârlı kabul edilir. Diğer durumlarda devre kârlı olmayacaktır - başka bir deyişle, devremizin swap faktörü yalnızca birden büyük olduğunda pozitif olacaktır.
Geri döndürülen sonuç, gelecekte alım-satım ve alım-satım mantığının geliştirilmesi için kendi kendine yeterli bir komut paketi olarak oluşturulan tamamen farklı bir depoya yazılır. Tüm devreyi hızlı ve kolay bir şekilde açmak için gereken her şeyi içerir:
struct EquationNormalized // the final structure with the formula in normalized form { Pair PairLeft[];// currency pairs on the left side Pair PairRight[];// currency pairs on the right side double SwapPlusRelative;// relative equivalent of the positive swap double SwapMinusRelative;// relative equivalent of the negative swap double SwapFactor;// resulting swap factor };
Ayrıca içerikle ilgili bilgilerin kolayca görüntülenmesini sağlayan iki yöntem ekledim, ancak bunlar bu makaleyle ilgili değildir ve bu nedenle burada sunmayacağım. Bunları ekteki kaynak kodunda görüntüleyebilirsiniz. Artık denklemin her bir bileşeni hakkındaki bilgiler, dizilerin öğeleri olarak ayrı ayrı yer almaktadır. Bu, daha sonra sürekli olarak dizgelerden ayrıştırmaya gerek kalmadan verilerle daha kolay çalışılmasını sağlar. Belki bu çözüm en başından itibaren kullanılabilirdi, ancak bu okunabilirliği bozardı.
Swap faktörünün hesaplanması ve denklem yapısının son ayarlaması
Bu, bu sistemin en önemli değişkeninin hesaplandığı son aşamadır - varyantlar bu değere göre karşılaştırılacaktır. En yüksek değere sahip olan en iyisidir.
void CalculateBestVariation(EquationNormalized &ii)// calculation of the best swap factor of the formula and final structure adjustment if needed { double SwapMinus=0.0;// total negative swap double SwapPlus=0.0;// total positive swap double SwapMinusReverse=0.0;// total negative swap double SwapPlusReverse=0.0;// total positive swap double SwapFactor=0.0;// swap factor of the direct pass double SwapFactorReverse=0.0;// swap factor of the reverse pass for ( int i=0; i<ArraySize(ii.PairLeft); i++ )// define the missing parameters for calculating the left side { for ( int j=0; j<ArraySize(Pairs); j++ ) { if ( Pairs[j].Name == ii.PairLeft[i].Name ) { ii.PairLeft[i].Margin=Pairs[j].Margin; ii.PairLeft[i].TickValue=Pairs[j].TickValue; ii.PairLeft[i].SwapBuy=Pairs[j].SwapBuy; ii.PairLeft[i].SwapSell=Pairs[j].SwapSell; break; } } } for ( int i=0; i<ArraySize(ii.PairRight); i++ )// define the missing parameters for calculating the right side { for ( int j=0; j<ArraySize(Pairs); j++ ) { if ( Pairs[j].Name == ii.PairRight[i].Name ) { ii.PairRight[i].Margin=Pairs[j].Margin; ii.PairRight[i].TickValue=Pairs[j].TickValue; ii.PairRight[i].SwapBuy=Pairs[j].SwapBuy; ii.PairRight[i].SwapSell=Pairs[j].SwapSell; break; } } } double TempSwap; // calculate all components taking into account a change in the structure for ( int i=0; i<ArraySize(ii.PairLeft); i++ )// for left parts { if ( ii.PairLeft[i].Side == "u" ) {// for direct trading TempSwap=ii.PairLeft[i].SwapBuy*ii.LotKLeft[i]; if ( TempSwap >= 0 ) SwapPlus+=TempSwap; else SwapMinus-=TempSwap; // for reverse trading TempSwap=ii.PairLeft[i].SwapSell*ii.LotKLeft[i]; if ( TempSwap >= 0 ) SwapPlusReverse+=TempSwap; else SwapMinusReverse-=TempSwap; } if ( ii.PairLeft[i].Side == "d" ) {// for direct trading TempSwap=ii.PairLeft[i].SwapSell*ii.LotKLeft[i]; if ( TempSwap >= 0 ) SwapPlus+=TempSwap; else SwapMinus-=TempSwap; // for reverse trading TempSwap=ii.PairLeft[i].SwapBuy*ii.LotKLeft[i]; if ( TempSwap >= 0 ) SwapPlusReverse+=TempSwap; else SwapMinusReverse-=TempSwap; } } for ( int i=0; i<ArraySize(ii.PairRight); i++ )// for right parts { if ( ii.PairRight[i].Side == "d" ) {// for direct trading TempSwap=ii.PairRight[i].SwapBuy*ii.LotKRight[i]; if ( TempSwap >= 0 ) SwapPlus+=TempSwap; else SwapMinus-=TempSwap; // for reverse trading TempSwap=ii.PairRight[i].SwapSell*ii.LotKRight[i]; if ( TempSwap >= 0 ) SwapPlusReverse+=TempSwap; else SwapMinusReverse-=TempSwap; } if ( ii.PairRight[i].Side == "u" ) {// for direct trading TempSwap=ii.PairRight[i].SwapSell*ii.LotKRight[i]; if ( TempSwap >= 0 ) SwapPlus+=TempSwap; else SwapMinus-=TempSwap; // for reverse trading TempSwap=ii.PairRight[i].SwapBuy*ii.LotKRight[i]; if ( TempSwap >= 0 ) SwapPlusReverse+=TempSwap; else SwapMinusReverse-=TempSwap; } } // calculate the swap factor for the direct pass if ( SwapMinus > 0.0 && SwapPlus > 0.0 ) SwapFactor=SwapPlus/SwapMinus; if ( SwapMinus == 0.0 && SwapPlus == 0.0 ) SwapFactor=1.0; if ( SwapMinus == 0.0 && SwapPlus > 0.0 ) SwapFactor=1000001.0; if ( SwapMinus > 0.0 && SwapPlus == 0.0 ) SwapFactor=0.0; // calculate the swap factor for the reverse pass if ( SwapMinusReverse > 0.0 && SwapPlusReverse > 0.0 ) SwapFactorReverse=SwapPlusReverse/SwapMinusReverse; if ( SwapMinusReverse == 0.0 && SwapPlusReverse == 0.0 ) SwapFactorReverse=1.0; if ( SwapMinusReverse == 0.0 && SwapPlusReverse > 0.0 ) SwapFactorReverse=1000001.0; if ( SwapMinusReverse > 0.0 && SwapPlusReverse == 0.0 ) SwapFactorReverse=0.0; // select the best approach and calculate the missing values in the structure if ( SwapFactor > SwapFactorReverse ) { ii.SwapPlusRelative=SwapPlus; ii.SwapMinusRelative=SwapMinus; ii.SwapFactor=SwapFactor; } else { ii.SwapPlusRelative=SwapPlusReverse; ii.SwapMinusRelative=SwapMinusReverse; ii.SwapFactor=SwapFactorReverse; bool bSigned; for ( int i=0; i<ArraySize(ii.PairRight); i++ )// if it is a reverse pass, then reverse the right structure of the formula { bSigned=false; if ( !bSigned && ii.PairRight[i].Side == "u" ) { ii.PairRight[i].Side="d"; bSigned=true; } if ( !bSigned && ii.PairRight[i].Side == "d" ) { ii.PairRight[i].Side="u"; bSigned=true; } } bSigned=false; for ( int i=0; i<ArraySize(ii.PairLeft); i++ )// if it is a reverse pass, then reverse the left structure of the formula { bSigned=false; if ( !bSigned && ii.PairLeft[i].Side == "u" ) { ii.PairLeft[i].Side="d"; bSigned=true; } if ( !bSigned && ii.PairLeft[i].Side == "d" ) { ii.PairLeft[i].Side="u"; bSigned=true; } } } bool bSigned; for ( int i=0; i<ArraySize(ii.PairRight); i++ )// reverse the right side anyway { bSigned=false; if ( !bSigned && ii.PairRight[i].Side == "u" ) { ii.PairRight[i].Side="d"; bSigned=true; } if ( !bSigned && ii.PairRight[i].Side == "d" ) { ii.PairRight[i].Side="u"; bSigned=true; } } }
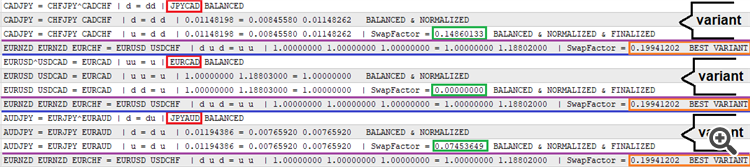
Sonucun sıralı çıktısını etkinleştirmek için, yalnızca başarılı bir şekilde filtrelenmiş formül varyantı bulunduğunda yazılan günlüğü uyguladım. Aşağıdaki gibidir:
Kırmızı renk, denklemin her iki tarafının da indirgendiği sonuç sembolü için kullanılır. Bir sonraki satır, lot katsayıları ile normalleştirilmiş varyantı göstermektedir. Üçüncü satır, hesaplanan swap faktörüyle varyantı göstermektedir. Dördüncü satır, kaba kuvvet oturumu sırasında bulunan varyantların en iyisidir ve bu da Comment fonksiyonu tarafından grafikte gösterilir. Bu prototip aşağıda eklenmiştir, böylece test edebilirsiniz. Aslında, swap alım-satımı için bir alım-satım asistanının prototipi olarak hizmet edebilir. Şimdilik çok az işlevi var, ancak bir sonraki makalede genişletmeye çalışacağım. Prototip iki versiyonda sunulmaktadır: MetaTrader 4 ve MetaTrader 5 için.
İlk testlerden elde edilen sonuçlar
Böylesine karmaşık bir konuda tek başına herhangi bir sonuca varmak oldukça zordur. Yine de, şu ana kadar birden büyük bir swap faktörü bulamamış olsam da, yararlı bir şeyler anlamayı başardım. Bu prototipin çalışmasını analiz ederken vardığım ilk sonuçlar şunlardır:
- Bazı döviz çiftleri için pozitif swapları artırabilir veya negatif swapları azaltabilirsiniz (pozisyonun sentetik bir eşdeğer olarak sunulması nedeniyle).
- Kârlı bir devre bulunamasa bile, parçalarından biri her zaman alternatif bir pozisyon olarak kullanılabilir - iki farklı işlem hesabında kilitleme için.
- Böyle bir sentetik pozisyonla kilitleme, her iki uçta da zıt pozitif bir swapa izin verdiği için swapsız hesapları kullanma ihtiyacını ortadan kaldırır.
- En popüler brokerlar ile daha iyi derinlemesine analiz yapmak gereklidir, bunun için işlevselliğin artırılmasına ihtiyaç vardır.
- Umarım karlı bir swap faktörünün elde edilebileceğini kanıtlayabilirim (şu ana kadar sadece bir tahmin).
- Swaplar akıllıca kullanılırsa küçük ama istikrarlı kâr sağlayabilir.
Sonuç
Umarım bu yaklaşım sizin için ilginçtir ve yeni fikirler edinmenizi sağlar. Yöntemin anlaşılması çok zordur, ancak aslında basit bir ilkeyi uygular: aynı hacimde iki zıt pozisyon açmak. Bu tür iki zıt pozisyonun basitçe açılması her zaman bir zarar yaratır. Hiçbir brokerda, bir yöndeki pozitif swapın, ters yöndeki negatif swaptan daha büyük olduğunu asla bulamazsınız. Elbette hiçbir zaman her iki yönde de pozitif swap bulamazsınız, çünkü bu matematiksel olarak imkansızdır.
Çok geniş bir konu olduğu için altta yatan matematiğin ayrıntılarını vermeyeceğim. Bu matematiğin tezahürlerinden yararlanmak daha iyidir. Açıklanan yöntemin uygulanmasıyla, pozisyon kilitlemede swapın neden olduğu kaybı azaltmak mümkündür. Ayrıca brokerların swap tablolarında bir boşluk bulmaya çalışabilir ve pozitif bir kâr faktörü (tüm pozisyonların kârlı bir toplam swapı) ile kilitlemenin tadını çıkarabilirsiniz - bu, fiyat dalgalanmalarına bağlı olmayan risksiz bir alım-satımdır.
Pozitif bir swap potansiyel kâr sağladığından, swap alım-satımı yöntemlerinin gerçekten hafife alındığını düşünüyorum. Açıklanan yöntem, swap alım-satımı yöntemlerinin olası varyasyonlarından sadece biri, ancak bu görevi seviyorum ve sonraki makalelerde fikri geliştirerek, kodu modernize ederek ve yeni ek işlevler oluşturarak devam etmeye çalışacağım. Ayrıca kâr tahmini ve alım-satım işlevselliği ile ilgili bazı fikirleri de açıklayacağım.
MetaQuotes Ltd tarafından Rusçadan çevrilmiştir.
Orijinal makale: https://www.mql5.com/ru/articles/9198
 Örneklerle formasyonlar (Bölüm I): Çoklu tepe
Örneklerle formasyonlar (Bölüm I): Çoklu tepe
 Sıfırdan bir alım-satım Uzman Danışmanı geliştirme (Bölüm 31): Geleceğe doğru (IV)
Sıfırdan bir alım-satım Uzman Danışmanı geliştirme (Bölüm 31): Geleceğe doğru (IV)
- Ücretsiz alım-satım uygulamaları
- İşlem kopyalama için 8.000'den fazla sinyal
- Finansal piyasaları keşfetmek için ekonomik haberler
Gizlilik ve Veri Koruma Politikasını ve MQL5.com Kullanım Şartlarını kabul edersiniz