Model aramada brute force yaklaşımı

Giriş

Bu makalede, piyasa modellerini arayacağız, belirlenen modellere dayalı Uzman Danışmanlar oluşturacağız ve bu modellerin geçerliliklerini koruyup korumadıklarını, ne kadar süreyle geçerli kaldıklarını kontrol edeceğiz. Bu makalenin kendi kendini uyarlayan ticaret sistemleri oluşturanlar için son derece yararlı olacağını düşünüyorum. Forex ticareti bağlamında brute force kavramıyla ne demek istediğimi açıklayarak başlamak istiyorum. Genel olarak, kaba kuvvet yaklaşımında, bir kod veya başka bir amaç için bir dizi belirleriz, ardından da bu diziyi kullanarak maksimum olasılıkla veya mevcut maksimum olasılıkla istenen sonuca ulaşmaya çalışırız. İstenen sonuç kripto para madenciliği yapma veya bir hesabı ya da Wi-Fi şifresini ele geçirmek olabilir. Uygulama alanı çok geniştir. Forex söz konusu olduğunda, dizimiz mümkün olan maksimum süre boyunca çalışarak maksimum kârı vermelidir. Dizi herhangi bir türde ve uzunlukta olabilir. Asıl önemli olan yararlı olmasıdır. Dizi türü nihayetinde algoritmamıza bağlıdır.

Bu tekniği incelemeye karar vermemi sağlayacak kadar özel olan şey nedir?

Düşüncelerimi her zaman diğer yatırımcılar için maksimum pratik uygulamaya sahip olacak şekilde ifade etmeye çalışırım. Peki bunu neden yapıyorum? Bu güzel bir soru. Deneyimlerimi diğer yatırımcılarla paylaşmak istiyorum. Birisi benim fikirlerimden yararlanıp ilginç ve kârlı bir şey uygularsa, bundan memnun olurum (bundan bir şey elde edip etmediğim önemli değildir). Fikirlerin tamamen bana ait olmayabileceğinin ve tekerleği yeniden icat ediyor olabileceğimin de farkındayım. Deneyimlerimizi paylaşmamız ve mümkün olduğunca etkili bir şekilde birlikte çalışmamız gerektiğine inanıyorum. Belki de başarının sırrı budur. Diğerlerinden soyutlanmış bir şekilde çalışarak tek başına önemli bir başarı elde etmek zordur. Bana göre, modeller konusu piyasanın fiziğini anlamak için temel öneme sahiptir. Bir yatırımcı olarak kariyeriniz, "yatırımcı olarak kariyer" ifadesi kulağa komik gelse de, temel fikirlerin anlaşılmasına bağlı olabilir. Umarım bu konuları araştıran insanlara faydalı olabilirim.

Brute force yaklaşımı ve sinir ağlarından farkı

Bir sinir ağı da aslında bir tür brute force’tur. Ancak algoritmaları basit brute force algoritmalarından çok farklıdır. Spesifik sinir ağı mimarilerinin ve unsurlarının ayrıntılarına girmeyeceğim, genel bir açıklama sunmaya çalışacağım. Bence spesifik bir mimariye bağlı kalırsak, algoritmamızın yeteneklerini önceden sınırlamış oluruz. Sabit bir mimari, telafisi mümkün olmayan bir sınırlamadır. Bir sinir ağı, bizim durumumuzda olası bir stratejinin bir tür mimarisidir. Sonuç olarak, bir sinir ağının yapılandırması her zaman bir ağ haritasına sahip belirli bir dosyaya karşılık gelir. Aslında bu her zaman belirli birimlerden oluşan bir koleksiyona işaret eder. 3D yazıcıda olduğu gibi: Öğenin parametrelerini ayarlarız ve devamında yazıcı onu üretir. Dolayısıyla bir sinir ağı, harita olmadan bir anlam ifade etmeyen genel bir koddur. Bu, herhangi bir gelişmiş programlama dilini alıp tüm yeteneklerini kullanmadan boş bir proje oluşturmaya benzerdir. Nihayetinde, boş şablon hiçbir şey yapamaz. Aynı şey sinir ağı için de geçerlidir. Brute force’un aksine, bir sinir ağı stratejilerde neredeyse sınırsız değişkenlik, herhangi bir sayıda kriter ve daha yüksek verimlilik sağlayabilir. Bu yaklaşımın tek dezavantajı, verimliliğin büyük ölçüde kod kalitesine bağlı olmasıdır. Sistem karmaşıklığının artması, programın kaynak yoğunluğunun artmasına neden olabilir. Sonuç olarak, stratejimiz eşdeğeri olan bir ağ haritasına dönüştürülür. Aynı şey brute force yaklaşımında da yapılır, ancak burada sayılardan oluşan basit bir dizi ile çalışırız. Bu dizi bir ağ haritasından çok daha basittir, hesaplanması daha kolaydır, ancak verimlilik açısından da bir sınırı vardır. Aşağıdaki şema yukarıdaki açıklamayı göstermektedir:

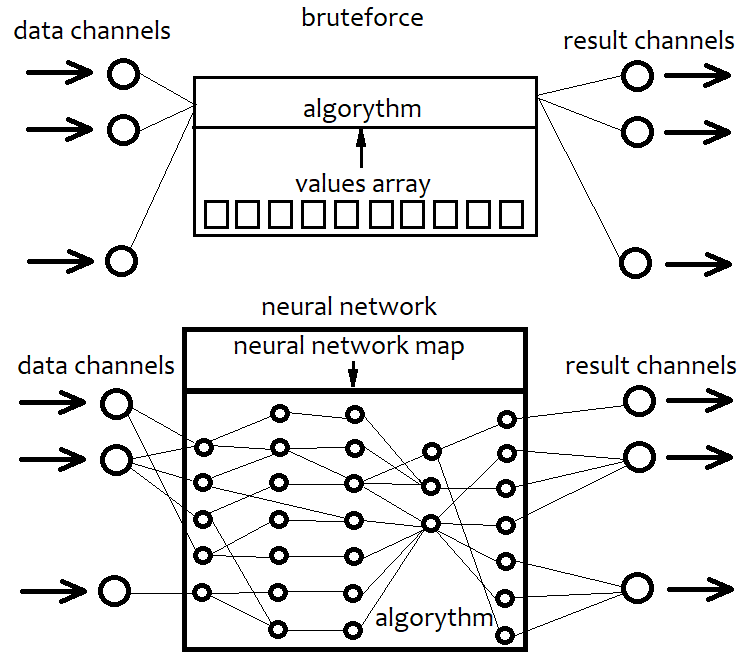
Başka bir deyişle, brute force yaklaşımında, kodumuzla etkileşime giren ve farklı sonuçlar üreten bir sayı dizisi seçeriz. Ancak algoritma sabit olduğundan, tüm esnekliği sayı dizisinde bulunur. Uzunluğu sabittir ve yapısı çok basittir. Bir sinir ağı ile çalışırken, en iyi sonucu verecek bir ağ haritası ararız. Her iki durumda da, sonuçta ortaya çıkan algoritmaya dönüştürülen belirli bir bayt dizisini veya veriyi ararız. Aralarındaki tek fark yetenekleri ve karmaşıklıklarıdır. 

Brute force ve optimizasyon algoritmam

Algoritmamda çok değişkenli Taylor açılımını kullandım. İşte bu yaklaşımı seçmemin nedeni. Mümkün olduğunca fazla sayıda değişken içeren çok basit bir algoritma sunmak istedim. Belirli bir formüle bağlı kalmak istemedim, çünkü herhangi bir fonksiyon sonuçta bir Taylor serisine veya bir Fourier serisine ayrıştırılabilir. Fourier serisinin bu amaç için çok uygun olmadığını düşünüyorum. Dahası, çok boyutlu eşdeğerine aşina değilim. Bu yüzden ilk seçeneği kullanmaya karar verdim. Ayrıca, uygulaması çok daha kolaydır. Tek boyutlu bir Taylor serisi şu şekilde görünür:

Y = Cs[0]+Cs[1]*(x-x0)^1+Cs[2]*(x-x0)^2+...+Cs[i]*(x-x0)^n

Burada kuvvetlerden önceki katsayılar 0'dan n'e kadar olan mertebeden türevler olarak işlev görür. Tüm parantezler açılarak daha basit bir forma dönüştürülebilir:

Y = C[0]+C[1]*x^1+C[2]*x^2+...+C[i]*x^n+... = Sum(0,+sonsuz)(C[i]x^i)

Bu durumda, yalnızca bir değişkenimiz vardır. Bu seri, seçilen herhangi bir x0 noktasının komşuluğundaki herhangi bir sürekli ve türevlenebilir fonksiyonu taklit edebilir. Formül ne kadar çok terime sahipse, fonksiyonumuzu o kadar doğru tanımlar. Eğer terim sayısı sonsuza eşitse, o zaman bu bizim fonksiyonumuzun mutlak eşdeğeridir. Burada herhangi bir fonksiyonun herhangi bir noktanın komşuluğundaki bir Taylor serisine nasıl ayrıştırılacağını göstermeyeceğim. Bu bilgi herhangi bir matematik kitabında mevcuttur. Ancak, genel formülün değişkenliğini artırmak adına birden fazla çubuktan gelen verileri kullanmak istediğimizden, tek boyutlu varyant bizim için yeterli değildir. Bu nedenle çok boyutlu varyantı kullanmalıyız:

Y = Sum(0,+sonsuz)(C[i]*Varyant(x1^p1*x2^p2...*xN^pN))

Bu formülü burada farklı bir şekilde yazmak oldukça zordur. Tek boyutlu varyant ile aynı mantığa sahiptir. Tüm olası kısmi türevleri sağlamalıyız. Terimlerin en yüksek kuvvetini sınırlarsak, kombinasyonları ve toplamları kullanarak bu terimlerin toplam sayısını hesaplayabiliriz. Algoritmamız, hesaplama kaynaklarının tüketimini sınırlamak için en yüksek derecenin sınırlandırılmasına sahip olacaktır. 

Ancak bu, brute force fonksiyonumuzun daha kullanışlı hale gelmesi için hala yeterli değildir. İlk terim C[0]'ı kaldırmak ve fonksiyonun ona ileteceğimiz negatif veya pozitif değerlere göre maksimum simetriye sahip olmasına izin vermek daha iyidir. Ayrıca, pozitif bir fonksiyon değerini alış sinyali olarak ve negatif bir fonksiyon değerini de satış sinyali olarak yorumlamak da uygun bir çözüm olacaktır. Bu sinyalin modülünün alt sınırındaki bir artış ideal olarak beklenen getiri ve kâr faktöründe bir artışa yol açmalıdır, ancak aynı zamanda kaçınılmaz olarak sinyal sayısında bir azalmaya yol açacaktır. Fonksiyon gereksinimlerimize ne kadar yakın olursa o kadar iyidir. Belirli bir mumun Close[i]-Open[i] değerlerini değişkenler olarak fonksiyona gireceğiz.

Tek yapmamız gereken, bu katsayıların rastgele varyantlarını oluşturmak ve onların sınayıcıda nasıl davrandığını kontrol etmektir. Elbette kimse bu katsayıları manuel olarak değerlendirmeyecektir. Bu nedenle, bu tür varyantları üretebilen ve aynı anda bu tür binlerce varyantı koruyabilen bir Uzman Danışmana veya strateji sınayıcının bazı işlevlerini uygulayabilen üçüncü taraf bir çözüme ihtiyacımız vardır. Başlangıçta, MQL4'te böyle bir Uzman Danışman yazmak zorunda kalmıştım - bu Uzman Danışmanı, talimatlarla birlikte makaleye ekledim, böylece herkes tarafından kullanılabilir. Ancak ben C# ile geliştirdiğim başka bir uygulamayı kullanacağım. Maalesef, malum nedenlerden dolayı bu uygulamayı ücretsiz olarak sunamıyorum. Yetenekleri araştırma alanının çok ötesine geçmektedir. Ancak, programlamayı bilen herkesin bu uygulamayı yeniden üretebilmesi için tüm yeteneklerini açıklayacak ve göstereceğim. Ekran görüntüleri, çalışma sonuçlarını analiz edeceğimiz makalenin ilerleyen kısımlarında verilecektir.

İşte uygulamanın başlıca özellikleri. Katsayı dizileri için arama 2 aşamada gerçekleştirilir. İlk aşama, yüklenen fiyatta, bir sonraki mumda maksimum beklenen getiriyi veya maksimum kâr faktörünü üreten dizileri arar. Strateji sınayıcıya benzer geçişler gerçekleştirilir. Aslında, basitçe bir sonraki çubuğun yönünü maksimum doğrulukla tahmin eden bir formül bulmaya çalışmaktadır. En iyi sonuçların belirli bir kısmı bellekte ve diskte dizi varyantları şeklinde saklanır. Yüklenen fiyatın yalnızca bir kısmı, yüklenen fiyat dosyasına göre yüzde cinsinden belirtilerek test edilebilir. Bu, ikinci adımda model olmayan rastgele sonuçları filtrelemek içindir. İkinci aşamada piyasa emirleri simüle edilir ve bakiye eğrisi oluşturulur - bu, yüklenen alanın tamamı için yapılır. Aynı zamanda, daha kaliteli varyantlar aranarak sinyal değerinde yumuşak bir artış gerçekleştirilir. Bu aşamada ayrıca daha düzgün grafikler elde etmek için gereken çeşitli filtreler de mevcuttur. Grafik ne kadar düzgünse, bulunan formül o kadar iyidir. Aramanın ikinci aşamasının tamamlanmasının ardından, düğmelerle listede gezinerek görsel olarak görülebilecek belirli sayıda en iyi varyant kalacaktır. İstenen varyantı seçtikten sonra, üçüncü sekmede MetaTrader 4 ve MetaTrader 5 için bir ticaret robotu oluşturabileceksiniz. Uzman Danışman, sayıların belirli yerlere basitçe doldurulduğu önceden derlenmiş bir şablona göre oluşturulur.

Görev için basit bir şablon oluşturma

Şablon ilk olarak MQL4'te oluşturulmuş ve daha sonra MQL5'e dönüştürülmüştür. Kod her iki platform için de uyarlanmıştır (önceki makalede olduğu gibi). Çözüm adaptasyonu için daha az zaman harcamak adına bu uyumluluğu sağlamaya çalışıyorum. MQL4'te olduğu gibi önceden tanımlanmış dizileri kullanmak için, Uzman Danışmana önceki makalemde açıklanan bazı ekstra kodlar eklenmelidir. Ayrıntılar için lütfen o makaleyi kontrol edin. Bu makale için bu bilgi gereklidir. Aslında zor değildir, herhangi bir geliştirici bu tür bir uyumluluğu uygulayabilir. Robot oluşturma sırasında otomatik olarak doldurulacak değişkenleri ve dizileri tanımlayarak başlayalım.

double C1[] = { %%%CVALUES%%% };//array of coefficients
int CNum=%%%CNUMVALUE%%%;//number of candlesticks in the formula
int DeepBruteX=%%%DEEPVALUE%%%;//formula depth
int DatetimeStart=%%%DATETIMESTART%%%;//start point in time
input bool bInvert=%%%INVERT%%%;//inverted trading
input double DaysToTrade=%%%DAYS%%%;//number of days into the future to trade

Burada C1, seçtiğimiz derecelerin önündeki katsayılar dizisidir. CNum, polinom değerini hesaplamak için kullanılacak fiyat grafiğindeki son mum sayısıdır. Ardından, çok boyutlu polinomun maksimum derecesi olan formülün derinliği gelir. Ben genellikle 1'i kullanıyorum, çünkü tek boyutlu Taylor serisinin aksine, çok boyutlu olanın derecesi arttıkça hesaplama karmaşıklığı da artmaktadır, çünkü toplam katsayı sayısı derecenin artmasıyla önemli ölçüde artar. Uzman Danışmanın çalışma süresini sınırlamak adına bir başlangıç noktası gereklidir, çünkü böyle bir sınırlamanın çalışmanın nereden başlayacağı bilgisine ihtiyacı vardır. Ters çevirme fonksiyonu, polinomun doğru yönde çalışmasını sağlamak için kullanılır. Derece katsayılarının önündeki tüm işaretleri ters çevirirsek, polinomun kendisi değişmeyecektir, yalnızca polinom tarafından üretilen sayılar farklı bir işarete sahip olacaktır. Buradaki en önemli kısım katsayıların oranıdır. Polinomun negatif değeri satış, pozitif değeri ise alış anlamına geliyorsa, ters çevirme yanlıştır. Değilse, o zaman doğru olur. Böylece, algoritmaya "polinomun değerlerini ters işaretle kullanması" talimatını veriyoruz. Ayrıca, bu değişkeni bir girdi değeri olarak yapmak daha iyidir, çünkü ticareti tersine çevirme yeteneğine ve gelecekte ticaret yapılmasına izin verdiğimiz gün sayısına ihtiyacımız olabilir.

Katsayıları içeren bir dizinin büyüklüğünü hesaplamanız gerekiyorsa, bu aşağıdaki şekilde yapılabilir:

int NumCAll=0;//size of the array of coefficients
void DeepN(int Nums,int deepC=1)//intermediate fractal
   {
   for ( int i=0; i<Nums; i++ )
      {
      if (deepC > 1)
         {       
         DeepN(Nums,deepC-1);
         } 
      else 
         {
         NumCAll++;
         }
      }   
   }

void CalcDeepN(int Nums,int deepC=1)//to launch calculations
   {
   NumCAll=0;
   for ( int i=0; i<deepC; i++ )
      {
      DeepN(Nums,i+1);
      }   
   }

Ara fraktal fonksiyon, tüm çarpanların toplam derecesi aynı olan terimlerin sayısını sayar. Bu, basitlik için yapılır, çünkü terimlerin hangi sırada toplandığı bizim için çok önemli değildir. İkinci fonksiyon, ilk fonksiyonu bir döngü içerisinde terim türü sayısı kadar çağırır. Örneğin, çok boyutlu seri açılımı diyelim ki 4 ile sınırlıysa, ilk fonksiyonu 1'den 4'e kadar tüm doğal sayılarla çağırırız.

Polinom değerini hesaplayacak olan fonksiyon neredeyse aynıdır. Ancak, bu durumda dizi kendi kendine oluşturulur ve büyüklüğünün ayarlanması gerekmez. Şu şekilde görünür:

double ValW;//the number where everything is multiplied (and then added to ValStart)
uint NumC;//the current number for the coefficient
double ValStart;//the number where to add everything
void Deep(double &Ci0[],int Nums,int deepC=1,double Val0=1.0)//calculate the sum of one degree
   {
   for ( int i=0; i<Nums; i++ )
      {
      if (deepC > 1)
         {
         ValW=(Close[i+1]-Open[i+1])*Val0;      
         Deep(Ci0,Nums,deepC-1,ValW);
         } 
      else 
         {
         ValStart+=Ci0[NumC]*(Close[i+1]-Open[i+1])*Val0/Point;
         NumC++;
         }
      }   
   }
   
void CalcDeep(double &Ci0[],int Nums,int deepC=1)//calculate the entire polynomial
   {
   NumC=0;
   ValStart=0.0;
   for ( int i=0; i<deepC; i++ )
      {
      Deep(Ci0,Nums,i+1);
      }   
   }

Hesaplanan her şey ValStart'a eklenecektir, yani sonuç bir global değişkene eklenecektir. Ayrıca başka bir global değişkene daha ihtiyaç vardır - ValW. Halihazırda var olan çarpımı bir değerle çarpmak için kullanılır. Bizim durumumuzda bu, ilgili çubuğun puan cinsinden hareketidir. Hareket hem yukarı hem de aşağı olabilir, bu da işaretle gösterilir. Dolayısıyla, bu fonksiyonlar çok ilginç bir yapıya sahiptir. Kendilerini içeriden çağırırlar ve bu çağrıların sayısı ve yapısı her zaman farklıdır. Bu bir tür çağrı ağacıdır. Çok değişkenli oldukları için bu fonksiyonları kullanmayı gerçekten seviyorum. Bu kez çok boyutlu Taylor serisini basit ve zarif bir şekilde uyguladık.

Polinomun sadece tek boyutlu versiyonunun kullanıldığı durum için ek bir fonksiyon uygulamak da mümkündür. Bu durumda, tüm seri büyük ölçüde basitleştirilir. Birinci derecedeki bazı çubukların hareketiyle çarpılan katsayıların toplamına dönüşür. Onların sayısı kullanılan çubukların sayısıyla aynı olur. Bu, tüm hesaplamaları basitleştirir. Derece 1 ise, basitleştirilmiş versiyon kullanılır. Aksi takdirde, herhangi bir derece için daha evrensel yöntem kullanılır.

double Val;
double PolinomTrade()//optimized polynomial
   {
   Val=0;
   if ( DeepBruteX <= 1 )
      {
      for ( int i=0; i<ArraySize(C1); i++ )
         {
         Val+=C1[i]*(Close[i+1]-Open[i+1])/Point;
         }
      return Val;   
      }
   else
      {
      CalcDeep(C1,CNum,DeepBruteX);
      return ValStart;
      }      
   }

Basit versiyon kullanıldığında, sonuçlar Val değişkenine eklenir.

Şimdi yeni bir çubuk göründüğünde çağrılacak ana metodu yazalım:

void Trade()
   {
   double Value;
   Value=PolinomTrade();
   
   if ( Value > ValueCloseE)
      {
      if ( !bInvert )
         {
         CloseBuyF();
         }      
      else 
         {
         CloseSellF();
         }
      }
      
   if ( Value < -ValueCloseE)
      {
      if ( !bInvert )
         {
         CloseSellF();
         }      
      else 
         {
         CloseBuyF();
         }      
      }   
   
   if ( double(TimeCurrent()-DatetimeStart)/86400.0 <= DaysToTrade && Value > ValueOpenE && Value <= ValueOpenEMax )
      {
      if ( !bInvert ) SellF();
      else BuyF();
      }
      
   if ( double(TimeCurrent()-DatetimeStart)/86400.0 <= DaysToTrade && Value < -ValueOpenE && Value >= -ValueOpenEMax )
      {
      if ( !bInvert ) BuyF();
      else SellF();
      }

   }

Bu fonksiyon çok basittir. Yapılması gereken tek şey, istediğimiz pozisyon açma ve kapama fonksiyonlarımızı uygulamaktır.

Çubuğun ortaya çıkışı aşağıdaki şekilde tespit edilebilir:

void CalcTimer()
   {
   if ( Time[1] > PrevTimeAlpha )
       {
       if ( PrevTimeAlpha > 0 )
          {
          Trade();
          }
       PrevTimeAlpha=Time[1];
       }
   }

Bence kod çok basit ve anlaşılırdır.

Kodum tarafından üretilen katsayılar yukarıda açıklanan dört model kullanılarak oluşturulur. Kolaylık açısından, tüm bu katsayılar [-1,1] aralığında yer almaktadır, çünkü değerlerin oranları değerlerin kendilerinden daha önemlidir. MQL5 program prototipimden bu sayıları üreten fonksiyon şu şekildedir:

   void GenerateC()
      {
      double RX;
      if ( DeepBrute > 1 ) CalcDeepN(CandlesE,DeepBrute);
      else NumCAll=CandlesE;
      for ( int j=0; j<VariantsE; j++ )
         {
         ArrayResize(Variants[j].Ci,NumCAll,0);
         Variants[j].CNum=CandlesE;
         Variants[j].ANum=NumCAll;
         Variants[j].DeepBruteX=DeepBrute;
         RX=MathRand()/32767.0;
         for ( int i=0; i<Variants[j].ANum; i++ )
            {
            if ( RE == RANDOM_TYPE_1 ) Variants[j].Ci[i]=double(MathRand())/32767.0;
            if ( RE == RANDOM_TYPE_2 )
               {
               if ( MathRand()/32767.0 >= 0.5  )
                  {
                  Variants[j].Ci[i]=double(MathRand())/32767.0;                  
                  }
               else
                  {
                  Variants[j].Ci[i]=double(-MathRand())/32767.0;                  
                  }
               }
            if ( RE == RANDOM_TYPE_3 )
               {
               if ( MathRand()/32767.0 >= RX  )
                  {
                  if ( MathRand()/32767.0 >= RX+(1.0-RX)/2.0  )
                     {
                     Variants[j].Ci[i]=double(MathRand())/32767.0;
                     ///Print(Variants[j].Ci[i]);
                     }
                  else
                     {
                     Variants[j].Ci[i]=double(-MathRand())/32767.0;                  
                     }        
                  }
               else
                  {
                  Variants[j].Ci[i]=0.0;                  
                  }
               }
            if ( RE == RANDOM_TYPE_4 )
               {
               if ( MathRand()/32767.0 >= RX  )
                  {
                  Variants[j].Ci[i]=double(MathRand())/32767.0;
                  }
               else
                  {
                  Variants[j].Ci[i]=0.0;                  
                  }
               }                              
            }
         }
      }

MQL4 ve MQL5'teki brute force prototipi makale ekinde mevcuttur. Burada ticaret fonksiyonu uygulamalarımı sunmuyorum, çünkü amaç sadece yaklaşımın bir şablon çerçevesinde nasıl uygulanabileceğini göstermektir. Uygulamanın tamamını görüntülemek isterseniz, lütfen eke bakınız. Tüm Uzman Danışmanlar ve diğer gerekli materyaller bu makalenin ekinde mevcuttur. Genel olarak şablonumda gereksiz fonksiyonlar veya değişkenler de dahil olmak üzere oldukça fazla şey vardır ve dolayısıyla optimize edilebilir. Şahsen ben bununla uğraşmıyorum. Çalışmayı engelleyen bir şey olursa, onu kaldıracağım. Benim için daha önemli olan şey, şu anda her şeyin iyi bir şekilde çalışıyor olmasıdır. Sürekli bir şeyler geliştiriyorum, bu yüzden her detayı mükemmel hale getirmek için zamanım yok. Ayrıca, kod düzenini ve okunabilirliği iyileştirebilecek olsa da, tüm prosedürleri ve değişkenleri sınıflarda depolamak için bir neden göremiyorum. Şablon çok basittir. Program tarafından kullanılacak olan fiyat dosyaları, geçmiş üzerinde çalışan ve çubuk verilerini program tarafından kolayca okunabilecek bir yapıya sahip bir metin dosyasına yazan özel bir Uzman Danışman tarafından oluşturulacaktır. Kolayca geliştirilebileceği için bu Uzman Danışmanın kodunu burada vermeyeceğim.

Modelleri bulmak ve analiz etmek için programı kullanma

Analiz için her biri bir ay uzunluğunda olan ve birbirini takip eden üç piyasa alanı seçtim. EURUSD, M5.

• İlk aralık:  2020.01.13 - 2020.02.16
• İkinci aralık:  2020.02.13 - 2020.03.15
• Üçüncü aralık:  2020.03.13 - 2020.04.18

Aralıklar, son gün her zaman Cuma olacak şekilde seçilmiştir. Bildiğiniz gibi Cuma günü haftanın son işlem günüdür. Aralıkların bu şekilde seçilmesi, borsa yeniden işlem görmeye başlayana kadar modelleri aramak için iki tam güne sahip olmamızı sağlar. Bu küçük bir püf noktası sayılır. Bizim durumumuzda bu önemli değildir, çünkü Uzman Danışmanı bir sınayıcıda test ediyoruz. Bulunan modellerin 12 varyantını burada açıklamaya karar verdim. Bunlardan altısı maksimum derecesi 1 olan polinomlar olacaktır. Diğer altısı da maksimum derecesi 2 olanlar olacaktır. Bence bu kadarı yeterlidir.

Programımın ilk sekmesi şu şekilde görünmektedir:

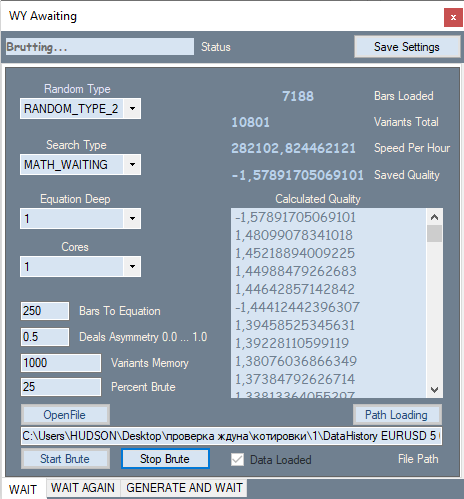
Sayı oluşturma türünü değiştirme imkanı sağlar, örneğin sadece pozitif, pozitif ve negatif, pozitif ve sıfırlar, pozitif ve negatif ve sıfırlar. Arama kriteri ikinci açılır kutuda ayarlanır. İki olası seçenek vardır: puan cinsinden beklenen getiri ve benim kâr faktörü formülümün benzeri. Formülümde bu değer -1 ile +1 arasında değişmektedir. Ayrıca, sıfır bölme hatası nedeniyle kâr faktörünün hesaplanamadığı durumlar da olamaz.

P_Factor = (Profit-Loss)/(Profit+Loss)

Ardından polinomun maksimum derecesi ve hesaplamalar için kullanılacak işlemci çekirdeği sayısı gelir. Metin kutularında, polinom için çubuk sayısı veya hesaplama sayısı ve önceki formüle çok benzeyen kendi icadım olan asimetri katsayısı belirtilir.

D_Asymmetry = |(BuyTrades-SellTrades)|/(BuyTrades+SellTrades)

Değerleri 0 ila 1 aralığındadır. Bu filtre, global bir trend sırasında tüm işlemlerin aynı yönde gerçekleştirildiği durumlardan kaçınmak adına programın benzer sayıda alış ve satış sinyaline sahip olmasını zorunlu kılmak için gereklidir. Daha sonra, tüm bulunan varyantlardan bellekte depolanması gereken en iyi varyantların sayısı ve yüklenen fiyatın yüzde kaçının brute force yinelemesi için kullanılacağı gelir. Burası açılış zamanına göre son çubuktan itibaren ölçülür ve arkasındaki parça optimizasyon için kullanılır. Geri kalan ifadeleri ve varyantları içeren listeyi yeterince basit oldukları için açıklamayacağım.

İkinci sekme şu şekilde görünür:

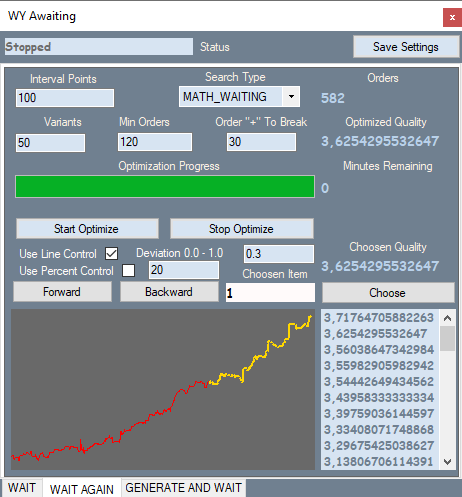
Sekmede, biraz sonra bahsedeceğimiz robotlardan ilkinin birinci aralıktaki grafiği görünmektedir. Programımdaki bu grafiği sınayıcının grafiği ile karşılaştırabilirsiniz. Aşağıda sunulacaktır. Brute force’un uygulandığı fiyat kısmındaki emirler sarı, diğerleri kırmızı ile gösterilmiştir. Burada tüm varyantların ekran görüntülerini vermeyeceğim - hepsi ekte mevcuttur.

Sekmede ne olduğunu görelim. Interval Points - polinomumuzun değer aralığını bölmek içindir. İlk sekmede brute force uyguladığımızda, varyantın ana parametrelerinin yanı sıra bu polinomun maksimum modül değeri de hesaplanır. Böylece, polinomun değer penceresini biliriz ve ardından bu pencereyi eşit parçalara bölerek, değeri kademeli olarak artırarak daha güçlü sinyalleri tespit etmeye çalışabiliriz. Bu işlem ikinci sekmede yapılır. Bu sekmede ayrıca arama türü ve optimizasyon belleğinde depolanan en iyi varyantların sayısı da bulunur. Diğer filtreler, model tanımımıza uymayan gereksiz varyantları filtrelememize olanak tanır. Line Control, her varyant için, grafik çizgisinin grafiğin başlangıcını ve sonunu birleştiren düz çizgiden göreceli sapmasını hesapladığı ek bir çalıştırma sağlar. 

Deviation = Max(|Profit[i]-LineProfit[i]|)/EndProfit

Burada Profit[i], i'ninci sıradaki bakiye eğrisinin değeridir, LineProfit[i] düz çizgi üzerindeki aynı değerdir, EndProfit ise grafiğin sonundaki değerdir.

Tüm değerler puan cinsinden ölçülür. Use Percent Control, grafiğin kırmızı kısmının yüzdesidir (bu durumda bu filtreyi kullanmadım). Minimum emir sayısı için de bir filtre vardır.

Aşağıdaki şekilde bot oluşturma sekmesi gösterilmektedir:

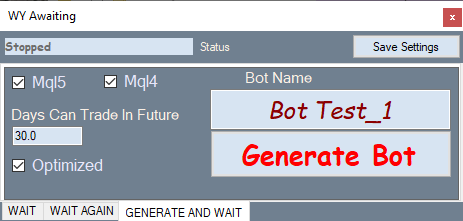
Nasıl çalışır: optimizasyon sekmesinden istediğiniz varyantı seçin, bu sekmeye geçin ve bir Uzman Danışman oluşturun.

Şimdi, oluşturulan robotları MetaTrader 4 Strateji Sınayıcıda test edelim. Onu seçtim, çünkü makası 1 olarak ayarlamaya ve böylece grafik ekranı üzerindeki etkisini pratik olarak ortadan kaldırmaya izin vermektedir. Aslında, bu şekilde bulunan robotların çoğunun beklenen getirisi, bir paritedeki ortalama makastan biraz daha yüksek olacaktır, bu nedenle düşük beklenen getirisi olan modelleri görsel olarak analiz edemeyiz. Her bir varyant yaklaşık iki saat boyunca brute force yapılmış ve optimize edilmiştir, bu da yüksek kaliteli bir model bulmak için yeterli değildir. Bir veya iki gün geçirmek daha iyidir. Ancak bu, en iyilerini bulmaktan ziyade bulunan modelleri analiz etmeyi amaçlayan bu makale için yeterlidir. Robotlarımı sınayıcıda test edecekseniz, lütfen DaysToTrade değişkenine dikkat edin. Değeri varsayılan olarak 3 gün olarak ayarlanmıştır. Dolayısıyla, brute force bölümünden sonra neredeyse hiç işlem olmayabilir.

İlk olarak, birinci derece polinoma dayalı olarak üretilen robotları ele alalım.

Birinci aralık.  2020.01.13 - 2020.02.16 

1. robot:

                                                             

Brute force bölümü

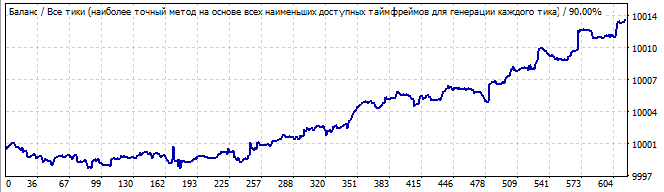
Gelecekte 10 gün 

İlk grafik, programımın ikinci sekmesinin ekran görüntüsünden bir varyantı göstermektedir. İkinci grafik, aynı robotun gelecekte 10 gün boyunca test edilmesidir. Nasıl çalıştığını görmek için 10 günün yeterli olduğunu düşünüyorum. Gördüğünüz gibi, model bir süre devam ediyor ve sonra aniden dönüp ters yöne gidiyor. Bu modelin iki ya da üç gün boyunca kâr elde etmek için yeterli olacağı düşünülebilir. İkinci robotu da aynı piyasa alanında görelim:

Brute force bölümü

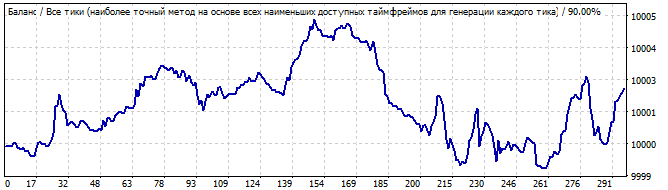
Gelecekte 10 gün

Burada sonuç o kadar düzgün değildir. Neden? Modelin bir ya da iki gün boyunca çalışması bekleniyordu, ancak geri dönüş oldukça yumuşak olmasına rağmen ilk saniyeden itibaren düşmeye başladı. Muhtemelen beklediğiniz sonuç bu değildir. Ama açıklanabilir. Bu konuya daha sonra döneceğiz.

Şimdi ikinci test aralığına geçelim.  2020.02.13 - 2020.03.15

Üçüncü robot:

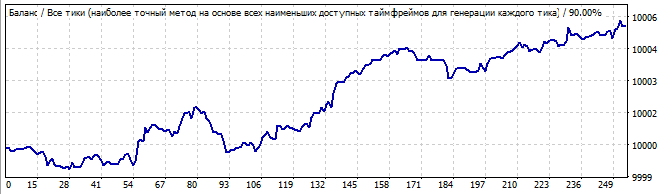
Brute force bölümü

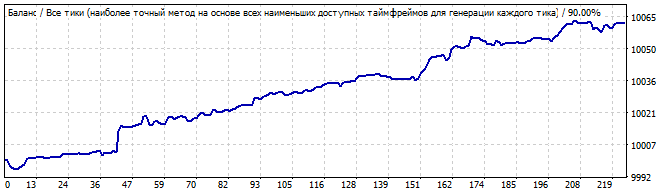
Gelecekte 10 gün

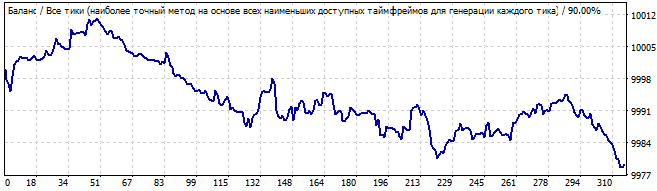
Bu kez durum daha iyi görünmektedir. Grafik düzgündür ve düz çizgiye çok yakındır. Bu durum, modelin istikrarlı olduğunu ve bir süre daha devam edeceğini göstermektedir. Ve öyle de oldu. Gelecekteki hareket de bir çizgiye benzemektedir, bu da model parametrelerinin çoğunun gelecekte de çalışmaya devam ettiği anlamına gelmektedir.

İşte dördüncü robot:

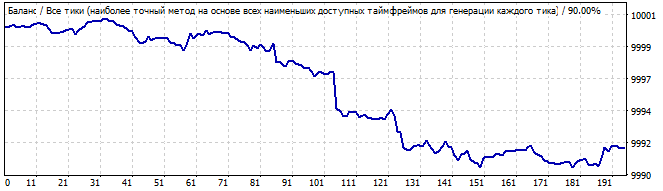
Brute force bölümü

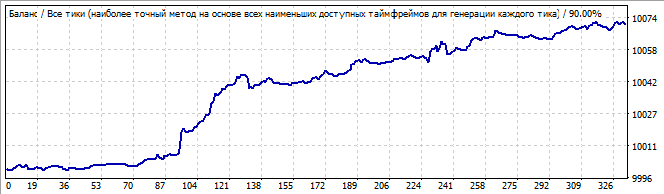
Gelecekte 10 gün

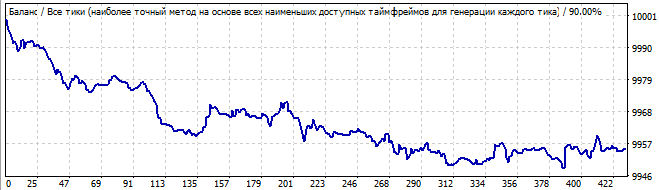
Yukarı doğru oldukça iyi bir hareketi vardır ve grafiğin başındaki keskin yükseliş dışında her şey düzgün ve istikrarlı görünmektedir. Ancak keskin artış göz ardı edilmemelidir: bu asimetri, bunun sadece bir tesadüf veya kazara bir sonuç olabileceğini düşündürmektedir. Doğal olarak, gelecekte tüm modelin ters yöne döndüğünü göreceğiz.

Şimdi üçüncü test aralığına geçelim.  2020.03.13 - 2020.04.18

Beşinci robot:

Brute force bölümü

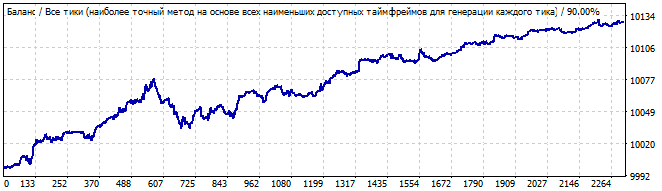
Gelecekte 10 gün

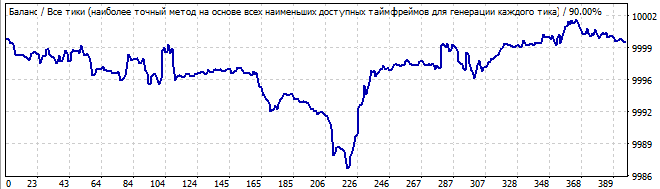
Durum benzerdir. Bariz asimetri, başlangıçta dalgalar ve sonunda zayıflama göstermektedir. Bu güvenilir bir model gibi görünmüyor. Bu modelde ticaret yapmazdım. Yine, gelecekte grafiğin ve tüm formülün tersine döndüğünü görüyoruz. Altıncı robotu burada göstermeyeceğim - grafiği arşivde mevcuttur. Yukarıdaki grafiklere çok benzemektedir.

Şimdi robotları ikinci derece bir polinoma göre test edelim.

Birinci aralık. 2020.01.13 - 2020.02.16 

Yedinci robot aşağıdaki gibidir:

Brute force bölümü

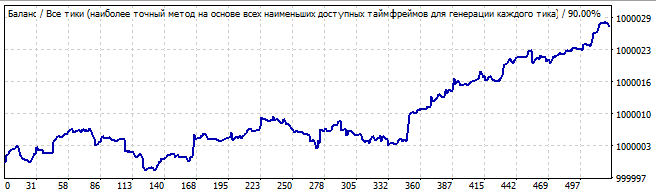
Gelecekte 10 gün

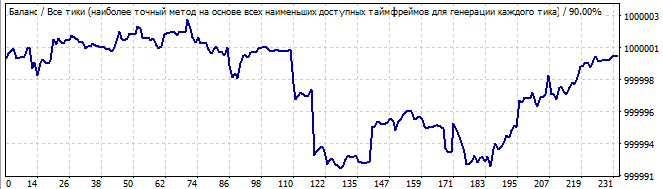
Bu robotların spesifik özelliği, brute force aralığında daha iyi çalışmalarıdır. Brute force bölümünden önceki aralıkta sonuçlar o kadar iyi değildir. Brute force aralığı her zaman keskin bir pozitif yarım dalga göstermektedir. Ancak kalan aralık tam bir karmaşadır. Bunlar belirli bir formülün sonuçlarıdır, davranış benzerdir. Başlangıçta küçük bir rastlantısallık ve ardından ters yönde bir hareket vardır.

Sekizinci varyant:

Brute force bölümü

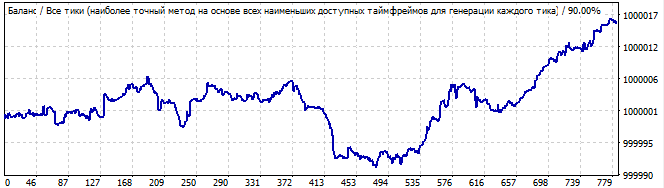
Gelecekte 10 gün

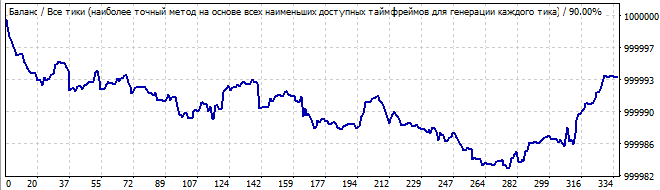
Bu çok daha kötüdür. Global bir model yoktur, ancak yine de brute force aralığında yukarı doğru bir hareket göstermektedir. Bu bir model değildir, bu yüzden grafik devamında aşağı dönmektedir.

Şimdi ikinci test aralığını kontrol edelim.  2020.02.13 - 2020.03.15

Dokuzuncu robot:

Brute force bölümü

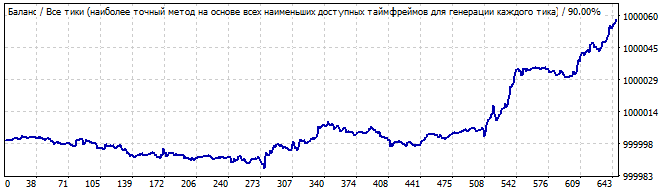
Gelecekte 10 gün

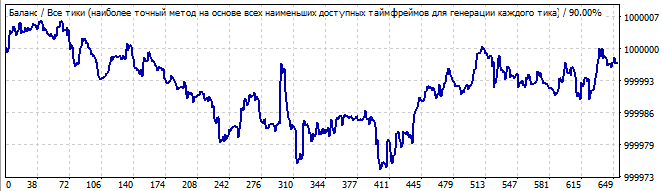
İlk grafikte bir dalganın başlangıcını ve gelecekte de sonunu görüyoruz. Herhangi bir global model yoktur, ancak terse dönüş ondan kâr elde etmeye çalışılabilecek kadar yumuşaktır.

Onuncu robot aşağıdaki gibidir:

Brute force bölümü

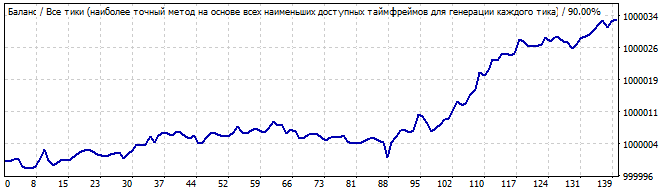
Gelecekte 10 gün

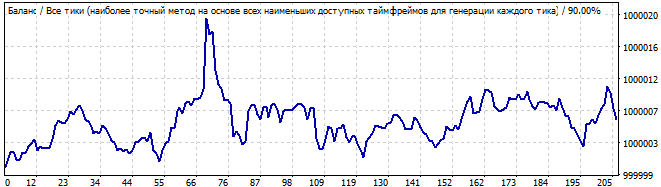
Grafik bu sefer daha iyidir. Bu sefer bir modele benzemektedir. Bu model en fazla bir ya da iki gün sürmektedir. Böyle bir grafikle ticaret yapma riskine girmezdim. Düz çizgiden önemli bir sapması vardır. 

Şimdi üçüncü test aralığına geçelim.  2020.03.13 -2020.04.18

On birinci robot:

Brute force bölümü

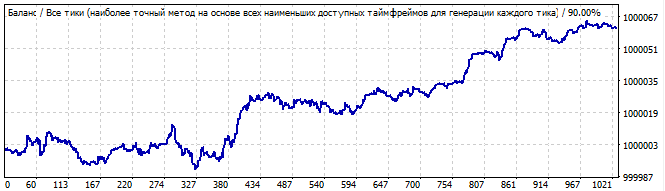
Gelecekte 10 gün

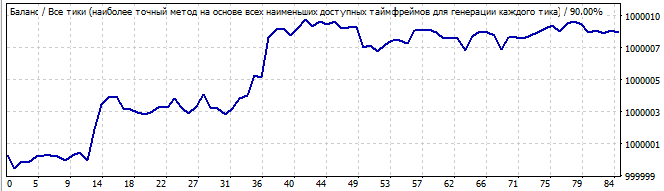
Grafik çok güzel değildir, ancak düz çizgiye biraz benzerliği vardır. Bu model gelecekte de devam edecektir, ancak çok fazla rastgele gürültü içerdiği için bunun düzenli sonuçlardan ziyade şans eseri olduğunu düşünüyorum. Ya da bu tam olarak gürültü değil, küçük dalgalar olabilir. 

On ikinci robot:

Brute force bölümü

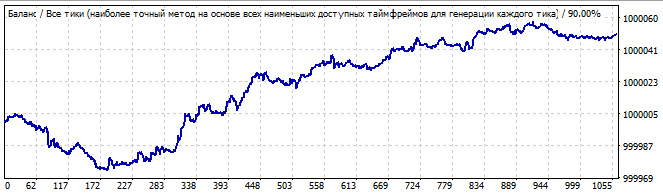
Gelecekte 10 gün

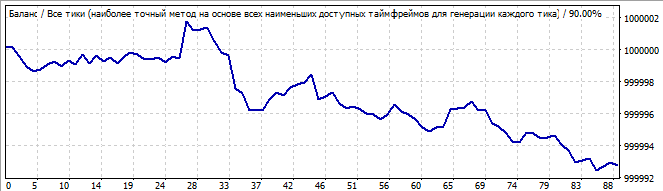
Oldukça çirkin bir grafik, ancak bir dalganın belirgin bir sonu ve onu takip eden büyük bir dalga daha vardır. Gelecekte bu büyük dalga yavaşça geri dönecek ve nihayet bir noktada tersine dönecektir. Bana öyle geldi ki, trendin terse dönüşü, polinom derecesi 2'den daha yüksek olan robotlarda daha yumuşak bir şekilde gerçekleşti. Daha az sürpriz gösterdiler. Bence biraz daha zaman harcamak ve üçüncü dereceyi test etmek mantıklıdır. Modeller, terimlerdeki çarpanların en yüksek toplam kuvvetine sahip polinom tarafından daha iyi tanımlanabilir.

Araştırmamızdan çıkan sonuçlar ve matematiksel gerçekler

Şimdi Uzman Danışmanlarımızın tüm test sonuçlarını özetleyebiliriz. Bunu yapmak zor görünebilir, çünkü brute force ve optimizasyon aralıkları modelleri gösterirken, gelecek segmentleri belirsiz bir resim göstermektedir. Pek sayılmaz:

• Geleceğe yönelik testlerin her birinde, her zaman grafiğin ve formülün tersine döndüğü bir nokta vardır.
• Tersine dönüş yumuşak bir şekilde ya da anında gerçekleşebilir, ancak her zaman oradadır.
• Grafiklerin büyük çoğunluğu genellikle gelecekte düşmektedir.
• Bazen model başlangıçta bir süre devam eder.
• Gelecekte yapılan tüm testler, modelin ters yönde çalıştığını göstermiştir.
• Bakiye eğrisi düz çizgiden saparsa, devam etme şansı çok daha düşüktür.
• Bulunan varyantların en iyisinde, model bir veya iki gün boyunca çalışmaya devam eder.

Şimdi bu gerçekleri açıklamaya çalışacağım. İlk ve en önemli gerçeği uzun zaman önce, henüz bu tür programlara sahip değilken keşfetmiştim. Bu basit bir matematiksel gerçektir. Aşağıda rastgele bir stratejinin bakiye grafiğini çizdim. Siyah çizgi küçük bir modele sahip olandır, mor çizgi ise büyük bir modele sahiptir. Grafik, sadece brute force aralığında değil, geçmiş boyunca işlem yapıldığı durumdaki yaklaşık davranışlarını göstermektedir:

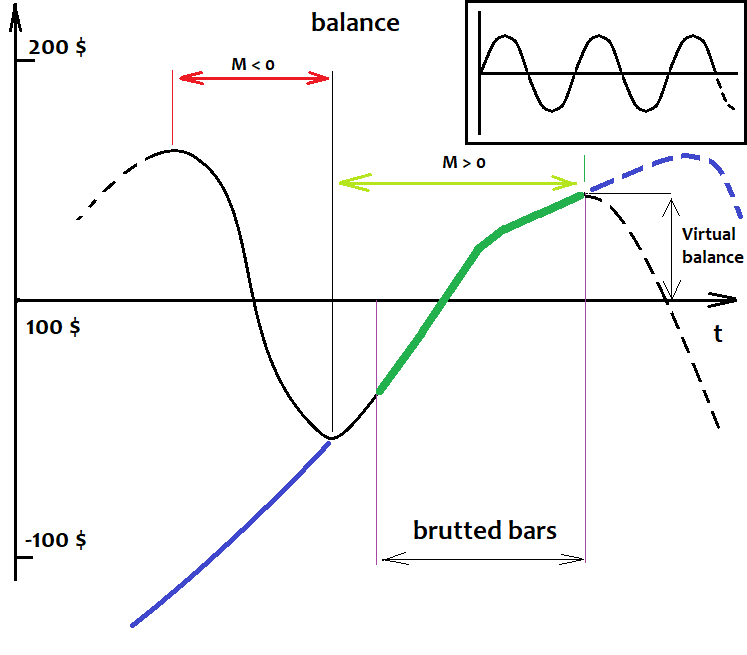
Bizim durumumuzda analiz edilen temel bakiye grafiği olduğu için buraya fiyatı eklemedim. Fiyat nasıl çizilmiş olursa olsun, onda stratejimizden daha fazlasını görmeyeceğiz.

Tüm robotlarımızı geçmişin en başından geleceğe kadar test ettiğimizi hayal edin. Elimizde gelecekteki fiyatlar olmasa da, yine de ne olacağını %100 doğrulukla tahmin edebiliriz. Saçmalık gibi mi geliyor? Hayır, bu saçmalık değil. Öncelikle, robotları mevcut tüm fiyat geçmişini kullanarak test ettiğimizi düşünelim. Ne göreceğiz? Bazı kafa karıştırıcı hareketler, yukarı ve aşağı ve benzeri. Burada neyi fark edebiliriz? Dalgalar. Şekilleri, dalga boyları ve genlikleri önemli değildir. Bir sinüzoid değildir, ama umurumuzda da değil. Önemli olan bu sürecin periyodik olmasıdır. Ayrıca, bir önceki makalemde sunduğum matematiksel araştırmama dayanarak, rastgele bir formüle dayanan bir stratejinin beklenen getirisi, geçmiş veri miktarı sonsuza gittiğinde sıfıra yönelecektir. Bunun etkisi nedir? Yukarıdaki varsayıma dayanarak, sonsuz sayıda işlem içeren herhangi bir bakiye eğrisinin başlangıç bakiye çizgisini sonsuz kere geçeceğini söyleyebiliriz. Herhangi bir nedenle bakiye hemen yukarı ya da aşağı gitse ve sürekli orada kalsa bile, bu çizgiyi hafifçe aşağı ya da yukarı kaydırabilir ve bakiyenin dalgalandığı bu denge noktasını bulabiliriz.

Geçmiş boyunca belirgin bir kazanç veya kayba yol açan formülleri dikkate almayacağız, ancak bu varyantlar da bu kategoriye atfedilebilir - bu sadece tüm geçmişimizden daha büyük olan büyük bir dalganın pozitif veya negatif yarım dalgasıdır. Bu varsayımlara göre, bulunan modeller sadece pozitif yarım dalgaların parçalarıdır. Bulunan parça ne kadar büyükse, denge noktasının çok daha aşağıda olma olasılığı o kadar yüksektir. Buna göre, şu anda pozitif bir yarım dalga varsa, yakında negatif bir dalga ortaya çıkacaktır. Matematiksel açıdan bakıldığında, tespit edilen yarım dalga ne kadar büyükse, negatif yönde hareket olasılığı da o kadar büyüktür. Ve tam tersi, eğer negatif bir yarım dalga tespit edersek, bu yarım dalga ne kadar büyük olursa, pozitif bir yarım dalganın başlama olasılığı da o kadar artar. Daha basit olabilir: eğer geçmiş boyunca beklenen getirisi sıfır olan bir stratejimiz varsa, o zaman tüm geçmiş birbirini takip eden ve sürekli değişen negatif ve pozitif beklenen getirili segmentlerden oluşur. Fiyat geçmişi boyunca herhangi bir döviz çifti için çalışan bu prensibi uygulayan bir Uzman Danışmanım vardır. Dolayısıyla, yukarıdaki varsayımlar Uzman Danışmanlar tarafından da onaylanmıştır. Genel olarak, bu prensip sadece ölçeklendirilmekle kalmaz, aynı zamanda sonsuz katmanlı hale getirilerek sistemin verimliliği artırılabilir. Tabii ki, trendin devam edişinde de ticaret yapmak mümkündür, ancak bunu yalnızca model çok belirgin ve eşitse, bulunan modelin %5-10'una kadar olan gelecek için ticaret yapmanızı öneririm. Risk çok yüksektir. Dahası, matematiğe karşı ticaret yapmak aptalcadır. Bu modelin yaklaşık kalan ömrünü tahmin etmek bir şekilde mümkün olsaydı deneyebilirdiniz. Ancak modelin doğası net olmadığı için bu mümkün değildir. Modelin niteliği açık olsa bile, böyle bir analizin yapılması son derece zordur.

Dalgalanmaların meydana geldiği seviye nasıl belirlenir?

Dalgaların ve hareketlerinin belirlenmesi gereken seviyenin nasıl tanımlanacağını cevaplamaya çalışacağım. Cevap çok basittir. Bunu belirlemenin bir yolu yok. Bu, seviyenin mevcut olmadığı ve uygun bir ticaret yapamayacağımız anlamına gelmez. Bu seviye sabit değildir ve sadece kafamızda mevcuttur. Şunu anlamak daha da önemlidir: bir yarım dalganın büyüklüğü sonsuza yöneldiğinde, bu yarım dalganın büyüklüğünün başlangıç bakiyesinden uzaklığına oranı da sonsuza yönelir. Başka bir deyişle, yarım dalga ne kadar güçlü olursa, bu seviyenin nerede olduğunu o kadar az düşünebiliriz, çünkü işlem sayısındaki artışla bu seviye sıfır noktasına yönelir. Tek yapmamız gereken çok güçlü yarım dalgalar bulmaktır. Aynı şeyi gösteren bir başka gerçek de, yarım dalga ne kadar büyük ve iyi olursa, sanal testin geri kalanında karşılaştırılabilir büyüklükte bir dalganın bulunma olasılığının o kadar düşük olmasıdır. Anlattıklarımı aşağıda görsel olarak göstermeye çalışacağım:

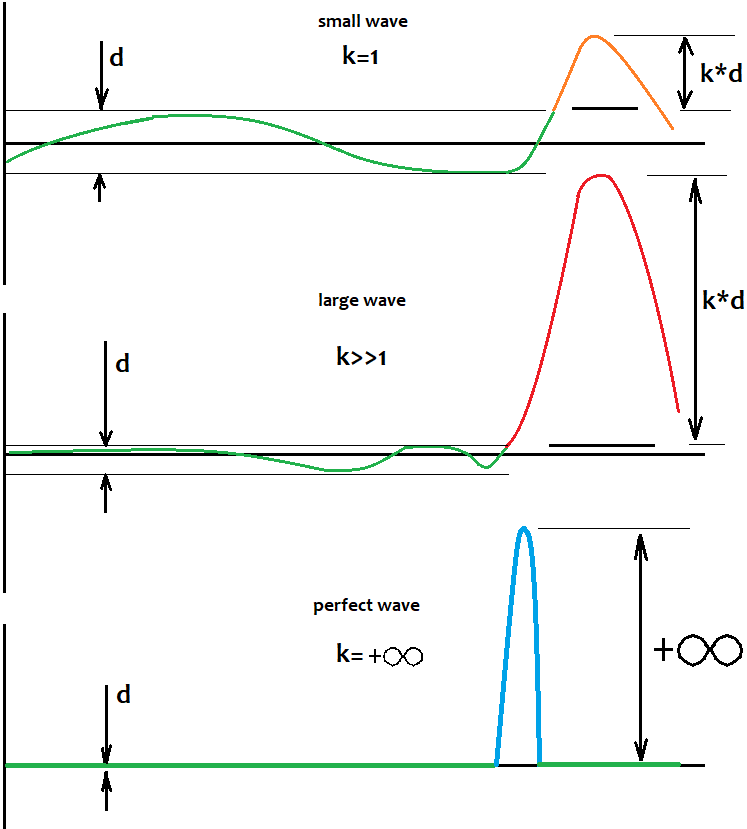
Bu seviye, modelin %100 olasılıkla döneceğini garanti etmez. Daha da önemlisi, yarım dalganın bir parçası olan bir modelin varlığı gerçeği bize büyük olasılıkla bu türden birden fazla dalganın olacağını ve hatta geçmiş boyunca var olabileceklerini söyler. Bu durumda, büyük bir geri çekilme hareketi olması ihtimali yüksektir. Onu yakalamaya çalışmalıyız. Global ölçekte çalışmayan çeşitli Uzman Danışmanları test ettiğimde bile, bu yerel olarak doğrudan veya tersine çevrilmiş bir şekilde çalıştı. Canlı dalgalar vardı ve grafik net bir şekilde yapılandırılmıştı.

Resmi tamamlamak için

Bana göre bu dalgaların en verimli şekilde nasıl ticaret yapılması gerektiğini göstermeye çalışacağım. Önce size bazı örnekler vereyim:

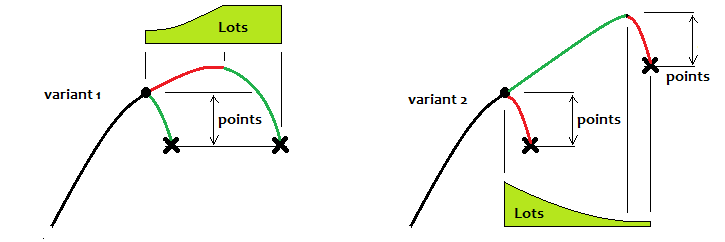
İlk seçenek modelin terse dönüşünde ticaret yapmaktır, ikincisi ise devamlılığında ticaret yapmaktır. İlk seçeneği ele alırsak, ideal olarak her zaman belirli bir seviyeye ulaşmalı ve ticaret döngüsünü orada durdurmalı ve ardından bir sonrakini beklemelisiniz. Kısmi bir martingale kullanıldığında, bir iyileşme olacaktır (ancak grafiğin yakında tersine dönmek üzere olduğu biliniyorsa). Aksi takdirde, beklenen getiri yine de "0" olacaktır. Trendin devam edişinde yalnızca model ideale yakın olduğunda ticaret yapabilirsiniz. Ancak bu ticaret kısa süreli olmalıdır. İkinci varyantta, bence, ters martingale kullanabilirsiniz. Dürüst olmak gerekirse, test ettiğim tüm stratejiler şu matematiksel gerçeği kanıtlamaktadır: sabit bir lotla ticaret yaparsanız ve fiyatın gelecekte nasıl davranacağını bilmiyorsanız (bu neredeyse hiç bilinmez), sonuç her zaman "0" olacaktır.

Ancak kazara global bir model yakaladığımız ve bunun çok işe yaradığı durumlar da var. Ancak bence bu tür durumları beklememekte fayda var. Bir ticaret planı seçmek ve onu takip etmek daha iyidir. Tek bir çözüm bulunmamaktadır. Bunu demo hesaplarda bile test etmek için henüz zamanım olmadı, çünkü bu 2-3 ay sürecektir. Bir ayda dört hafta var ve her hafta sonu iki günlük brute force uygulanmalıdır. Ve daha sonra günün her saati çalışan bir bilgisayarda test edilmelidir. Şu anda bunu yapma imkanım yok. Belki gelecekte bir demo hesap üzerinde deneyler yaparım ve ayrı bir sinyal oluştururum.

Sonuç

Bu makalede, piyasaya uygulandığı şekliyle modeller ve bunların fiziği hakkında basit ama çok önemli sonuçlar çıkardık. Bunlar şu şekildedir: piyasa kaotik değildir ve grafiklerin farklı dönemlerinde içerisinde gizlenmiş birçok model vardır. Üst üste binerler ve kaos yanılsaması yaratırlar. Model, tekrarlanabilen ve tersine dönebilen periyodik bir süreçtir. Modeller tekrarlandığından, bu dalgalar ticaret stratejilerinde kullanılabilecek sınırlı bir genliğe sahip olabilir. Bu makaleyi mümkün olduğunca anlaşılır kılmaya ve minimum düzeyde matematik sunmaya çalıştım. Umarım bu bilgiler ticaret sistemleri geliştirmenizde size yardımcı olur. Başka çıkarımlarınız varsa, lütfen yorumlarınızı ekleyin. Ne yazık ki, daha yüksek zaman dilimlerinde brute force uygulayamadım çünkü bu çok fazla zaman alıyor. Okuyucular daha derin analizlerle ilgilenirlerse, bu konuya başka makalelerde devam etmeye hazırım. Bu makale daha ziyade bir konu tanıtımı ve gösterimi niteliğindedir.