Модель движения цены и ее основные положения. (Часть 3): Расчет оптимальных параметров биржевой игры

Введение

Если в предыдущих статьях (Часть 1 и Часть 2) были представлены  фундаментальные принципы и латентные механизмы генерации ценовой динамики, что носило чисто теоретический характер и даже выходило за рамки наблюдаемого (являясь, однако, основой оного), то в этой статье и последующих я  постараюсь заложить основы новой инженерной дисциплины (где, соответственно, многие выкладки будут носить оценочный характер), что  позволяла бы делать практически полезные выводы из наблюдаемой динамики цены и непосредственно применять их в трейдинге. В данной статье речь пойдет об инженерных подходах и алгоритмах, что, вообще, в состоянии обеспечить устойчивую прибыль, и вероятностных расчетах тех оптимальных значений тейкпрофита и стоплосса, что позволили бы достичь максимума среднестатистической прибыли.

1. Модель.

В предыдущей статье (Часть 2)  была  получена формула (II.3) для плотности потока вероятности  цены (для краткости здесь и в дальнейшем формула (N) статьи Часть R нумеруется, как (R.N), где R – римская цифра). Такой поток вероятности в редуцированном или наблюдаемом виде выражается уже в вероятностях движения цены «вверх» или «вниз», точнее, порождает эти вероятности. Сформулируем подход к практической оценке таких вероятностей.

 

В дискретном (отталкивающимся от понятия бара) представлении времени, когда участок истории  цены  (что может быть ценой открытия, закрытия, максимума или минимума)  представим в виде ряда  (здесь порядок нумерации таков, что последующие бары имеют номера большие предыдущих),  цена движется скачками, что позволяет в крупных масштабах или на достаточно большом   говорить о вероятностях таких скачков, оцениваемых для вероятности движения цены вверх, как ,  где   - число членов множества , или вниз , где   - число членов   .  При этом можно вычислить протяженность среднего скачка 

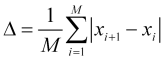                                                                                                    (1.1)

цены .  На практике может быть установлено, что хаотично движущаяся посредством разнообразных скачков цена за период   за счет случайного блуждания уходит от своего текущего среднего (определяемого такими вероятностями) положения на величину порядка

              ,                                                                                                      (1.2)

(это подтверждают показания индикатора «Casual Channel», линии канала коего есть    или отклонения (1.2) от скользящего среднего с периодом  ).

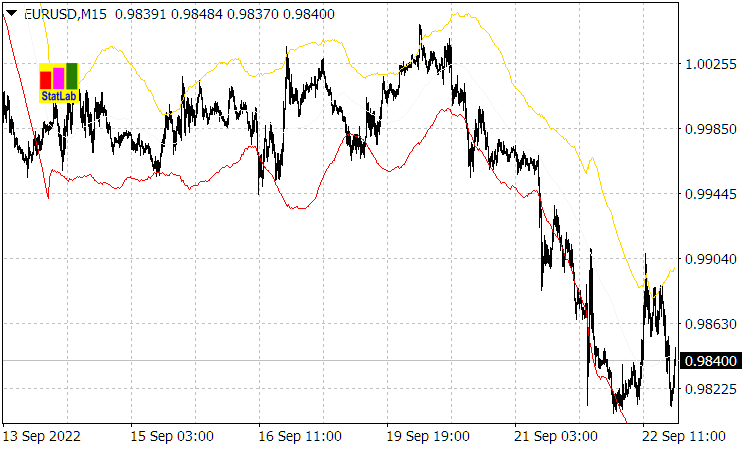
Рис. 1.  Индикатор «Casual Channel»

Очевидно, что характерное время случайного отклонения цены на величину   порядка  , где   - временная протяженность бара соответствующего таймфрейма.  Такое же в точности  отклонение  (1.2) цены  от среднего было бы и в том случае, если бы она случайно двигалась посредством одинаковых скачков точно  равных  .    

 

Поэтому, в представляемом здесь модельном упрощении будем считать, что  цена движется одинаковыми скачками  , направлениям которых присущи  вероятности   и   . 

 

Отметим вычисленные представленными выше способами скачок   и вероятности были актуальны для уже прошлого интервала   в целом, т.е. как средние для этого интервала величины, а не для текущих ценовых движений, которые формируются под действием несколько иных скачков     и, главное, вероятностей   и   , что нужно еще прогнозировать.

 

Следует также сразу подчеркнуть, что, поскольку, как я уже высказался ранее (в статье  Часть 2), методы обычной классической статистики и ее математический аппарат к формирующейся из суперпозиций вероятностных волн ценовой динамике плохо применимы и работают там с большими погрешностями, то анализ основанный на использовании наблюдаемых данных и соответствующие вероятностно-статические расчеты носят приближенный  характер.   

2. Практическое определение ранее действовавших вероятностей и нормированная скорость цены. Принцип применения этих параметров для расчета будущего распределения цены.

Средняя скорость движения цены за  интервал усреднения     равна

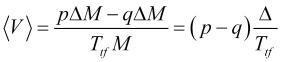                                                                                  (2.1)

и характеризует скорость изменения скользящей средней    (где   -  индекс бара) с соответствующим периодом усреднения, а не какие-то флуктуации скорости. Стало быть, средняя скорость есть практически вычисляемая величина

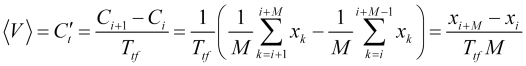                .         (2.2)

Приравнивая (2.1) к (2.2)  получаем эмпирически  определяемый параметр

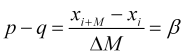               ,                                                                                           (2.3)

что назовем нормированной  скоростью  цены, т.к.  , а  . То, что    легко показать. В самом деле, к примеру, из  (1.1)  следует неравенство

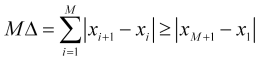              ,                                                                           (2.4)

откуда и  (2.3) вытекает   . Можно также представить  , а поскольку вероятность   ,  то и   . Из   (2.3)  и    находим  вероятности 

                 и  ,                                                                        (2.5)

а также еще одно выражение для нормированной скорости

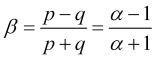                 ,                                                                                    (2.6)                               

где  параметр

                .                                                                   (2.7)

В дальнейших расчетах нам также понадобится параметр  

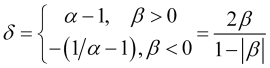               ,                                                            (2.8)

через который сама нормированная скорость выражается так

                .                                                                                            (2.9)

 

Вероятности (2.5) скачков, вычисленные на интервале   цен, являются  средними по этому интервалу и участвуют в формировании конечной цены , поэтому, если заранее в текущий момент , когда известна цена , знать эти  средние вероятности,  то можно предсказать, какая  будет цена    в  будущий момент  , точнее,   распределение вероятности   этой  цены.  При сопоставлении графиков цены   и нормированной скорости   (из которой вычисляются   и  )  прослеживается их сильное подобие (по совпадению местоположений их вершин), показывающее, что именно эта скорость (точнее, соответствующие ей вероятности) и формировала текущую цену  .

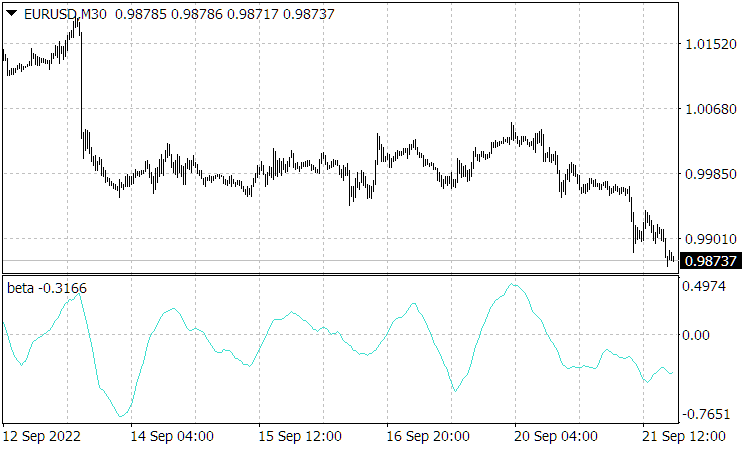
Рис. 2. На рисунке показан график нормированной скорости.

 

Это и понятно. В самом деле, из (2.3) следует . Значит, цену   будет  формировать из цены   массив будущих скоростей    или их средние по данному интервалу, величины

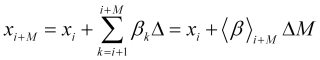  ,                         (2.10)                                                              

где средняя на будущем интервале нормированная скорость, отображаемая на ее графике в точке  

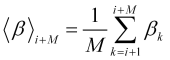            ,                                                     (2.11)

а средние на этом интервале вероятности   и  , находятся при подстановке    в формулы (2.5)  (очевидно, что если в (2.10)  член   порядка  , то возникает подобие графиков   и  ). Тогда спрогнозировав достаточно  гладкие функции   на   баров вперед мы и вычислим нужные вероятности    и  , что  позволят  рассчитать в момент   распределение  вероятности    будущей цены   и ее  нужные для торговли  характеристики (направление открытия позиций и положения стоп ордеров).

 

Суть применяемого здесь прогноза нормированной скорости такова. Временная функция   нормированной скорости колеблется в интервале    около своего математического ожидания равного нулю (или малой величины  , выражающей скорость глобального тренда, если таковой охватывает весь рассматриваемый участок). В этом случае, к примеру, простейший статистический прогноз по условному математическому ожиданию, что тогда примет вид  , будет приближать прогнозирующую функцию к нулю или   по закону  , т.е. по мере падения функции автокорреляции соответствующего процесса  , что только резко снизит число позиций, открываемых по условию типа  и сделает игру еще менее прибыльной, чем игру с тривиальным прогнозом по последнему значению . С другой стороны, динамика цены неплохо моделируется и предсказывается колебательными процессами суть чего была раскрыта в предыдущих статьях. На данном этапе развития теории, прогноз  функции   (имеющей колебательный характер) на   баров вперед делался на основе Фурье экстраполяции просчитываемой на основе эмпирических данных истории  , т.к. использование предложенной в прошлых статьях вейвлет экстраполяции в данном случае пока не дало заметных преимуществ.

3. Добротность тренда. Подход к оценке протяженностей текущего и будущего трендов, горизонт адекватной работы.

Если тренд длится время большее времени усреднения  , то закономерное приращение цены за время усреднения (согласно (2.1) и (2.3) ) порядка

               .                                    (3.1)

Неопределенность  этого приращения 

                ,                                                                                               (3.2)

тогда  полный  размах  движения цены (см. Рис. 1), когда она движется от одной границы канала индикатора Casual Channel до другой и при сем среднестатистически дрейфует с нормированной скоростью  ,   оценивается, как

                 ,                                                               (3.3)

где

                 .                                                                                 (3.4)         

Если играть по тренду, то желательно, чтобы величина смещения (3.1) была значительно больше неопределенности (3.2) этого  смещения

               ,                                                                (3.5)

откуда, и из (2.6) , (2.9),  для  требуемого времени  усреднения  получаем оценку снизу

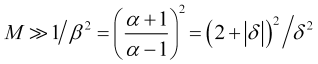              ,                                                   (3.6)

при выполнении которой, в соответствии с (3.4), время  усреднения  (в барах) рассчитывается, как 

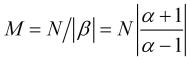              .                                                                                  (3.7)

Если же неопределенностью   приращения  цены пренебречь нельзя, то время усреднения считается как положительный корень квадратного уравнения (3.4)

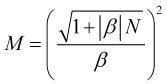               .                                                                                        (3.7.1)

 

Определим добротность тренда

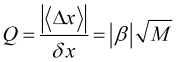               ,                                                                                        (3.8)

как отношение его закономерного приращения к его неопределенности или зашумленности. Вполне понятно, что для стабильной прибыльной игры чисто по тренду требуется высокая добротность  . Но просчитывающий величину добротности тренда индикатор «Quality Trend» (Рис. 3), в лучшем случае, для валюты достигает значения нескольких единиц. Более того, даже идентифицировав качественный тренд нет возможности определить, когда он кончится из-за непредсказуемости появления сильных внешних событий, способных нарушить собственную динамику рынка и завершить тренд или даже его развернуть. Поэтому, прибыльная стратегия может отталкиваться лишь от взятия прибыли на сравнительно небольших колебаниях в направлении тренда.

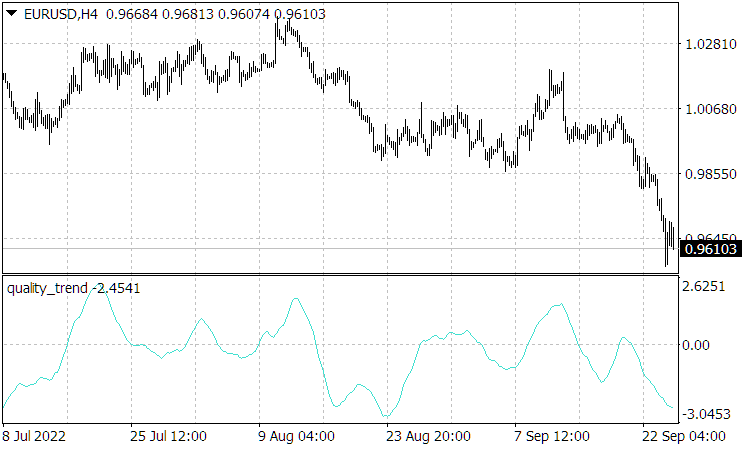
Рис. 3. Индикатор «Quality Trend», где приращение цены не берется по модулю, т.е. знак показаний индикатора указывает на направление тренда.

Отметим, что показания индикатора « Quality Trend», будучи пропорциональными  нормированной скорости, как то было показано из соотношения (2.10) для оной, оказываются по положениям своих пиков подобными ценовой истории и, соответственно, показания « Quality Trend» получаются не отстающими. Более того, показания этого индикатора могут и опережать (и часто и опережают) движения цены, поскольку уже до смены тенденции соответствующая скорость движения (роста для повышающего тренда или падения для понижающего) цены уменьшается. Однако, такое прогнозирующее поведение данного индикатора имеет место только при отсутствии сильных воздействий на рынок, нарушающих его собственное движение. И после таких воздействий в течении времени их релаксации показания индикатора « Quality Trend» становятся «обычными» отстающими, с отставанием определяемым его периодом усреднения.

 

Проанализируем поведение функции   и оценим на основе этого возможные протяженности трендов при условии отсутствия сильных сторонних воздействий на рынок. С уменьшением периода усреднения  могут увеличиваться вычисляемые на этом периоде значения   нормированной скорости (ведь ее «мгновенные» значения в постоянно изменяющемся рынке с большей амплитудой меняются, чем усредненные и, чем больше усреднение, тем меньше такие вариации), т.е.  в соотношении для добротности перемножаются члены, для которых   и наоборот  , что делает возможным существование максимумов у функции  . Однако, на очень малом интервале, когда действующие на нем истинные вероятности   и   скачков, из-за малого изменения на нем рыночной ситуации, постоянны, их статистически рассчитываемые величины   и   на этом малом периоде усреднения, скорее всего, будут сильно отличаться от истинных вероятностей, т.к. с уменьшением периода неопределенности   и   рассчитываемых на нем вероятностей растут. Поэтому, для периода усреднения  , обеспечивающего расчет более менее достоверных вероятностей, должны выполняться соотношения типа  , что определит его минимальное значение. В противном случае, когда   (но это, заметим, более широкий случай, чем случай больших колебаниях мгновенной нормированной скорости на малых интервалах усреднения, поскольку такое соотношение может иметь место и на больших интервалах при быстром изменением истинной вероятности  ), статистически рассчитываемые значения вероятностей нельзя использовать. Отметим, что в случаях сильных флуктуаций нормированной скорости рассчитываемая на ее основе функция   также сильно колеблется вблизи своего максимума, поэтому используемый для анализа рыночной ситуации максимум нужно выбирать такой, что формируется плавно, что, как следует из вышеизложенного, достигается при достаточно больших периодах усреднения. При выполнении же условия  , что предполагается в дальнейшей теории выполненным, оцениваемые вероятности   и  можно отождествить с действующими вероятностями   и   , что также тогда будем записывать, как   и  .

 

Далее, именно на тех участках, где постоянны вероятности   и   формируется устойчивый тренд, а падение превалирующей вероятности, что обозначим   (т.е.  ), будет уменьшать скорость роста приращения   и может даже (при достижении обратного соотношения  ) развернуть тренд, что приводит и к падению рассчитываемой добротности. Напротив, высокая добротность и ее рост говорит не только о сильном преобладании превалирующей вероятности   над  , но и о ее постоянстве и даже возрастании. Поэтому, чем больше добротность (3.8) тренда, тем больше вероятность, что он там, т.е.  на всем интервале  , действительно наличествует, а малая величина добротности   характеризует, напротив, флет. Понятно, также, что, если мы, увеличив период усреднения  , охватим им не только тренд (что тогда имеет протяженность  ), но и флет и, тем более, участок истории цены с противоположно направленным трендом, то добротность резко упадет; поэтому протяженность   тренда идентифицируется по пику добротности   .

 

Если же мы увеличим период   настолько, что охватим им однонаправленный тренд большего масштаба  , чем масштаб меньшего трендового участка с протяженностью  , то добротность тренда, напротив, как правило, будет возрастать, поскольку из-за подобия графиков в разных таймфреймах, при условии  , масштаб нормированных скоростей в (3.8) с ростом   меняться практически не будет, а   будет расти. Кроме того (и это требует уже коррекции подсчета величины  , фигурирующей в формуле (3.8) добротности), зашумление тренда резко повышают те крупные и мелкие хаотичные скачки цены, что выходят за рамки статистического распределения, формируемого «стандартными» (соответствующими рассматриваемой модели) скачками с вероятностями   и  . Такие нестандартные скачки одинаковы для всех масштабов и создают «дополнительное» зашумление тренда, поэтому вес этого дополнительного зашумления снижается с ростом масштабов, в которых идентифицируется тренд. Все вышеизложенное приводит к тому, что на функции   при наличии глобального однонаправленного тренда определится целый ряд пиков добротности, что будут возрастать с увеличением   или ростом масштабов идентифицируемых трендовых участков.

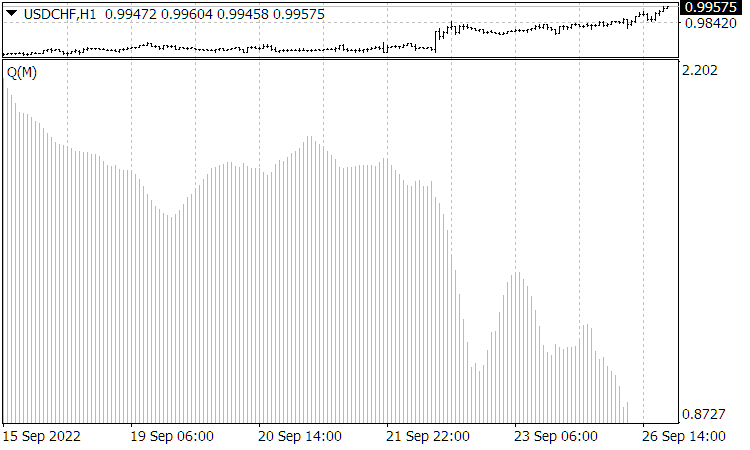
Рис 4. Функция    на текущий момент. Здесь на шкале абсцисс фигурирует не время, а период усреднения для «Quality Trend»   от 10 до 160.

  

И, наконец, игра идет не на уже сформированной истории, а в реальном времени, поэтому, необходимо знание ряда прогнозов  , основанного на множестве   прогнозных значений нормированной скорости. Стало быть, для оценки возможной протяженности   вновь возникшего тренда нужно пройтись по всему спектру периодов усреднения и выявить ряд максимумов прогнозной добротности  , когда ее прогнозирование идет вперед на   баров от текущего бара, т.е. вычисляется

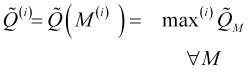               ,                                                                 (3.9)                 

где   - есть функция идентификации -ГО максимума. При этом нужно также  установить и максимальный пик

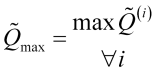                 ,                                                                                    (3.10) 

и  соответствующую ему точку на шкале усреднений.  

 

Очевидно, что на меньших интервалах усреднения   идущих до максимального пика   прогнозной добротности, если, конечно, на этих интервалах добротность тоже значима и растет монотонно или последовательностью возрастающих (опирающихся также на растущую подушку) пиков, будет иметь место соответствующий однонаправленный тренд (с откатами после каждого пика добротности). После   максимального пика   добротности, когда она начинает падать в масштабах соответствующего усреднения  , имеет место замедление тренда, что может вскоре привести к его развороту. Последнее наиболее вероятно, когда сама величина пика   очень значима в том смысле, что добротность для рассматриваемого биржевого инструмента редко достигает значений больших  . Во любом случае, усиливающийся тренд будет продолжаться до отметки    до достижения которой нужно закрыть открытую по этому тренду позицию.   

 

Попробуем теперь оценить протяженности   трендовых участков, что перспективны для торговли, которые не обязательно должны быть равны прогнозируемой протяженности    тренда. Во-первых, прибыль, из-за малой достоверности работы самой прогнозирующей математики (что относится ко всем ее видам, хоть различным частотным и иным экстраполяторам, хоть нейронным сетям, хоть ARIMA и т.д.) нужно брать на сравнительно небольших – ближайших участках   идентифицируемого будущего тренда  , на которых этот тренд с наибольшей вероятностью должен формироваться. Поэтому, что собственно следует и из предыдущего абзаца, обязательно должно выполняться неравенство  .  Во-вторых, в представленной модели используются оценки будущих значений  вероятностей   и   и предполагается постоянство средних скачков   цены, что есть прогнозы, работающие, когда рынок развивается по инерции и по собственным законам. Однако, как было показано в первой статье (Часть 1)  интервал предсказуемого развития рынка начинается от последнего сильного внешнего события и продолжается вплоть до наступления последующего такого события. Поэтому, существует горизонт адекватной работы   всего разрабатываемого здесь математического аппарата, где величина   равна числу баров от текущего бара до будущего бара наступления сильного внешнего события. Если, что крайне важно, попытаться использовать такой математический аппарат за  данным горизонтом, то это приведет к некорректности его работы и к неизбежным убыткам. Для определения возможного горизонта адекватной работы подобного математического аппарата необходимо отталкиваться от фундаментального анализа или исследований экспертов, оценивающих силу влияния всех происходящих и будущих политических  и экономических событий на состояние рынка.  Поэтому, протяженность перспективного для торговли участка прогнозируемого тренда оценивается сверху соотношением

              ,                                                                        (3.11)   

а снизу его  нужно  оценивать на основе ранее установленного  соотношения  малости  неопределенности (флуктуаций) вероятности по сравнению с самой вероятностью

               ,                                                                                    (3.12)

что также определяется по графику прогнозируемой добротности   и соответствует тем участкам, где этот график изменяется достаточно плавно. Ожидаемое же на этом участке тренда закономерное изменение цены

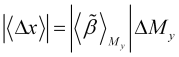               ,                                                                                    (3.13)

что соответствует порядку получаемой прибыли при чисто трендовой стратегии.

 

В-третьих, выбор протяженности   участка тренда для игры должен также основываться на представляемых ниже расчетах, что, по существу, позволяют установить интервал   величин  , на которых, в принципе, в заданных рыночных условиях возможно получение среднестатистической прибыли, т.е.  . Кроме всего этого, трейдер сам выбирает таймфрейм для игры, а истинная (а не модельная, рассчитываемая по формуле (3.8)) добротность падает с уменьшением таймфрейма из-за зашумления цены на всех таймфреймах ее немодельными – одинаковыми на всех таймфреймах – скачками. Поэтому трейдеру на выбор предлагаются или варианты с высокой добротностью тренда, но длительным ожиданием прибыли, что имеет место для больших таймфреймов; или быстрое получение прибыли, но на трендах с более низкой добротностью (и, соответственно, большими рисками потерь), что характерно для малых таймфреймов.

4. Вероятностный расчет тех значений тейкпрофита и стоплосса, что дают максимальную прибыль при постоянстве действующих вероятностей и выражение последней.

Постановка задачи. 

Цена движется единичными скачками в вертикальном измерении от нулевой отметки. Вероятность скачка цены вверх , вероятность скачка цены вниз ,  соответственно,   Вероятности, конечно, здесь есть прогнозируемые средние    и , что сейчас не суть важно.  Вверху на расстоянии «а»  находится тейкпрофит, внизу – на расстоянии «в» от нулевой отметки стоплосс  (при рассмотрении в координатных осях  ).  Найти параметры биржевой игры, обеспечивающие максимум  прибыли.

 

Решение задачи.

              Цена может попасть в точку с координатой «n» или  снизу из точки  «n-1»  или  сверху из точки   «n+1». Поэтому, вероятность нахождения цены в точке «n» равна 

               .                                                                                     (4.1)

Из (4.1) получаем уравнение в конечных  разностях 

                                                                                (4.2)

 

Случай равновероятных  скачков. 

              Рассмотрим сначала случай равновероятных скачков    При этом из  (4.2) получаем

               ,                                           (4.3)

где    - постоянная, откуда находим

               .                                                                                                 (4.4)

              Вероятность  нахождения цены  в стартовый для  ее движения момент на нулевой отметке  , поэтому, 

               .                                                                                                      (4.5)

              Положим, что стоплосс «в» в сумме с тейкпрофитом «а»  составляют характерный, оцененный здесь (3.4) в средних скачках   цены, размах   движения цены в за период   ее усреднения (и движения), на котором полагается постоянство вероятностей   и  . Вероятность, что цена, находящая уже в точке стоплосса, где  , достигнет тейкпрофита равна нулю  , подставляя что в (4.5),  получим

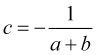                                                                                                                       (4.6)

что  вместе  с  (4.5) даст вероятность  достижения тейкпрофита равную

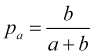                                                                                                                        (4.7)

а вероятность срабатывания  стоплосса

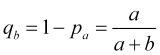               .                                                                                         (4.8)

Поэтому при равновероятных скачках цены в разных направлениях средняя прибыль в числе скачков

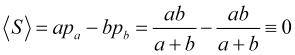                                                                          (4.9)

всегда равна  нулю (спред, конечно, делает ее отрицательной) независимо от положения  тейкпрофита и  стоплосса, которые  могут  быть любыми. 

 

Есть тенденция движения к тейкпрофиту.

 

Пусть     (точнее   ) тогда,  перемножая все уравнения (4.2), находим

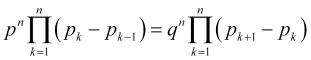               ,                                                      (4.10)

сокращая в (4.10) одинаковые множители, используя обозначение (2.7)   и учитывая, что   ,  получим 

                .                                                                                 (4.11)

Представим    в  виде суммы разностей смежных членов ряда    вероятностей, используя далее соотношения (4.11) и формулу суммирования геометрической  прогрессии

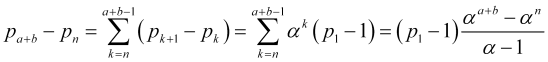 ,             (4.12)

 , поэтому,

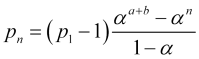                                                                                                   (4.13)

 , следовательно,

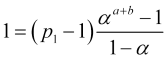              ,                                                                                           (4.14)

деля  (4.13) на (4.14)  находим вероятность достижения тейкпрофита  «а»               

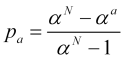              .                                                                                                      (4.15)

Вероятность срабатывания стоплосса, соответственно,  равна  ,  тогда  средняя на одну позицию прибыль в скачках   цены равна

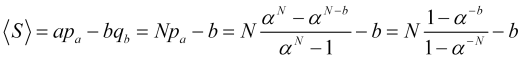               ,         (4.16)

что  является  в представлении (4.16) функцией  величины стоплосса  «в», который в  этом представлении есть просто число скачков, а фактически есть величина   . Прибыль же есть   .  Понятно, что с ростом вероятности движения цены в сторону открытой позиции средняя прибыть (4.16)  растет и, в пределе, когда    принимает  значение   ,  т.е.    растущая функция  от   .

 

Найдем максимум среднестатистической прибыли (4.16) при условии заданных величин N  и   , для этого приравняем ее производную к нулю

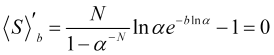                ,                                                             (4.17)

откуда находим величину искомого стоплосса в скачках    цены 

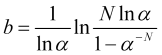               .                                                                                        (4.18)

 

Поскольку   , то  логарифм   положительный и    и, соответственно, величина  логарифма 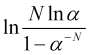   должна быть положительна, что выполняется  при условии

               ,                                                                                               (4.19)

или   

      ,                                                      (4.20)                                                                                      

где  . Неравенство (4.20) строго выполняется при любом  , поскольку экспонента  проходит выше прямой   и только касается ее в точке  . 

Вторая  производная  от  функции  (4.16)

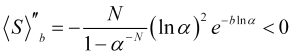                                                                            (4.21)

при этих  условиях всегда  отрицательна, т.е.  кривизна  функции     направлена вниз и мы имеем в  точке  (4.18) максимум.  Вид функции (4.16)  при N=100 и    показан  на  рисунке 5. 

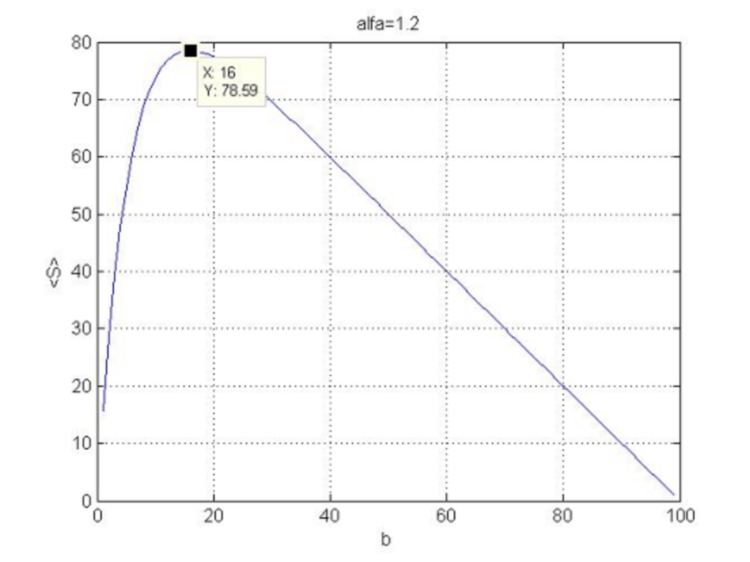
Рис.5. Зависимость функции  прибыли от  стоплосса.

Подчеркнем, чтобы средняя прибыль   была  положительна  коэффициент   должен существенно превышать единицу. В самом деле,  если    ,  где    и можно пренебречь вторым членом разложения, оставив только первый член   ,  то средняя за сделку прибыль 

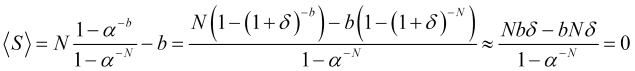    (4.22)

будет (как и в случае равных вероятностей противоположных скачков) равна нулю. Если же вторым членом разложения пренебречь нельзя, то с учетом, что количества скачков   достаточно велики или , имеем

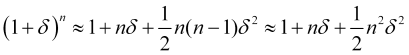               ,                               (4.23)

что даст положительное значение для средней прибыли  (4.16)

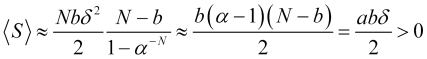               ,                          (4.24)

поскольку   ,     (и, стало быть,  ).

              Приближенная средняя прибыль (4.24)  относительно аргумента представляет собой перевернутую квадратичную параболу, максимум которой достигается при   (что есть равенство стоплосса и тейкпрофита), когда   .

 

Теперь очень существенный момент. В выше представленной теории вычислялась  средняя  прибыль, что рассчитывалась только на основе средних значений цены, которая, на самом деле, сильно  флуктуирует и может размахами своих флуктуаций даже сильно превышать соответствующие ее средние смещения. Стоп ордера же (тейкпрофит и стоплосс) закрываются же не по средним значениям цены, а, как раз, по краям полосы ее колебаний. Поэтому, чтобы представленный, отталкивающийся от средних величин, математический аппарат более менее работал, стоплосс должен быть много больше   неопределенности   цены (чтобы его флуктуационное срабатывание мало отличалось от модельного срабатыванию по среднему и этим флуктуациями можно было пренебречь), т.е., согласно (1.2), 

                .                                                                                                         (4.25)

Тогда, используя выражения (3.7.1) для периода усреднения  получим из (4.25)  функцию для  которой должно выполняться  неравенство

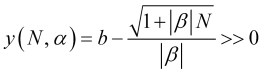               ,                                                                 (4.26)

являющееся критерием малости флуктуаций цены, где   находится из соотношения  (2.6). Подставляя в (4.26) стоплосс (4.18)  построим  график (Рис. 6) этой  функции, из которого видно, что такая функция никак не намного больше нуля, а, напротив, принципиально отрицательна, т.е. соотношение  (4.25), при оптимальном стоплоссе  (4.18) никогда не выполняется.

 

Код MATLAB

>> [N,a]=meshgrid([3:200],[1.01:0.01:3]);
>> b=log(N.*log(a)./(1-a.^(-N)))./log(a);
>> beta=(a-1)./(a+1);
>> s=(N.*beta+1).^(1/2)./beta;
>> y=b-s;
>> plot3(N,a,y)
>> grid on

   

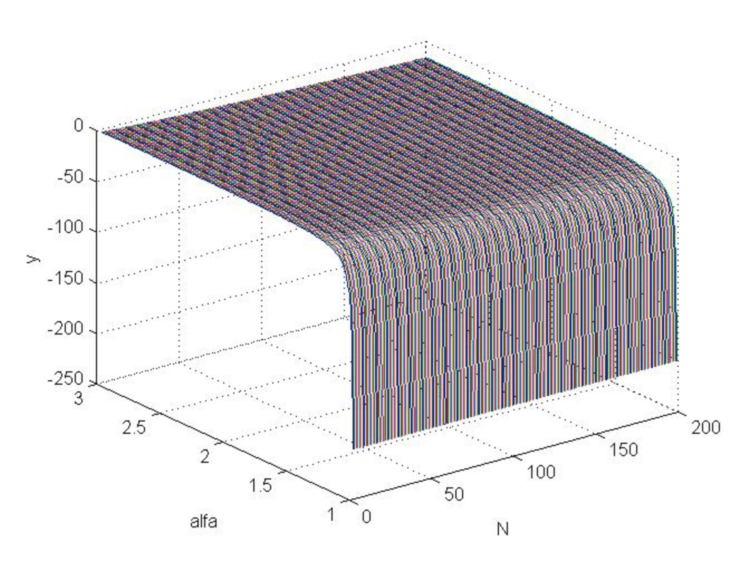
Рис.6. График  функции «y» при изменении  Альфа от 1 до 3  и    N  от 3  до 200.

 

 

Таким образом, использование рассчитанных выше величин стоп ордеров приведет к среднестатистическим убыткам, поскольку флуктуации цены оказываются принципиально больше оптимального в модели ее усредненного движения стоплосса

               .                                                                                                              (4.27)

Значит надо изменять размер самого стоплосса, а не искать период усреднения, делающий сравнительно малым  (4.25)  оптимальный  стоплосс  (4.18) (поскольку эта задача не имеет решения), что, конечно,  изменит и прибыль.

 

Оптимальный для модели усредненного движения цены тейкпрофит, вообще говоря, совпадает с точкой прогнозного скользящего среднего цены, отстоящей от текущего бара на  баров вперед. Но если учитывать сильные отклонения цены от среднего, на которых и закрываются стоп ордера, то, как видно из графика индикатора «Casual Channel» (Рис.1), для обеспечения прибыльной игры такой оптимальный тейкпрофит нужно уменьшить на величину больше среднего отклонения

              ,                                                                                                  (4.28)

где коэффициент   должен  быть несколько больше единицы для слабых трендов (на коих прибыли практически нет) и порядка   для сильных трендов,  являясь здесь именно тем  параметром точное  значение которого нужно искать путем оптимизации,  а стоплосс нужно увеличивать на туже величину, т.е. 

               .                                                                                                  (4.29)

Тогда, стоплосс, как величина отстоящая от среднего значения возможного отклонения (за   будущих баров) цены против открытой позиции на  , будет срабатывать гораздо реже и, более того, с вероятностью меньшей  , а тейкпрофит будет срабатывать, наоборот, чаше с вероятностью большей  . Соответственно, для максимальной прибыли  получим оценку

               , (4.30)

где    - величина из (4.16),   или, с учетом   (3.7.1)

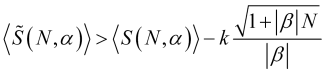                                                                    (4.31)

функцию чего (при оптимальном b  из  (4.18))  можно построить и найти  максимизирующее  ее  значение  N ,  а затем из  него период усреднения. 

 

Код MATLAB для  k=3

>> [N,a]=meshgrid([3:200],[1.01:0.01:3]);
>> b=log(N.*log(a)./(1-a.^(-N)))./log(a);
>> beta=(a-1)./(a+1);
>> s=(N.*beta+1).^(1/2)./beta;
>> s0=N.*(1-a.^(-b))./(1-a.^(-N))-b;
>> Profit=s0-3*s;
>> plot3(N , a, Profit)
>> grid on 

 

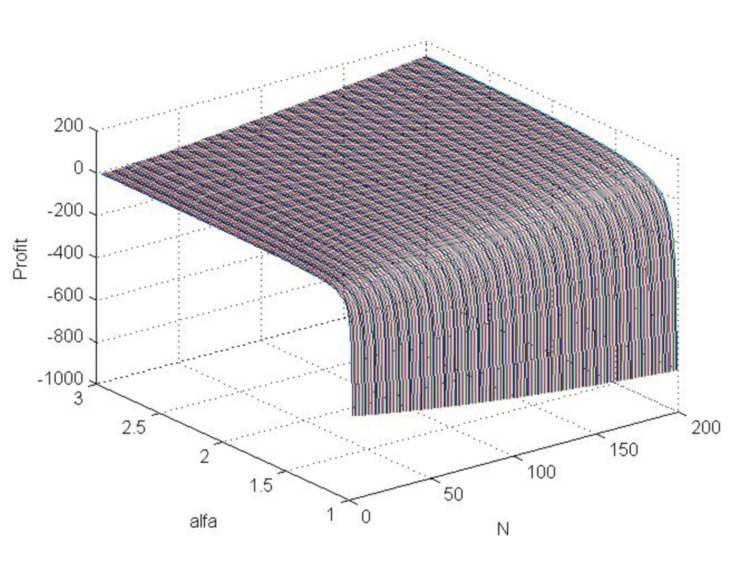
Рис.7. График функции прибыли (в модельных скачках цены) при изменении  Альфа от 1 до 3  и N от 3 до 200.

Из графика видна, что прибыль с положительным математическим ожиданием, в принципе, возможна и возрастает при увеличении  Альфа  и   N. 

 

Для нахождения лучшего - перспективного для торговли - периода  усреднения нужно построить прогнозную функцию добротности , для чего был разработан скрипт «CalculateScientificTradePeriod», и определить этот перспективный период    по тому положению максимума    функции добротности, где  , когда этот максимум достигается плавно (выполняется соотношение (3.12)) и не расположен дальше горизонта адекватной работы. И, если таким способом  найденное значение  обеспечит положительное (и превышающее, как минимум, пару спредов) значение профита (4.31) и достаточно большую вероятность выигрыша  (4.15), что и задает интервал  , то  на него, в данной ситуации, и должно опираться торговое решение. Для расчета оптимальных – максимизирующих среднюю прибыль - тейкпрофита, стоплосса и определения дальнейшей тенденции движения цены и ее будущей траектории был разработан индикатор «ScientificTrade», алгоритмы которого опираются на всю выше представленную теорию.

 

Заметим, что алгоритм скрипта «CalculateScientificTradePeriod» очень ресурсоемкий, поэтому используется именно скрипт, а не индикатор, что запускал бы этот алгоритм на каждом тике и подвесил бы компьютер. Для отображения информации рассчитываемой скриптом используется  индикатор «FindScientificTradePeriod».  

 

 

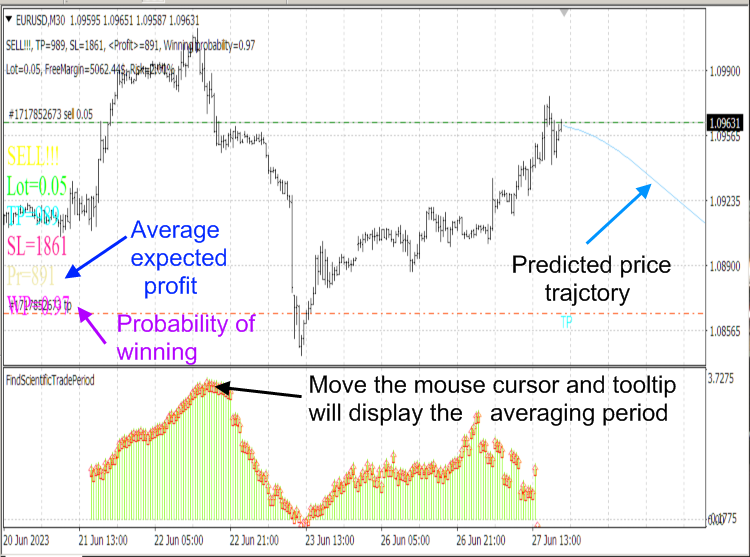
Рис.8.  Индикаторы «ScientificTrade» и  « FindScientificTradePeriod ». 

 

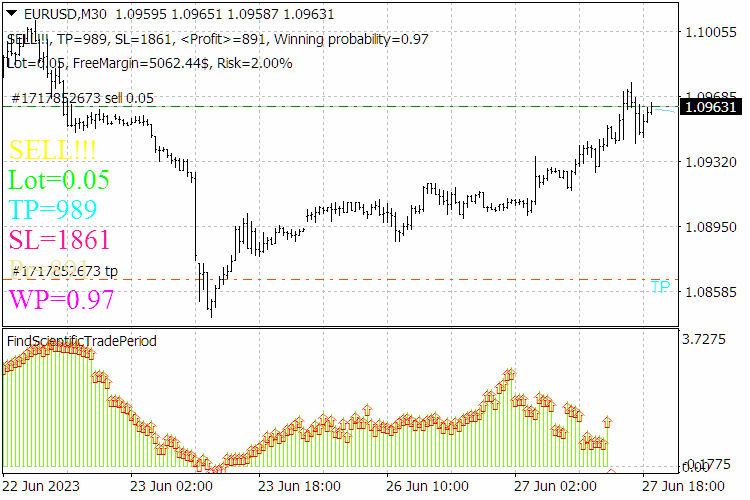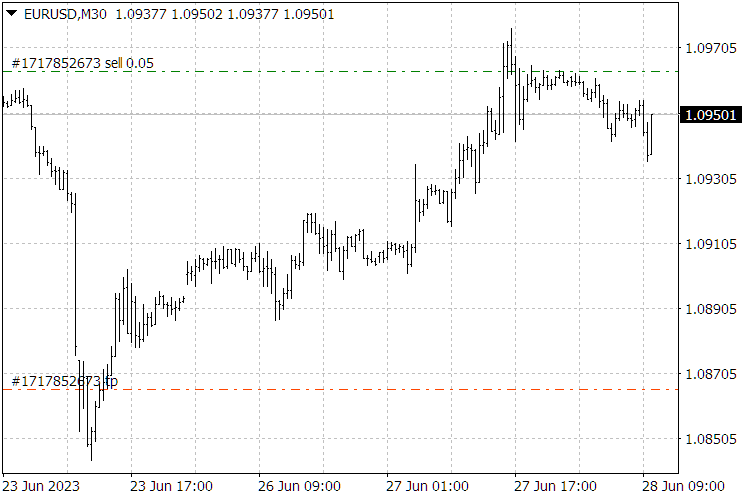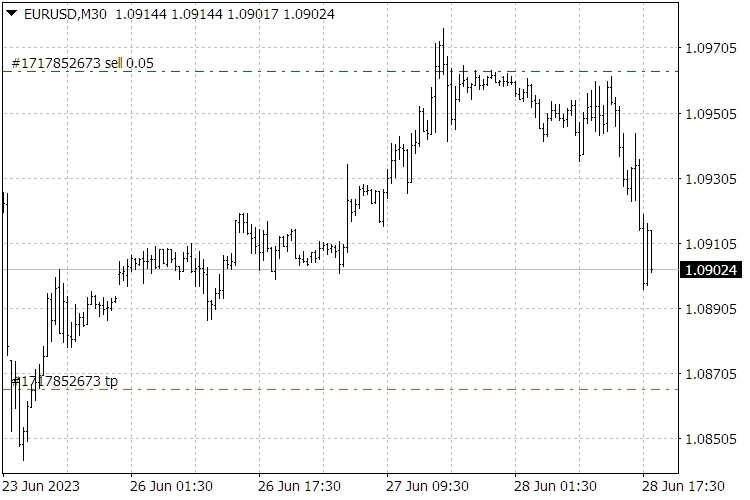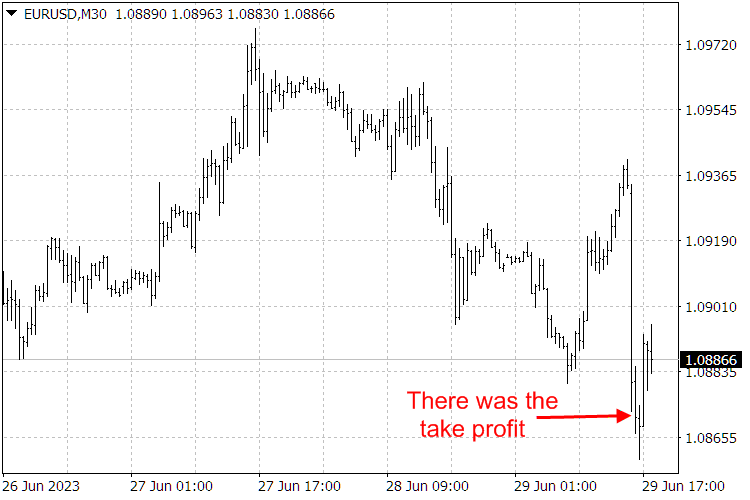
Рис.9.  Результаты  работы  индикатора    «ScientificTrade» . 

5. Неустранимая в рамках самого математического аппарата погрешность используемых здесь расчетов. Подход к идентификации моментов закономерно происходящих отскоков и разворотов цены.

Как было уже ранее сказано, тенденции предсказываемые индикатором  «ScientificTrade»  и рассчитываемые данным индикатором положения стоплосса и тейкпрофита  отталкиваются от прогнозных  значений   и  , что могут оказаться ошибочными и из-за ненадежности работы самого прогнозирующего аппарата  (в данном индикаторе Фурье экстраполятора). Поэтому такие прогнозы могут оказаться ложными и в рамках горизонта адекватной работы всего выше представленного  математического аппарата.

Для исключения хотя бы части случаев ложных математических прогнозов тенденции, рассчитываемые индикатором «ScientificTrade» на интервале, определяемом для него с помощью  скрипта  «CalculateScientificTradePeriod»,  должны  совпадать с прогнозными тенденциями, даваемыми авторитетными экспертами от фундаментального анализа на данном интервале. Понятно, что, если и «ScientificTrade»   и эксперты дают одинаковый ложный прогноз (о чем мы заведомо знать не можем),  то потери  также  неизбежны. Следует, однако, заметить, что эксперты, по моим наблюдениям (достаточной статистики нет, поэтому сие мнение субъективно), чаше ошибаются, чем  индикатор «ScientificTrade» в совокупности со скриптом «CalculateScientificTradePeriod», что, на мой  взгляд, обусловлено тем, что  собственные законы развития рынка оказывают на него более сильные воздействия, чем большинство внешних событий, и вызывают также смены тенденций, моменты наступления которых (в отличии от представленной здесь теории) эксперты установить не в состоянии; причем такие, вызываемые внутренними причинами развороты рынка возникают часто до наступления сильных внешних событий и чаще их, о механизмах чего будет сказано чуть ниже.        

Для выражения сути выше обозначенной проблемы следует сначала заметить, что  цена, даже при развитии рынка по собственным законам (когда цена не подталкивается сильными внешними событиями), не всегда движется эквидистантными скачками – сия концепция есть использованная здесь упрощенная модель, позволяющая хоть что-то понять и рассчитать в хаосе рынка. В действительности цена изредка, вопреки средне статическим тенденциям, по которым она медленно в среднем (но с большими флуктуациями) в определенную сторону дрейфует, совершает кратковременные (выходящие за рамки классической статистики) сильные движения. Причем, если такие сильные движения не вызываются внешними воздействиями на рынок, а обусловлены его собственными процессами, то они, как правило, направлены против статистических тенденций; поэтому, такие сильные движения сбивают стоплоссы и создают максимальные потери у большинства мелких трейдеров.

Фактически (если исключить из рассмотрения целенаправленное сбивание стоплоссов поставщиками торговых услуг и котировок) здесь работает принцип Ле Шателье в совокупности с диалектическим законом перехода количества в качество, когда при достижении конкретной, также зависящей от рынка, планки роста (или падения) определенного рыночного инструмента происходит резкий скачок качества, что, в соответствии с принципом Ле Шателье (действие коего распространяется на любую сложную находящуюся в равновесии систему, включая и экономику, которая, точнее, основное время эволюционирует, проходя через близкие квазиравновесные состояния), стремится противостоять росту вышеупомянутого количества, резко (скачком) его снижая. В такой ситуации, поскольку рынок, как система, при его монотонном развитии постепенно проходит через близкие квазиравновесные состояния, принцип Ле Шателье на его небольшие изменения не реагирует, а действует скачком, когда уже накапливаются большие количественные изменения в данной системе. С позиций волновой модели (Часть 1)  рынка такие скачки можно объяснить набегающей близостью (или равенством) фаз парциальных вероятностных волн соответствующего рыночного инструмента.

Теоретически приближение естественного скачка цены может быть идентифицировано посредством соотношения  (II.17). Однако, практически о приближении такого скачка гораздо проще судить по графику прогнозной добротности. А именно, если  прогнозная добротность в некий будущий момент   (отстоящий от текущего бара на   баров) превысит или приблизится к определенной критической для данного рыночного инструмента на соответствующем таймфрейме величине  , т.е.     (если рассматривать текущую, а не прогнозную ситуацию, то просто  ), то в этот момент возможна смена глобальной тенденции.

Вообще, естественные скачки цены (любого характера, как глобальные, так и мелкие) на уровне амплитуд вероятности ее распределения описываются антисимметричными вейвлетами (Часть 1  соотношение (I.17)), когда после реализации близости и даже равенства фаз всех парциальных ценовых волн, из которых складывается ее полная амплитуда вероятности, фаза последней, за счет антисимметрии соответствующих вейвлетов, инвертируются, что приводит к резкому изменению реально действующих вероятностей   и , что будут тогда в корне отличаться от прогнозных вероятностей  и  .  Понятно, что такие критические ситуации, когда за счет собственных законов рынка происходят скачки качества, нужно  или  исключать из торговли. Заметим, кстати, что подобная антисимметрия парциальных ценовых волн,  обеспечивает их  сходство с фермионами, чем обусловлено постоянное стремление к смене ценовых уровней их значительная ширина (что трактуется как результат флуктуаций цены). Поэтому, эволюцию рыночных инструментов  более правильно описывать не обычной статистикой, а статистикой Ферми-Дирака.  

В связи с описанным эффектом инверсии ценовой волны (Часть 1) на самой интенсивной фазе ее движения (максимуме модуля амплитуды ее вероятности) забавно также заметить, что, казалось бы, наиболее оптимальные, основанные на самой высокой добротности   параметры торговли должны были бы обеспечивать и максимальную прибыль. Однако, эти параметры торговли, что, так или иначе (интуитивно или на основе плавных математических экстраполяций), выявляемы большинством трейдеров на основе привычных (характерных для всего наблюдаемого в физическом макромире) представлений о монотонности процессов и их инерции, на самом деле, обеспечивают максимальные убытки.

В результате и здесь оказывается верным житейский «закон», что деньги текут к деньгам, основная масса которых находится в банках, поэтому рынок вытягивает деньги из мелких трейдеров. Ведь рынок, по выше упомянутым причинам, по мере своей эволюции, в конце концов, вдруг (что он делает регулярно) начинает развивается вопреки прогнозируемым основной массой трейдеров тенденциям или, как раз, наоборот, играя против этих трейдеров, в чем нет людского «злого умысла». Дело в том, что у рынка, нет постоянной инерции (на основе коей до поры до времени «обогащаются» мелкие трейдеры), характерной для физических макропроцессов, и, в определенные (непредсказуемые для экспертов и трейдеров невооруженных соответствующей теорией) моменты, он с легкостью под действием своих работающих на его эмерджентном уровне законов (в чем и состоит его сильное влияние на собственные процессы, превосходящее влияние даже сильных внешних событий) способен переворачивать фазы всех отдельных парциальных ценовых волн, испускаемых разными участниками рынка. 

В целом рынком правит хаос. Поэтому, если какой-то рыночный порядок идентифицируется в максимальной степени, то он должен быть нарушен, что можно считать достаточно хорошо соблюдающимся законом рынка, без знания которого невозможно получать стабильную прибыть.

Заключение

В статье представлен разработанный мною инженерный подход к созданию прибыльной стратегии биржевой игры. Этот подход показывает, что рынок оставляет трейдеру чрезвычайно узкий набор условий для открытия и закрытия позиций, что могли бы обеспечить ему  игру с положительным математическом ожиданием прибыли. И этот набор условий неидентифицируем классическими методами. Но игра с положительным математическим ожиданием прибыли, в принципе, возможна, что в какой-то мере подтверждает мой личный использования (правда, статистика пока невелика) индикатора «ScientificTrade» , который основан на этом инженерном подходе и использовании для прогнозирования Фурье экстраполяции. Конечно, этот индикатор еще нужно совершенствовать и на текущий момент его главный недостаток заключается в использовании недостаточно точного математического аппарата прогнозирования.