Введение

Первоначально после представления основ волновой вероятностной модели цены мною планировалось сразу перейти к рассмотрению  процесса случайного блуждания цены в волновом вероятностном поле с получением практически важных (для трейдинга) выводов. Но в обсуждении первой части мне были заданы существенные, на мой  взгляд вопросы, которые я бы сформулировал так: «Как  соотносятся  случайные блуждания цены с волновой моделью ее  эволюции и как трактуемы соответствующие мгновенные состояния (значения) цены, что мы видим на графиках, с  позиций  данной  модели?» И я счел правильным в отдельной статье ответить на эти вопросы с представлением всех сопутствующих сему теоретических представлений, что также крайне важны, так как используются для прогнозирования волнового вероятностного поля.

Уравнение эволюции вероятностного поля цены

Прежде чем устанавливать суть отношений случайных блужданий цены с ее вероятностным волновым движением, уместно сначала представить более подробно саму аналитику последнего с выводом уравнения, которому подчиняется волновое поле. 

Уравнение непрерывности вероятностного поля     цены

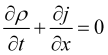           ,                                                                                                    (1)

где   ,    - поток вероятности ценового поля, а - скорость этого  потока. С учетом уравнения

                                                                                                                         (2)

на собственные значения оператора 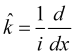   для волнового вектора и их действительного характера, поток вероятности можно  записать так

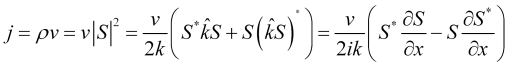             ,    (3)

где     волновой вектор  поля цены.

Волновое поле   определяет истинное состояние цены. Допустим, что функция волнового поля гладкая, что обуславливает существование ее производной   по времени. Тогда, будущее значение    функции волнового поля можно найти через ее производную. И если на рынок не действуют сильные внешние воздействия, что нарушают гладкость , то знание волнового поля   в текущий момент времени позволяет его рассчитать в последующие моменты времени, что, подчеркнем, справедливо внутри временного интервала, ограниченного сильными внешними воздействиями на рынок. В этом случае уравнение эволюции цены записывается в виде

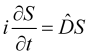           ,                                                                                                         (4) 

где   линейный (из-за принципа суперпозиции парциальных составляющих волнового поля ) оператор эволюции.

Интеграл  от плотности вероятности цены по всей ценовой шкале есть константа или единица, если плотность вероятности нормирована, поэтому:

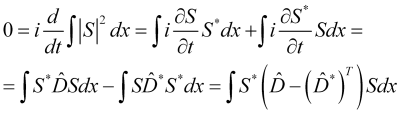                                           (5)

где    - операция транспонирования. Стало быть,  

         ,                                                                                               (6)

то есть оператор эволюции эрмитов. Найдем его вид.

Используя (4) и (6), получим

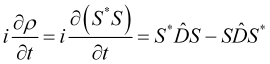                                                                          (7)

С  другой стороны, из (1) и (3) имеем

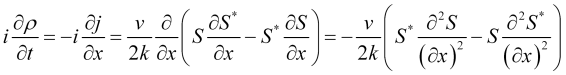         (8)

Сравнивая  (7) и (8), видно, что оператор эволюции имеет вид

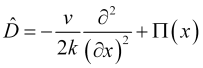              ,                                                                          (9)

где    имеет смысл потенциала, в котором распространяется вероятностное поле цены; и тогда уравнение для расчета эволюции волнового поля цены запишется

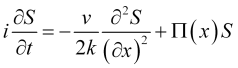              ,                                                                (10)

что по своему аналитическому содержанию тождественно одномерному уравнению Шредингера. В самом деле, учитывая, что в квантовой механике  импульс  , множитель в уравнении (10) для квантовой теории  равен 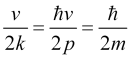 .  Заменяя  этот множитель в (10)  на его квантомеханический аналог и умножая (10) на постоянную планка    и заменяя   на  привычную для физиков    получим

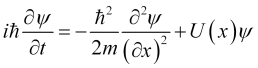                                                                         (10.1)

одномерное  уравнение  Шредингера, где квантомеханический потенциал связан с потенциалом поля цены соотношением  , поскольку потенциал  имеет размерность частоты, а квантомеханический потенциал имеет размерность энергии.   

По-видимому,  уравнение (10) есть общее уравнение эволюции вероятностных волновых полей, что могут иметь различный генезис.

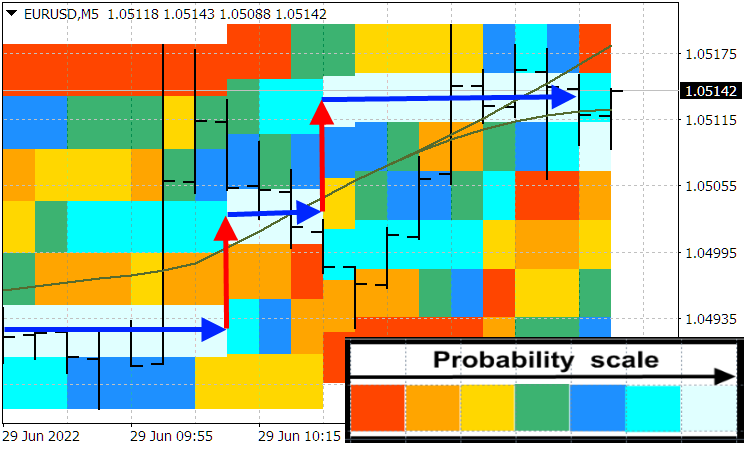
Отметим, что если потенциал   имеет характер глубокой ямы, которую ценовая волна не преодолевает, отражаясь от стенок этой ямы (и чуть – с экспоненциальным затуханием - проникая в нее), то есть движение цены финитное, то, в соответствии с элементарными квантово-механическими решениями данной задачи, получается дискретный спектр ценовых значений.  Что, собственно, также (даже в этой простейшей линейной модели) будет объяснять существование ценовых уровней, между которыми цена перемещается скачками. И, зная текущий потенциал, мы легко можем найти эти ценовые уровни, между которыми цена перемещается скачками. И практика показывает, что такие ценовые уровни действительно существуют. На следующем скриншоте показаны синими стрелками эти ценовые уровни, а красными стрелками показаны ценовые скачки. Из рисунка также видно, что при ценовых скачках значение цены становится более неопределенным, чем ее значение на ценовом уровне.

Индикатор Probabilities distribution of price

Критерий приближения скачка цены

В первой части было сказано, что скачки цен могут вызываться не только внешними, но и внутренними причинами. И если в первом случае предсказать появление таких скачков на основе истории котировки невозможно, то во втором – отнюдь не менее распространенном - случае имеется шанс распознать их приближения. Остановимся в самых общих чертах на аналитике идентификации приближения скачков второго типа. Для удобства дальнейшего анализа будем нумеровать формулу (N) первой части  как  (I.N).  Докажем сначала, что соотношение неопределенности (I.16)  минимизирует вейвлет Морле, доказательство чего было, для краткости, опущено в первой части. 

Соотношение (I.16) достигает минимума  при  , что является корнем (I.15)  при дискриминанте, равном нулю.  Введем операторы   и  ,  тогда  (I.11)  для своей минимальной величины запишется  так

              .                                                                  (11)

Из (11) следует

                                                                                                           (12)

или

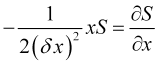              ,                                                                                     (13)

что  имеет решение 

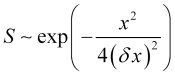                 ,                                                                               (14)

Соотношение  (14), с учетом того, что оператор волнового числа удовлетворяет уравнение на собственные значения

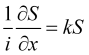                 ,                                                                                                   (15)

что имеет решение  ,  и даст, после нормировки, формулу  (I.17)  или   

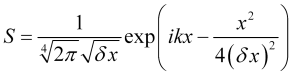                  .                                                  (16)               

Минимум (I.16) или минимум произведения неопределенностей   достигается, когда вектор состояния  не меняется при Фурье преобразовании, что имеет место, если вероятностное поле имеет вид (16). Гаусс, моделирующий  гармоническую составляющую поля в обоих представлениях (координатном и частотном), симметричен. Более-менее симметричным является и плотность распределения вероятности цены вокруг своего среднего на горизонтальном участке движения цены или до скачка. Однако при скачке функция плотности вероятности , а значит, и огибающая вероятностного поля   цены, становится асимметричной, что говорит о росте произведения . Таким образом, рост величины   может служить критерием возможного скачка цены, если он вызывается внутренними рыночными процессами.

Тогда, в соответствии с соотношением (11), что минимизирует величину  , можно заключить, что возрастание принципиально положительной функции 

                                                                                                        (17)

может служить критерием приближающегося скачка цены.

Редуцируемые значения цены и их случайные блуждания

Проблема о сути взаимосвязи и отношении видимых на мониторах значениях цены и ее волнового вероятностного поля очень непростая и требует для своего разрешения не только рассмотрение чисто технических аспектов формирования цен, но и глубокого философского анализа. Поэтому мне также придется здесь это представить. 

Итак, сначала о чисто технических  аспектах ценообразования. На графиках котировок мы видим лишь те значения  цены, что (1) или предоставляет нашему брокеру или дилеру (у которого мы открыли торговый счет) поставщик или агрегатор ликвидности, (2) или формирует сам банк или прайм-брокер, если мы открыли счет у такового. Назовем эти видимые на мониторах значения цены редуцируемыми. Появление таких редуцируемых цен имеет свою историю, что важна для понимания всей сложности взаимосвязей их образования и, вкратце, такова. Спрос и предложение, что определяют цены, сначала формировали крупные банки под надзором национального регулятора.

Эти банки должны были ориентироваться  на общемировые спрос и предложение. Сбором и обработкой информации по курсам Форекс занялась компания Thomson Reuters, что поставляла эту информацию в реальном времени, базируясь на крупных сделках множества международных финансовых организаций, задавая банкам ориентир для цен покупки и продажи. Затем, с появлением сети Интернет, брокеры Форекс стали дистанционно открывать счета  своих клиентов и организовывать торги на облачных платформах. Сейчас банки и крупные брокеры, называемые прайм-брокерами, что оперируют заявками с большими объемами, стали самостоятельно формировать курсы валют для своих клиентов, отказавшись от услуг поставщиков ликвидности. Но Thomson Reuters (а затем и ряд других компаний) предложила свои услуги мелким клиентам, объединив заявки на одной онлайн-платформе с формированием интегрального стакана цен, где суммируются по уровням цены обезличенные ордера, в чем состоит суть агрегатора валютной ликвидности. 

В настоящее время существуют два основных вида  доступа к валютной ликвидности.

1. Маркет-мейкинг – поставщик валютной ликвидности, исполняющий заявки заключивших с ним договора клиентов брокеров. Эти  банки работают с только с  крупными брокерами и объемами,
2. Агрегаторы ликвидности, которыми, соответственно, пользуются мелкие брокеры.

У основных поставщиков ликвидности имеется полная информация о формирующемся у них стакане цен с ценами спроса и предложения и их  объемами. Исходя из нижней грани предложений на продажу, поставщик определяет  для своих клиентов цену Ask, а из  верхней грани спроса на  покупку поставщик формирует цену Bid, то есть редуцируемая цена является, вообще говоря, двухкомпонентной. И, кстати, говоря о волновом поле цены, мы имеем ввиду какую-то одну из этих компонент. 

Причем, соответствующие цены, по существу, определяют все те связанные с поставщиком котировок трейдеры, что на основе своих данных о рынке формируют свои заявки. Все участники рынка получают свои данные уже из единого для всего мира информационного пространства. И этот процесс получения данных практически мгновенен. Поэтому, во-первых, в редуцировании цены неким поставщиком котировок участвует не только этот поставщик, но и множество его клиентов, чья роль в формировании значений цен гораздо больше, чем роль самого поставщика. А во-вторых, из-за единства информационного пространства и мгновенного доступа клиентов к нему редуцируемые разными поставщиками ликвидности цены оказываются очень близки.

Теперь об онтологии отношения редуцируемых цен и эмерджентных ценовых волн. Для раскрытия этого составим блок-схему, где представлены основные элементы сложной системы взаимоотношений вероятностного и редуцируемого для рынка.

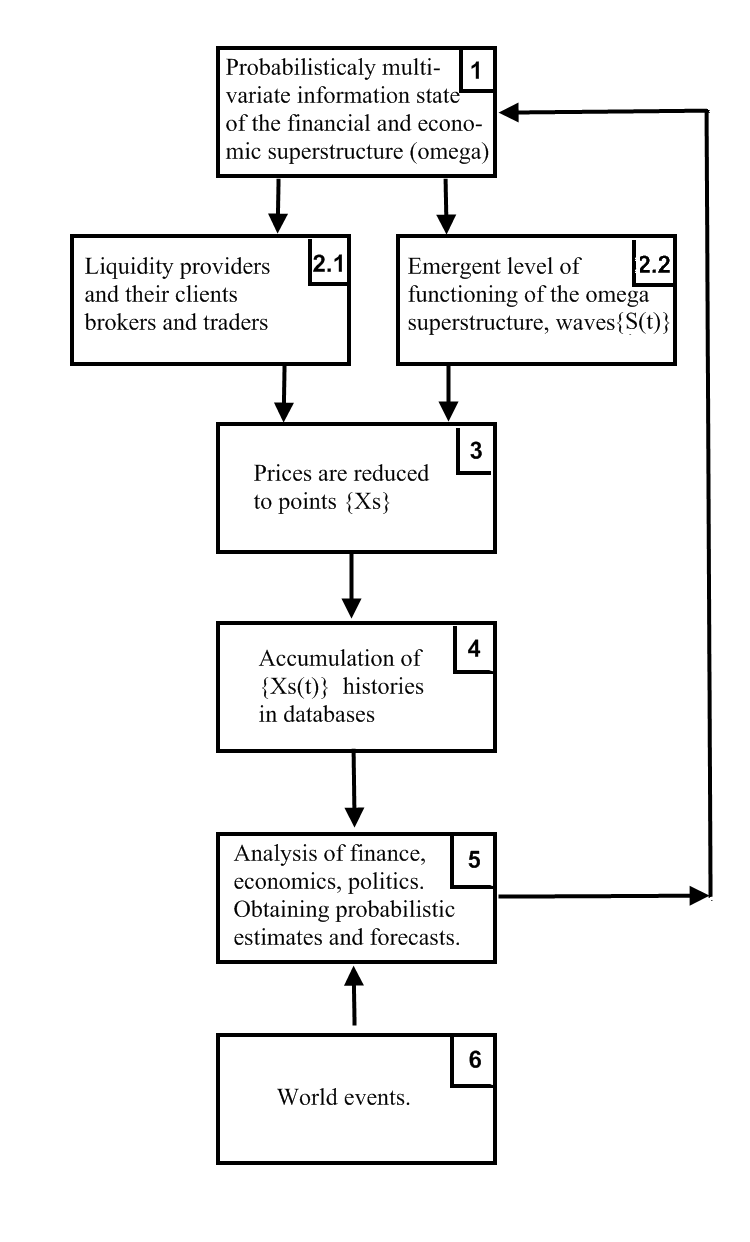
Распространяющиеся в своем эмерджентном пространстве волны вероятности  цены порождаемы, по существу, всей финансово-экономической надстройкой  человеческой цивилизации, что можно символически записать  , чему соответствует связь на блок-схеме  {1 → 2.2}. Состояние финансово-экономической надстройки  {1} (блоки блок-схемы обозначаются в тексте фигурными скобками) вероятностно-многовариантное из-за обратной связи  {5 → 1}, где блок {5} (точнее, финансовые, экономические и политические аналитики  всего мира) генерирует вероятностные прогнозы и оценки. И, собственно, из-за вероятностного состояния надстройки {1}  (и это единственное доступное нам знание о ней)  вероятностен и порождаемый ей эмерджентный мир {2.2}  ценовых  волн, что исчерпывающе отражает состояние этой  надстройки.  Клиенты  какого-то поставщика ликвидности  получают интересующие их финансовые данные также из надстройки {1} (точнее от экспертов, описывающих ее состояние), но только они выбирают частную и однозначную, близкую им по их пониманию рынка информацию из многовариантных данных надстройки {1}, выбор чего (из-за незнания внешним наблюдателем, оценивающим ситуацию, умонастроений всех этих клиентов) может трактоваться как случайный. Понятно, что связь  {1 → 2.1} не отражает надстройки {1} исчерпывающе, а просто случайно выбирает одну из ее сторон. Поставщик ликвидности    редуцирует цену  инструмента на основе сформированного для него заявками его клиентов   стакана цена, чему соответствует связь  {2.1 → 3} нашей блок схемы, процедура чего носит уже в большой мере  закономерный характер. Но, если взглянуть на реальность со стороны суммирующего частности мира {2.2} эмерджентных вероятностных полей (из коего не видно действий отдельных трейдеров и не идентифицируемы их мотивации), то получится, что та же самая цена    редуцируется из волнового поля  случайным образом.

Таким образом, рассматривая реальность по-разному (здесь проявляется как бы роль наблюдателя в редуцировании уже самого алгоритма формирования наблюдаемой им реальности)  можно идентифицировать  две грани одного и  того же, случайного по своей сути, явления редукции, когда случайность  на грани  {1 → 2.1 → 3} возникает на этапе  {1 → 2.1}, а на грани {1 → 2.2 → 3} появляется на этапе  {2.2 → 3}. Однако предсказать  эволюцию цены можно только на пути использования представления эмерджентного пространства, что исчерпывающе отражает надстройку {1}, поскольку процедура  редуцирования цены поставщиком ликвидности базируется лишь на случайном отражении одной из частных сторон  , утрачивая при сем основной массив необходимой для прогноза информации. Подчеркнем, что исчерпывающе выражают цену только ее волновое поле, то есть связь  носит не только более общий характер, чем {1 → 2.1}, но и порождает более информативное. Поэтому редуцирование цены есть неполное или упрощенное (редуцирование, от  лат. reductio,  одно из значений которого есть упрощение) отражение ее волнового поля.

Редуцированные цены, путем цепочки  связей {3 → 4 → 5 → 1 → 2.2}, имеют обратное воздействие на  и волновое поле S(t). Но рыночное редуцирование, в отличие от редукции состояния в  квантовой механике, не приводит к схлопыванию волновой функции, а лишь может слегка влиять на  последующую эволюцию цены, описываемую уравнением (10).  Дело, на мой взгляд, заключается в том, что энергия прибора, которым экспериментатор  действует на микрообъект, несопоставимо больше энергии самого микрообъекта, чем обусловлено сильное сжатие состояния микрообъекта (или его локализация в конкретной пространственной точке или состоянии).

Если же речь идет о финансовом редуцировании или редуцировании цены, то лоты трейдеров, на которые опирается поставщик ликвидности при редуцировании цены некоторого инструмента, несопоставимо меньше всего суммарного объема этого инструмента на всем финансовом рынке, чем и обусловлена малость влияния на волновое поле такого инструмента при его редуцировании. Обобщая вышеизложенное, можно заключить, что эволюция волнового поля цены и истории ее котировок есть две формы (полная неявная и сокращенная явная) существования  одного и того же феномена цены;  или, отталкиваясь от представления самостоятельного эмерджентного функционирования рынка, можно сказать, что  ансамбль историй котировок некого инструмента, редуцируемый всеми поставщиками его ликвидности, является неполным отражением эволюции волнового поля цены того же  инструмента на том же участке истории.

И наконец можно уже раскрыть суть случайного блуждания цены с позиций ее волнового поля. Будем считать, что текущая плотность вероятности    цены задает вероятность   ее  редуцирования  на малом  интервале .  Разные поставщики ликвидности могут давать несколько отличные друг от друга цены одного и того же инструмента. Но очевидно, что чаще  всего редуцируется  цена, близкая к средней величине

                                                                                   (18)

(не путать , которое не отстает, со скользящим средним, что отстает на полпериода своего усреднения). При каждом таком редуцировании (также как и при являющимся его аналогом акте квантомеханического измерения) наблюдаемая цена флуктуирует около средней величины (18) с уже установленном в первой части квадратом неопределенности

            .                                                                                   (19)

что, собственно, и порождает видимый уже на мониторах процесс случайного блуждания цены. Причем, отдельные, вызываемые редукцией, случайные скачки  и даже их небольшие последовательности (что могут даже формировать похожие на тренд участки, см. True and illusory currency market trends, которые являются участками ложного тренда и на которых не случайно нельзя заработать), в  общем-то, малоинформативны  (в смысле малой пользы для трейдинга), важно  движение  среднего   и их распределение около него. В процессе  движения среднего и редуцирования формируются последовательности ,  где  есть случайные значения, которые с соответствующей распределению вероятностью попадают в интервалы типа  , что и является  выражением случайного блуждания цены. Значение среднего , около коего случайно «скачет» редуцируемая цена, формируемо волновым вероятностным полем, поэтому процесс генерации последовательности   можно условно назвать случайным блужданием цены в волновом вероятностном поле.

Подчеркнем, что это среднее  и распределение вероятностей   формируемы отнюдь не классическими статистическими процессами, а интерферирующими друг с другом волнами амплитуд вероятности в эмерджентном пространстве. Поэтому, строго говоря, методы обычной  классической статистики к рынку плохо применимы и работают там с большими погрешностями. Однако, поскольку волнового поля цены мы пока еще не научились  видеть, то  именно  на основе  практически  определяемых (из графиков цен)  вероятностей направлений этих случайных  скачков можно в первом приближении судить и об эволюции среднего, что позволяет выработать подход к идентификации оптимальных (в рамках такой упрощенной модели) параметров биржевой игры, о чем будет следующая статья.

Заключение

Друзья, то что мы с вами каждый день наблюдаем на графиках котировок есть довольно детальное отражение самого настоящего квантового мира, что описываем квантовыми законами (волновыми полями, специфическими редукционными процессами, уравнением Шредингера и т.п.) и квантовой логикой! Этот квантовый мир создается огромным коллективом участников рынка и существует эмерджентным  образом, как качественно иная надстройка над деятельностью данного коллектива. Понимание  этого и соответствующий  математический  аппарат позволят нам создавать гораздо более эффективные продукты - квантовые советники и квантовые  индикаторы, которые будут основаны на уравнениях  эволюции соответствующих волновых полей.