Você está perdendo oportunidades de negociação:
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Registro
Login
Você concorda com a política do site e com os termos de uso
Se você não tem uma conta, por favor registre-se
Não sei, tenho escrito o que é a fórmula e todas as variáveis estão definidas. Deixe-me também esclarecer - este é o montante de lucro obtido a cada mês (não o lucro total para m meses).
Resta derivar a fórmula para a soma da série, você escreveu que o faz facilmente - faça-o. Depois pegue a derivada, equacione-a a zero.
Em minhas anotações, sua fórmula para a retirada do mês atual é parecida com esta:
Conseqüentemente, quebrar a derivada desta função em forma de besta é tão difícil quanto a anterior.
Acho que você pode tentar pré-prologaritmizar f e depois procurar por seu máximo... Talvez seja mais fácil dessa forma.
avtomat:
E então, na segunda etapa, abra a válvula que divide o fluxo em duas partes. Isto mudará o fluxo de entrada.
Você ainda não vê a solução?
Não, eu não sei o que você está pensando. Diga-me.
Há alguns que mesmo o teorema de Pitágoras, como interpretado por eles, não pode ser compreendido.
OFFTOP:
Na escola eles deram a prova mais sucinta do teorema de Pitágoras.
Nota, a idéia básica mais simples (não-padrão) é p.2. Não se usa conhecimento de propriedades de triângulos similares, também não é necessário conhecimento de trigonometria para entender a existência da função f Isto é, tal prova pode ser dada nas escolas primárias depois de bem (não como de costume) explicar às crianças qual é a área.
OFFTOP:
Na escola eles deram a prova mais sucinta do teorema de Pitágoras.
Em que nota?
A fórmula S = c^2 * f(alpha) não é óbvia para um aluno do 7º ano. É um dado adquirido que é mais ou menos assim.
Assim, quebrar a derivada desta função em forma de besta é tão difícil quanto a anterior.
Todo o processo está preso com a derivada?
Esta função é x0*k*(1-(1+q-k)^2)/(k-q)?
Se assim for, não há problema, eu os resolvi facilmente, só preciso lembrar um pouco. A variável q?
em que classe?
A fórmula S = c^2 * f(alpha) não é óbvia para um aluno do 7º ano. É um dado adquirido que é mais ou menos assim.
Quase qualquer criança que tenha sido introduzida ao conceito de área de uma figura suficientemente bem para sentir que terá pouca dificuldade em compreender a prova acima.
Se uma criança realmente entende o que é área, ela entende a medida dela e também entende que a área de qualquer figura pode ser expressa através de suas características (neste caso, a hipotenusa e o ângulo) que definem de forma única a figura.
Não é necessário nenhum conhecimento das propriedades de triângulos e trigonometria similares.
Recentemente estive em visita e vi duas pirâmides de pedra (semelhantes às pirâmides egípcias). Peguei-as em minhas mãos e as coloquei em suas bases (elas são ligeiramente diferentes em tamanho):
E veio com outra prova do teorema de Pitágoras (claro da construção).
Integer:
Весь процесс уперся в производную?
Вот эта функция - x0*k*(1-(1+q-k)^2)/(k-q)?
Если это так, то это как бы не проблема, я их легко решал, только вспомнить надо немного. Переменная q?
Não, o problema é o derivado de k de: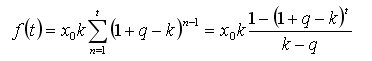
Ela tem que ser igualada a zero e resolvida com respeito a k.
Não posso fazer isso da maneira inteligente, por isso vou simplificar:
Digamos que há 10.000 no depósito no início do período. A cada período, adicionamos 5% ao depósito e os reinvestimos no depósito. Cada período nos é permitido retirar apenas 3%.
Se você retirar todos os 3% de seu dinheiro a cada período, todos nós recebemos mais de 4k$ (e não ligamos a mínima para o depósito), caso contrário, recebemos apenas 0,5k$ (mas com muito sobre o depósito).
Quase qualquer criança que tenha sido introduzida ao conceito de área de uma figura suficientemente bem para sentir que terá pouca dificuldade em compreender a prova acima.
Se uma criança realmente entende o que é uma área, ela entende a medida dela e também entende que a área de qualquer figura pode ser expressa através de suas características (neste caso a hipotenusa e o ângulo), que definem de forma única a figura.
Mas não é uma prova rigorosa.
Não posso fazer isso da maneira inteligente, por isso vou simplificar:
É por isso que precisamos de uma solução analítica geral, não para desenhar tais tabelas, mas para substituir dois valores de entrada em uma fórmula simples e obter a resposta.
Esse é o ponto, tudo o que está acima é "parece que é assim que vai ser". Que "de alguma forma pode ser expresso através de algo".
Mas não é uma prova rigorosa.
Que tipo de prova concreta é essa?! É óbvio: