Análise de Cluster (Parte I): usando a inclinação das linhas indicadoras
Introdução
A análise de cluster é um dos elementos mais importantes da inteligência artificial. Os dados, geralmente exibidos como tuplas de números ou de pontos, são agrupados em clusters ou pilhas. O objetivo é atribuir com sucesso um ponto observado a um cluster ou categoria, atribuir as propriedades conhecidas dessa categoria ao novo ponto observado e, então, agir em conformidade. Neste artigo, verificaremos se a inclinação do indicador pode indicar a natureza lateral ou de tendência do mercado.
Numeração e nomes
O indicador HalfTrend, que usarei como exemplo, é escrito na linguagem MQL4. Índice de barras ou candles (iB) no gráfico de preços é medido a partir de seu valor mais alto (rates_total) - do índice da barra mais antiga até zero, da barra mais recente e da barra atual. Quando a função OnCalculate() é chamada pela primeira vez após iniciar o indicador, o valor prev_calculated é igual a zero, uma vez que nenhum cálculo foi feito ainda. Nas subsequentes chamadas, este valor permite determinar as barras que já foram calculadas e as que ainda não.
O indicador usa uma linha indicadora de duas cores implementada por dois buffers de dados - up[] e down[]. Cada um tem sua própria cor. Apenas um dos dois buffers recebe um valor maior que zero de cada vez, o outro é colocado em zero na mesma posição (o elemento do buffer com o mesmo índice iB). Isso significa que ele não é exibido.
Para facilitar tanto quanto possível o posterior uso da análise de cluster aplicada em outros indicadores ou programas, no indicador HalfTrend foram feitas as alterações mínimas necessárias. No código do indicador as strings adicionadas são marcadas com os seguintes comentários:
//+------------------------------------------------------------------+ //| added for cluster analysis | //+------------------------------------------------------------------+ .... //+------------------------------------------------------------------+
Na íntegra, as funções e os dados da análise de cluster são fornecidos no arquivo ClusterTrend.mqh anexado ao artigo. Todos os cálculos são baseados na seguinte estrutura de dados para todos os clusters:
struct __IncrStdDev { double µ, // average σ, // standard deviation max,min, // max. and min. values S2; // auxiliary variable uint ID,n; // ID and no. of values };
µ - valor médio; σ - desvio padrão ou raiz da variância que indica como os valores no cluster variam em torno da média; Max e min - valores máximo e mínimo do cluster; S2 - variável auxiliar; n - número de valores no cluster, ID - identificador do cluster.
Essa estrutura de dados é feita como uma matriz bidimensional:
__cluster cluster[][14];
Como em MQL5 apenas a primeira dimensão das matrizes multidimensionais é definida dinamicamente, a ela é atribuído o número de tipos de valores estudados, o que torna mais fácil alterá-la. A segunda dimensão é o número de valores de classificação que são estabelecidos na seguinte matriz unidimensional:
double CatCoeff[9] = {0.0,0.33,0.76,1.32,2.04,2.98,4.21,5.80,7.87};
Ambas as string estão diretamente abaixo uma da outra, uma vez que o número de coeficientes em CatCoeff predetermina um tamanho fixo para a segunda dimensão do cluster. Tamanho esse que deve ser mais 5. Vou explicar o motivo abaixo. Como as duas matrizes são predefinidas mutuamente, elas podem ser facilmente alteradas.
Só é verificada a diferença entre o valor do indicador e seu valor anterior: x[iB] - x[iB+1]. Esta diferença é convertida em pontos (_Point) para que diferentes instrumentos de negociação possam ser comparados, como EURUSD com 5 casas decimais e XAUUSD (ouro) com duas.
Tarefas
Durante a negociação, é importante saber se o mercado está numa lateralização ou numa tendência forte/fraca. Quando estamos perante uma lateralização, precisamos negociar a partir da borda do canal, perto de um indicador de média, em direção ao indicador, de volta ao centro do canal; já quando vemos uma tendência é necessário operar com ela a partir do indicador de média e a partir do centro do canal, ou seja, é o oposto. Assim, um indicador ideal dentro de um Expert Advisor deve distinguir claramente entre esses dois estados. O EA precisa de um número que reflita a ação do mercado. Ele também precisa de patamares para saber se o valor do indicador aponta para uma tendência ou uma lateralização. Muitas vezes parece que a análise visual é suficiente para isso. No entanto, ela é bastante difícil de expressar em termos numéricos. A análise de cluster é um método matemático para agrupar dados ou categorizá-los. Isso nos ajuda a separar essas duas condições do mercado.A análise de cluster identifica ou calcula por meio da otimização:
- número de clusters
- centros de cluster
- atribuição de pontos a apenas um dos clusters, se possível (= sem clusters sobrepostos).
- todas ou o maior número possível de tuplas numéricas (possivelmente excluindo os dados discrepantes) possam ser atribuídas a um cluster,
- o tamanho do cluster seja mínimo
- os clusters se sobreponham o mínimo possível (caso contrário, não fica claro a qual cluster um ponto pertence),
- o número de clusters seja mínimo.
Quanto mais pontos, valores, elementos e clusters, mais intensivos serão os cálculos.
Notação O
Os custos computacionais são apresentados com notação O. Por exemplo, O(n) significa que o cálculo deve acessar todos os elementos n apenas uma vez. Os valores do algoritmo de classificação são exemplos bem conhecidos da importância desta magnitude. Os mais rápidos são geralmente O(nlog(n)), os mais lentos, O(n²). Esse critério era especialmente importante para grandes quantidades de dados em uma época em que os computadores eram muito menos poderosos. Hoje, as capacidades de computação são muito mais amplas, mas ao mesmo tempo, em algumas áreas, a quantidade de dados também aumenta significativamente (análise óptica de objetos e categorização de objetos).
O primeiro e mais famoso algoritmo de análise de cluster é o método médias k. Ele atribui n observações ou vetores com dimensão dc para k clusters, minimizando distâncias (euclidianas) aos centros dos clusters. Isso provoca custos computacionais O(n^(dk+1)). Temos apenas uma dimensão d, que corresponde à diferença do indicador em relação ao valor anterior, mas todo o histórico de preços, por exemplo, contas de demonstração MQ para velas GBPUSD D1 inclui 7265 barras ou velas (n na fórmula). Como no início não sabemos de quantos clusters precisamos, uso k=9 clusters ou categorias. De acordo com esta proporção, os custos serão O(7265^(1*9+1)) ou O(4,1*10^38). Bastante para o computador médio. O método apresentado aqui atinge o agrupamento em 16 ms, que é 454.063 valores por segundo. Ao calcular as barras no GBPUSD M15 usando este programa, obtemos 556 388 barras e, novamente, 9 clusters. O cálculo dura 140 ms ou 3.974.200 valores por segundo. O cálculo mostra que o clustering é ainda melhor do que O(n), o que pode ser explicado pela forma como o terminal organiza os dados - os custos computacionais para calcular o indicador também estão incluídos neste período.
Indicador
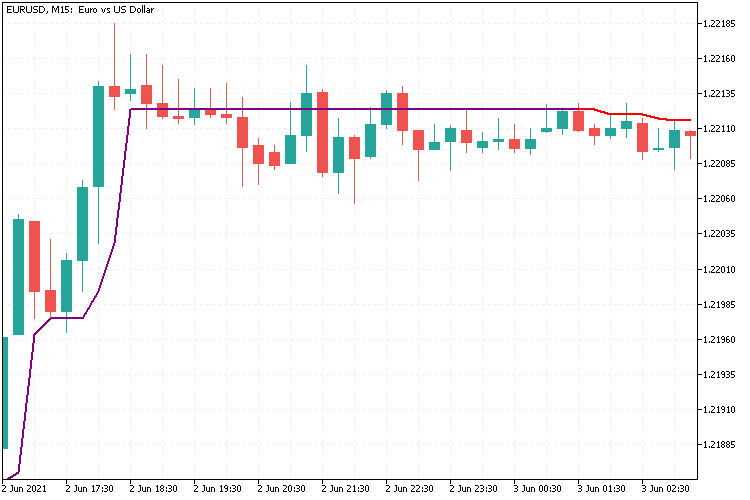
Eu uso o indicador HalfTrend da MetaQuotes (anexado ao artigo). Muitas vezes está dentro de uma lateralização:
A questão que surge é se há patamar indicando lateralização e tendência (não importa se é alta ou baixa). É claro que, se a linha do indicador for horizontal, o mercado estará dentro de uma lateralização. Mas até que altura de inclinação as mudanças permanecem insignificantes e o mercado é considerado lateral, e de que altura podemos falar sobre a tendência? Vamos imaginar que o EA veja apenas um número, no qual está concentrada toda a imagem do gráfico, mas não a geral, como vemos na imagem acima. Este problema é resolvido usando a análise de cluster. Mas antes de prosseguirmos, vamos primeiro considerar as mudanças feitas no indicador.
Mudanças feitas no indicador
Uma vez que o indicador precisa ser minimamente alterado, o agrupamento foi movido para o arquivo externo ClusterTrend.mqh integrado ao início do indicador:
Naturalmente, o arquivo está anexado ao artigo. Mas só isso não é suficiente. Para simplificar nossas tentativas, foi adicionada a variável NumValues:
input int NumValues = 1;
O valor de 1 indica que apenas um tipo de valor deve ser examinado. Por exemplo, se desejarmos analisar um indicador que calcula duas médias e quisermos estimar a inclinação de ambas, bem como a distância entre elas, NumValues deverá ser igual a 3. Em seguida, a matriz usada para o cálculo é ajustada automaticamente. Se o valor for zero, não é realizada a análise de cluster. Esta carga adicional pode ser facilmente desabilitada nas configurações.
Além disso, temos variáveis globais:
string ShortName;
long StopWatch=0;
ShortName – nome abreviado do indicador em OnInit():
ShortName = "HalfTrd "+(string)Amplitude;
IndicatorSetString(INDICATOR_SHORTNAME,ShortName);
que será usado para identificação ao imprimir os resultados.
StopWatch é usado para cronometragem. É definido imediatamente antes do primeiro valor passado para a análise de cluster e é lido após a impressão dos resultados:
if (StopWatch==0) StopWatch = GetTickCount64();
...
if (StopWatch!=0) StopWatch = GetTickCount64()-StopWatch;
Como a maioria dos outros indicadores, o HalfTrend tem um grande ciclo que percorre todas as barras disponíveis no histórico de preços. O indicador calcula seus valores para que a barra no gráfico com o índice iB = 0 contenha os preços atuais mais recentes e para que o maior índice possível represente o início do histórico de preços (primeiras barras). Antes do final do ciclo, o valor analisado é calculado e enviado para a função de cluster para ser avaliado. Todo o trabalho é automatizado. Os detalhes são indicados a seguir.
No bloco de código logo antes do final do ciclo, precisamos nos certificar de que a análise de cluster com preços históricos seja realizada apenas uma vez para cada barra, e não sempre que um novo preço aparecer:
//+------------------------------------------------------------------+
//| added for cluster analysis |
//+------------------------------------------------------------------+
if ( (prev_calculated == 0 && iB > 0 ) // não usamos uma barra real
|| (prev_calculated > 9 && iB == 1)) // é usada a última barra: iB = 1
{
Em seguida, verificamos se esta é a primeira barra de inicialização para definir o temporizador e redefinir os resultados anteriores (se houver):
if (prev_calculated==0 && iB==limit) { // apenas na primeira passagem/barra
StopWatch = GetTickCount64(); // ativamos o cronômetro
if (ArraySize(Cluster) > 0) ArrayResize(Cluster,0); // se tudo for recalculado, removemos os resultados anteriores
}
Em seguida, o valor do indicador é determinado usando os índices da barra iB atual e da (iB+1) anterior. Como a linha do indicador é bicolor (veja acima) e é implementado com os dois buffers up[] e down[], um dos quais é sempre 0,0 e, portanto, não é exibido, o valor do indicador é o buffer que está acima de zero:
double actBar = fmax(up[iB], down[iB]), // obtemos o valor real da barra [iB]
prvBar = fmax(up[iB+1], down[iB+1]); // obtemos o valor anterior
Para garantir que os valores no início do cálculo afetem os resultados da análise de cluster (embora o indicador não tenha sido calculado), introduzimos a seguinte verificação de segurança:
if ( (actBar+prvBar) < _Point ) continue; // ignoramos as cotações ausentes na posição inicial ou intermediária
Agora podemos transferir a diferença absoluta entre os valores do indicador atual e o anterior.
enterVal(fabs(actBar-prvBar)/_Point, // diferença absoluta na inclinação da linha do indicador
0, // índice do tipo de valor
1.0 - (double)iB/(double)rates_total, // velocidade de aprendizado: usamos 1-iB/rates_total ou iB/rates_total, dependendo do que estiver no intervalo 0 .. 1
NumValues // é usado para inicialização (número de tipos de valores) e se < 1, não acontece o clustering
);
Por que usamos a diferença absoluta fabs(actBar-prvBar) no primeiro argumento? Se tivéssemos de enviar uma diferença líquida, teríamos que definir o dobro de clusters (para valores maiores e menores que zero). Nesse caso, o resultado será influenciado pelo fato de o preço ter subido ou caído dentro do histórico de preços disponível. Isso pode distorcer os resultados. Em última análise, para mim é importante a quantidade de inclinação, não sua direção. Eu acho que é razoável supor que no mercado Forex as quedas e subidas nos preços são um tanto equivalentes . Talvez a situação seja diferente no mercado de ações.
O segundo argumento (0) é o índice do tipo do valor passado (0=primeiro, 1=segundo,...). Por exemplo, com duas linhas indicadoras e suas diferenças, precisamos definir 0, 1 e 2 para o valor correspondente.
Terceiro argumento
1.0 - (double)iB/(double)rates_total, // velocidade de aprendizado: usar 1-iB/rates_total ou iB/rates_total, dependendo do que estiver no intervalo 0 .. 1
diz respeito à velocidade de aprendizado. O índice iB muda do valor maior para 0. rates_total é o número total de barras. Desse modo, iB/rates_total é a proporção do que ainda não foi calculado e cai de quase 1 (nada está calculado) a zero (tudo está calculado). Portanto, este valor aumenta de quase 0 (nada aprendido) para 1 (tudo aprendido). Explicarei a importância dessa relação a seguir.
O último parâmetro é necessário para a inicialização e para determinar se os clusters devem ser calculados. Se for maior que zero, indica (veja acima) o número de tipos de valores, por exemplo, linhas indicadoras. Desse modo, determina o tamanho da primeira dimensão da matriz global Cluster []] [] no arquivo ClusterTrend.mqh (veja acima).
No final de um loop grupo ciclo percorrendo o histórico de preços, todos os resultados são exibidos imediatamente na guia Expert Advisors, uma string para cada categoria/cluster:
prtStdDev(_Symbol+" "+EnumToString(Period())+" "+ShortName, // é exibido no início de cada string
0, // tipo de valor exibido
NumValues); // se <=0, esse tipo não é exibido
Aqui, o primeiro argumento é informativo e é impresso no início de cada linha, o segundo (0) indica o tipo de indicador calculado (0=primeiro, 1=segundo, ...). Em seguida, temos NumValues. Se for igual a 0, esse tipo de indicador não é exibido.
O bloco adicionado fica assim:
//+------------------------------------------------------------------+ //| added for cluster analysis | //+------------------------------------------------------------------+ if ( (prev_calculated == 0 && iB > 0 ) // we don't use the actual bar || (prev_calculated > 9 && iB == 1)) // during operation we use the second to last bar: iB = 1 { if (prev_calculated==0 && iB==limit) { // only at the very first pass/bar StopWatch = GetTickCount64(); // start the stop whatch if (ArraySize(Cluster) > 0) ArrayResize(Cluster,0); // in case everything is recalculated delete prev. results } double actBar = fmax(up[iB], down[iB]), // get actual indi. value of bar[iB] prvBar = fmax(up[iB+1], down[iB+1]); // get prev. indi. value if ( (actBar+prvBar) < _Point ) continue; // skip initially or intermediately missing quotes enterVal(fabs(actBar-prvBar)/_Point, // abs. of slope of the indi. line 0, // index of the value type 1.0 - (double)iB/(double)rates_total, // learning rate: use either 1-iB/rates_total or iB/rates_total whatever runs from 0 .. 1 NumValues // used for initialization (no. of value types) and if < 1 no clustering ); } //+------------------------------------------------------------------+ } // end of big loop: for(iB = limit; iB >= 0; iB--) .. //+------------------------------------------------------------------+ //| added for cluster analysis | //+------------------------------------------------------------------+ if (prev_calculated < 1) // print only once after initialization { prtStdDev(_Symbol+" "+EnumToString(Period())+" "+ShortName, // printed at the beginning of each line 0, // the value type to be printed NumValues); // if <=0 this value type is not printed if (StopWatch!=0) StopWatch = GetTickCount64()-StopWatch; Print ("Time needed for ",rates_total," bars on a PC with ",TerminalInfoInteger(TERMINAL_CPU_CORES), " cores and Ram: ",TerminalInfoInteger(TERMINAL_MEMORY_PHYSICAL),", Time: ", TimeToString(StopWatch/1000,TIME_SECONDS),":",StringFormat("%03i",StopWatch%1000) ); } //+------------------------------------------------------------------+
Essas são todas as mudanças que eu queria fazer no indicador.
Análise de cluster no arquivo ClusterTrend.mqh
O arquivo está localizado na mesma pasta do indicador, portanto, deve ser como ClusterTrend.mqh.
Na parte inicial, existem simplificações associadas a #definir. #define crash(strng) causa deliberadamente a divisão por 0, que o compilador não reconhece, porque o indicador não é capaz de completar seu próprio trabalho. Pelo menos, alert() é chamado apenas uma vez e declara uma especificação errada de dimensão. É necessário corrigir isso e recompilar o indicador.
A estrutura de dados usada para esta análise já foi descrita acima.
Vamos considerar a essência dessa abordagem.
A média, a variância e a análise de cluster usam os dados geralmente disponíveis. Primeiro, os dados devem ser coletados. Em seguida, o clustering é realizado num ou mais loops. Tradicionalmente, a média de todos os valores anteriores, que chegam sucessivamente, é calculada num segundo loop sobre os dados comuns para soma. Isso leva muito tempo. No entanto, consegui encontrar o artigo "Incremental calculation of weighted mean and variance" de Tony Finch, em que este calcula a média e a variância de forma incremental, ou seja, todos os dados de uma só vez, em vez de somá-los todos e dividir o resultado pelo número de valores. Assim, o novo valor médio (simples) para todos os valores anteriores, incluindo o recém passado, é calculado pela fórmula (4), pg. 1:
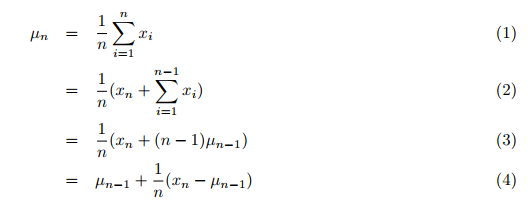
Onde:
- µn = média atualizada,
- µn-1 = média anterior,
- n = número atual de valores (incluindo o novo),
- xn = novo enésimo valor.
Mesmo a variância é calculada em tempo real e não no segundo ciclo após a média. Em seguida, é calculada a variância incremental (fórmulas 24, 25; pg. 3):
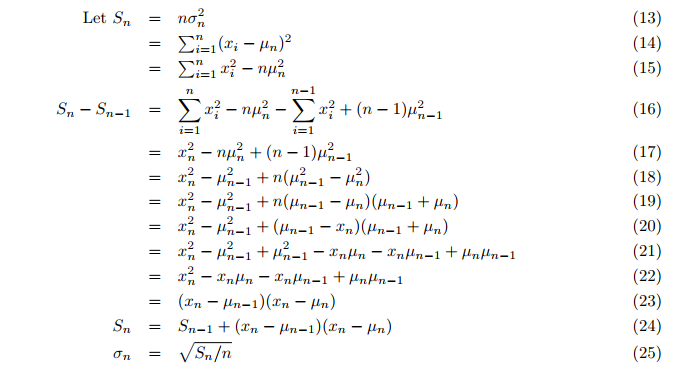
Onde:
- Sn = valor atualizado da variável auxiliar S,
- σ = variância.
Assim, a média e a variância da população geral podem ser calculadas numa passagem, sempre atualizando o novo valor mais recente na função incrStdDeviation(..):
Com base nisso, o valor médio calculado desta forma pode ser usado para classificação após a primeira parte dos dados históricos. Você pode perguntar: por que não usar apenas uma média móvel que apresenta resultados úteis de forma rápida e fácil com poucos dados? A média móvel varia. Para a classificação, precisamos de um valor de comparação relativamente constante. Imagine que precisamos medir o nível de água de um rio. É claro que o valor comparativo do nível normal de água não deve mudar com a altura atual. Assim, durante tendências fortes, as diferenças na média móvel também aumentam, e a diferença com esse valor se torna desnecessariamente menor. Quando o mercado fica estável, a média também diminui, aumentando a diferença em relação à linha de base. Por isso, precisamos de um valor muito estável que seja a média do valor máximo possível.
Finalmente, chegamos ao clustering. Normalmente, todos os valores são usados para formar clusters. No entanto, uma média incremental nos dá outra possibilidade: usamos os primeiros 50% dos dados históricos para a média e os 50% mais recentes para o clustering (continuando com a média). Essa porcentagem (50%) é aqui chamada de velocidade de aprendizado no sentido de que a média é "aprendida" apenas até 50%. Porém, seu cálculo não para depois de atingir 50%, mas agora está tão estável que dá bons resultados. No entanto, a introdução de 50% é essencialmente minha própria decisão, por isso eu inseri duas outras médias para comparação: 25% e 75%. Elas começam a calcular sua média após atingir sua velocidade de aprendizado. Graças a isso, podemos ver em que direção e o quanto a inclinação mudou.
Criação da média e do cluster
Praticamente, tudo é gerenciado pela função enterVal() do arquivo ClusterTrend.mqh:
//+------------------------------------------------------------------+ //| | //| enter a new value | //| | //+------------------------------------------------------------------+ // use; enterVal( fabs(indi[i]-indi[i-1]), 0, (double)iB/(double)rates_total ) void enterVal(const double val, const int iLne, const double learn, const int NoVal) { if (NoVal<=0) return; // nothing to do if true if( ArrayRange(Cluster,0)<NoVal || Cluster[iLne][0].n <= 0 ) // need to initialize setStattID(NoVal); incrStdDeviation(val, Cluster[iLne][0]); // the calculation from the first to the last bar if(learn>0.25) incrStdDeviation(val, Cluster[iLne][1]); // how does µ varies after 25% of all bars if(learn>0.5) incrStdDeviation(val, Cluster[iLne][2]); // how does µ varies after 50% of all bars if(learn>0.75) incrStdDeviation(val, Cluster[iLne][3]); // how does µ varies after 75% of all bars if(learn<0.5) return; // I use 50% to learn and 50% to devellop the categories int i; if (Cluster[iLne][0].µ < _Point) return; // avoid division by zero double pc = val/(Cluster[iLne][0].µ); // '%'-value of the new value compared to the long term µ of Cluster[0].. for(i=0; i<ArraySize(CatCoeff); i++) { if(pc <= CatCoeff[i]) { incrStdDeviation(val, Cluster[iLne][i+4]); // find the right category return; } } i = ArraySize(CatCoeff); incrStdDeviation(val, Cluster[iLne][i+4]); // tooo big? it goes to the last category }
val é o valor obtido do indicador; iLine é o índice do tipo de valor, learn é a velocidade de aprendizado ou a proporção trabalho/histórico. Finalmente, NoVal permite saber o número de tipos de valores (se houver) que devem ser calculados.
Primeiro, verificamos (NoVal<=0), se o clustering é feito intencionalmente ou não.
Em seguida, vemos (ArrayRange(Cluster,0) < NoVal) se a primeira dimensão da matriz Cluster[][] tem o tamanho dos tipos de valor a serem calculados. Caso contrário, é realizada a inicialização, são zerados todos os valores e o identificador é atribuído pela função setStattID(NoVal) (veja abaixo).
Quero que a quantidade de código seja pequena e não seja difícil de implementar. Isso facilitará nos lembrarmos dela rapidamente depois de algum tempo. Assim, o valor val atribuído à estrutura de dados correspondente por meio da mesma função incrStdDeviation(val, Cluster[][]) é processado nesse mesmo local.
A função incrStdDeviation(val, Cluster[iLne][0]) calcula a média do primeiro ao último valor. Como já mencionado, o primeiro índice [iLine] denota o tipo de valor e o segundo índice [0] denota uma estrutura de dados do tipo de valor a ser calculado. Como já sabemos, precisamos de 5 elementos a mais do que há na matriz estática CatCoeff[9]. Agora podemos ver o porquê:
- [0] .. [3] são necessários para os distintos valores médios [0]:100%, [1]:25%, [2]:50%, [3]:75%,
- [4] .. [12] são necessários para 9 categorias CatCoeff[9]: 0.0, .., 7.87
- [13] é exigido como a última categoria para valores maiores do que a maior categoria CatCoeff[8] (neste caso 7,87).
Agora podemos ver porquê precisamos de uma média estável. Para encontrar uma categoria ou cluster, calculamos a proporção val/Cluster[iLne][0].µ. É o valor da média do tipo com índice iLine. Portanto, os coeficientes da matriz CatCoeff[] são multiplicadores da média total, transformando a equação:
pc = val/µ => pc*µ = val
Isso significa que não apenas pré-definimos o número de clusters (isso é necessário para a maioria dos métodos de clustering), também pré-definimos as propriedades dos clusters, o que é bastante incomum, mas é por esta razão que este método de agrupamento apenas requer uma passagem, enquanto outros os métodos precisamo de várias, para encontrar as propriedades ideais (veja acima).O primeiro coeficiente (CatCoeff [0]) é zero. Foi escolhido porque o indicador HalfTrend é usado para realizar uma passagem horizontal ao longo de várias barras, portanto, a diferença nos valores do indicador, neste caso, é igual a zero. Assim, espera-se que esta categoria atinja um tamanho significativo. Todas as outras atribuições são cumpridas desde que:
pc <= CatCoeff[i] => val/µ <= CatCoeff[i] => val <= CatCoeff[i]*µ.
Como não podemos fugir de termos dados discrepantes que destruam as categorias especificadas em CatCoeff[], há uma categoria adicional para os valores desses dados:
i = ArraySize(CatCoeff);
incrStdDeviation(val, Cluster[iLne][i+4]); // muito grande? Vamos incluí-lo na última categoria
Avaliação e exibição de resultados
Imediatamente, após o final do loop do indicador grande e apenas durante a primeira passagem (prev_calculated < 1), os resultados são impressos no log usando prtStdDev(), em seguida StopWatch para e também exibe:
//+------------------------------------------------------------------+ //| added for cluster analysis | //+------------------------------------------------------------------+ if (prev_calculated < 1) { prtStdDev(_Symbol+" "+EnumToString(Period())+" "+ShortName, 0, NumValues); if (StopWatch!=0) StopWatch = GetTickCount64()-StopWatch; Print ("Time needed for ",rates_total," bars on a PC with ",TerminalInfoInteger(TERMINAL_CPU_CORES), " cores and ",TerminalInfoInteger(TERMINAL_MEMORY_PHYSICAL)," Ram: ",TimeToString(StopWatch/1000,TIME_SECONDS)); } //+------------------------------------------------------------------+
prtStdDev(..) primeiro exibe o cabeçalho com HeadLineIncrStat(pre) e, em seguida, para cada tipo de valor (índice iLine) mostra todos os 14 resultados em cada string usando retIncrStat():
void prtStdDev(const string pre, int iLne, const int NoVal) { if (NoVal <= 0 ) return; // if true no printing if (Cluster[iLne][0].n==0 ) return; // no values entered for this 'line' HeadLineIncrStat(pre); // print the headline int i,tot = 0,sA=ArrayRange(Cluster,1), sC=ArraySize(CatCoeff); for(i=4; i<sA; i++) tot += (int)Cluster[iLne][i].n; // sum up the total volume of all but the first [0] category retIncrStat(Cluster[iLne][0].n, pre, "learn 100% all["+(string)sC+"]", Cluster[iLne][0], 1, Cluster[iLne][0].µ); // print the base the first category [0] retIncrStat(Cluster[iLne][1].n, pre, "learn 25% all["+(string)sC+"]", Cluster[iLne][1], 1, Cluster[iLne][0].µ); // print the base the first category [0] retIncrStat(Cluster[iLne][2].n, pre, "learn 50% all["+(string)sC+"]", Cluster[iLne][2], 1, Cluster[iLne][0].µ); // print the base the first category [0] retIncrStat(Cluster[iLne][3].n, pre, "learn 75% all["+(string)sC+"]", Cluster[iLne][3], 1, Cluster[iLne][0].µ); // print the base the first category [0] for(i=4; i<sA-1; i++) { retIncrStat(tot, pre,"Cluster["+(string)(i)+"] (<="+_d22(CatCoeff[i-4])+")", Cluster[iLne][i], 1, Cluster[iLne][0].µ); // print each category } retIncrStat(tot, pre,"Cluster["+(string)i+"] (> "+_d22(CatCoeff[sC-1])+")", Cluster[iLne][i], 1, Cluster[iLne][0].µ); // print the last category }
Aqui tot += (int)Cluster[iLne][i].n é o número de valores nas categorias 4-13, somados para obter um valor comparativo (100%) para estas categorias. Os dados exibidos são mostrados abaixo:
GBPUSD PERIOD_D1 HalfTrd 2 ID Cluster Num. (tot %) µ (mult*µ) σ (Range %) min - max GBPUSD PERIOD_D1 HalfTrd 2 100100 learn 100% all[9] 7266 (100.0%) 217.6 (1.00*µ) 1800.0 (1.21%) 0.0 - 148850.0 GBPUSD PERIOD_D1 HalfTrd 2 100025 learn 25% all[9] 5476 (100.0%) 212.8 (0.98*µ) 470.2 (4.06%) 0.0 - 11574.0 GBPUSD PERIOD_D1 HalfTrd 2 100050 learn 50% all[9] 3650 (100.0%) 213.4 (0.98*µ) 489.2 (4.23%) 0.0 - 11574.0 GBPUSD PERIOD_D1 HalfTrd 2 100075 learn 75% all[9] 1825 (100.0%) 182.0 (0.84*µ) 451.4 (3.90%) 0.0 - 11574.0 GBPUSD PERIOD_D1 HalfTrd 2 400000 Cluster[4] (<=0.00) 2410 ( 66.0%) 0.0 (0.00*µ) 0.0 0.0 - 0.0 GBPUSD PERIOD_D1 HalfTrd 2 500033 Cluster[5] (<=0.33) 112 ( 3.1%) 37.9 (0.17*µ) 20.7 (27.66%) 1.0 - 76.0 GBPUSD PERIOD_D1 HalfTrd 2 600076 Cluster[6] (<=0.76) 146 ( 4.0%) 124.9 (0.57*µ) 28.5 (26.40%) 75.0 - 183.0 GBPUSD PERIOD_D1 HalfTrd 2 700132 Cluster[7] (<=1.32) 171 ( 4.7%) 233.3 (1.07*µ) 38.4 (28.06%) 167.0 - 304.0 GBPUSD PERIOD_D1 HalfTrd 2 800204 Cluster[8] (<=2.04) 192 ( 5.3%) 378.4 (1.74*µ) 47.9 (25.23%) 292.0 - 482.0 GBPUSD PERIOD_D1 HalfTrd 2 900298 Cluster[9] (<=2.98) 189 ( 5.2%) 566.3 (2.60*µ) 67.9 (26.73%) 456.0 - 710.0 GBPUSD PERIOD_D1 HalfTrd 2 1000421 Cluster[10] (<=4.21) 196 ( 5.4%) 816.6 (3.75*µ) 78.9 (23.90%) 666.0 - 996.0 GBPUSD PERIOD_D1 HalfTrd 2 1100580 Cluster[11] (<=5.80) 114 ( 3.1%) 1134.9 (5.22*µ) 100.2 (24.38%) 940.0 - 1351.0 GBPUSD PERIOD_D1 HalfTrd 2 1200787 Cluster[12] (<=7.87) 67 ( 1.8%) 1512.1 (6.95*µ) 136.8 (26.56%) 1330.0 - 1845.0 GBPUSD PERIOD_D1 HalfTrd 2 1300999 Cluster[13] (> 7.87) 54 ( 1.5%) 2707.3 (12.44*µ) 1414.0 (14.47%) 1803.0 - 11574.0 Time needed for 7302 bars on a PC with 12 cores and Ram: 65482, Time: 00:00:00:016
O que nós vemos? Vamos de coluna em coluna. A primeira coluna contém o símbolo, período gráfico, nome do indicador e sua "Amplitude" conforme especificado em ShortName. A segunda coluna exibe o ID de cada estrutura de dados. 100nnn indica que este é apenas um cálculo médio com os últimos três dígitos que indicam a velocidade de aprendizado (100, 25, 50 e 75). 400nnn .. 1300nnn - categorias, clusters ou pilhas. Aqui, os últimos três dígitos indicam a categoria ou multiplicador para a média µ, que também é mostrado na terceira coluna Cluster em parênteses. Tudo está claro e é autoexplicativo.
Agora a parte mais interessante. A quarta coluna mostra o número de valores na categoria correspondente e a porcentagem entre parênteses. Curiosamente, na maior parte do tempo o indicador está em uma posição horizontal (categoria # 4 - 2.409 barras ou 66,0% dias), ou seja, a negociação numa faixa pode ser bem-sucedida em dois terços das vezes. No entanto, houve mais máximos (locais) nas categorias # 8, # 9 e # 10, enquanto houve surpreendentemente poucos valores na categoria # 5 (112, 3,1%). Agora esse fato pode ser interpretado como uma lacuna entre dois patamares. Ele nos dá os seguintes valores aproximados:
se fabs(slope) < 0.5*µ => no mercado está acontecendo uma lateralização, é necessário operar dentro da faixa
se fabs(slope) > 1.0*µ => no mercado está acontecendo uma tendência, precisamos "selar" a onda
As primeiras 4 strings com identificadores 100nnn nos permitem avaliar a estabilidade do valor µ. Como disse, não queremos um valor que flutue muito. Nós vemos que µ diminui de 217,6 (pontos por dia) em 100100 para 182,1 em 100075 (para um determinado µ são usados apenas os últimos 25% dos valores), ou 16%. Não muito, acho eu. O que isso nos diz? Que a volatilidade do GBPUSD diminuiu. O primeiro valor nesta categoria é de 28/05/2014 00:00:00. Talvez isso deva ser levado em consideração.
Ao calcular a média, a variância σ exibe informações valiosas, o que nos leva à coluna 6 (σ (Range %)) Mostra o quão próximos os valores individuais estão da média. Para valores normalmente distribuídos, 68% de todos os valores estão dentro da variância. Em termos de variância, isso significa que quanto menor, mais precisa é a média. A razão σ/(max-min) das duas últimas colunas é mostrada entre parênteses. É também uma medida da qualidade da variância e da média.
Agora vamos ver se os resultados de GBPUSD D1 são repetidos em intervalos de tempo menores, em particular em M15. Para fazer isso, basta mudar o período gráfico de D1 para M15:
GBPUSD PERIOD_M15 HalfTrd 2 ID Cluster Num. (tot %) µ (mult*µ) σ (Range %) min - max GBPUSD PERIOD_M15 HalfTrd 2 100100 learn 100% all[9] 556389 (100.0%) 18.0 (1.00*µ) 212.0 (0.14%) 0.0 - 152900.0 GBPUSD PERIOD_M15 HalfTrd 2 100025 learn 25% all[9] 417293 (100.0%) 18.2 (1.01*µ) 52.2 (1.76%) 0.0 - 2971.0 GBPUSD PERIOD_M15 HalfTrd 2 100050 learn 50% all[9] 278195 (100.0%) 15.9 (0.88*µ) 45.0 (1.51%) 0.0 - 2971.0 GBPUSD PERIOD_M15 HalfTrd 2 100075 learn 75% all[9] 139097 (100.0%) 15.7 (0.87*µ) 46.1 (1.55%) 0.0 - 2971.0 GBPUSD PERIOD_M15 HalfTrd 2 400000 Cluster[4] (<=0.00) 193164 ( 69.4%) 0.0 (0.00*µ) 0.0 0.0 - 0.0 GBPUSD PERIOD_M15 HalfTrd 2 500033 Cluster[5] (<=0.33) 10528 ( 3.8%) 3.3 (0.18*µ) 1.7 (33.57%) 1.0 - 6.0 GBPUSD PERIOD_M15 HalfTrd 2 600076 Cluster[6] (<=0.76) 12797 ( 4.6%) 10.3 (0.57*µ) 2.4 (26.24%) 6.0 - 15.0 GBPUSD PERIOD_M15 HalfTrd 2 700132 Cluster[7] (<=1.32) 12981 ( 4.7%) 19.6 (1.09*µ) 3.1 (25.90%) 14.0 - 26.0 GBPUSD PERIOD_M15 HalfTrd 2 800204 Cluster[8] (<=2.04) 12527 ( 4.5%) 31.6 (1.75*µ) 4.2 (24.69%) 24.0 - 41.0 GBPUSD PERIOD_M15 HalfTrd 2 900298 Cluster[9] (<=2.98) 11067 ( 4.0%) 47.3 (2.62*µ) 5.5 (23.91%) 37.0 - 60.0 GBPUSD PERIOD_M15 HalfTrd 2 1000421 Cluster[10] (<=4.21) 8931 ( 3.2%) 67.6 (3.75*µ) 7.3 (23.59%) 54.0 - 85.0 GBPUSD PERIOD_M15 HalfTrd 2 1100580 Cluster[11] (<=5.80) 6464 ( 2.3%) 94.4 (5.23*µ) 9.7 (23.65%) 77.0 - 118.0 GBPUSD PERIOD_M15 HalfTrd 2 1200787 Cluster[12] (<=7.87) 4390 ( 1.6%) 128.4 (7.12*µ) 12.6 (22.94%) 105.0 - 160.0 GBPUSD PERIOD_M15 HalfTrd 2 1300999 Cluster[13] (> 7.87) 5346 ( 1.9%) 241.8 (13.40*µ) 138.9 (4.91%) 143.0 - 2971.0 Time needed for 556391 bars on a PC with 12 cores and Ram: 65482, Time: 00:00:00:140
Claro, a inclinação média agora é muito menor. Ela desce de 217,6 pips por dia para 18,0 pips em 15 minutos. Mas aqui se pode ver um comportamento semelhante:
se fabs(slope) < 0.5*µ => no mercado está acontecendo uma lateralização, é necessário operar dentro da faixa
se fabs(slope) > 1.0*µ => no mercado está acontecendo uma tendência, precisamos "selar" a onda
Tudo o mais relacionado à interpretação do período gráfico diário permanece relevante.
Conclusão
Usando o indicador HalfTrend como exemplo, mostramos que a categorização simples ou análise de cluster pode fornecer informações muito valiosas sobre o comportamento do indicador, que de outra forma acarretaria muitos recursos computacionais para ser obtido. Normalmente, a média e a variância são calculadas em loops separados, seguidas por loops adicionais para clustering. Aqui, fizemos tudo num ciclo grande que também calcula o indicador. O primeiro dado é usado para treinamento e o segundo, para aplicar o que foi aprendido. Tudo isso em menos de um segundo, mesmo com uma grande quantidade de dados. Isso permite exibir informações relevantes rapidamente, o que é especialmente valioso na hora de operar.
Tudo é pensado para que os usuários possam inserir de forma rápida e fácil as linhas de código necessárias para tal análise em seu próprio indicador. Isso não apenas permite que eles verifique se tal indicador pode determinar o estado atual do mercado, mas também fornece diretrizes para o desenvolvimento posterior de suas próprias ideias.
O que vem agora?
No próximo artigo, aplicaremos essa abordagem aos indicadores padrão. Isso permitirá que olhemos para eles de uma nova maneira e expandamos o que pensamos sobre eles. Também haverá exemplos de como proceder se você quiser usar este kit de ferramentas sozinho.
Traduzido do Inglês pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/en/articles/9527
 Combinatória e teoria da probabilidade para negociação (Parte I): fundamentos
Combinatória e teoria da probabilidade para negociação (Parte I): fundamentos
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso