クラスター分析(第I部):インジケーターラインの傾きをマスターする
717
0
概要
クラスター分析は、人工知能の最も重要な要素の1つです。観察されたものは、通常、数または点のタプルの形で、クラスターまたはヒープにグループ化されます。目標は、監視対象の点をクラスターまたはカテゴリに正常に割り当てることにより、そのカテゴリの既知のプロパティを監視対象の新しい点に割り当て、それに応じて動作することです。ここでの目標は、指標の傾きが市場が横ばいであるかトレンドに従っているのかを示しているかどうか、そしてどれだけよく示しているかを確認することです。
番号付けと命名規則
例として使用されるインジケーター「HalfTrend」は、MQL4の伝統に基づいて構築されているため、価格チャートのバーまたはローソク足のインデックス(iB)は、最も古いバーの最大値(rate_total)から最新のバー、現在のバーのゼロまで降順に番号付けされています。prev_calculatedの値は、インジケーターの開始後に初めてOnCalculate()関数が呼び出されたときはまだ何も計算されていないためにゼロですが、後続の呼び出しでは、どのバーがすでに計算されているか、どのバーが計算されていないかを検出するために使用できます。
インジケーターは2色のインジケーターラインを使用します。これは、それぞれが独自の色を持つ、2つのデータバッファup[]とdown[]によって実現されます。2つのバッファのうち1つだけが一度にゼロより大きい有効な値を受け取ります。もう1つは同じ位置でゼロが割り当てられます(同じインデックスiBのバッファ要素)。これは、描画されないことを意味します。
他の指標またはプログラムでこのクラスター分析をさらに簡単に使用できるようにするために、HalfTrendインジケーターへの追加は可能な限り少なくしました。インジケーターのコードに追加された行は、次のコメントによって囲まれています。
//+------------------------------------------------------------------+ //| added for cluster analysis | //+------------------------------------------------------------------+ .... //+------------------------------------------------------------------+
クラスター分析の関数とデータは完全にClusterTrend.mqhに含まれています。このファイルは添付されています。計算全体の基礎となるのは、すべてのクラスターが持つ次のデータ構造体です。
struct __IncrStdDev { double µ, // average σ, // stdandard deviation max,min, // max. and min. values S2; // auxiliary variable uint ID,n; // ID and no. of values };
µは平均、σは標準偏差 - 分散の根で、クラスター内の値が平均にどれだけ近いかを示します。maxとminはそれぞれクラスター内の最大値と最小値であり、S2は補助変数です。nはクラスター内の値の数であり、IDはクラスターの識別子です。
このデータ構造は、2次元配列で構成されています:
__cluster cluster[][14];
MQL5では、多次元配列の最初の次元のみを動的に調整できるため、検査する値の型の数がそれに割り当てられ、
簡単に変更できます。2番目の次元は分類値の数であり、次の1次元配列に固定されています。
double CatCoeff[9] = {0.0,0.33,0.76,1.32,2.04,2.98,4.21,5.80,7.87};
CatCoeffの係数の数は、クラスターの2番目の次元の固定サイズを条件付けるため、両方の線は互いのすぐ下にあります。5より大きくする必要があります。その理由を以下に説明します。両方の配列は相互に条件付けを行うため、簡単に一緒に変更できます。
インジケーター値とその前の値の違い(x[iB] - x[iB+1])のみが調べられます。これらの差はポイント(_Point)に変換され、小数点以下5桁のEURUSDと小数点以下2桁のXAUUSD(金)などのさまざまな取引商品の比較を可能にします。
課題
取引するには、市場が横ばいであるか、弱いまたは強いトレンドがあるかを知ることが不可欠です。横方向の動きでは、適切な平均インジケーターの周りのチャネルの境界からインジケーターに戻って、チャネルの中心に戻って取引しますが、トレンドでは 、平均指標から離れ、チャネルの中心から離れ、つまりその逆のトレンドの方向に取引する必要があります。したがって、EAが使用するほぼ完全なインジケーターは、これら2つの状態を明確に分離する必要があります。EAには、市場の動きが反映された数値が必要であり、この場合、インジケーターの数値がトレンドまたはフラットのどちらを示しているかを知るためのしきい値が必要です。視覚的には、この点に関して評価を行うのはしばしば簡単に思えますが、視覚的な感覚を数式や数値に具体化するのは難しいことがよくあります。クラスター分析は、データをグループ化する、またはデータをカテゴリに割り当てる数学的方法で、市場のこれら2つの状態を分離するのに役立ちます。クラスター分析は、最適化を通じて以下を定義または達成します。
- クラスターの数
- クラスターの中心
- クラスターの1つのみへの点の割り当て - 可能であれば(=重複するクラスターなし)。
- 数のタプルのすべてまたはできるだけ多く(外れ値を除く)を1つのクラスターに割り当てること
- クラスターのサイズが可能な限り小さいこと
- それらができるだけ重ならないこと(その場合、点が1つまたはその隣接するクラスターに属するかどうかは明確ではありません)、
- クラスターの数ができるだけ少ないこと
これは、特に多くの点、値、または要素と多くのクラスターがある場合、問題が計算上非常に高価になる可能性があるという事実につながります。
ランダウの記号
計算量はランダウの記号によって表現されます。たとえばO(n)は計算がn個の要素すべてに1回だけアクセスする必要があることを意味します。この量の重要性のよく知られた例は、並び替えアルゴリズムの値です。通常、最も速いものにはO(nlog(n))があり、最も遅いものにはO(n²)があります。昔だけでなく、これは大量のデータや当時それほど高速ではなかったコンピューターにとって重要な基準でした。今日、コンピューターは何倍も高速ですが、同時に、一部の領域では、データの量(環境の光学分析とオブジェクトの分類)が非常に増加しています。
クラスター分析で最初で最も有名なアルゴリズムはk平均法です。クラスターの中心までの(ユークリッド)距離を最小化することにより、d次元のn個の観測値またはベクトルをk個のクラスターに割り当てます。これにより、O(n^(dk+1))の計算コストが発生します。次元dは1つだけで、それぞれのインジケーターは前の値と異なりますが、たとえば、 GBPUSD D1(毎日)ローソク足のMQのデモ口座には、式のnである7265バーまたは相場のデモ口座が含まれています。最初は、いくつのクラスターが有用または必要であるかがわからないため、k=9のクラスターまたはカテゴリを使用します。この関係はO(7265^(1*9+1))またはO(4,1*10^38)の努力につながります。通常の取引用コンピューターには多すぎます。ここに示す方法では、16ミリ秒でクラスタリングを実現できます。これは1秒あたり454.063の値になります。このプログラムでGBPUSD m15(15分足)のバーを計算すると、556.388バーと9つのクラスターがあり、1秒あたり140ミリ秒または3.974.200の値が必要です。結局のところ、指標を計算するための計算作業もこの期間に流れ込むため、MQのターミナルがデータを編成する方法によって正当化できるO(n)よりもクラスタリングが優れていることを示しています。
インジケーター
インジケーターとして、以下に添付されているMQの「HalfTrend」を使用します。水平方向に走る通路が長くなっています。
このインジケーターに対する私の質問は、明確な分離があるかどうか、つまり、横ばいの兆候として解釈できるしきい値と、上昇または下降のトレントを示すしきい値があるかどうかでした。もちろん、このインジケーターが正確に水平である場合、市場が横ばいであることがすぐにわかります。しかし、傾斜のどの高さまで市場の変化が非常に小さくて市場はまだ横ばいであると見なされ、どの高さからトレンドを想定する必要があるのでしょうか。EAが1つの数値のみを表示し、チャート全体の画像が集中していて、上の画像のように大きな画像が表示されていないことを想像してみてください。これは、クラスター分析によって解決されます。ただし、クラスター分析に移る前に、まずインジケーターで行われた変更を検討します。
インジケーターの変更
インジケーターの変更はできるだけ少なくする必要があるため、クラスタリングは外部ファイルClusterTrend.mqhに移動されました。このファイルは、インジケーターの先頭に
でインクルードされています。もちろん、このファイルは添付されています。しかし、これだけでは十分ではありません。自分での試行をできるだけ簡単にするために、入力変数NumValuesが追加されました。
input int NumValues = 1;
この値1は、1つの値タイプ(のみ)を調べる必要があることを意味します。たとえば、2つの平均を計算するインジケーターを分析し、両方の傾きを評価する場合、3番目にこれら2つのNumValues間の距離を3に設定する必要があります。次に、計算が行われる配列が自動的に調整されます。値がゼロに設定されている場合、クラスター分析は実行されません。したがって、この追加の負荷は、設定によって簡単にオフにできます。
さらに、グローバル変数があります。
string ShortName;
long StopWatch=0;
ShortName は、OnInit()でインジケーターの短い名前が割り当てられます。
ShortName = "HalfTrd "+(string)Amplitude;
IndicatorSetString(INDICATOR_SHORTNAME,ShortName);
これは、結果を出力する際の識別に使用されます。
StopWatchはタイミングに使用され、クラスター分析のために最初の値が渡される直前に設定され、結果が出力された後に読み取られます。
if (StopWatch==0) StopWatch = GetTickCount64();
...
if (StopWatch!=0) StopWatch = GetTickCount64()-StopWatch;
ほとんどすべてのインジケーターと同様に、これは価格履歴の使用可能なすべてのバーを大きなループに入れます。このインジケーターは、インデックスiB=0のチャートのバーに現在の最近受け取った価格が含まれ、可能な最大のインデックスが価格履歴の始まりである最も古いバーを表すように値を計算します。このループが終了する前の最後の最後の括弧である閉じ括弧として、分析される値が計算され、評価のためにクラスター関数に渡されます。すべてが自動化されています。以下でさらに説明します。
ループが終了する直前のコードブロックで最初に行われることは、過去の価格を使用したクラスター分析が、新しい価格が到着するたびにではなく、各バーに対して1回だけ実行されることを確認することです。
//+------------------------------------------------------------------+
//| added for cluster analysis |
//+------------------------------------------------------------------+
if ( (prev_calculated == 0 && iB > 0 ) // we don't use the actual bar
|| (prev_calculated > 9 && iB == 1)) // during operation we use the second to last bar: iB = 1
{
次に、ストップウォッチを設定して前の結果(あれば)を無効にするための初期化の最初のバーであることを確認します。
if (prev_calculated==0 && iB==limit) { // only at the very first pass/bar
StopWatch = GetTickCount64(); // start the stop whatch
if (ArraySize(Cluster) > 0) ArrayResize(Cluster,0); // in case everything is recalculated delete prev. results
}
次に、バーインデックスiBと前のバーのインデックス(iB+1)を使用してインジケーター値が決定されます。このインジケーターラインは2色であり(上記を参照)、2つのバッファup[]とdown[]で実現されています。1つは常に0,0で描画されないので、インジケーター値は2つのバッファのうちのゼロより大きい1つです。
double actBar = fmax(up[iB], down[iB]), // get actual indi. value of bar[iB]
prvBar = fmax(up[iB+1], down[iB+1]); // get prev. indi. value
インジケーターがまったく計算されていなくても、クラスター分析が計算の開始時の値の影響を受けることを確認するために、次の安全性チェックがあります。
if ( (actBar+prvBar) < _Point ) continue; // skip initially or intermediately missing quotes
これで、インジケーター値とその前の値との絶対差を渡すことができます。
enterVal(fabs(actBar-prvBar)/_Point, // abs. of slope of the indi. line
0, // index of the value type
1.0 - (double)iB/(double)rates_total, // learning rate: use either 1-iB/rates_total or iB/rates_total whatever runs from 0 .. 1
NumValues // used for initialization (no. of value types) and if < 1 no clustering
);
最初の引数で絶対差fabs(actBar-prvBar)を使用するのはなぜでしょうか。純粋な差を渡した場合、クラスターの数を2倍(正と負に1つずつ)にする必要があります。価格が使用可能な価格履歴内で全体的に上昇したか下降したかが関係するようになり、結果が歪む可能性があります。最終的に、(私にとって)重要なのは傾きの方向ではなく強さです。外国為替市場では、価格の上昇と下降はある程度同等であると考えるのが妥当だと思います。おそらく株式市場とは異なります。
2番目の引数0は、渡された値のタイプのインデックスです(0=最初、1=2番目..)。つまり、2つのインジケーターラインとそれらの違いがあるため、それぞれの値に0、1、および2を設定する必要があります。
3番目の引数
1.0 - (double)iB/(double)rates_total, // learning rate: use either 1-iB/rates_total or iB/rates_total whatever runs from 0 .. 1
は学習率に関します。インデックスiBは、最大値から0まで実行されます。rates_total は、すべてのバーの総数です。したがって、iB/rates_totalは、まだ計算されていないものの比率であり、ほぼ1(何も計算されていない)からゼロ(すべてが計算されている)になります。したがって、1からこの値を引いた値はほぼ0(何も学習されていない)から増加します)から1(完了)に増加します。この比率の重要性を以下に説明します。
最後のパラメータは、初期化に必要でクラスターを計算する必要があるかです。ゼロより大きい場合は、値タイプの数を指定し(上記を参照)(インジケーターライン)。したがって、ファイルClusterTrend.mqh内のグローバル配列Cluster[]][]の最初の次元のサイズを決定します(上記を参照)。
価格履歴全体にわたる大きなループの終了直後に、すべての結果がカテゴリ/クラスターごとに1行ずつエキスパートタブに出力されます。
prtStdDev(_Symbol+" "+EnumToString(Period())+" "+ShortName, // printed at the beginning of each line
0, // the value type to be printed
NumValues); // if <=0 this value type is not printed
ここで、最初の引数は情報用であり、各行の先頭に出力されます。2番目の0は、計算されたインジケータータイプ(0最初、1=2番目、..)を示し、最後に上記のようにNumValuesを示します。0の場合、このインジケータータイプは出力されません。
全体として、追加されたブロックは次のようになります。
//+------------------------------------------------------------------+ //| added for cluster analysis | //+------------------------------------------------------------------+ if ( (prev_calculated == 0 && iB > 0 ) // we don't use the actual bar || (prev_calculated > 9 && iB == 1)) // during operation we use the second to last bar: iB = 1 { if (prev_calculated==0 && iB==limit) { // only at the very first pass/bar StopWatch = GetTickCount64(); // start the stop whatch if (ArraySize(Cluster) > 0) ArrayResize(Cluster,0); // in case everything is recalculated delete prev. results } double actBar = fmax(up[iB], down[iB]), // get actual indi. value of bar[iB] prvBar = fmax(up[iB+1], down[iB+1]); // get prev. indi. value if ( (actBar+prvBar) < _Point ) continue; // skip initially or intermediately missing quotes enterVal(fabs(actBar-prvBar)/_Point, // abs. of slope of the indi. line 0, // index of the value type 1.0 - (double)iB/(double)rates_total, // learning rate: use either 1-iB/rates_total or iB/rates_total whatever runs from 0 .. 1 NumValues // used for initialization (no. of value types) and if < 1 no clustering ); } //+------------------------------------------------------------------+ } // end of big loop: for(iB = limit; iB >= 0; iB--) .. //+------------------------------------------------------------------+ //| added for cluster analysis | //+------------------------------------------------------------------+ if (prev_calculated < 1) // print only once after initialization { prtStdDev(_Symbol+" "+EnumToString(Period())+" "+ShortName, // printed at the beginning of each line 0, // the value type to be printed NumValues); // if <=0 this value type is not printed if (StopWatch!=0) StopWatch = GetTickCount64()-StopWatch; Print ("Time needed for ",rates_total," bars on a PC with ",TerminalInfoInteger(TERMINAL_CPU_CORES), " cores and Ram: ",TerminalInfoInteger(TERMINAL_MEMORY_PHYSICAL),", Time: ", TimeToString(StopWatch/1000,TIME_SECONDS),":",StringFormat("%03i",StopWatch%1000) ); } //+------------------------------------------------------------------+
インジケーターの変更はこれですべてです。
ClusterTrend.mqhファイルのクラスター分析
ファイルはインジケーターと同じフォルダーにあるため、「"ClusterTrend.mqh"」の形式でインクルードします。
まず#defineによる簡略化がいくつかあります。インジケータープログラムがそれ自体を終了することは実際には(まだ?)不可能であるため、#define crash(strng)はコンパイラが認識しない0による除算を人為的に引き起こします。これもこれでは完全には成功しませんが、少なくとも、間違った次元指定を要求するalert()が呼び出されるのは1回だけです。修正して、インジケーターを再コンパイルします。
この分析に使用されるデータの構造体は、すでに上記で説明されています。
それでは、このアプローチのアイデアの核心に取り掛かりましょう。
実際には、平均、分散、およびクラスター分析は、合計で使用可能である必要があるデータを使用して計算されます。まずデータを収集し、次に2番目のステップでこれらの値とクラスタリングが1つ以上のループによって実行されます。従来、1つずつ到着する以前のすべての値の平均は、合計するすべてのデータの大きなループの2番目のループで計算されていました。これには非常に時間がかかります。ただし、私が見つけたTony Finch氏による出版物「加重平均と分散の増分計算」では、平均と分散は増分的に計算されます。つまり、すべてのデータを計算してから値の数で合計を割るのではなく、すべてのデータを1回通過して、計算します。 したがって、新しく送信された値を含む以前のすべての値の新しい(単純な)平均は、式(4), p.1に従って計算されます。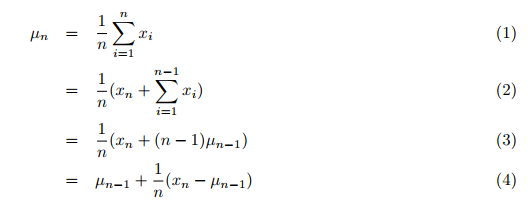
ここで
- µn = 更新された平均値
- µn-1 = 前の平均値
- n = 値の現在の数(新しい値を含む)
- xn = 新しいn番目の値
分散でさえ、平均後の2番目のループではなく、オンザフライで計算されます。次に、増分分散が計算されます(式24,25; p. 3)。
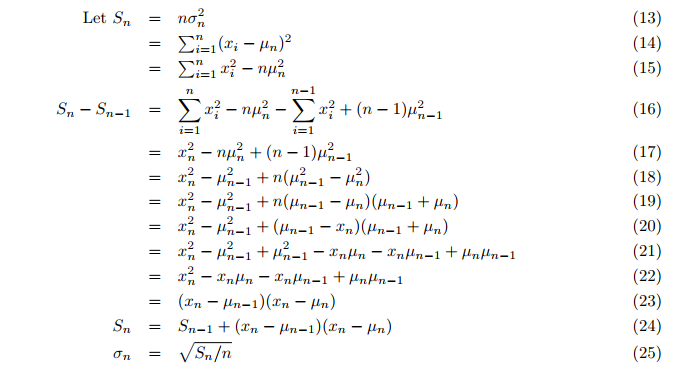
ここで、
- Sn = 補助変数Sの更新された値
- σ = 分散
したがって、母集団の平均と分散は1回のパスで計算できて、関数incrStdDeviation(..)の最新値にたいして常に最新になります。
これに基づいて、この方法で計算された平均値は、履歴データの最初の部分の後の分類にすでに使用できます。移動平均を使用できないのはなぜかと疑問に思われるかもしれません。移動平均を使用すると、少量のデータですばやく簡単に有用な結果が得られます。移動平均は調整されます。ただし、分類の目的には、比較的一定の比較値が必要です。川の水位を測定することを想像してみてください。通常の水位の比較値が現在の高さで変化してはならないことは明らかです。たとえば、強いトレンドがあるときは、移動平均の差も大きくなり、この値の差は不当に小さくなります。そして、市場が横ばいになると、平均も減少し、これにより、この基本値との差が実際に増加します。可能な限り平均的な、非常に安定した値が必要なのです。
ここで、クラスタリングの問題が発生します。 従来、クラスターは再びすべての値を使用して形成していましたが、平均値の増分計算によって、平均値に履歴データの最も古い50％を使用し、クラスタリングには最新の50％を使用する(平均値の計算を続行します)という別の可能性が生じます。この割合(50％)は、50％までは平均値のみが「学習」されるという意味で、ここでは学習率と呼ばれます。 50％に達しても計算は停止しませんが、それまでには安定していて、良好な結果が得られます。それでも、50％という数字は私の恣意的な決定であるため、比較のために他に2つの平均値(25％と75％)を作成しました。学習率に達した後に平均値を計算します。これでは、傾斜がどのように、どれだけ変化したかがわかりません。
平均とクラスターの作成
ほとんどすべてが、ファイルClusterTrend.mqhの関数enterVal()によって管理されます。
//+------------------------------------------------------------------+ //| | //| enter a new value | //| | //+------------------------------------------------------------------+ // use; enterVal( fabs(indi[i]-indi[i-1]), 0, (double)iB/(double)rates_total ) void enterVal(const double val, const int iLne, const double learn, const int NoVal) { if (NoVal<=0) return; // nothing to do if true if( ArrayRange(Cluster,0)<NoVal || Cluster[iLne][0].n <= 0 ) // need to inicialize setStattID(NoVal); incrStdDeviation(val, Cluster[iLne][0]); // the calculation from the first to the last bar if(learn>0.25) incrStdDeviation(val, Cluster[iLne][1]); // how does µ varies after 25% of all bars if(learn>0.5) incrStdDeviation(val, Cluster[iLne][2]); // how does µ varies after 50% of all bars if(learn>0.75) incrStdDeviation(val, Cluster[iLne][3]); // how does µ varies after 75% of all bars if(learn<0.5) return; // I use 50% to learn and 50% to devellop the categories int i; if (Cluster[iLne][0].µ < _Point) return; // avoid division by zero double pc = val/(Cluster[iLne][0].µ); // '%'-value of the new value compared to the long term µ of Cluster[0].. for(i=0; i<ArraySize(CatCoeff); i++) { if(pc <= CatCoeff[i]) { incrStdDeviation(val, Cluster[iLne][i+4]); // find the right category return; } } i = ArraySize(CatCoeff); incrStdDeviation(val, Cluster[iLne][i+4]); // tooo big? it goes to the last category }
valはインジケーターから受け取った値です。iLineは値型のインデックス、learnは学習率または完了/履歴の比率、NoVal は計算される値型がある場合いくつあるかを知るために使用します。
最初は、クラスタリングが意図されているかどうかのテスト(NoVal<=0)です。
配列Cluster[][]の最初の次元が計算される値型のサイズを持っているかどうかの確認(ArrayRange(Cluster,0) < NoVal)が続きます。 持っていない場合、初期化が実行されて、すべての値がゼロに設定され、IDは関数setStattID(NoVal)によって割り当てられます(以下を参照)。
コードの量を少なくして、他の人がコードを使いやすくし、自分がしばらく作業をしなかった後で再び理解できるようにしたいと思います。値valは、1つの同じ関数incrStdDeviation(val, Cluster[][])を介して対応するデータ構造に割り当てられ、そこで処理されます。
incrStdDeviation(val, Cluster[iLne][0])関数は、最初の値から最後の値までの平均を計算します。すでに述べたように、最初のインデックス[iLine] は値タイプを示し、2番目のインデックス[0]は計算の値タイプのデータ構造を示します。上からわかるように、静的配列CatCoeff[9]の要素の量よりも5つ多く必要です。 これで、理由がわかります。
- [0] .. [3]は、さまざまな平均に必要です([0]:100%、[1]:25%、[2]:50%、[3]:75%)
- [4] .. [12]は、CatCoeff[9]の9つのカテゴリに必要です(0.0, .., 7.87)
- [13]は、CatCoeff[8]の最大のカテゴリ(ここでは7.87)よりも大きい値の最後のカテゴリとして必要です。
これで、何に対して安定した平均値が必要かを理解できます。カテゴリまたはクラスターを見つけるために、val/Cluster[iLne][0].µ. の比率を計算します。これは、インデックスiLineを持つ値型の全体的な平均です。したがって、配列CatCoeff[]の係数は、方程式を変換すると、全体の平均値の乗数になります。
pc = val/µ => pc*µ = val
これは、クラスターの数を事前定義(ほとんどのクラスタリング方法で必要)しただけでなく、クラスターのプロパティも事前定義したことを体系的に意味します。これはかなり珍しいことですが、これがこのクラスタリング方法で必要なパスが1つだけである理由です。 一方、他の方法では、クラスターの最適なプロパティを見つけるためにすべてのデータを数回パスする必要があります(上記を参照)。(CatCoeff[0])の最初の係数はゼロです。 これが選択されたのは、インジケーター「HalfTrend」が複数のバーに対して水平に実行されるように設計されているため、インジケーター値の差がゼロになるためです。したがって、このカテゴリはかなりのサイズに達すると予想されます。 他のすべての割り当ては、次の場合に行われます。
pc <= CatCoeff[i] => val/µ <= CatCoeff[i] => val <= CatCoeff[i]*µ.
CatCoeff[]の特定のカテゴリを爆破する外れ値が確かに存在するため、そのような値には追加のカテゴリがあります。
i = ArraySize(CatCoeff);
incrStdDeviation(val, Cluster[iLne][i+4]); // tooo big?最後のカテゴリに移動します
評価と出力
インジケーターの大きなループの終了直後、最初のパスの場合のみ(prev_calculated < 1) 結果はprtStdDev()によって操作ログに出力されます。 次に、StopWatchが停止し、同様に出力されます(s.a)。
//+------------------------------------------------------------------+ //| added for cluster analysis | //+------------------------------------------------------------------+ if (prev_calculated < 1) { prtStdDev(_Symbol+" "+EnumToString(Period())+" "+ShortName, 0, NumValues); if (StopWatch!=0) StopWatch = GetTickCount64()-StopWatch; Print ("Time needed for ",rates_total," bars on a PC with ",TerminalInfoInteger(TERMINAL_CPU_CORES), " cores and ",TerminalInfoInteger(TERMINAL_MEMORY_PHYSICAL)," Ram: ",TimeToString(StopWatch/1000,TIME_SECONDS)); } //+------------------------------------------------------------------+
prtStdDev(..)は、最初にHeadLineIncrStat(pre)で見出しを出力し、次にretIncrStat()を使用して値タイプ(インデックスiLine)ごとに14個すべての結果を1行で出力します。
void prtStdDev(const string pre, int iLne, const int NoVal) { if (NoVal <= 0 ) return; // if true no printing if (Cluster[iLne][0].n==0 ) return; // no values entered for this 'line' HeadLineIncrStat(pre); // print the headline int i,tot = 0,sA=ArrayRange(Cluster,1), sC=ArraySize(CatCoeff); for(i=4; i<sA; i++) tot += (int)Cluster[iLne][i].n; // sum up the total volume of all but the first [0] category retIncrStat(Cluster[iLne][0].n, pre, "learn 100% all["+(string)sC+"]", Cluster[iLne][0], 1, Cluster[iLne][0].µ); // print the base the first category [0] retIncrStat(Cluster[iLne][1].n, pre, "learn 25% all["+(string)sC+"]", Cluster[iLne][1], 1, Cluster[iLne][0].µ); // print the base the first category [0] retIncrStat(Cluster[iLne][2].n, pre, "learn 50% all["+(string)sC+"]", Cluster[iLne][2], 1, Cluster[iLne][0].µ); // print the base the first category [0] retIncrStat(Cluster[iLne][3].n, pre, "learn 75% all["+(string)sC+"]", Cluster[iLne][3], 1, Cluster[iLne][0].µ); // print the base the first category [0] for(i=4; i<sA-1; i++) { retIncrStat(tot, pre,"Cluster["+(string)(i)+"] (<="+_d22(CatCoeff[i-4])+")", Cluster[iLne][i], 1, Cluster[iLne][0].µ); // print each category } retIncrStat(tot, pre,"Cluster["+(string)i+"] (> "+_d22(CatCoeff[sC-1])+")", Cluster[iLne][i], 1, Cluster[iLne][0].µ); // print the last category }
ここで、tot += (int)Cluster[iLne][i].nは、これらのカテゴリの比較値(100％)を得るために合計された、カテゴリ4〜13の値の数です。以下が出力です。
GBPUSD PERIOD_D1 HalfTrd 2 ID Cluster Num. (tot %) µ (mult*µ) σ (Range %) min - max GBPUSD PERIOD_D1 HalfTrd 2 100100 learn 100% all[9] 7266 (100.0%) 217.6 (1.00*µ) 1800.0 (1.21%) 0.0 - 148850.0 GBPUSD PERIOD_D1 HalfTrd 2 100025 learn 25% all[9] 5476 (100.0%) 212.8 (0.98*µ) 470.2 (4.06%) 0.0 - 11574.0 GBPUSD PERIOD_D1 HalfTrd 2 100050 learn 50% all[9] 3650 (100.0%) 213.4 (0.98*µ) 489.2 (4.23%) 0.0 - 11574.0 GBPUSD PERIOD_D1 HalfTrd 2 100075 learn 75% all[9] 1825 (100.0%) 182.0 (0.84*µ) 451.4 (3.90%) 0.0 - 11574.0 GBPUSD PERIOD_D1 HalfTrd 2 400000 Cluster[4] (<=0.00) 2410 ( 66.0%) 0.0 (0.00*µ) 0.0 0.0 - 0.0 GBPUSD PERIOD_D1 HalfTrd 2 500033 Cluster[5] (<=0.33) 112 ( 3.1%) 37.9 (0.17*µ) 20.7 (27.66%) 1.0 - 76.0 GBPUSD PERIOD_D1 HalfTrd 2 600076 Cluster[6] (<=0.76) 146 ( 4.0%) 124.9 (0.57*µ) 28.5 (26.40%) 75.0 - 183.0 GBPUSD PERIOD_D1 HalfTrd 2 700132 Cluster[7] (<=1.32) 171 ( 4.7%) 233.3 (1.07*µ) 38.4 (28.06%) 167.0 - 304.0 GBPUSD PERIOD_D1 HalfTrd 2 800204 Cluster[8] (<=2.04) 192 ( 5.3%) 378.4 (1.74*µ) 47.9 (25.23%) 292.0 - 482.0 GBPUSD PERIOD_D1 HalfTrd 2 900298 Cluster[9] (<=2.98) 189 ( 5.2%) 566.3 (2.60*µ) 67.9 (26.73%) 456.0 - 710.0 GBPUSD PERIOD_D1 HalfTrd 2 1000421 Cluster[10] (<=4.21) 196 ( 5.4%) 816.6 (3.75*µ) 78.9 (23.90%) 666.0 - 996.0 GBPUSD PERIOD_D1 HalfTrd 2 1100580 Cluster[11] (<=5.80) 114 ( 3.1%) 1134.9 (5.22*µ) 100.2 (24.38%) 940.0 - 1351.0 GBPUSD PERIOD_D1 HalfTrd 2 1200787 Cluster[12] (<=7.87) 67 ( 1.8%) 1512.1 (6.95*µ) 136.8 (26.56%) 1330.0 - 1845.0 GBPUSD PERIOD_D1 HalfTrd 2 1300999 Cluster[13] (> 7.87) 54 ( 1.5%) 2707.3 (12.44*µ) 1414.0 (14.47%) 1803.0 - 11574.0 Time needed for 7302 bars on a PC with 12 cores and Ram: 65482, Time: 00:00:00:016
では、何がわかるでしょうか。列ごとにみてみましょう。最初の列には、ShortNameに割り当てられた銘柄、時間枠、インジケーターの名前、およびその「Amplitude」が表示されます。2番目の列は、各データ構造のIDを示しています。1000nnnは、100、25、50、および75からの学習率を示す最後の3桁の平均計算を示しています。400nnn .. 1300nnnは、カテゴリ、クラスター、またはヒープです。ここで、最後の3桁は、平均µのカテゴリまたは乗数を示します。これは、括弧内のクラスターの下の3番目の列にも示されています。それは明確で自明です。
これからが面白くなります。列4は、それぞれのカテゴリの値の数と括弧内のパーセンテージを示しています。ここで興味深いのは、インジケーターがほとんどの場合水平であるということです(Cat.#4 2409バーまたは日数66.0％)。これは、3分の2の時間でレンジ取引で成功する可能性があることを示しています。しかし、カテゴリ8、9、10には、より多くの(ローカル)最大値がありますが、カテゴリ5は、驚くほど少ない値(112、3.1％)を受け取っています。これは2つのしきい値間のギャップとして解釈できるようになり、次の大まかな値を提供できます。
fabs(slope) < 0.5*µの場合は、市場が横ばいなので、レンジ取引を試します
fabs(slope) > 1.0*µの場合は、市場にトレンドがあるので、波に乗ってみます
IDが100nnnの最初の4行は、µがどれだけ安定しているかを推定するのに役立ちます。説明したように、あまり変動する値は必要ありません。µが100100の217.6(1日あたりのポイント)から100075の182.1(このµに使用されるのは値の最後の25％のみ)または16％に低下することがわかります。少ないですが多すぎないと思います。しかし、これで何がわかるのしょうか。GBPUSDのボラティリティは減少しました。このカテゴリの最初の値の日付は2014.05.28 00:00:00です。おそらくこれを考慮に入れる必要があります。
平均値を計算すると、分散σは貴重な情報を示します。これにより列6(σ (Range %))に移動します。これは、個々の値が平均値にどれだけ近いかを示します。正規分布の値の場合、すべての値の68％が分散内にあります。分散の場合、これは、平均値が小さいほど良い、つまり、平均値がより正確(あいまいさが少ない)であることを意味します。括弧内の値の後ろには、最後の2列の比率σ/(max-min)があります。これは、分散と平均の質の尺度でもあります。
次に、GBPUSD D1の結果が、M15ローソク足のような短い時間枠で繰り返されるかどうかを見てみましょう。チャートの時間枠をD1からM15に切り替えます。
GBPUSD PERIOD_M15 HalfTrd 2 ID Cluster Num. (tot %) µ (mult*µ) σ (Range %) min - max GBPUSD PERIOD_M15 HalfTrd 2 100100 learn 100% all[9] 556389 (100.0%) 18.0 (1.00*µ) 212.0 (0.14%) 0.0 - 152900.0 GBPUSD PERIOD_M15 HalfTrd 2 100025 learn 25% all[9] 417293 (100.0%) 18.2 (1.01*µ) 52.2 (1.76%) 0.0 - 2971.0 GBPUSD PERIOD_M15 HalfTrd 2 100050 learn 50% all[9] 278195 (100.0%) 15.9 (0.88*µ) 45.0 (1.51%) 0.0 - 2971.0 GBPUSD PERIOD_M15 HalfTrd 2 100075 learn 75% all[9] 139097 (100.0%) 15.7 (0.87*µ) 46.1 (1.55%) 0.0 - 2971.0 GBPUSD PERIOD_M15 HalfTrd 2 400000 Cluster[4] (<=0.00) 193164 ( 69.4%) 0.0 (0.00*µ) 0.0 0.0 - 0.0 GBPUSD PERIOD_M15 HalfTrd 2 500033 Cluster[5] (<=0.33) 10528 ( 3.8%) 3.3 (0.18*µ) 1.7 (33.57%) 1.0 - 6.0 GBPUSD PERIOD_M15 HalfTrd 2 600076 Cluster[6] (<=0.76) 12797 ( 4.6%) 10.3 (0.57*µ) 2.4 (26.24%) 6.0 - 15.0 GBPUSD PERIOD_M15 HalfTrd 2 700132 Cluster[7] (<=1.32) 12981 ( 4.7%) 19.6 (1.09*µ) 3.1 (25.90%) 14.0 - 26.0 GBPUSD PERIOD_M15 HalfTrd 2 800204 Cluster[8] (<=2.04) 12527 ( 4.5%) 31.6 (1.75*µ) 4.2 (24.69%) 24.0 - 41.0 GBPUSD PERIOD_M15 HalfTrd 2 900298 Cluster[9] (<=2.98) 11067 ( 4.0%) 47.3 (2.62*µ) 5.5 (23.91%) 37.0 - 60.0 GBPUSD PERIOD_M15 HalfTrd 2 1000421 Cluster[10] (<=4.21) 8931 ( 3.2%) 67.6 (3.75*µ) 7.3 (23.59%) 54.0 - 85.0 GBPUSD PERIOD_M15 HalfTrd 2 1100580 Cluster[11] (<=5.80) 6464 ( 2.3%) 94.4 (5.23*µ) 9.7 (23.65%) 77.0 - 118.0 GBPUSD PERIOD_M15 HalfTrd 2 1200787 Cluster[12] (<=7.87) 4390 ( 1.6%) 128.4 (7.12*µ) 12.6 (22.94%) 105.0 - 160.0 GBPUSD PERIOD_M15 HalfTrd 2 1300999 Cluster[13] (> 7.87) 5346 ( 1.9%) 241.8 (13.40*µ) 138.9 (4.91%) 143.0 - 2971.0 Time needed for 556391 bars on a PC with 12 cores and Ram: 65482, Time: 00:00:00:140
もちろん、平均勾配は今でははるかに小さくなっています。1日あたり217.6ポイントから15分で18.0ポイントに低下します。しかし、同様の動作がここでも見られます。
fabs(slope) < 0.5*µの場合は、市場が横ばいなので、レンジ取引を試します
fabs(slope) > 1.0*µの場合は、市場にトレンドがあるので、波に乗ってみます
毎日の時間枠の解釈について述べたことはすべて、その有効性を保持しています。
終わりに
「HalfTrend」インジケーターを例として使用すると、インジケーターの動作に関する非常に価値のある情報が、単純な分類またはクラスター分析で取得できることを示すことができました。それ以外の場合は、非常に計算量が多くなります。通常、平均と分散は別々のループで計算され、その後にクラスタリング用の追加のループが続きます。ここでは、データの最初の部分が学習に使用され、2番目の部分が学習内容を適用するためのインジケーターも計算する1つの大きなループですべてを判定できます。50万を超えるデータがあっても、これらすべてが1秒未満で完了するので、この情報を最新かつオンザフライで判断して表示することが可能になります。これは、取引にとって非常に価値があります。
すべては、ユーザーがそのような分析に必要なコード行を自分のインジケーターにすばやく簡単に挿入できるように設計されています。自分の指標がトレンドvsフラットの質問に答えるかどうか、どのようにそしてどれだけうまく答えるかをテストできるだけでなく、自分のアイデアをさらに発展させるためのベンチマークが提供されます。
次の段階
次の記事では、このアプローチを標準指標に適用します。新しい見解と解釈の拡張がもたらされるでしょう。そしてもちろん、これらは、このツールキットを自分で使用したい場合の進め方の例でもあります。
MetaQuotes Ltdにより英語から翻訳されました。
元の記事: https://www.mql5.com/en/articles/9527
DoEasyライブラリのグラフィックス(第76部): フォームオブジェクトと事前定義されたカラースキーム
DoEasyライブラリのグラフィックス(第75部): 基本的なグラフィック要素でプリミティブとテキストを処理するメソッド
DoEasyライブラリのグラフィックス(第77部): 影オブジェクトクラス
DoEasyライブラリのグラフィックス(第74部): CCanvasクラスを使用した基本的グラフィック要素
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索