
Guia Prático MQL5 - Programando os Canais Móveis
Introdução
É bem conhecido que a direção dos preços do mercado pode ser expressada, indicando uma tendência no gráfico, ou, de fato, sua ausência, significando que ela está lateralizada. Considera-se que os indicadores de técnicas que pertencem ao grupo dos osciladores funcionam de forma eficiente quando o mercado está lateralizado. No entanto, pode existir uma determinada faixa de flutuação dos preços mesmo quando uma tendência aparece.
Neste artigo, vou tentar esclarecer uma forma dinâmica de construção dos canais equidistantes, frequentemente denominados como canais móveis. Deve-se notar que uma das estratégias mais populares para tais canais é a estratégia de Victor Barishpolts. Nós iremos abordar os aspectos de sua estratégia que estão relacionados com as regras de formação dos canais móveis. Além disso, nós vamos tentar estender essas regras, que, na opinião do autor, aumentaria a flexibilidade do sistema de canais.
1. Fundamentos dos canais equidistantes
Primeiramente,nós vamos trabalhar com esquemas utilizados como base para programar um canal equidistante. Eu recomendaria utilizar a Ajuda para ler sobre a ferramenta de análise técnica "Canal Equidistante".
Sabe-se que o canal é construído a partir de três pontos, e cada um deles possuem uma coordenada de preço e hora. Para começar, vamos prestar atenção às coordenadas de tempo, já que a sua sequência influência no tipo de canal. Como exemplo, nós vamos utilizar um canal cuja linha principal é construída a partir de dois mínimos locais. O terceiro ponto será responsável pelo máximo local. A posição dos pontos pode servir como critério para a tipificação do canal.
Ao desenhar o canal, não se utilizam os raios para a esquerda, nem os raios para a direita, salvo indicação contrária.
O primeiro tipo refere-se a um caso em que o mínimo aparece primeiro, seguido pelo máximo e o mínimo novamente. É apresentada uma visão esquemática desta situação na Fig.1.
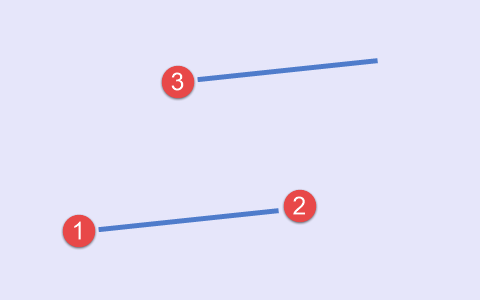
Fig.1 Primeiro tipo de conjunto de pontos, esquema
No gráfico de preço abaixo, o primeiro tipo apresentado tem o seguinte aspecto (Fig.2).
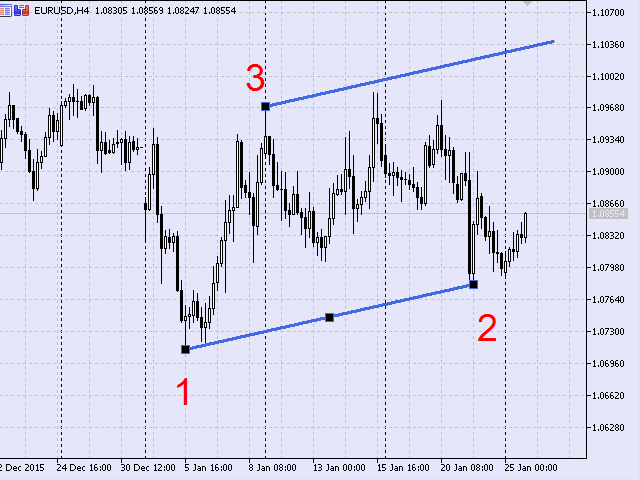
Fig.2 Primeiro tipo de conjunto de pontos, gráfico de preço
O segundo tipo refere-se a um caso quando aparecem um máximo seguido por um par de mínimos no gráfico (Figura 3).
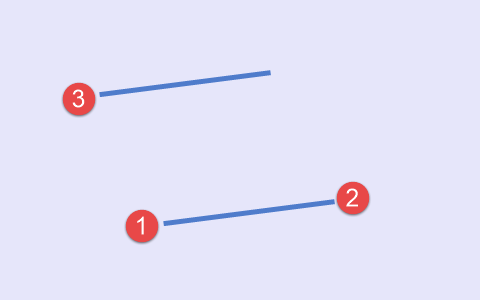
Fig.3 Segundo tipo de conjunto de pontos, esquema
O máximo local que aparece no início, eventualmente se tornará um terceiro ponto. Ele é seguido por um par de mínimos que formam uma linha principal.
O terceiro tipo é construído com base no esquema "mínimo-mínimo-máximo". Neste caso, a linha principal espera até que o máximo local seja formado (Fig.4).
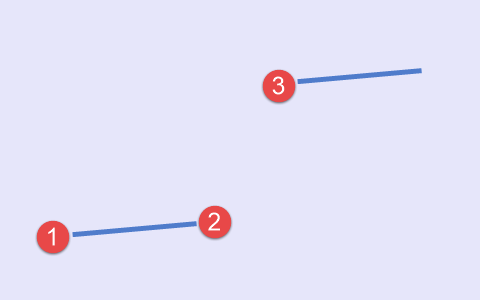
Fig.4 Terceiro tipo de conjunto de pontos, esquema
Os últimos dois tipos são casos bastante específicos.
A quarta opção se aplica quando o terceiro e o primeiro ponto se coincidem na hora de sua construção. (Fig.5).
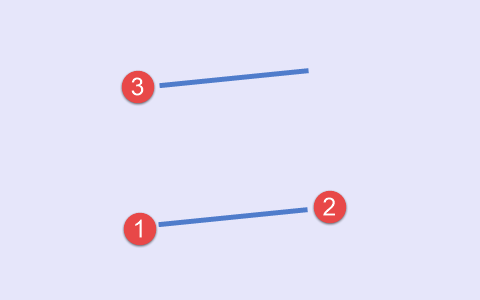
Fig.5 Quarto tipo de conjunto de pontos, esquema
E, finalmente, o quinto tipo, que ocorre quando há a coincidência das coordenadas de tempo do segundo e do terceiro ponto (Fig.6).
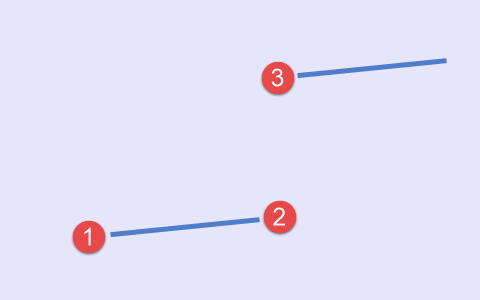
Fig.6 Quinto tipo de conjunto de pontos, esquema
E estes são os cinco tipos de canais equidistantes que nós iremos trabalhar. Na próxima seção, tentaremos programar os pontos utilizados para a construção das linhas do canal.
2. Tipos auxiliares de dados
Geralmente, são utilizados os pontos dos fractais para desenhar as linhas de tendência do canal. Desta maneira, um ponto é, simultaneamente, um fractal e uma base para desenhar uma linha reta.
Agora, tentaremos resumir e codificar os pontos dos fractais utilizando a POO.
2.1 Classe do ponto fractal
A característica desta classe envolve estar no comando do ponto que está entre os pontos utilizados para a construção do canal equidistante.
Nós vamos nomear a classe indicada como CFractalPoint, e como boa prática da programação MQL5, vamos ligá-la a classe de interface CObject como uma relação de herança.
//+------------------------------------------------------------------+ //| Classe do ponto fractal | //+------------------------------------------------------------------+ class CFractalPoint : public CObject { //--- === Os membros de dados === --- private: datetime m_date; // data e hora double m_value; // valor ENUM_EXTREMUM_TYPE m_extreme_type; // tipo de extremo int m_idx; // índice (de 0 a 2) //--- === Métodos === --- public: //--- Construtor/destrutor void CFractalPoint(void); void CFractalPoint(datetime _date,double _value, ENUM_EXTREMUM_TYPE _extreme_type,int _idx); void ~CFractalPoint(void){}; //--- métodos-get datetime Date(void) const {return m_date;}; double Value(void) const {return m_value;}; ENUM_EXTREMUM_TYPE FractalType(void) const {return m_extreme_type;}; int Index(void) const {return m_idx;}; //--- métodos-set void Date(const datetime _date) {m_date=_date;}; void Value(const double _value) {m_value=_value;}; void FractalType(const ENUM_EXTREMUM_TYPE extreme_type) {m_extreme_type=extreme_type;}; void Index(const int _bar_idx){m_idx=_bar_idx;}; //--- serviço void Copy(const CFractalPoint &_source_frac); void Print(void); }; //+------------------------------------------------------------------+
A classe possui 4 membros para a transferência de dados:
- m_date — a coordenada de tempo do ponto no gráfico;
- m_Value — a coordenada de preço do ponto no gráfico;
- m_extreme_type – tipo de extremo;
- m_idx – índice.
A enumeração ENUM_EXTREMUM_TYPE será responsável para o tipo de extremo:
//+------------------------------------------------------------------+ //| Tipo de extremo | //+------------------------------------------------------------------+ enum ENUM_EXTREMUM_TYPE { EXTREMUM_TYPE_MIN=0, // mínima EXTREMUM_TYPE_MAX=1, // máxima };
O objetivo principal dos métodos CFractalPoint é garantir o recebimento e a atualização dos valores dos membros privados listados acima.
Por exemplo, vamos criar de forma programática um ponto de fractal no gráfico H4 do EURUSD, datado em 26/01/2016 08:00, indicado na Fig.7. O fractal foi formado na máxima da vela, no valor de 1,08742.
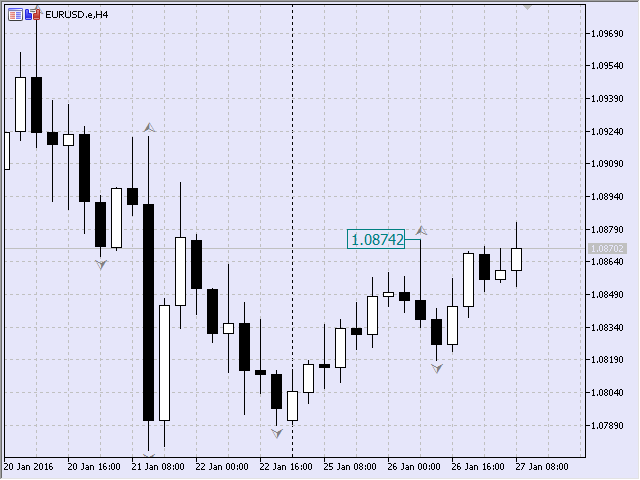
Fig.7 Exemplo de fractal
Isto é aspecto de como pode parecer o código pode alcançar o objetivo.
//--- dados para o ponto fractal datetime pnt_date=D'26.01.2016 08:00'; double pnt_val=1.08742; ENUM_EXTREMUM_TYPE pnt_type=EXTREMUM_TYPE_MAX; int pnt_idx=0; //--- cria um ponto fractal CFractalPoint myFracPoint(pnt_date,pnt_val,pnt_type,pnt_idx); myFracPoint.Print();
No registro aparece o seguinte:
---=== Dados do ponto Fractal ===--- Date: 2016.01.26 08:00 Price: 1.08742 Type: EXTREMUM_TYPE_MAX Index: 0
Isso implica que o ponto fractal foi localizado na barra datada em 26/01/2016, ao preço de 1,08742. Este fractal é um máximo local. O índice zero indica que ele será o primeiro ponto no conjunto de pontos análogos.
2.2 Classe do conjunto de pontos fractais
Agora, nós podemos prosseguir com a criação de um conjunto de pontos fractais que será usado para a construção do canal equidistante. Para este fim, nós criaremos a classe CFractalSet que irá identificar e reunir estes pontos em um conjunto.
Esta classe será incluída no Expert Advisor, em vez do indicador, portanto, os canais irão se referir aos objetos gráficos do tipo CChartObjectChannel e não aos buffers do indicador.
CFractalSet é uma classe que deriva da classe CArrayObj da Biblioteca Padrão. cI selecionou o tipo protected de herança para construir uma interface da classe altamente especializada.
//+------------------------------------------------------------------+ //| Classe do conjunto de pontos | //+------------------------------------------------------------------+ class CFractalSet : protected CArrayObj { //--- === Os membros de dados === --- private: ENUM_SET_TYPE m_set_type; // tipo do conjunto de pontos int m_fractal_num; // número fixo de pontos int m_fractals_ha; // manipulador do indicador de fractal CisNewBar m_new_bar; // objeto da nova barra CArrayObj m_channels_arr; // objeto do array do indicador color m_channel_colors[4]; // cor dos canais bool m_is_init; // flag de inicialização //--- configurações do canal de int m_prev_frac_num; // fractais anteriores int m_bars_beside; // barras do lado esquerdo/direito do fractal int m_bars_between; // número de barras intermediárias bool m_to_delete_prev; // remover canais anteriores? bool m_is_alt; // indicador de fractal alternativo? ENUM_RELEVANT_EXTREMUM m_rel_frac; // ponto relevante bool m_is_array; // desenhar seta? int m_line_wid; // espessura da linha bool m_to_log; // manter o registro? //--- === Métodos === --- public: //--- Construtor/destrutor void CFractalSet(void); void CFractalSet(const CFractalSet &_src_frac_set); void ~CFractalSet(void){}; //--- void operator=(const CFractalSet &_src_frac_set); //--- manipuladores bool Init( int _prev_frac_num, int _bars_beside, int _bars_between=0, bool _to_delete_prev=true, bool _is_alt=false, ENUM_RELEVANT_EXTREMUM _rel_frac=RELEVANT_EXTREMUM_PREV, bool _is_arr=false, int _line_wid=3, bool _to_log=true ); void Deinit(void); void Process(void); //--- serviço CChartObjectChannel *GetChannelByIdx(const int _ch_idx); int ChannelsTotal(void) const {return m_channels_arr.Total();}; private: int AddFrac(const int _buff_len); int CheckSet(const SFracData &_fractals[]); ENUM_SET_TYPE GetTypeOfSet(void) const {return m_set_type;}; void SetTypeOfSet(const ENUM_SET_TYPE _set_type) {m_set_type=_set_type;}; bool PlotChannel(void); bool Crop(const uint _num_to_crop); void BubbleSort(void); }; //+------------------------------------------------------------------+
Segue a lista de membros desta classe.
- m_set_type - tipo do conjunto de pontos. Abaixo está a enumeração responsável pela classificação do conjunto;
- m_fractal_num - Número fixo de pontos incluídos no conjunto;
- m_fractals_ha - manipulador do indicador de fractal;
- m_new_bar – objeto da nova barra;
- m_channels_arr – objeto do array do indicador;
- m_channel_colors[4] — array de cores para exibir os canais;
- m_is_init — flag de inicialização.
Ele é seguido pelo bloco de membros responsáveis pela configuração do canal. - m_prev_frac_num — número de fractais anteriores utilizados para a construção do primeiro canal. Se há 3 pontos, então, o canal será construído logo após a sua inicialização;
- m_bars_beside — barras do lado esquerdo/direito do fractal. Se, por exemplo, é indicado 5, então, será usado um total de 11 barras para encontrar um fractal;
- m_bars_between — número de barras intermediárias. De fato, este é um mínimo de barras que devem estar presente entre os pontos adjacentes do fractal;
- m_to_delete_prev — permissão para remover os canais anteriores;;
- m_is_alt — flag de utilização do indicador fractal alternativo;
- m_rel_frac — selecção do ponto relevante. Se as barras intermediárias forem suficientes, então o tipo deste ponto irá mostrar qual barra que deve ser ignorada;
- m_is_array — flag de desenho da seta;
- m_line_wid — espessura da linha;
- m_to_log — flag de registro.
É apresentado a seguir a enumeração que processa os tipos dos conjuntos de pontos:
//+------------------------------------------------------------------+ //| Tipo do conjunto de pontos de extremo | //+------------------------------------------------------------------+ enum ENUM_SET_TYPE { SET_TYPE_NONE=0, // não definido SET_TYPE_MINMAX=1, // min-max-min SET_TYPE_MAXMIN=2, // max-min-max };
Neste exemplo, o valor de SET_TYPE_MAXMIN corresponde à seguinte sequência de pontos fractais: máximo, mínimo e máximo (Fig.8).
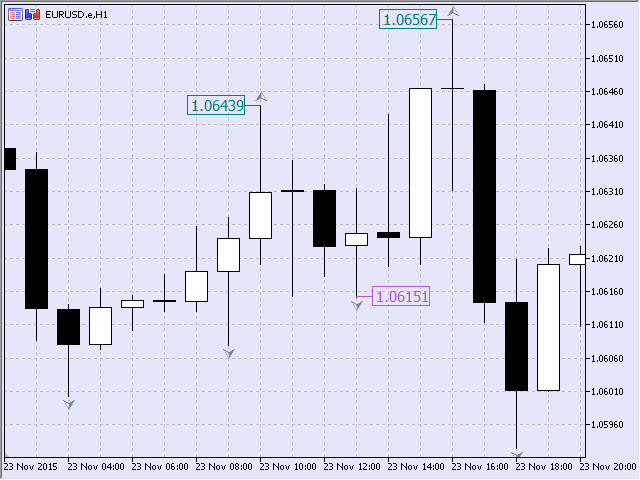
Fig.8 Conjunto do tipo "max-min-max"
Apresso-me em dizer que a sequência de pontos não pode ser seguida o tempo todo. Ocasionalmente, pode haver um caso em que o primeiro mínimo será seguido por mais um mínimo. Como exemplo, podemos referir-se ao terceiro tipo de conjunto de pontos, descrito na primeira seção (Fig.4). Em todo caso, vamos considerar um conjunto completo se ele tiver um par de mínimos e um máximo, ou um par de máximos e um mínimo.
A enumeração que processa os tipos do ponto relevante possui a seguinte forma:
//+------------------------------------------------------------------+ //| Type do ponto relevante | //+------------------------------------------------------------------+ enum ENUM_RELEVANT_EXTREMUM { RELEVANT_EXTREMUM_PREV=0, // anterior RELEVANT_EXTREMUM_LAST=1, // último };
Vamos prosseguir para os métodos. Primeiramente, vamos listar os manipuladores.
- Init() – inicializa o conjunto. O método é responsável pela inicialização correta da operação do objeto que apresenta o conjunto de pontos fractais.
- Deinit() - desinicialização do conjunto.
- Process() - controla o fluxo de preço. De fato, este método em específico identifica os pontos e exibe o canal.
Métodos do serviço:
- AddFrac() — addiciona os pontos fractais ao conjunto
- CheckSet() - verifica o estado atual do conjunto.
- PlotChannel() - desenha o canal equidistante.
- Crop() – corta o conjunto.
- BubbleSort() - ordena os pontos no conjunto segundo o horário de sua aparição.
2.3 Possibilidades adicionais da construção de um canal
Deixe-me lembrá-lo mais uma vez que a classe CChartObjectChannel da Biblioteca Padrão foi usada para a construção do canal e endereçamento de suas propriedades. Nós vamos considerar alguns pontos cuja implementação algorítmica pode aumentar a flexibilidade da construção dos canais de forma automática.
2.3.1 Sincronização das linhas
É mais conveniente avaliar visualmente o gráfico com os canais no momento em que ambas as linhas do canal dão início a partir da mesma barra. Oficialmente, o quarto tipo do canal corresponde a esta abordagem (Fig.5). Obviamente, os canais podem pertencer a outros tipos. Por esta razão, as coordenadas de preço e tempo dos pontos fractais são modificados no método CFractalSet::PlotChannel(), a fim de ajustar ao quarto tipo do canal. Ele também é importante (é implementado) para guardar o ângulo e a largura do canal.
Considere o seguinte canal equidistante no gráfico de preços (Fig.9).
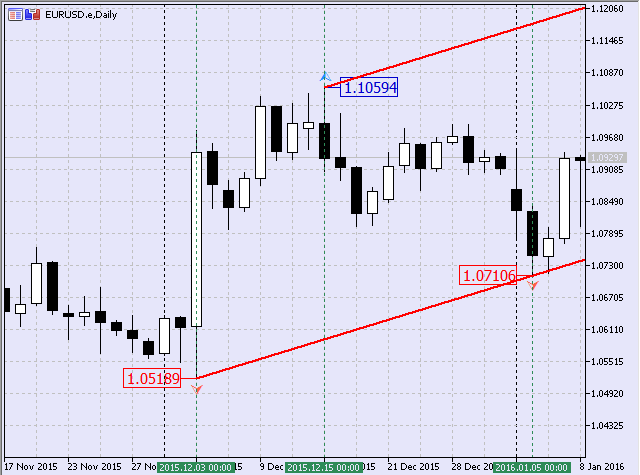
Fig.9 Canal Equidistante com base nos pontos iniciais
Eu gostaria de esclarecer desde o início que ele foi construído manualmente. Ele tem os seguintes pontos fractais:
- $1.05189 em 03/12/2015 (mínima);
- $1.07106 em 05/01/2016 (mínima);
- $1.10594 em 05/01/2016 (máxima).
Se exibirmos um canal semelhante com a classe CFractalSet, obteremos a seguinte imagem (Fig.10).
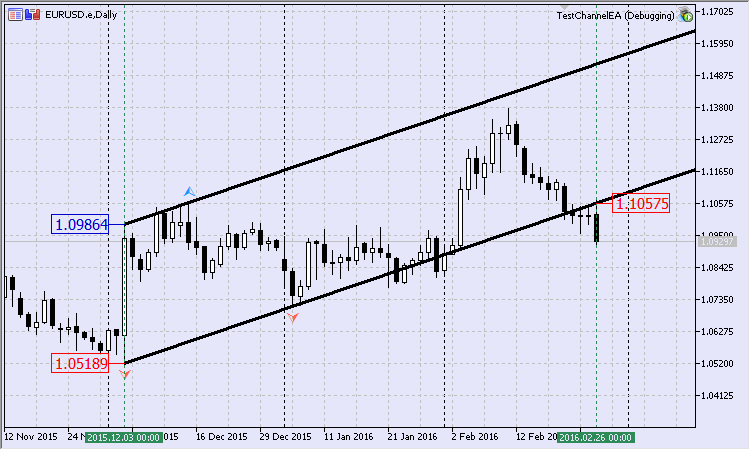
Fig.10 Canal equidistante segundo os pontos calculados
As diferenças insignificantes advêm do fato de que a construção do canal na Fig. 10 se baseia nos pontos calculados. Os valores do preço e do tempo do segundo e do terceiro ponto estão sendo calculados. O último ponto deve coincidir com o a coordenada de tempo com o primeiro ponto.
Eu vou dividir em 2 partes a tarefa de desenhar um canal segundo os pontos calculados.
A primeira parte vai se concentrar em coordenadas de tempo, onde início do canal e no final são definidos. O bloco de código seguinte está presente no método indicado:
//--- 1) coordenadas de tempo //--- início do canal int first_date_idx=ArrayMinimum(times); if(first_date_idx<0) { Print("Erro na obtenção da coordenada de tempo!"); m_channels_arr.Delete(m_channels_arr.Total()-1); return false; } datetime first_point_date=times[first_date_idx]; //--- fim do canal datetime dates[]; if(CopyTime(_Symbol,_Period,0,1,dates)!=1) { Print("Erro na obtenção da coordenada de tempo!"); m_channels_arr.Delete(m_channels_arr.Total()-1); return false; } datetime last_point_date=dates[0];
Desta forma, todos os pontos terão as seguintes coordenadas de tempo:
//--- coordenadas de tempo finais times[0]=times[2]=first_point_date; times[1]=last_point_date;
A segunda parte da tarefa refere-se as coordenadas de preços — um novo preço é determinado tanto para o terceiro ponto quanto para o primeiro.
Vamos determinar primeiro a rapidez com que o preço das linhas do canal se alteram, de barra em barra, e se o canal está indo para cima ou para baixo.
//--- 2) coordenadas de preço //--- 2.1 ângulo da linha //--- barras entre o primeiro e o segundo ponto datetime bars_dates[]; int bars_between=CopyTime(_Symbol,_Period, times[0],times[1],bars_dates ); if(bars_between<2) { Print("Erro na obtenção do número de barras entre os pontos!"); m_channels_arr.Delete(m_channels_arr.Total()-1); return false; } bars_between-=1; //--- diferencial comum double price_differential=MathAbs(prices[0]-prices[1]); //--- velocidade do preço (variação do preço na primeira barra) double price_speed=price_differential/bars_between; //--- direção do canal bool is_up=(prices[0]<prices[1]);
Agora, as coordenadas de preço dos pontos poderão ser atualizadas. É importante saber qual ponto foi formada anteriormente. Além disso, precisamos saber onde o canal está caminhando — se é para cima ou para baixo:
//--- 2.2 novo preço do primeiro ou do terceiro ponto if(times[0]!=times[2]) { datetime start,end; start=times[0]; end=times[2]; //--- se o terceiro ponto é anterior ao primeiro bool is_3_point_earlier=false; if(times[2]<times[0]) { start=times[2]; end=times[0]; is_3_point_earlier=true; } //--- barras entre o primeiro e o terceiro ponto int bars_between_1_3=CopyTime(_Symbol,_Period, start,end,bars_dates ); if(bars_between_1_3<2) { Print("Erro na obtenção do número de barras entre os pontos!"); m_channels_arr.Delete(m_channels_arr.Total()-1); return false; } bars_between_1_3-=1; //--- se o canal é ascendente if(is_up) { //--- se o ponto 3 é anterior if(is_3_point_earlier) prices[0]-=(bars_between_1_3*price_speed); else prices[2]-=(bars_between_1_3*price_speed); } //--- ou se o canal for descendente else { //--- se o ponto 3 é anterior if(is_3_point_earlier) prices[0]+=(bars_between_1_3*price_speed); else prices[2]+=(bars_between_1_3*price_speed); } }Anteriormente, o primeiro ponto foi formado antes em nosso exemplo, o que significa que o preço do terceiro ponto deve ser atualizado.
Finalmente, nós vamos atualizar as coordenadas do segundo ponto:
//--- 2.3 novo preço do ponto 2 if(times[1]<last_point_date) { datetime dates_for_last_bar[]; //--- barras entre o ponto 2 e a última barra bars_between=CopyTime(_Symbol,_Period,times[1],last_point_date,dates_for_last_bar); if(bars_between<2) { Print("Erro na obtenção do número de barras entre os pontos!"); m_channels_arr.Delete(m_channels_arr.Total()-1); return false; } bars_between-=1; //--- se o canal é ascendente if(is_up) prices[1]+=(bars_between*price_speed); //--- ou se o canal for descendente else prices[1]-=(bars_between*price_speed); }
O que nós obtemos:
- $1.05189 em 03/12/2015 (mínima);
- $1.10575 em 26/12/2016 (valor calculado);
- $1.09864 em 03/12/2015 (valor calculado).
O canal pode ser desenhado com ou sem a utilização dos raios para a direita. No entanto, esta opção refere-se apenas para o canal atual. Todos os objetos do canal anterior sobre o gráfico estarão sem o raio para a direita.
2.3.2 Consideração dos pontos fractais anteriores
Foi adicionado a opção de recorrer ao histórico para procurar os pontos fractais, com base nos parâmetros dados, à classe CFractalSet. Tal possibilidade só é utilizada durante a inicialização do exemplo da classe. Lembre-se que o membro m_prev_frac_num é responsável pelos "pontos do passado".
Vamos analisar o exemplo (Fig.11). Suponha-se que logo após a inicialização do Expert Advisor TestChannelEA, nós teremos de encontrar vários pontos fractais no gráfico. Eles podem ser fractais marcados com figuras relevantes.
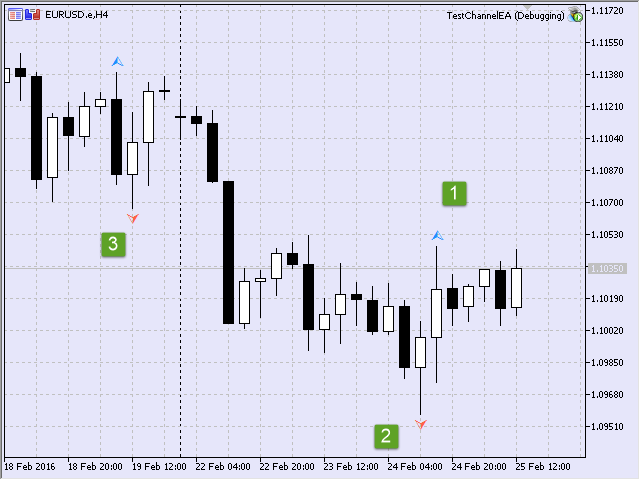
Fig.11 Pontos Fractais durante a inicialização
Se tomarmos os três pontos, então, nós seremos capazes de construir um canal (Fig.12).
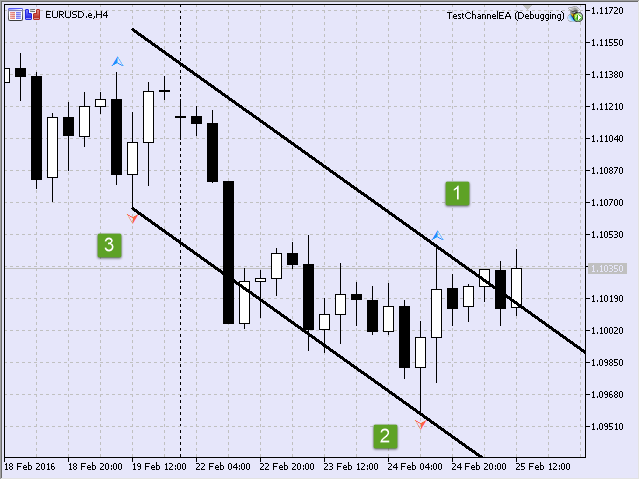
Fig.12 Primeiro canal construído durante a inicialização
Há uma mensagem no log:
2016.02.25 15:49:23.248 TestChannelEA (EURUSD.e,H4) Adicionado os fractais anteriores: 3
Não é difícil perceber que os pontos são adicionados ao conjunto da direita para a esquerda. E o canal é construído sobre pontos que devem ser reunidos a partir da esquerda para a direita. O método privado de ordenação CFractalSet::BubbleSort(), de fato, permite organizar os pontos antes de desenhar o canal atual.
A seguir, é apresentado o bloco de código que é responsável pelo conjunto de pontos durante a inicialização do método CFractalSet::Init():
//--- Se os pontos fractais anteriores foram adicionados if(m_prev_frac_num>0) { //--- 1) Carregando o histórico [start] bool synchronized=false; //--- Contado do loop int attempts=0; //--- 10 tentativas para aguardar a sincronização while(attempts<10) { if(SeriesInfoInteger(_Symbol,0,SERIES_SYNCHRONIZED)) { synchronized=true; //--- sincronização estabelecida, saída break; } //--- aumento do contador attempts++; //--- aguarda 50 milissegundos até a próxima iteração Sleep(50); } //--- if(!synchronized) { Print("Falha na obtenção do número de barras no ",_Symbol); return false; } int curr_bars_num=Bars(_Symbol,_Period); if(curr_bars_num>0) { PrintFormat("Número de barras no histórico do terminal baseado no símbolo/período no momento atual: %d", curr_bars_num); } //--- 1) Carregando o histórico [end] //--- 2) Dados calculados para o indicador solicitado [start] double Ups[]; int i,copied=CopyBuffer(m_fractals_ha,0,0,curr_bars_num,Ups); if(copied<=0) { Sleep(50); for(i=0;i<100;i++) { if(BarsCalculated(m_fractals_ha)>0) break; Sleep(50); } copied=CopyBuffer(m_fractals_ha,0,0,curr_bars_num,Ups); if(copied<=0) { Print("Falha ao copiar os fractais superiores. Error = ",GetLastError(), "i=",i," copied= ",copied); return false; } else { if(m_to_log) Print("Cópia dos fractais superiores com sucesso.", " i = ",i," copied = ",copied); } } else { if(m_to_log) Print("Cópia dos fractais superiores com sucesso. ArraySize = ",ArraySize(Ups)); } //--- 2) Dados calculados para o indicador solicitado [end] //--- 3) Adição de pontos fractais [start] int prev_fracs_num=AddFrac(curr_bars_num-1); if(m_to_log) if(prev_fracs_num>0) PrintFormat("Adicionado os fractais anteriores: %d",prev_fracs_num); //--- se o canal pode ser visualizado if(prev_fracs_num==3) if(!this.PlotChannel()) Print("Falha ao exibir o canal!"); //--- 3) Adição de pontos fractais [end] }
Ele pode ser dividido em 3 sub-blocos:
- carregando o histórico de cotações;
- cálculo dos dados do indicador de fractal;
- adicionando os pontos fractais ao conjunto.
Desta forma, o canal pode ser desenhado no momento de sua inicialização. Ele exige algum tempo, especialmente nos casos em que os dados do gráfico não está sincronizado com os dados do servidor.
2.3.3 Consideração de barras entre os pontos fractais adjacentes
Pontos fractais utilizados (primeiro e segundo, terceiro e quarto), que estão localizados ao lado do outro nos gráficos anteriores. Para eliminar os pontos mais próximos você pode adicionar algum tipo de filtro. Esta função pode ser desenvolvida pelo membro m_bars_between - um número de barras intermediárias entre os pontos adjacentes. Se você definir um número igual a 1, então, o segundo ponto não entrará no conjunto, e ele será substituído pelo terceiro ponto atual.
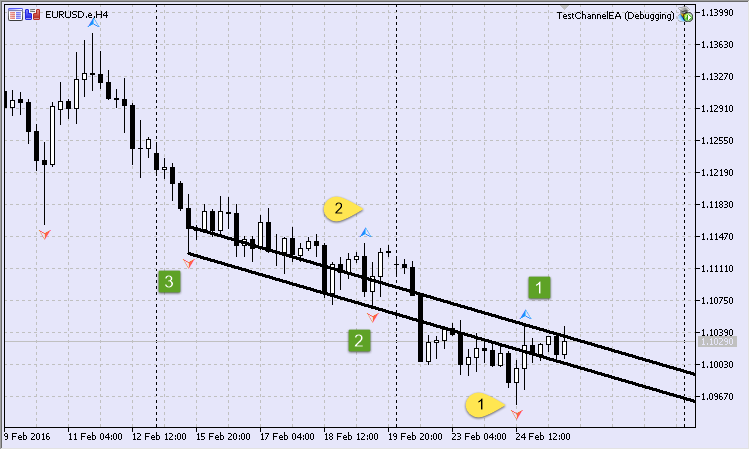
Fig.13 Primeiro canal levando em conta as barras intermediárias
Nós vamos construir um canal com base na condição de que haverá, pelo menos, 1 barra (Fig. 13) entre os pontos fractais adjacentes (Fig.13). Acontece que os pontos seguintes ao primeiro e segundo ponto devem ser ignorados. Eles são destacadas em amarelo.
Por exemplo, o primeiro ponto que faltava terá o seguinte log:
2016.02.25 16:11:48.037 TestChannelEA (EURUSD.e,H4) O ponto anterior será ignorado: 2016.02.24 12:00 2016.02.25 16:11:48.037 TestChannelEA (EURUSD.e,H4) As barras intermediárias não são suficientes. Um ponto será ignorado.
Então, o canal procurado ficará mais estreito e, provavelmente, não será funcional do ponto de vista do trader.
No que tange ao código, a verificação do número permitido de barras intermediárias é executada no corpo do método privado CFractalSet::CheckSet().
//--- se verificar o número de barras entre o último ponto e o atual if(m_bars_between>0) { curr_fractal_num=this.Total(); if(curr_fractal_num>0) { CFractalPoint *ptr_prev_frac=this.At(curr_fractal_num-1); if(CheckPointer(ptr_prev_frac)!=POINTER_DYNAMIC) { Print("Erro na obtenção do objeto de pontos fractais do conjunto!"); return -1; } datetime time1,time2; time1=ptr_prev_frac.Date(); time2=ptr_temp_frac.Date(); //--- barras entre os pontos datetime bars_dates[]; int bars_between=CopyTime(_Symbol,_Period, time1,time2,bars_dates ); if(bars_between<0) { Print("Erro na obtenção dos dados para o horário de abertura da barra!"); return -1; } bars_between-=2; //--- em várias barras if(bars_between>=0) //--- se as barras intermediárias não são suficientes if(bars_between<m_bars_between) { bool to_delete_frac=false; if(m_to_log) Print("Barras intermediárias não são suficientes. Será ignorado um ponto."); // ... } } }
A variável bars_between recebe um número de barras entre os dois pontos fractais adjacentes. Se o seu valor for inferior ao permitido, então um ponto é ignorado. Vamos descobrir a partir da próxima seção se é um ponto atual ou anterior.
2.3.4 Seleção do ponto fractal relevante
Quando as barras intermediárias não são suficientes, e um dos pontos tiver de ser ignorado, você pode especificar qual ponto deve ser ignorado. No exemplo acima, o ponto mais antigo, em termos do tempo de aparecimento, foi ignorado, porque o último ponto foi considerado o ponto fractal relevante. Vamos tornar o ponto anterior relevante, e ver o seu resultado (Fig.14).
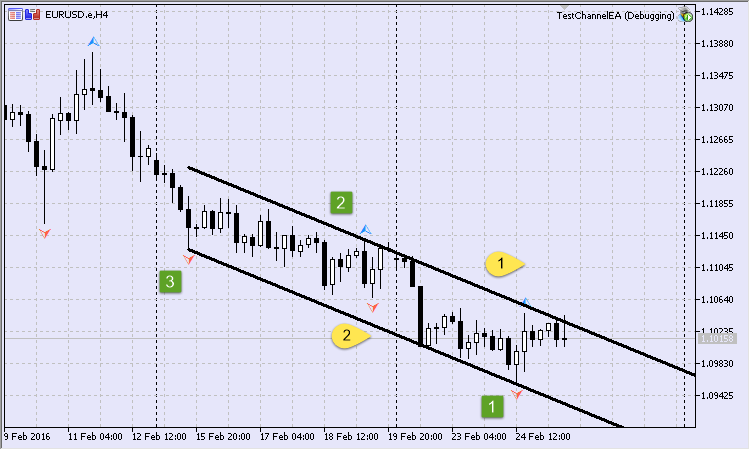
Fig.14 Primeiro canal com uma consideração de barras intermediárias e um ponto relevante anterior
Por exemplo, vamos obter o seguinte log para o primeiro ponto ignorados
2016.02.25 16:46:06.212 TestChannelEA (EURUSD.e,H4) Ponto atual será ignorado: 2016.02.24 16:00 2016.02.25 16:46:06.212 TestChannelEA (EURUSD.e,H4) Barras intermediárias não são suficientes. Um ponto será ignorado.
Possivelmente, este canal parece mais útil, uma vez que ele limita todas as barras adjacentes. É difícil dizer de antemão, se o ponto relevante anterior ou o último se tornará mais produtivo ao desenhar o canal.
Se olharmos para o código (e é o mesmo bloco de código no corpo do método privado CFractalSet::CheckSet()), veremos que dois fatores afetam o comportamento do método: o tipo do ponto atual e a flag de inicialização selecionada.
//--- se as barras intermediárias não são suficientes if(bars_between<m_bars_between) { bool to_delete_frac=false; if(m_to_log) Print("Barras intermediárias não são suficientes. Será ignorado um ponto."); //--- se o ponto anterior é relevante if(m_rel_frac==RELEVANT_EXTREMUM_PREV) { datetime curr_frac_date=time2; //--- se houve inicialização if(m_is_init) { continue; } //--- se não houver inicialização else { //--- remove ponto atual to_delete_frac=true; curr_frac_date=time1; } if(m_to_log) { PrintFormat("O ponto atual será descartado: %s", TimeToString(curr_frac_date)); } } //--- se o último ponto é relevante else { datetime curr_frac_date=time1; //--- se houve inicialização if(m_is_init) { //--- remove o ponto anterior to_delete_frac=true; } //--- se não houver inicialização else { curr_frac_date=time2; } if(m_to_log) PrintFormat("O ponto anterior foi ignorado: %s", TimeToString(curr_frac_date)); if(curr_frac_date==time2) continue; } //--- se o ponto foi removido if(to_delete_frac) { if(!this.Delete(curr_fractal_num-1)) { Print("Erro ao apagar o último ponto do conjunto!"); return -1; } } }
Na próxima seção, vamos olhar para o conjunto de canais equidistantes e obter a imagem do movimento de preço, variando os seus parâmetros.
3. Criando os canais móveis automaticamente
A versão do Expert Advisor chamado de ChannelsPlotter foi criado para testar o desenho dos canais. Os resultados da operação do Expert Advisor foram exibidos na Fig.15. Obviamente, os canais começam a "oscilar", com base nos fractais normais e na ausência de uma tendência clara do mercado. Portanto, foi adicionado uma opção para utilizar o indicador de fractais alternativo , onde qualquer outro número de barras adjacentes ao extremo são definidos. O indicador X-bars Fractals foi emprestado da Base de Código.
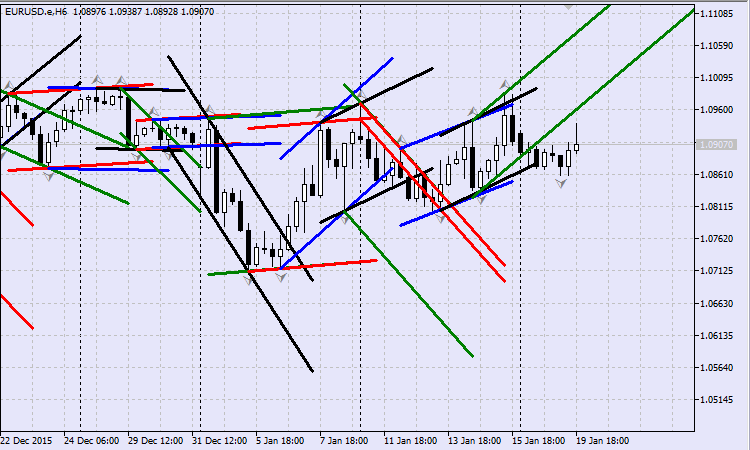
Fig.15 Canais móveis com base nos fractais habituais
Se você executa o Expert Advisor com uma seleção de indicadores fractais alternativos, então um resultado satisfatório dá um aumento no número de barras em que formam um grupo para encontrar o extremo. Assim, se olharmos para um fractal em um grupo constituído por 23 barras, então, o resultado pode aparecer como mostrado na Fig.16.
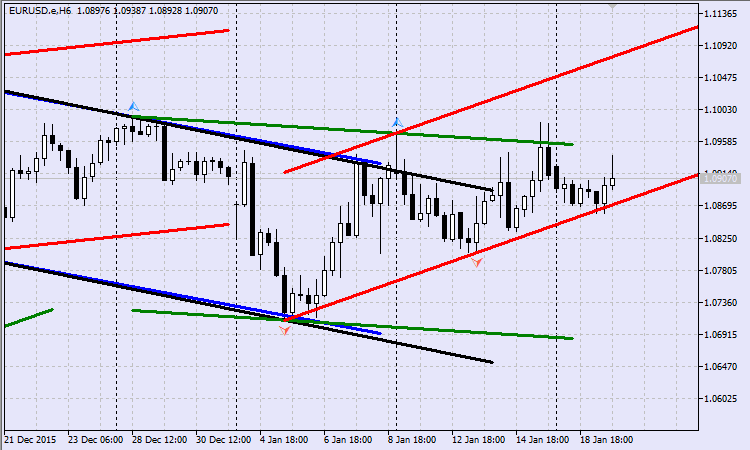
Fig.16 Canais móveis com base em fractais alternativos
Desta forma, quanto menos as barras adjacentes participarem na determinação do fractal, mais ruído do "canal" aparecerá no gráfico de preço.
Conclusão
Neste artigo, eu tentei apresentar um método de programação do sistema de canais equidistantes. Foram considerados alguns detalhes na construção dos canais. Foi usada a ideia de Victor Barishpoltz como um framework.. No meu próximo artigo, vou analisar os sinais de negociação gerados pelos canais móveis.
local dos arquivos:
Na minha opinião, é mais conveniente criar e armazenar arquivos na pasta do projeto. Por exemplo, a localização pode ser a seguinte: <pasta de dados>\MQL5\Projects\ChannelsPlotter. Não se esqueça de compilar o indicador fractal alternativo - X-bars_Fractals. O código fonte do indicador deve estar localizado na pasta — <pasta de dados>\MQL5\Indicators.
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/1862
 Expert Advisor Universal: Estratégias Personalizadas e Classes Auxiliares de Negociação (Parte 3)
Expert Advisor Universal: Estratégias Personalizadas e Classes Auxiliares de Negociação (Parte 3)
 Método da área
Método da área
 Expert Advisor Universal: Modos de Negociação das Estratégias (Parte 1)
Expert Advisor Universal: Modos de Negociação das Estratégias (Parte 1)
 Calculadora de sinais
Calculadora de sinais
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso