Generalized Normal (version 1) Parameters Support PDF CDF Mean Median Mode Variance Skewness Ex. kurtosis Entropy Known also as the exponential power distribution, or the generalized error distribution, this is a parametric family of symmetric distributions. It includes all normal and Laplace distributions, and as limiting cases it includes all...
8. 특정 분위수에 대한 신뢰 구간의 경계를 넘어 슬라이딩 윈도우에서 출구(High-Low)를 기다리고 거래에 들어갑니다.
5. Renko는 "Renko 브릭"에 의해 지정된 범위의 이탈을 1 "brick"의 값으로 간주하며, 브레이크아웃은 "brick"의 값, 즉 "벽돌" 10pp, 새로운 Renko 벽돌을 그리려면 가격이 이미 형성된 Renko 막대 10pp + 1pp(또는 10pp + 1pp만큼 더 낮음) 이상으로 올라가고 새 "벽돌"을 그려야 합니다. 저것들. 사실, 가격은 시간을 고려하지 않고 "Renko 브릭"의 가치로 이산화됩니다. Renko는 가격의 노이즈 구성 요소를 제거하지만 모든 필터와 마찬가지로 지연이 있습니다. 새로운 Renko 막대를 그리려면 가격이 2 범위 = 2 Renko 벽돌 높이를 통과해야 합니다.
7.8은 ATR 지표로, 일반적으로 당신이 쓰는 것을 변동성 분석이라고 하지만 여기서도 영원한 문제는 ATR 기간입니다. 기간이 짧으면 노이즈가, 기간이 크면 노이즈가 발생합니다 지연
8. 특정 분위수에 대한 신뢰 구간의 경계를 넘어 슬라이딩 윈도우에서 출구(High-Low)를 기다리고 거래에 들어갑니다.
글쎄, 그것은 너무 - 알고리즘의 대략적인 스케치, 단지 주제를 개발하고 그 이상은 아닙니다 :)Cgfcb,j
정말 감사합니다. 좋은 의견입니다.
zz의 구성에 대한 몇 마디. 카기 변종.
눈금 차트는 파란색으로 표시되며 임계값은 3p입니다. 카운터 이동이 3p 이상인 경우. 극값이 그려지고 그렇지 않은 경우 계속 진행합니다. 저것들. 스윙은 2.66을 포함할 수 있습니다. 3.66; 이러한 임계값(세그먼트)의 n번째 수와 분수 값. Renko형 구성에서는 이 분수 값을 버리지만 원리는 동일합니다. 저것들. 정수 값 2,3 등 저것들. 우리는 구성에서 분수 정점이 고려되지 않는 방법을 봅니다. 아래 그림은 Renko 변형을 보여줍니다.
이제 차이점이 명확하다고 생각합니다. 따라서 임계값(3p의 세그먼트)에 대한 스윙 길이의 비율이 발생하는 빈도 Kagi의 경우:
Fig.b) 곡선의 누적 합. k=1에서의 카이제곱 분포가 이 곡선에 맞습니다.
그리고 이것은 Renko를 구축하기위한 임계 값 (세그먼트)에 대한 스윙 비율의 발생 빈도의 누적 합계입니다. k=2에서 카이제곱.
눈금 차트는 파란색으로 표시되며 임계값은 3p입니다. 카운터 이동이 3p 이상인 경우. 극값이 그려지고 그렇지 않은 경우 계속 진행합니다. 저것들. 스윙은 2.66을 포함할 수 있습니다. 3.66; 이러한 임계값(세그먼트)의 n번째 수와 분수 값. Renko형 구성에서는 이 분수 값을 버리지만 원리는 동일합니다. 저것들. 정수 값 2,3 등 저것들. 우리는 구성에서 분수 정점이 고려되지 않는 방법을 봅니다. 아래 그림은 Renko 변형을 보여줍니다.
이제 차이점이 명확하다고 생각합니다. 따라서 임계값(3p의 세그먼트)에 대한 스윙 길이의 비율이 발생하는 빈도 Kagi의 경우:
Fig.b) 곡선의 누적 합. k=1에서의 카이제곱 분포가 이 곡선에 맞습니다.
그리고 이것은 Renko를 구축하기위한 임계 값 (세그먼트)에 대한 스윙 비율의 발생 빈도의 누적 합계입니다. k=2에서 카이제곱.
저것들. 순수한 지수를 얻을 때 분수 부분만 버리면 됩니다.
스윙... 어머... :)))
확인. 나는 용어에 대해 깊이 들어가지 않을 것이다. 한번.
우리는 무엇이든 가장 순수한 지수를 가지고 있습니다.
이러한 구성 요소의 합은 알려진 분산을 사용하여 음의 이항 분포(연속 SW에 대한 Erlang 분포)가 될 것임을 다시 강조합니다. 극한에서 찾고 있는 정규 분포.
맙소사. 이런 일이 일어날 줄은 상상도 못했습니다.
맙소사. 이런 일이 일어날 줄은 상상도 못했습니다.
아니요. 나는 이 지표들을 믿지 않는다.
그들은 거짓말을하고 있습니다.
지표를 믿지 마십시오. 날 믿어.
아니요. 나는 이 지표들을 믿지 않는다.
그들은 거짓말을하고 있습니다.
지표를 믿지 마십시오. 날 믿어.
Muller는 조금 다르게 말했습니다. 당신은 아무도 믿을 수 없습니다 ..., 저는 할 수 있습니다. )
Muller는 조금 다르게 말했습니다. 당신은 아무도 믿을 수 없습니다 ..., 저는 할 수 있습니다. )
당신은 오늘 열한 번째로 나를 웃게하기 위해 귀찮게했습니다)))). 다음 분기를 읽을 때 열 번.
하지만 나는 확실히 믿을 수 있다. 나는 뮬러가 아니다
이는 3Z 카기에 대한 임계값 변화에 따른 극단의 차이를 판단한 결과이다. 그림 b) - 누적 곡선.
ZZ Renko도 마찬가지입니다.
흥미로운 기능을 발견했습니다. 카이제곱 분포:
보세요, k=1에서 ZZ Kagi의 유사성을 k=2에서 지수인 ZZ Renko 차트와 정확히 같은 지수로 볼 수 있습니다.
카이제곱 분포는 k가 증가함에 따라 정규화되는 경향이 있습니다.
글쎄 잘 모르겠어...
기능은 흥미롭지만 어떻게 사용합니까? "전혀"라는 단어에서 Kagi 또는 Renko를 알지 못하기 때문에 아무것도 제안하기 어렵습니다.
하지만 노력하겠습니다.
1. 우리는 정규 분포를 달성하려는 욕망을 포기하고 수세기 동안 찾아야합니다. 이미 발견된 규칙으로 작업하는 것은 이미 매우, 아주 많습니다.
2. https://en.wikipedia.org/wiki/Generalized_normal_distribution
3. 간단히 말해서, k=1인 xi-square는 정규 분포 MF의 제곱의 합이고, k=2인 xi-square는 MF와 Laplace 분포의 합입니다.
4. k = 2인 경우에 관심이 있었습니다. 연구에 따르면 시장은 라플라스 분포(더 정확하게는 이중 기하 분포)에 의해 지배됩니다.
5. 여기에는 명확하지 않습니다-이 Renkos에서 고려되는 것은 무엇입니까 ?? 차이의 합(높음-낮음)?
6. 그렇다면 Renko의 차이(High-Low)는 Laplace 분포에 속하는 CV입니다. 이 또한 실험적으로 확인해야 합니다.
7. 그런 다음 슬라이딩 윈도우(특정 샘플 크기에 대해)의 차이(높음-낮음)의 합은 알려진 분위수 함수를 사용하여 k=2인 xi-제곱을 형성합니다.
https://keisan.casio.com/exec/system/1180573197
8. 특정 분위수에 대한 신뢰 구간의 경계를 넘어 슬라이딩 윈도우에서 출구(High-Low)를 기다리고 거래에 들어갑니다.
글쎄요, 이것은 알고리즘의 대략적인 스케치입니다. 주제를 개발하기 위한 것뿐입니다. :)))
5. 여기에는 명확하지 않습니다.이 Renkos에서 고려되는 것은 무엇입니까 ?? 차이의 합(높음-낮음)?
7. 그런 다음 슬라이딩 윈도우(특정 샘플 크기에 대해)의 차이(높음-낮음)의 합은 알려진 분위수 함수를 사용하여 k=2인 xi-제곱을 형성합니다.
https://keisan.casio.com/exec/system/1180573197
8. 특정 분위수에 대한 신뢰 구간의 경계를 넘어 슬라이딩 윈도우에서 출구(High-Low)를 기다리고 거래에 들어갑니다.
5. Renko는 "Renko 브릭"에 의해 지정된 범위의 이탈을 1 "brick"의 값으로 간주하며, 브레이크아웃은 "brick"의 값, 즉 "벽돌" 10pp, 새로운 Renko 벽돌을 그리려면 가격이 이미 형성된 Renko 막대 10pp + 1pp(또는 10pp + 1pp만큼 더 낮음) 이상으로 올라가고 새 "벽돌"을 그려야 합니다. 저것들. 사실, 가격은 시간을 고려하지 않고 "Renko 브릭"의 가치로 이산화됩니다. Renko는 가격의 노이즈 구성 요소를 제거하지만 모든 필터와 마찬가지로 지연이 있습니다. 새로운 Renko 막대를 그리려면 가격이 2 범위 = 2 Renko 벽돌 높이를 통과해야 합니다.
7.8은 ATR 지표로, 일반적으로 당신이 쓰는 것을 변동성 분석이라고 하지만 여기서도 영원한 문제는 ATR 기간입니다. 기간이 짧으면 노이즈가, 기간이 크면 노이즈가 발생합니다 지연
여기
거래, 자동 거래 시스템 및 거래 전략 테스트에 관한 포럼
지그재그 양치기
노바자 , 2018.08.26 23:22
이는 3Z 카기에 대한 임계값 변화에 따른 극단의 차이를 판단한 결과이다. 그림 b) - 누적 곡선.
ZZ Renko도 마찬가지입니다.
흥미로운 기능을 발견했습니다. 카이제곱 분포:
보세요, k=1에서 ZZ Kagi의 유사성을 k=2에서 지수인 ZZ Renko 차트와 정확히 같은 지수로 볼 수 있습니다.
카이제곱 분포는 k가 증가함에 따라 정규화되는 경향이 있습니다.
Novaja는 극한값 사이의 약간의 차이점에 대해 이야기합니다... 범위(높음-낮음) 또는 기타 정보에 대해? 이해가 안가네요... 너무 건조하고 간결하게 써져있네요...
그런데 xi-square 처럼 보이기 때문에 관심을 갖게 되었습니다. 명확한 패턴을 찾는 것은 드뭅니다.
글쎄 잘 모르겠다...
기능은 흥미롭지만 어떻게 사용합니까? "전혀"라는 단어에서 Kagi 또는 Renko를 알지 못하기 때문에 아무것도 제안하기 어렵습니다.
하지만 노력하겠습니다.
1. 우리는 정규 분포를 달성하려는 욕망을 포기하고 수세기 동안 찾아야합니다. 이미 발견된 규칙으로 작업하는 것은 이미 매우, 아주 많습니다.
2. https://en.wikipedia.org/wiki/Generalized_normal_distribution
3. 간단히 말해서, k=1인 xi-square는 정규 분포 MF의 제곱의 합이고, k=2인 xi-square는 MF와 Laplace 분포의 합입니다.
4. k = 2인 경우에 관심이 있었습니다. 연구에 따르면 시장은 라플라스 분포(더 정확하게는 이중 기하 분포)에 의해 지배됩니다.
5. 여기에는 명확하지 않습니다-이 Renkos에서 고려되는 것은 무엇입니까 ?? 차이의 합(높음-낮음)?
6. 그렇다면 Renko의 차이(High-Low)는 Laplace 분포에 속하는 CV입니다. 이 또한 실험적으로 확인해야 합니다.
7. 그런 다음 슬라이딩 윈도우(특정 샘플 크기에 대해)의 차이(높음-낮음)의 합은 알려진 분위수 함수를 사용하여 k=2인 xi-제곱을 형성합니다.
https://keisan.casio.com/exec/system/1180573197
8. 특정 분위수에 대한 신뢰 구간의 경계를 넘어 슬라이딩 윈도우에서 출구(High-Low)를 기다리고 거래에 들어갑니다.
글쎄, 그것은 너무 - 알고리즘의 대략적인 스케치, 단지 주제를 개발하고 그 이상은 아닙니다 :)Cgfcb,j
정말 감사합니다. 좋은 의견입니다.
zz의 구성에 대한 몇 마디. 카기 변종.
눈금 차트는 파란색으로 표시되며 임계값은 3p입니다. 카운터 이동이 3p 이상인 경우. 극값이 그려지고 그렇지 않은 경우 계속 진행합니다. 저것들. 스윙은 2.66을 포함할 수 있습니다. 3.66; 이러한 임계값(세그먼트)의 n번째 수와 분수 값. Renko형 구성에서는 이 분수 값을 버리지만 원리는 동일합니다. 저것들. 정수 값 2,3 등 저것들. 우리는 구성에서 분수 정점이 고려되지 않는 방법을 봅니다. 아래 그림은 Renko 변형을 보여줍니다.
이제 차이점이 명확하다고 생각합니다. 따라서 임계값(3p의 세그먼트)에 대한 스윙 길이의 비율이 발생하는 빈도 Kagi의 경우: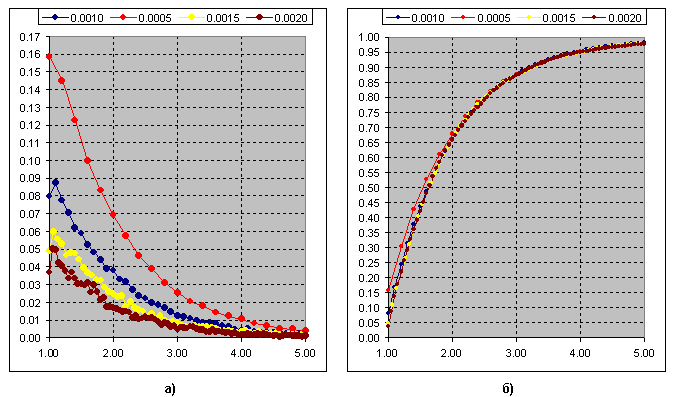
Fig.b) 곡선의 누적 합. k=1에서의 카이제곱 분포가 이 곡선에 맞습니다.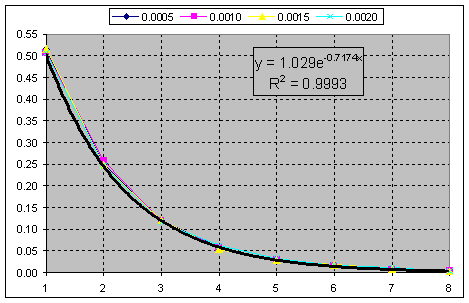
그리고 이것은 Renko를 구축하기위한 임계 값 (세그먼트)에 대한 스윙 비율의 발생 빈도의 누적 합계입니다. k=2에서 카이제곱.
저것들. 순수한 지수를 얻을 때 분수 부분만 버리면 됩니다.
정말 감사합니다. 좋은 의견입니다.
zz의 구성에 대한 몇 마디. 카기 변종.
눈금 차트는 파란색으로 표시되며 임계값은 3p입니다. 카운터 이동이 3p 이상인 경우. 극값이 그려지고 그렇지 않은 경우 계속 진행합니다. 저것들. 스윙은 2.66을 포함할 수 있습니다. 3.66; 이러한 임계값(세그먼트)의 n번째 수와 분수 값. Renko형 구성에서는 이 분수 값을 버리지만 원리는 동일합니다. 저것들. 정수 값 2,3 등 저것들. 우리는 구성에서 분수 정점이 고려되지 않는 방법을 봅니다. 아래 그림은 Renko 변형을 보여줍니다.
이제 차이점이 명확하다고 생각합니다. 따라서 임계값(3p의 세그먼트)에 대한 스윙 길이의 비율이 발생하는 빈도 Kagi의 경우:
Fig.b) 곡선의 누적 합. k=1에서의 카이제곱 분포가 이 곡선에 맞습니다.
그리고 이것은 Renko를 구축하기위한 임계 값 (세그먼트)에 대한 스윙 비율의 발생 빈도의 누적 합계입니다. k=2에서 카이제곱.
저것들. 순수한 지수를 얻을 때 분수 부분만 버리면 됩니다.
스윙... 어머... :)))
확인. 나는 용어에 대해 깊이 들어가지 않을 것이다. 한번.
우리는 무엇이든 가장 순수한 지수를 가지고 있습니다.
이러한 구성 요소의 합은 알려진 분산을 사용하여 음의 이항 분포(연속 SW에 대한 Erlang 분포)가 될 것임을 다시 강조합니다. 극한에서 찾고 있는 정규 분포.