포스팅하기로 약속한 내용입니다. Matrix의 전체 출력 파일은 데이터가 쉼표로 구분된 동일한 유형의 수천 블록으로 구성됩니다. 이해의 편의를 위해 이 블록은 표 형식으로 표시됩니다(숫자를 더 잘 보려면 클릭해야 함). 지금 - 설명:
첫 번째 블록 라인: #310: 카이제곱 = 2814.626 첫 번째 - Lag 변수의 값입니다. 그런 다음 - 변수의 독립성에 대한 카이 제곱 검정의 값입니다.
두 번째 라인: 카이제곱 컷오프와 함께 종속/독립 결론.
테이블의 노란색 셀은 캡입니다. 해당 행과 열의 교차점에서 동시에 관찰된 알파벳 문자를 탐색할 수 있습니다. 소스와 리시버의 알파벳이 동일하고 해당 막대(소스 및 리시버)의 수익률이 속하는 분위수와 동일함을 상기시킵니다.
예를 들어, source=10 열과 receiver=13 행의 교차점에서 셀 값 75/60을 찾습니다. 이는 "10번째 분위수에 속하는 소스(과거 막대)의 반환과 13번째 분위수에 속하는 수신자의 반환(현재에 더 가까운 막대)" 조합이 75 관찰되었음을 의미합니다. 역사적으로 몇 번이고 그러한 조합의 이론적 수는 독립적인 경우 60과 같습니다.
시안색 셀은 카이제곱을 계산하는 데 필요한 행 또는 열의 실제 주파수 합계입니다.
소스와 수신기가 독립된 경우 카이제곱 자체는 거의 항상 경계보다 작아야 합니다. 블록의 두 번째 줄에 지정됩니다. 보시다시피 거의 3배에 달하는 훨씬 더 큽니다. 이것은 이 경우 막대의 매우 강한 의존성을 나타냅니다.
그리고 Shannon의 정의가 순전히 공식적으로 적용되는 상호 정보의 정의가 있습니다. 그러나 종속성이 존재한다고 가정합니다.
상호 정보 정의의 철학적 깊이와 모순을 탐구하고 싶다면 - 탐구하십시오. 나는 이것에 대해 걱정하지 않고 독립성에 대해 신경 쓰지 않고 확률이 있는 "미국식" 공식을 사용하는 것을 선호합니다.
약간 잘못되었습니다. 나무 껍질..., TI의 의미를 번역하면 다음과 같다. 엔트로피라는 개념이 있습니다. 이 아름답고 이해할 수 없는 외래어 뒤에는 인위적으로 고안된 어떤 형상이 있다는 것을 분명히 이해해야 합니다. 교과서에서 더 정직한 교과서에서는 공리적으로 도입된 불확실성 척도를 직접적으로 씁니다. 그것이 밝혀진 방법은 실제로 회선입니다. 대략적으로 말하면 산술 공식의 도움으로 상태와 빈도를 설명하는 큰 테이블이 단일 숫자로 접혀 있습니다. 주파수 만 접히고 상태 자체 (그런데 자체 측정 값도 가질 수 있음)는 총 수의 관점에서만 흥미 롭습니다.
믿음으로. 비슷한 작업이 있습니다. 대략적으로 말하면 내 시스템도 비슷한 방식으로 간주됩니다. 그러나 그곳에서만 상태의 확률에 측정값을 곱하고 합산하여 수치를 얻고 이에 대한 수렴 정리를 증명하는 등의 작업을 수행합니다. 여기는 그렇지 않습니다. 여기서 주파수 자체는 측정값(확률이라고 함) 또는 로그의 역할을 합니다. 로그는 Shannon 이 세 가지 조건(단조롭게 성장해야 함 등)에서 공식화한 산술 문제 중 일부를 해결합니다.
그 후 Shannon은 다음과 같이 말합니다. - 친구 여러분, 제가 최근에 발견한 숫자, 즉 엔트로피라고 하는 두 개의 다른 태블릿에서 숫자를 더할 수 있는 방법에 대한 합리적이고 분명한 규칙을 생각해 냈습니다. 친구(대부분 군인)는 다음과 같이 묻습니다. - 좋습니다. 하지만 어떻게? - 아주 간단합니다. - 섀넌이 반짝이는 눈으로 대답합니다. - 한 판이 다른 판과 어떤 식으로든 연결되어 있지 않다고 가정해 보겠습니다. 글쎄요, 그것들은 독립적이며 삶에서 일어나는 일입니다. 그리고 이번 기회에 저는 엔트로피의 추가에 관한 정리를 가지고 있습니다. 놀라운 결과가 있습니다. 숫자를 더하기만 하면 됩니다! - 좋습니다. 하지만 태블릿이 이해할 수 없는 방식으로 연결되어 있다면 어떻게 될까요? - 여기에서는 모든 것이 동일합니다. 두 개의 초기 플레이트에서 하나의 큰 정사각형 플레이트를 만들고 각 셀에서 확률을 곱합니다. 우리는 열의 셀에 숫자를 추가하고, 열에 별도로 추가하고, 새 테이블을 만들고, 하나씩 나누고, 0에는 너무 이르고, 물고기는 포장되었습니다 ... Op-la, 결과적으로 하나를 얻습니다. 내가 조건부 엔트로피라고 부르는 숫자! 흥미롭게도 조건부 엔트로피는 첫 번째 판에서 두 번째 판으로 또는 그 반대로 계산할 수 있습니다! 그리고 이 불행한 이중성을 고려하기 위해 완전한 상호 엔트로피를 발명했는데, 이것은 동일한 숫자입니다! - 그래서 무엇을, - 친구들이 팝콘을 씹고, - 그리고 한 숫자를 다른 숫자와 비교하는 것이 원래 테이블의 데이터 본질을 이해하는 것보다 훨씬 쉽다는 사실. 그리고 관계의 의미와 신뢰성을 이해해야 할 때 훨씬 더 쉽습니다. 이해하는 것은 지루합니다. 커튼.
제 공연에서 TI의 간략한 역사는 이렇습니다. 내 자신의 연구 및 학술 사전 진술을 기반으로 작성되었습니다(이전 인용 참조).
이제 중요합니다. 이 전체 이야기의 핵심은 조건부 엔트로피에 숨겨져 있습니다. 사실 한 자리 숫자로 연산을 하고 싶다면 상호 정보 등을 세지 않아도 조건부 엔트로피 계산법을 마스터하면 충분하다. 한 사람과 다른 사람의 관계에 대한 일정한 척도를 줄 사람은 바로 그녀입니다. 동시에 플레이트의 숫자는 "고정"이어야 하며 또한 플레이트의 상호 연결도 "고정"이어야 함을 이해해야 합니다. 게다가 판의 원래 숫자는 적절한 출처에서 가져와야 합니다.
Markov 체인의 경우에 TI의 확장이 있다고 말해야 합니다. 의사가 지시한 대로인 것 같습니다. 그러나 아니요, 시장의 전환 확률은 일반적인 비정상성으로 인해 일정하지 않습니다. 또한 CM이 시스템이 현재 상태에서 어떻게 끝났는지 신경 쓰지 않는다면 시장에 매우 중요합니다.
수학 : 나는 당신의 작업 알파벳이 무엇인지 모릅니다. 지연 거리로 분리된 몇 개의 막대 시스템이 있습니다. 과거에는 하나의 막대가 소스이고 두 번째 막대가 수신기입니다. 둘 다 알파벳이 동일합니다(물론 막대 반환에 대해 이야기하는 경우).
자기 상관과 유사하지만 측정값이 다른 것이 분명합니다. 내 이의 제기는 CM 사례와 정확히 동일합니다. 글쎄, 다른 모든 것, 고정성 등.
추신. 당신이 정말로 이것을 (TI) 거래하고 성공적으로 거래한다면 반대와 함께 그와 함께 boh해야합니다. 도움이 된다면 모니터에 최소한 토끼 발을 올려 놓으십시오.
네 흥미롭네요. 실제로, 연결 가정 하에 시스템의 조건부 상태에 대한 주파수 행렬이 조건부 엔트로피 측면에서 재구성되면 한 변수에서 다른 변수의 일부 결정론을 가질 가능성을 특성화하는 하나의 숫자를 제공합니다. 이러한 초기 행렬의 PDF가 균일하면 시스템의 최대 엔트로피가 있습니다(물론 조건부 엔트로피라고 말하고 싶었습니다). 그리고 불규칙성이 있으면 엔트로피가 줄어 듭니다. 첫 번째 근사치로 한 자리 숫자로 계산할 수 있습니다. 당신은 이것을 올바르게 지적했습니다. 그리고 Aleksey가 쓴 것처럼 Lag의 개념에 의해 수신자와 분리된 변수 세트에 대한 상호 정보는 이미 매우 구체적인 목적, 즉 정보 변수를 선택하기 위해 계산되었습니다.
지금까지는 개인적으로 TI와 거래하지 않습니다. 이번 주제는 "첫 글쓰기 시도"였다고 생각합니다.
HideYourRichess : Вот так выглядит краткая история ТИ в моём исполнении. Составлена по мотивам моих собственных изысканий и утверждений академического словарика (см. цитаты ранее).
매우 흥미로운. Shannon 은 우리가 아직도 그것을 분류하고 있는 그런 혼란을 만들었다 ...
Markov 체인의 경우에 TI의 확장이 있다고 말해야 합니다. 의사가 지시한 대로인 것 같습니다. 그러나 아니요, 시장의 전환 확률은 일반적인 비정상성으로 인해 일정하지 않습니다. 또한 CM이 시스템이 현재 상태에서 어떻게 끝났는지 신경 쓰지 않는다면 시장에 매우 중요합니다.
문제의 사실은 반환 흐름이 Markov 프로세스가 아니라는 것입니다. 제로 막대의 반환은 첫 번째 막대뿐만 아니라 두 번째, 세 번째 등의 반환에도 크게 의존합니다. 어쨌든 이것이 바로 본점 연구를 직접적으로 해석할 수 있는 방법이다.
추신. 당신이 정말로 이것을 (TI) 거래하고 성공적으로 거래한다면, 반대와 함께 그와 함께 boh해야합니다. 도움이 된다면 모니터에 최소한 토끼 발을 올려 놓으십시오.
아니요, 거래하지 않습니다. 그러나 그것을 상업적으로 발전시키는 것은 매우 흥미로울 것입니다. 나는 alsu ( Alexey 가 어딘가에 사라졌다, 미안하다)로부터 RBC 채널의 프로그램을 어렴풋이 기억하고 있다고 들었습니다. 그 프로그램에서 어떤 불손한 상인이 실제로 비슷한 것을 거래했습니다. 그리고 입어, 이 나쁜 놈아, 약한 돈이 아니야. 그리고 그는 자신의 시스템을 "시장의 비효율을 잡는 것"이라고 부릅니다.
그리고 저는 오랫동안 엔트로피에 대해 생각해 왔습니다. 그리고 여기에서도 무언가가 던져졌습니다. 그러나 그것은 TI가 아니라 통계 물리학의 엔트로피에 더 가깝고 다중 통화를 나타냅니다. 일반적으로 카르마는 몇 년 동안 내 귓가에 엔트로피적인 것을 속삭여 왔지만 나는 그것을 듣고 그것이 나에게 원하는 것을 계속 이해하려고 노력합니다 ...
나는 나의 평소의 무례한 솔직함으로 그렇게 말할 것입니다. 우리는 "수학은 과학의 여왕"이라는 썩은 오래된 슬로건을 잘못되고 해로운 것으로 거부합니다. 수학은 여왕이 아니라 과학의 종입니다. 의미와 신중함이 먼저 와야 하고, 그 다음에 공식이 와야 합니다. 그러나 그 반대는 아닙니다. 위대한 수학자들이 이것을 아주 잘 이해했다는 것이 놀랍고, 수학을 모르는 사람들도 이것을 이해합니다. 그러나 이 두 극단 사이에 있는 사람들은 단호히 이것을 이해하기를 원하지 않습니다. 여기에서 동일한 위대한 Shannon 은 매우 협소한 특정 문제를 해결해야 했습니다. 그는 간단하게 행동했고 이 특정 문제를 해결하는 데 적합한 새로운 장치를 생각해 냈습니다. 그는 그것을 다른 과학의 프로크루스테스(Procrustean) 침대에 밀어넣지 않고 새로운 것을 생각해 냈습니다. 그는 엔트로피라는 새로운 개념을 생각해 냈고 다른 사람들이 생각하는 것이 아니라 자신에게 필요한 정보를 계산하고 결론을 추론하는 방법을 배웠습니다. 나는 당신에게 행운을 빕니다!
문제의 사실은 반환 흐름이 Markov 프로세스가 아니라는 것입니다. 제로 막대의 반환은 첫 번째 막대뿐만 아니라 두 번째, 세 번째 등의 반환에도 크게 의존합니다. 어쨌든 이것이 바로 본점 연구를 직접적으로 해석할 수 있는 방법이다.
아니요, 거래하지 않습니다. 그러나 그것을 상업적으로 발전시키는 것은 매우 흥미로울 것입니다. 나는 alsu ( Alexey 가 어딘가에 사라졌다, 미안하다)로부터 RBC 채널의 프로그램을 어렴풋이 기억하고 있다고 들었습니다. 그 프로그램에서 어떤 불손한 상인이 실제로 비슷한 것을 거래했습니다. 그리고 입어라, 이 나쁜 놈아, 약한 돈이 아니다. 그리고 그는 자신의 시스템을 "시장의 비효율을 잡는 것"이라고 부릅니다.
그리고 저는 오랫동안 엔트로피에 대해 생각해 왔습니다. 그리고 여기에서도 무언가가 던져졌습니다. 그러나 그것은 TI가 아니라 통계 물리학의 엔트로피에 더 가깝고 다중 통화를 나타냅니다. 일반적으로 카르마는 몇 년 동안 내 귓가에 엔트로피적인 것을 속삭여 왔지만 나는 그것을 듣고 그것이 나에게 원하는 것을 계속 이해하려고 노력합니다 ...
정말 궁금합니다.
그러나 Alexey, 수익률 분포에 대한 어떤 가설이 카이-제곱 추정에 해당하는지 더 명확하게 공식화할 수 있습니까?
EView가 있는 사람들은 그런 질문을 하지 않죠 히히
친절하세요. 가능하다면 개인용 또는 여기 EViews를 버릴 수 있습니까?
EView가 있는 사람들은 그런 질문을 하지 않죠 히히
예, 질문이 어리석습니다. 동의합니다. 보증은 모델 자체와 동일합니다.
그리고 어떤 버전이 있습니까? 그들은 "5"가 구식이라고 말합니다.
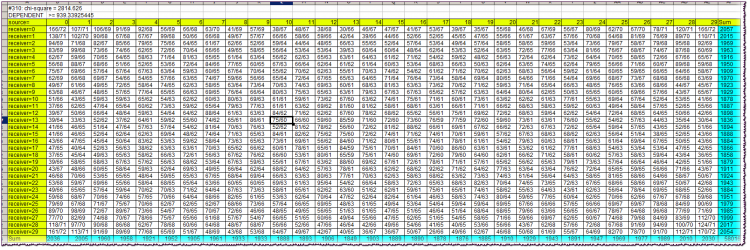
첫 번째 블록 라인: #310: 카이제곱 = 2814.626첫 번째 - Lag 변수의 값입니다. 그런 다음 - 변수의 독립성에 대한 카이 제곱 검정의 값입니다.
두 번째 라인: 카이제곱 컷오프와 함께 종속/독립 결론.
테이블의 노란색 셀은 캡입니다. 해당 행과 열의 교차점에서 동시에 관찰된 알파벳 문자를 탐색할 수 있습니다. 소스와 리시버의 알파벳이 동일하고 해당 막대(소스 및 리시버)의 수익률이 속하는 분위수와 동일함을 상기시킵니다.
예를 들어, source=10 열과 receiver=13 행의 교차점에서 셀 값 75/60을 찾습니다. 이는 "10번째 분위수에 속하는 소스(과거 막대)의 반환과 13번째 분위수에 속하는 수신자의 반환(현재에 더 가까운 막대)" 조합이 75 관찰되었음을 의미합니다. 역사적으로 몇 번이고 그러한 조합의 이론적 수는 독립적인 경우 60과 같습니다.
시안색 셀은 카이제곱을 계산하는 데 필요한 행 또는 열의 실제 주파수 합계입니다.
소스와 수신기가 독립된 경우 카이제곱 자체는 거의 항상 경계보다 작아야 합니다. 블록의 두 번째 줄에 지정됩니다. 보시다시피 거의 3배에 달하는 훨씬 더 큽니다. 이것은 이 경우 막대의 매우 강한 의존성을 나타냅니다.
아카이브된 전체 파일은 많은 공간을 차지하므로 여기에 게시할 수 없습니다.
예, 질문이 어리석습니다. 동의합니다. 보증은 모델 자체와 동일합니다.
그리고 어떤 버전이 있습니까? 그들은 "5"가 구식이라고 말합니다.
독립성이 요구되는 Shannon의 엔트로피 정의가 있습니다.
그리고 Shannon의 정의가 순전히 공식적으로 적용되는 상호 정보의 정의가 있습니다. 그러나 종속성이 존재한다고 가정합니다.
상호 정보 정의의 철학적 깊이와 모순을 탐구하고 싶다면 - 탐구하십시오. 나는 이것에 대해 걱정하지 않고 독립성에 대해 신경 쓰지 않고 확률이 있는 "미국식" 공식을 사용하는 것을 선호합니다.
약간 잘못되었습니다. 나무 껍질..., TI의 의미를 번역하면 다음과 같다. 엔트로피라는 개념이 있습니다. 이 아름답고 이해할 수 없는 외래어 뒤에는 인위적으로 고안된 어떤 형상이 있다는 것을 분명히 이해해야 합니다. 교과서에서 더 정직한 교과서에서는 공리적으로 도입된 불확실성 척도를 직접적으로 씁니다. 그것이 밝혀진 방법은 실제로 회선입니다. 대략적으로 말하면 산술 공식의 도움으로 상태와 빈도를 설명하는 큰 테이블이 단일 숫자로 접혀 있습니다. 주파수 만 접히고 상태 자체 (그런데 자체 측정 값도 가질 수 있음)는 총 수의 관점에서만 흥미 롭습니다.
믿음으로. 비슷한 작업이 있습니다. 대략적으로 말하면 내 시스템도 비슷한 방식으로 간주됩니다. 그러나 그곳에서만 상태의 확률에 측정값을 곱하고 합산하여 수치를 얻고 이에 대한 수렴 정리를 증명하는 등의 작업을 수행합니다. 여기는 그렇지 않습니다. 여기서 주파수 자체는 측정값(확률이라고 함) 또는 로그의 역할을 합니다. 로그는 Shannon 이 세 가지 조건(단조롭게 성장해야 함 등)에서 공식화한 산술 문제 중 일부를 해결합니다.
그 후 Shannon은 다음과 같이 말합니다. - 친구 여러분, 제가 최근에 발견한 숫자, 즉 엔트로피라고 하는 두 개의 다른 태블릿에서 숫자를 더할 수 있는 방법에 대한 합리적이고 분명한 규칙을 생각해 냈습니다. 친구(대부분 군인)는 다음과 같이 묻습니다. - 좋습니다. 하지만 어떻게? - 아주 간단합니다. - 섀넌이 반짝이는 눈으로 대답합니다. - 한 판이 다른 판과 어떤 식으로든 연결되어 있지 않다고 가정해 보겠습니다. 글쎄요, 그것들은 독립적이며 삶에서 일어나는 일입니다. 그리고 이번 기회에 저는 엔트로피의 추가에 관한 정리를 가지고 있습니다. 놀라운 결과가 있습니다. 숫자를 더하기만 하면 됩니다! - 좋습니다. 하지만 태블릿이 이해할 수 없는 방식으로 연결되어 있다면 어떻게 될까요? - 여기에서는 모든 것이 동일합니다. 두 개의 초기 플레이트에서 하나의 큰 정사각형 플레이트를 만들고 각 셀에서 확률을 곱합니다. 우리는 열의 셀에 숫자를 추가하고, 열에 별도로 추가하고, 새 테이블을 만들고, 하나씩 나누고, 0에는 너무 이르고, 물고기는 포장되었습니다 ... Op-la, 결과적으로 하나를 얻습니다. 내가 조건부 엔트로피라고 부르는 숫자! 흥미롭게도 조건부 엔트로피는 첫 번째 판에서 두 번째 판으로 또는 그 반대로 계산할 수 있습니다! 그리고 이 불행한 이중성을 고려하기 위해 완전한 상호 엔트로피를 발명했는데, 이것은 동일한 숫자입니다! - 그래서 무엇을, - 친구들이 팝콘을 씹고, - 그리고 한 숫자를 다른 숫자와 비교하는 것이 원래 테이블의 데이터 본질을 이해하는 것보다 훨씬 쉽다는 사실. 그리고 관계의 의미와 신뢰성을 이해해야 할 때 훨씬 더 쉽습니다. 이해하는 것은 지루합니다. 커튼.
제 공연에서 TI의 간략한 역사는 이렇습니다. 내 자신의 연구 및 학술 사전 진술을 기반으로 작성되었습니다(이전 인용 참조).
이제 중요합니다. 이 전체 이야기의 핵심은 조건부 엔트로피에 숨겨져 있습니다. 사실 한 자리 숫자로 연산을 하고 싶다면 상호 정보 등을 세지 않아도 조건부 엔트로피 계산법을 마스터하면 충분하다. 한 사람과 다른 사람의 관계에 대한 일정한 척도를 줄 사람은 바로 그녀입니다. 동시에 플레이트의 숫자는 "고정"이어야 하며 또한 플레이트의 상호 연결도 "고정"이어야 함을 이해해야 합니다. 게다가 판의 원래 숫자는 적절한 출처에서 가져와야 합니다.
Markov 체인의 경우에 TI의 확장이 있다고 말해야 합니다. 의사가 지시한 대로인 것 같습니다. 그러나 아니요, 시장의 전환 확률은 일반적인 비정상성으로 인해 일정하지 않습니다. 또한 CM이 시스템이 현재 상태에서 어떻게 끝났는지 신경 쓰지 않는다면 시장에 매우 중요합니다.
나는 당신의 작업 알파벳이 무엇인지 모릅니다. 지연 거리로 분리된 몇 개의 막대 시스템이 있습니다. 과거에는 하나의 막대가 소스이고 두 번째 막대가 수신기입니다. 둘 다 알파벳이 동일합니다(물론 막대 반환에 대해 이야기하는 경우).
자기 상관과 유사하지만 측정값이 다른 것이 분명합니다. 내 이의 제기는 CM 사례와 정확히 동일합니다. 글쎄, 다른 모든 것, 고정성 등.
추신. 당신이 정말로 이것을 (TI) 거래하고 성공적으로 거래한다면 반대와 함께 그와 함께 boh해야합니다. 도움이 된다면 모니터에 최소한 토끼 발을 올려 놓으십시오.
HideYourRichss를 읽으십시오 .
네 흥미롭네요. 실제로, 연결 가정 하에 시스템의 조건부 상태에 대한 주파수 행렬이 조건부 엔트로피 측면에서 재구성되면 한 변수에서 다른 변수의 일부 결정론을 가질 가능성을 특성화하는 하나의 숫자를 제공합니다. 이러한 초기 행렬의 PDF가 균일하면 시스템의 최대 엔트로피가 있습니다(물론 조건부 엔트로피라고 말하고 싶었습니다). 그리고 불규칙성이 있으면 엔트로피가 줄어 듭니다. 첫 번째 근사치로 한 자리 숫자로 계산할 수 있습니다. 당신은 이것을 올바르게 지적했습니다. 그리고 Aleksey가 쓴 것처럼 Lag의 개념에 의해 수신자와 분리된 변수 세트에 대한 상호 정보는 이미 매우 구체적인 목적, 즉 정보 변수를 선택하기 위해 계산되었습니다.
지금까지는 개인적으로 TI와 거래하지 않습니다. 이번 주제는 "첫 글쓰기 시도"였다고 생각합니다.
HideYourRichess : Вот так выглядит краткая история ТИ в моём исполнении. Составлена по мотивам моих собственных изысканий и утверждений академического словарика (см. цитаты ранее).
매우 흥미로운. Shannon 은 우리가 아직도 그것을 분류하고 있는 그런 혼란을 만들었다 ...
Markov 체인의 경우에 TI의 확장이 있다고 말해야 합니다. 의사가 지시한 대로인 것 같습니다. 그러나 아니요, 시장의 전환 확률은 일반적인 비정상성으로 인해 일정하지 않습니다. 또한 CM이 시스템이 현재 상태에서 어떻게 끝났는지 신경 쓰지 않는다면 시장에 매우 중요합니다.
문제의 사실은 반환 흐름이 Markov 프로세스가 아니라는 것입니다. 제로 막대의 반환은 첫 번째 막대뿐만 아니라 두 번째, 세 번째 등의 반환에도 크게 의존합니다. 어쨌든 이것이 바로 본점 연구를 직접적으로 해석할 수 있는 방법이다.
추신. 당신이 정말로 이것을 (TI) 거래하고 성공적으로 거래한다면, 반대와 함께 그와 함께 boh해야합니다. 도움이 된다면 모니터에 최소한 토끼 발을 올려 놓으십시오.
아니요, 거래하지 않습니다. 그러나 그것을 상업적으로 발전시키는 것은 매우 흥미로울 것입니다. 나는 alsu ( Alexey 가 어딘가에 사라졌다, 미안하다)로부터 RBC 채널의 프로그램을 어렴풋이 기억하고 있다고 들었습니다. 그 프로그램에서 어떤 불손한 상인이 실제로 비슷한 것을 거래했습니다. 그리고 입어, 이 나쁜 놈아, 약한 돈이 아니야. 그리고 그는 자신의 시스템을 "시장의 비효율을 잡는 것"이라고 부릅니다.
그리고 저는 오랫동안 엔트로피에 대해 생각해 왔습니다. 그리고 여기에서도 무언가가 던져졌습니다. 그러나 그것은 TI가 아니라 통계 물리학의 엔트로피에 더 가깝고 다중 통화를 나타냅니다. 일반적으로 카르마는 몇 년 동안 내 귓가에 엔트로피적인 것을 속삭여 왔지만 나는 그것을 듣고 그것이 나에게 원하는 것을 계속 이해하려고 노력합니다 ...
문제의 사실은 반환 흐름이 Markov 프로세스가 아니라는 것입니다. 제로 막대의 반환은 첫 번째 막대뿐만 아니라 두 번째, 세 번째 등의 반환에도 크게 의존합니다. 어쨌든 이것이 바로 본점 연구를 직접적으로 해석할 수 있는 방법이다.
아니요, 거래하지 않습니다. 그러나 그것을 상업적으로 발전시키는 것은 매우 흥미로울 것입니다. 나는 alsu ( Alexey 가 어딘가에 사라졌다, 미안하다)로부터 RBC 채널의 프로그램을 어렴풋이 기억하고 있다고 들었습니다. 그 프로그램에서 어떤 불손한 상인이 실제로 비슷한 것을 거래했습니다. 그리고 입어라, 이 나쁜 놈아, 약한 돈이 아니다. 그리고 그는 자신의 시스템을 "시장의 비효율을 잡는 것"이라고 부릅니다.
그리고 저는 오랫동안 엔트로피에 대해 생각해 왔습니다. 그리고 여기에서도 무언가가 던져졌습니다. 그러나 그것은 TI가 아니라 통계 물리학의 엔트로피에 더 가깝고 다중 통화를 나타냅니다. 일반적으로 카르마는 몇 년 동안 내 귓가에 엔트로피적인 것을 속삭여 왔지만 나는 그것을 듣고 그것이 나에게 원하는 것을 계속 이해하려고 노력합니다 ...
정말 궁금합니다.
그러나 Alexey, 수익률 분포에 대한 어떤 가설이 카이-제곱 추정에 해당하는지 더 명확하게 공식화할 수 있습니까?
유명한 "갈색"이나 더 멋진 것?
;)