예를 들어, 포인트의 근접 정도에 따라 계수를 표시할 수 있습니다. 수동으로 테스트했을 때 더 도움이 될 것입니다. 강한 추세에 있는 20명의 어드바이저 중(H4) 6개 조각으로 -6 + 6(막대)은 진입점을 보였으며 그 반대의 경우도 이 특정 기간의 추세가 2와 일치하지 않았으며 여기에서 논할 사항이 없습니다. 이것은 이론이 아닙니다. 이를 확인하고 확인했습니다.
전문가 평가에는 다양한 방법이 있습니다. 복잡성이 다양합니다. 예를 들어, 가장 단순한 것 - 모든 전문가의 신호 합계가 취해지면 구매 신호가 우세하면 구매합니다. 퍼지 논리 방법이 있습니다. 출력은 전문가 신호의 특수 회선에 의해 얻어지며 각각 고유한 가중치가 할당됩니다(코드베이스에 유사한 조언자가 있음). NN - 연관 기계를 사용하여 전문가를 결합하는 방법이 있습니다(Khaikin이 잘 설명함). 일반적으로 많은 방법이 있습니다. 문헌을 읽으십시오.
전문가 평가에는 다양한 방법이 있습니다. 복잡성이 다양합니다. 예를 들어, 가장 단순한 것 - 모든 전문가의 신호 합계가 취해지면 구매 신호가 우세하면 구매합니다. 퍼지 논리 방법이 있습니다. 출력은 전문가 신호의 특수 회선에 의해 얻어지며 각각 고유한 가중치가 할당됩니다(코드베이스에 유사한 조언자가 있음). NN - 연관 기계를 사용하여 전문가를 결합하는 방법이 있습니다(Khaikin이 잘 설명함). 일반적으로 많은 방법이 있습니다. 문헌을 읽으십시오.
방법을 사용하면 그가 유일한 투투가 아니라는 모든 것이 분명합니다. 물론 이러한 문제를 처리해야 하지만 이에 대한 기술적인 질문에 관심이 있고 이미 이 주제를 썼습니다. 누가 그것들을 결합하는 것이 더 나은 방법을 알려줄 수 있다면 매우 감사합니다. 전체 코드를 하나의 어드바이저에 던지거나 어떻게든 하나의 차트에 연결합니다. 이것이 제가 필요한 전부이고 기술적인 측면은 많지 않지만 잘못된 방향으로 많이 주문되지 않았습니다.
첫 번째 근사치로 p는 사용된 지표의 수가 증가함에 따라 거의 선형적으로 증가한다고 가정할 수 있습니다(위 그림 참조). 차례로, n개의 지표가 동시에 트리거될 확률은 지표 수가 증가함에 따라 기하급수적으로 감소합니다. 이는 트랜잭션 빈도가 그만큼 빠르게 감소한다는 것을 의미합니다. 즉, 수익성과 거래 빈도라는 두 가지 경쟁 프로세스가 있습니다.
- 우리는 p가 사용된 지표의 수가 증가함에 따라 선형적으로 증가한다고 가정할 수 없습니다... 포물선과 비슷합니다 :)
- 모든 지표가 동시에 작동해야 한다고 누가 말했는지 ... 최적의 수만 (포물선에서는 -b / 2a가 될 것입니다)
그러나 결론은 여전히 우울합니다. 거래에 사용할 지표가 적을수록 좋습니다. 가장 최적의 - 하나!
방법을 사용하면 그가 유일한 투투가 아니라는 모든 것이 분명합니다. 물론 이러한 문제를 처리해야 하지만 이에 대한 기술적인 질문에 관심이 있고 이미 이 주제를 썼습니다. 누가 그것들을 결합하는 것이 더 나은 방법을 제안해 주시면 대단히 감사하겠습니다. 전체 코드를 하나의 어드바이저에 던지거나 어떻게든 하나의 차트에 연결합니다. 이것이 제가 필요한 전부이고 기술적인 측면은 많지 않지만 잘못된 방향으로 많이 주문되지 않았습니다.
여기에 간단한 옵션이 있습니다
double Signal (int i ){double val1 =iWPR(NULL,0,14, i );double val2 =iDeMarker(NULL,0,14, i );double val3 =iRSI(NULL,0,14,PRICE_CLOSE, i );double BBL =iBands(NULL,0,20,1,0,PRICE_CLOSE,MODE_LOWER, i );double BBU =iBands(NULL,0,20,1,0,PRICE_CLOSE,MODE_UPPER, i );// // ------------ buy int BufferUP =0;if( val1 >=(-20)) BufferUP ++;if( val2 >=0.7) BufferUP ++;if( val3 >=70) BufferUP ++;if( BBU <=Close[ i ]) BufferUP ++;//--------------sell int BufferDN =0;if( val1 <=(-80)) BufferDN ++;if( val2 <=0.3) BufferDN ++;if( val3 <=30) BufferDN ++;if( BBL >=Close[ i ]) BufferDN ++;return( BufferUP - BufferDN );}
포물선은 어디에서 왔습니까, 빈센트? 그리고 0에 가까운 값에서 어떻게 동작합니까(확률은 음수가 될 수 없음)?
너무 심각하게 받아들이지 마세요, Alexey... 이것이 제가 대략적으로 내 실제 관찰을 공식화한 방법입니다. 전문가(지표)의 수가 증가하면서 얼마 동안(이것이 필요하지는 않지만) 올바른 확률이 예측은 증가할 것입니다... 그리고 그것은 떨어지기 시작할 것입니다 ... 즉. 당신이 사용해야하는 최적의 수가 있습니다 ...
예를 들어, 포인트의 근접 정도에 따라 계수를 표시할 수 있습니다. 수동으로 테스트했을 때 더 도움이 될 것입니다. 강한 추세에 있는 20명의 어드바이저 중(H4) 6개 조각으로 -6 + 6(막대)은 진입점을 보였으며 그 반대의 경우도 이 특정 기간의 추세가 2와 일치하지 않았으며 여기에서 논할 사항이 없습니다. 이것은 이론이 아닙니다. 이를 확인하고 확인했습니다.
전문가 평가에는 다양한 방법이 있습니다. 복잡성이 다양합니다. 예를 들어, 가장 단순한 것 - 모든 전문가의 신호 합계가 취해지면 구매 신호가 우세하면 구매합니다. 퍼지 논리 방법이 있습니다. 출력은 전문가 신호의 특수 회선에 의해 얻어지며 각각 고유한 가중치가 할당됩니다(코드베이스에 유사한 조언자가 있음). NN - 연관 기계를 사용하여 전문가를 결합하는 방법이 있습니다(Khaikin이 잘 설명함). 일반적으로 많은 방법이 있습니다. 문헌을 읽으십시오.
이것은 여전히 초등하지만 완전히 잘못된 수학입니다.
세 명의 조언자의 신호가 독립적이라고 가정하면 원하는 확률은 1 - (1-0.55)(1-0.65)(1-0.75) = 1 - 0.03975 = 0.960625입니다.
뒤늦게라도 2센트를 더하겠습니다.
고문의 확률은 모두에 대한 수익성 있는 거래의 비율입니다.
즉, 첫 번째의 경우 수익성 있는 거래와 무익한 거래의 비율은 0.55 / (1 - 0.55) = 1.2222, 두 번째 - 0.65 / (1 - 0.65) = 1.8571, 세 번째 - 0.75 / (1 - 0.75) = 3.0000.
이 비율을 곱하면 - 1.2222 * 1.8571 * 3.0000 = 6.8095 - 수익성 있는 거래와 무익한 거래의 최종 비율이 됩니다.
공식 y = x / (1 - x)를 사용하여 파생된 경우 이제 역변환은 x = y / (1 + y)입니다.
여기에서 "결합된" 고문의 확률 - 6.8095 / (1 + 6.8095) = 0.8720을 도출합니다. 즉, 수익성있는 거래의 최종 비율은 0.8720입니다. 고문의 확률이기도 하다.
추신: 왜 우리는 곱셈(1.2222 * 1.8571 * 3.0000)을 하는지, 모르겠습니다! 프로그래밍 방식으로 확인하기 위해 1시간 30분을 망쳤습니다. 0.8720(평균)으로 나타납니다.
전문가 평가에는 다양한 방법이 있습니다. 복잡성이 다양합니다. 예를 들어, 가장 단순한 것 - 모든 전문가의 신호 합계가 취해지면 구매 신호가 우세하면 구매합니다. 퍼지 논리 방법이 있습니다. 출력은 전문가 신호의 특수 회선에 의해 얻어지며 각각 고유한 가중치가 할당됩니다(코드베이스에 유사한 조언자가 있음). NN - 연관 기계를 사용하여 전문가를 결합하는 방법이 있습니다(Khaikin이 잘 설명함). 일반적으로 많은 방법이 있습니다. 문헌을 읽으십시오.
방법을 사용하면 그가 유일한 투투가 아니라는 모든 것이 분명합니다. 물론 이러한 문제를 처리해야 하지만 이에 대한 기술적인 질문에 관심이 있고 이미 이 주제를 썼습니다.
누가 그것들을 결합하는 것이 더 나은 방법을 알려줄 수 있다면 매우 감사합니다. 전체 코드를 하나의 어드바이저에 던지거나 어떻게든 하나의 차트에 연결합니다. 이것이 제가 필요한 전부이고 기술적인 측면은 많지 않지만 잘못된 방향으로 많이 주문되지 않았습니다.
간단한 요약과 관련하여 예를 들면 다음과 같습니다. 나는 다른 사람의 칠면조를 가져 와서 추세의 강도를 결정하기 위해 조각을 뽑고 코드를 최소화했습니다 (원본은 너무 많은 메모리를 먹습니다).
위/아래 힘을 오른쪽 상단 모서리에 백분율로 표시합니다. 75% 이상 - 입력합니다. 여기 http://highwayfx.ucoz.ru/forum/3-8-1 페이지 끝에 여전히 역사 옵션이 있습니다.
예를 들어, 한 고문은 고전적이고 두 번째 고문은 별에 따르고 세 번째 고문은 민속 표지판에 따름). 그리고 동일한 데이터에 대해 다른 TA 전략을 사용할 때 독립성이 작동하지 않습니다. 그리고 여기서 계산하는 방법은 큰 문제입니다.
예를 들어 MAI를 사용할 수 있습니다 ... 완전히 다른 성격의 전문가를 결합 할 수 있습니다 ...
첫 번째 근사치로 p는 사용된 지표의 수가 증가함에 따라 거의 선형적으로 증가한다고 가정할 수 있습니다(위 그림 참조). 차례로, n개의 지표가 동시에 트리거될 확률은 지표 수가 증가함에 따라 기하급수적으로 감소합니다. 이는 트랜잭션 빈도가 그만큼 빠르게 감소한다는 것을 의미합니다. 즉, 수익성과 거래 빈도라는 두 가지 경쟁 프로세스가 있습니다.
- 우리는 p가 사용된 지표의 수가 증가함에 따라 선형적으로 증가한다고 가정할 수 없습니다... 포물선과 비슷합니다 :)
- 모든 지표가 동시에 작동해야 한다고 누가 말했는지 ... 최적의 수만 (포물선에서는 -b / 2a가 될 것입니다)
그러나 결론은 여전히 우울합니다. 거래에 사용할 지표가 적을수록 좋습니다. 가장 최적의 - 하나!
- 여러 지표를 하나로 결합하면 행복할 것입니다!
방법을 사용하면 그가 유일한 투투가 아니라는 모든 것이 분명합니다. 물론 이러한 문제를 처리해야 하지만 이에 대한 기술적인 질문에 관심이 있고 이미 이 주제를 썼습니다.
누가 그것들을 결합하는 것이 더 나은 방법을 제안해 주시면 대단히 감사하겠습니다. 전체 코드를 하나의 어드바이저에 던지거나 어떻게든 하나의 차트에 연결합니다. 이것이 제가 필요한 전부이고 기술적인 측면은 많지 않지만 잘못된 방향으로 많이 주문되지 않았습니다.
여기에 간단한 옵션이 있습니다
반환된 역사
파란색 - UP
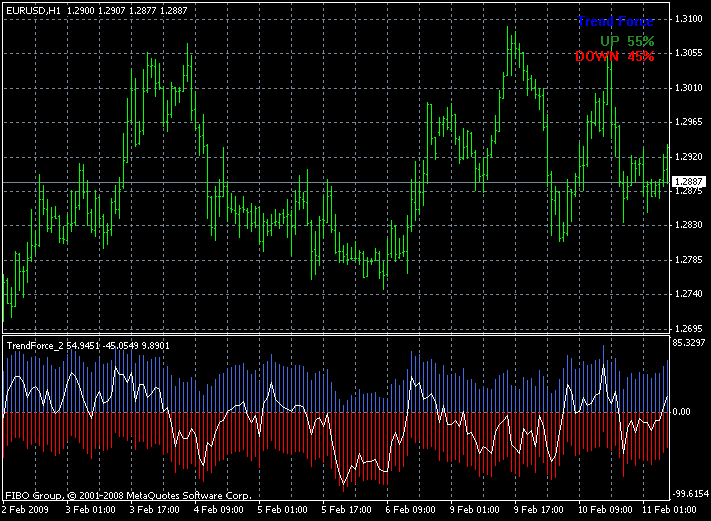
홍당무 = 아래
흰색 = UP 및 DOWN 백분율 간의 학교 차이
- 사용된 지표의 수가 증가함에 따라 p가 선형적으로 증가한다고 가정할 수 없습니다... 포물선과 비슷합니다 :)
포물선은 어디에서 왔습니까, 빈센트? 그리고 0에 가까운 값에서 어떻게 동작합니까(확률은 음수가 될 수 없음)?
안녕하세요 알렉세이입니다.
몬테카를로에서 문제를 푸는 것이 더 쉽습니다.
글쎄, 당신이 준다, 세르게이. 나는 아직 당신의 결론을 이해하지 못했습니다. 음식을 주셔서 감사합니다.
그리고 여기에 질문이 있습니다. p=0.5에서 확률이 증가하지 않는 이유는 무엇입니까?
포물선은 어디에서 왔습니까, 빈센트? 그리고 0에 가까운 값에서 어떻게 동작합니까(확률은 음수가 될 수 없음)?
너무 심각하게 받아들이지 마세요, Alexey... 이것이 제가 대략적으로 내 실제 관찰을 공식화한 방법입니다. 전문가(지표)의 수가 증가하면서 얼마 동안(이것이 필요하지는 않지만) 올바른 확률이 예측은 증가할 것입니다... 그리고 그것은 떨어지기 시작할 것입니다 ... 즉. 당신이 사용해야하는 최적의 수가 있습니다 ...