아니오, 작동하지 않습니다. 이 공식에 따르면 BGN은 상관관계가 있음을 알 수 있습니다. 모든 시간 r은 마이너스 0.5의 영역에 있습니다.
인증 코드는 다음과 같습니다.
확인했습니다.
세르게이, 제대로 합시다.
1. 우리는 견적과 유사한 BP와 협력합니다. 이러한 계열은 SW를 MO와 통합하여 얻습니다. MO가 0인 CB의 예: dX=rnorm(n+1,0,10), 여기서 n+1은 가우시안 분포를 갖는 CV 구성원의 수이고, 0은 제 경우에는 0과 같은 MO이고, 귀하의 예에서는 10이고, 10은 너비입니다. 제 경우에는 이 분포의 100개 - 귀하의 경우에는 100개입니다. 가격과 유사한 VR을 구축하려면 원본 시리즈를 통합해야 합니다(누적 합계 찾기).
다음은 통합 SW의 증가분 분포(왼쪽 그림)와 VR 배경에 대한 증가분 분포(오른쪽 그림의 빨간색 및 파란색 선)입니다.
Sergey, 우리가 지금 연구하고 있는 것은 VR(파란색)의 속성이며, 귀하의 게시물에서 첫 번째 차이, 맨 처음 차이(dX in 내 표기법 및 X). 물론, 당신은 R=0.5를 얻게 될 것이고 다른 것이 없어야 합니다(그것은 기초적인 것으로 판명되었습니다). 따라서 이제 MO가 0인 통합 SW(오른쪽 그림에서 파란색)에 대해 제안한 공식을 사용하여 r을 계산하면 예상되는 0을 얻을 수 있습니다.
나는 당신이 말하는 것을 POI = 0과 통합 CB했습니다. 전체 코드는 다음과 같습니다.
언뜻보기에는 모든 것이 괜찮은 것 같습니다. 하지만 함정이 있습니다. 상관 배열을 공식에 대한 입력으로 사용하겠습니다. 트렌드 + 노이즈의 형태로. y=a*x+b+rnorm(). 이것은 POI = 0을 대신 설정하여 간단히 수행할 수 있습니다. 예를 들어 0.5라고 가정해 보겠습니다.
그림에서 곡선(파란색)이 명확하게 상관관계가 있음을 알 수 있습니다. 그것을 두 개의 배열 A와 B로 나누어 상관 계수를 계산하면 0.993으로 판명됩니다. 그리고 공식에 따르면 0.225.
사실은 정의에 따라 상관 계수(CC)가 두 배열 사이에서 고려된다는 것입니다. 당신은 같은 것을 사용하고 있습니다. 따라서 배열을 자체와 비교할 수 있습니다. 이것을 ACF라고 합니다. 두 개의 배열이 형성되고 A, 원래 배열 및 두 번째 배열 B가 A에 대해 시간 이동되고 그래프가 그려집니다. 즉, 이동에 대한 QC의 의존성입니다. 이동이 없으면 QC는 자연스럽게 = 1입니다. 다음은 마지막 파란색 곡선의 ACF 플롯입니다.
이것이 응용 프로그램이 나온 방법입니다. 저것들. 나는 당신이 이 공식에 따라 무언가를 고려하지만 이것은 QC가 아니라는 내 자신의 의견을 유지합니다. 숫자가 일치하지 않습니다
그러나 우리는 빗나갔다. 먼저 Hurst를 올바르게 계산한 다음 KK와 어떻게 다른지 확인해야 합니다.
원래 BP(증가가 아님)와 동일한 BP 사이의 상관 계수를 찾고 있지만 500 카운트를 오른쪽으로 이동했습니다. 저것들. 두 항상 양의 BP 사이의 상관 계수를 찾고 있습니다! 음, 물론 항상 긍정적이고 매우 클 것입니다(약 1).
Sergey, 나는 당신을 이해하지 못합니다! 원래 VR과 동일하지만 이동된 VR 간의 상관 계수는 무엇이라고 생각합니까? Nafik 우리는 그를 필요로?! 초기 VR 의 첫 번째 차이 시리즈 에서 인접한 판독값 간의 상관 계수에 관심이 있습니다. 이전 증가에 대한 예상 증가의 의존성을 보여주는 사람은 바로 그 사람입니다. 1/2만큼 이동한 Hurst와 동일한 인덱스입니다.
이것은 일련의 통합 CB 및 EURGBP 비율이 어떻게 보이는지(왼쪽 그림)이고, 여기에 서로 다른 시간 프레임에 대한 증분 진폭이 이중 로그 눈금에서 어떻게 보이는지 보여줍니다(오른쪽 그림). , TF의 로그는 가로 좌표를 따라 표시됩니다.
Hers는 이러한 선의 기울기의 탄젠트가 임의의 통합 값의 경우 1/2이고(이러한 견적으로 거래하는 것은 의미가 없음), 후퇴 시장의 경우 1/2 미만이고 1/2 이상이라고 주장합니다. 유행하는 것. SW에 대한 이 각도가 무엇인지 봅시다. 여기에서 기사에서 조언한 대로 LSM 직선을 그리고 그 기울기를 찾을 수 있지만 이 값은 두 점마다 직선을 그려서 로컬에서 찾을 수 있습니다. 결과적으로 각 TF에 대한 RH를 얻습니다.
여기에서 원은 NE(빨간색)의 RP와 파란색을 나타냅니다. EURGBP 견적의 경우 분 단위의 TF는 가로 좌표를 따라 표시됩니다. 십자형은 1/2의 이동으로 원래 시리즈의 첫 번째 차이 시리즈에 대한 인접 판독값 간의 상관 계수를 보여줍니다. 이 페이지의 첫 번째 메시지에 제공된 공식에 따라 상관 계수를 찾았습니다. VR의 예측 가능성을 평가하는 이 두 가지 방법 간의 일치는 만족스러운 반면 제 경우에는 공식이 훨씬 적습니다(하나만). 실제로 보여야 했던 것입니다.
또한 Random 계열은 정의에서 다음과 같이 HX=1/2 및 r=0(그림에 오프셋 있음)을 부여했습니다. 롤백 추세(지속성 방지)는 kotir에 대해 명확하게 볼 수 있으며, TF가 클수록 작습니다.
아니오, 작동하지 않습니다. 이 공식에 따르면 BGN은 상관관계가 있음을 알 수 있습니다. 모든 시간 r은 마이너스 0.5의 영역에 있습니다.
인증 코드는 다음과 같습니다.
확인했습니다.
세르게이, 제대로 합시다.
1. 우리는 견적과 유사한 BP와 협력합니다. 이러한 계열은 SW를 MO와 통합하여 얻습니다. MO가 0인 CB의 예:
dX=rnorm(n+1,0,10), 여기서 n+1은 가우시안 분포를 갖는 CV 구성원의 수이고, 0은 제 경우에는 0과 같은 MO이고, 귀하의 예에서는 10이고, 10은 너비입니다. 제 경우에는 이 분포의 100개 - 귀하의 경우에는 100개입니다. 가격과 유사한 VR을 구축하려면 원본 시리즈를 통합해야 합니다(누적 합계 찾기).
다음은 통합 SW의 증가분 분포(왼쪽 그림)와 VR 배경에 대한 증가분 분포(오른쪽 그림의 빨간색 및 파란색 선)입니다.
Sergey, 우리가 지금 연구하고 있는 것은 VR(파란색)의 속성이며, 귀하의 게시물에서 첫 번째 차이, 맨 처음 차이(dX in 내 표기법 및 X). 물론, 당신은 R=0.5를 얻게 될 것이고 다른 것이 없어야 합니다(그것은 기초적인 것으로 판명되었습니다). 따라서 이제 MO가 0인 통합 SW(오른쪽 그림에서 파란색)에 대해 제안한 공식을 사용하여 r을 계산하면 예상되는 0을 얻을 수 있습니다.
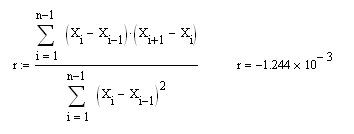
그리고 물론 이것은 일련의 dX 증분에 대한 r과 동일합니다(그러나 다른 공식에서).
이제 우리가 이 점에 대해 합의를 이루기를 바랍니다.
추신 당신은 또한 이것을 할 수 있습니다:
좋아, 순서대로 가자.
나는 당신이 말하는 것을 POI = 0과 통합 CB했습니다. 전체 코드는 다음과 같습니다.
언뜻보기에는 모든 것이 괜찮은 것 같습니다. 하지만 함정이 있습니다. 상관 배열을 공식에 대한 입력으로 사용하겠습니다. 트렌드 + 노이즈의 형태로. y=a*x+b+rnorm(). 이것은 POI = 0을 대신 설정하여 간단히 수행할 수 있습니다. 예를 들어 0.5라고 가정해 보겠습니다.
그림에서 곡선(파란색)이 명확하게 상관관계가 있음을 알 수 있습니다. 그것을 두 개의 배열 A와 B로 나누어 상관 계수를 계산하면 0.993으로 판명됩니다. 그리고 공식에 따르면 0.225.
사실은 정의에 따라 상관 계수(CC)가 두 배열 사이에서 고려된다는 것입니다. 당신은 같은 것을 사용하고 있습니다. 따라서 배열을 자체와 비교할 수 있습니다. 이것을 ACF라고 합니다. 두 개의 배열이 형성되고 A, 원래 배열 및 두 번째 배열 B가 A에 대해 시간 이동되고 그래프가 그려집니다. 즉, 이동에 대한 QC의 의존성입니다. 이동이 없으면 QC는 자연스럽게 = 1입니다. 다음은 마지막 파란색 곡선의 ACF 플롯입니다.
이것이 응용 프로그램이 나온 방법입니다. 저것들. 나는 당신이 이 공식에 따라 무언가를 고려하지만 이것은 QC가 아니라는 내 자신의 의견을 유지합니다. 숫자가 일치하지 않습니다
그러나 우리는 빗나갔다. 먼저 Hurst를 올바르게 계산한 다음 KK와 어떻게 다른지 확인해야 합니다.
다양한 시계열을 분석한 재미있는 작품입니다 .
허스트 지수를 사용합니다.
그림에서 곡선(파란색)이 명확하게 상관관계가 있음을 알 수 있습니다. 그것을 두 개의 배열 A와 B로 나누어 상관 계수를 계산하면 0.993으로 판명됩니다. 그리고 공식에 따르면 0.225.
여기서 나는 완전히 이해하지 못했습니다.
트렌디한 VR을 어떤 어레이로 나누셨나요? Y=a*X+b 선과 MO가 0인 임의 구성요소에서 이들 사이의 상관 계수를 찾고 있습니까?
다양한 시계열을 분석한 흥미로운 작품 이 있습니다.
허스트 지수를 사용합니다.
여기서 나는 완전히 이해하지 못했습니다.
지금은 이해.
원래 BP(증가가 아님)와 동일한 BP 사이의 상관 계수를 찾고 있지만 500 카운트를 오른쪽으로 이동했습니다. 저것들. 두 항상 양의 BP 사이의 상관 계수를 찾고 있습니다! 음, 물론 항상 긍정적이고 매우 클 것입니다(약 1).
Sergey, 나는 당신을 이해하지 못합니다! 원래 VR과 동일하지만 이동된 VR 간의 상관 계수는 무엇이라고 생각합니까? Nafik 우리는 그를 필요로?! 초기 VR 의 첫 번째 차이 시리즈 에서 인접한 판독값 간의 상관 계수에 관심이 있습니다. 이전 증가에 대한 예상 증가의 의존성을 보여주는 사람은 바로 그 사람입니다. 1/2만큼 이동한 Hurst와 동일한 인덱스입니다.
고맙습니다. 우리는 볼 것이다.
여기 가 진리인 것 같습니다.
구현하려고했지만 코스의 경우 1에 매우 가깝습니다.
______________
나는 기사를 다시 읽었습니다. 갈퀴를 밟은 것 같습니다.
통화 쌍의 경우 파생 상품에 대해 Hurst 지수를 계산해야 하며 환율에 대해 계산했습니다.
나는 기사를 다시 읽었습니다. 갈퀴를 밟은 것 같습니다.
음다 :-)
앞으로 달리고 있습니다.
이것은 일련의 통합 CB 및 EURGBP 비율이 어떻게 보이는지(왼쪽 그림)이고, 여기에 서로 다른 시간 프레임에 대한 증분 진폭이 이중 로그 눈금에서 어떻게 보이는지 보여줍니다(오른쪽 그림). , TF의 로그는 가로 좌표를 따라 표시됩니다.
Hers는 이러한 선의 기울기의 탄젠트가 임의의 통합 값의 경우 1/2이고(이러한 견적으로 거래하는 것은 의미가 없음), 후퇴 시장의 경우 1/2 미만이고 1/2 이상이라고 주장합니다. 유행하는 것. SW에 대한 이 각도가 무엇인지 봅시다. 여기에서 기사에서 조언한 대로 LSM 직선을 그리고 그 기울기를 찾을 수 있지만 이 값은 두 점마다 직선을 그려서 로컬에서 찾을 수 있습니다. 결과적으로 각 TF에 대한 RH를 얻습니다.
여기에서 원은 NE(빨간색)의 RP와 파란색을 나타냅니다. EURGBP 견적의 경우 분 단위의 TF는 가로 좌표를 따라 표시됩니다. 십자형은 1/2의 이동으로 원래 시리즈의 첫 번째 차이 시리즈에 대한 인접 판독값 간의 상관 계수를 보여줍니다. 이 페이지의 첫 번째 메시지에 제공된 공식에 따라 상관 계수를 찾았습니다. VR의 예측 가능성을 평가하는 이 두 가지 방법 간의 일치는 만족스러운 반면 제 경우에는 공식이 훨씬 적습니다(하나만). 실제로 보여야 했던 것입니다.
또한 Random 계열은 정의에서 다음과 같이 HX=1/2 및 r=0(그림에 오프셋 있음)을 부여했습니다. 롤백 추세(지속성 방지)는 kotir에 대해 명확하게 볼 수 있으며, TF가 클수록 작습니다.
여기에서 원은 NE(빨간색)의 RP와 파란색을 나타냅니다. EURGBP 견적의 경우 분 단위의 TF는 가로 좌표를 따라 표시됩니다.
랜덤 시리즈는 정의에서 다음과 같이 RH=1/2 및 r=0(그림에 오프셋이 있음)을 제공했습니다. 롤백 추세(지속성 방지)는 kotir에 대해 명확하게 볼 수 있으며, TF가 클수록 작습니다.
이것이 아마도 파이퍼들이 유로파운드를 사랑하는 이유일 것입니다.
이것이 아마도 파이퍼들이 유로파운드를 사랑하는 이유일 것입니다.
그것은 분명하다!
그것은 분명하다!
순수한 호기심에서 - 나는 극도로 끈질긴 쌍을 찾고 싶습니다.
또는 최악의 경우 지속성이 발생하는 조건):