パターン検索への総当たり攻撃アプローチ（第VI部）：循環最適化

内容

• はじめに
• ルーティーン
• 新しい最適化アルゴリズム
• 最も重要な最適化基準
• 取引設定の自動検索
• 結論
• リンク

はじめに

前回の記事の内容を考慮すると、これはアルゴリズムに導入したすべての関数の表面的な説明にすぎないと言えます。これらは、EA作成の完全な自動化だけでなく、最適化と結果の選択の完全な自動化、その後の自動取引での使用、または後で説明するより進歩的なEAの作成などの重要な機能にも関係します。

取引端末、汎用EA、アルゴリズム自体の共生のおかげで、必要なコンピューティング能力があれば、手動による開発を完全に排除することも、最悪の場合、改善にかかる労力を一桁減らすこともできます。この記事では、これらのイノベーションの最も重要な側面について説明していきます。

ルーティーン

私にとって、このようなソリューションを作成し、その後時間をかけて修正する上で最も重要な要素は、日常的なアクションを最大限に自動化できる可能性を理解することでした。この場合、日常的なアクションには、必須ではない人間の作業がすべて含まれます。

• アイデアの生成
• 理論の作成
• 理論に従ってコードを書く
• コード修正
• 継続的なEAの再最適化
• 継続的なEAの選択
• EAのメンテナンス
• 端末操作
• 実験と実践
• その他

ご覧のとおり、このルーチンの範囲は非常に広いです。これらすべてが自動化できることを証明できたので、私はこれをまさにルーティンとして扱います。一般的なリストを提供しました。アルゴリズムトレーダー、プログラマー、またはその両方など、あなたが誰であるかは関係ありません。プログラミングの仕方を知っているかどうかは関係ありません。知らない場合でも、いずれにせよ、このリストの少なくとも半分に遭遇することになります。私が話しているのは、市場でEAを購入し、チャート上で起動し、ボタンを1つ押すだけで落ち着いた場合の話ではありません。もちろん、これは非常にまれではありますが、起こります。

これらすべてを理解した上で、まず最も明らかなことを自動化する必要がありました。この最適化すべてについては、以前の記事で概念的に説明しました。ただし、このようなことをおこなうと、すでに実装されている機能に基づいて全体を改善する方法がわかり始めます。この点に関する私にとっての主なアイデアは次のとおりです。

• 最適化メカニズムの改善
• EAを結合する仕組み（結合ボット）の作成
• すべてのコンポーネントの対話パスの正しいアーキテクチャ

もちろん、これはかなり短い列挙です。すべてを詳しく説明します。最適化を改善するとは、複数の要素を一度に組み合わせることを意味します。これらすべては、システム全体を構築するために選択されたパラダイム内で検討されます。

• ティックを排除することで最適化を加速
• 取引意思決定ポイント間の利益曲線制御を排除することで、最適化を加速
• カスタム最適化基準を導入することにより、最適化の品質を向上
• フォワード期間の効率を最大化

このWebサイトのフォーラムでは、最適化がそもそも必要かどうか、また最適化の利点は何かについて、現在も進行中の議論を見つけることができます。以前は、主に個々のフォーラムやWebサイトユーザーの影響により、私はこの行動に対してかなり明確な態度をとっていました。今では、この意見はまったく気になりません。最適化に関しては、それを正しく使用する方法と目的を知っているかどうかにすべてかかっています。正しく使用すると、このアクションにより望ましい結果が得られます。一般に、このアクションは非常に便利であることがわかります。

多くの人は最適化を好みません。それには客観的な理由が2つあります。

• 基本的な事項（なぜ何をどのようにおこなうのか、結果の選択方法、および経験不足も含む、これに関連するすべてのこと）の理解不足
• 最適化アルゴリズムの不完全さ

実際、両方の要素がお互いを強化します。公平を期すために言うと、MetaTrader 5オプティマイザーは構造的に完璧に実行されていますが、最適化基準と可能なフィルターに関してはまだ多くの改善が必要です。これまでのところ、これらすべての機能は子供の砂場に似ています。プラスのフォワード期間を達成する方法、そして最も重要なことに、このプロセスを制御する方法について考えている人はほとんどいません。私は長い間このことについて考えてきました。実際、今回の記事のかなりの部分がこのトピックに当てられます。

新しい最適化アルゴリズム

バックテストの基本的な既知の評価基準に加えて、結果の選択とその後の設定の適用をより効率的におこなうために、アルゴリズムの値を倍増するのに役立ついくつかの組み合わせ特性を考え出すことができます。これらの特性の利点は、作業設定を見つけるプロセスを高速化できることです。これをおこなうために、MetaTraderと同様のストラテジーテスターレポートのようなものを作成しました。

図1

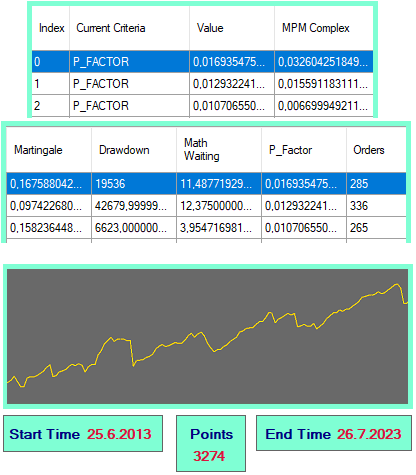
このツールを使用すると、クリックするだけで好みのオプションを選択できます。クリックすると設定が生成され、すぐに端末内の適切なフォルダーに移動して、汎用EAがそれを読み取って取引を開始できるようにします。必要に応じて、ボタンをクリックしてEAを生成することもできます。内部に組み込まれた設定を備えた別のEAが必要な場合に備えて、EAが構築されます。利益曲線もあり、表から次のオプションを選択すると再描画されます。

テーブル内で何がカウントされるかを見てみましょう。これらの特性を計算するための主な要素は次のデータです。

1. ポイント：対応する商品の「_Point」内のバックテスト全体の利益
2. 注文：完全にオープンした注文と決済した注文の数（「オープン注文は1つだけ存在できる」というルールに従って、厳密な順序で相互に続く）
3. ドローダウン：バランスドローダウン

これらの値に基づいて、次の取引特性が計算されます。

• 数学的待機：ポイント単位の数学的期待値
• Pファクター：範囲[-1 ...0...1]に正規化された利益率の類似物（私の基準）
• マーチンゲール：マーチンゲールの適用可能性（私の基準）
• MPMComplex：前の3つの指標を複合した指標（私の基準）

これらの基準がどのように計算されるかを見てみましょう。

方程式1

ご覧のとおり、私が作成した基準はすべて非常にシンプルで、最も重要なことに、理解しやすいものです。各基準の増加は確率理論の観点からバックテスト結果がより優れていることを示しているため、MPMComplex基準で行ったように、これらの基準を掛け合わせることが可能になります。共通のメトリクスを使用すると、重要度によって結果をより効率的に並べ替えることができます。大規模な最適化の場合、より多くの高品質のオプションを保持し、より多くの低品質のオプションを削除することができます。

また、これらの計算ではすべてがポイントで発生することに注意してください。これは最適化プロセスに良い影響を与えます。計算では、厳密に正の一次量が使用され、常に最初に計算されます。残りはすべてそれらに基づいて計算されます。テーブルにない主な数量を列挙する価値があると思います。

• ポイントプラス：収益性の高い各注文またはゼロ注文の利益のポイント単位の合計
• ポイントマイナス：各不採算注文の損失モジュールのポイント単位の合計
• ドローダウン：バランスによるドローダウン（独自の方法で計算）

ここで最も興味深いのは、ドローダウンがどのように計算されるかです。私たちの場合、これは最大相対バランスドローダウンです。私のテストアルゴリズムが資金曲線の監視を拒否しているという事実を考慮すると、他のタイプのドローダウンは計算できません。ただし、このドローダウンを計算する方法を示すことは役立つと思います。

図2

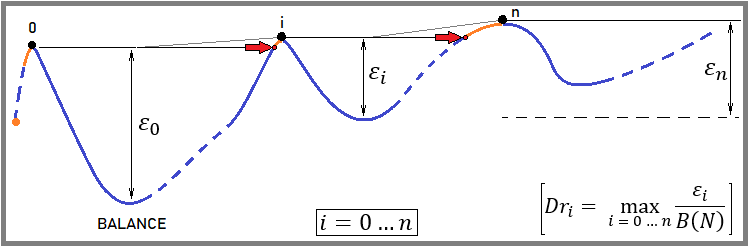
これは非常に簡単に定義されています。

1. バックテストの開始点（最初のドローダウンカウントダウンの開始点）を計算する
2. 取引が利益から始まる場合は、最初の負の値が表示されるまで、バランスの増加に応じてこのポイントを上方に移動する（ドローダウン計算の開始を示す）
3. バランスが基準点のレベルに達するまで待つその後、それを新しい基準点として設定する
4. ドローダウン検索の最後のセクションに戻り、そのセクションの最低点を探す（このセクションのドローダウン量はこの点から計算される）
5. バックテスト全体または取引曲線全体に対してプロセス全体を繰り返す

最後のサイクルは常に未完了のままになります。ただし、テストが続けば増加する可能性があるにもかかわらず、ドローダウンも考慮されます。しかし、これはここでは特に重要なことではありません。

最も重要な最適化基準

次に、最も重要なフィルターについて話しましょう。実際、この基準は最適化の結果を選択する際に最も重要です。残念なことに、この基準はMetaTrader 5オプティマイザーの機能には含まれていません。そこで、誰もがこのアルゴリズムを独自のコードで再現できるように、理論的な資料を提供しましょう。実際、この基準はあらゆるタイプの取引に多機能であり、スポーツ賭博、暗号通貨、その他考えられるあらゆるものを含む、あらゆる利益曲線に対して機能します。基準は次のとおりです。

方程式2

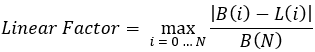
この方程式の中身を見てみましょう。

• N：バックテストまたは取引セクション全体を通じて、完全にオープンおよび決済された取引ポジションの数
• B(i)：対応する決済ポジション「i」の後のバランスラインの値
• L(i)：ゼロからバランスの最後の点（最終バランス）まで引かれた直線

このパラメータを計算するには2つのバックテストを実行する必要があります。最初のバックテストで最終的なバランスが計算されます。その後、各バランスポイントの値を保存して対応する指標を計算できるため、不必要な計算をおこなう必要がなくなります。それにもかかわらず、この計算はバックテストの繰り返しと呼ぶことができます。この方程式はカスタムテスターで使用でき、EAに組み込むことができます。

この指標全体は、より深く理解するために変更できることに注意することが重要です。例えば、次のようになります。

方程式3

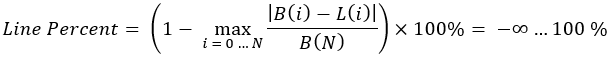
この方程式は、認識と理解の点でより困難です。しかし、実用的な観点から見ると、このような基準は、値が高いほどバランス曲線が直線に近づくため便利です。以前の記事でも同様の問題に触れましたが、その背後にある意味については説明していませんでした。まず次の図を見てみましょう。

図3

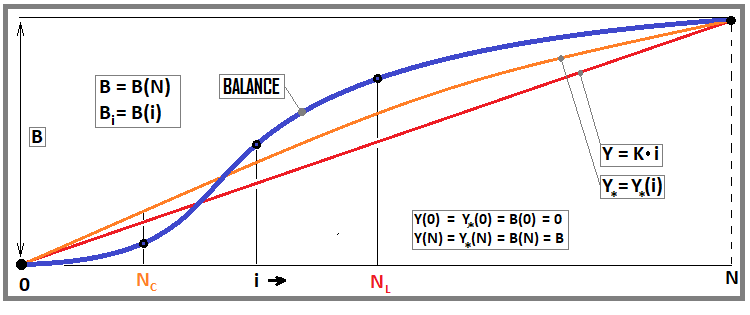
この図は、バランスラインと2つの曲線を示しています。そのうちの1つは方程式（赤）に関連し、2番目の曲線は次の修正基準（方程式11）に関係します。さらに詳しく説明しますが、ここでは方程式に焦点を当てましょう。

バックテストをバランスのある単純な点の配列として想像すると、それを統計サンプルとして表し、それに確率論の方程式を適用できます。直線が私たちが目指しているモデルであり、利益曲線自体が私たちのモデルを目指している実際のデータフローであると考えます。

直線性係数は、利用可能な取引基準セット全体の信頼性を示すことを理解することが重要です。データの信頼性が高いということは、将来の期間がより長く、より良いものになる可能性があることを示している可能性があります（将来の収益性の高い取引）。厳密に言うと、当初は確率変数を考慮した上で検討を始めるべきだったのですが、このような表現の方が分かりやすいのではないかと思いました。

ランダムなスパイクの可能性を考慮して、線形性係数の代替類似物を作成してみましょう。これをおこなうには、後続の分散計算に便利な確率変数とその平均を導入する必要があります。

方程式4

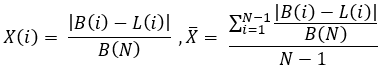
よりよく理解するために、「N」個の完全にオープンなポジションと決済されたポジションがあり、それらは厳密に次々と続くことを明確にする必要があります。これは、バランスラインのこれらのセグメントを接続する「N+1」個の点があることを意味します。すべてのラインのゼロ点は共通であるため、そのデータは最後の点と同様に結果を改善の方向に歪めます。したがって、それらを計算から除外し、計算を実行する「N-1」個の点が残ります。

2行の値の配列を1行に変換する式の選択は非常に興味深いことがわかりました。次の分数に注意してください。

方程式5

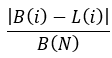
ここで重要なことは、すべての場合において最終バランスですべてを割ることです。したがって、すべてを相対値に換算することで、テストされたすべての戦略について例外なく計算された特性が同等であることが保証されます。直線性係数の最初の単純な基準に同じ部分が存在するのは偶然ではありません。これは同じ考慮事項に基づいて構築されているためです。しかし、代替基準の構築を完了しましょう。これをおこなうには、分散などのよく知られた概念を使用できます。

方程式6

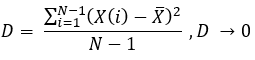
分散は、サンプル全体の平均からの二乗偏差の算術平均に他なりません。私はすぐにそこにランダム変数、つまり上で定義した式を代入しました。理想的な曲線の平均偏差はゼロであり、その結果、特定のサンプルの分散もゼロになります。これらのデータに基づいて、この分散は、その構造（使用される確率変数またはサンプル（必要に応じて））により、代替の線形性係数として使用できることが容易に推測できます。さらに、両方の基準を組み合わせて使用​​すると、サンプルパラメータをより効果的に制限できますが、正直に言うと、私は最初の基準のみを使用します。

同様の、より便利な基準を見てみましょう。これも、定義した新しい線形性係数に基づいています。

方程式7

見てわかるように、これは最初の基準（方程式2）に基づいて構築された同様の基準と同じです。ただし、これら2つの基準は考えられる限界からはほど遠いものです。この検討を支持する明らかな事実は、この基準があまりにも理想化されており、理想的なモデルにより適しているため、多かれ少なかれ重要な対応を達成するためにEAを調整するのは非常に困難であるということです。方程式を適用してしばらくすると明らかになるマイナス要因を列挙する価値はあると思います。

1. 取引回数の大幅な削減（結果の信頼性の低下）
2. 効率的なシナリオの最大数の拒否(戦略によっては、曲線が必ずしも直線に向かうとは限りません)

目標は良い戦略を破棄することではなく、逆に、これらの欠点のない新しく改善された基準を見つけることであるため、これらの欠点は非常に重要です。これらの欠点は、いくつかの推奨ラインを一度に導入することで完全または部分的に解消でき、それぞれを許容可能なモデルまたは推奨モデルとみなすことができます。これらの欠点を解消した、新しく改良された基準を理解するには、対応する置き換えを理解するだけで済みます。

方程式8

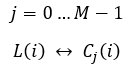
次に、リストから各曲線の適合係数を計算できます。

方程式9

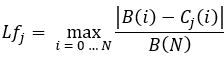
同様に、各曲線のランダムなスパイクを考慮した代替基準を計算することもできます。

方程式10

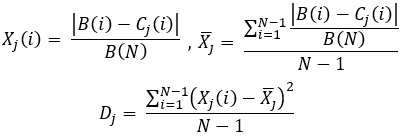
次に、次のことを計算する必要があります。

方程式11

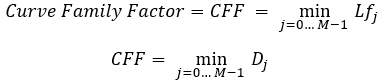
ここで、曲線ファミリー係数と呼ばれる基準を導入します。実際、このアクションにより、取引曲線に最も類似した曲線が同時に見つかり、それに対応する係数もすぐに見つかります。最小のマッチング係数を持つ曲線が実際の状況に最も近くなります。その値を修正された基準の値として受け取ります。もちろん、計算は2つのバリエーションのどちらが良いかに応じて2つの方法でおこなうことができます。

これはすべて非常に素晴らしいことですが、多くの人が気づいているように、ここにはそのような曲線群の選択に関連するニュアンスがあります。このようなファミリーを正しく説明するには、さまざまな考慮事項に従うことができますが、私の考えは次のとおりです。

• すべての曲線に変曲点があってはなりません(後続の各中間点は、厳密に前の中間点よりも高い必要があります)。
• 曲線は凹面である必要があります(曲線の急勾配は一定であることも、増加するだけであることもできます)。
• 曲線の凹面は調整可能である必要があります(例えば、たわみの量は、何らかの相対値または割合を使用して調整する必要があります)。
• 曲線モデルの単純さ(最初は単純で理解しやすいグラフィカルモデルに基づいてモデルを作成することをお勧めします)。

これは、この曲線群の最初のバリエーションにすぎません。必要なすべての構成を考慮して、より広範なバリエーションを作成することが可能であり、品質設定を失うことを完全に防ぐことができます。このタスクは後で引き受けることにしますが、ここでは凹曲線族の元の戦略についてのみ触れておきます。私は数学の知識を使って、そのようなファミリーを非常に簡単に作ることができました。この一連の曲線が最終的にどのようになるかをすぐに示しましょう。

図4

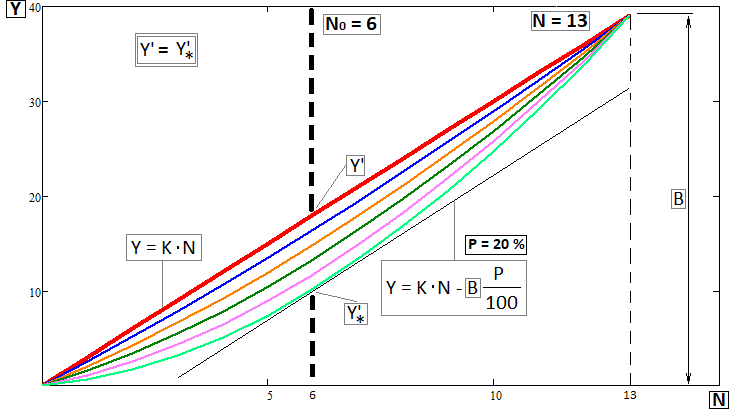
このようなファミリーを構築するとき、私は垂直の支持体の上にある弾性ロッドの抽象化を使用しました。このようなロッドのたわみの程度は、力の作用点とその大きさによって異なります。これがここで扱っているものと多少似ているだけであることは明らかですが、視覚的に類似したある種のモデルを開発するには十分です。この状況では、もちろん、まず最初に極値の座標を決定する必要があります。これはバックテストチャート上の点の1つと一致する必要があり、そこでX軸はゼロから始まる取引指数で表されます。私は次のように計算します。

方程式12

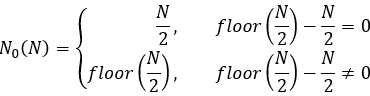
ここには、偶数および奇数の「N」の場合の2つのケースがあります。「N」が偶数であることが判明した場合、インデックスは整数である必要があるため、単純に2で割ることはできません。ちなみに、最後の図ではまさにこのケースを描きました。そこでは、力の適用点が開始点に少し近づいています。もちろん、終了に少し近づいてその逆をおこなうこともできますが、図で示したように、これは少数の取引でのみ重要になります。取引数が増加すると、これらすべてが最適化アルゴリズムにとって重要な役割を果たさなくなります。

「P」のたわみ値を割合で設定し、バックテストの「B」の最終バランスを設定し、極値の座標を事前に決定したら、受け入れられた曲線の各ファミリーの式を構築するためのさらなるコンポーネントの計算を順次開始できます。次に、バックテストの開始と終了を結ぶ直線の急勾配が必要です。

方程式13

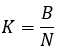
これらの曲線のもう1つの特徴は、横軸が「N0」である点における各曲線の接線角度が「K」と同一であるという事実です。方程式を作成するときに、タスクからこの条件を要求しました。これは最後の図（図4）でもグラフで見ることができ、そこにもいくつかの方程式と恒等式があります。次へ移りましょう。次に、次の値を計算する必要があります。

方程式14

 

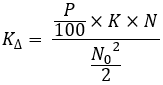
「P」はファミリーの曲線ごとに異なるように設定されることに注意してください。厳密に言うと、これらはファミリーから1つの曲線を構築するための方程式です。これらの計算は、ファミリーの曲線ごとに繰り返す必要があります。次に、別の重要な比率を計算する必要があります。

方程式15

これらの構造の意味を掘り下げる必要はありません。これらは、曲線を構築するプロセスを簡素化するためにのみ作成されています。最後の補助比率を計算することが残っています。

方程式16

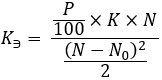
ここで、取得したデータに基づいて、構築された曲線の点を計算するための数式を受け取ることができます。ただし、最初に、曲線は単一の方程式で記述されないことを明確にする必要があります。「N0」点の左側には1つの方程式があり、もう1つは右側に作用します。理解しやすくするために、次のようにすることができます。

方程式17

これで、最終的な方程式がわかります。

方程式18

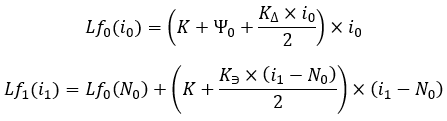
これは次のように示すこともできます。

方程式19

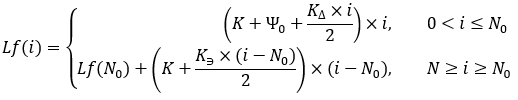
厳密に言えば、この関数は個別の補助関数として使用する必要があります。しかし、それにもかかわらず、小数点「i」で値を計算することができます。もちろん、これは私たちの問題の文脈において、私たちにとって有益な利点をもたらす可能性は低いです。

このような数学を説明しているので、アルゴリズムの実装例を提供する義務があります。誰もが、自分のシステムに簡単に適応できる既成のコードを入手することに興味があると思います。必要な量の計算を簡素化する主な変数とメソッドを定義することから始めましょう。

//+------------------------------------------------------------------+
//| Number of lines in the balance model                             |
//+------------------------------------------------------------------+
#define Lines 11 

//+------------------------------------------------------------------+
//| Initializing variables                                           |
//+------------------------------------------------------------------+
double MaxPercent = 10.0;
double BalanceMidK[,Lines];
double Deviations[Lines];
int Segments;
double K;

//+------------------------------------------------------------------+
//| Method for initializing required variables and arrays            |
//| Parameters: number of segments and initial balance               |
//+------------------------------------------------------------------+
void InitLines(int SegmentsInput, double BalanceInput) 
{
  Segments = SegmentsInput;
  K = BalanceInput / Segments;
  ArrayResize(BalanceMidK,Segments+1);
  ZeroStartBalances();
  ZeroDeviations();
  BuildBalances();
}

//+------------------------------------------------------------------+
//| Resetting variables for incrementing balances                    |
//+------------------------------------------------------------------+
void ZeroStartBalances()
{
  for (int i = 0; i < Lines; i++ ) 
  {
      for (int j = 0; j <= Segments; j++)
      {
          BalanceMidK[j,i] = 0.0;
      }
  }
}

//+------------------------------------------------------------------+
//| Reset deviations                                                 |
//+------------------------------------------------------------------+
void ZeroDeviations()
{
  for (int i = 0; i < Lines; i++)
  {
      Deviations[i] = -1.0;
  }
}

コードは再利用できるように設計されています。次の計算の後、最初にInitLinesメソッドを呼び出すことで、別のバランス曲線の指標を計算できます。バックテストの最終バランスと取引数を指定する必要があります。その後、このデータに基づいて曲線の構築を開始できます。

//+------------------------------------------------------------------+
//| Constructing all balances                                        |
//+------------------------------------------------------------------+
void BuildBalances()
{
   int N0 = MathFloor(Segments / 2.0) - Segments / 2.0 == 0 ? Segments / 2 : (int)MathFloor(Segments / 2.0);//calculate first required N0
   for (int i = 0; i < Lines; i++)
   {
       if (i==0)//very first and straight line 
       {
           for (int j = 0; j <= Segments; j++)
           {
               BalanceMidK[j,i] = K*j;
           }
       }
       else//build curved lines
       {
           double ThisP = i * (MaxPercent / 10.0);//calculate current line curvature percentage
           double KDelta = ( (ThisP /100.0) * K * Segments) / (MathPow(N0,2)/2.0 );//calculation first auxiliary ratio
           double Psi0 = -KDelta * N0;//calculation second auxiliary ratio
           double KDelta1 = ((ThisP / 100.0) * K * Segments) / (MathPow(Segments-N0, 2) / 2.0);//calculate last auxiliary ratio
           //this completes the calculation of auxiliary ratios for a specific line, it is time to construct it

           for (int j = 0; j <= N0; j++)//construct the first half of the curve 
           {
               BalanceMidK[j,i] = (K + Psi0 + (KDelta * j) / 2.0) * j;
           }
           for (int j = N0; j <= Segments; j++)//construct the second half of the curve 
           {
               BalanceMidK[j,i] = BalanceMidK[i, N0] + (K + (KDelta1 * (j-N0)) / 2.0) * (j-N0);
           }
       }
   }
}

Linesによって、ファミリーに含まれる曲線の数が決定されることに注意してください。凹面は、対応する図で示したとおり、ゼロ（直線）などからMaxPercentまで徐々に増加します。次に、各曲線の偏差を計算し、最小のものを選択します。

//+------------------------------------------------------------------+
//| Calculation of the minimum deviation from all lines              |
//| Parameters: initial balance passed via link                      |
//| Return: minimum deviation                                        |
//+------------------------------------------------------------------+
double CalculateMinDeviation(double &OriginalBalance[])
{
   //define maximum relative deviation for each curve 
   for (int i = 0; i < Lines; i++)
   {
       for (int j = 0; j <= Segments; j++)
       {
          double CurrentDeviation = OriginalBalance[Segments] ? MathAbs(OriginalBalance[j] - BalanceMidK[j, i]) / OriginalBalance[Segments] : -1.0;
          if (CurrentDeviation > Deviations[i])
          {
              Deviations[i] = CurrentDeviation;
          }           
       }
   }
    
   //determine curve with minimum deviation and deviation itself 
   double MinDeviation=0.0;
   for (int i = 0; i < Lines; i++)
   {
       if ( Deviations[i] != -1.0 && MinDeviation == 0.0)
       {
           MinDeviation = Deviations[i];
       }
       else if (Deviations[i] != -1.0 && Deviations[i] < MinDeviation)
       {
           MinDeviation = Deviations[i];
       }
   }
   return MinDeviation;
}

これは次のように使用する必要があります。

1. OriginalBalanceオリジナルバランス配列を定義する
2. その長さSegmentsInputと最終的なバランスBalanceInputを決定し、InitLinesメソッドを呼び出す
3. BuildBalancesメソッドを呼び出して曲線を構築する
4. 曲線がプロットされるので、曲線のファミリーに対して改良されたCalculateMinDeviation基準を考慮する

これで基準の計算が完了しました。CurveFamilyFactorの計算は特に難しいことはないと思います。ここで提示する必要はありません。

取引設定の自動検索 

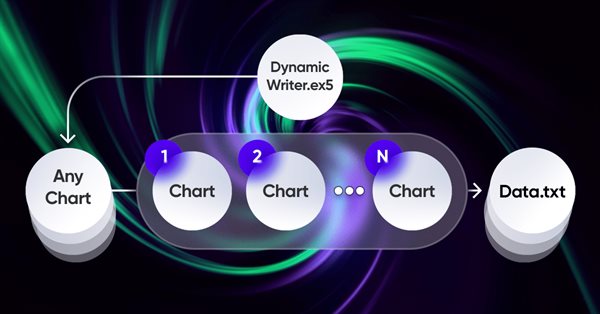
アイデア全体の中で最も重要な要素は、端末とプログラム間の対話システムです。実際、これは高度な最適化基準を備えた循環オプティマイザーです。最も重要なものについては前のセクションで説明しました。システム全体が機能するためには、まず、MetaTrader 5端末の1つであるクオートのソースが必要です。前回の記事ですでに示したように、クオートは私にとって都合の良い形式でファイルに書き込まれます。これはEAを使用しておこなわれますが、一見するとかなり奇妙に機能します。

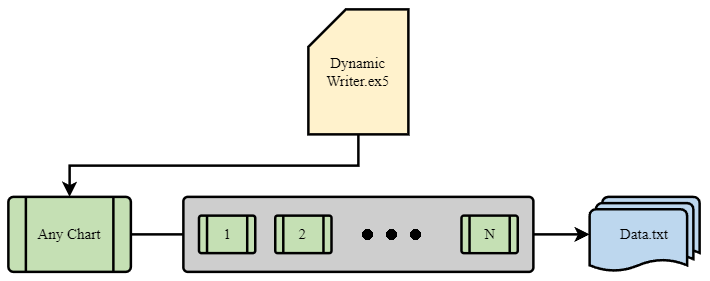
EAの機能に独自のスキームを使用することは、非常に興味深く有益な経験であることがわかりました。ここでは私が解決する必要があった問題のデモンストレーションにすぎませんが、これらはすべてEAの取引にも使用できます。

 

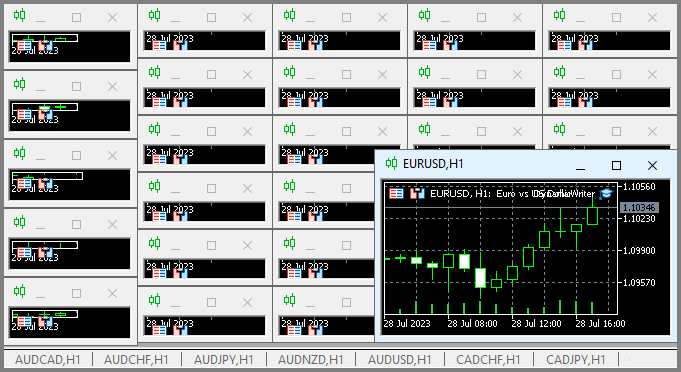
このスキームの特徴は、任意のグラフを選択できることです。データの重複を避けるために取引ツールとしては使用されませんが、ティックハンドラまたはタイマーとしてのみ機能します。チャートの残りの部分は、クオートを生成する必要がある金融商品の期間を表しています。

クオートの書き込みは、乱数発生器を使用してクオートをランダムに選択する形でおこなわれます。必要に応じて、このプロセスを最適化できます。書き込みは、次の基本関数を使用して一定の時間が経過した後におこなわれます。

//+------------------------------------------------------------------+
//| Function to write data if present                                |
//| Write quotes to file                                             |
//+------------------------------------------------------------------+
void WriteDataIfPresent()
{
    // Declare array to store quotes 
    MqlRates rates[];
    ArraySetAsSeries(rates, false);

    // Select a random chart from those we added to the workspace 
    ChartData Chart = SelectAnyChart();
    
    // If the file name string is not empty 
    if (Chart.FileNameString != "")
    {
        // Copy quotes and calculate the real number of bars
        int copied = CopyRates(Chart.SymbolX, Chart.PeriodX, 1,
                        int((YearsE*(365.0*(5.0/7.0)*24*60*60)) / double(PeriodSeconds(Chart.PeriodX))),
                        rates);
        
        // Calculate ideal number of bars
        int ideal = int((YearsE*(365.0*(5.0/7.0)*24*60*60)) / double(PeriodSeconds(Chart.PeriodX)));
        
        // Calculate percentage of received data 
        double Percent = 100.0 * copied / ideal;
        
        // If the received data is not very different from the desired data, 
        // then we accept them and write them to a file
        if (Percent >= 95.0)
        {
            // Open file (create it if it does not exist, 
            // otherwise, erase all the data it contained)
            OpenAndWriteStart(rates, Chart, CommonE); 
            WriteAllBars(rates); // Write all data to file
            WriteEnd(rates); // Add to end
            CloseFile(); // Close and save data file
        }
        else 
        {
            // If there are much fewer quotes than required for calculation 
            Print("Not enough data"); 
        }
    }
}

WriteDataIfPresent関数は、コピーされたデータが、指定されたパラメータに基づいて計算された理想的なバー数の95%以上である場合、選択したチャートからのクオートに関する情報をファイルに書き込みます。コピーされたデータが95%未満の場合、「データが足りません」というメッセージが表示されます。指定された名前のファイルが存在しない場合、関数はそれを作成します。

このコードが機能するには、以下を追加で記述する必要があります。

//+------------------------------------------------------------------+
//| ChartData structure                                              |
//| Objective: Storing the necessary chart data                      |
//+------------------------------------------------------------------+
struct ChartData {
    string FileNameString;
    string SymbolX;
    ENUM_TIMEFRAMES PeriodX;
};

//+------------------------------------------------------------------+
//| Randomindex function                                             |
//| Objective: Get a random number with uniform distribution         |
//+------------------------------------------------------------------+
int Randomindex(int start, int end) {
    return start + int((double(MathRand())/32767.0)*double(end-start+1));
}

//+------------------------------------------------------------------+
//| SelectAnyChart function                                          |
//| Objective: View all charts except current one and select one of  |
//|       them to write quotes                                       |
//+------------------------------------------------------------------+
ChartData SelectAnyChart() {
    ChartData chosenChart;
    chosenChart.FileNameString = "";
    int chartCount = 0;
    long currentChartId, previousChartId = ChartFirst();

    // Calculate number of charts
    while (currentChartId = ChartNext(previousChartId)) {
        if(currentChartId < 0) {
            break;  
        }
        previousChartId = currentChartId;
        
        if (currentChartId != ChartID()) {
            chartCount++;
        }
    }

    int randomChartIndex = Randomindex(0, chartCount - 1);
    chartCount = 0;
    currentChartId = ChartFirst(); 
    previousChartId = currentChartId;
    
    // Select random chart
    while (currentChartId = ChartNext(previousChartId)) {
        if(currentChartId < 0) {
            break;
        }
        
        previousChartId = currentChartId;
        
        // Fill in selected chart data
        if (chartCount == randomChartIndex) {
            chosenChart.SymbolX = ChartSymbol(currentChartId);
            chosenChart.PeriodX = ChartPeriod(currentChartId);
            chosenChart.FileNameString = "DataHistory" + " " + chosenChart.SymbolX + " " + IntegerToString(CorrectPeriod(chosenChart.PeriodX));
        }
        
        if (chartCount > randomChartIndex) {
            break;
        }

        if (currentChartId != ChartID()) {
            chartCount++;
        }
    }
       
    return chosenChart;
}

このコードは、現在端末で開くことができるさまざまなチャートから、さまざまな通貨の過去の金融市場データ(クオート)を記録および分析するために使用されます。

• ChartData構造体は、ファイル名、銘柄（通貨ペア）、時間枠など、各チャートに関するデータを保存するために使用されます。 
• Randomindex(start, end)関数は、「start」と「end」の間の乱数を生成します。これは、使用可能なチャートの1つをランダムに選択するために使用されます。
• SelectAnyChart()は、現在のチャートを除く、開いている使用可能なすべてのチャートを反復処理し、そのうちの1つをランダムに選択して処理します。

生成されたクオートはプログラムによって自動的に取得され、その後、収益性の高い構成が自動的に検索されます。プロセス全体を自動化するのは非常に複雑ですが、それを1つの図に凝縮してみました。

図5

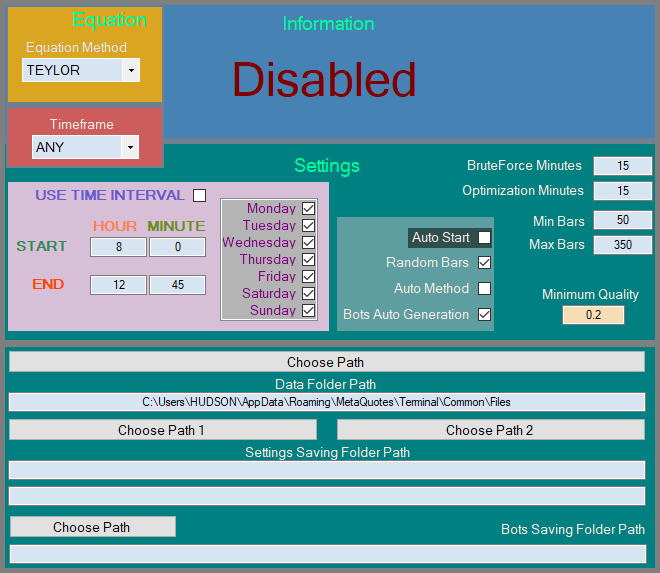
このアルゴリズムには3つの状態があります。

1. 無効
2. クオート待機
3. 有効

クオートを記録するためのEAがまだファイルを1つも生成していない場合、または指定されたフォルダーからすべてのクオートを削除した場合、アルゴリズムは単にファイルが表示されるのを待ち、しばらく停止します。MQL5スタイルで実装した改良された基準については、総当たり攻撃と最適化の両方に対しても実装されています。

図6

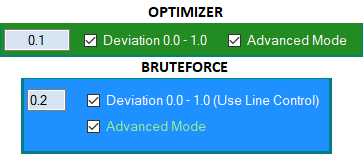
詳細モードは曲線ファミリー係数を操作しますが、標準アルゴリズムは直線性係数のみを使用します。残りの改善点は広範すぎるため、この記事には収まりません。次の記事では、汎用複数通貨テンプレートに基づいてアドバイザーを結合するための新しいアルゴリズムを紹介します。テンプレートは1つのチャート上で起動されますが、各EAを独自のチャート上で起動する必要なく、結合されたすべての取引システムを処理します。この記事では、その機能の一部が使用されています。

結論

この記事では、取引システムの開発と最適化のプロセスを自動化する分野における新しい機会とアイデアをより詳細に検討しました。主な成果は、新しい最適化アルゴリズムの開発、端末同期メカニズムと自動オプティマイザーの作成、そして重要な最適化基準である曲線係数と曲線群です。これにより、開発時間を短縮し、得られる結果の品質を向上させることができます。

重要な追加要素は、逆順期間のコンテキストでより現実的なバランスモデルを表す凹型曲線のファミリーです。各曲線適合係数を計算することで、自動取引に最適な設定をより正確に選択できるようになります。

リンク

• パターン検索への総当たり攻撃アプローチ（第V部）：新鮮な角度
  
• パターン検索への総当たり攻撃アプローチ（第IV部）：最低限の機能
• パターン検索への総当たり攻撃アプローチ（第III部）：新たな地平線
  
• パターン検索への総当たり攻撃アプローチ（第II部）：イマージョン
  
• パターン検索への総当たり攻撃アプローチ