MetaTrader 5 / 例
English Русский 中文 Español Deutsch Português
preview
ニューラルネットワークが簡単に

ニューラルネットワークが簡単に

MetaTrader 5 — 例 | 16 3月 2020, 11:40
3 072 0
Dmitriy Gizlyk
Dmitriy Gizlyk

目次

イントロダクション

人工知能は、生活のさまざまな側面で扱われています。 多くの新しい出版物が登場し、"ニューラルネットワークはトレーニングされています.."しかし、人工知能にはまだ可能性があります。 アイデアは複雑で、超自然的で不可解なようです。 したがって、このような最先端の奇跡は、科学者のグループによってのみ作成することができます。 類似プログラムは、家庭のPCを使用して開発することができないように思われています。 しかし、実はそれほど難しいものではありません。 ニューラルネットワークとは何か、そしてどのようにトレードに適用できるかを理解してみましょう。

1. AI ネットワーク構築の原則

Wikipedia では、次のニューラル ネットワーク定義が提供されています。

人工ニューラルネットワーク(ANN)は、動物の脳を構成する生物学的ニューラルネットワークに触発されたコンピューティングシステムです。 ANNは、人工ニューロンと呼ばれる接続されたユニットまたはノードのコレクションに基づいており、生物学的脳のニューロンをゆるやかにモデル化します。

つまり、ニューラルネットワークは人工ニューロンからなるエンティティであり、その中に組織化された関係があります。 これらの関係は、生物学的脳に似ています。

下図は、シンプルなニューラル ネットワーク図を示します。 ここで、円はニューロンを示し、線はニューロン間の接続を視覚化します。 ニューロンは、3つのグループに分かれている層に位置します。 青はインプットニューロンの層を示し、ソース情報のインプットを意味します。 緑と青は出力ニューロンであり、ニューラルネットワークの動作結果を出力します。 その間には、隠れ層を形成する灰色のニューロンがあります。 

シンプルなニューラル ネットワークの例

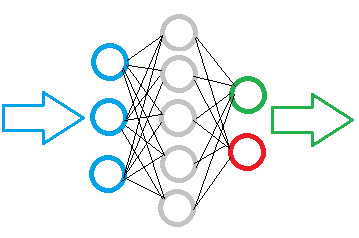
それにも関わらず、ネットワーク全体は、インプットシグナルの要素と結果の唯一の要素を持つ同じニューロンで構築されています。 インプットデータはニューロン内で処理され、シンプルな論理結果が出力されます。 たとえば、「はい」または「いいえ」の場合があります。 トレードに適用されると、結果はトレードシグナルとして、またはトレード方向として出力することができます。

ニューロン

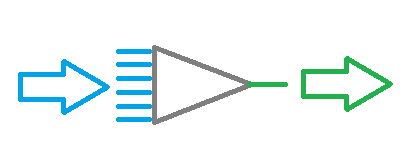
初期情報はインプットニューロン層にインプットされ、次に処理され、処理結果は次の層ニューロンのソース情報として機能します。 出力ニューロンの層に到達するまで、操作はある層から別の層に繰り返されます。 したがって、初期データは、あるレイヤーから別のレイヤーに処理およびフィルタリングされ、その後に結果が生成されます。

タスクの複雑さと作成されたモデルによって、各レイヤーのニューロンの数は異なる場合があります。 ネットワーク のバリエーションによっては、複数の非表示レイヤーが含まれる場合があります。 このような高度なニューラルネットワークは、より複雑な問題を解決することができます。 ただし、この場合、より多くの計算リソースが必要になります。

したがって、ニューラルネットワークモデルを作成する際には、処理するデータ量と目的の結果を定義する必要があります。 モデルレイヤー内の必要なニューロンの数に影響します。

10 個の要素のデータ配列をニューラル ネットワークにインプットする必要がある場合、インプットネットワーク層には 10 個のニューロンが含まれている必要があります。 これより、データ配列の 10 個の要素をすべて受け入れられます。 余分なインプットニューロンは過剰になります。

出力ニューロンの品質は、期待される結果によって決まります。 明確な論理結果を得るためには、1つの出力ニューロンで十分です。 複数の質問に対する回答を受け取りたい場合は、それぞれの質問に対して 1 つのニューロンを作成します。

非表示のレイヤーは、受信した情報を処理し、分析する分析センターとして機能します。 したがって、層内のニューロンの数は、前の層データの変動性、すなわち各ニューロンがイベントの特定の仮説を示唆するに依存します。

隠しレイヤーの数は、ソース データと予想される結果との因果関係によって決まります。 たとえば、5 why" 手法のモデルを作成する場合、論理的な解決策は 4 つの隠し層を使用する方法です。

要約:

  • ニューラルネットワークは同じニューロンで構築されているため、1つのクラスのニューロンでモデルを構築するのに十分です。
  • モデル内のニューロンは、層に編成されています。
  • ニューラルネットワークのデータフローは、インプットニューロンから出力ニューロンまで、モデルのすべての層を通じてシリアルデータ伝送として実装されています。
  • インプットニューロンの数は、1回のパスで分析されるデータの量に依存し、出力ニューロンが結果のデータ量に依存する場合は、その数によって異なります。
  • 出力で論理結果が形成されるため、ニューラルネットワークに与えられた質問は明確な答えを出す可能性を提供する必要があります。


2. 人工ニューロンの構造

ニューラルネットワーク構造を考えたので、人工ニューロンモデルの作成に移りましょう。 すべての数学的計算と意思決定は、このニューロン内で行われます。 ここで疑問が生じます。つまり、同じソースデータに基づいて、同じ式を使用して、多くの異なるソリューションをどのように実装できるでしょうか。 解決策は、ニューロン間の接続を変更することです。 各接続に対して加重係数が決定されます。 この加重によって、インプット値が結果に与える影響の度合いが設定されます。

ニューロンの数学的モデルは、2つの関数から構成されています。 インプットデータの積は、その重量係数で最初に集計されます。

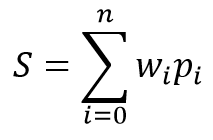
受け取った値に基づいて、結果はいわゆる活性化関数で計算されます。 実際には、異なる亜種の有効化関数が使用します。 最も頻繁に使用するものは次のとおりです。

  • シグモイド関数 — "0"から"1" までの戻り値の範囲
  • 双曲線正接 — "-1" から "1" までの戻り値の範囲 

活性化関数の選択は、解決される問題に依存します。 たとえば、ソース データ処理の結果として論理応答が予想される場合は、シグモイド関数が適します。 トレードには、ハイパボリックタンジェントを使用することが好ましいです。 値 "-1" は売りシグナルに対応し、"1" は買いシグナルに対応します。 中程度の結果は不確実性を示します。


3. ネットワークトレーニング

前述したように、各ニューロンとニューラルネットワーク全体の結果変動は、ニューロン間の接続に対して選択された加重に依存します。 加重選択の問題はニューラルネットワーク学習と呼ばれます。

ネットワークは、さまざまなアルゴリズムと方法に従ってトレーニングできます。

  • 教師あり学習;
  • 教師なし学習;
  • 強化学習

学習方法は、ソースデータとニューラルネットワーク用に設定されたタスクによって異なります。

教師付き学習は、提起された質問に対応する正解を持つ十分な初期データセットがある場合に使用します。 学習プロセス中に、初期データがネットワークにインプットされ、出力が既知の正解で検証されます。 その後、加重は、エラーを減らすために調整されます。

教師なし学習は、対応する正解のない初期データのセットがある場合に使用します。 この方法では、ニューラル ネットワークは類似のデータ セットを検索し、ソース データを同様のグループに分割できます。

強化学習は、正解がないときに使用しますが、望ましい結果を理解します。 学習プロセス中に、ソース データがネットワークにインプットされ、問題の解決が試みられます。 結果を確認した後、フィードバックは、特定の報酬として送信されます。 学習中に、ネットワークは最大の報酬を受け取ろうとします。

この記事では、教師あり学習を使用します。 例として、バックプロパゲーションアルゴリズムを使用します。 このアプローチにより、リアルタイムでの継続的なニューラルネットワークトレーニングが可能になります。

この方法は、その加重の補正の出力ニューラルネットワークエラーの使用に基づいています。 学習アルゴリズムは2つの段階から成ります。 まず、インプットデータに基づいてネットワークが結果の値を計算し、その結果を参照値で検証し、エラーが計算されます。 次に、ネットワーク出力からインプットへのエラーの伝搬とともに、すべての加重係数を調整して逆パスを実行します。 データのやり取り型のアプローチであり、ネットワークは段階的にトレーニングされます。 ヒストリーデータを使用して学習した後、ネットワークはオンラインモードでさらにトレーニングすることができます。

逆伝播法ではストキャスティクススロープ降下法を使用し、許容できる誤差の最小値に達します。 オンラインモードでネットワークをさらにトレーニングする可能性は、長い時間間隔にわたってこの最小レベルを維持することができます。

4. MQLを使って独自のニューラルネットワークを構築

では、この記事の実用的な部分に移りましょう。 ニューラルネットワーク(NN)操作をより良く視覚化するために、MQL5言語のみを使用して、サードパーティのライブラリを使用せずに例を作成します。 まず、ニューロン間の基本的なつながりに関するデータを格納するクラスを作成します。

4.1. コネクション

まず、1 つの接続の重み係数を格納する СConnection クラスを作成します。 CObject クラスの子として作成されます。 クラスには、ウェイトを格納する 「加重」と、直近のワイト変更の値を格納する deltaWeight という 2 つのダブル型変数が含まれます(学習で使用します)。 変数を操作するための追加のメソッドを使用する必要を回避するために、パブリックにしましょう。 変数の初期値はクラスコンストラクタで設定されます。 

class СConnection : public CObject
  {
public:
   double            weight;
   double            deltaWeight;
                     СConnection(double w) { weight=w; deltaWeight=0; }
                    ~СConnection(){};
   //--- methods for working with files
   virtual bool      Save(const int file_handle);
   virtual bool      Load(const int file_handle);
  };

接続に関する詳細情報の保存を有効にするには、ファイルにデータを保存する (保存) とこのデータを読み取る (読み込む) 方法を作成します。 このメソッドは、古典的なスキームに基づいています: ファイルハンドルは、メソッドパラメータで受信され、検証され、データが書き込まれます (または、読み取り、 Load メソッドで)。

bool СConnection::Save(const int file_handle)
  {
   if(file_handle==INVALID_HANDLE)
      return false;
//---
   if(FileWriteDouble(file_handle,weight)<=0)
      return false;
   if(FileWriteDouble(file_handle,deltaWeight)<=0)
      return false;
//---
   return true;
  }

次のステップでは、加重を格納する配列を作成します: CArrayObj に基づいて CArrayCon. ここでは、2 つの仮想メソッドをオーバーライドします。 最初の要素は新しい要素を作成するために使用され、2番目の要素はクラスを識別します。

class CArrayCon  :    public CArrayObj
  {
public:
                     CArrayCon(void){};
                    ~CArrayCon(void){};
   //---
   virtual bool      CreateElement(const int index);
   virtual int       Type(void) const { return(0x7781); }
   };

新しい要素を作成する CreateElement メソッドのパラメータでは、この新しい要素のインデックスを渡します。 メソッドの有効性を確認し、配列を格納するデータのサイズを確認し、必要に応じてサイズを変更します。 次に、ランダムな初期ウェイトを指定して、СConnection クラスの新しいインスタンスを作成します。

bool CArrayCon::CreateElement(const int index)
  {
   if(index<0)
      return false;
//---
   if(m_data_max<index+1)
     {
      if(ArrayResize(m_data,index+10)<=0)
         return false;
      m_data_max=ArraySize(m_data)-1;
     }
//---
   m_data[index]=new СConnection(MathRand()/32767.0);
   if(!CheckPointer(m_data[index])!=POINTER_INVALID)
      return false;
   m_data_total=MathMax(m_data_total,index);
//---
   return (true);
  }

4.2. ニューロン

次のステップは、人工ニューロンを作成することです。 先に述べたように、ニューロンの活性化関数として双曲線正接を使用します。 結果の値の範囲は "-1" "1" の間にあります。 "-1" は売りシグナルを示し、"1" は買いシグナルを意味します。

前の CConnection 要素と同様に、Cニューロンの人工ニューロン クラスは CObject クラスから継承されます。 しかし、その構造はもう少し複雑です。 

class CNeuron  :  public CObject
  {
public:
                     CNeuron(uint numOutputs,uint myIndex);
                    ~CNeuron() {};
   void              setOutputVal(double val) { outputVal=val; }
   double            getOutputVal() const { return outputVal; }
   void              feedForward(const CArrayObj *&prevLayer);
   void              calcOutputGradients(double targetVals);
   void              calcHiddenGradients(const CArrayObj *&nextLayer);
   void              updateInputWeights(CArrayObj *&prevLayer);
   //--- methods for working with files
   virtual bool      Save(const int file_handle)                         { return(outputWeights.Save(file_handle));   }
   virtual bool      Load(const int file_handle)                         { return(outputWeights.Load(file_handle));   }

private:
   double            eta;
   double            alpha;
   static double     activationFunction(double x);
   static double     activationFunctionDerivative(double x);
   double            sumDOW(const CArrayObj *&nextLayer) const;
   double            outputVal;
   CArrayCon         outputWeights;
   uint              m_myIndex;
   double            gradient;
  };

クラスコンストラクタパラメータでは、発信ニューロン接続数と、その層内のニューロンの序数を渡します(ニューロンの後の識別に使用します)。 メソッド本体で定数を設定し、受信したデータを保存し、送信接続の配列を作成します。

CNeuron::CNeuron(uint numOutputs, uint myIndex)  :  eta(0.15), // net learning rate
                                                    alpha(0.5) // momentum  
  {
   for(uint c=0; c<numOutputs; c++)
     {
      outputWeights.CreateElement(c);
     }

   m_myIndex=myIndex;
  }

setOutputVal メソッドと getOutputVal メソッドは、ニューロンの結果の値にアクセスするために使用します。 このニューロンの結果の値は、feedForward メソッドで計算されます。 ニューロンの前の層は、このメソッドのパラメータとしてインプットされます。

void CNeuron::feedForward(const CArrayObj *&prevLayer)
  {
   double sum=0.0;
   int total=prevLayer.Total();
   for(int n=0; n<total && !IsStopped(); n++)
     {
      CNeuron *temp=prevLayer.At(n);
      double val=temp.getOutputVal();
      if(val!=0)
        {
         СConnection *con=temp.outputWeights.At(m_myIndex);
         sum+=val * con.weight;
        }
     }
   outputVal=activationFunction(sum);
  }

メソッド本体には、以前のすべての層ニューロンを通るループがあります。 結果として得られるニューロン値と加重の積もメソッド本体で合計されます。 合計を計算した後、結果のニューロン値は activationFunction メソッドで計算されます (ニューロン活性化関数は別のメソッドのように実装されます)。

double CNeuron::activationFunction(double x)
  {
//output range [-1.0..1.0]
   return tanh(x);
  }

次のメソッドブロックは、NN学習で使用します。 アクティベーション関数の派生関数を計算するメソッドを作成します。 これより、結果として得られるニューロン値の誤差を補正するために、加算関数に必要な変更を決定することができます。

double CNeuron::activationFunctionDerivative(double x)
  {
   return 1/MathPow(cosh(x),2);
  }

次に、2 つのスロープ計算方法を作成して、加重調整を行います。 結果として得られる値の誤差は、出力層のニューロンと隠れ層のニューロンに対して異なる方法で計算されるため、2つのメソッドを作成する必要があります。 出力レイヤーの場合、エラーは結果値と参照値の差として計算されます。 隠れ層ニューロンの場合、誤差はニューロン間の接続の加重に基づいて加重付けされたトレーリングの層のすべてのニューロンのスロープの合計として計算されます。 この計算は、別の sumDOW メソッドとして実装されます。

void CNeuron::calcHiddenGradients(const CArrayObj *&nextLayer)
  {
   double dow=sumDOW(nextLayer);
   gradient=dow*CNeuron::activationFunctionDerivative(outputVal);
  }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CNeuron::calcOutputGradients(double targetVals)
  {
   double delta=targetVals-outputVal;
   gradient=delta*CNeuron::activationFunctionDerivative(outputVal);
  }

次に、このスロープは、そのエラーに活性化関数の派生関数を掛けることによって決定されます。

隠れ層のニューロンエラーを決定するsumDOWメソッドを、より詳細に考察します。 メソッドは、パラメータとしてニューロンの次の層へのポインタを受け取ります。 メソッド本体では、最初に'sum' の結果値をゼロに設定し、次の層のすべてのニューロンをループで実行し、ニューロンのスロープの積とその接続の加重を合計します。

double CNeuron::sumDOW(const CArrayObj *&nextLayer) const
  {
   double sum=0.0;
   int total=nextLayer.Total()-1;
   for(int n=0; n<total; n++)
     {
      СConnection *con=outputWeights.At(n);
      CNeuron *neuron=nextLayer.At(n);
      sum+=con.weight*neuron.gradient;
     }
   return sum;
  }

上記の準備タスクが完了したら、加重を再計算する updateInputWeights メソッドを作成するだけです。 今回のモデルでは、ニューロンは発信ウェイトを保存するので、ウェイト更新方法はパラメータでニューロンの前の層を受け取ります。

void CNeuron::updateInputWeights(CArrayObj *&prevLayer)
  {
   int total=prevLayer.Total();
   for(int n=0; n<total && !IsStopped(); n++)
     {
      CNeuron *neuron= prevLayer.At(n);
      СConnection *con=neuron.outputWeights.At(m_myIndex);
      con.weight+=con.deltaWeight=eta*neuron.getOutputVal()*gradient + alpha*con.deltaWeight;
     }
  }

メソッド本体には、前の層のすべてのニューロンを通るループが含まれています。

重量調整は、イータ(偏差への反応を減らすため)とアルファ(慣性係数)の2つの係数を使用して行われることに注意してください。 このアプローチにより、トレーリングの学習繰り返しの数の影響を一定の平均化し、ノイズデータを除外することができます。

4.3. ニューラルネットワーク

人工ニューロンを作成した後、作成オブジェクトを単一のエンティティ、ニューラルネットワークに組み合わせる必要があります。 結果として得られるオブジェクトは柔軟性を持ち、さまざまな構成のニューラル ネットワークを作成できるようにする必要があります。 これにより、さまざまなタスクに対して、結果として得られるソリューションを使用できるようになります。

前述のように、ニューラルネットワークはニューロンの層で構成されています。 したがって、最初のステップは、ニューロンを1つの層に結合することです。 CLayer クラスを作成しましょう。 その中の基本的なメソッドは、CArrayObjから継承されます。

class CLayer: public CArrayObj
  {
private:
   uint              iOutputs;
public:
                     CLayer(const int outputs=0) { iOutputs=outpus; };
                    ~CLayer(void){};
   //---
   virtual bool      CreateElement(const int index);
   virtual int       Type(void) const { return(0x7779); }
   };

CLayer クラス初期化メソッドのパラメータで、次のレイヤーの要素数を設定します。 また、CreateElement (レイヤーの新しいニューロンの作成) と Type (オブジェクト識別方法) の 2 つの仮想メソッドを書き直しましょう。

新しいニューロンを作成する場合は、メソッドパラメータでインデックスを指定します。 受け取ったインデックスの有効性は、メソッド本体でチェックされます。 次に、ニューロン オブジェクトインスタンスへのポインタを格納するための配列のサイズを確認し、必要に応じて配列のサイズを大きくします。 その後、ニューロンを作成します。 新しいニューロンインスタンスが正常に作成された場合は、初期値を設定し、配列内のオブジェクトの数を変更します。 次に、メソッドを 'true' で終了します。

bool CLayer::CreateElement(const uint index)
  {
   if(index<0)
      return false;
//---
   if(m_data_max<index+1)
     {
      if(ArrayResize(m_data,index+10)<=0)
         return false;
      m_data_max=ArraySize(m_data)-1;
     }
//---
   CNeuron *neuron=new CNeuron(iOutputs,index);
   if(!CheckPointer(neuron)!=POINTER_INVALID)
      return false;
   neuron.setOutputVal((neuronNum%3)-1)   
//---
   m_data[index]=neuron;
   m_data_total=MathMax(m_data_total,index);
//---
   return (true);
  }

同様のアプローチを使用して、ネットワークレイヤーへのポインタを格納するためのCArrayLayerクラスを作成します。

class CArrayLayer  :    public CArrayObj
  {
public:
                     CArrayLayer(void){};
                    ~CArrayLayer(void){};
   //---
   virtual bool      CreateElement(const uint neurons, const uint outputs);
   virtual int       Type(void) const { return(0x7780); }
   };

前のクラスとの差は、新しい配列要素を作成する CreateElement メソッドに表示されます。 このメソッドパラメータでは、作成する現在のレイヤーとさらにレイヤー内のニューロンの数を指定します。 メソッド本体で、レイヤー内のニューロンの数を確認します。 作成されたレイヤーにニューロンがない場合は、'false' で終了します。 次に、ポインタを格納する配列のサイズを変更する必要があるかどうかを確認します。 その後、オブジェクトインスタンスを作成することができます: 新しいレイヤーを作成し、ニューロンを作成するループを実装します。 各ステップで作成されたオブジェクトを確認します。 エラーの場合は、'false' 値を指定します。 すべての要素を作成した後、配列内の作成されたレイヤーへのポインタを保存し、'true' で終了します。

bool CArrayLayer::CreateElement(const uint neurons, const uint outputs)
  {
   if(neurons<=0)
      return false;
//---
   if(m_data_max<=m_data_total)
     {
      if(ArrayResize(m_data,m_data_total+10)<=0)
         return false;
      m_data_max=ArraySize(m_data)-1;
     }
//---
   CLayer *layer=new CLayer(outputs);
   if(!CheckPointer(layer)!=POINTER_INVALID)
      return false;
   for(uint i=0; i<neurons; i++)
      if(!layer.CreatElement(i))
         return false;
//---
   m_data[m_data_total]=layer;
   m_data_total++;
//---
   return (true);
  }

レイヤーとレイヤーの配列の別々のクラスの作成は、クラスを変更することなく、異なる構成を持つさまざまなニューラルネットワークの作成を可能にします。 これは、層ごとに所望の数の層とニューロンをインプットできる柔軟なエンティティです。

次に、ニューラルネットワークを作成するCNetクラスについて考えてみましょう。

class CNet
  {
public:
                     CNet(const CArrayInt *topology);
                    ~CNet(){};
   void              feedForward(const CArrayDouble *inputVals);
   void              backProp(const CArrayDouble *targetVals);
   void              getResults(CArrayDouble *&resultVals);
   double            getRecentAverageError() const { return recentAverageError; }
   bool              Save(const string file_name, double error, double undefine, double forecast, datetime time, bool common=true);
   bool              Load(const string file_name, double &error, double &undefine, double &forecast, datetime &time, bool common=true);
//---
   static double     recentAverageSmoothingFactor;
private:
   CArrayLayer       layers;
   double            recentAverageError;
  };

すでに上記のクラスで多くの必要なタスクを実装しているため、ニューラルネットワーククラス自体には最小限の変数とメソッドがあります。 クラスコードには、平均誤差を計算して格納するための統計変数が2つだけ(recentAverageSmoothingFactorとrecentAverageError)と、ネットワーク層を含む「レイヤー」配列へのポインタがあります。

このクラスのメソッドについて詳しく考えてみましょう。 int データ配列へのポインタは、クラス コンストラクタのパラメータに渡されます。 配列内の要素の数はレイヤー数を示し、配列の各要素には適切な層のニューロンの数が含まれます。 したがって、このユニバーサルクラスは、任意の複雑度レベルのニューラルネットワークを作成するために使用することができます。

CNet::CNet(const CArrayInt *topology)
  {
   if(CheckPointer(topology)==POINTER_INVALID)
      return;
//---
   int numLayers=topology.Total();
   for(int layerNum=0; layerNum<numLayers; layerNum++) 
     {
      uint numOutputs=(layerNum==numLayers-1 ? 0 : topology.At(layerNum+1));
      if(!layers.CreateElement(topology.At(layerNum), numOutputs))
         return;
     }
  }

メソッド本体で、渡されたポインタの有効性を確認し、ニューラルネットワーク内にレイヤを作成するループを実装します。 出力レベルには、発信接続のゼロ値が指定されます。

feedForward メソッドは、ニューラル ネットワーク値の計算に使用します。 このパラメータでは、ニューラル ネットワークの結果の値が計算されるインプット値の配列を受け取ります。

void CNet::feedForward(const CArrayDouble *inputVals)
  {
   if(CheckPointer(inputVals)==POINTER_INVALID)
      return;
//---
   CLayer *Layer=layers.At(0);
   if(CheckPointer(Layer)==POINTER_INVALID)
     {
      return;
     }
   int total=inputVals.Total();
   if(total!=Layer.Total()-1)
      return;
//---
   for(int i=0; i<total && !IsStopped(); i++) 
     {
      CNeuron *neuron=Layer.At(i);
      neuron.setOutputVal(inputVals.At(i));
     }
//---
   total=layers.Total();
   for(int layerNum=1; layerNum<total && !IsStopped(); layerNum++) 
     {
      CArrayObj *prevLayer = layers.At(layerNum - 1);
      CArrayObj *currLayer = layers.At(layerNum);
      int t=currLayer.Total()-1;
      for(int n=0; n<t && !IsStopped(); n++) 
        {
         CNeuron *neuron=currLayer.At(n);
         neuron.feedForward(prevLayer);
        }
     }
  }

メソッド本体で、受信ポインタとネットワークのゼロ層の有効性を確認します。 次に、受信した初期値をゼロ層ニューロンの結果値として設定し、第1の隠れ層から出力ニューロンまで、ニューラルネットワーク全体のニューロンの結果値を段階的に再計算して二重ループを実装します。

この結果は、出力層のニューロンから結果の値を収集するループを含む getResults メソッドを使用して取得されます。

void CNet::getResults(CArrayDouble *&resultVals)
  {
   if(CheckPointer(resultVals)==POINTER_INVALID)
     {
      resultVals=new CArrayDouble();
     }
   resultVals.Clear();
   CArrayObj *Layer=layers.At(layers.Total()-1);
   if(CheckPointer(Layer)==POINTER_INVALID)
     {
      return;
     }
   int total=Layer.Total()-1;
   for(int n=0; n<total; n++)
     {
      CNeuron *neuron=Layer.At(n);
      resultVals.Add(neuron.getOutputVal());
     }
  }

ニューラルネットワーク学習プロセスは、backPropメソッドで実装されています。 このメソッドは、パラメータ内の参照値の配列を受け取ります。 このメソッド本体で、受信した配列の有効性を確認し、結果の層の平均２乗誤差を計算します。 次に、ループ内で、すべての層のニューロンのスロープを再計算します。 その後、直近のメソッドレイヤーで、以前に計算されたスロープに基づいてニューロン間の接続の加重を更新します。

void CNet::backProp(const CArrayDouble *targetVals)
  {
   if(CheckPointer(targetVals)==POINTER_INVALID)
      return;
   CArrayObj *outputLayer=layers.At(layers.Total()-1);
   if(CheckPointer(outputLayer)==POINTER_INVALID)
      return;
//---
   double error=0.0;
   int total=outputLayer.Total()-1;
   for(int n=0; n<total && !IsStopped(); n++)
     {
      CNeuron *neuron=outputLayer.At(n);
      double delta=targetVals[n]-neuron.getOutputVal();
      error+=delta*delta;
     }
   error/= total;
   error = sqrt(error);

   recentAverageError+=(error-recentAverageError)/recentAverageSmoothingFactor;
//---
   for(int n=0; n<total && !IsStopped(); n++)
     {
      CNeuron *neuron=outputLayer.At(n);
      neuron.calcOutputGradients(targetVals.At(n));
     }
//---
   for(int layerNum=layers.Total()-2; layerNum>0; layerNum--)
     {
      CArrayObj *hiddenLayer=layers.At(layerNum);
      CArrayObj *nextLayer=layers.At(layerNum+1);
      total=hiddenLayer.Total();
      for(int n=0; n<total && !IsStopped();++n)
        {
         CNeuron *neuron=hiddenLayer.At(n);
         neuron.calcHiddenGradients(nextLayer);
        }
     }
//---
   for(int layerNum=layers.Total()-1; layerNum>0; layerNum--)
     {
      CArrayObj *layer=layers.At(layerNum);
      CArrayObj *prevLayer=layers.At(layerNum-1);
      total=layer.Total()-1;
      for(int n=0; n<total && !IsStopped(); n++)
        {
         CNeuron *neuron=layer.At(n);
         neuron.updateInputWeights(prevLayer);
        }
     }
  }

プログラムの再起動時にシステムを再トレーニングする必要がないように、ローカルファイルにデータを保存するための'Save'メソッドと、保存されたデータをファイルからロードするための'Load'メソッドを作成しましょう。

すべてのクラス メソッドは、添付ファイルで使用できます。

結論

この記事の目的は、自宅でニューラル ネットワークを作成する方法を示すためにありました。 もちろん、これは氷山の一角に過ぎません。 この記事では、1957年にフランク・ローゼンブラットによって導入されたパーセプトロンというバージョンの1つです。 モデル導入から60年以上が経過し、他にも様々なモデルが登場しています。 しかし、パーセプトロンモデルは依然として実行可能であり、良い結果を生成します- 自分でモデルをテストすることができます。 人工知能のアイデアに深く入りたい人は、一連の記事でもすべてをカバーすることは不可能であるため、関連する記事を読む必要があります。

レファレンス

  1. Wikipedia
  2. パーセプトロン(ロシア語)

この記事で使用するプログラム

# 名前 タイプ 詳細
1 NeuroNet.mqh クラスライブラリ ニューラルネットワーク(パーセプトロン)を作成するためのクラスのライブラリ


MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/7447

添付されたファイル |
ZIPをダウンロード
NeuroNet.mqh (38.34 KB)
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動
MetaTraderプログラムを簡単かつ迅速に開発するためのライブラリ(第24部): 未決取引リクエストの使用 - リクエストオブジェクトクラス MetaTraderプログラムを簡単かつ迅速に開発するためのライブラリ(第24部): 未決取引リクエストの使用 - リクエストオブジェクトクラス
前の記事では、保留中取引リクエストの概念を確認しました。保留中リクエストは、実際には、特定の条件によって実行される一般的な取引注文です。本稿では、保留中リクエストオブジェクトの完全なクラス(基本リクエストオブジェクトとその子孫)を作成します。
MetaTraderプログラムを簡単かつ迅速に開発するためのライブラリ(第28部): 指値取引リクエストの決済、削除、変更 MetaTraderプログラムを簡単かつ迅速に開発するためのライブラリ(第28部): 指値取引リクエストの決済、削除、変更
これは、保留中リクエストの概念に関する3番目の記事です。ここでは、ポジションの決済、指値注文の削除、ポジションと指値注文パラメータの変更のためのメソッドを作成することにより、指値取引リクエストのテストを完了します。
連続ウォークフォワード最適化(パート3):ロボットをオートオプティマイザに適応させる 連続ウォークフォワード最適化(パート3):ロボットをオートオプティマイザに適応させる
3番目であるこの記事は、前の 2 つの記事間のブリッジとして機能します。最初の記事で検討されている.dll との相互作用のメカニズムと、2 番目の記事で説明したレポートダウンロード用のオブジェクトについて説明します。 DLLからインポートし、トレードヒストリーを持つXMLファイルを形成するクラスのラッパ作成のプロセスを分析します。 このラッパとデータのやり取りするメソッドも検討します。
MetaTraderプログラムを簡単かつ迅速に開発するためのライブラリ(第27部): 取引リクエストの使用 - 指値注文 MetaTraderプログラムを簡単かつ迅速に開発するためのライブラリ(第27部): 取引リクエストの使用 - 指値注文
この記事では、取引リクエストの開発を継続し、指値注文の発注を実装し、検出された取引クラス使用の欠点を排除します。