
キャンバスクラスの学習。アンチエイリアスと影
目次
イントロダクション
Canvasクラスで描画するときに様々な動的効果を表示することが可能です。例えば、アンチエイリアシングアルゴリズムによってグラフィック構成を実装すると、より魅力的な外観になります。またはスプラインと呼ばれるインジケータラインを表示するメソッドもあります。あるいは、オシロスコープで周波数特性を描き、ダイナミックなインジケータを描画することもできます。いずれの場合も、描画は個人的な開発に新鮮さをもたらします。
1. 座標とキャンバス
キャンバスはグラフ座標で構築されています。この場合、グラフのサイズはピクセル単位で測定されます。チャートの左上隅が、座標(0,0)を有しています。
キャンバス上に描画するとき、着色されたプリミティブの座標が int型で独占的に与えられていることに注意してください。そして、アンチエイリアシング法 PixelSetAAを使用してプリミティブを描画する座標はdouble、 CircleAAメソッドで座標に与えられている int、および円の大きさdouble。
| メソッド | 座標 | サイズ |
|---|---|---|
| PixelSetAA | double | - |
| LineAA | int | - |
| PolylineAA | int | - |
| PolygonAA | int | - |
| TriangleAA | int | - |
| CircleAA | int | double |
PixelSetAAメソッドの座標は、(120.3、25.56)と同様とすることができます。 PixelSetAA.mq5スクリプトは、11点の2列を描画します。左側の列で、 X 軸方向に0.1ポイントの増分で、 Y軸は3.0です。右側の X 軸方向の各ポイントの増分は0.1で、 Y軸の増分は3.1です。
これらが描画されているかを確認するために、 PixelSetAA.mq5スクリプトにズームインしました。
![]()
図1。PixelSetAAメソッド操作
より良い外観のためのアンチエイリアシングおよび描画用の座標を持つテキストの境界線を追加しました:
![]()
図2。PixelSetAA法のビジュアル操作
ご覧の通り、ピクセルは座標で与えられた色で着色されています。点が座標の1つを有する場合は、異なる色の彩度(左カラム)を使用して二つの画素で描画されます。
ポイントの両方の座標は小数で与えられている例では、様々な色の彩度(右欄)を持つ3ピクセルで描画されます。様々な色の彩度を有するこの図は、平滑化効果をもたらします。
2. アンチエイリアシングアルゴリズム
アンチエイリアシングとプリミティブを描画キャンバスクラスのメソッドは、ポイントのカラー方式の一般的な計算を使用する PixelSetAA画面上に表示します。
| メソッド | 画像演算の最終的なメソッド |
|---|---|
| PixelSetAA | PixelSetAA |
| LineAA | PixelSetAA |
| PolylineAA | LineAA -> PixelSetAA |
| PolygonAA | LineAA -> PixelSetAA |
| TriangleAA | LineAA -> PixelSetAA |
| CircleAA | PixelSetAA |
アンチエイリアシングと描画メソッド PixieSetのデモンストレーションは、図1で確認できます。
アンチエイリアシングで描画する際、 PixieSetAAメソッドは、Canvasクラスのベースとして作用します。したがって、アンチエイリアシングアルゴリズムが正確に実装されているメソッドは興味深いものになると信じています。
PixelSetAAメソッドの座標 X と Y はdouble型です。 PixelSetAAメソッドは 画素の間に位置することができます。:
//+------------------------------------------------------------------+ //|アンチエイリアスとピクセルを描画します| //+------------------------------------------------------------------+ void CCanvas::PixelSetAA(const double x,const double y,const uint clr) {
次に、3つの配列を宣言します。rr[]配列は、仮想ピクセル(描画可能)の物理的なピクセルをカバーする、計算の補助配列です。配列xx[]と yy[]は、画像の平滑化効果を与えるピクセルを描画するために使用される座標の配列です。
void CCanvas::PixelSetAA(const double x,const double y,const uint clr) { static double rr[4]; static int xx[4]; static int yy[4];
以下の図は、仮想ピクセルと物理ピクセルのカバレッジと接続を示しています。
![]()
図3。物理的なピクセルのカバレッジ
仮想ピクセル(計算された座標)が、頻繁分率座標を有しており、4つの物理ピクセルを同時にカバーすることができることを意味します。この場合、アンチエイリアシングアルゴリズムは、その主な任務を実行するために必要とします。このように、それはの見た目をだまします。 - 人間の目にとって穏やかな配色と少しぼやけた画像が表示されます。
次のブロックは、予備的な計算が含まれています。最も近い整数に丸め、座標の値を取得します。
static int yy[4]; //---試算 int ix=(int)MathRound(x); int iy=(int)MathRound(y);
より深く理解するため、数学関数 MathRoundで、このコードを実行することをお勧めします(四捨五入します)
void OnStart() { Print("MathRound(3.2)=",DoubleToString(MathRound(3.2),8),"; (int)MathRound(3.2)=",IntegerToString((int)MathRound(3.2))); Print("MathRound(3.5)=",DoubleToString(MathRound(3.5),8),"; (int)MathRound(3.5)=",IntegerToString((int)MathRound(3.5))); Print("MathRound(3.8)=",DoubleToString(MathRound(3.8),8),"; (int)MathRound(3.8)=",IntegerToString((int)MathRound(3.8))); } //+------------------------------------------------------------------+
実行結果
MathRound(3.8)=4.00000000; (int)MathRound(3.8)=4 MathRound(3.5)=4.00000000; (int)MathRound(3.5)=4 MathRound(3.2)=3.00000000; (int)MathRound(3.2)=3
Followed by the calculation of dx and dy delta — difference between incoming coordinates x and y and their rounded values ix and iy:
int iy=(int)MathRound(y); double rrr=0; double k; double dx=x-ix; double dy=y-iy;
dxとdyがゼロかどうか確認する必要があります。その後、 PixelSetAAメソッドを終了します。
double dy=y-iy; uchar a,r,g,b; uint c; //---アンチエイリアシングに必要はありません if(dx==0.0 && dy==0.0) { PixelSet(ix,iy,clr); return; }
デルタがゼロに等しくないなら、画素配列の準備を進めます。
PixelSet(ix,iy,clr); return; } //---ピクセルの配列を準備 xx[0]=xx[2]=ix; yy[0]=yy[1]=iy; if(dx<0.0) xx[1]=xx[3]=ix-1; if(dx==0.0) xx[1]=xx[3]=ix; if(dx>0.0) xx[1]=xx[3]=ix+1; if(dy<0.0) yy[2]=yy[2]=iy-1; if(dy==0.0) yy[2]=yy[2]=iy; if(dy>0.0) yy[2]=yy[2]=iy+1;
このブロックは、具体的には、平滑化画像の錯覚のための基礎になります。
PrepareArrayPixels.mq5スクリプトを書き、それがどのように動作するかをビデオを記録し、このブロックの動作を可視化します。
ビデオ1。PrepareArrayPixels.mq5スクリプトの動作
画素配列が充填された後、「重み」は、仮想画素が実画素をカバーしないメソッドを確認するために計算されます。
yy[2]=yy[2]=iy+1; //---計算半径及びそれらの二乗和 for(int i=0;i<4;i++) { dx=xx[i]-x; dy=yy[i]-y; rr[i]=1/(dx*dx+dy*dy); rrr+=rr[i]; }
最後のステップは - ぼかしを描きます:
rrr+=rr[i];
}
//---ドローピクセル
for(int i=0;i<4;i++)
{
k=rr[i]/rrr;
c=PixelGet(xx[i],yy[i]);
a=(uchar)(k*GETRGBA(clr)+(1-k)*GETRGBA(c));
r=(uchar)(k*GETRGBR(clr)+(1-k)*GETRGBR(c));
g=(uchar)(k*GETRGBG(clr)+(1-k)*GETRGBG(c));
b=(uchar)(k*GETRGBB(clr)+(1-k)*GETRGBB(c));
PixelSet(xx[i],yy[i],ARGB(a,r,g,b));
}
3. オブジェクトの影
影を描画すると、このようにマイナーなボリューム効果を作成し、グラフィックオブジェクトによりソフトな輪郭のアウトラインを与えるので、グラフィックオブジェクトは、フラットに見えなくなります。また、影の効果は非常に興味深く、有益な特性を持っています:通常のオブジェクトの影が透明であり、かつ追加のボリュームが作成されます。
影の最も一般的なタイプを以下に示します。
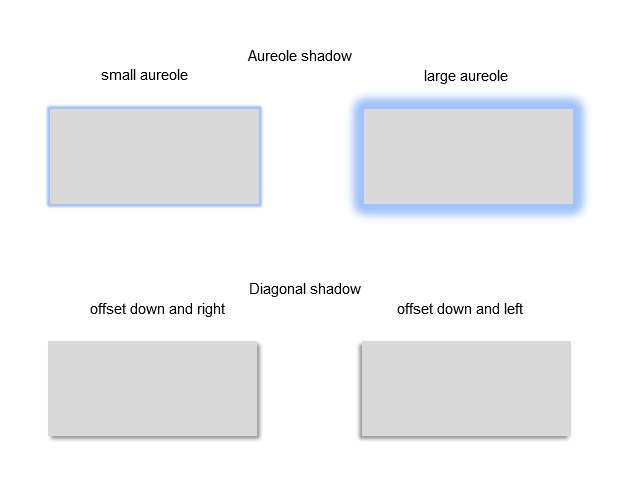
図4。影の種類
「aureole」影の幅を設定することができます。「外部対角線」の影はシフトしている角度の設定を有することができます。両方のタイプには、色選択の設定があります。
影の描画に関連するアルゴリズムを選択するために、影で構成されないかを確認しなければなりません。画像内の便利なズームの出番です。画像4で非常に近い検査を参照してください:
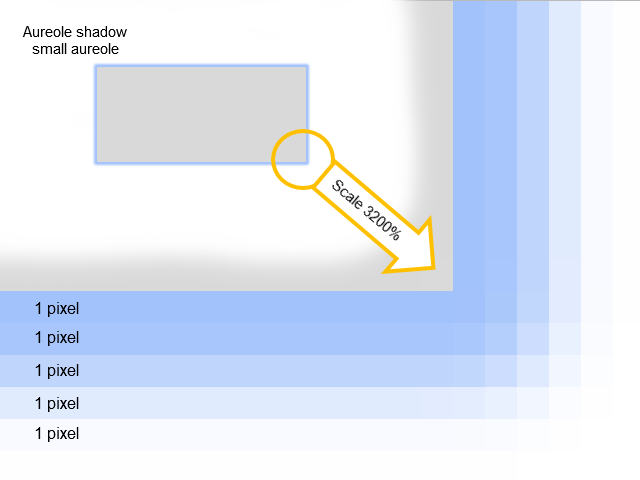
図5。どのような影が構成されているか
"aureole"影が1ピクセル幅のいくつかのアウトラインから構築されていることが明らかになりました。これらのアウトラインは色の緩やかな変化があります。
ガウスぼかし(ガウスぼかしアルゴリズムに関する情報は以下に提供します)- 影を描画する際に、最も一般的なグラフィックフィルタを使用しようとしています。画像のすべてのピクセルに適用される変換を計算する際に、このフィルタは正規分布を使用しています。画像の各画素のぼかし計算は、(パラメータはフィルタを使用する前に与えられている)、すべての周辺画素に十分配慮して行われる必要があります。
実際のぼけの半径が言及されたという事実にもかかわらず、ピクセルグリッドN×N個の計算に使用されます。
![]()
ここで、Radiusはぼかし半径です。
下図は、3に等しいぼかし半径ピクセルグリッドの例を示しています。
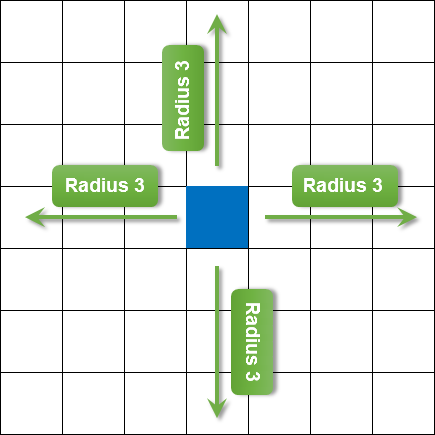
図6。ぼかし半径
このフィルタの高速計算理論は今回は扱いません。ガウスフィルタの分離特性が使用されることだけ言及します: X 軸に沿ってぼかし適用し、 Y軸に進みます。これで、品質に影響を与えることなく、より高速な計算を行うことができます。
計算された画素に隣接する画素の影響に正規分布を使用しています。画素が算出された画素から、さらに下位に効果があります。ガウスのアルゴリズムによって正規分布を計算するために、数値解析ライブラリALGLIBを使用します。 GQGenerateRecToExel.mq5スクリプトは、正規分布のモデリングを実証するのに役立ちます。 ALGLIBライブラリスクリプトは、正規分布の係数を計量の配列を受け取り、ファイル<data catalogue>\MQL5\Files\GQGenerateRecToExel.csv.にこれらの値を表示します。GQGenerateRecToExel.csvファイルデータに基づいて構築されたチャートがどのように見えるかを表したものです:
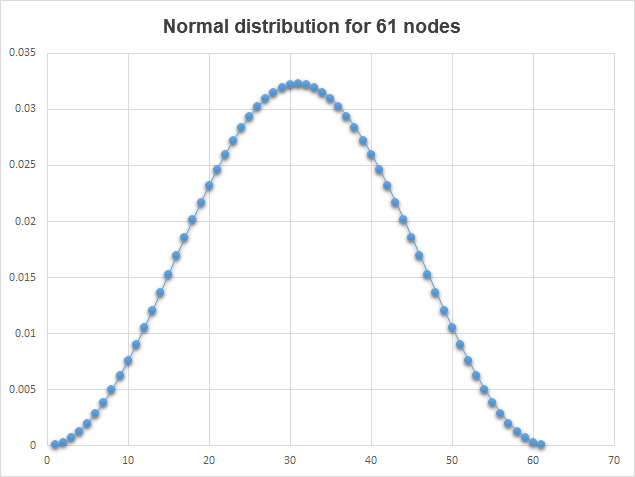
図7. 正規分布
例として、 GQGenerateRecToExel.mq5スクリプトを使用して、正規分布の重み係数の配列の取得をチェックします。同じ GetQuadratureWeights関数はこれ以降のスクリプトで使用します。
//+------------------------------------------------------------------+ //||直交の重みの配列を取得します //+------------------------------------------------------------------+ bool GetQuadratureWeights(const double mu0,const int n,double &w[]) { CAlglib alglib; //クラスAlglibの静的メンバ double alp[]; //配列のアルファ係数 double bet[]; //配列のベータ係数 ArrayResize(alp,n); ArrayResize(bet,n); ArrayInitialize(alp,1.0); //数値配列アルファを初期化 ArrayInitialize(bet,1.0); //数値配列のベータ版を初期化 double out_x[]; int inf=0; //| Info - error code: | //||*-3内部固有値問題ソルバー //|収束| //| * -2 Beta[i]<=0 | //|*-1間違ったN渡されました| //| * 1 OK | alglib.GQGenerateRec(alp,bet,mu0,n,inf,out_x,w); if(inf!=1) { Print("Call error in CGaussQ::GQGenerateRec"); return(false); } return(true); }
この関数は、w[]配列の正規分布の係数を計量し、inf変数の分析を通じて、 ALGLIBライブラリ関数を呼び出した結果をチェックします。
リソースとキャンバス、影を描画するときに(ResourceReadImage)グラフィカルなリソースからデータを読み取り、このデータを持つ配列を充填します。
リソースの操作中に、画素配列はuint形式で保存されていることに注意を払う必要があります(: ARGBカラー表現)。また、1次元配列に変換する、2Dの幅と高さのイメージ知っている必要があります。長い行の画像の行:変換アルゴリズムは以下の通りです。下の図は、4×3画素、1次元配列に変換された3×4ピクセルの2つの画像を示しています:
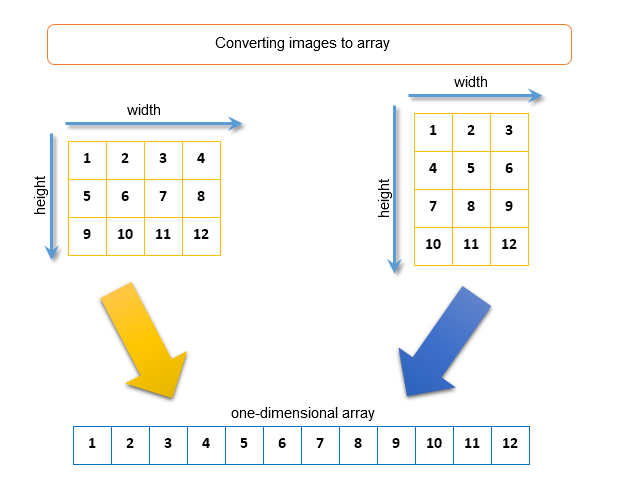
図8。一次元配列に画像を変換します
4. ガウスのぼかしアルゴリズムの例
ガウスぼかしは、 ShadowPLayers.mq5アルゴリズムを適用します。2つのファイルCanvas.mqh、数値解析ライブラリALGLIBスクリプトが必要とされます。
#property script_show_inputs #include <Canvas\Canvas.mqh> #include <Math\Alglib\alglib.mqh>
Input parameters:
//--- input input uint radius=4; // radius blur input color clrShadow=clrBlack; // shadow color input uchar ShadowTransparence=160; // transparency shadows input int ShadowShift=3; // shadow shift input color clrDraw=clrBlue; // shadow color input uchar DrawwTransparence=255; // transparency draws //---
2つのキャンバスを作成します。下のキャンバスは、影の描画に使用される層の関数を実行し、上のキャンバスはグラフィック図形を描画する作業レイヤーとして機能します。これらの例はドキュメント・セクションで利用できますので、両方のキャンバスのサイズは、ここで指定されていないチャートを取得するための関数に等しいですチャートでの作業):
//---キャンバスを作成します CCanvas CanvasShadow; CCanvas CanvasDraw; if(!CanvasShadow.CreateBitmapLabel("ShadowLayer",0,0,ChartWidth, ChartHeight,COLOR_FORMAT_ARGB_NORMALIZE)) { Print("Error creating canvas: ",GetLastError()); return; } if(!CanvasDraw.CreateBitmapLabel("DrawLayer",0,0,ChartWidth ,ChartHeight,COLOR_FORMAT_ARGB_NORMALIZE)) { Print("Error creating canvas: ",GetLastError()); return; }
それでは、少しキャンバス上に描画してみましょう。まず、影の数字のワークピースが低いキャンバス(影がデフォルトで透明に描かれている)を描画し、その後、上部のキャンバス上に四角形を描画します。
//---キャンバス上の描画 CanvasShadow.Erase(ColorToARGB(clrNONE,0)); CanvasShadow.FillRectangle(ChartWidth/10,ChartHeight/10, ChartWidth/2-ChartWidth/10,ChartHeight/10*9,ColorToARGB(clrShadow,ShadowTransparence)); CanvasShadow.FillRectangle(ChartWidth/2,ChartHeight/12,ChartWidth/3*2, ChartHeight/2,ColorToARGB(clrShadow,ShadowTransparence)); CanvasShadow.Update(); CanvasDraw.Erase(ColorToARGB(clrNONE,0)); CanvasDraw.FillRectangle(ChartWidth/10-ShadowShift,ChartHeight/10-ShadowShift,ChartWidth/2-ChartWidth/10-ShadowShift, ChartHeight/10*9-ShadowShift,ColorToARGB(clrDraw,DrawwTransparence)); CanvasDraw.Update();
以下の画像を取得する必要があります(注意:長方形の「影」はまだぼやけていません):
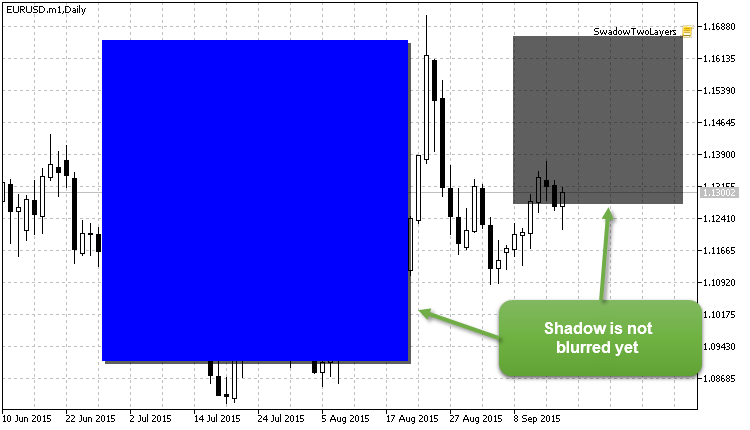
図9。影はまだ、ぼかされていません
下のキャンバス上でぼかしが実行されます(CanvasShadow)。この目的のため、データを読み込む必要があります( ResourceReadImage)、キャンバスのグラフィックリソース( CanvasShadow。 ResourceNameの())、データを持つ1次元配列(res_data)):
//+------------------------------------------------------------------+ //||グラフィック・リソースからデータを読み出し //+------------------------------------------------------------------+ ResetLastError(); if(!ResourceReadImage(CanvasShadow.ResourceName(),res_data,res_width,res_height)) { Print("Error reading data from the graphical resource ",GetLastError()); Print("attempt number two"); //--- 試行番号2:画像の幅と高さが分かっています ResetLastError(); if(!ResourceReadImage(CanvasShadow.ResourceName(),res_data,res_width,res_height)) { Print("Error reading data from the graphical resource ",GetLastError()); return; } }
アルファ、赤、緑、青:次のステップでは、 GetQuadratureWeights関数を使用して、正規分布の係数を計量し、4つの配列に1次元配列を分解する配列を取得します。グラフィック効果は、各色の成分に適用されなければならないため、色の分解が主に必要とされます。
//+------------------------------------------------------------------+ //|R、G、Bの画像の分解| //+------------------------------------------------------------------+ ... if(!GetQuadratureWeights(1,NNodes,weights)) return; for(int i=0;i<size;i++) { clr_temp=res_data[i]; a_data[i]=GETRGBA(clr_temp); r_data[i]=GETRGBR(clr_temp); g_data[i]=GETRGBG(clr_temp); b_data[i]=GETRGBB(clr_temp); }
次のセクションは、ぼかし"マジック"です。最初に、画像が沿ってぼかされるX軸、 Y軸に沿って同じプロセスが続きます。このアプローチは、品質を損なうことなく、計算を高速化することができます。 X 軸に沿ってぼかしの例を見てみましょう:
//+------------------------------------------------------------------+ //||水平方向(軸X)をぼかします //+------------------------------------------------------------------+ uint XY; //ピクセル配列内の座標 double a_temp=0.0,r_temp=0.0,g_temp=0.0,b_temp=0.0; int coef=0; int j=(int)radius; for(uint Y=0;Y<res_height;Y++) // 画像の幅にサイクル { for(uint X=radius;X<res_width-radius;X++) //画像の高さのサイクル { XY=Y*res_width+X; a_temp=0.0; r_temp=0.0; g_temp=0.0; b_temp=0.0; coef=0; for(int i=-1*j;i<j+1;i=i+1) { a_temp+=a_data[XY+i]*weights[coef]; r_temp+=r_data[XY+i]*weights[coef]; g_temp+=g_data[XY+i]*weights[coef]; b_temp+=b_data[XY+i]*weights[coef]; coef++; } a_data[XY]=(uchar)MathRound(a_temp); r_data[XY]=(uchar)MathRound(r_temp); g_data[XY]=(uchar)MathRound(g_temp); b_data[XY]=(uchar)MathRound(b_temp); } //---左のアーチファクトを除去 for(uint x=0;x<radius;x++) { XY=Y*res_width+x; a_data[XY]=a_data[Y*res_width+radius]; r_data[XY]=r_data[Y*res_width+radius]; g_data[XY]=g_data[Y*res_width+radius]; b_data[XY]=b_data[Y*res_width+radius]; } //---右側のアーチファクトを除去 for(uint x=res_width-radius;x<res_width;x++) { XY=Y*res_width+x; a_data[XY]=a_data[(Y+1)*res_width-radius-1]; r_data[XY]=r_data[(Y+1)*res_width-radius-1]; g_data[XY]=g_data[(Y+1)*res_width-radius-1]; b_data[XY]=b_data[(Y+1)*res_width-radius-1]; } }
よって、2つのネストされたループを参照してください。
for(uint Y=0;Y<res_height;Y++) // 画像の幅にサイクル { for(uint X=radius;X<res_width-radius;X++) //画像の高さのサイクル { ... } }
このネストは、画像の各画素を通るパスを確保します:
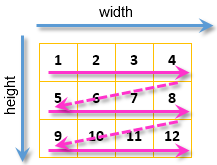
図10。画像の各画素のパス
ネストされたループは、各画素ごとにX 軸に沿ってぼかしの計算します。
for(uint X=radius;X<res_width-radius;X++) //画像の高さのサイクル { XY=Y*res_width+X; a_temp=0.0; r_temp=0.0; g_temp=0.0; b_temp=0.0; coef=0; for(int i=-1*j;i<j+1;i=i+1) { a_temp+=a_data[XY+i]*weights[coef]; r_temp+=r_data[XY+i]*weights[coef]; g_temp+=g_data[XY+i]*weights[coef]; b_temp+=b_data[XY+i]*weights[coef]; coef++; } a_data[XY]=(uchar)MathRound(a_temp); r_data[XY]=(uchar)MathRound(r_temp); g_data[XY]=(uchar)MathRound(g_temp); b_data[XY]=(uchar)MathRound(b_temp); }
ぼかし半径に等しい補助的ピクセルは、左側の画素毎に、右に選択されています。以前、正規分布の重み係数の配列を取得するには、GetQuadratureWeights関数を使用しました。次の互換性が得られます:左側のピクセルの数+ぼかしの計算に必要なピクセル+右側の重み係数の配列要素=重み付け係数の要素の配列の数。この方法は、各隣接した画素が重み付け係数の配列の特定の値に相当します。
ぼかしを各色毎に算出するメソッドです:すべての隣接する画素は、それに対応する重み係数が乗算され、そして得られた値をまとめます。半径のぼかしが4に等しい、赤い画像を計算するには、以下のようにします:
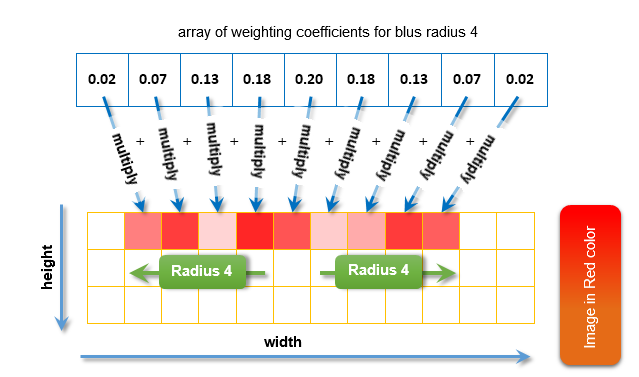
図11。ぼかしの計算
ぼかしアルゴリズムを適用するときにぼやけていなかったピクセルのストライプは、画像のエッジに沿って残ります。これらのストライプの幅は、ぼかし半径に等しいです。ぼかし半径が大きいほど、ぼやけされなかった画素のストライプがあります。アルゴリズムでは、これらのアーティファクトは、ぼやけたピクセルをコピーすることによって削除されます。
//---左のアーチファクトを除去 for(uint x=0;x<radius;x++) { XY=Y*res_width+x; a_data[XY]=a_data[Y*res_width+radius]; r_data[XY]=r_data[Y*res_width+radius]; g_data[XY]=g_data[Y*res_width+radius]; b_data[XY]=b_data[Y*res_width+radius]; } //---右側のアーチファクトを除去 for(uint x=res_width-radius;x<res_width;x++) { XY=Y*res_width+x; a_data[XY]=a_data[(Y+1)*res_width-radius-1]; r_data[XY]=r_data[(Y+1)*res_width-radius-1]; g_data[XY]=g_data[(Y+1)*res_width-radius-1]; b_data[XY]=b_data[(Y+1)*res_width-radius-1]; }
同様のぼかし操作を、 Y軸に対して実行します。結果として、得られる4つの配列a1_data[], r1_data[], g1_data[], b1_data[]が得られ、それぞれアルファ、赤、緑、青でぼかします。これは、各画素について、これら四つの成分から色を収集し、CanvasShadowキャンバスに適用します。:
//--- for(int i=0;i<size;i++) { clr_temp=ARGB(a1_data[i],r1_data[i],g1_data[i],b1_data[i]); res_data[i]=clr_temp; } for(uint X=0;X<res_width;X++) { for(uint Y=radius;Y<res_height-radius;Y++) { XY=Y*res_width+X; CanvasShadow.PixelSet(X,Y,res_data[XY]); } } CanvasShadow.Update(); CanvasDraw.Update(); Sleep(21000);
影を有する層をぼかした結果:
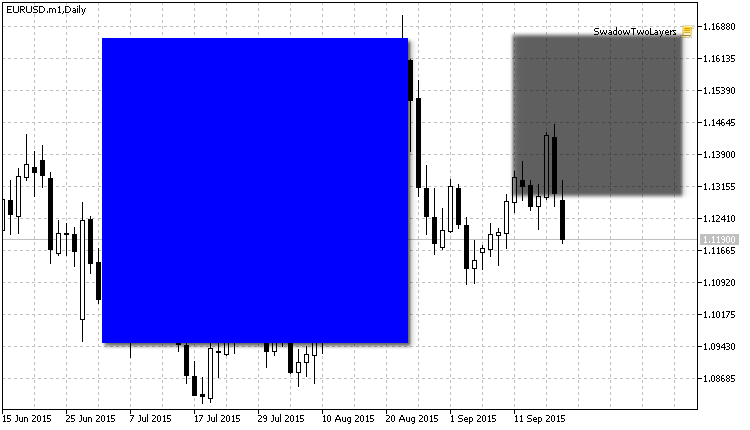
図12。影はぼかされました
5. 影を描画するクラス
キャンバス上の描画の例は、ガウスクラスで実装されています。 CGaussクラスは、このようなプリミティブを描画することができます:
| プリミティブ | デスクリプション |
|---|---|
| LineVertical | 影で垂直線を描画します |
| LineHorizontal | 影で水平線を描画します |
| Line | 影で任意の線を引きます |
| Polyline | 影でポリラインを描きます |
| Polygon | 影でポリゴンを描画します |
| Rectangle | 影で四角形を描画します |
| Circle | 影で円を描きます |
| FillRectangle | 影で塗りつぶされた四角形を描画 |
| FillTriangle | 影で満たされた三角形を描きます |
| FillPolygon | 影で満たされたポリゴンを描画 |
| FillCircle | 影で塗りつぶされた円を描きます |
| FillEllipse | 影で満たされた楕円を描きます |
| Fill | 影で領域を塗りつぶします |
| TextOut | 影でテキストを表示します |
影でプリミティブを描画するBlur.mq5スクリプトのデモビデオ:
ビデオ2。影でプリミティブを描画
数値解析ライブラリALGLIBは、ガウスクラスで影の色を計算するために使用されます。このクラスで1つの影タイプがあります - シフト右の外側斜め下方描かれた影(図4参照)。
CGaussの一般的な考え方は、2つのキャンバスを作成することです。下のキャンバスは、影の描画に使用される層の関数を実行し、上のキャンバスはグラフィック図形を描画する作業レイヤーとして機能します。両方のキャンバスのサイズは、グラフのサイズに等しいです。描画影の座標の計算が容易になります。下のキャンバスは、作成したときに、影の大きさによって水平方向および垂直方向にシフトしていることが特徴です。
影の描画アルゴリズムは、以下の原理で動作します。ぼかし半径に等しいオブジェクトの量は、その後、下のキャンバスに描かれています。各オブジェクトの色は、このように透明性を完了するために与えられた影の色を得て、ガウスアルゴリズムにより計算されます。
結論
本稿では、オブジェクトの計算例および描画ぼかしと共に、CCanvasクラスのアンチエイリアスのアルゴリズムをカバーしています。これにより、数値解析ライブラリALGLIBをボケや色合いを形成する計算に適用しました。
加えて、ガウスの様々な実施例に基づいて描かれていた影と図形要素を描画するためのクラスを取り上げました。
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/1612
 グラフィカルインタフェースX: Easy And Fast (簡単で手早い)ライブラリの更新(ビルド2)
グラフィカルインタフェースX: Easy And Fast (簡単で手早い)ライブラリの更新(ビルド2)
 MQL5とQLUAの比較ーなぜMQL5での取引操作は28倍速いのか?
MQL5とQLUAの比較ーなぜMQL5での取引操作は28倍速いのか?
 グラフィカルインタフェースIX:プログレスバーと折れ線グラフコントロール(チャプター2)
グラフィカルインタフェースIX:プログレスバーと折れ線グラフコントロール(チャプター2)
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索