MQL5で古典的な戦略を再構築する（第3回）：FTSE100予想

MetaTrader 5 — 例 | 21 11月 2024, 15:40

人工知能(AI)は、現代の投資家戦略において、無限とも言える可能性を秘めた活用例を提供します。しかし、どの戦略に自分の資本を託すべきかを決める前に、各戦略を細かく分析する時間を十分に確保できる投資家は、ほとんどいないのが現状です。本連載では、AI ベースの戦略が持つ広大な可能性を探りながら、投資家一人ひとりのプロファイルに最適な戦略を見つけるための手助けをします。

取引戦略の概要

ロンドン証券取引所(LSE) は、先進国で最も歴史ある証券取引所の1つで、1801年に設立された英国の主要な証券取引所です。ニューヨーク証券取引所や東京証券取引所とともに、世界の「ビッグ3」の一角を担っています。LSEはヨーロッパ最大の証券取引所であり、公式Webサイトによれば、現在同取引所に上場している企業全体の時価総額は約4.4兆英国ポンドに達します。

フィナンシャル・タイムズ証券取引所(FTSE)100は、LSEから派生した株価指数であり、ロンドン証券取引所に上場している時価総額上位100社を追跡します。これらの企業は一般的に「優良株」と呼ばれ、その長年の実績や信頼性から、比較的安全な投資対象とみなされています。FTSE 100指数の計算方法を正確に理解することで、指数の現在の終値や構成銘柄トップ10のパフォーマンスを基に、FTSE 100の将来の終値を予測する新たな取引戦略を構築できる可能性があります。

方法論の概要

私たちは、AI搭載のエキスパートアドバイザー(EA)をMQL5で完全に構築しました。このため、モデルを頻繁に調整する必要がなく、さまざまな時間枠で柔軟に使用できるようになっています。さらに、モデルパラメータ、例えば予測する未来の期間を動的に調整することが可能です。今回のモデルでは、合計12の入力データを用い、FTSE 100指数の将来の終値を20ステップ先まで予測しました。

データの前処理として、各モデル入力を正規化・スケーリングするためにZ標準化を採用しました。これは列ごとの平均値と標準偏差値を利用しておこなっています。ターゲットとなるデータは、FTSE 100指数の20ステップ先の将来の終値です。このターゲットを基に、指数の将来の終値を予測する多重線形回帰モデルを作成しました。

すべての機械学習モデルが同じように設計されているわけではありません。予測タスクにおいてその違いは特に顕著です。たとえば、決定木アルゴリズムについて考えてみましょう。ツリーアルゴリズムは、一般にデータをグループ化して処理します。モデルが予測をおこなう際には、入力データに最も一致するグループの平均値を返します。そのため、ツリーベースのアルゴリズムは外挿をおこなわず、将来の予測には向いていません。具体例を挙げると、5つの異なる瞬間における類似した入力をツリーベースのモデルに与えた場合、それらが十分に似ていれば、すべてに同じ終値を予測する可能性があります。一方、線形回帰モデルは外挿が可能であり、証券の将来の終値について予測を提供する能力を持っています。

スクリプトとしての初期デザイン

最初に、システムの各部分がどのように連携して動作するかを理解するために、MQL5で簡単なスクリプトとしてアイデアを構築します。まずは、グローバル変数を定義します。

//+------------------------------------------------------------------+
//|                                                        UK100.mq5 |
//|                                        Gamuchirai Zororo Ndawana |
//|                          https://www.mql5.com/ja/gamuchiraindawa |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Zororo Ndawana"
#property link      "https://www.mql5.com/ja/gamuchiraindawa"
#property version   "1.00"
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+

//1) ADM.LSE  - Admiral
//2) AAL.LSE  - Anglo American
//3) ANTO.LSE - Antofagasta
//4) AHT.LSE  - Ashtead
//5) AZN.LSE  - AstraZeneca
//6) ABF.LSE  - Associated British Foods
//7) AV.LSE   - Aviva
//8) BARC.LSE - Barclays
//9) BP.LSE   - BP
//10) BKG.LSE - Berkeley Group 
//11) UK100   - FTSE 100 Index

//+-------------------------------------------------------------------+
//| Global variables                                                  |
//+-------------------------------------------------------------------+
int fetch = 2000;
int look_ahead = 20;
double mean_values[11],std_values[11];
string list_of_companies[11] = {"ADM.LSE","AAL.LSE","ANTO.LSE","AHT.LSE","AZN.LSE","ABF.LSE","AV.LSE","BARC.LSE","BP.LSE","BKG.LSE","UK100"};
vector intercept = vector::Ones(fetch);
matrix target = matrix::Zeros(1,fetch);
matrix coefficients;
matrix input_matrix = matrix::Zeros(12,fetch);

最初に行うタスクは、入力データの取得と正規化です。入力データを1つの行列に格納し、ターゲットデータは独自の行列に保持されます。

void OnStart()
  {
//--- Fetch the target
target.CopyRates("UK100",PERIOD_CURRENT,COPY_RATES_CLOSE,1,fetch);

//--- Fill in the input matrix
for(int i = 0; i < 11; i++)
   {
      //--- Add the symbol to market watch
      SymbolSelect(list_of_companies[i],true);
      //--- Fetch historical data
      vector temp = vector::Zeros(fetch);
      temp.CopyRates(list_of_companies[i],PERIOD_CURRENT,COPY_RATES_CLOSE,1+look_ahead,fetch);
      //--- Store the mean value and standard deviation, also scale the data
      mean_values[i] = temp.Mean();
      std_values[i] = temp.Std();
      temp = ((temp - mean_values[i]) / std_values[i]);
      //--- Add the data to the matrix
      input_matrix.Row(temp,i);
   }
//--- Add the intercept
input_matrix.Row(intercept,11);

//--- Show the input data
Print("Input data:");
Print(input_matrix);

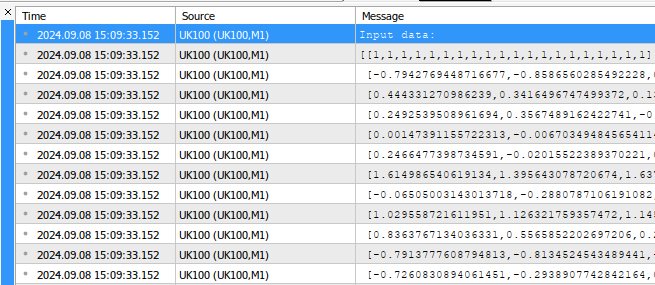
図1：スクリプトの出力例

入力データを取得したら、次はモデルのパラメータを計算します。幸い、多重線形回帰モデルの係数は、閉じた形式の式で計算できます。以下にモデル係数の例を示します。

//--- Calculating coefficient values
coefficients = target.MatMul(input_matrix.PInv());

//--- Display the coefficient values
Print("UK100 Coefficients:");
Print(coefficients.Transpose());

UK100係数

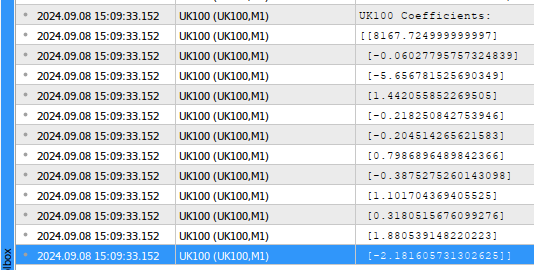
図2：モデルパラメーター

結果をまとめて解釈してみましょう。最初の係数値は、すべてのモデル入力が0の場合におけるターゲットの平均値を表します。これは数学的にはバイアスパラメーターの定義に該当しますが、この取引アプリケーションにおいて直感的な意味はほとんどありません。技術的に説明すれば、FTSE 100に含まれるすべての株式が0英国ポンドで評価された場合、FTSE 100の平均将来価値も0英国ポンドになることを示しています。次に、2番目の係数項は、他のすべての株式が同じ価格で終了すると仮定した場合における、FTSE 100の将来価値の限界変化を表します。これにより、たとえばAdmiralの株式が1単位増加するたびに、インデックスの将来の終値がわずかに低下することが予測されることがわかります。

モデルから予測を取得するのは簡単です。各株式の現在の価格に対応する係数値を掛け、それらの積をすべて合計するだけで済みます。モデルの構築方法が明確になったので、次のステップとしてEAの開発を開始する準備が整いました。

EAの導入

まず、プログラムの動作を変更するためにユーザーが変更できる入力を定義します。

//+------------------------------------------------------------------+
//|                                                  FTSE 100 AI.mq5 |
//|                                        Gamuchirai Zororo Ndawana |
//|                          https://www.mql5.com/ja/gamuchiraindawa |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Zororo Ndawana"
#property link      "https://www.mql5.com/ja/gamuchiraindawa"
#property version   "1.00"

//+------------------------------------------------------------------+
//| User inputs                                                      |
//+------------------------------------------------------------------+
input int look_ahead = 20;       // How far into the future should we forecast?
input int rsi_period = 20;       // The period of our RSI
input int profit_target = 20;     // After how much profit should we close our positions?
input bool ai_auto_close = true; // Should the AI automatically close positions?

次に、ポジションの管理に役立つ取引ライブラリをインポートします。

//+------------------------------------------------------------------+
//| Libraries we need                                                |
//+------------------------------------------------------------------+
#include  <Trade/Trade.mqh>
CTrade Trade;

ここで、EA全体で必要となるいくつかのグローバル変数を定義します。

//+------------------------------------------------------------------+
//| Global variables                                                 |
//+------------------------------------------------------------------+
double position_profit = 0;
int fetch = 20;
matrix coefficients;
matrix input_matrix = matrix::Zeros(12,fetch);
double mean_values[11],std_values[11],rsi_buffer[1];
string list_of_companies[11] = {"ADM.LSE","AAL.LSE","ANTO.LSE","AHT.LSE","AZN.LSE","ABF.LSE","AV.LSE","BARC.LSE","BP.LSE","BKG.LSE","UK100"};
ulong open_ticket;

ここで、訓練データを取得するための関数を定義します。訓練データを取得し、それを入力行列に追加する前にデータを正規化および標準化することを目的としていることを思い出してください。

//+------------------------------------------------------------------+
//| This function will fetch our training data                       |
//+------------------------------------------------------------------+
void fetch_training_data(void)
  {
//--- Fetch the target
   target.CopyRates("UK100",PERIOD_CURRENT,COPY_RATES_CLOSE,1,fetch);

//--- Add the intercept
   input_matrix.Row(intercept,0);

//--- Fill in the input matrix
   for(int i = 0; i < 11; i++)
     {
      //--- Add the symbol to market watch
      SymbolSelect(list_of_companies[i],true);
      //--- Fetch historical data
      vector temp = vector::Zeros(fetch);
      temp.CopyRates(list_of_companies[i],PERIOD_CURRENT,COPY_RATES_CLOSE,1+look_ahead,fetch);
      //--- Store the mean value and standard deviation, also scale the data
      mean_values[i] = temp.Mean();
      std_values[i] = temp.Std();
      temp = ((temp - mean_values[i]) / std_values[i]);
      //--- Add the data to the matrix
      input_matrix.Row(temp,i+1);
     }
  }

訓練データを取得した後は、モデル係数を適合するための関数も定義する必要があります。

//+---------------------------------------------------------------------+
//| This function will fit our multiple linear regression model         |
//+---------------------------------------------------------------------+
void model_fit(void)
  {
//--- Calculating coefficient values
   coefficients = target.MatMul(input_matrix.PInv());
  }

モデルの訓練と適合が完了したら、次にモデルから予測を得る手順に進みます。まず、現在の市場データをモデルに入力するために取得し、それを正規化します。正規化されたデータを用いて線形回帰式を適用することで、モデルから予測を取得します。最後に、取得したモデルの予測をバイナリフラグとして保存し、潜在的な市場の反転を追跡できるようにします。

//+---------------------------------------------------------------------+
//| This function will fetch a prediction from our model                |
//+---------------------------------------------------------------------+
void model_predict(void)
  {
//--- Add the intercept
   intercept = vector::Ones(1);
   input_matrix.Row(intercept,0);

//--- Fill in the input matrix
   for(int i = 0; i < 11; i++)
     {
      //--- Fetch historical data
      vector temp = vector::Zeros(1);
      temp.CopyRates(list_of_companies[i],PERIOD_CURRENT,COPY_RATES_CLOSE,0,1);
      //--- Normalize and scale the data
      temp = ((temp - mean_values[i]) / std_values[i]);
      //--- Add the data to the matrix
      input_matrix.Row(temp,i+1);
     }

//--- Calculate the model forecast
   forecast = (
                 (1 * coefficients[0,0]) +
                 (input_matrix[0,1] * coefficients[0,1]) +
                 (input_matrix[0,2] * coefficients[0,2]) +
                 (input_matrix[0,3] * coefficients[0,3]) +
                 (input_matrix[0,4] * coefficients[0,4]) +
                 (input_matrix[0,5] * coefficients[0,5]) +
                 (input_matrix[0,6] * coefficients[0,6]) +
                 (input_matrix[0,7] * coefficients[0,7]) +
                 (input_matrix[0,8] * coefficients[0,8]) +
                 (input_matrix[0,9] * coefficients[0,9]) +
                 (input_matrix[0,10] * coefficients[0,10]) +
                 (input_matrix[0,11] * coefficients[0,11])
              );
//--- Store the model's state
//--- Whenever the system and model state aren't the same, we may have a potential reversal
   if(forecast > iClose("UK100",PERIOD_CURRENT,0))
     {
      model_state = 1;
     }

   else
      if(forecast < iClose("UK100",PERIOD_CURRENT,0))
        {
         model_state = -1;
        }
  }
//+------------------------------------------------------------------+

端末から現在の市場データを取得する関数も必要になります。

//+------------------------------------------------------------------+
//| Update our market data                                           |
//+------------------------------------------------------------------+
void update_market_data(void)
  {
//--- Update the bid and ask prices
   bid = SymbolInfoDouble("UK100",SYMBOL_BID);
   ask = SymbolInfoDouble("UK100",SYMBOL_ASK);
//--- Update the RSI readings
   CopyBuffer(rsi_handler,0,1,1,rsi_buffer);
  }

次に、市場センチメントを分析し、それがモデルと一致するかを確認する関数を作成します。モデルが購入を提案した場合、まず1つのビジネスサイクルにわたる週単位の時間枠で価格の変化を確認します。価格レベルが上昇している場合、RSI指標を使用して市場センチメントが強気であるかどうかを判断します。市場センチメントが強気の場合は買いポジションを設定しますが、そうでない場合はポジションを設定せずに終了します。

//+------------------------------------------------------------------+
//| Check if we have an opportunity to sell                          |
//+------------------------------------------------------------------+
void check_sell(void)
  {
   if(iClose("UK100",PERIOD_W1,0) < iClose("UK100",PERIOD_W1,12))
     {
      if(rsi_buffer[0] < 50)
        {
         Trade.Sell(0.3,"UK100",bid,0,0,"FTSE 100 AI");
         //--- Remeber the ticket
         open_ticket = PositionGetTicket(0);
         //--- Whenever the system and model state aren't the same, we may have a potential reversal
         system_state = -1;
        }
     }
  }

//+------------------------------------------------------------------+
//| Check if we have an opportunity to buy                           |
//+------------------------------------------------------------------+
void check_buy(void)
  {
   if(iClose("UK100",PERIOD_W1,0) > iClose("UK100",PERIOD_W1,12))
     {
      if(rsi_buffer[0] > 50)
        {
         Trade.Buy(0.3,"UK100",ask,0,0,"FTSE 100 AI");
         //--- Remeber the ticket
         open_ticket = PositionGetTicket(0);
         //--- Whenever the system and model state aren't the same, we may have a potential reversal
         system_state = 1;
        }
     }
  }

アプリケーションを初期化するときに、まず RSI指標を準備します。そこから、RSI指標を検証します。このテストに合格したら、多重線形回帰モデルの作成に進みます。まず、訓練データを取得し、次にモデル係数を計算します。最後に、ユーザーの入力を検証して、ユーザーがリスクレベルを制御するための基準を定義したことを確認します。

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- Prepare the technical indicator
   rsi_handler = iRSI(Symbol(),PERIOD_CURRENT,rsi_period,PRICE_CLOSE);

//--- Validate the indicator handler
   if(rsi_handler == INVALID_HANDLE)
     {
      //--- We failed to load the indicator
      Comment("Failed to load the RSI indicator");
      return(INIT_FAILED);
     }

//--- This function will fetch our training data and scaling factors
   fetch_training_data();

//--- This function will fit our multiple linear regression model
   model_fit();

//--- Ensure the user's inputs are valid
   if((ai_auto_close == false && profit_target == 0))
     {
      Comment("Either set AI auto close true, or define a profit target!")
      return(INIT_FAILED);
     }

//--- Everything went well
   return(INIT_SUCCEEDED);
  }

EAが使用されていないときはいつでも、使用しなくなったリソースを解放します。特に、メインチャートからRSI指標とEAを削除します。

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//--- Free up the resources we are no longer using
   IndicatorRelease(rsi_handler);
   ExpertRemove();
  }

最後に、更新された価格を受け取るたびに、まずFTSE 100銘柄を選択し、更新された市場データとテクニカル指標の値を取得します。その後、モデルから新しい予測を取得し、それに基づいて適切なアクションを実行します。システムにポジションがない場合、ポジションを建てる前に現在の市場センチメントがモデルの予測と一致しているかを確認します。一方、すでにポジションがある場合は、潜在的な反転の可能性をテストします。これは、モデルの予測状態とシステムの現在の状態が一致していない場合に簡単に検出できます。

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//--- Since we are dealing with a lot of different symbols, be sure to select the UK1OO (FTSE100)
//--- Select the symbol
   SymbolSelect("UK100",true);

//--- Update market data
   update_market_data();

//--- Fetch a prediction from our AI model
   model_predict();

//--- Give the user feedback
   Comment("Model forecast: ",forecast,"\nPosition Profit: ",position_profit);



//--- Look for a position
   if(PositionsTotal() == 0)
     {
      //--- We have no open positions
      open_ticket = 0;

      //--- Check if our model's prediction is validated
      if(model_state == 1)
        {
         check_buy();
        }

      else
         if(model_state == -1)
           {
            check_sell();
           }
     }

//--- Do we have a position allready?
   if(PositionsTotal() > 0)
     {

      //--- Should we close our positon manually?
      if(PositionSelectByTicket(open_ticket))
        {
         if((profit_target > 0) && (ai_auto_close == false))
           {
            //--- Update the position profit
            position_profit = PositionGetDouble(POSITION_PROFIT);
            if(profit_target < position_profit)
              {
               Trade.PositionClose("UK100");
              }
           }
        }

      //--- Should we close our positon using a hybrid approach?
      if(PositionSelectByTicket(open_ticket))
        {
         if((profit_target > 0) && (ai_auto_close == true))
           {
            //--- Update the position profit
            position_profit = PositionGetDouble(POSITION_PROFIT);
            //--- Check if we have passed our profit target or if we are expecting a reversal
            if((profit_target < position_profit) || (model_state != system_state))
              {
               Trade.PositionClose("UK100");
              }
           }
        }


      //--- Are we closing our system just using AI?
      else
         if((system_state != model_state) &&
            (ai_auto_close == true) &&
            (profit_target == 0))
           {
            Trade.PositionClose("UK100");
           }
     }
  }
//+------------------------------------------------------------------+

UK100バックテスト

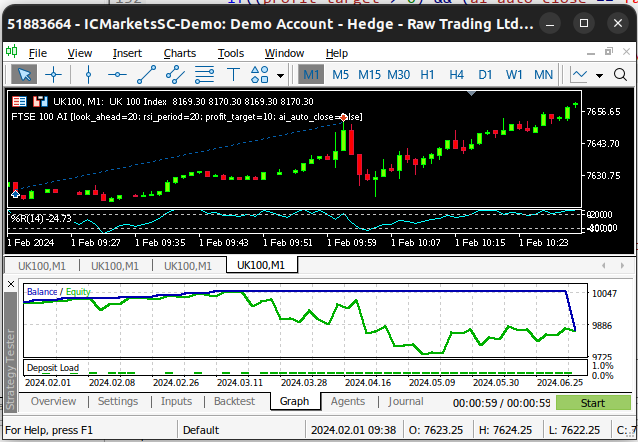
図3：EAのバックテスト

EAの最適化

これまでのところ、私たちの取引アプリケーションは不安定であるように見えますが、米国の経済学者ハリー・マーコウィッツの提唱したアイデアを活用することで、その安定性を向上させることができます。マーコウィッツは、現代ポートフォリオ理論(MPT)の基礎を確立した人物として知られています。本質的に、彼は個々の資産のパフォーマンスは、投資家のポートフォリオ全体のパフォーマンスと比較すると無視できるほど小さいことに気付きました。

図4：ノーベル賞受賞者ハリー・マーコウィッツの写真

取引アプリケーションのパフォーマンスを安定させるために、マーコウィッツのアイデアのいくつかを適用してみましょう。まずは必要なライブラリをインポートすることから始めましょう。

#Import the libraries we need
import pandas            as pd
import numpy             as np
import seaborn           as sns
import MetaTrader5       as mt5
import matplotlib.pyplot as plt
from   scipy.optimize    import  minimize

検討中の保有銘柄のリストを作成する必要があります。

#Create the list of stocks
stocks = ["ADM.LSE","AAL.LSE","ANTO.LSE","AHT.LSE","AZN.LSE","ABF.LSE","AV.LSE","BARC.LSE","BP.LSE","BKG.LSE","UK100"]

端末を初期化します。

#Initialize the terminal
if(!mt5.initialize()):
    print('Failed to load the MT5 Terminal')

True

次に、各銘柄のリターンを格納するデータフレームを作成します。

#Create a dataframe to store our returns
amount  = 10000
returns = pd.DataFrame(columns=stocks,index=np.arange(0,amount))

MetaTrader 5端末から必要なデータを取得します。

#Fetch the data
for stock in stocks:
     temp = pd.DataFrame(mt5.copy_rates_from_pos(stock,mt5.TIMEFRAME_M1,0,amount))
     returns[[stock]] = temp[['close']]

この作業では、通常の終値ではなく、各銘柄のリターンを使用します。

#Store the data as returns
returns = returns.pct_change()
returns.dropna(inplace=True)

デフォルトでは、実際のパーセント収益を得るには、各エントリに100を掛ける必要があります。

#Let's look at our dataframe
returns = returns * (10.0 ** 2)

では、手持ちのデータを見てみましょう。

returns

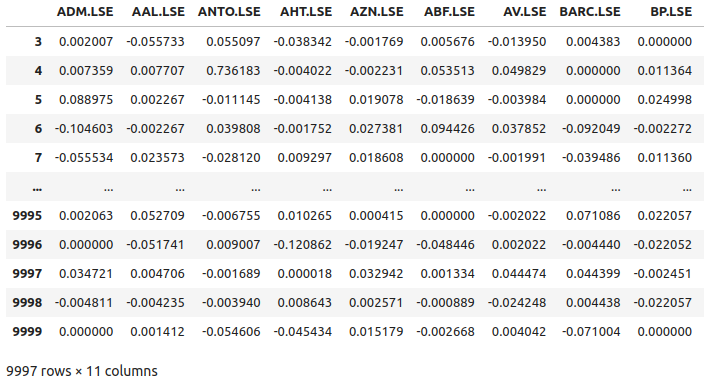
図5：FTSE100種構成銘柄のリターンの一部

では、保有している各銘柄の市場リターンをプロットしてみましょう。例えば、Ashtead Group (AHT.LSE)のような特定の銘柄が、保有している11銘柄のポートフォリオの平均パフォーマンスから大きく逸脱し、強力で明確なテールを持っていることが確認できます。本質的に、マーコウィッツのアルゴリズムは、経験的に分散の大きい銘柄の選択を減らし、分散の小さい銘柄の選択を増やすのに役立ちます。このマーコウィッツのアプローチは、分析的であり、私たちの側での推測作業を排除します。

#Let's visualize our market returns
returns.plot()

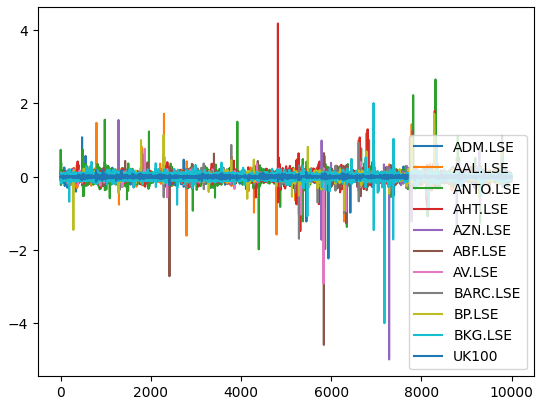
図6：FTSE100種株価指数バスケットからの市場リターン

データに意味のある相関レベルがあるかどうか確認してみましょう。残念ながら、興味深いと思える有意な相関レベルはありませんでした。

#Let's analyze the correlation coefficients
fig, ax = plt.subplots(figsize=(8,8)) 
sns.heatmap(returns.corr(),annot=True,linewidths=.5, ax=ax)

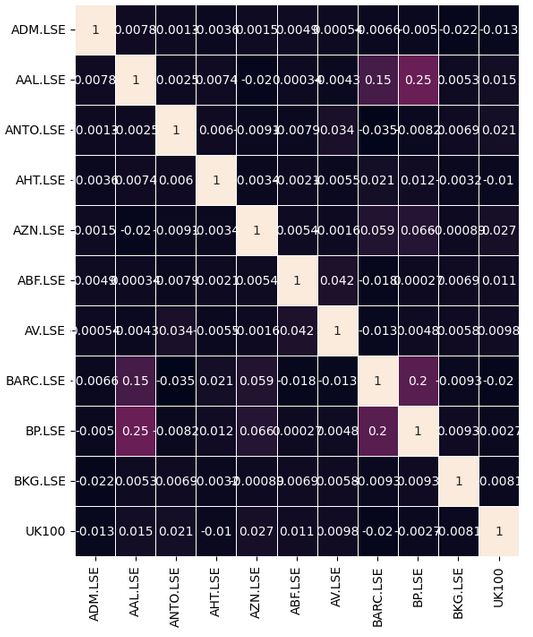
図7：FTSE100の相関ヒートマップ

いくつかの関係は簡単には見つけられず、明確にするためにはいくつかの前処理手順が必要です。保有する株式バスケット間の相関関係を直接探すだけでなく、各株式の現在の値とUK100銘柄の将来の値との相関関係を調べることもできます。これは、リードラグ相関と呼ばれる古典的な手法です。

まず、株式バスケットを20位後ろに押し戻し、UK100銘柄を20位前に押し出します。

# Let's also analyze for lead-lag correlation
look_ahead  = 20
lead_lag    = pd.DataFrame(columns=stocks,index=np.arange(0,returns.shape[0] - look_ahead))
for stock in stocks:
    if stock == 'UK100':
        lead_lag[[stock]] = returns[[stock]].shift(-20)
    else:
        lead_lag[[stock]] = returns[[stock]].shift(20)

# Returns
lead_lag.dropna(inplace=True)

相関行列に変化があったかどうか確認してみましょう。残念ながら、この手順では改善は得られませんでした。

#Let's see if there are any stocks that are correlated with the future UK100 returns
fig, ax = plt.subplots(figsize=(8,8)) 
sns.heatmap(lead_lag.corr(),annot=True,linewidths=.5, ax=ax)

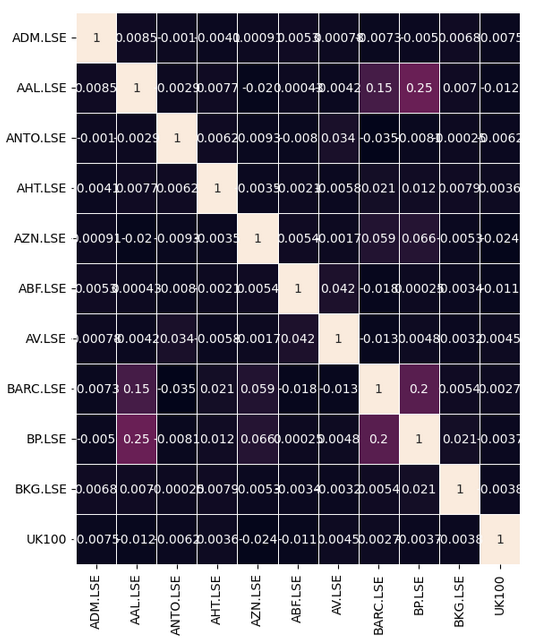
図8：リードラグ相関ヒートマップ

それでは、ポートフォリオ全体の分散を最小化してみましょう。ポートフォリオのリスクを最小化するために、さまざまな株式を売買できるようにポートフォリオをモデル化します。この目標を達成するために、SciPyの最適化ライブラリを使用します。最適化するのは11種類の重みで、各重みはそれぞれの株式に割り当てる資本を表します。各重みの係数は、各株式を買うべきか（正の係数）、売るべきか（負の係数）を示します。より具体的には、すべての係数が-1から1まで（両端を含む）、または区間表記[-1,1]であることを確認します。

これに加えて、保有する資本をすべて使い、それ以上は使いたくありません。そのため、最適化手順に制約を設定する必要があります。具体的には、ポートフォリオ内のすべての重みの合計が1になるようにする必要があります。これは、保有する資本をすべて割り当てたことを意味します。係数の一部は負になるので、すべての係数の合計が1になるのが難しくなる可能性があることを思い出してください。そのため、この制約を変更して、各重みの絶対値のみを考慮する必要があります。言い換えると、11個の重みをベクトルに格納する場合、L1ノルムが1になるようにする必要があります。

まず、重みをランダムな値で初期化し、リターンの行列の共分散を計算します。

#Let's attempt to minimize the variance of the portfolio
weights = np.array([0,0,0,0,0,0,-1,1,1,0,0])
covariance = returns.cov()

ここで、初期の分散レベルを記録しておきます。

#Store the initial portfolio variance
initial_portfolio_variance = np.dot(weights.T,np.dot(covariance,weights))
initial_portfolio_variance

0.011959689589562724

最適化を実行するときは、関数からの出力が最小になるような関数への最適な入力を探します。この関数はコスト関数と呼ばれます。ここでのコスト関数は、現在の重み付けでのポートフォリオの分散になります。幸い、これは線形代数コマンドを使用して簡単に計算できます。

#Cost function
def cost_function(x):
    return(np.dot(x.T,np.dot(covariance,x)))

次に、ポートフォリオの重みが1になるように指定する制約を定義します。

#Constraints
def l1_norm(x):
    return(np.sum(np.abs(x))) - 1

constraints = {'type': 'eq', 'fun':l1_norm}

SciPy では、最適化を実行するときに初期推測値を提供する必要があります。

#Initial guess
initial_guess = weights

重みがすべて-1から1の間になるように、境界のタプルを使ってSciPyに命令を渡します。

#Add bounds
bounds =   [(-1,1)] * 11

ここでは、逐次最小二乗計画(SLSQP: Sequential Least SQuares Programming)アルゴリズムを使用して、ポートフォリオの分散を最小化します。SLSQPアルゴリズムは、1980年代にドイツの優秀なエンジニアであるDieter Kraftによって開発されました。元のルーチンはFORTRANで実装されており、アルゴリズムの概要を説明したKraftの元の科学論文は、こちらで参照できます。SLSQPは準ニュートンアルゴリズムであり、目的関数の2次導関数（ヘッセ行列）を推定することで、目的関数の最適値を見つけます。

#Minimize the portfolio variance
result = minimize(cost_function,initial_guess,method="SLSQP",constraints=constraints,bounds=bounds)

この最適化手順が成功したので、結果を見てみましょうう。

result

message:Optimization terminated successfully
success:True
status:0
     fun:0.0004706570068070814
       x: [ 5.845e-02 -1.057e-01 8.800e-03 2.894e-02 -1.461e-01
            3.433e-02 -2.625e-01 6.867e-02 1.653e-01 3.450e-02
            8.675e-02]
     nit:12
     jac: [ 3.820e-04 -9.886e-04 3.242e-05 4.724e-04 -1.544e-03
            4.151e-04 -1.351e-03 5.850e-04 8.880e-04 4.457e-04
            4.392e-05]
    nfev:154
    njev:12

SciPyソルバーが見つけた最適な重みを保存しましょう。

#Store the optimal weights
optimal_weights = result.x

L1ノルム制約が違反されていないことを検証しましょう。コンピュータのメモリ浮動精度が限られているため、重みの合計が正確に1にならないことに注意してください。

#Validating the weights add up to one
np.sum(np.abs(optimal_weights))

0.9999999998893961

新しいポートフォリオの分散を保存します。

#Store the new portfolio variance
otpimal_variance = cost_function(optimal_weights)

パフォーマンスを比較するためのデータフレームを作成します。

#Portfolio variance
portfolio_var = pd.DataFrame(columns=['Old Var','New Var'],index=[0])

分散レベルをデータフレームに保存します。

portfolio_var.iloc[0,0] = initial_portfolio_variance * (10.0 ** 7)
portfolio_var.iloc[0,1] = otpimal_variance * (10.0 ** 7)

ポートフォリオの分散をプロットします。ご覧のとおり、分散レベルは大幅に低下しています。

portfolio_var.plot.bar()

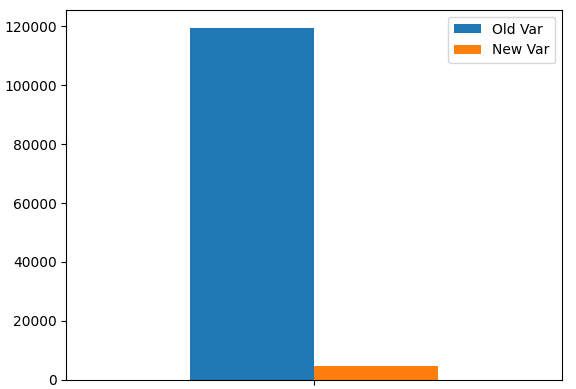
図9：新しいポートフォリオの分散

次に、最適な重みに従って各市場で建てるべきポジション数を取得しましょう。データによると、UK100銘柄で1つのロングポジションを建てる場合、Admiral Group (ADM.LSE)でポジションを開くべきではなく、Anglo-American (AAL.LSE)で同等の2つのショートポジションを建てる必要があります。

int_weights = (optimal_weights / optimal_weights[-1]) // 1
int_weights

array([ 0., -2., 0., 0., -2., 0., -4., 0., 1., 0., 1.])

EAの更新

ここで、FTSE 100市場に関する新たな理解を活用するために、取引アルゴリズムの更新に目を向けることができます。まず、SciPyを使用して計算した最適な重みを読み込みます。

int    optimization_weights[11] = {0,-2,0,0,-2,0,-4,0,1,0,1};

最適化手順をトリガーするための設定も必要です。損失限度を設定し、未決取引の損失がその損失限度を超える場合には、リスクレベルを最小限に抑えるために他のFTSE 100市場で取引を開始します。

input double  loss_limit = 20;        // After how much loss should we optimize our portfolio?

ここで、ポートフォリオのリスクレベルを最小化する手順を呼び出す関数を定義しよう。このルーチンを実行するのは、口座が損失リミットを突破した場合、または株式閾値を超えるリスクがある場合のみであることを思い出してください。

      //--- Should we optimize our portfolio variance using the optimal weights we have calculated
      if((loss_limit > 0))
        {
         //--- Update the position profit
         position_profit = AccountInfoDouble(ACCOUNT_EQUITY) - AccountInfoDouble(ACCOUNT_BALANCE);
         //--- Check if we have passed our profit target or if we are expecting a reversal
         if(((loss_limit * -1) < position_profit))
           {
            minimize_variance();
           }
        }

この関数は実際にポートフォリオの最適化を実行し、株式リストを反復処理して、建てるべきポジションの数とタイプを確認します。

//+------------------------------------------------------------------+
//| This function will minimize the variance of our portfolio        |
//+------------------------------------------------------------------+
void minimize_variance(void)
  {
   risk_minimized = true;

   if(!risk_minimized)
     {
      for(int i = 0; i < 11; i++)
        {
         string current_symbol = list_of_companies[i];

         //--- Add that stock to the portfolio to minimize our variance, buy
         if(optimization_weights[i] > 0)
           {
            for(int i = 0; i < optimization_weights[i]; i++)
              {
               Trade.Buy(0.3,current_symbol,ask,0,0,"FTSE Optimization");
              }
           }
         //--- Add that stock to the portfolio to minimize our variance, sell
         else
            if(optimization_weights[i] < 0)
              {
               for(int i = 0; i < optimization_weights[i]; i--)
                 {
                  Trade.Sell(0.3,current_symbol,bid,0,0,"FTSE Optimization");
                 }
              }
        }
     }
  }

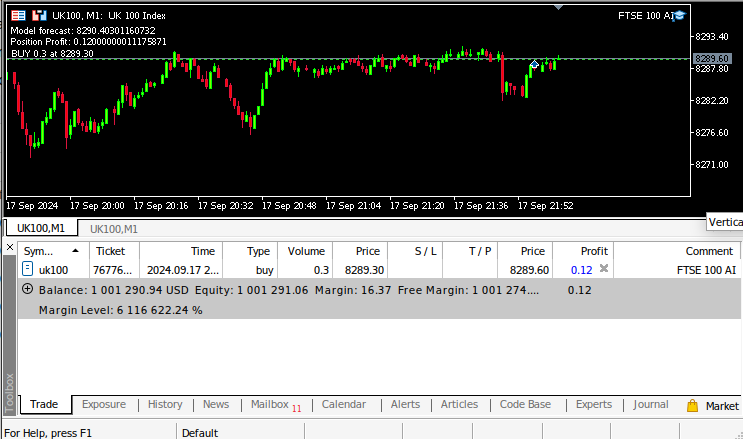
図10：アルゴリズムのフォワードテスト

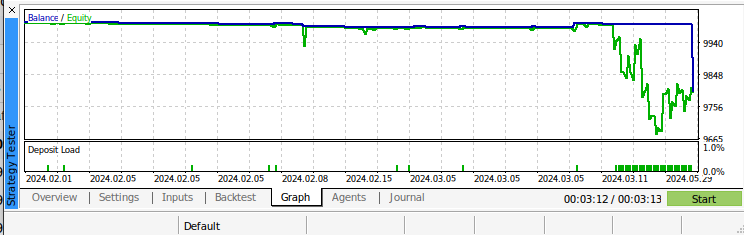
図11：アルゴリズムのバックテスト

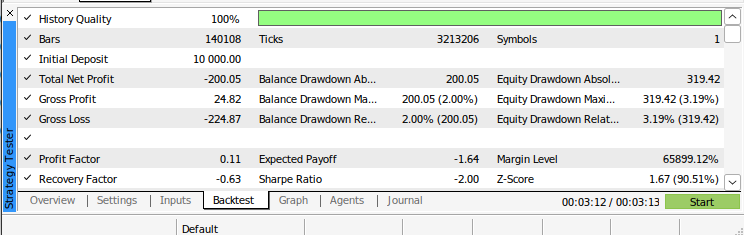
図12：アルゴリズムのバックテスト結果

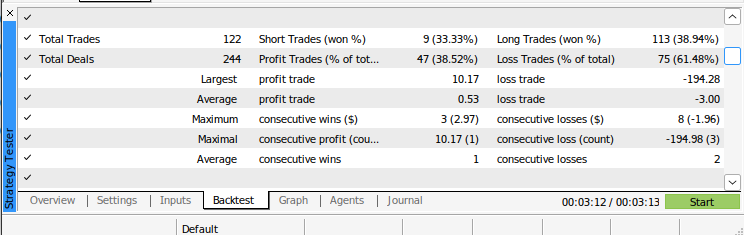
図13：アルゴリズムのバックテストによる追加結果

結論

この記事では、PythonとMQL5を使用してテクニカル分析とAIのアンサンブルをシームレスに構築する方法を示しました。このアプリケーションは、MetaTrader 5端末で利用可能なすべての時間枠に動的に調整できます。最新の最適化アルゴリズムを使用して、最新のポートフォリオ最適化の基本となる主要な原則を概説しました。ポートフォリオ選択のプロセスで人間のバイアスを最小限に抑える方法を示しました。さらに、市場データを使用して最適な決定を下す方法を紹介しました。アルゴリズムにはまだ改善の余地があります。たとえば、今後の記事では、リスクフリー収益率を考慮しながらリスクレベルを最適化するなど、2つの基準を同時に最適化する方法を示します。

ただし、今日概説した原則のほとんどは、より微妙な最適化手順を実行する場合でも同じままであり、コスト関数と制約を調整し、ニーズに適した最適化アルゴリズムを特定するだけで済みます。

MetaQuotes Ltdにより英語から翻訳されました。
元の記事: https://www.mql5.com/en/articles/15818

添付されたファイル |

ZIPをダウンロード

UK100.mq5 (3.16 KB)

Minimizing_Portfolio_Variance.ipynb (369.35 KB)

FTSE_100_AI.mq5 (12.63 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。