古典的な戦略を再構築する（第8回）：USDCADをめぐる為替市場と貴金属市場

本連載では、取引戦略におけるAIの広範な応用可能性を探ります。その目的は、AIベースの戦略への投資を検討する際に、十分な情報に基づいた意思決定をおこなうための知識を提供することです。最終的には、読者が自身のリスク許容度に合った戦略を見つけ出す一助となれば幸いです。

取引戦略の概要

今回は、通貨と貴金属市場の関係に焦点を当てます。貴金属は、電子機器からヘルスケアに至るまで、さまざまな産業に欠かせない現代経済の重要な要素です。貴金属の価格変動は、完成品の生産者にコスト増をもたらし、インフレを引き起こして生産レベルを低下させる可能性があります。また、貴金属を輸出する国にとっては需要が減少し、国内経済にも影響を与えることがあります。

例えば、金はカナダやアメリカで最大の鉱物輸出品の1つです。金は腐食に対する自然な耐性を持つため、精密電子機器の製造や宝飾品産業からの需要が高まっています。一方、パラジウムは多くの産業、特に自動車産業で不可欠とされています。自動車には20種類以上の部品に触媒コンバーターが必要とされ、特に排気管に組み込まれる触媒コンバーターにはかなりの量のパラジウムが使われています。  両国が自動車産業の主要輸出国であるため、パラジウム価格の変動はこれらの国の製造業に直接影響を及ぼします。

過去には、金価格とドルは逆相関の傾向がありました。ドルの価値が下がると、投資家はドルから資金を引き上げて金を利用したヘッジをおこなうことが多かったためです。しかし、近年の量的緩和政策により、両者の相関は必ずしも明確でなくなっています。

方法論の概要

私たちは、コンピュータがこれら3つの市場の価格データから独自の戦略を学習することを目指しています。もちろん、人間の直感的な理解や魅力的に思える戦略に信頼を寄せたくなることもあります。しかし、アルゴリズムを用いて戦略を学習させることで、コンピュータは人間が長い時間をかけて見つけるかもしれない関係性を迅速に発見する可能性があります。また、学習結果は戦略の精度の限界も明らかにしてくれるかもしれません。

通貨市場予測における貴金属市場の有用性を検証するため、次の3つの予測変数グループを用いてUSDCADの為替レートを予測することに挑戦しました。

1. USDCADペアの相場
2. XAUUSDとXPDUSDの相場
3. 上記のセット全体

データはMetaTrader 5端末から直接取得し、MQL5で作成したカスタムスクリプトを用いてCSV形式で書き出し、Pythonで処理しました。さらに、XAUUSDとUSDCADの間には-0.5、XPDUSDとUSDCADの間には-0.66という統計的に有意な負の相関が見られました。一方で、XAUUSDとXPDUSDの間には中程度の相関(0.37)が確認されました。

データの可視化も試みましたが、目視で明確な関係性は見出せませんでした。3D散布図を使用してデータをより高次元でプロットしましたが、データの分離が難しいことが判明しました。

そのため、上述した3つの予測変数グループを用いてUSDCADの為替レートを予測するいくつかのモデルを訓練しました。最もパフォーマンスが良かったのは、最初のグループ（USDCADの相場）を用いた線形モデルでした。しかし、線形モデルはパラメータ調整が不要なため、次に良い結果を示した線形サポートベクター回帰モデル(LSVR)を最適なモデルとして採用しました。

LSVRモデルでは、過剰適合を避けつつハイパーパラメーターを調整することができ、未知のデータに対してデフォルトのLSVRモデルよりも優れたパフォーマンスを示しました。しかし、同じ検証データでの線形モデルのパフォーマンスには及びませんでした。モデル選択は、トレーニングと検証の両方で5分割の時系列交差検証を用い、ランダムシャッフルなしで計算した平均RMSEによって実行しました。

最終的に、チューニングしたLSVRモデルをONNX形式にエクスポートし、MQL5でAIを統合した独自のエキスパートアドバイザー(EA)を構築しました。

データ収集

MetaTrader 5端末からデータを取得するために、便利なスクリプトを用意しました。このスクリプトを、分析したいチャートに添付するだけでデータ収集を開始できます。

このスクリプトは、指定したバーの数を取得し、データをCSV形式で出力します。時間情報を書き出すことも重要です。これは後にCSVファイルをPythonで1つのデータフレームに統合する際に必要となるためです。この際、すべてのデータは共通の日付のデータのみを結合します。

また、スクリプトには「#property script_show_inputs」というプロパティが含まれていることに注意してください。このプロパティを含めないと、スクリプトの入力設定を調整できなくなります。

//+------------------------------------------------------------------+
//|                                                     ProjectName  |
//|                                     Copyright 2020, CompanyName  |
//|                                     http://www.companyname.net   |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Zororo Ndawana"
#property link          "https://www.mql5.com/ja/users/gamuchiraindawa"
#property version   "1.00"
#property script_show_inputs

//---Amount of data requested
input int size = 100000; //How much data should we fetch?

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void OnStart()
  {
//---File name
   string file_name = "Market Data " + Symbol() + ".csv";

//---Write to file
   int file_handle=FileOpen(file_name,FILE_WRITE|FILE_ANSI|FILE_CSV,",");

   for(int i= size;i>=0;i--)
        {
        if(i == size)
        {
        FileWrite(file_handle,"Time","Open","High","Low","Close");
        }

        else
        {
        FileWrite(file_handle,iTime(Symbol(),PERIOD_CURRENT,i),
                iOpen(Symbol(),PERIOD_CURRENT,i),
                iHigh(Symbol(),PERIOD_CURRENT,i),
                iLow(Symbol(),PERIOD_CURRENT,i),
                iClose(Symbol(),PERIOD_CURRENT,i));
        }
        }

  }
//+------------------------------------------------------------------+

データの準備ができたので、Pythonでデータクリーニングを開始します。

データクリーニング

まず、必要な標準ライブラリをインポートします。

#Import the libraries we need
import pandas as pd
import numpy as np

以下は、このデモで使用しているライブラリのバージョンです。

#Display library versions
print(f"Pandas version {pd.__version__}")
print(f"Numpy version {np.__version__}")

Pandas version 2.2.1
Numpy version 1.26.4

次に、取得したCSVデータを読み込みます。

#Read in the data we need
usdcad = pd.read_csv("\\home\\volatily\\.wine\\drive_c\\Program Files\\MetaTrader 5\\MQL5\\Files\\Market Data USDCAD.csv")
usdcad = usdcad[::-1]
xauusd = pd.read_csv("\\home\\volatily\\.wine\\drive_c\\Program Files\\MetaTrader 5\\MQL5\\Files\\Market Data XAUUSD.csv")
xauusd = xauusd[::-1]
xpdusd = pd.read_csv("\\home\\volatily\\.wine\\drive_c\\Program Files\\MetaTrader 5\\MQL5\\Files\\Market Data XPDUSD.csv")
xpdusd = xpdusd[::-1]

インデックスとしてtime列を使用します。

#Set the time column as the index
usdcad.set_index("Time",inplace=True)
xauusd.set_index("Time",inplace=True)
xpdusd.set_index("Time",inplace=True)

データを結合します。

#Let's merge the data
merged_data = usdcad.merge(xauusd,suffixes=('',' XAU'),left_index=True,right_index=True)
merged_data = merged_data.merge(xpdusd,suffixes=('',' XPD'),left_index=True,right_index=True)

以下が私たちのデータです。

merged_data

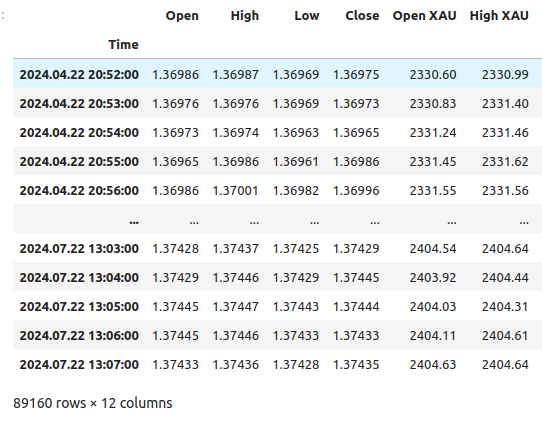
図1：結合されたデータフレーム

どの程度先の未来を予測したいのかを明確にします。

#Define the forecast horizon
look_ahead = 20

テストしたい予測変数の3つのグループを定義します。

#Define the predictors and target
ohlc_predictors = ['Open','High','Low','Close']
new_predictors = ['Open XAU','High XAU','Low XAU','Close XAU','Open XPD','High XPD','Low XPD','Close XPD']
predictors = ohlc_predictors + new_predictors

データにラベルを付けます。

#Let's add labels to the data
merged_data["Target"] = merged_data["Close"].shift(-look_ahead)

また、データを可視化する際に役立つラベルを作成します。これらのラベルは、各市場の変化をまとめたものです。

#Let's also add labels to help us visualize the relationships
merged_data["Binary Target"] = np.nan
merged_data["XAU Target"] = np.nan
merged_data["XPD Target"] = np.nan

#Define the target values
#Changes in the USDCAD Exchange rate
merged_data.loc[merged_data["Close"] > merged_data["Target"],"Binary Target"] = 0
merged_data.loc[merged_data["Close"] < merged_data["Target"],"Binary Target"] = 1
#Changes in the price of Gold
merged_data.loc[merged_data["Close XAU"] > merged_data["Close XAU"].shift(-look_ahead),"XAU Target"] = 0
merged_data.loc[merged_data["Close XAU"] < merged_data["Close XAU"].shift(-look_ahead),"XAU Target"] = 1
#Changes in the price of Palladium
merged_data.loc[merged_data["Close XPD"] > merged_data["Close XPD"].shift(-look_ahead),"XPD Target"] = 0
merged_data.loc[merged_data["Close XPD"] < merged_data["Close XPD"].shift(-look_ahead),"XPD Target"] = 1

#Drop any NA values
merged_data.dropna(inplace=True)

探索的データ分析

データを可視化するために、まず必要なライブラリをインポートします。

#Explorartory data analysis
import seaborn as sns
import matplotlib.pyplot as plt

ライブラリのバージョンを表示します。

#Display library version
print(f"Seaborn version: {sns.__version__}")

Seaborn version:0.13.2

まず、結合したデータフレームのインデックスをリセットします。

#Reset the index
merged_data.reset_index(inplace=True)

次に、相関ヒートマップを作ってみます。これにより、2つの貴金属とUSDCADペアの間に非常に強い相関があることが視覚的に確認できます。この相関は、これらの金属が両国の国内総生産に果たす役割についての基本分析と一致しています。しかし、残念ながらこの強い相関があるにもかかわらず、USDCAD為替レートの予測モデルにおいては、より高いパフォーマンスの向上には結びつきませんでした。

#Correlation heatmap
fig , ax = plt.subplots(figsize=(7,7))
sns.heatmap(merged_data.loc[:,predictors].corr(),annot=True,ax=ax)

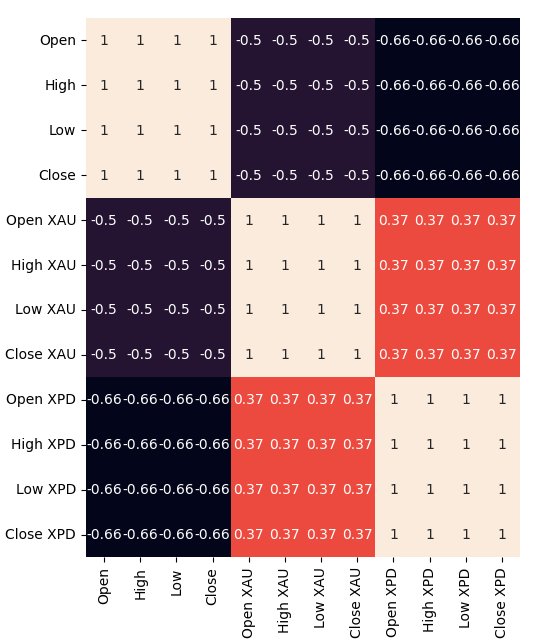
図2：相関ヒートマップ

金またはパラジウムの価格が上昇したケース（列1）と下落したケース（列2）を集めて、2種類のカテゴリプロットを作成しました。このプロットでは、各データポイントを色分けし、USDCAD為替レートが上昇した場合はオレンジ色のドット、下落した場合は青いドットで表しています。ご覧のとおり、両方の列で、USDCAD為替レートが上昇したケースと下落したケースが混在しています。これは、選択した貴金属価格の変動とUSDCAD為替レートの変動が関連していない可能性を示唆しています。

#Let's create categorical plots
sns.catplot(data=merged_data,x="XAU Target",y="Close",hue="Binary Target")

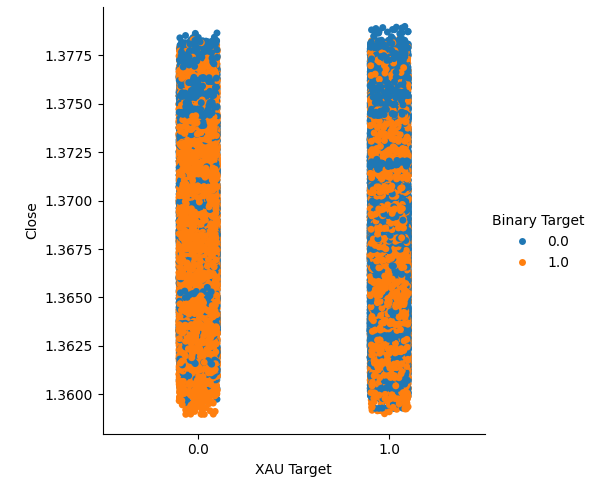
図3：金価格とUSDCAD終値のカテゴリプロット

#Let's create categorical plots
sns.catplot(data=merged_data,x="XPD Target",y="Close",hue="Binary Target")

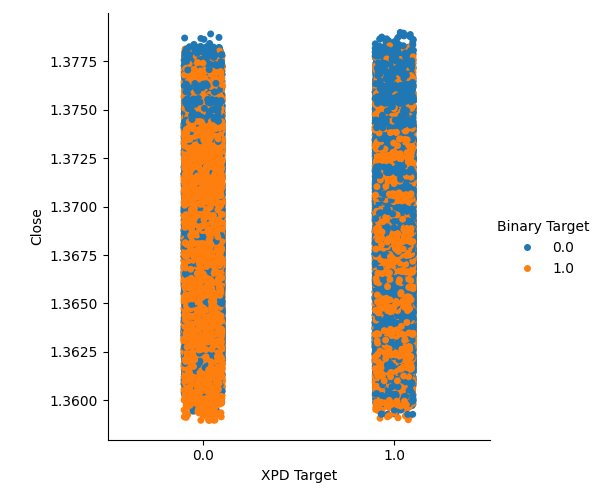
図4：USDCAD価格に対するパラジウム価格のカテゴリプロット

次に、パラジウムとUSDCAD市場の終値差を視覚化した散布図を作成しました。しかし、残念ながら、このプロットからは明確な関係を見出すことはできませんでした。各ポイントは、前述と同様にオレンジ色と青色のカラーマップで色分けしています。

#Let's visualize scatter plots
sns.scatterplot(data=merged_data,x="Close XPD",y="Close",hue="Binary Target")

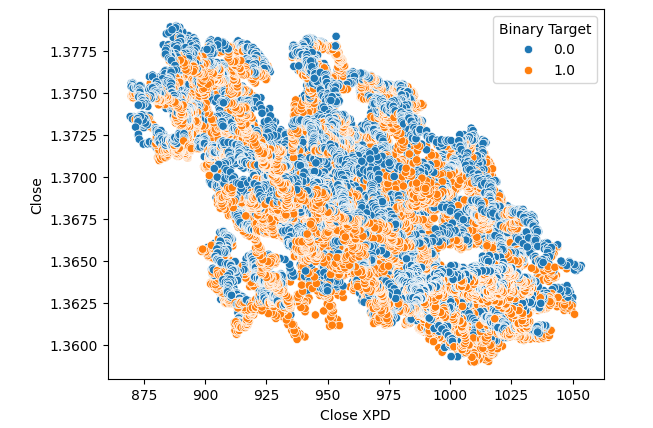
図5：XPDUSDとUSDCADの散布図

散布図において、パラジウムの代わりに金価格を代用しても改善はみられませんでした。

#Let's visualize scatter plots
sns.scatterplot(data=merged_data,x="Close XAU",y="Close",hue="Binary Target")

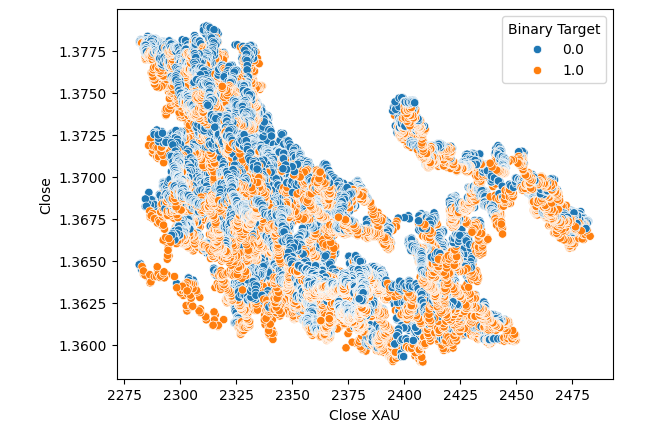
図6：USDCAD終値とXAUUSDの散布図

また、2つの金属同士の関係性を調べるため、金とパラジウムの価格に基づく散布図を作成しました。そして、各ポイントにはUSDCADペアの変化に応じて色を付けましたが、残念ながら関係性は明確にはなりませんでした。

#Let's visualize scatter plots
sns.scatterplot(data=merged_data,x="Close XPD",y="Close XAU",hue="Binary Target")

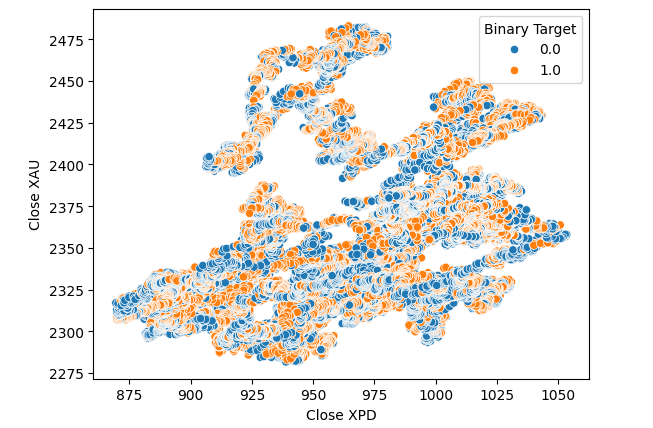
図7：XPDUSDとXAUUSDの散布図

効果を確認するために同時に十分な変数を表示していないため、関係が隠れている可能性があります。そこで、パラジウム、金、USDCADの終値を使用して3D散布図を作成しました。しかし、残念ながら、得られたプロットでは、データ内の分離レベルが低いクラスタのようなものが強調され、基本的にはこれまでに得た知見を繰り返す結果となりました。

#Visualizing 3D data
fig = plt.figure(figsize=(7,7))
ax = fig.add_subplot(111,projection='3d')
colors = ['blue' if movement == 0 else 'orange' for movement in merged_data.loc[0:1100,"Binary Target"]]
ax.scatter(merged_data.loc[0:1100,"Close"],merged_data.loc[0:1100,"Close XAU"],merged_data.loc[0:1100,"Close XPD"],c=colors)

#Set labels
ax.set_xlabel('USDCAD')
ax.set_ylabel('XAUUSD')
ax.set_zlabel('XPDUSD')

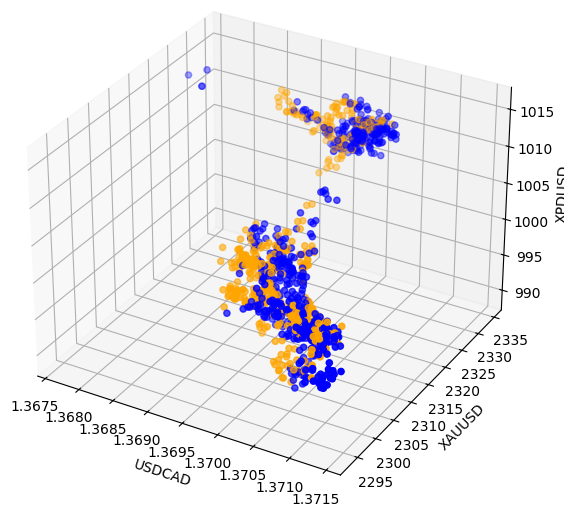
図8：市場データを3Dで可視化する

データモデリング

データのモデリングを始める準備をしましょう。まず、標準ライブラリをインポートします。

#Modelling the data
import sklearn
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import RobustScaler

ライブラリのバージョンを表示します。

#Print library version
print(f"Sklearn version {sklearn.__version__}")

Sklearn version 1.4.1.post1

モデルの訓練を始める前に、まずデータをスケールし、標準化します。

#Scale the data
scaled_data = pd.DataFrame(RobustScaler().fit_transform(merged_data.loc[:,predictors]),columns=predictors)

ここで、データを2つに分割します。一方は訓練と最適化に使用し、もう一方は検証と過剰適合のテストに使用します。

#Split the data
train_X,test_X,train_y,test_y = train_test_split(scaled_data,merged_data.loc[:,"Target"],shuffle=False,test_size=0.5)

次に、モデルをインポートします。

#Preparing to model the data
from sklearn.model_selection import TimeSeriesSplit
from sklearn.linear_model import LinearRegression
from sklearn.ensemble import RandomForestRegressor , GradientBoostingRegressor , BaggingRegressor
from sklearn.svm import LinearSVR
from sklearn.neighbors import KNeighborsRegressor
from sklearn.neural_network import MLPRegressor
from sklearn.metrics import root_mean_squared_error

時系列分割オブジェクトを作成します。

#Create the time series split object
tscv = TimeSeriesSplit(gap=look_ahead,n_splits=5)

モデルをリストに格納し、繰り返し処理できるようにします。

#Create a list of models
models = [
        LinearRegression(),
        RandomForestRegressor(),
        GradientBoostingRegressor(),
        BaggingRegressor(),
        LinearSVR(),
        KNeighborsRegressor(),
        MLPRegressor(hidden_layer_sizes=(100,10))
]

精度レベルを格納するデータフレームを作成します。

#List of models
columns = [
        "Linear Regression",
        "Random Forest",
        "Gradient Boost",
        "Bagging",
        "Linear SVR",
        "K-Neighbors",
        "Neural Network"
]

#Create a dataframe to store our error metrics
ohlc_error = pd.DataFrame(columns=columns,index=np.arange(0,5))
new_error = pd.DataFrame(columns=columns,index=np.arange(0,5))
all_error = pd.DataFrame(columns=columns,index=np.arange(0,5))

使用する予測変数を定義します。

#Setting the current predictors
current_predictors = predictors

上で定義された予測変数を用いて各モデルを交差検証します。

#Perform cross validation
for j in np.arange(0,len(models)):
        model = models[j]
        for i,(train,test) in enumerate(tscv.split(train_X)):
        model.fit(train_X.loc[train[0]:train[-1],current_predictors],train_y.loc[train[0]:train[-1]])
        all_error.iloc[i,j] = root_mean_squared_error(train_y.loc[test[0]:test[-1]],model.predict(train_X.loc[test[0]:test[-1],current_predictors]))

通常のOHLCデータを使って、誤差レベルを観察してみましょう。可視化および要約統計に基づくと、線形回帰モデルがこのタスクにおいて最も優れたパフォーマンスを発揮したことが明らかです。

ohlc_error

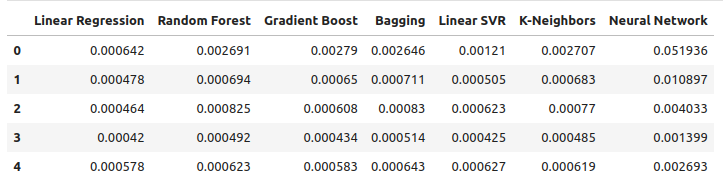
図9：OHLCのUSDCADデータを使って予測した場合の誤差レベル

データをプロットします。

ohlc_error.plot()

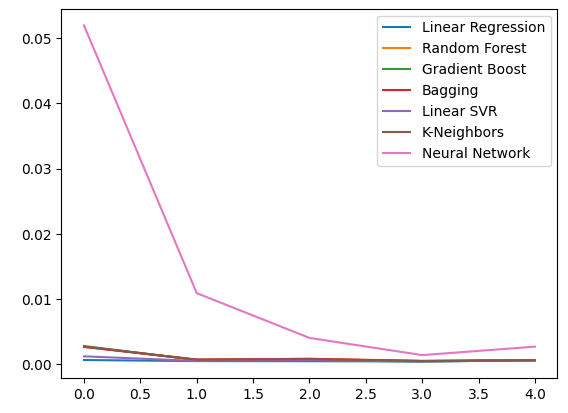
図10：予測変数の最初のセットを用いたモデルの精度

箱ひげ図を作成します。

fig = plt.figure(figsize=(5,5))
plt.boxplot(ohlc_error)

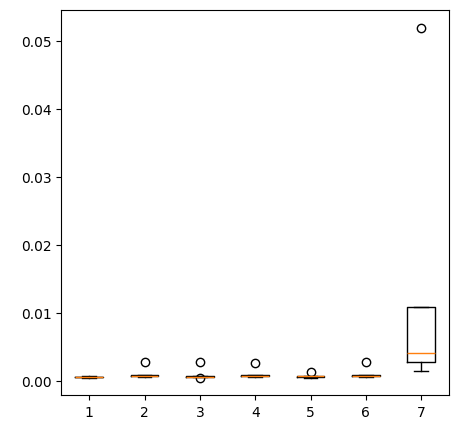
図11：最初の予測変数群で予測した場合のモデル精度

貴金属を使って USDCADの為替レートを予測する際の誤差レベルを観察してみましょう。線形回帰は依然として最もパフォーマンスの高いモデルですが、他のモデルとの間にはもはや大きな差はありません。

new_error

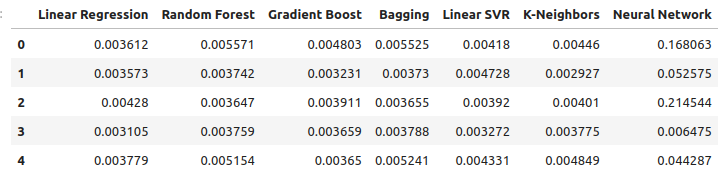
図12：新しい誤差レベル

新しい誤差レベルをプロットします。

new_error.plot()

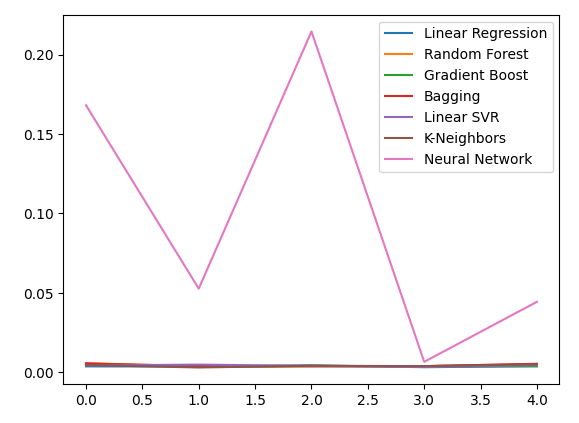
図13：新しい誤差レベル

新しい結果の箱ひげ図を作成します。

fig = plt.figure(figsize=(5,5))
plt.boxplot(new_error)

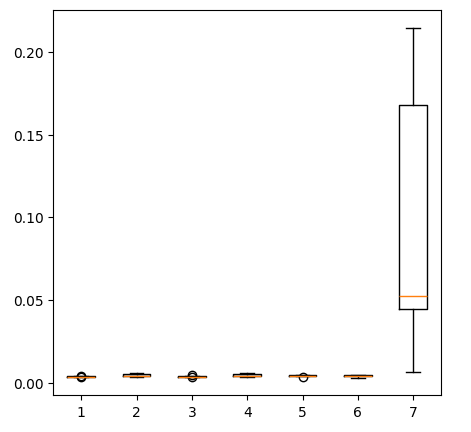
図14：貴金属市場データ使用時の誤差レベル

ここでは、利用可能なすべてのデータを用いた場合のパフォーマンスを考察します。線形モデルが他のすべてのモデルよりも優れていることが明らかです。次に、2番目に優れたモデルであるLinearSVRを最適化し、線形回帰よりも優れたパフォーマンスを発揮できるように試みます。

all_error

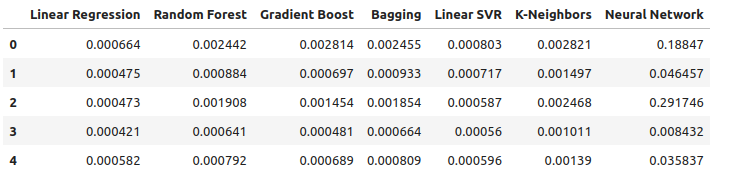
図15：保有するすべてのデータを使用した場合の精度

誤差レベルをプロットします。

all_error.plot()

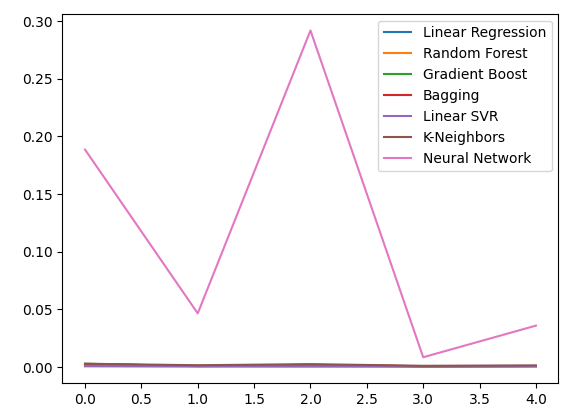
図16：保有するすべてのデータを使用した場合の精度の折れ線グラフ

保有するすべてのデータを使用して得られた誤差 レベルのボックスプロットを作成すると、単純な線形回帰が依然として最適な選択であることが明らかになります。

fig = plt.figure(figsize=(5,5))
plt.boxplot(all_error)

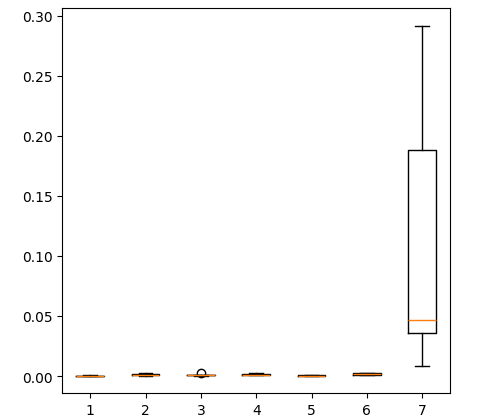
図17：保有するすべてのデータを使用した場合の精度の箱ひげ図

5 つの検証セット全体にわたるモデルの平均誤差レベルは、これまでのところ線形モデルが最良の選択であることを明確に示していますが、LinearSVR も遅れを取っていません。

all_error.mean()

Linear Regression 0.000523
Random Forest      0.001333
Gradient Boost       0.001227
Bagging                  0.001343
Linear SVR             0.000653
K-Neighbors            0.001837
Neural Network       0.114188
dtype: object

特徴量の重要性

モデルの最適化を始める前に、まずどの特徴量が重要かを評価しましょう。貴金属市場に関連するデータがこのテストでその価値を示すことを期待します。まず、相互情報量(MI)のレベルをテストします。MIは、予測子の1つの値を知ることで、ターゲットの値についてどの程度の確実性が得られるかを表す尺度です。MIは対数スケールであるため、実際には2を超えるMIスコアを見つけることはまれです。

まず、必要なライブラリをインポートします。

#Mutual information score
from sklearn.feature_selection import mutual_info_regression

ここで、各予測変数のMIスコアを計算します。

#Prepare the data for plotting
mi = mutual_info_regression(train_X,train_y)
mi = mi.reshape(1,12)
mi_scores = pd.DataFrame(mi,columns=predictors)

MIスコアをプロットすると、USDCAD市場のデータが貴金属市場のすべてのデータよりも有益である可能性が示唆されます。これは、交差検証テストによって確認されており、USDCAD市場の相場のみを使用した線形モデルが最も低い誤差を生成することが確認されました。

#Prepare the data for plotting
mi = mutual_info_regression(train_X,train_y)
mi = mi.reshape(1,12)
mi_scores = pd.DataFrame(mi,columns=predictors)
#Plot the scores
mi_scores.plot.bar()

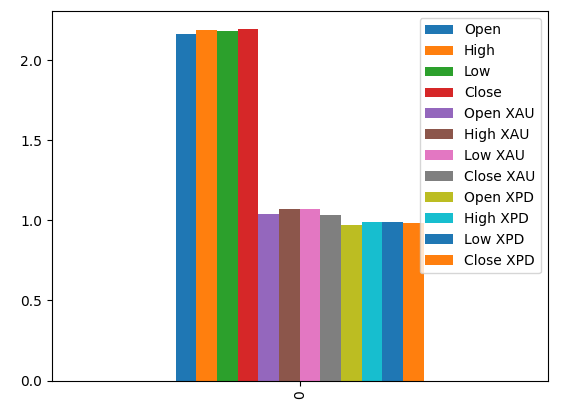
図18：3つのデータセットの相互情報スコア

次にSHAP値を計算します。SHAP値は、機械学習モデルにおけるグローバルな特徴の重要性を特定するのに役立つブラックボックス的な説明変数です。

SHAPライブラリをインポートします。

#The Linear SVR appears to be performing second best
import shap

LSVRモデルを初期化します。

#Initialize the model
model = LinearSVR()
model.fit(train_X,train_y)

SHAP値を計算します。

#Compute SHAP values
explainer = shap.Explainer(model,train_X)
explanations = explainer(train_X)

グローバルな特徴量の重要性を表示します。

#Plot SHAP values
shap.plots.violin(explanations)

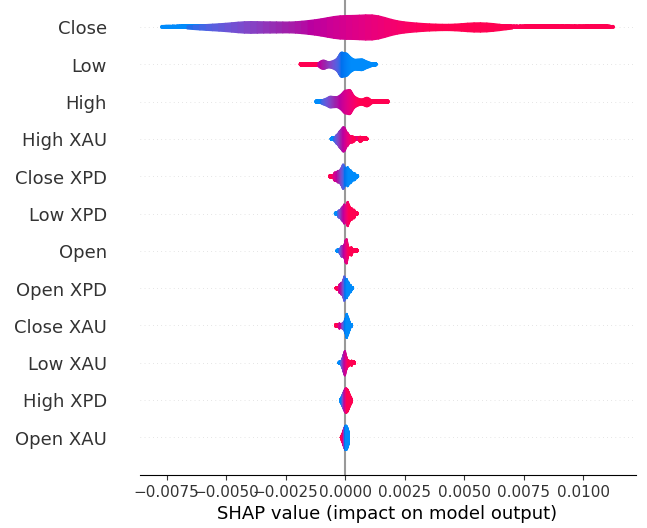
図19：SHAPの重要度

SHAPの解釈は、相互情報の評価とは一致しません。この不一致の問題については、以前の記事で詳しく取り上げましたが、特徴量の重要性を評価するのは難しく、あまり重要視しすぎないようにする必要があります。ただし、どちらの解釈も、貴金属市場には有用な情報が含まれていることを示唆しています。

ハイパーパラメータの調整

モデルをチューニングすることで、デフォルトのモデルを使用する場合よりも未知のデータに対して優れたパフォーマンスを発揮できる可能性があります。

モデルを調整するために、まず必要なライブラリをインポートします。

#Parameter tuning
from sklearn.model_selection import RandomizedSearchCV

ここでモデルを初期化します。

#Reinitialize the model
model = LinearSVR()

次にチューニングパラメータを定義します。モデルを指定し、可能なパラメータ値の辞書を渡した後、実行する反復の総回数を指定します。5分割交差検証を実施して負の平均二乗誤差を測定します。これは、検証誤差が最も低いモデルを選択することを意味します。最後に、n_jobsを-1に設定することで、利用可能なすべてのCPUコアで並列に検索を実行できます。

#Define the tuner
tuner = RandomizedSearchCV(
        model,
        {
        "epsilon" : [0,10,100,1000],
        "tol":[0.01,0.001,0.0001,0.00001,0.0000001],
        "C":[1,10,100,1000,10000],
        "loss":['epsilon_insensitive', 'squared_epsilon_insensitive']  
        },
        n_iter=1000,
        cv=5,
        n_jobs=-1,
        scoring="neg_mean_squared_error"
)

チューナーを適合させます。

#Let's fit the tuner
tuner_results = tuner.fit(train_X,train_y)

以下が、見つかった最高のパラメータです。

#Let's see the best parameters we found
tuner_results.best_params_

{'tol':1e-05, 'loss': 'squared_epsilon_insensitive', 'epsilon':0, 'C':10000}

過剰適合のテスト

過剰適合をテストするには、まずモデルを初期化する必要があります。

#Testing for overfitting
benchmark =  LinearRegression()
default_lsvr = LinearSVR()
customized_lsvr = LinearSVR(tol=1e-05,loss='squared_epsilon_insensitive',epsilon=0,C=10000)

ここでインデックスをリセットし、交差検証を実行できるようにします。

#Reset the indexes
test_y = test_y.reset_index()
test_X = test_X.reset_index()

データを書式設定します。

#Format the data
test_y = test_y.loc[:,"Target"]
test_X = test_X.loc[:,predictors]

誤差レベルを格納するデータフレームを作成します。

#Create dataframes to store our error levels
test_error = pd.DataFrame(columns=["Linear Regression","LSVR","Customized LSVR"],index=[0,1,2,3,4])

訓練セットでモデルを訓練します。

#Fit the models on the training set
benchmark.fit(train_X,train_y)
default_lsvr.fit(train_X,train_y)
customized_lsvr.fit(train_X,train_y)

モデルをリストに保存します。

models = [benchmark,default_lsvr,customized_lsvr]

テストセットで各モデルを交差検証します。

for j in np.arange(0,len(models)):
        model = models[j]
        for i,(train,test) in enumerate(tscv.split(test_X)):
        model.fit(test_X.loc[train[0]:train[-1],:],test_y.loc[train[0]:train[-1]])
        test_error.iloc[i,j] = root_mean_squared_error(test_y.loc[test[0]:test[-1]],model.predict(test_X.loc[test[0]:test[-1],:]))

以下がテストの誤差です。

test_error

Linear Regression	LSVR	Customized LSVR
0.000598	0.000542	0.000743
0.000472	0.000573	0.000722
0.000318	0.000451	0.000333
0.000341	0.000366	0.000499
0.00043	0.000839	0.00043

5つのフォールド全体の平均パフォーマンスによれば、線形モデルは依然として最も優れたパフォーマンスを示しました。ただし、デフォルトモデルを上回るパフォーマンスを発揮することができました。

#Let's calculate our mean performances
test_error.mean()

Linear Regression      0.000432
LSVR                          0.000554
Customized LSVR      0.000545
dtype: object

テスト誤差を可視化します。

#Let's visualize our error
test_error.plot()

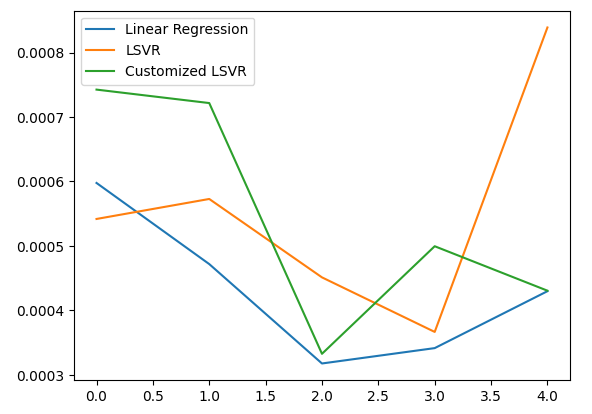
図20：テスト誤差の可視化

テストの誤差率を箱ひげ図にします。

#Create a boxplot of the error
sns.boxplot(data=test_error)

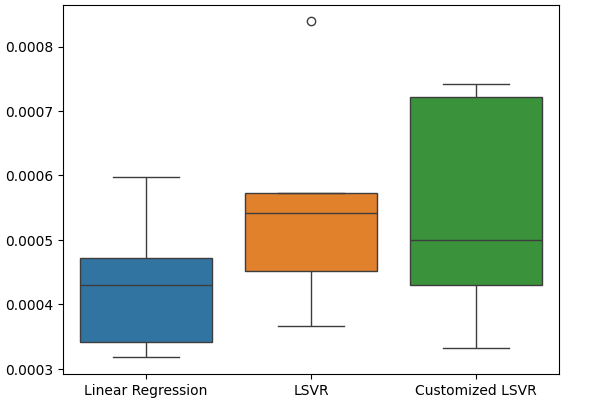
図21：テスト誤差の可視化

ONNXにエクスポートするモデルの準備

モデルをONNX形式にエクスポートする前に、まず平均を減算し、標準偏差で割ることでデータをスケーリングおよび標準化する必要があります。その後、スケーリング係数をCSVファイルに書き出し、MQL5で手順を再現できるようにします。

まず、スケーリング係数を格納するためのデータフレームを作成します。

#Let's scale our data
scaling_factors = pd.DataFrame(columns=predictors,index=['mean','standard deviation'])
X = merged_data.loc[:,predictors]
y = merged_data.loc[:,"Target"]

次に平均と標準偏差を保存し、最後にスケーリングプロシージャを実行します。

#Let's fill each column
for i in np.arange(0,len(predictors)):
        scaling_factors.iloc[0,i] = X.iloc[:,i].mean()
        scaling_factors.iloc[1,i] = X.iloc[:,i].std()
        X.iloc[:,i] = ( ( X.iloc[:,i] - scaling_factors.iloc[0,i] ) / scaling_factors.iloc[1,i])

スケーリング係数を保存します。

#Save the scaling factors as a CSV
scaling_factors.to_csv("/home/volatily/.wine/drive_c/Program Files/MetaTrader 5/MQL5/Files/usd_cad_xau_xpd_scaling_factors.csv")

モデルをONNXにエクスポートする

ONNXは、Open Neural Network Exchangeの略で、オープンソースの相互運用可能な機械学習フレームワークです。開発者は、言語に依存しないフレームワークを使用して機械学習モデルを作成、共有、展開することができます。このフレームワークは、各機械学習モデルをノードとグラフのツリーとして表現することで実現されており、ONNX APIをサポートする任意の言語で元のモデルを再構成することが可能です。

まず、必要なライブラリをインポートします。

#Let's prepare to export our model to ONNX format
import onnx
import netron
import skl2onnx
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType

ライブラリのバージョンを表示します。

#Display library versions
print(f"Onnx version: {onnx.__version__}")
print(f"Netron version: {netron.__version__}")
print(f"Skl2onnx version: {skl2onnx.__version__}")

Onnx version:1.15.0
Netron version:7.8.0
Skl2onnx version:1.16.0

次に、モデルの入力タイプを定義します。

#Define the input type
initial_types = [('float_input',FloatTensorType([1,12]))]

保有するすべてのデータでモデルを訓練します。

#Train the model on all the data we have
customized_lsvr = LinearSVR(tol=1e-05,loss='squared_epsilon_insensitive',epsilon=0,C=10000)
customized_lsvr.fit(X,y)

モデルをONNX形式に変換します。

#Covert the sklearn model
onnx_model = convert_sklearn(customized_lsvr,initial_types=initial_types)

ONNXモデルを保存します。

#Save the onnx model
onnx_name = "USDCAD XAUUSD XPDUSD M1 Float.onnx"
onnx.save(onnx_model,onnx_name)

ONNXモデルを表示します。

#View the onnx model
netron.start(onnx_name)

図22：netronで可視化されたONNXモデル

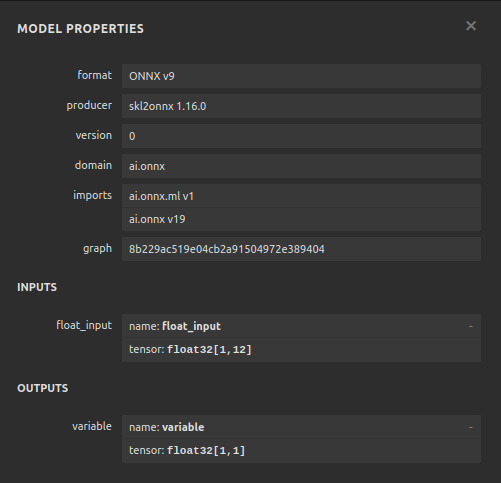
図23：ONNXモデルのパラメータは、モデルの入力と出力に関する私たちの予想と一致している

MQL5での実装

MQL5でAIを統合したEAを実装するには、まず先にエクスポートしたONNXモデルをロードする必要があります。

//+------------------------------------------------------------------+
//|                                                    USDCAD AI.mq5 |
//|                                        Gamuchirai Zororo Ndawana |
//|                          https://www.mql5.com/ja/gamuchiraindawa |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Zororo Ndawana"
#property link      "https://www.mql5.com/ja/gamuchiraindawa"
#property version   "1.00"

//+------------------------------------------------------------------+
//| Resources                                                        |
//+------------------------------------------------------------------+
#resource  "\\Files\\USDCAD XAUUSD XPDUSD M1 Float.onnx" as const uchar onnx_buffer[];

次に、ポジションを建てたり閉じたりできるように、取引ライブラリをロードしなければなりません。

//+------------------------------------------------------------------+
//| Libraries we need                                                |
//+------------------------------------------------------------------+
#include <Trade/Trade.mqh>
CTrade Trade;

また、プログラム全体で必要となるグローバル変数をいくつか定義しておきましょう。

//+------------------------------------------------------------------+
//| Global variables                                                 |
//+------------------------------------------------------------------+
long onnx_model;
double mean_values[12],std_values[12];
vectorf model_output = vectorf::Zeros(1);
int model_forecast,state;
double ask,bid;

プログラムで使用するヘルパー関数を定義しましょう。ONNXモデルをロードし、入出力シェイプを設定する関数が必要です。成功すればtrueを返し、そうでなければfalseを返す関数を使います。この関数は、まず先に作成したバッファからモデルを作成し、次に入出力シェイプの設定と検証を試みます。

//+------------------------------------------------------------------+
//| This function is responsible for loading our ONNX model          |
//+------------------------------------------------------------------+
bool load_onnx(void)
  {
//--- First we must create the model from the buffer
   onnx_model = OnnxCreateFromBuffer(onnx_buffer,ONNX_DEFAULT);

//--- Now we shall define our I/O shape
   ulong input_shape [] = {1,12};
   ulong output_shape []  = {1,1};

   if(!OnnxSetInputShape(onnx_model,0,input_shape))
        {
        Comment("Failed to set ONNX input shape!");
        return(false);
        }

   if(!OnnxSetOutputShape(onnx_model,0,output_shape))
        {
        Comment("Failed to set ONNX output shape!");
        return(false);
        }

//--- Everything went fine
   return(true);
  }
//+------------------------------------------------------------------+

この関数は、スケーリング値が格納されたCSVファイルを読み込み、定義したグローバルスコープ配列に格納します。

//+------------------------------------------------------------------+
//| This function will read our scaling factors and store them       |
//+------------------------------------------------------------------+
bool load_scaling_factors(void)
  {
//--- Read in the file
   string file_name = "usd_cad_xau_xpd_scaling_factors.csv";

//--- Try open the file
   int result = FileOpen(file_name,FILE_READ|FILE_CSV|FILE_ANSI,","); //Strings of ANSI type (one byte symbols).

//--- Check the result
   if(result != INVALID_HANDLE)
        {
        Print("Opened the file");
        //--- Store the values of the file

        int counter = 0;
        string value = "";

        while(!FileIsEnding(result) && !IsStopped()) //read the entire csv file to the end
        {

        if(counter > 100)  //if you aim to read 10 values set a break point after 10 elements have been read
                break; //stop the reading progress

        value = FileReadString(result);
        Print("Trying to read string: ",value," count value: ",counter);

        //--- Check where we are
        if((counter >= 14) && (counter < 26))
        {
                mean_values[counter - 14] = (float) value;
        }
        //--- Check where we are
        if((counter >= 27) && (counter < 39))
        {
                std_values[counter - 27] = (float) value;
        }
        //--- Reading a new row
        if(FileIsLineEnding(result))
        {
                Print("row++");
        }

        counter++;
        }
        //---Close the file
        ArrayPrint(mean_values);
        ArrayPrint(std_values);
        FileClose(result);
        return(true);
        }
//--- We failed to find the file
   else
        {
        Comment("Failed to find the file containing scaling factors");
        return(false);
        }
  }

また、市場から更新された価格相場を取得する関数も必要です。

//+------------------------------------------------------------------+
//| Update market prices                                             |
//+------------------------------------------------------------------+
void update_market_prices(void)
  {
   ask = SymbolInfoDouble(_Symbol,SYMBOL_ASK);
   bid = SymbolInfoDouble(_Symbol,SYMBOL_BID);
  }

最後に、モデルから予測値を取得する関数が必要です。予測関数は、モデルにデータを渡す前に、まずデータをスケーリングします。

//+------------------------------------------------------------------+
//| Model predict                                                    |
//+------------------------------------------------------------------+
void model_predict(void)
  {
//--- First fetch the market data

   vectorf model_input  =
        {
        iOpen("USDCAD",PERIOD_CURRENT,0),iHigh("USDCAD",PERIOD_CURRENT,0),iLow("USDCAD",PERIOD_CURRENT,0),iClose("USDCAD",PERIOD_CURRENT,0),
        iOpen("XAUUSD",PERIOD_CURRENT,0),iHigh("XAUUSD",PERIOD_CURRENT,0),iLow("XAUUSD",PERIOD_CURRENT,0),iClose("XAUUSD",PERIOD_CURRENT,0),
        iOpen("XPDUSD",PERIOD_CURRENT,0),iHigh("XPDUSD",PERIOD_CURRENT,0),iLow("XPDUSD",PERIOD_CURRENT,0),iClose("XPDUSD",PERIOD_CURRENT,0)
        };

//--- Now standardize and scale the data
   for(int i =0; i < 12; i++)
        {
        model_input[i] = ((model_input[i] - mean_values[i]) / std_values[i]);
        }

//--- Now fetch a prediction from our model
   OnnxRun(onnx_model,ONNX_DEFAULT,model_input,model_output);

//--- Store our model's forecat
   if(model_output[0] > iClose("USDCAD",PERIOD_CURRENT,0))
        {
        model_forecast = 1;
        }
   else
        if(model_output[0] < iClose("USDCAD",PERIOD_CURRENT,0))
        {
        model_forecast = -1;
        }
  }

EAを初期化する際、まずONNXファイルを読み込み、次にスケーリング値を読み込みます。これらの手順のいずれかが失敗した場合、すべてのプロセスを中止します。

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- This function will load our ONNX model
   if(!load_onnx())
        {
        return(INIT_FAILED);
        }

//--- This function will load our scaling factors
   if(!load_scaling_factors())
        {
        return(INIT_FAILED);
        }
//---
   return(INIT_SUCCEEDED);
  }

EAがチャートから削除されるたびに、不要になったリソースを解放します。

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//--- Free up the resources we do not need
   OnnxRelease(onnx_model);
   ExpertRemove();
  }

最後に、買値と売値に変化があるたびに、更新された価格をメモリに保存し、AIモデルから新しい予測を取得します。  ポジションがない場合は、AIモデルが提案するポジションを取りますが、ポジションがある場合は、AIモデルの予測が現在のポジションに反していないか確認します。

void OnTick()
  {
//--- Update the market prices
   update_market_prices();

//--- Fetch a forecast from our model
   model_predict();

//--- Find a trading oppurtunity
   if(PositionsTotal() == 0)
        {
        if(model_forecast == -1)
        {
        Trade.Sell(0.2,_Symbol,ask,0,0,"USDCAD AI");
        state = -1;
        }

        else
        if(model_forecast == 1)
        {
                Trade.Buy(0.2,_Symbol,ask,0,0,"USDCAD AI");
                state = 1;
        }
        }

//--- Check for reversals
   if(PositionsTotal() > 0)
        {
        if(state != model_forecast)
        {
        Alert("Reversal detected by our AI system, closing all positions now!");
        Trade.PositionClose(_Symbol);
        }
        }

  }
//+------------------------------------------------------------------+

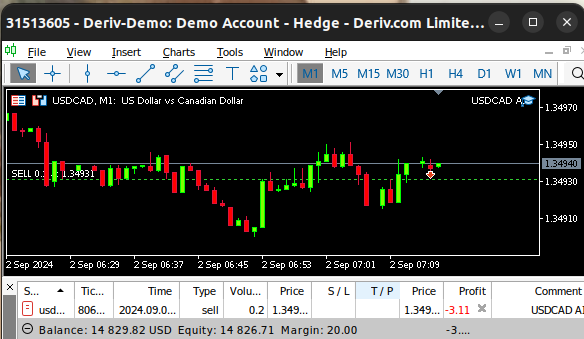
図24：EAの動作

図25：私たちのAIシステムが逆転の可能性を検知した

結論

本日の記事では、相互に関連する市場の間に存在する可能性のある隠れた関係性を明らかにする手法を示しました。しかし、実証分析の結果、通常の市場データとより単純な線形モデルを使用する方が良い可能性があることが分かりました。この理由として、市場データにはノイズが含まれる可能性が高いため、単純なモデルの方が有効であることが考えられます。また、ノイズの多いデータでは、複雑なモデルは入力データの変動に敏感になりやすく、その結果、単純なモデルの方がより良いパフォーマンスを発揮する傾向があることも示唆されています。