知っておくべきMQL5ウィザードのテクニック（第24回）：移動平均

MetaTrader 5 — トレーディングシステム | 16 8月 2024, 15:07

はじめに

MQL5ウィザードについての本連載の続きとして、移動平均指標を取り上げ、一部のトレーダーにとって斬新な方法で、この指標をすでに利用可能なツールのライブラリにどのように追加できるかを見ていきます。移動平均には、チャートに取り付け可能な単一の時系列としてだけでなく、オシレーターやエンベロープ指標としても非常に多くのバリエーションがあります。

ピタゴラス平均と呼ばれる3つの移動平均(MA)の特別なカテゴリ内で、これらの複数のアプリケーションまたはバリエーションを検討します。この名前下にある3つのMAは、算術平均(AM)、幾何平均(GM)、調和平均(HM)です。最初の算術平均は、MAと聞いて誰もが最初に思い浮かべるものです。これは単純に、セット内の任意の数の値の平均です。ウィキペディアには、これら3つの手段を図にまとめた非常に興味深いものがあります。以下をご覧ください。

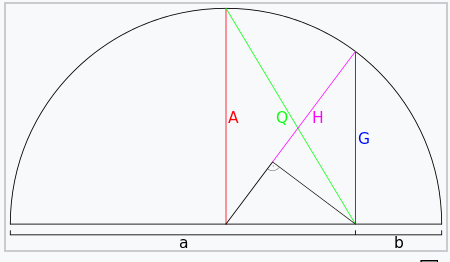
上に示されているのは、直径が2つの値aとbに不均等に分割された半円です。この2つの値の算術平均は、図では赤でAと表示されていますが、これは予想通り半円の半径に相当します。念のため、算術平均の公式を以下に示します。

ここで

AMは算術平均
xは平均が計算される集合の値
nは集合のサイズ

次に、幾何平均は式で与えられます。

ここで

GMは幾何平均
xとnは上記のAMと同じものを表す

上の半円上のGM値は、Gと書かれた青い弦と同じ長さであり、大きなa値よりも小さなb値に重みが置かれています。また、注目すべきは、すべての値が負であっても、GMは常に正になるということです。このシナリオは、セットにすべて負の数値が含まれている場合は、計算されたGMに負の値を割り当てることで対処できますが、負の値と正の値が混在している場合は、実際のGMを作成することが困難になります。

調和平均の場合、半円表現はHと記された線であり、その長さはaとbの平均に相当します。その式は次のように表されます。

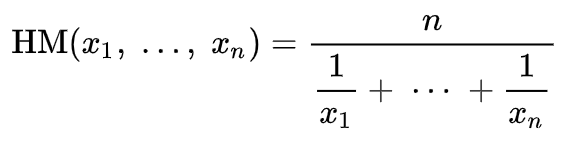
ここで

HMはもちろん調和平均
xとnは上記と同じ

もし何らかの理由でbの値がゼロであったとしたら、半円図からわかるように、幾何平均も調和平均もゼロになります（調和平均を計算するときに「ゼロ除算」を得るにもかかわらずです）。興味深いことに、これは平均が計算される数値の数に関係なく（つまり2以上であれば）当てはまります。これらの数値のどれかがゼロである限り、すべての値の幾何平均と調和平均はゼロです。

この性質は要するに、集合の最小値がゼロに近い度合いを測るものです。しかし、これはトレーダーにとって何を意味するのでしょうか。考慮されている移動平均のデータによって、さまざまな意味を持ちます。

もしそれが単なる証券価格であれば、移動平均線は支持の良い代用品となるでしょう。なぜでしょうか。GMとHMは低い値に重みを置いています。これは、例えば、これらの平均値を下回る価格ブレイクは、通常の移動平均を下回るブレイクよりも大きな意味を持つ可能性があることを意味します。したがって、GMとHMは、ほとんどのプライスアクションの支持側で役立つ可能性があります。抵抗側ではどうでしょうか。以下の式から、GMとHMの反転した等価物を得ることができます。

HM' = AM + (AM - HM)

GM' = AM + (AM - GM)

ここで

HM'は反転調和平均
GM'は反転幾何平均
AM、GM、HMは上記と同じ

GMとHMの反転した等価物または反転を導入することで、ある意味、平均にバランスを加えることになります。なぜなら、これらの反転の重み付けは、平均が計算される値のどのセットにおいても、より大きな値に傾くからです。これはまた、抵抗に関する質問に答えるために、抵抗レベルを定義するためのより効果的なプロキシとして機能する、より高い価格加重平均としてGM'またはHM'のいずれかを使用できるようになることを意味します。

ここでの目的にとって、GMとHMの違いは程度の問題です。これは、両者とも値が小さい方に重みを置いているためです。主な違いは、HMの方がGMよりもゼロに対する重みが高いことです。

カスタム実装

ここでは、これらの単純な平均値をMQL5でどのように活用し、そのユニークな特性を生かすことができるかを見ていきます。まずは基本的な算術平均です。この3つの平均の中で最も普通なのは、平均の基本をそのまま取り入れたものであり、この平均を使用する最も簡単な方法は、価格のクロスオーバーを監視することです。価格構造を追跡する際の移動平均の用途は数多くありますが、これは間違いなく最も単純明快で一般的なものでしょう。そのため、主に上記ですでに紹介したGMおよびHMの他のあまり一般的でない手段との比較目的として、この適用をここで紹介します。

ウィザードで選択されたシグナルクラスは、取引される証券のロングとショートの条件を決定する際に重み付け、つまり発言権を割り当てることができるため、ベンチマークと比較は、特にシグナルクラスについて、MQL5ウィザードが組み立てたEAに固有のものです。vectorデータ型のおかげで、この関数から簡単にAMバッファを得ることができます。

//+------------------------------------------------------------------+
//| Arithmetic Mean                                                  |
//+------------------------------------------------------------------+
double CSignalAM::AM(int Index, int Mask = 8)
{  vector _am;
   _am.CopyRates(m_symbol.Name(), m_period, Mask, Index, m_fast);
   return(_am.Mean());
}

また、移動平均のクロスオーバーを追跡する上で鍵となる現在の価格ギャップを、以下の関数で測定することができます。

   double            CrossOver(int Index)
   {                 m_close.Refresh(-1);
      return(AM(Index) - m_close.GetData(Index));
   }

通常、手動で取引する場合は、GMとHMをカスタム指標としてコード化する方が理にかなっています。これはEAのためのもので、手動で取引するわけではないので、内蔵のクラス価格バッファにアクセスする関数で十分です。

GMのようなHM平均は、低い値に重みがあり、上で見たように、これをミラーリングして、高い値に重みがある別の平均、HM'を作ることができます。つまり、HMとHM'は両極端に偏重した平均であるため、乖離を拾いやすいのです。さて、相違点といえば、まず思い浮かぶのはオシレーターとその証券価格のトレンドの違いでしょう。このような試合は非常に短期間で起こるので、それをキャッチするためには警戒が必要です。あるいは、週足では強い強気トレンドが形成されているにもかかわらず、1時間足では価格が下落しているように、1つの証券の価格が異なる時間軸で完全に乖離している場合もあります。

しかし、調和平均の「偏り」を利用するには、高値と安値の乖離に注目します。具体的には、高値の変化と安値の変化の方向性が異なる場合にのみ、ポジションを建てるようにします。しかし、これにはまだ2つの方法があります。高値の下落と安値の上昇でポジションを建てるか、高値の上昇と安値の下落でポジションを建てるかです。この記事では後者を探っていますが、すべてのソースは記事の最後に添付されているので、読者はこれをカスタマイズして、ここで取り上げていない、より一般的な包み足ダイバージェンス(engulf divergence)を試すことができます。

高値の調和平均が上昇し、同時に安値の調和平均が下落するのを見計らってポジションを建てます。ロングまたはショートのポジションを建てる際の目安となるフォローアップ指標はここでカスタマイズできますが、フォローアップとして使用するのは、単純に終値の変化です。前のバーでダイバージェンスが発生した後、終値が上昇したらロングを建て、その逆も然りです。

AMで見たように、これを実装するためのコードも2つあります。まず、HM関数とそのミラーを以下に示します。

//+------------------------------------------------------------------+
//| Harmonic Mean                                                    |
//+------------------------------------------------------------------+
double CSignalHM::HM(int Index, int Mask = 8)
{  vector _hm, _hm_i;
   _hm_i.CopyRates(m_symbol.Name(), m_period, Mask, Index, m_slow);
   _hm = (1.0 / _hm_i);
   return(m_slow / _hm.Sum());
}
//+------------------------------------------------------------------+
//| Inverse Harmonic Mean                                            |
//+------------------------------------------------------------------+
double CSignalHM::HM_(int Index, int Mask = 8)
{  double _am = AM(Index, Mask);
   double _hm = HM(Index, Mask);
   return(_am + (_am - _hm));
}

ダイバージェンス関数は次のようになります。

   double            Divergence(int Index)
   {                 return((HM_(Index, 2) - HM_(Index + 1, 2)) - (HM(Index, 4) - HM(Index + 1, 4)));
   }

ベク取るを使用してデータをコピーし読み込む際、「レートマスク」インデックスは不可欠です。なぜなら、様々な価格(OHLC)を素早く切り替えることができ、同時にvectorデータ型に内蔵された統計関数を使用することで、多くのコードを書く必要がなくなるからです。さらに、これらのピタゴラス平均のテスト関数は、速い期間と遅い期間の2つの移動平均期間を使用します。これは、特にエントリポイントとエグジットポイントを決定するためにクロスオーバー戦略を使用する場合、一般的な慣行です。調和平均と幾何平均の両バッファについては、遅い期間に頼って値を計算しています。速い期間は算術平均バッファのみに使用されています。

もちろん、これはご自分の戦略やアプローチに合うように変更したり調整したりすることができますが、ここでは純粋にテストを目的としています。

最後に、調和と同様の幾何平均がボリンジャーバンドと同様の方法で適用されます。調和は小さな値に重みがあり、その度合いもやや大きいようです。よく知られているように、ボリンジャーバンドは移動平均に2つの標準偏差を加えたものであるため、この程度の重み付けはボリンジャーバンドのような指標を導き出すのに理想的です。その実装に入る前に、幾何平均とそのミラー（高値加重等価値）を求めるコードは以下のようになります。

//+------------------------------------------------------------------+
//| Geometric Mean                                                   |
//+------------------------------------------------------------------+
double CSignalGM::GM(int Index, int Mask = 8)
{  vector _gm;
   _gm.CopyRates(m_symbol.Name(), m_period, Mask, Index, m_slow);
   return(pow(_gm.Prod(), 1.0 / m_slow));
}
//+------------------------------------------------------------------+
//| Inverse Geometric Mean                                           |
//+------------------------------------------------------------------+
double CSignalGM::GM_(int Index, int Mask = 8)
{  double _am = AM(Index, Mask);
   double _gm = GM(Index, Mask);
   return(_am + (_am - _gm));
}

今回も、vectorデータ型とその組み込み関数を使用して、コーディングプロセスを簡略化します。バンドのバッファは2つで、上のバンドと下のバンドからなります。これらも以下の2つの関数から取得されます。

   double            BandsUp(int Index)
   {  vector _bu;
      _bu.CopyRates(m_symbol.Name(), m_period, 2, Index, m_slow);
      return(GM_(Index, 2) + (2.0 * _bu.Std()));
   }

   double            BandsDn(int Index)
   {  vector _bd;
      _bd.CopyRates(m_symbol.Name(), m_period, 4, Index, m_slow);
      return(GM(Index, 4) - (2.0 * _bd.Std()));
   }

この2つの関数は、それぞれBandsUpとBandsDn関数の上のバンド価格と下のバンド価格を返すだけです。これらの返された値は、多くの形態で分析するために、並列バッファに簡単に再構成することができます。単にロングポジションやショートポジションの可能性があるかどうかを確認するために、クロスオーバー方式でそれらを使用しているだけです。ロングポジションを確認するには、価格が下のバンドを下から超えたこと、つまり下のバンドより下にあったが、今は上にあることを確認する必要があります。同様に、ショートポジションを確認するには、価格が上のバンドより上にあったが、その後の価格バーで上のバンドより下になった場合、上のバンドの上からの価格クロスを確認する必要があります。

カスタムシグナルクラス

これら3つのピタゴラスMAはそれぞれ、EAで使用するために、そのうちの1つを選択できる追加パラメータを持つ1つのクラスに組み合わせることができます。ただし、これらのシグナルを別々のシグナルクラスとして実装しているのは、それぞれの平均の理想的な重みを最適化することで、シグナルクラスの重み設定を検討し、どのシグナルが、ひいてはどの平均が、EAでの予測や注文に有用であるかを把握するためです。

ただし、相対的な重要性を把握する前に、各信号クラスを個別に独立したテストを最初に実行して、最終的に得られる相対的な重みが、最初に実行したテストの検証（または反証）として役立つようにすることをお勧めします。そこで、まず3つの平均それぞれについてEAを開発し、それぞれのパフォーマンスを評価するために個別にテストします。これらの結果が得られたら、3つの平均を組み合わせたEAでテストをおこない、それぞれの平均の相対的な重みを最適化します。

算術平均シグナルクラスのロング/ショート条件を開発するには、単純に、上記でコードを共有したCrossover関数が返すクロスオーバー値の変化を確認します。ロングとショートの条件コードは非常に短いです。

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalAM::LongCondition(void)
{  int result = 0;
   if(CrossOver(StartIndex()) > 0.0 && CrossOver(StartIndex()+1) < 0.0)
   {  result = int(round(100.0 * ((CrossOver(StartIndex()) - CrossOver(StartIndex()+1))/fmax(fabs(CrossOver(StartIndex()))+fabs(CrossOver(StartIndex()+1)),fabs(CrossOver(StartIndex()+1))+fabs(CrossOver(StartIndex()+2))))));
   }
   return(result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalAM::ShortCondition(void)
{  int result = 0;
   if(CrossOver(StartIndex()) < 0.0 && CrossOver(StartIndex()+1) > 0.0)
   {  result = int(round(100.0 * ((CrossOver(StartIndex()+1) - CrossOver(StartIndex()))/fmax(fabs(CrossOver(StartIndex()))+fabs(CrossOver(StartIndex()+1)),fabs(CrossOver(StartIndex()+1))+fabs(CrossOver(StartIndex()+2))))));
   }
   return(result);
}

いつものように、潜在的なシグナルがある場合には、結果の値を正規化することが肝心です。AMについては、現在のクロスオーバー値の変化を、事前のクロスオーバー値の最大の大きさで割ったものを使用しています。明らかに、これは大幅にカスタマイズできる領域です。独自の実装は歓迎です。ここで選択された実装は算術平均を活用する傾向があるため使用されています。

調和平均のロングとショートの条件は、次にDivergence関数を使用して、ロングとショートの両方のポジションの潜在的なオープンをフィルタリングします。以下に示すように、ショートとロングの条件があります。

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalHM::LongCondition(void)
{  int result = 0;
   m_close.Refresh(-1);
   if(Divergence(StartIndex()+1) > 0.0 && m_close.GetData(StartIndex()) > m_close.GetData(StartIndex()+1))
   {  result = int(round(100.0 * (Divergence(StartIndex()+1)/(fabs(Divergence(StartIndex()))+fabs(Divergence(StartIndex()+1))))));
   }
   return(result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalHM::ShortCondition(void)
{  int result = 0;
   m_close.Refresh(-1);
   if(Divergence(StartIndex()+1) > 0.0 && m_close.GetData(StartIndex()) < m_close.GetData(StartIndex()+1))
   {  result = int(round(100.0 * (Divergence(StartIndex()+1)/(fabs(Divergence(StartIndex()))+fabs(Divergence(StartIndex()+1))))));
   }
   return(result);
}

調和平均では、高値が上昇し、安値が下落するような陽転を探し、それに続いて終値が上昇すれば強気、終値が下落すれば弱気となります。この2つの出来事は同じバーで起こるのではなく、連続して起こります。このダイバージェンスは、通常、高値の下落と安値の上昇を特徴とする、より一般的なエンゴルフィングパターンとは多くの点で正反対です。

ロングかショートのどちらかのオープニングが決まったら、次の問題は、これらのシグナルクラス関数のロングとショートの条件で常に出力される結果の整数値を決定することです。ここでもまた、結果を定量化する上でいくつかのアプローチが可能であり、そのうちのいくつかは調和平均以外の指標と関連づけることができます。しかし、ここでの目的では、結果の量を決定する際に調和平均にさらに頼りたいと思います。そのため、0～100の範囲の整数値を導き出す際に、過去の値の大きさに対する現在の乖離の比率を使用しています。

したがって、この結果は、現在の乖離が大きいほど、強気または弱気になることを意味します。この結果比率の分母（パーセンテージで0～100の範囲に正規化する）には、現在と以前のダイバージェンス値が入ります。これは幾何平均を適用することにつながります。

GMは、上記で共有したように、GMバッファに基づくボリンジャーバンドの上限値と下限値を計算することによって実装されます。これを実行可能なシグナルにするには、前述のように、下のバンドと価格のクロスと上のバンドと価格のクロスを確認して、それぞれ強気と弱気の設定を確認します。ロングとショートの条件のコードは以下のようになります。

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalGM::LongCondition(void)
{  int result = 0;
   m_close.Refresh(-1);
   if(m_close.GetData(StartIndex()) > m_close.GetData(StartIndex() + 1) && m_close.GetData(StartIndex()) > BandsDn(StartIndex()) && m_close.GetData(StartIndex() + 1) < BandsDn(StartIndex() + 1))
   {  result = int(round(100.0 * ((m_close.GetData(StartIndex()) - m_close.GetData(StartIndex()+1))/(fabs(m_close.GetData(StartIndex()) - m_close.GetData(StartIndex()+1)) + fabs(BandsUp(StartIndex()) - BandsDn(StartIndex()))))));
   }
   return(result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalGM::ShortCondition(void)
{  int result = 0;
   m_close.Refresh(-1);
   if(m_close.GetData(StartIndex()) < m_close.GetData(StartIndex() + 1) && m_close.GetData(StartIndex()) < BandsUp(StartIndex()) && m_close.GetData(StartIndex() + 1) > BandsUp(StartIndex() + 1))
   {  result = int(round(100.0 * ((m_close.GetData(StartIndex()+1) - m_close.GetData(StartIndex()))/(fabs(m_close.GetData(StartIndex()) - m_close.GetData(StartIndex()+1)) + fabs(BandsUp(StartIndex()) - BandsDn(StartIndex()))))));
   }
   return(result);
}

算術平均と調和平均で追跡した結果のサイズも、幾何平均に近づく傾向があり、他の指標は使用されません。そのため、GMの場合は、ボリンジャーバンドの上のバンドと下のバンドのギャップに対する終値の変化の比率を算出します。繰り返しますが、この結果は、バンドギャップの圧縮に対して価格が大きく動くほど、エントリまたはクローズのシグナルが大きくなることを意味します。クローズシグナルは、ロングとショートの条件がオープンの閾値を設定するだけでなく、その逆ポジションがクローズされる閾値も決定するからです。入力設定には常にオープンの閾値とクローズの閾値があります。ショートポジションを建てる前にロングポジションをクローズする必要があるため、後者は前者よりも小さくする必要があります。また、その逆も同様です。

さらに、シグナルを確立するためにGMが導き出したボリンジャーバンドの代替的な実装の可能性は、ベースライン平均の傾きとバンドの上下のギャップの大きさを追跡するオプション、および他のいくつかの反復を見ることができます。ここでの用途は、ボリンジャーバンドを使用したり確認したりする唯一の方法ではありません。

戦略テストとパフォーマンス評価

まずそれぞれのピタゴラス移動平均をEAで別々にテストし、それぞれの独立した結果を得たら、3 つのピタゴラス平均シグナルを組み合わせたEAをテストし、このEAを最適化して、それぞれの平均の相対的な重み付けを求めます。

統一性を持たせるため、2023年の20分足で1つの銘柄EURJPYのテストをおこないます。算術平均については、次のような結果が得られます。

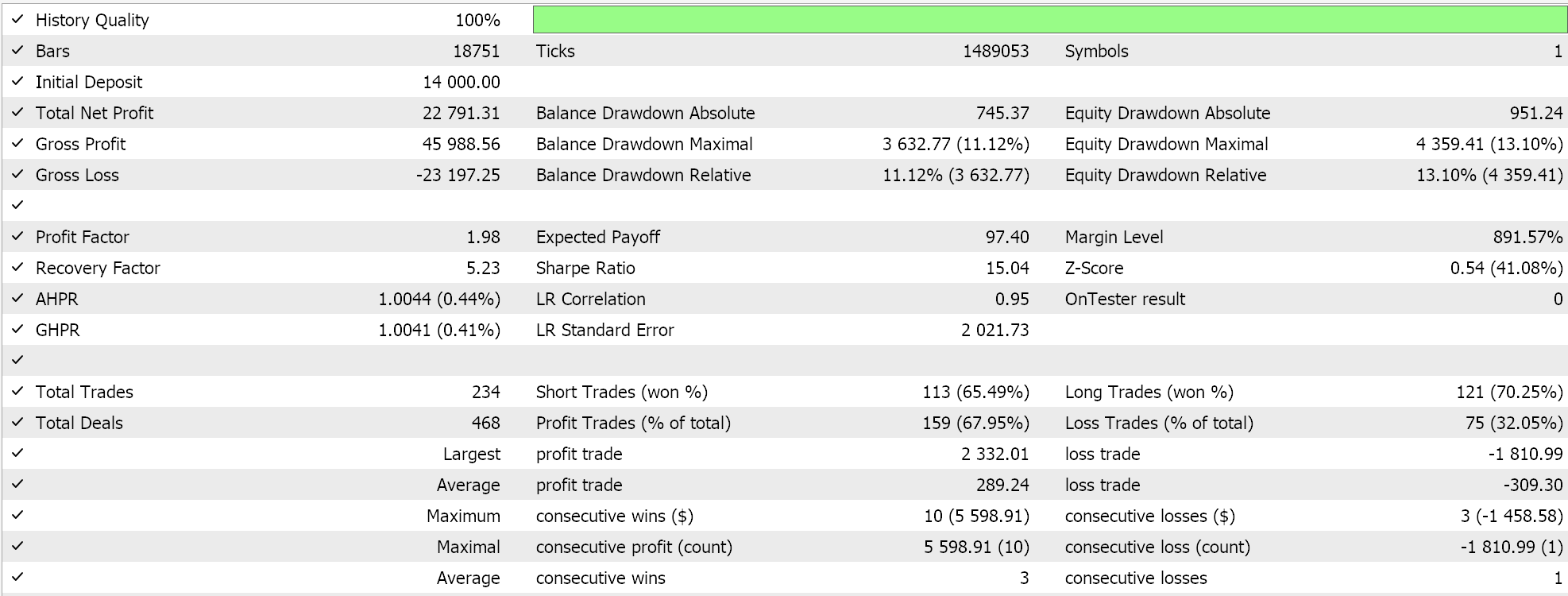
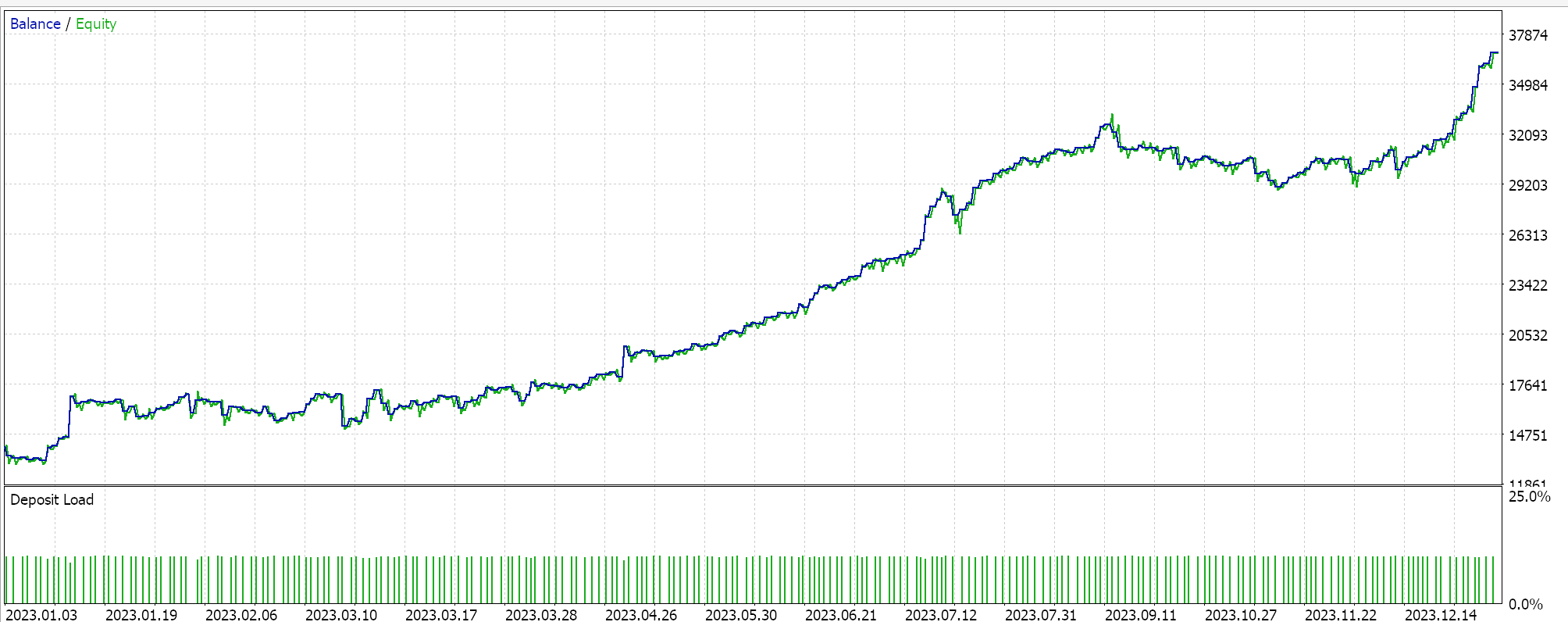
調和平均については、以下のようになります。

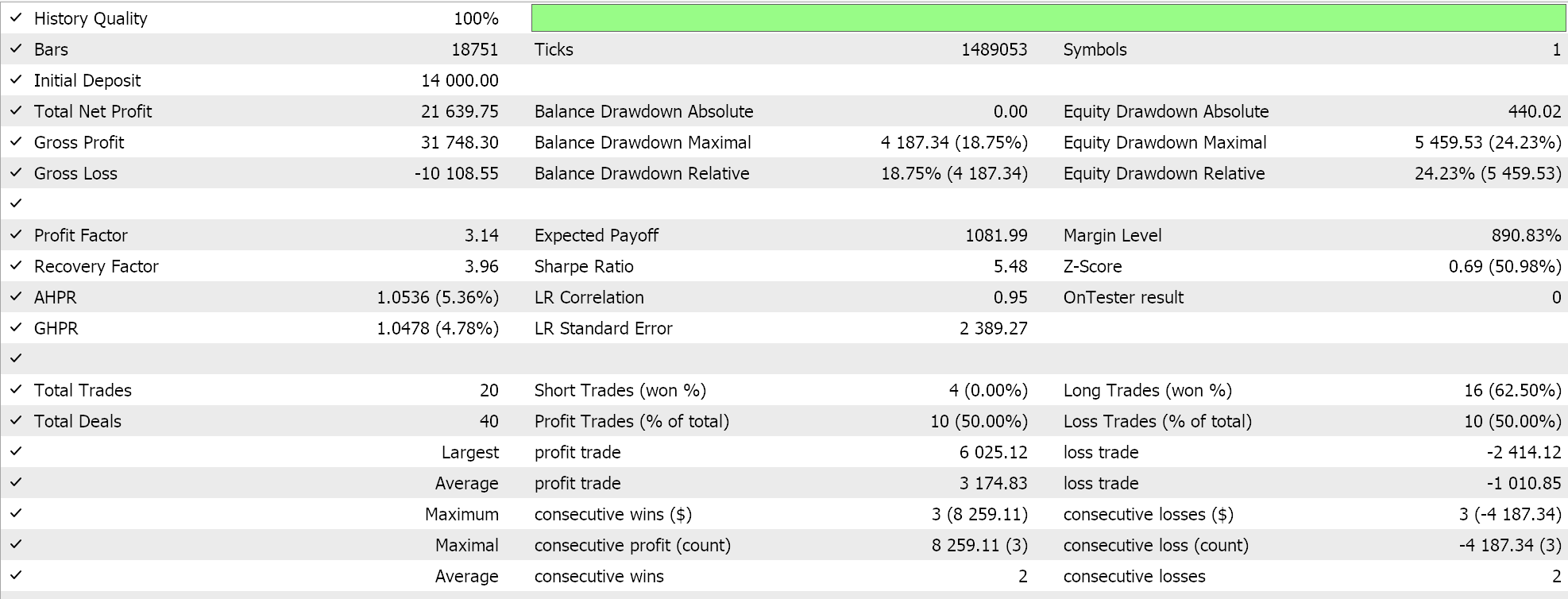
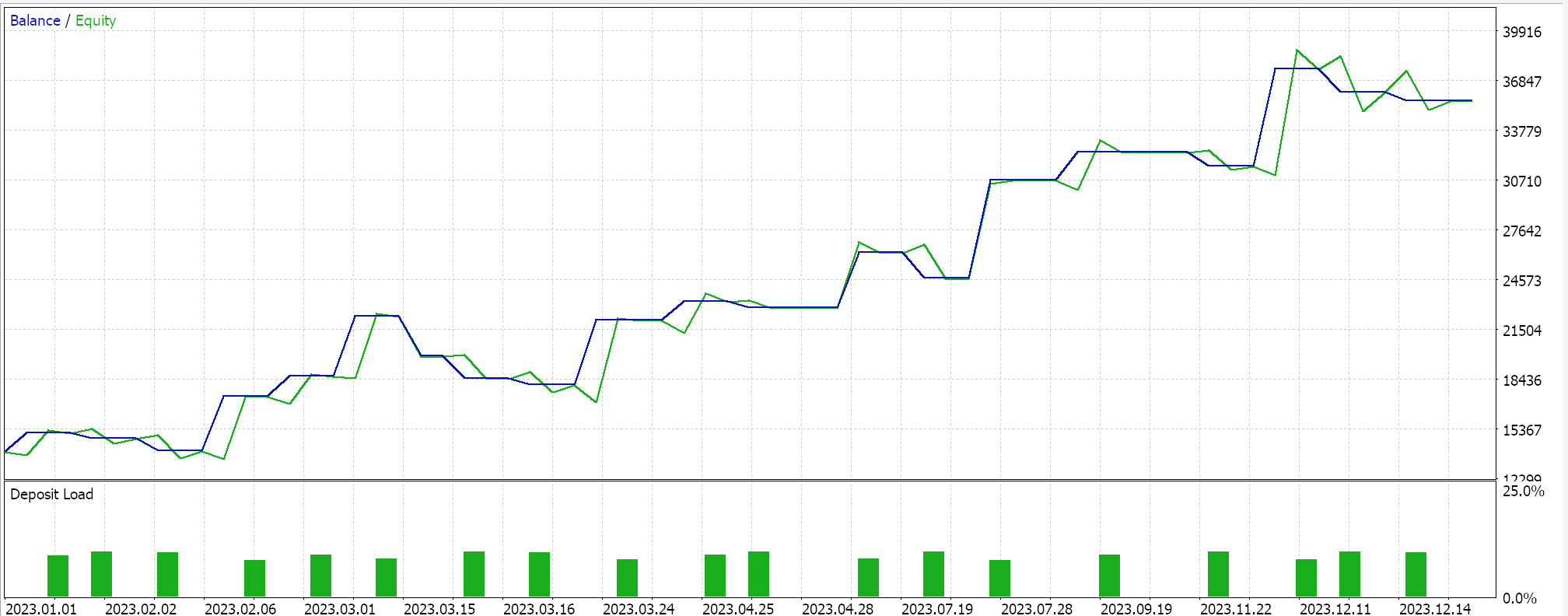
最後に、幾何平均については、以下のようになります。

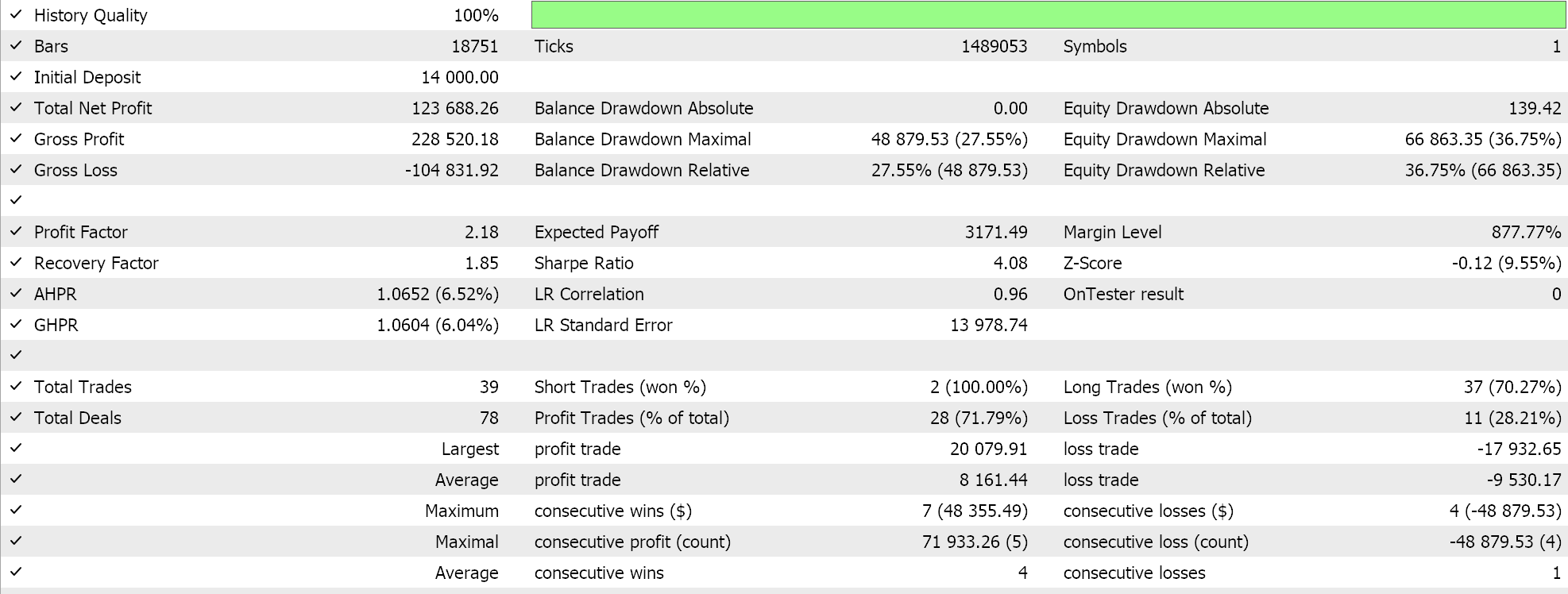
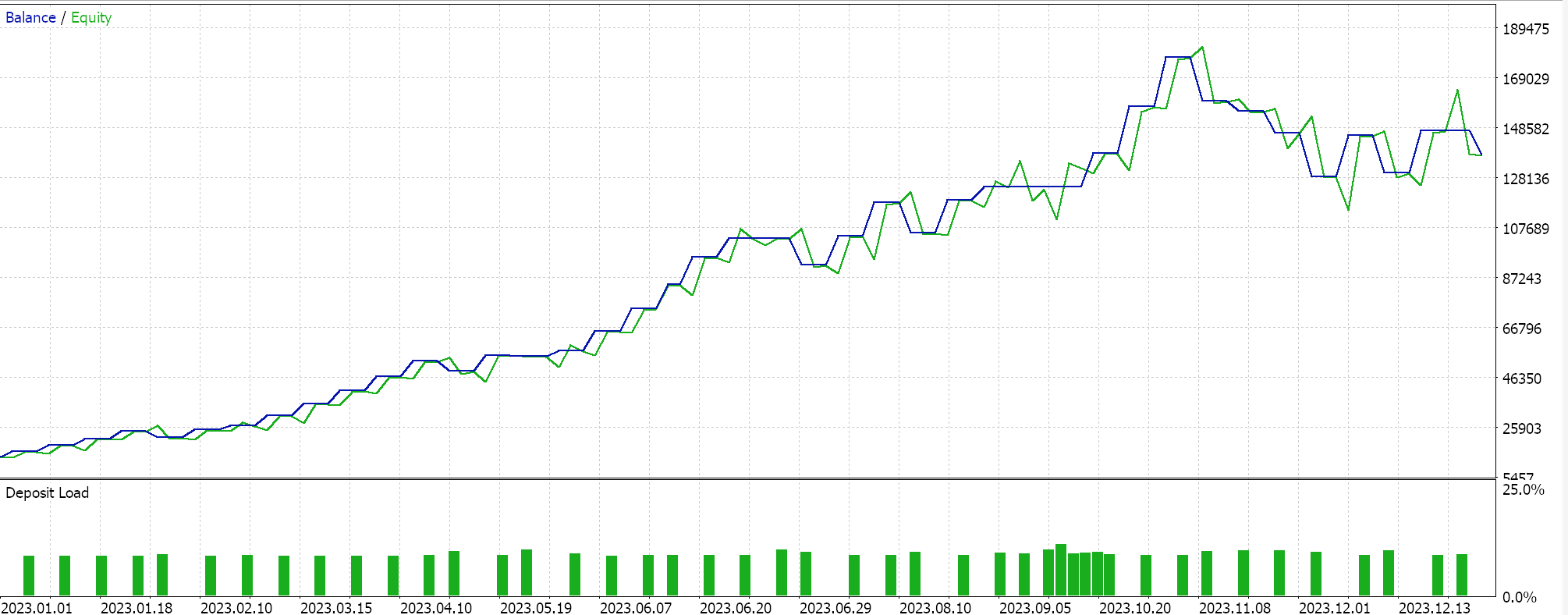
独立したパフォーマンスからは、幾何平均が大きな影響力を持ち、次いで単純クロスオーバー算術平均、そして遅れをとっているのが調和平均発散であるようです。結果は、もちろん、非常に小さなウィンドウでテストしているという事実と、各手段のエントリシグナルの解釈と実装方法について特定のカスタマイズをおこなっているという事実の影響を受けています。相対的な性能の結論を出すにはより多くのテストが必要なのは明らかですが、これはパフォーマンスの比較的大きな変動を示しており、予備テストでは有望なシグナルとなる可能性があります。

ここで、3つの平均値をすべて使用してテストをおこない、相対的な重み付けを最適化しようとすると、次のような良い結果が得られます。

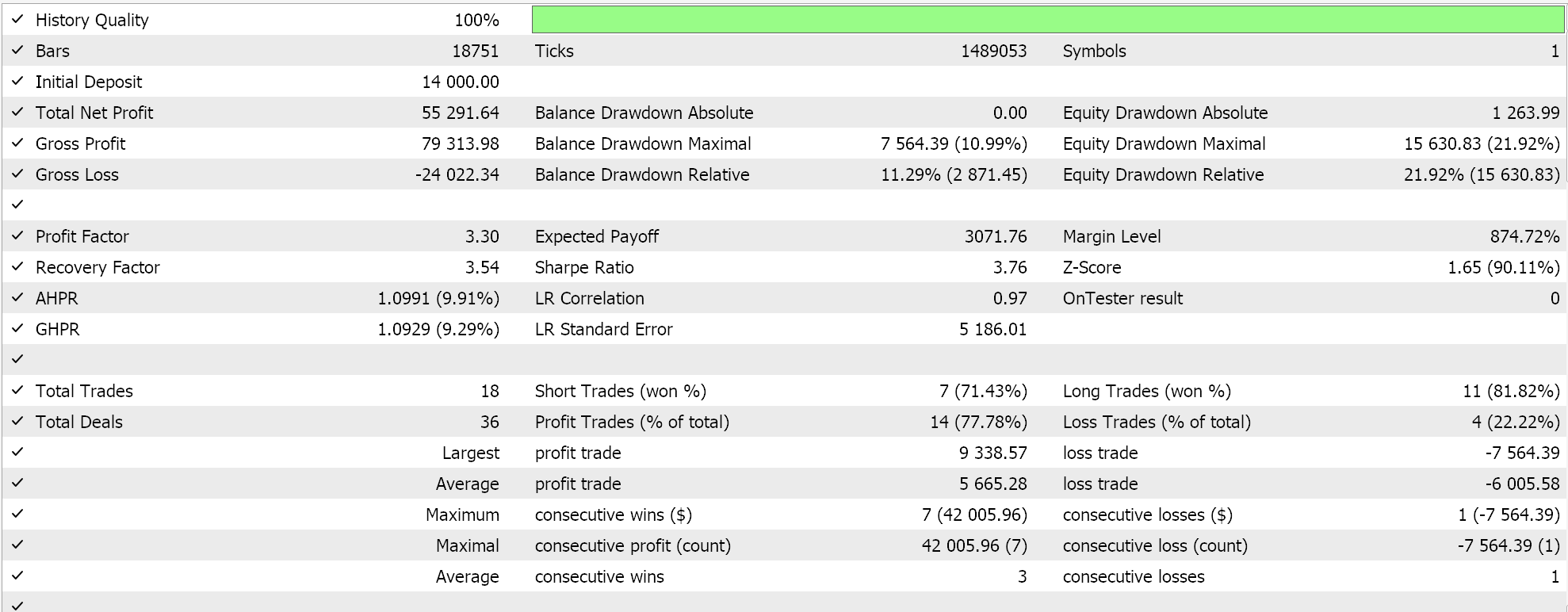
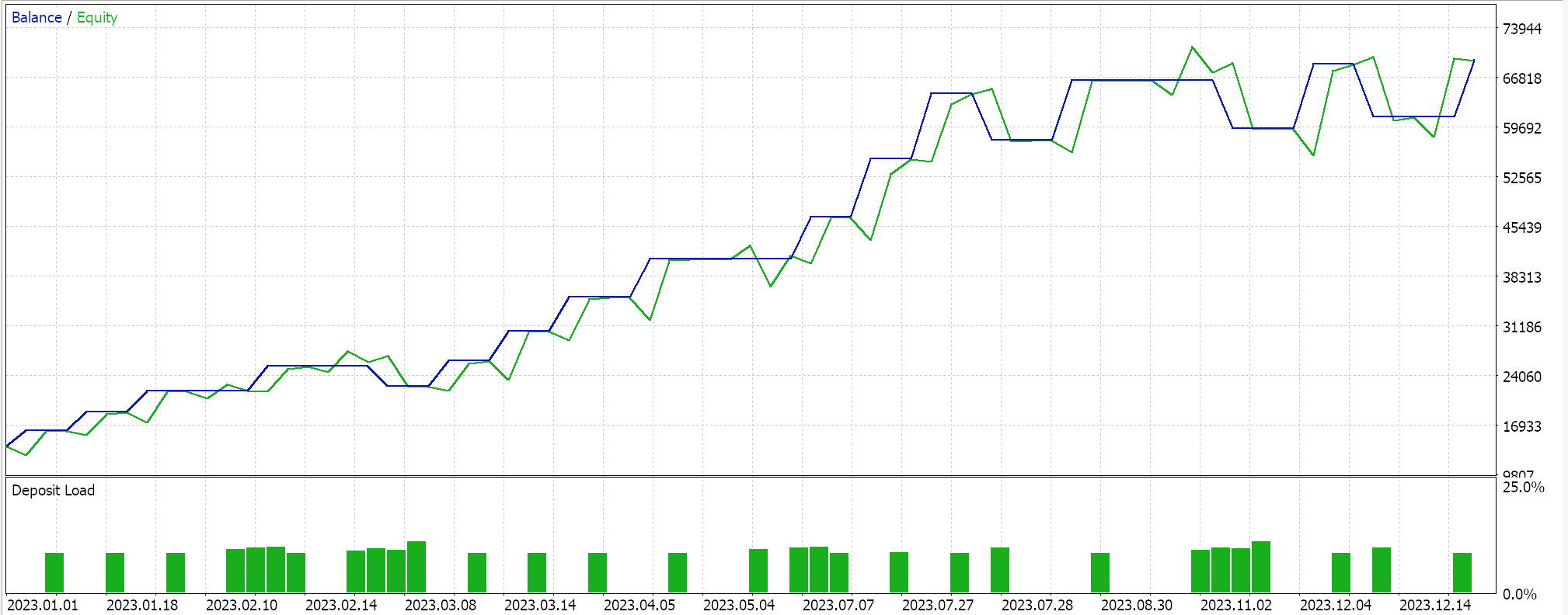
明らかに、幾何平均の独立した結果は依然として有望な指標であり、もちろん、より長い期間にわたるテストの対象となります。興味深いことに、あるいは皮肉なことに、3つのシグナルすべてが一緒に機能するためには、最も優れた独立したシグナルに最小の重み付け0.4を与える必要があります。調和平均と算術平均の独立して遅れたパフォーマンスには、1.0と0.9という重い重みが与えられています。これは、3つの平均を合わせた総合的なパフォーマンスが、幾何平均の独立したパフォーマンスを下回るだけでなく、算術平均と調和平均の独立したパフォーマンスを加えても、GMのパフォーマンスの方がまだ良い理由を説明するかもしれません。EAの組み合わせの設定は以下の通りです。

s_all

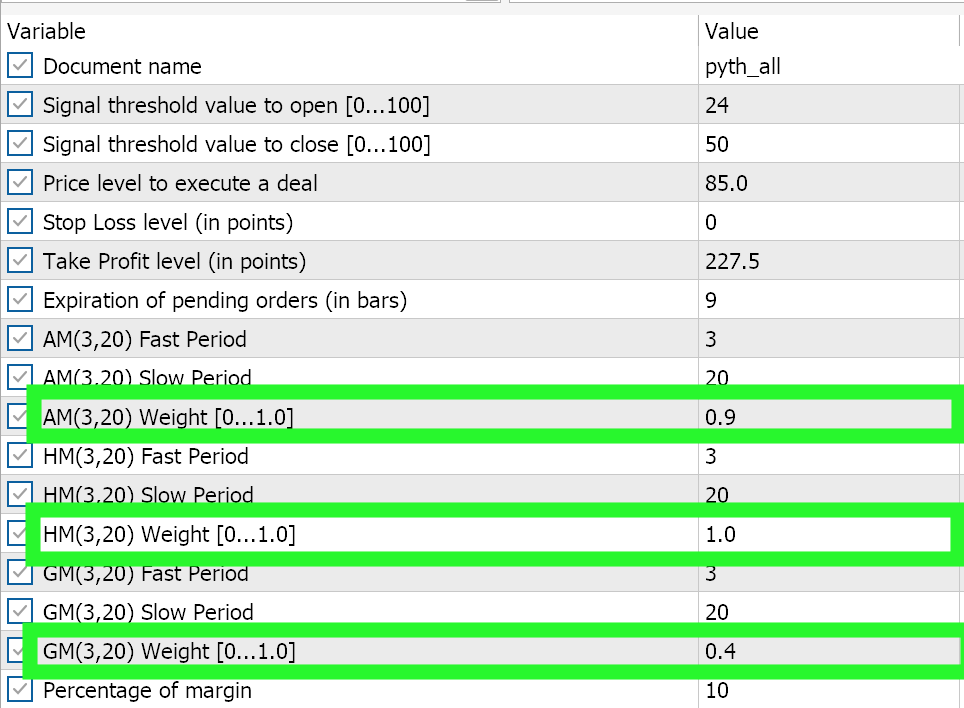
結論

過去の実績は将来の結果を保証するものではありません。すでに述べたように、できれば長期にわたる広範なテストが常に必要であり、今回のような1年という短い期間でテストするよりも安全です。いつものように、こちらとこちら.で紹介されているガイドラインに従って、これらのシグナルの添付コードを組み立てます。この記事で検討した3つの平均のうち、最も小さい値に加重される幾何平均は、ボリンジャーバンドの設定で有望であることを示していますが、この相対的なパフォーマンスについてより明確な結論を得るために、同様のバンドの設定で調和平均を見ていません。また、ボリンジャーバンドやAMクロスオーバー、HMダイバージェンス以外にも、OSMAや TRIXなどのオシレーター形式の移動平均があります。ピタゴラス平均の相対的なポテンシャルを計るには、これらの方法と他の方法を考慮することができます。

MetaQuotes Ltdにより英語から翻訳されました。
元の記事: https://www.mql5.com/en/articles/15135

添付されたファイル |

ZIPをダウンロード

SignalWZ_24_AM.mqh (8.42 KB)

SignalWZ_24_HM.mqh (8.35 KB)

SignalWZ_24_GM.mqh (8.72 KB)

pyth_all.mq5 (7.72 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動

リプレイシステムの開発（第43回）：Chart Traderプロジェクト(II)

プログラミングを学びたいと夢見る人のほとんどは、実際に自分が何をしているのかわかっていません。彼らの活動は、ある方法で物事を創造しようとすることから成っています。しかし、プログラミングとは、適切な解決策を仕立てることではありません。このようなやり方は、解決策よりも多くの問題を引き起こす可能性があります。ここでは、より高度で、それゆえに異なることをします。

リプレイシステムの開発（第42回）：Chart Traderプロジェクト（I）

もっと面白いものを作りましょう。ネタバレはしたくないので、理解を深めるために記事を読んでください。リプレイ/シミュレーターシステムの開発に関する本連載の最初の段階から、私は、開発中のシステムと実際の市場の両方で同じようにMetaTrader 5プラットフォームを使用することがアイディアであると述べてきました。これが適切におこなわれることが重要です。ある道具を使用して訓練して戦い方を学んだ末、戦いの最中に別の道具を使用しなければならないというようなことは誰もしたくありません。

GIT：それは何か？

今回は、開発者にとって非常に重要なツールを紹介しましょう。GITに馴染みのない方は、この記事を読んでGITとは何か、MQL5でどのように使用するかをご覧ください。

PythonとMQL5を使用した取引戦略の自動パラメータ最適化

取引戦略とパラメータを自己最適化するアルゴリズムには、いくつかの種類があります。これらのアルゴリズムは、過去と現在の市場データに基づいて取引戦略を自動的に改善するために使用されます。この記事では、そのうちの1つをpythonとMQL5の例で見ていきます。