
トレーディングにおける数学:トレード結果の推定方法
ナシーム N. タレブ
はじめに:数学は科学の女王である
トレーダーには皆、一定レベルの数学的知識背景が求められますが、この意見には根拠はありません。問題はただ、この求められる最低限のレベルをどう定義できるか、ということです。トレード経験が増すと、フォーラムの掲示や多様な書籍を読み、トレーダーは単独で視野を広げることがよくあります。読者にもっと低いレベルの数学的背景しか求めない本がありますが、逆に学習したり純粋な科学やまた別の分野での知識を磨くよう促します。本稿ではいくらか推定したり、その推定を解釈してみようと思います。
二悪から選択するなら最低限の悪を選択すべし
成功しているトレーダーよりも数学者は世界にもっと存在します。この事実はトレーディングにおける複雑な計算やメソッドに反対する人の論点とされることが多いものです。トレーディングはトレードの規則を開発する能力(分析能力)だけではなく、こういったルール(規則)を観察する能力であると反論することができます。また、金融市場の価格設定を正確に説明するセオリーはまだいまのところ生み出されていません(生み出されることは決してないだろうと私は思います)。金融市場それ自体のセオリー作成(数学的性質の発見)は哲学的観点では判断不能なパラドックスである市場の死を意味します。それでも、市場について満足のいく数学的説明が十分ないまま市場に行くか、それともまったく説明がないままいくかという疑問に直面した場合、一番害のないものを選択します。:トレーディングシステムを推定する方法を選択するのです。
正規分布の異常性は何か?
確率論における基本的概念は正規(ガウス)分布の概念です。なぜそのような名前になっているのでしょうか?自然のプロセスの多くは正規分布であることがわかっています。より正確に言えば、最も自然なプロセスは限界では正規分布に帰着するのです。簡単な例を考察します。0~100 の間隔で一様分布があると仮定します。一様分布とは間隔上の任意の値が下がる確率で、3.14(パイ)が下がる確率は77(7 が二つの私が好きな数字です)が下がる確率と同じであることを意味します。最新のコンピュータはかなり良い疑似乱数列を作成するのに役立ちます。
この一様分布の正規分布を取得する方法は?一様分布から複数の無作為な数字(たとえば5個)を毎回取り、これら数字の平均値(これは「サンプルを取る」と言います)をみつけ、そのサンプルの量が多い場合は、新規に取得する分布は正規の傾向になることが判ります。中心極限定理によると、これは一様分布から採られたサンプルだけでなく、その他分布のひじょうに大きな分類に関連しているのです。正規分布の特性がひじょうによく研究されているため、正規分布のプロセスとして表されているなら、プロセスを分析することはずっと簡単になります。そこで、百聞は一見に如かず。簡単な MQL4 のインディケータでこの中心極限定理の確認をしてみることができます。
異なる N 値(サンプル量)を持つ任意のチャートでこのインディケータを起動し、経験的周波数分布がどんどん滑らかになっていくのを見ます。
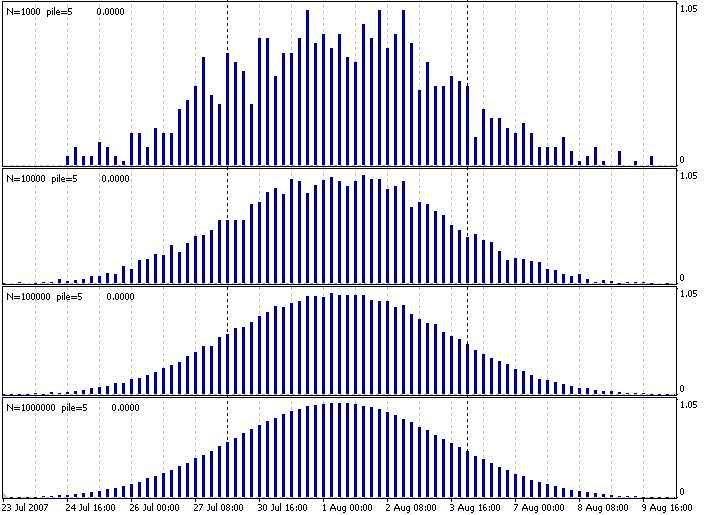
図1 一様分布の正規分布を作り出すインディケータ
ここで、N は0~100の間隔で一様分布している数字 pile=5 の平均を取った回数です。外見がひじょうに似通った 4 つのチャートを取得しました。限界でいくぶん正規化すると(補助的に単一スケールに)、いくつか標準正規分布が実現されます。唯一の問題は、金融市場における価格設定(より正確には、価格増加とこの増加から派生するその他)は一般的に言えば、正規分布には当てはまらないことです。金融市場におけるかなり稀なイベント(たとえば価格が50%落ちる)の確率は低いのですが、正規分布ではまだかなり高いのです。正規分布を基にリスクを推定する場合、これを覚えておく必要があるのはそのためです。
量の質への変換
正規分布をモデル化するというこの簡単な例でさえ、処理されるデータ量はかなりに及ぶことを示しています。初期データが多いほど、結果の精度は高く妥当性も高いものです。サンプルの最小数は 30 を超えるべきであるとみなされています。トレード結果を推定したければ(たとえばテスターでの Expert Advisor)、30件以下のトレードはシステムのパラメータの一部に関して統計的に信頼性ある結論を得るには不十分である、ということです。分析するトレードが多ければ多いほど、トレードがただ幸いにもさっと手に入ったあまり信頼性のないトレーディングシステムのエレメントである可能性は低いのです。したがって、連続した150件のトレードの最終利益は、15件のトレードだけで推定されるシステムよりは、そのシステムを利用する根拠を持つのです。
数学的期待値とリスク推定としての分散
分布の性質としてもっとも重要な2点は、数学的期待値(平均値)と分散です。標準正規分布では数学的期待値はゼロです。そこでは、分布の中心もゼロに位置しています。正規分布の平坦度、あるいは急峻は数学的期待領域内の乱数値の拡散計測によって特徴づけられます。それは、乱数値の数学的期待値に関して値がどのように拡散するかを示す分散です。
数学的期待値はひじょうに簡単な方法で見つけることができます。加算集合に対して、分布値をすべて合計し、取得される合計値を値の数量で除算するのです。たとえば、自然数一式は無限ですが、可算です。それは各値がそのインデックス(順番)と照合されるためです。不可算セットに対しては、積分が行われます。一連のトレードの数学的期待値を推定するには、トレード結果をすべて合計し、得た数量をトレード数で割ります。取得した値は各トレードの期待平均結果を示すこととなるのです。数学的期待値が正であれば、平均して利益が上がります。負であれば、平均して損失が出るのです。
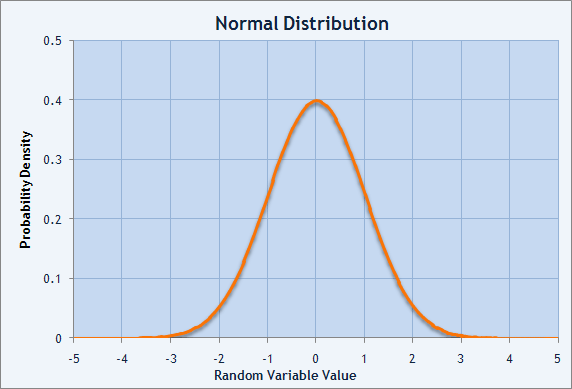
図2 正規分布の確立密度チャート
分布の拡散観測は数学的期待値から得るランダムな値の二乗偏差の合計です。分布のこの特徴は分散と呼ばれます。通常、ランダムに分布している値の数学的期待値は M(X) と呼ばれます。そして、分散は D(X) = M((X-M(X))^2 ) と表記されます。分散の平方根は標準偏差と呼ばれます。それもシグマ(σ)として定義されます。それは、数学的期待値がゼロで、正規分布、あるいはガウス分布と呼ばれる標準偏差 1 の正規分布です。
標準偏差値が高いほど、トレード資本は変動しやすくリスクは高くなります。数学的期待値が正(収益性ある戦略)で、それが $100 であり、標準偏差が $500 であれば、1ドル得るのに合計額をリスクにさらすこととなり、それは数倍大きいものです。たとえば、30件のトレード結果があるとします。
|
|
|---|
この一連のトレードに対する数学的期待値を求めるには、すべての結果を合計して、これを30で割るのです。そうすると平均値 M(X) は $4.26 となります。標準偏差を見つけるには、トレードそれぞれの結果から平均値を引き、それを二乗し二乗の合計を求めます。取得した値を29(トレード数引く1)で割ります。そうすると、9 353.623 に等しい分散 D を取得します。分散の平方根を作ったところで、$96.71である標準偏差、シグマを取得します。
チェックデータは以下のテーブルに表示しています。
| トレードNo. | X (結果) |
X-M(X) (差) |
(X-M(X))^2 (差の二乗) |
|---|---|---|---|
| 1 | -17.08 | -21.34 | 455.3956 |
| 2 | -41.00 | -45.26 | 2 048.4676 |
| 3 | 147.80 | 143.54 | 20 603.7316 |
| 4 | -159.96 | -164.22 | 26 968.2084 |
| 5 | 216.97 | 212.71 | 45 245.5441 |
| 6 | 98.30 | 94.04 | 8 843.5216 |
| 7 | -87.74 | -92.00 | 8 464.00 |
| 8 | -27.84 | -32.10 | 1 030.41 |
| 9 | 12.34 | 8.08 | 65.2864 |
| 10 | 48.14 | 43.88 | 1 925.4544 |
| 11 | -60.91 | -65.17 | 4 247.1289 |
| 12 | 10.63 | 6.37 | 40.5769 |
| 13 | -125.42 | -129.68 | 16 816.9024 |
| 14 | -27.81 | -32.07 | 1 028.4849 |
| 15 | 88.03 | 83.77 | 7 017.4129 |
| 16 | 32.93 | 28.67 | 821.9689 |
| 17 | 54.82 | 50.56 | 2 556.3136 |
| 18 | -160.10 | -164.36 | 27 014.2096 |
| 19 | -83.37 | -87.63 | 7 679.0169 |
| 20 | 118.40 | 114.14 | 13 027.9396 |
| 21 | 145.65 | 141.39 | 19 991.1321 |
| 22 | 48.44 | 44.18 | 1 951.8724 |
| 23 | 77.39 | 73.13 | 5 347.9969 |
| 24 | 57.48 | 53.22 | 2 832.3684 |
| 25 | 67.75 | 63.49 | 4 030.9801 |
| 26 | -127.10 | -131.36 | 17 255.4496 |
| 27 | -70.18 | -74.44 | 5 541.3136 |
| 28 | -127.61 | -131.87 | 17 389.6969 |
| 29 | 31.31 | 27.05 | 731.7025 |
| 30 | -12.55 | -16.81 | 282.5761 |
取得したのは、数学的期待値 $4.26 と標準偏差 $96.71 です。それはリスクと平均トレードの間のベストな比率ではありません。以下の収益チャートはこのことを裏付けます。
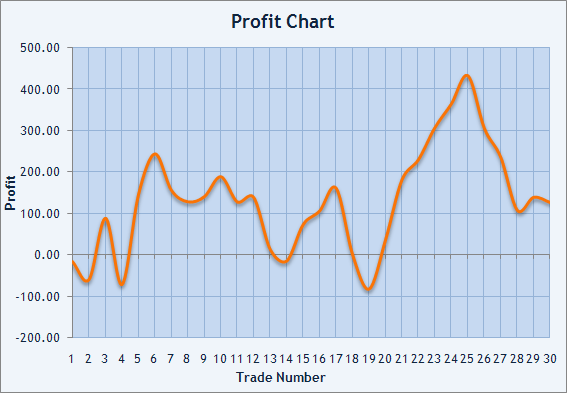
図3 行われたトレードに対するバランスグラフ
私はランダムにトレードするのでしょうか?Z スコア
一連のトレードの結果として得られる利益はまぐれである、とする仮定そのものはほとんどのトレーダーにとっては皮肉に聞こえます。多大な時間を費やして成功するトレーディングシステムを検索し、見つけたシステムがすでに限られた期間で実利を上げていることを観察すると、トレーダーは市場に対する適切なアプローチ法を見つけたと思うものです。その人たちはこれがただのまぐれだと思うでしょうか?特に初心者にとってこれはちょっとややこしすぎます。それでもなお、結果を客観的に推定することは基本です。この場合、またしても、正規分布が救いとなります。
トレードそれぞれの結果がどのようなものか、わかりません。一つ言えることは、利益を得る(+)か損失を出す(-)かだということです。利益と損失は異なるトレーディングシステムに違った方法で繰り返し順番に発生します。たとえば、ストップロスが実行される時点で期待利益が期待損失より5倍少なければ、収益性あるトレード(プラストレード)は損失を招くトレード(マイナストレード)をかなり勝ち越すと予測するのは合理的でしょう。Zスコアにより、収益性あるトレードが損失を出すトレードとどの程度頻繁に入れ替わるか推定するのが可能になります。
トレーディングシステムに対する Z は以下の式で計算されます。
Z=(N*(R-0.5)-P)/((P*(P-N))/(N-1))^(1/2) ここで |
一連とは、お互いに続くプラス(たとえば +++)、またはお互いに続くマイナス(たとえば--)の連続を言います。R はそのような一連の数をカウントします。

図4 二連続の利益と損失の比較.
図4では 、「自動売買チャンピオンシップ 2006」で第1位を取った Expert Advisor の利益と損失のシーケンスの一部 をブルーで表示しています。その競争アカウント Z スコア値は -3.85 で、確率 99.74%は括弧内に示されています。これは、確率 99.74% でこのアカウントのトレードは、トレード間に正の依存性があることを意味しています( Z スコアが負)。:利益には利益が続き、損失には損失が続いた、ということです。そうなのでしょうか?この「チャンピオンシップ」を見守っていた方は、 ローマン・リッチが同じ方向で実行しているトレードを頻繁に3件オープンする Expert Advisor MACD の彼のバージョンを出したことを覚えておられることでしょう。
正規分布での乱数の正の値と負の値の典型的な連続は赤で表示されています。これら連続が異なっていることがわかります。ですが、この違いはどのように計測できるのでしょうか?Z スコアがこの疑問に答えてくれます。:みなさんの利益と損失のシーケンスは、トレード間に依存性がまったくなくほんとうにランダムなシーケンスに対する期待よりも多くのあるいは少ないストリップ(利益の連続あるいは損失の連続)を持つのでしょうか?Z スコアがゼロに近ければ、トレード分布は正規分布とは異なると言うことはできません。トレードシーケンスの Z スコアは連続するトレード間に存在するかもしれない依存性を伝えます。
この点では、Z の値は標準正規分布(平均=0、シグマ=1)に従って分布するランダムな値のゼロからの偏差の確率と同様の方法で解釈されます。範囲 ±3σ 内の正規分布ランダム値が落ちる確率が 99.74% であれば、同じ確率 99.74% でこの間隔外でこの値が下がることは、このランダムな値が既存の正規分布にないことを伝えます。これは『3 シグマルール』が次のように読まれる理由です。:通常のランダムな値はその平均から 3 シグマ以内の距離で偏差する。
Z の記号は依存性タイプを伝えるのです。プラスは、収益性あるトレードに損失を出すトレードが続くであろうことを意味します。マイナスは利益が利益に続き、損失には再び損失が続くことを告げます。以下の小さいテーブルは正規分布との比較としてトレード間の依存性のタイプと確率を示すものです。
| Z スコア | 依存性確率(%) | 依存性タイプ |
|---|---|---|
| -3 | 99.73 | 正 |
| -2.9 | 99.63 | 正 |
| -2.8 | 99.49 | 正 |
| -2.7 | 99.31 | 正 |
| -2.6 | 99.07 | 正 |
| -2.5 | 98.76 | 正 |
| -2 | 95.45 | 正 |
| -1.5 | 86.64 | 中間 |
| -1.0 | 68.27 | 中間 |
| 0.0 | 0.00 | 中間 |
| 1.0 | 68.27 | 中間 |
| 1.5 | 86.64 | 中間 |
| 2.0 | 95.45 | 負 |
| 2.5 | 98.76 | 負 |
| 2.6 | 99.07 | 負 |
| 2.7 | 99.31 | 負 |
| 2.8 | 99.49 | 負 |
| 2.9 | 99.63 | 負 |
| 3.0 | 99.73 | 負 |
トレード間の正の依存性は、利益が新たな利益を生むことを意味します。一方で損失は新しい損失を生むのです。負の依存性は利益に損失が続き、また損失に利益が続くことを意味します。見つかった依存性により、オープンするポジションサイズを調整し(理想的に)、またはその一部をスキップし、トレードシーケンスを見るため、仮想的にだけオープンするするのです。
保有期間利回り(HPR)
ラルフ・ビンス氏は著書 The Mathematics of Money Management で、HPR(保有期間利回り)の概念を用いています。10% の利益を出したトレードは HPR=1+0.10=1.10 です。10% の損失に終わったトレードは HPR=1-0.10=0.90 です。トレードに対する HPR の値はトレードが終了したあとの残高値(BalanceClose)をトレード開始時の残高値(BalanceOpen)で割っても求めることができます。HPR=BalanceClose/BalanceOpen です。よって、すべてのトレードには金額での結果と HPR で表現される結果の両方があるのです。これでトレードされる契約サイズで個別にシステムを比較することができるのです。そのような比較に使用される指数のひとつは算術平均、AHPR(平均保有期間利回り)です。
AHPR を得るには、全 HPR を合計し、その値をトレード金額で割ります。上記トレード30件の例を用いてこれら計算を考察します。アカウント上 $500 でトレードを開始したとします。新しいテーブルを作成します。
| トレード No. | 残高($) | 結果($) | 終了時残高($) | HPR |
|---|---|---|---|---|
| 1 | 500.00 | -17.08 | 482.92 | 0.9658 |
| 2 | 482.92 | -41.00 | 441.92 | 0.9151 |
| 3 | 441.92 | 147.8 | 589.72 | 1.3344 |
| 4 | 589.72 | -159.96 | 429.76 | 0.7288 |
| 5 | 429.76 | 216.97 | 646.73 | 1.5049 |
| 6 | 646.73 | 98.30 | 745.03 | 1.1520 |
| 7 | 745.03 | -87.74 | 657.29 | 0.8822 |
| 8 | 657.29 | -27.84 | 629.45 | 0.9576 |
| 9 | 629.45 | 12.34 | 641.79 | 1.0196 |
| 10 | 641.79 | 48.14 | 689.93 | 1.0750 |
| 11 | 689.93 | -60.91 | 629.02 | 0.9117 |
| 12 | 629.02 | 10.63 | 639.65 | 1.0169 |
| 13 | 639.65 | -125.42 | 514.23 | 0.8039 |
| 14 | 514.23 | -27.81 | 486.42 | 0.9459 |
| 15 | 486.42 | 88.03 | 574.45 | 1.1810 |
| 16 | 574.45 | 32.93 | 607.38 | 1.0573 |
| 17 | 607.38 | 54.82 | 662.20 | 1.0903 |
| 18 | 662.20 | -160.10 | 502.10 | 0.7582 |
| 19 | 502.10 | -83.37 | 418.73 | 0.8340 |
| 20 | 418.73 | 118.4 | 537.13 | 1.2828 |
| 21 | 537.13 | 145.65 | 682.78 | 1.2712 |
| 22 | 682.78 | 48.44 | 731.22 | 1.0709 |
| 23 | 731.22 | 77.39 | 808.61 | 1.1058 |
| 24 | 808.61 | 57.48 | 866.09 | 1.0711 |
| 25 | 866.09 | 67.75 | 933.84 | 1.0782 |
| 26 | 933.84 | -127.10 | 806.74 | 0.8639 |
| 27 | 806.74 | -70.18 | 736.56 | 0.9130 |
| 28 | 736.56 | -127.61 | 608.95 | 0.8267 |
| 29 | 608.95 | 31.31 | 640.26 | 1.0514 |
| 30 | 640.26 | -12.55 | 627.71 | 0.9804 |
AHPR は算術平均として取得されます。それは 1.0217 です。すなわち、各トレードで平均 (1.0217-1)*100%=2.17% を得るのです。そうなのでしょうか?2.17 に30 をかけると、収入は 65.1% となるのがわかります。初期額 $500 に65.1% をかけて $325.50 を得ます。同時に、実利益は (627.71-500)/500*100%=25.54% となります。よってHPR の算術平均で必ずしもシステムを適切に推定できるわけではありません。
算術平均と共に、ラルフ・ビンスが紹介するのは、GHPR(幾何学的保有期間利回り)と呼ぶ幾何平均です。それは実質的につねに AHPR より少ないものです。幾何平均はゲームごとの成長要因で、以下の式で求められます。
GHPR=(BalanceClose/BalanceOpen)^(1/N) ここで |
最大の GHPR を持つシステムは、再投資を基にトレードを行う場合には、最高の利益を出します。下の GHPR は、再投資を基にトレードを行えば、システムが資金を失うことを意味します。AHPR、GHPR 間の違いをうまく説明するのはサスケンのアカウント履歴です。彼は長期にわたり「チャンピオンシップ」のリーダーでした。AHPR=9.98% には感動しますが、最終的な GHPR=-27.68% はすべてを大局的に見ます。
シャープレシオ
投資の効率は利益の分散の観点で推定されることが多いものです。そのような指標の一つがシャープレシオです。この指標は無リスク金利(RFR)によって減少する AHPR がシーケンスの標準偏差(SD)とどのように関連するかを示すものです。RFR の値は通常銀行の預金金利、または国庫債務の金利に等しく取られてています。われわれの例では、以下です。:AHPR=1.0217, SD(HPR)=0.17607、RFR=0。
シャープレシオ=(AHPR-(1+RFR)) ÷ SD ここで |
シャープレシオ=(1.0217-(1+0))/0.17607=0.0217/0.17607=0.1232。正規分布に対しては、 99% を超えるランダムな値が平均値 M(X) 周辺の ±3σ (シグマ=SD)範囲にあります。3 を超えるシャープレシオの値はひじょうに良いということになります。以下の図5 では、トレード結果の分布が正規で、シャープレシオ=3 であれば、3 シグマルールに従えばトレードごとの負けの確率は 1% を下回る、ということがわかります。
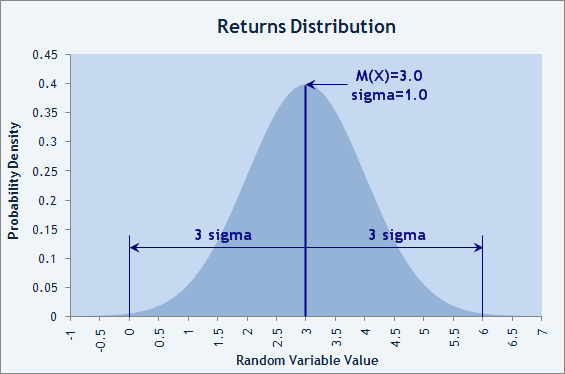
図5 負けの確率が1% より低い取引結果の正規分布
RobinHood という名前の出場者のアカウントは以下を裏付けます。彼の EA は 1 件も負けを出さず、自動売買チャンピオンシップ 2006 で26件のトレードを行いました。シャープレシオ=3.07 です!
直線回帰(LR)と線形相関係数(CLC)
トレード結果の安定性を推定する方法はまだほかにもあります。シャープレシオにより、資本が負っているリスクを推定することが可能ですが、残高曲線の平滑度合いも推定してみることができます。各トレード終了時に残高値を入れると、破線を描くことができます。これらの点は資本変化の平均方向を示す一定の直線と一致します。Hendrick によって作成された Expert Advisor Phoenix_4 の残高グラフを利用してこの好機の例を考察します。
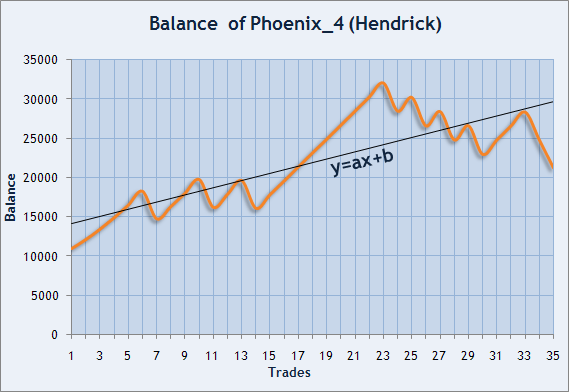
図6 自動売買チャンピオンシップ 2006 出場者、ヘンドリックの残高グラフ
この直線が一致する点にできるだけ近づく係数 a と b を求める必要があります。われわれの場合、x はトレード番号、y はトレード終了時の残高値です。
|
|
|---|
近似ストレートの係数は通常、最小二乗法(LS 法)によって求められます。わかっている係数 а と b でこの直線を取得したとします。すべての x に対して、値は2つあります。y(x)=a*x+b および残高(x) です。y(x) からの残高(x) の偏差は d(x)=y(x) - 残高(x) と表されます。SSD(偏差の二乗の合計)は SD=Summ{d(n)^2} のように計算されます。LS 法によって直線を求めることは、SD が最小である a や b を求めることを意味します。この直線も既定のシーケンスに対する直線回帰 (LR) と呼ばれます。
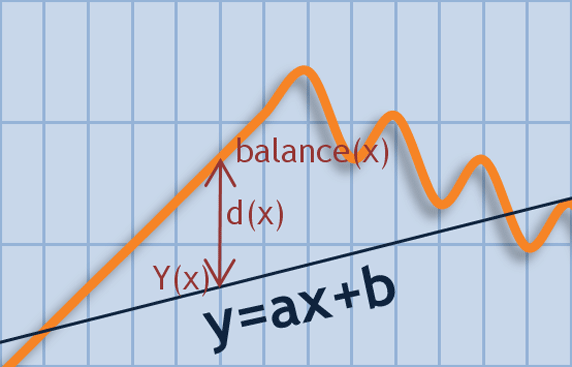
図7 直線 y=ax+b からの残高値偏差
LS 法によって直線 y=a*x+b の係数を取得したので、求めた直線からの残高値偏差を金額で推定することが可能です。シーケンス d(x) に対し算術平均を計算するとМ(d(x) がゼロに近い(より正確には、一部の計算精度の度合ではゼロです)ことを確認できます。同時に、SD の SSD はゼロではなく、そこには一定の限界値があります。SD/(N-2) の平方根は直線に関する残高グラフにおける値の広がりを示し、それにより、アカウントの初期状態と同一の値でトレーディングシステムを推定することができます。このパラメータを LR 標準エラーと呼ぶことにします。
以下は「自動売買チャンピオンシップ 2006」の上位15件のアカウントについてのこのパラメータ値です。
| 番号 | ログイン | LR 標準エラー($) | 利益($) |
|---|---|---|---|
| 1 | Rich | 6 582.66 | 25 175.60 |
| 2 | ldamiani | 5 796.32 | 15 628.40 |
| 3 | GODZILLA | 2 275.99 | 11 378.70 |
| 4 | valvk | 3 938.29 | 9 819.40 |
| 5 | Hendrick | 3 687.37 | 9 732.30 |
| 6 | bvpbvp | 9 208.08 | 8 236.00 |
| 7 | Flame | 2 532.58 | 7 676.20 |
| 8 | Berserk | 1 943.72 | 7 383.70 |
| 9 | vgc | 905.10 | 6 801.30 |
| 10 | RobinHood | 109.11 | 5 643.10 |
| 11 | alexgomel | 763.76 | 5 557.50 |
| 12 | LorDen | 1 229.40 | 5 247.90 |
| 13 | systrad5 | 6 239.33 | 5 141.10 |
| 14 | emil | 2 667.76 | 4 658.20 |
| 15 | payday | 1 686.10 | 4 588.90 |
直線に対する残高グラフの近似化度合は金額、絶対値の双方で測定可能です。これには相関率を利用します。相関率 r は数字の2つのシーケンス間の相関関係度合を測定します。その値は-1 ~ +1 の範囲にあります。r=+1 であれば、2つのシーケンスは同一の動きをし、相関関係は正であることを示します。
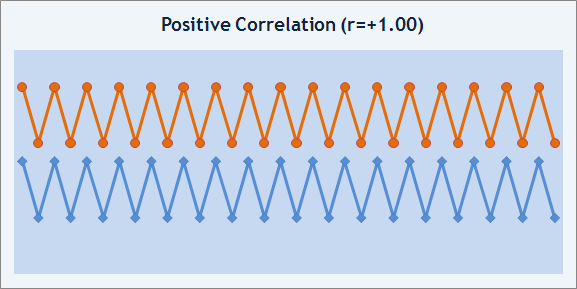
図8 正の相関関係例
r=-1 であれば、2つのシーケンスは逆に変化し、負の相関関係です。
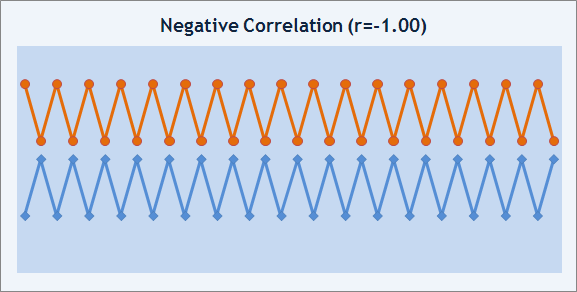
図9 負の相関関係例
r=0 であれば、 シーケンス間に依存性は存在しないことを意味します。r=0 はシーケンス間に相関関係が存在しないことを意味しているのではない、と強調する必要があると思われます。それはただそのような相関関係が見つからないと言っているにすぎません。これはご記憶ください。われわれの場合、数字のシーケンスを2つ比較する必要があります。ひとつはチャートの残高シーケンス、もう一つは直線回帰上で対応する点のシーケンスです。
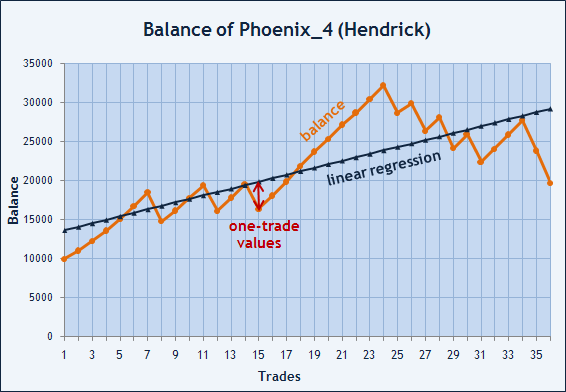
図10 直線回帰における残高値と点
以下は同一データをテーブルで表したものです。
|
|
残高値を X、直線回帰ライン上のポイントシーケンスを Y として表記します。シーケンス X と Y の間の線形相関の係数を計算するには、まず平均値 M(X) と M(Y) を求める必要があります。それから、新しいシーケンス T=(X-M(X)) × (Y-M(Y)) を作成し、その平均値を M(T)=cov(X, Y)=M((X-M(X)) × (Y-M(Y))) として計算します。求められたcov(X,Y) の値を X と Y の共分散と呼びます。これはプロダクト (X-M(X)) × (Y-M(Y)) の数学的期待値です。われわれの例については、共分散値は 21 253 775.08 です。M(X) と M(Y) は等しく、それぞれの値が 21 382.26 であることにご注意ください。それは「残高」が平均値で、一致する直線の平均が等しいことを意味します。
T=(X-M(X)) × (Y-M(Y)) M(T)=cov(X,Y)=M((X-M(X)) × (Y-M(Y))) ここで |
残っているのは、Sx と Sy の計算だけです。Sx を計算するには、値 (X-M(X))^2 の合計を求める、すなわちその平均値から X の SSD を求めるのです。分散の計算方法とLS 法のアルゴリズムを思い出します。ごらんのように、すべて関連しています。求めた SSD はシーケンスの数量、われわれの場合 36(0~35)で割ります。そして、出た値の平方根を抽出します。そうして Sx の値を取得しました。Sy の値は同様の方法で計算します。われわれの例では、Sx=583.098245、Sy=4610.181675となります。
Sx=Summ{(X-M(X))^2}/N
Sy=Summ{(Y-M(Y))^2}/N
r=cov(X,Y)/(Sx* Sy)
ここで |
これで相関係数値を r=21 253 775.08/(5839. 098245 × 4610. 181675)=0.789536583 と求めることができます。1より低い値ですが、ゼロからは遠く離れています。よって、残高グラフはトレンドライン値 0.79 と相互に関連している、と言えます。別システムと比較することで、徐々に相関係数の値をどう解釈するのか学習していきます。「チャンピオンシップ」の「レポート」ページではこのパラメータはLR 相関と名付けられています。「チャンピオンシップ」の枠組みの中でこのパラメータを計算するのに設けられた違いは、LR 相関のサインはトレードの収益性を示す、ということでした。
問題は、残高グラフと任意の直線間の相関係数を計算できたことです。「チャンピオンシップ」の目的としては、それはトレンドラインを上昇するために計算されたので、従って、LR 相関がゼロより上であれば、トレードには収益性があるのです。それがゼロを下回れば、負けです。時として、アカウントが利益を示す場面で、LR 相関が負になるという面白い効果が現れます。これはどちらにしても、トレードが負けつつあることを意味します。そのような状況の例は Aver のところで見られます。純利益トータルは $2 642 ですが、一方LR 相関は -0.11 です。この場合には相関関係はなさそうです。それはアカウントの将来が判断できなかっただけであることを示しています。
MAE と MFE が多くを語る
われわれは「損失を削減し、利益を増やす」ことを頻繁に望みます。最終的なトレード結果を見ると、保護的ストップ(ストップロス)が有効か、利益修正が効果的か結論を出すことができません。ポジションのオープン日付けとクローズ日付、最終結果が利益を上げたか負けかを確認するだけです。これは人についてその人の誕生日と死亡日で判断するようなものです。トレードのライフ期間の浮動利益やトータルとしてのすべてのポジションについては知らず、トレーディングシステムの性質を判断することはできません。それはどのくらいリスクを伴うものでしょうか?どのように利益に到達したのでしょうか?架空利益は失われましたか?これらに対してはパラメータ、MAE(最大逆行幅) とMFE(最大順行幅)が答えになる可能性があります。
オープンポジション(それがクローズされるまで)はすべて、継続的に利益の変動を経ます。トレードはすべて、オープンからクローズまでの間に、最大利益と最小損失に到達します。MFE は好ましい方向で最大価格変動を示します。それぞれ MAE は逆方向での最大価格変動を示します。両方の指数をポイントで測定するのは合理的であると思われます。ただし、異なる通貨ペアがトレードされていたら、それを金額で表現する必要があります。
終了済みトレードは結果(収益)および2種類の指数-MFE と MAE、に対応します。トレード結果が利益 $100 、MAEが -$1000 であれば、このトレードがベストであるとは言えません。数多くのトレードを行うことは利益につながりますが、1トレードにつき MAE の負の値が大きいことは、システムが損失を出すポジションに「長居」しすぎたことを伝えます。そのようなトレードは遅かれ早かれ失敗する運命にあります。
同様に、MFE の値も有用な情報を提供します。ポジションが正しい方向でオープンした場合、1トレードごとの MFE は $3000 になりますが、トレードがそれから利益 $500 でクローズすると、固定されていない利益保護のシステムを念入りに作るのは良いと言えます。後者が好ましい方向に変動する場合、価格の後に移動できるのは「トレーリングストップ」です。短期利益が体系的であれば、システムは大幅に改善されます。MFE はこのことを語ってくれるのです。
視覚的分析の方が便利なので、MAE と MFEの値分布のグラフ表現を利用するのが良いでしょう。 トレードをすべてグラフにすれば、結果がどのように得られたか確認することができます。たとえば、まったくこれまで負けトレードを知らない RobinHood の「レポート」を見ると、各トレードのドローダウン(MAE)は -$120 ~ -$2500であるのがわかります。
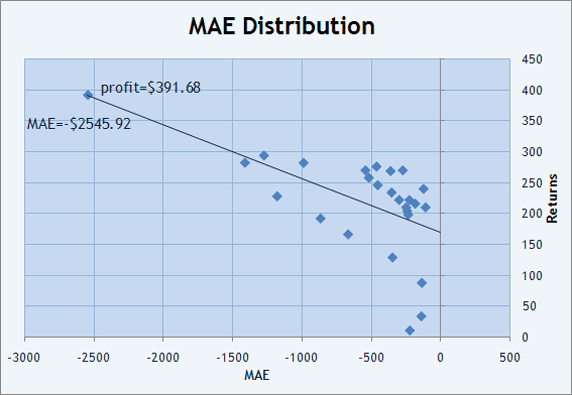
図11 MAExReturns の平面上のトレード分布
また、LS 法によって利益 × MAE に一致する直線を描くことができます。図11では、それは赤で示され、負の傾斜となっています(左から右へ直線の値は減少しています)。パラメータの相関関係(利益、MWE)=-0.59 により、チャートに分布する点が直線にどのくらい近いか推定することができます。負の値はフィッティングラインの傾斜が負の傾きであることを示します。
別の出場者のアカウントに目を通すと、相関係数が通常は正であることがわかります。上の例では、ラインの減少の傾きは負けトレードにならないよう、ますますドローダウンが増える傾向にあることを告げてくれているのです。ここで、パラメータ LR 相関=1の理想的値にどの価格が支払われたのか理解することができます。
同様に、相関(利益、MFE) =0.77 と相関(MFE, MAE)=-0.59 の値を求めることと共に、「利益」と MFE の分布グラフを作成することもできます。相関(利益、MFE)は正で1(0.77)の傾向があります。これは戦略が浮動利益の長い「待ち」を許可しないでおこうとしていることを伝えます。おそらく、利益は十分上がることなく、トレードはテイクプロフィットでクローズする可能性が高いということです。おわかりのように、MAE と MFE の分布は視覚的推定を与え、相関(利益、MFE)および相関(利益、MAE)はチャートなしでもトレードの性質を伝えてくれます。
「チャンピオンシップ」出場者の「レポート」にある相関(MFE, MAE)、相関(NormalizedProfits, MAE)、相関(NormalizedProfits, MFE)の値は追加情報として提供されています。
トレード結果の正規化
トレーディングシステムを作成する過程で、通常ポジションに対するサイズ修正が行われます。これで、特定の基準でより最適なパラメータを見つけるための、システムパラメータの最適化がもっと簡単にできるようになるのです。ただ、インプットを求めたあと、論理的な質問が生じます。どのようなサイジング管理システム(資金管理、MM)を適用すべきか?オープンしているポジションサイズは直接アカウント上の資金に関連しています。そのため、アカウント上で $50,000 と同じように $5,000 でトレードを行うことは合理的ではないかもしれません。また、MM システムはポジションをオープンすることができますが、それは正比例ではありません。$50,000 でオープンしているアカウントのポジションは必ずしも $5,000 でオープンしているものの10倍ではないということです。
ポジションサイズも現時点の市場相、直近の複数トレード分析結果などによって変化するのです。よって、適用される資金管理システムは本質的にトレーディングシステムの最初の書き方を変える可能性があります。それでは、採用される資金管理システムの影響をどのように推定することができるのでしょうか?それは有用でしょうか?それともわれわれのトレード方法の不利な側面を悪化させるだけでしょうか?最初に同じデポジットサイズである複数アカウントのトレード結果を比較するにはどうすればよいのでしょうか?可能な解決法はトレード結果の正規化だろうと思われます。
NP=TradeProfit ÷ TradeLots × MinimumLots ここで |
正規化は次のように実現されます。トレード結果(利益か損失)それぞれをポジションボリュームで割り、それからそこに最小許容ポジションサイズを掛ける。たとえば、USDJPY のオーダーNo.4399142 、ロット 2.3 買い、は利益 $4 056 でクローズしました。20 + $118.51 (swaps) = $4 174.71. この例は GODZILLA (Nikolay Kositsin)のアカウントから抜粋しました。結果を 2.3 で割って、0.1 (最小許容ポジションサイズ)を掛け、利益 $4 056.20/2.3 * 0.1 = $176.36 とスワップ = $5.15を取得します。これらはロットサイズ 0.1 のオーダーに対する結果です。全トレード結果に対して同じように計算を行い、「正規化された利益(NP)」を取得します。
まず考えるべきことは、相関(NormalizedProfits, MAE)および(NormalizedProfits, MAE)の値を求め、それを初期の相関(利益、MAE)および(利益、MFE)と比較することです。パラメータ間の差が大きければ、採用した方法は初期システムを本質的に変えてしまった可能性があります。それらは ММ を採用することは収益性あるシステムを「殺す」可能性があり、負けつつあるシステムを利益を上げるシステムに変えることはできないことを告げています。「チャンピオンシップ」では、TMR のアカウントが相関(NormalizedProfits, MFE)の値が 0.23 から 0.63 に代わる場面でトレーダーが「黒字でクローズする」ことのできた稀な例です。
戦略の攻撃性を推定する方法は?
採用された MM 方法が戦略にどのように影響するのか測定する中で、正規化されたトレードからさらに利益を上げることができるのです。ポジションサイズが10倍に増えると、最終結果は初期結果と10倍変わることは明白です。では与えられた倍数ではなく現在の動向に応じてトレードサイズを変更したらどうなるのでしょうか?信用管理企業からもたらされる結果は通常特定のモデル-たいていは株式指数、と比較されます。ベータ係数は指数と比較して何倍アカウント資金が変動するかを示します。正規化したトレードを指数とするなら、初期システム(ロット0.1 のトレード)と比較して、結果がどの程度変わりやすいか知ることができるのです。
よってまず、共分散-cov(Profits, NormalizedProfits)、を計算します。それから、正規化トレードのシーケンスに NP と名付け、正規化トレードの分散を計算します。このためには、M(NP) と呼ばれる正規化トレードの数学的期待値を計算します。M(NP) は正規化トレードに対する平均的なトレード結果を示すものです。それから、正規化トレードの SSD を求めます。すなわち、(NP-M(NP))^2を合計するのです。取得される結果はトレード数で割り、D(NP) と名前をつけます。これが正規化トレードの分散です。測定対象システムの共分散、利益、理想的指数、 NormalizedProfits cov(Profits, NormalizedProfits)をインデックス分散 D(NP) で割ります。結果は、正規化トレードとの比較として、資本が元のトレード(「チャンピオンシップ」のトレード)結果より何倍変わりやすいか推定できるパラメータ値なのです。このパラメータは「レポート」では、「マネーコンパウンド」と呼ばれています。それはある程度のレベルまでのトレードの攻撃性を表します。
MoneyCompounding=cov(Profits, NP) ÷ D(NP)= M((Profits-M(Profits)) × (NP-M(NP))) ÷ M((NP-M(NP))^2) ここで |
ここで「自動売買チャンピオンシップ 2006」出場者のテーブルを読む方法を修正することができます。
| 番号 | ログイン | LR 標準エラー($) | LR 相関 | シャープレシオ | GHPR | Z スコア(%) | マネーコンパウンド | 利益($) |
|---|---|---|---|---|---|---|---|---|
| 1 | Rich | 6 582.66 | 0.81 | 0.41 | 2.55 | -3.85(99.74) | 17.27 | 25 175.60 |
| 2 | ldamiani | 5 796.32 | 0.64 | 0.21 | 2.89 | -2.47 (98.65) | 28.79 | 15 628.40 |
| 3 | GODZILLA | 2 275.99 | 0.9 | 0.19 | 1.97 | 0.7(51.61) | 16.54 | 11 378.70 |
| 4 | valvk | 3 938.29 | 0.89 | 0.22 | 1.68 | 0.26(20.51) | 40.17 | 9 819.40 |
| 5 | Hendrick | 3 687.37 | 0.79 | 0.24 | 1.96 | 0.97(66.8) | 49.02 | 9 732.30 |
| 6 | bvpbvp | 9 208.08 | 0.58 | 0.43 | 12.77 | 1.2(76.99) | 50.00 | 8 236.00 |
| 7 | Flame | 2 532.58 | 0.75 | 0.36 | 3.87 | -2.07(96.06) | 6.75 | 7 676.20 |
| 8 | Berserk | 1 943.72 | 0.68 | 0.20 | 1.59 | 0.69(50.98) | 17.49 | 7 383.70 |
| 9 | vgc | 905.10 | 0.95 | 0.29 | 1.63 | 0.58(43.13) | 8.06 | 6 801.30 |
| 10 | RobinHood | 109.11 | 1.00 | 3.07 | 1.74 | N/A (N/A) | 41.87 | 5 643.10 |
| 11 | alexgomel | 763.76 | 0.95 | 0.43 | 2.63 | 1.52(87.15) | 10.00 | 5 557.50 |
| 12 | LorDen | 1229.40 | 0.8 | 0.33 | 3.06 | 1.34(81.98) | 49.65 | 5 247.90 |
| 13 | systrad5 | 6 239.33 | 0.66 | 0.27 | 2.47 | -0.9(63.19) | 42.25 | 5 141.10 |
| 14 | emil | 2 667.76 | 0.77 | 0.21 | 1.93 | -1.97(95.12) | 12.75 | 4 658.20 |
| 15 | payday | 1686.10 | 0.75 | 0.16 | 0.88 | 0.46(35.45) | 10.00 | 4 588.90 |
勝者のアカウントの LR 標準エラーは最小ではありませんでした。同時に、もっとも利益を上げた Expert Advisor の残高グラフは LR 相関の値が 1.0 からあまり離れていないため、かなり滑らかです。シャープレシオは基本的に 0.20~0.40 の範囲内に収まっています。外部シャープレシオ=3.07 の EA だけが MAE と MFE の値があまり良くないことが判明しました。
トレードごとの GHPR は基本的に 1.5~3% の範囲に位置しています。そこでは勝者はGHPR の値が最大だったわけではありません。かといって最小だったのでもありませんが。極値 GHPR=12.77% はトレードに異常があったことを再び伝えています。このアカウントは LR 標準エラー=$9 208.08のもっとも大きな変動を経ていたことがわかります。
Z スコアは「チャンピオンシップ」の出場者上位15人についてなにも一般化になっていませんが、値 |Z|>2.0 はトレード間のアカウントに依存する性質を理解するために、トレード履歴に対する注意を喚起します。よってRich のアカウントについてのZ=-3.85 は、3つのアカウントを同時にオープンしたことで、実質上その結果に至ったとわかります。では、ldamiani のアカウント状況はどうでしょうか?
最後に、上記テーブルに関する最後の列、マネーコンパウンド も 8~50 と値範囲は大きく、最大許容トレードサイズは、最小サイズである 0.1 ロットの50倍、5.0 ロットとされていたため、50 はこの「チャンピオンシップ」での最大値となっています。ただ不思議なことに、このパラメータは勝者では最大ではありません。上位3組の値は17.27、28.79、16.54 です。勝者は最大許容ポジションサイズを最大限使用しなかったのでしょうか?いいえ、しています。問題はおそらく、契約サイズを標準的に増やす際、MM 法がトレードのリスクに大きくは影響しなかったことです。これは資金管理がトレーディングシステムにとってひじょうに重要であることの目に見える証拠です。
15位はpayday が取りました。この出場者の EA は 、コード内の小さなエラーにより、1.0より大きなサイズではトレードを開始しませんでした。このエラーが発生せず、ポジションサイズが 5.0 ロットまで5倍増えていたらどうなったのでしょうか?そうすると利益が比例して増えていたことでしょう。 $4 588.90 から $22 944.50へ、でしょうか?そうなると彼は第2位を獲得したのでしょうか? それともリスクが増大したことで回復不能のドローダウンを経験することになったでしょうか?alexgomelが第1位となったのでしょうか?彼の EA も 1.0 ロットだけでトレードを行ったのです。それとも、Expert Advisor がもっとも頻繁に 1.0 ロットより小さいサイズでトレードをオープンした vgc が勝者となった可能性があります。3人の残高グラフはすべて良い滑らかなものでした。ごぞんじのように、「チャンピオンシップ」のプロットは「チャンピオンシップ」が終了しても継続します。
おわりに「赤子を湯水と共に捨てるなかれ」
人の意見はさまざまです。本稿ではトレーディング戦略を推定するひじょうに一般的方法を提供しています。トレード結果を推定するためにもっと数多くの基準を設けることが可能です。個別に取り上げられている性質は完全で客観的な推定を提供するものではありませんが、一緒に取り入れることでこの問題の偏ったアプローチを避けることができます。
トレードの否定的な点を見つけるために、良好な結果(十分なトレードシーケンスで利益を得た)に対して「反対尋問」を行うことができます。この意味するところは、こういった性質がすべて、良好な最終結果-アカウントに得た純利益、だけに満足せず、注意すべきトレードのウィークポイントを知らせてくれるほど、既存のトレーディング戦略の有効性を性格づけるものではない、ということです。
理想のトレーディングシステムを作成することはできません。どんなシステムでもメリットがあれば、その含むところはあるものです。独断的にトレード方法を拒否しないために、またトレーディングシステムや Expert Advisor をさらに発展させる方法を知るため予測検証が行われます。この点では、自動売買チャンピオンシップ 2006 の間に蓄積された統計データがすべてのトレーダーにとって強力な支援となってくれることでしょう。
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/1492
 初心者向け MQL4 言語テクニカルインディケータと組み込み関数
初心者向け MQL4 言語テクニカルインディケータと組み込み関数
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索


