MQL5の圏論（第13回）：データベーススキーマを使用したカレンダーイベント

MetaTrader 5 — テスター | 14 8月 2023, 08:27

388

Stephen Njuki

はじめに

圏論に関するこの連載の前回の記事では、順序理論が圏論とどのように連携できるかを検討し、この結合の概念をMQL5でどのように実装できるかを検討しました。また、これらの概念のいくつかを使用した取引システムのケーススタディについても検討しました。

前回の記事では、部分順序と線形順序という2つの順序理論の概念に焦点を当てました。要約すると、部分順序は、反対称関係を使用した前順序に焦点を当てたタイプの集合ランク付け法です。これは、反射関係と推移関係も持つことを意味します。一方、線形順序は、未定義の関係が許可されないことを意味する比較可能性をさらに要求することにより、部分順序のより焦点を当てた形式です。

この記事では、新しい概念の導入から一休みし、データベーススキーマを使用する言語分類子に概念を統合することを目標に、これまでに取り上げてきた内容の一部を一歩下がって確認します。

カレンダーイベントの効果的な分類の必要性

カレンダーイベントはほぼ毎日生成され、そのほとんどは数か月前に事前にマークされています。MetaTrader経済指標カレンダーを介して提供されており、中国、米国、日本、ドイツ、EU、英国、韓国、シンガポール、スイス、カナダ、ニュージーランド、オーストラリア、ブラジルの通貨およびマクロ経済指標がハイライトされています。このリストは動的であるため、将来さらに多くの国が追加される可能性があります。これらの指標は多くの場合書式設定されますが、必ずしも予測値、実際の値、および以前の値を主に特徴とする数値で書式設定されるわけではありません。「頻繁に書式設定される」と述べたことに注意してください。これは、すべての指標に数値があるわけではないためです。また、実際の数値の数値と書式は指標間でもかなり異なるためです。言い換えれば、比較できないことがたくさんあり、これはある意味で問題になります。

これらの通貨や経済の指標の読み取り値を使用するには、トレーダーは確実かつ一貫して数値を読み取り、投稿されたテキストを正確に解釈できる必要があります。いくつかの典型的なカレンダーイベントを見てこれを説明しましょう。

上には、中国、米国、日本、ドイツの4つのイベントがあり、それぞれ指数、利回り、金額、未定義の値を取得しています。この情報は、以下に示すような簡単な方法でMQL5で抽出できます。

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void SampleRetrieval(string Currency)
   {
      MqlCalendarValue _value[];
      datetime _stop_date=datetime(__start_date+int(PeriodSeconds(__stop_date_increment)));
//--- get events
      MqlCalendarEvent _event[];
      int _events=CalendarEventByCurrency(Currency,_event);
      printf(__FUNCSIG__+" for Currency: "+Currency+" events are: "+IntegerToString(_events));
      //
      for(int e=0;e<_events;e++)
      {
         int _values=CalendarValueHistoryByEvent(_event[e].id, _value, __start_date, _stop_date);
         //
         for(int v=0;v<_values;v++)
         {
            //
            printf(__FUNCSIG__+" Calendar Event code: "+_event[e].event_code+", for value: "+TimeToString(_value[v].period)+" on: "+TimeToString(_value[v].time)+", has... ");
            //
            if(_value[v].HasPreviousValue())
            {
               printf(__FUNCSIG__+" Previous value: "+DoubleToString(_value[v].GetPreviousValue()));
            }
            
            if(_value[v].HasForecastValue())
            {
               printf(__FUNCSIG__+" Forecast value: "+DoubleToString(_value[v].GetForecastValue()));
            }
            
            if(_value[v].HasActualValue())
            {
               printf(__FUNCSIG__+" Actual value: "+DoubleToString(_value[v].GetActualValue()));
            }
         }
      }
   }

抽出後の問題は、分析に使用するために抽出された値をどのように整理および並べ替えるかという点にあります。数値がすべてインデックスのように0～100の範囲の標準的なものである場合、各イベントの相対的な重要性を簡単に判断できるため、カレンダーイベント間の相対比較が簡単になります。ただし、個々のイベントと特定の株式や通貨の値動きとの相関関係など、分析は「第三者」を介して行う必要があります。

それに加えて、ドイツに関する上記の連邦銀行理事会メンバーによる講演など、いくつかのイベントには比較可能な数値がありません。

しかし、さらに関連性があるのは、トレーダーがイベントを識別する方法であると考えられる、イベント自体のテキスト説明です。たとえば、EURUSDのような外国為替ペアを分析する場合、理想的には、EURイベントと同等のUSDイベントを考慮する必要があります。しかし、次のような出来事をどうやって阻止するのでしょうか。

cal_5

一見同等に見えるUSD側の対応物は次のとおりです。

と

ユーロを選択するとき、ユーロのセンチメントとドイツのセンチメントのどちらを使用するのでしょうか。それとも両方を重み付けして使用するのでしょうか。重み付けするとしたら、どのような重みを使用するのでしょうか。USD側では、ミシガンまたはフィラデルフィアのどちらの値を使用するのでしょうか。

したがって、MQL5によってすでに提供されているもの以外に、イベントを分類する追加の方法が必要です。これは、経済や通貨間で数値を簡単に比較できるだけでなく、特に取引を実行する目的にも役立ちます。

既存の分類方法は非常に初歩的なもので、IDによるイベントの選択、国によるイベントの選択、通貨によるイベントの選択が含まれます。これらのイベントの価値を考慮した分類は他にもほとんどありませんが、これらの分類と大きな違いはありません。また、国別および通貨別に選択すると、主にユーロのおかげで曖昧さが生じますが、これは役に立ちません。イベントが指数のように後ろ向きなのか、センチメントのように前向きなのかという基本的な側面が欠けています。また、同じイベントについて通貨間で比較する必要性は、上記のEURUSDペアのように明確に定義されていない場合もあります。

圏論の概念とデータベーススキーマ

これまで圏論で扱ってきたことを簡単に要約すると、集合の基本単位である要素を調べることから始めて（集合は以前の記事では始域と呼ばれていました）、次に集合、次にその型と射、最後に、構成とそれが示す多くの特性と形式を見てきました。

グラフの近似であり、データベーススキーマと呼ばれる、テーブルに設定される個々のデータを時期尚早に気にすることなく、データが準拠する概念的なレイアウトをキャプチャします。確立されたデータベースは、参照整合性を強制し、データの重複を回避するインデックス付きストレージツールです。

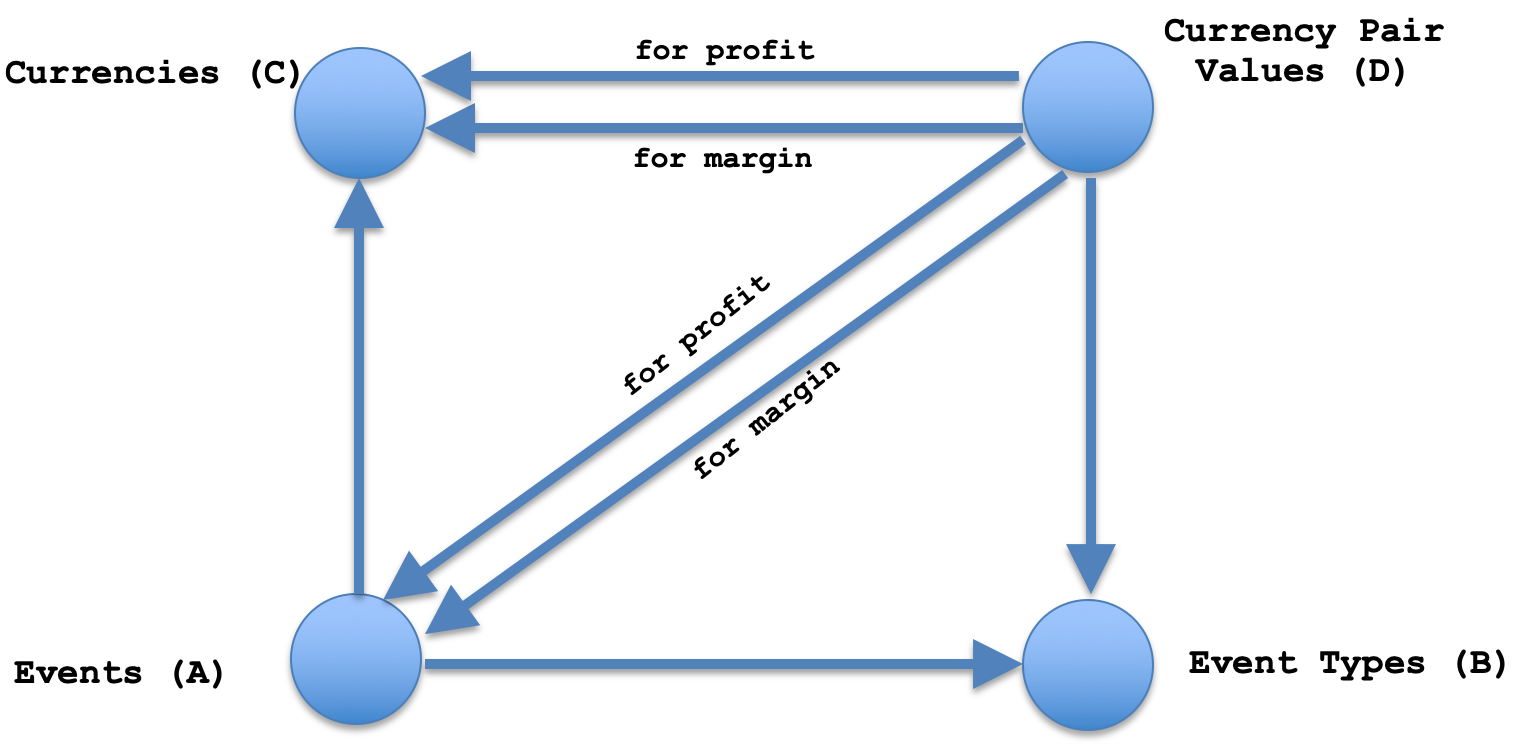
圏論とデータベーススキーマの間の潜在的な相乗効果は、圏論の構成がその特性の一部をデータベーススキーマに提供できるという事実にあります。したがって、単純なデータベースを使用してカレンダーイベントを分類することから始めれば、プルバック、グラフ、注文など、さまざまな「レンズ」を通してスキーマを簡単に見ることができます。以下は、カレンダーイベントを定義できるテーブルを図で表したものです。

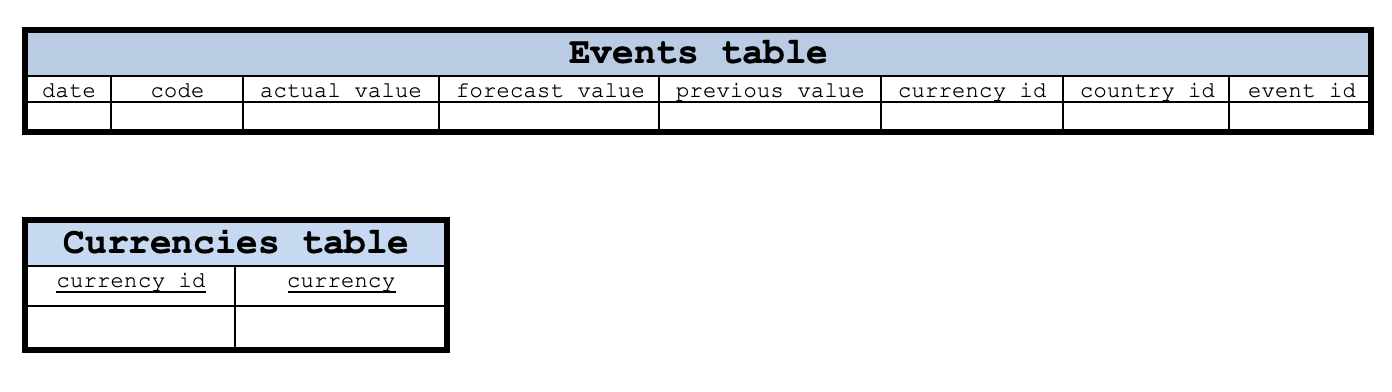
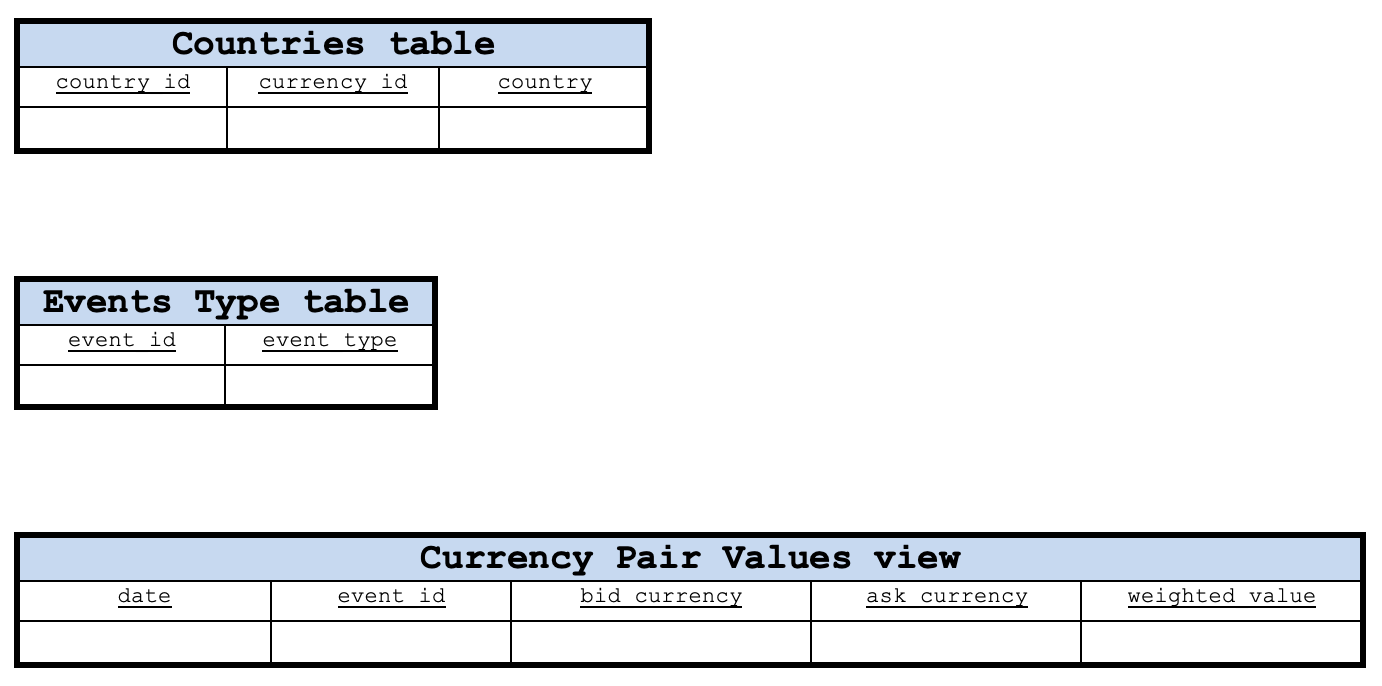
この基本レイアウトでは、イベントテーブルの日付列とコード列の両方が主キーとして機能します。コード列を思い出してください。コード列には、カレンダーイベントから読み取られたイベントコードデータが保持されます。通貨、国、およびイベントタイプのテーブルには、主キーをそれぞれCurrency_id、country_id、event_id列として簡単に設定できます。ただし、通貨ペア値テーブルでは、主キーのdate列とevents_id列を組み合わせる必要があります。

上記はテーブル間の接続が示されていないためスキーマではなく、単にデータベース内のテーブルを示しているだけです。ただし、スキーマを作成することはできます。その一部を以下に示します。

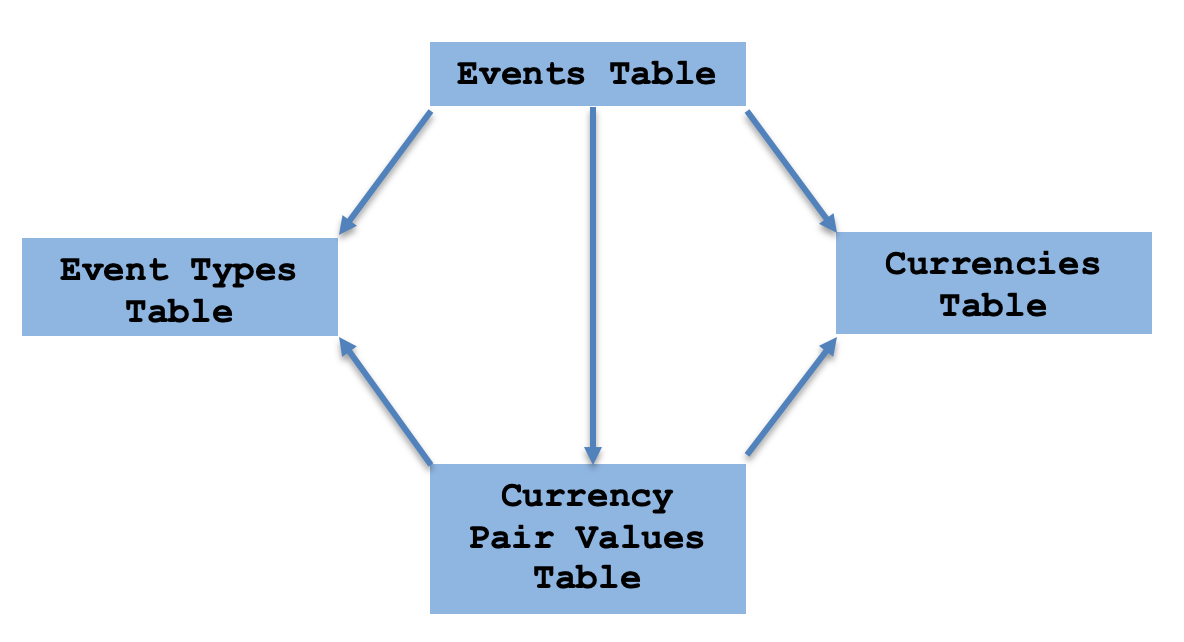
この図式的な配置は、圏論の積積として簡単に見ることができます。これが意味するのは、イベントテーブルと通貨ペアの値ビューの間に普遍性があるということです。

要約すると、通常、余積の普遍性は区分曲線を処理する場合に役立ちます。たとえば、2つの領域AとBで記録された温度がそれぞれ線形および二次的に変化する実験を考えてみましょう。組み合わせた領域の温度プロファイルを研究するために、AuB余積の普遍的な特性により、各領域の個々の温度プロファイルを曲線データに基づいて1つの関数に貼り付けることができます。これは、誰かが明確に定義された旅程を持たずにその地域への旅行を決定する場合、予想されることの合理的な代用となります。

トレーダーとしての私たちの目的にとって、個々の通貨のイベント値が同時にリリースされることはないため、上記の構成は非常に役立ちます。したがって、たとえばユーロのセンチメント数値が今日発表された場合、米ドルのセンチメント数値は2週間以内に発表される可能性があります。古いUSD（最新）の値を使用して通貨ペアの値を算出することもできますが、圏論を使用すると、実際に普遍的な特性を使用して、ダイアグラムが交換されるため更新されない通貨の期待または予測することができます。

MQL5での実装

圏理論とスキーマはMQL5で正方形の通勤として表すことができるため、以前の記事のCSquareCommuteクラスを次のように少し変更できます。

//+------------------------------------------------------------------+
//| Square Commute Class to illustrate Universal Property            |
//+------------------------------------------------------------------+
template <typename TA,typename TB,typename TC,typename TD>
class CCommuteSquare
   {
      public:
      
      CHomomorphism<TA,TB>          ab;
      CHomomorphism<TA,TC>          ac;
      CHomomorphism<TD,TB>          db;
      CHomomorphism<TD,TC>          dc;
      
      CHomomorphism<TD,TA>          da;   //universal property
      
      virtual void                  SquareAssert()
                                    {
                                       ab.domain=ac.domain;
                                       ab.codomain=db.codomain;
                                       dc.domain=db.domain;
                                       dc.codomain=ac.codomain;
                                       
                                       da.domain=db.domain;
                                       da.codomain=ac.domain;
                                    }
      
                                    CCommuteSquare(){};
                                    ~CCommuteSquare(){};
   };

元のクラスに追加したものは、単に普遍性に対する追加の準同型写像です。したがって、これを定義したら、次の重要なことは、それぞれのデータを取得する各集合の要素を定義する方法になります。これは、以下にリストされているように、イベント集合（イベントテーブルとして表示）に対して実行できます。

//sample constructor for event set
CElement<string> _e_event;_e_event.Cardinality(7);
//

この要素が定義されると、トレーダーは上で共有したlist-1またはその他の適切なオプションを使用して、この要素にデータを簡単に入力できます。読者の方が自分の戦略により適した方法を思いつくことができると確信しているので、ここでは実証には労力は費やしませんでした。以前の記事で説明したように、要素にデータを入力すると、上に示したCSquareCommuteクラスのそれぞれの始域に簡単に追加できます。イベント値や通貨集合要素も以下のように構築できます。

//sample constructor for type set
CDomain<string> _d_type;_d_type.Cardinality(_types);
//data population
CElement<string> _e_type;_e_type.Cardinality(1);
      //sample constructor for currency set
CDomain<string> _d_currency;_d_currency.Cardinality(_currencies);
//data population
CElement<string> _e_currency;_e_currency.Cardinality(1);

これは、通貨ペアの値要素につながります。この集合では、通貨を共通の取引ペアにペアリングします。このペアには、市場監視から選択された場合の価格チャートがあり、各通貨の2つのイベント値を組み合わせたペアの実効値である新しい数値が追加されます。したがって、たとえば、EUR通貨に写像されるユーロ圏の小売売上高と、USDに写像される米国の小売売上高がある場合、設定された通貨ペア値にはEURUSDペアとその有効小売売上高がリストされます。その要素を構築するためのリストを以下に示します。

//sample constructor for values set
CDomain<string> _d_values;_d_values.Cardinality(_values);
//data population
CElement<string> _e_values;_e_values.Cardinality(4);

そうは言っても、通貨ペアのビュー（上記のMQL5リストでは通貨ペアの値）がなぜ重要なのかという疑問が生じるかもしれません。イベントカレンダーで報告される2つの通貨のイベント値を、これら2つの通貨の通貨ペアの単一の値に統合します。この単一の値は、たとえば、ペアの価格時系列やこのペアの他の指標シリーズなど、さらなる研究の機会を提供する時系列を形成することができます。

これまで説明した内容を要約すると、この分類の設計と実装に含まれる手順は、まず生のカレンダーイベントをデータベーススキーマに分類することです。これにより、繰り返しのテキストが識別され、インデックスの使用が可能になります。他のすべてのテーブルにリンクするイベントテーブルを持つ単純なスキーマをこの設計に使用できます。

この設計では、上記の最初のリスト1に示すように簡単に抽出できるカレンダーイベントを反復処理し、データベースに値を入力します。車輪の再発明ではありませんが、構造体として表される付随テーブルを備えたデータベースのクラスは次のようになります。

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class CDatabase
  {
      public:
      
      STableEvents               events;
      STableEventTypes           event_types;
      STableCountries            countries;
      STableCurrencies           currncies;
      
      
                                 CDatabase(void);
                                 ~CDatabase(void);
  };

これがSQLと異なるのは、SQLでは通常、コンピュータの記憶領域（ハードドライブ）にデータが保存される野に対して、データが一時的なRAMに保存されることです。ただし、このクラスを使用すると、既存のデータベースにエクスポートできます。また、MQL5 IDEにはデータベース処理機能があるため、最終的には、コンピューティングリソースを節約するために、RAMではなく物理データベースからこれらの値を読み取ることができます。

データベースを取得したら、上記のクラスからSquare Commuteを構築します。このプロセスには、以下の図に示すようにコーナー集合を定義するだけが含まれます。集合ごとにその要素構造を定義し、そのリストはすでに上で共有されています。要素が定義されると、データベースからのデータが要素に入力され、CSquareCommuteクラスのインスタンスに追加されます。

集合を取得したら、これらの集合間の準同型写像を定義する楽しい作業に取り掛かります。イベント集合からイベントタイプ集合への準同型写像は、単にイベントをそのタイプに写像することになります。これは、データベースの設計点から、イベントテーブルにはタイプのインデックスの列しか持てないということです。実際のタイプとそのインデックスはイベントタイプテーブル内にあり、2 つの間の外部キー関係は準同型写像と同等になります。これはデータベースではないため、タイプ集合には、イベント集合の一部としてすでにリストされているすべてのタイプが繰り返しなしで含まれているだけです。つまり、イベント集合が始域で、イベントタイプが終域です。したがって、準同型写像は以下のリストを使用して簡単に定義できます。

      //ab homomorphisms
      CHomomorphism<string,string> _ab;
      
      CElement<string> _e;
      for(int s=0;s<_sc.ab.domain.Cardinality();s++)
      {
         _e.Let();
         if(_sc.ab.domain.Get(s,_e))
         {
            string _s="";
            if(_e.Get(0,_s))
            {
               CMorphism<string,string> _m;
               _m.Morph(_sc.ab.domain,_sc.ab.codomain,s,EventType(_s));
               
               _ab.Morphisms(_ab.Morphisms()+1);
               _ab.Set(_ab.Morphisms()-1,_m);
            }
         }
      }

同様に、イベントから通貨への準同型写像は、以下のリストで実現できる単純な写像です。

      //ac homomorphisms
      CHomomorphism<string,string> _ac;
      
      for(int s=0;s<_sc.ac.domain.Cardinality();s++)
      {
         _e.Let();
         if(_sc.ac.domain.Get(s,_e))
         {
            string _s="";
            if(_e.Get(1,_s))
            {
               CMorphism<string,string> _m;
               int _c=EventCurrency(_s);
               if(_c!=-1)
               {
                  _m.Morph(_sc.ac.domain,_sc.ac.codomain,s,_c);
                  
                  _ac.Morphisms(_ac.Morphisms()+1);
                  _ac.Set(_ac.Morphisms()-1,_m);
               }
            }
         }
      }

ただし、核心は残りの3つの準同型写像です。つまり、通貨ペア値集合からのイベントタイプ集合への写像、通貨ペア値集合からの通貨集合への写像、そして最後に、イベント集合から戻された通貨ペア値への普遍性写像です。比較的単純な最初の2つから始めてこれを明確にすると、通貨ペアの値からイベントタイプへの写像と、通貨ペアの値から通貨への写像が得られます。これにより、構成は積になります。準同型写像の基本的な規則に従って、始域内の要素は終域内の1つの要素にのみ写像できることに注意してください。これは、複数の通貨を参照する場合、逆方向の写像はできないことを意味します。これにより、ペアがその値を参照するたびにイベント値が複数のペアに写像されることになり、通貨についても同様に、そこから通貨ペアの値セットへの写像で同様の繰り返しの問題が発生します。したがって、イベント値への写像のためのこれの実装は次のようになります。

      //db homomorphisms
      CHomomorphism<string,string> _db;
      
      for(int s=0;s<_values;s++)
      {
         _e.Let();
         if(_sc.db.domain.Get(s,_e))
         {
            string _s="";
            if(_e.Get(3,_s))
            {
               int _t=TypeToInt(_s);
               CMorphism<string,string> _m;
               //
               _m.Morph(_sc.db.domain,_sc.db.codomain,s,_t);
               
               _db.Morphisms(_db.Morphisms()+1);
               _db.Set(_db.Morphisms()-1,_m);
            }
         }
      }

同様に、通貨への写像は次のようになります。

      //dc homomorphisms
      CHomomorphism<string,string> _dc;
      
      for(int s=0;s<_values;s++)
      {
         _e.Let();
         if(_sc.dc.domain.Get(s,_e))
         {
            string _s="";
            if(_e.Get(0,_s))//morphisms for margin currency only
            {
               int _c=EventCurrency(_s);
               
               CMorphism<string,string> _m;
               //
               _m.Morph(_sc.dc.domain,_sc.dc.codomain,s,_c);
               
               _dc.Morphisms(_dc.Morphisms()+1);
               _dc.Set(_dc.Morphisms()-1,_m);
            }
         }
      }

ここで注目すべきは、入札通貨と証拠金通貨の重み付けパラメータです。これらは、各経済のベンチマーク金利やインフレ率の最適化や相対的な重み付けによって達成できます（このリストはすべてを網羅しているわけではありません）。トレーダーは自分の戦略と市場見通しに基づいて選択を行う必要があります。イベントから返される通貨ペア値に対する最終的な準同型写像は、イベント集合内の2つのエントリに対する通貨ペア値の1つの要素に写像されます。上記の2つの写像に使用される重み付けに基づいて、普遍性写像は次のようにリストされます。

      //da homomorphisms
      CHomomorphism<string,string> _da;
      
      for(int s=0;s<_values;s++)
      {
         _e.Let();
         if(_sc.da.domain.Get(s,_e))
         {
            string _s_c="",_s_t="";
            if(_e.Get(0,_s_c) && _e.Get(3,_s_t))// for margin currency
            {
               for(int ss=0;ss<_sc.ac.domain.Cardinality();ss++)
               {
                  CElement<string> _ee;
                  if(_sc.da.codomain.Get(ss,_ee))
                  {
                     string _ss_c="",_ss_t="";
                     if(_ee.Get(1,_ss_c) && _ee.Get(6,_ss_t))// for margin currency
                     {
                        if(_ss_c==_s_c && _ss_t==_s_t)
                        {
                           CMorphism<string,string> _m;
                           //
                           _m.Morph(_sc.da.domain,_sc.da.codomain,s,ss);
                           
                           _da.Morphisms(_da.Morphisms()+1);
                           _da.Set(_da.Morphisms()-1,_m);
                           
                           _sc.da=_da; _sc.SquareAssert();
                           
                           break;
                        }
                     }
                  }
               }
            }
         }
      }
      
      _da.domain=_sc.da.domain;
      _da.codomain=_sc.da.codomain;
      _sc.da=_da; _sc.SquareAssert();

したがって、これは、個々の通貨のカレンダーイベントに基づいて通貨ペアに対する有効なウェイトを生成する最後のステップとなります。

カレンダーイベントの分類

イベントタイプの表を作成する際には、イベントタイプに到達する前にデータの臨界量を考慮する規律ある方法論に従うことが賢明かもしれません。問題文で述べたように、イベントの分類は重要です。したがって、これらのイベントを比較可能なタイプに分類する際に考えられる方法論には、以下が含まれます。データ収集：MQL5組み込みクラスを使用したデータの基本的な抽出は、上で共有しました。イベントのグループ化が続き、指数、センチメント測定値、国債利回り、インフレ測定値などの標準グループを使用できます。その後、特徴抽出がおこなわれ、各イベントがキーワードに対して解析され、どのグループに最もよく属するかを決定します。次に、モデルのトレーニングと特徴分類の評価が続き、トレーニングデータセットとテストデータセットを作成し、モデルのトレーニングから開始します。続いて、テストデータセットでモデルをテストして、イベントがどの程度適切に分類されているかを確認します。そして最後に、分析後の反復的な改善により、モデルを過度に適合させることなく微調整できる方法を検討することで、これが結論付けられます。

イベントタイプを作成したら、上図に示すevent_typesテーブルにこれらを設定します。これは、グループを割り当てるために、すべてのイベントに対してイベントテーブルのイベントタイプID列が更新されることを意味します。新しい行を挿入したり行を更新したりする格納済みプロシージャは、これに関する上記のモデルの実装に役立ちます。

要素のデータ型がデータ列に対応する各配列インデックスを持つ文字列配列であるため、イベントのセットへのこの追加は、上記の構成に対する唯一の重要な変更がイベントからイベント値への準同型性であることを意味します。「小売売上高」のように、どの通貨でも説明テキストが同一である値のみを含めるのではなく、より広範囲のイベントに対応できるようになります。

取引決定に関する情報提供

上記の構成から通貨ペア値始域を作成することは、タイムスタンプ付きの通貨ペア値があることを意味します。このタイムスタンプにより、これらの値の大きさ（場合によっては方向）を最終的な価格の変化と比較することができます。データ集合のトレーニングとテストを含む慎重な分析プロセスでは、各イベントタイプが最終的な価格変動とどのように、どの程度相関しているかを確認できます。

イベント値と後続の値動きの相関関係に関するこのデータを使用することで、分析結果に基づいて売買取引をおこなうためのルールを設定できるだけでなく、相関の大きさに基づいてポジションのサイズを設定することもできます。

加重通貨ペアの値を使用して最終的な値動きをタグ付けするシステムの精度は、複数のイベントが加重平均で結合され、この「指標」が最終的な値動きと相関付けられる場合に向上する可能性があります。これにより、どの重みがどのイベントに適用されるかという疑問が生じます。この答えは最適化によって答えることができ、あるいはトレーダー自身のマクロ経済学の理解がこのプロセスを導くこともできます。どちらの方法を選択する場合でも、このより全体的なアプローチにより、より正確な予測が得られるはずです。

ケーススタディ：MQL5での実装と評価

簡潔にするために、これは完全な取引システムではなく、すでに述べたように、イベント、タイプ、通貨、および値の4つの集合で構成される構成を考慮した最初の部分のみになります。データベースクラスを使用せずにカレンダーイベントデータを直接取得し、CSquareCommuteクラスのインスタンスにデータを入力し、生成できる準同型写像を読み取ります。繰り返しますが、これは純粋に可能性を実証することを目的とした最初のステップにすぎません。そのための入力は主に3つです。すなわち、焦点を当てるイベントのタイプ、買い/証拠金通貨の重み付け、売り/利益通貨の重み付けです。説明したように、これらの重みは2つの通貨のカレンダー値を1つに結合するためのものです。この調査の読み取り値を生成する際には、PMI関連のイベントのみを考慮し、通貨EUR、GBP、USD、CHF、JPYのみと、EURUSD、GBPUSD、USDCHF、USDJPYのペアのみの値を調べます。すべてのコードは記事の最後に添付されています。普遍性の準同型写像の出力を実行すると、以下のようなログが得られるはずです。

2023.07.11 13:51:52.966 ct_13 (GBPUSD.i,H1) void OnStart() d to a homomorphisms are... 
2023.07.11 13:51:52.966 ct_13 (GBPUSD.i,H1) 
2023.07.11 13:51:52.966 ct_13 (GBPUSD.i,H1) {(EUR,USD,45.85000000,TYPE_PMI),(GBP,USD,47.00000000,TYPE_PMI),(USD,CHF,45.05000000,TYPE_PMI),(USD,JPY,48.75000000,TYPE_PMI)}
2023.07.11 13:51:52.966 ct_13 (GBPUSD.i,H1) |
2023.07.11 13:51:52.966 ct_13 (GBPUSD.i,H1) (EUR,USD,45.85000000,TYPE_PMI)|----->(markit-manufacturing-pmi,EUR,44.60000000,44.60000000,44.80000000,2023.06.01 11:00,TYPE_PMI)
2023.07.11 13:51:52.966 ct_13 (GBPUSD.i,H1) |
2023.07.11 13:51:52.966 ct_13 (GBPUSD.i,H1) {(markit-manufacturing-pmi,EUR,44.60000000,44.60000000,44.80000000,2023.06.01 11:00,TYPE_PMI),(markit-manufacturing-pmi,EUR,44.80000000,44.20000000,43.60000000,2023.06.23 11:00,TYPE_PMI),(markit-services-pmi,EUR,55.90000000,55.90000000,55.10000000,2023.06.05 11:00,TYPE_PMI),(markit-services-pmi,EUR,55.10000000,55.50000000,52.40000000,2023.06.23 11:00,TYPE_PMI),(markit-composite-pmi,EUR,53.30000000,53.30000000,52.80000000,2023.06.05 11:00,TYPE_PMI),(markit-composite-pmi,EUR,52.80000000,53.00000000,50.300000

PMIイベントと上記で事前に選択した通貨およびペアのみを入力すると、マージン通貨の射が1つだけ得られます。この場合はたまたまユーロです。合計値がユーロの入力値よりも高かったのは、単に米ドルの同等のPMI数値が高く、EURUSDペアの印刷値が単に加重平均であったためです。この特定のテストでは、EURとUSDの両方に等しい重み付けが使用されました。

結論

記事が長すぎくなるため、この分類を取引システムにどのように適用できるかを示すケーススタディは共有しませんでしたが、この記事には独自の実装を可能にする十分なコードと資料が含まれていると思います。要約すると、圏論とデータベーススキーマがどのように連携し、カレンダーイベントを分類するだけでなく、価格変動に対するカレンダーイベントの影響を定量化するのに役立つ普遍的な特性を備えた製品などの構成を定義するのに役立つかについて見てきました。

通貨ペアの価値がある場合に簡単にペアリングできるようにするイベントの標準的な分類を超えたこれのメリットは、圏理論の普遍性公理を使用することです。これは、（イベント値または通貨のコーナー集合を使用せずに）イベント集合から通貨ペア値集合に直接写像できる準同型写像を定義するのに役立ちます。これにより、前述したように、通貨のイベント値の一方のみが新しく、もう一方がまだ数日または数週間保留されている場合でも、通貨ペアの値を予測することができます。

MetaQuotes Ltdにより英語から翻訳されました。
元の記事: https://www.mql5.com/en/articles/12950

添付されたファイル |

ZIPをダウンロード

ct_13.mqh (25 KB)

ct_13.mq5 (22.43 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。