MQL5の圏論（第14回）：線形順序を持つ関手

はじめに

1950年代にサミュエル・アイレンベルグとサンダース・マック・レインによって導入された圏論は、相そのものではなく、各相における変換に重点を置いて体系を研究する手段とみなすことができます。Haskellのような言語による関数型プログラミングから、自然言語の構造と構成性を研究する言語学、さまざまな位相幾何学的構成と不変量を理解するための統一的なアプローチを提供する代数的位相幾何学まで、幅広い用途で使用されています。

この連載では、圏論はこれまで、サブ圏レベルの情報と構造（私たちの場合は主に集合（オブジェクト））に関わるという意味で局限されてきました。私たちは、圏内のすべての関係性と特性を見てきました。

この記事とそれに類するいくつかの記事の目的は、今後、圏からズームアウトして、さまざまな圏が相互に持つことができる関係を検討し始めることです。これは、正式には関手と呼ばれています。そこで、さまざまな圏とその可能な関係を見ていくことにします。トレーダーのデータセットの中には、研究する価値のある圏の候補がいくつかありますが、圏論の超越的な特質を強調するために、枠にとらわれず、この記事ではカリフォルニア沖で収集された潮汐データとNASDAQ指数のボラティリティを結びつけて考えてみたいと思います。潮汐に、この指数の変動を予感させるものはあるのでしょうか。記事の最後までに、この疑問にある程度答えられるようにしたいと思います。

この記事と、それに続くいくつかの記事は、それ自体新しい概念を紹介するものではなく、すでに取り上げられていることを見直し、より広範なスケールを意味する別の適用を検討するものです。

潮汐とNASDAQ指数

潮汐データは、アメリカ海洋大気庁(NOAA)が公表し、Webサイトを通じて一般に公開されています。このデータは、1日に4回、基準点から外れた潮汐の高さを記録します。一年中、その日の潮の満ち引きの時刻と高度だけが記録されます。これがプレビューです。

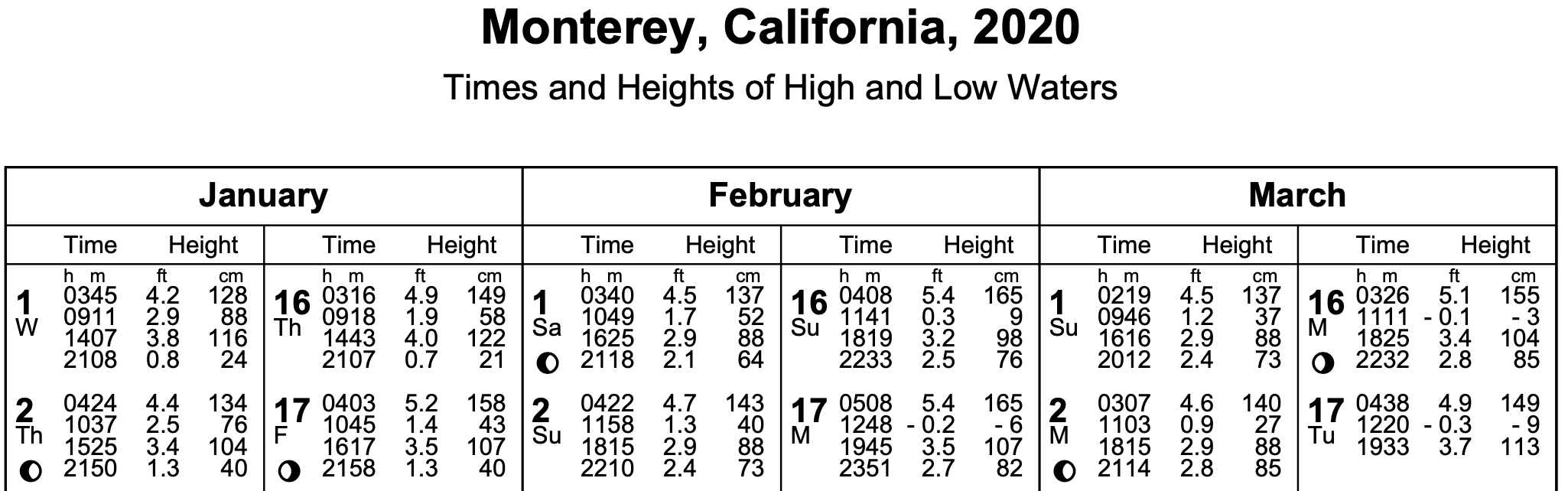
すべての海は4つの地域に分けられ、それぞれの地域内の多くの測定局から潮汐値が集められます。例えば、南米チリからアラスカまでの南北アメリカ西海岸には33の観測所があります。この分析では、2020年のカリフォルニア州モントレー局のデータを使用します。

NASDAQは定評のある証券取引所ですが、ここでは主に、MSFT、AAPL、GOOG、AMZNなど、カリフォルニアに本社を置く数多くのハイテク企業で構成される指数として見ています。この指数はほとんどの証券会社で取引できるため、その価格フィードから、産業に革命を起こし、カリフォルニアのイノベーション精神を体現しているこれらの企業の時価総額が、カリフォルニア沖で収集された潮汐データと何らかの形でリンクしているかどうかを確認することで、私たちの圏を知ることができます。

圏論関手を用いたデータの写像

しかし、モノイド、モノイド群、グラフ、次数について考察した記事では、関手を扱っていることが示唆されていました。なぜなら、これらの概念はそれぞれ圏として考えることができ、それらの関係はしばしば記事の基礎となっていたからです。例えば、モノイド間の射は事実上の関手だったわけです。

正式には、関手とは、各圏内のオブジェクトとその射によって定義される構造と関係を保持する、圏間の写像のことです。CとDが圏であるならば、CからDへの関手F

は2つのことで構成されます。すなわち、Cのすべてのオブジェクトcに対して、Dに関連するオブジェクトF(c)が存在することと、Cのすべての2つのオブジェクトb,cに対して、Dには、射f

に、関連した射F(f)

が存在することです。関手にはまた、合成 を保持する追加の公理があります。つまり、Cに射

および射

がある場合、Fは次のようなCにおいて合成

を保存します。また、Cの恒等射はDの各写像されたオブジェクトに対して保存されるため、

の場合

になります。異なる圏を関連付けることの重要性は、忖度に由来します。圏に分類される各システムには、ある圏を別の圏に翻訳するだけでなく、より広いコンテキストの中での各圏の「相対的な位置づけ」やおそらく重要性を確立する方法が、デフォルトでは存在しないことが多くなります。このため、例えば、重み付けされた射のポートフォリオを持つ取引可能証券の圏を、別の取引戦略の圏に写像する関手が存在します。このような関手がトレーダーにとって有益かどうかは、観点の問題かもしれませんが、関手が時間差で写像されるのであれば、例えば、ポートフォリオ証券からどのような戦略を使うべきか、あるいは現在の戦略から次にどのような証券を保有すべきかを確立することができるでしょう。

線形順序または全順序は、他律性と反射性の公理を満たすだけでなく、反対称性と比較可能性の要件も満たします。つまり、通常、線形順序のデータはすべて数値でなければならないか、あるいはテキストであれば、二項演算「<=」があいまいさなしかつ未定義の結果をもたらすことなく適用できるような離散的なものでなければなりません。NOAAのWebサイトに掲載されている潮汐データは、1日を1つのデータとすると多次元的です。それぞれの高さに対して4つのdatetimeエントリがあり、高さの4つの浮動小数点値、そして日のdatetimeエントリがあります。各データポイントについて、その日の日時の値を比較する線形順序をとると、海洋データは、各ポイントで2つのデータ、つまり日時としての日付と浮動小数点データとしての潮位の2つのデータを持つ単純な時系列になります。

この線形順序を圏として表現すると、連続する2つのデータ点間の二項演算が射となり、各データ ポイントがオブジェクトになります。オブジェクトには、4つのデータ、4つの日付、高さの記録、4つの高さの値が含まれます。 これらの潮汐値は毎日取得されるため、このデータを日ごとにグループ化します。しかし、すべての日に4つのデータポイントがあるわけではないので、このデータをもう少し正規化する必要があります。3つしかないものもあります。私たちの圏には単純な同型写像関係があり、各ドメイン（日）の要素数に一貫性を持たせることが重要です。

NASDAQのボラティリティ圏は、時間的な順序に基づく価格データポイントを射としてリンクさせるという点で、潮汐と同様の方法をとるでしょう。

比較分析と洞察

潮汐の圏をNASDAQ指数の圏に写像する場合、そこから予測利益を得るためには、タイムラグをもってこれをおこなう必要があります。しかし、まず最初に潮汐クラス圏のインスタンスを作成する必要があります。これは以下のようになります。

protected:

      ...
      
      CCategory _category_ocean,_category_nasdaq;
      
      CDomain<string> _domain_ocean,_domain_nasdaq;
      
      CHomomorphism<string,string> _hmorph_ocean,_hmorph_nasdaq; 

この関手を予測に使用することに興味があるので、圏は新しいバーごとに再定義されるという点でダイナミックになりますが、そこからNASDAQ圏への関手は一定です。したがって、ラグが1日であることから、ログに記録された海洋高度をリンクする前述の3つの射は、csvファイルから潮汐データを読み取ることによって、以下のように定義することができます。

void CTrailingCT::SetOcean(int Index)
   {
      ...
      
      if(_handle!=INVALID_HANDLE)
      {
         ...
         
         while(!FileIsLineEnding(_handle))
         {
            ...
            
            if(_date>_data_time)
            {
               _category_ocean.SetDomain(_category_ocean.Domains(),_domain_ocean);
               
               break;
            }
            else if(__DATETIME.day_of_week!=6 && __DATETIME.day_of_week!=0 && datetime(int(_data_time)-int(_date))<=PeriodSeconds(PERIOD_D1))//_date<=_data_time && datetime(int(_data_time)-(1*PeriodSeconds(PERIOD_D1)))<=_date)
            {
               _element_value.Let();_element_value.Cardinality(1);_element_value.Set(0,DoubleToString(_value));
               _domain_ocean.Cardinality(_elements);_domain_ocean.Set(_elements-1,_element_value);
               
               _elements++;
            }
         }
         
         FileClose(_handle);
      }
      else
      {
         printf(__FUNCSIG__+" failed to load file. Err: "+IntegerToString(GetLastError()));
      }
   } 

同様に、NASDAQのボラティリティについても、以下のリストでセットを構成します。

void CTrailingCT::SetNasdaq(int Index)
   {
      m_high.Refresh(-1);
      m_low.Refresh(-1);
      
      _value=0.0;
      
      _value=(m_high.GetData(Index+StartIndex()+m_high.MaxIndex(Index,_category_ocean.Homomorphisms()))-m_low.GetData(Index+StartIndex()+m_low.MinIndex(Index,_category_ocean.Homomorphisms())))/m_symbol.Point();
      
      _element_value.Let();_element_value.Cardinality(1);_element_value.Set(0,DoubleToString(_value));
      _domain_nasdaq.Cardinality(1);_domain_nasdaq.Set(0,_element_value);
      
      _category_nasdaq.SetDomain(_category_nasdaq.Domains(),_domain_nasdaq);
   } 

その射もまた、似て非なる方法で組み立てられています。さて、定義ですでに述べたように、関手は2つの圏をまたいで対象だけを写像するのではなく、射も写像します。これは、一方が他方をチェックしていることを意味します。NASDAQへの潮汐データの関手の一部であるオブジェクトの写像から始めると、次のように初期化されます。

double CTrailingCT::GetOutput()
   {
      ...
      
      ...
      
      _domain.Init(3+1,3);
      
      for(int r=0;r<4;r++)
      {
         CDomain<string> _d;_d.Let();
         _category_ocean.GetDomain(_category_ocean.Domains()-r-1,_d);
         
         for(int c=0;c<_d.Cardinality();c++)
         {
            CElement<string> _e; _d.Get(c,_e);
            
            string _s; _e.Get(0,_s);
            
            _domain[r][c]=StringToDouble(_s);
         }
      }
      
      _codomain.Init(3);
      
      for(int r=0;r<3;r++)
      {
         CDomain<string> _d;
         _category_nasdaq.GetDomain(_category_nasdaq.Domains()-r-1,_d);
         
         CElement<string> _e; _d.Get(0,_e);
         
         string _s; _e.Get(0,_s);
            
         _codomain[r]=StringToDouble(_s);
      }
      
      _inputs.Init(3);_inputs.Fill(m_consant_morph);
      
      M(_domain,_codomain,_inputs,_output,1);
      
      return(_output);
   } 

同じように、私たちの射関手の構成は次のような形になります。

double CTrailingCT::GetOutput()
   {
      ...
      
      ...
      
      _domain.Init(3+1,3);
      
      for(int r=0;r<4;r++)
      {
         ...
         
         if(_category_ocean.Domains()-r-1-1>=0){ _category_ocean.GetDomain(_category_ocean.Domains()-r-1-1,_d_old); }
         
         for(int c=0;c<_d_new.Cardinality();c++)
         {
            ...
            
            CElement<string> _e_old; _d_old.Get(c,_e_old);
            
            string _s_old; _e_old.Get(0,_s_old);
            
            _domain[r][c]=StringToDouble(_s_new)-StringToDouble(_s_old);
         }
      }
      
      _codomain.Init(3);
      
      for(int r=0;r<3;r++)
      {
         ...
         
         if(_category_nasdaq.Domains()-r-1-1>=0){ _category_nasdaq.GetDomain(_category_nasdaq.Domains()-r-1-1,_d_old); }
         
         ...
         
         CElement<string> _e_old; _d_old.Get(0,_e_old);
         
         string _s_old; _e_old.Get(0,_s_old);
            
         _codomain[r]=StringToDouble(_s_new)-StringToDouble(_s_old);
      }
      
      _inputs.Init(3);_inputs.Fill(m_consant_morph);
      
      M(_domain,_codomain,_inputs,_output,1);
      
      return(_output);
   } 

ここでの作業の大部分は、MQL5で潮汐データにアクセスできるようにすることです。そのため、データは共通データフォルダ内のcsvファイルから、潮汐の圏の要素と同様の表形式でアクセスされます。データの形式には、正しい値を選択する際に取引サーバの時刻と同期させるためのdatetimeフィールドが含まれています。MQL5 IDEには、そのような二次データにアクセスするための他の選択肢があり、IDEからネイティブな接続設計が可能であるため、そのような選択肢の1つにデータベースを介する方法があります。つまり、ローカルマシンにデータベースがあるか、クラウドに接続できるのであれば、この方法を検討することができます。しかし、読者がここに掲載されたテスト結果を簡単に再現できるようにしたいので、ここでの目的では、共通フォルダにあるcsvファイルを使用しています。

私たちの関手は、圏をまたいで2つのものを写像します。つまり、重複を避けるために、単純に一方の接続を他方の接続を確認または検証することになります。最初の段階では、どちらの設定が私たちの取引システムにとって理想的なのかわからないので、両方テストしてみます。

そこで、最初のセットアップでは、オブジェクトを横断する関手に、終域（NASDAQ集合）内のオブジェクト間の射を確認または検証させます。これを図式化すると以下のようになります。

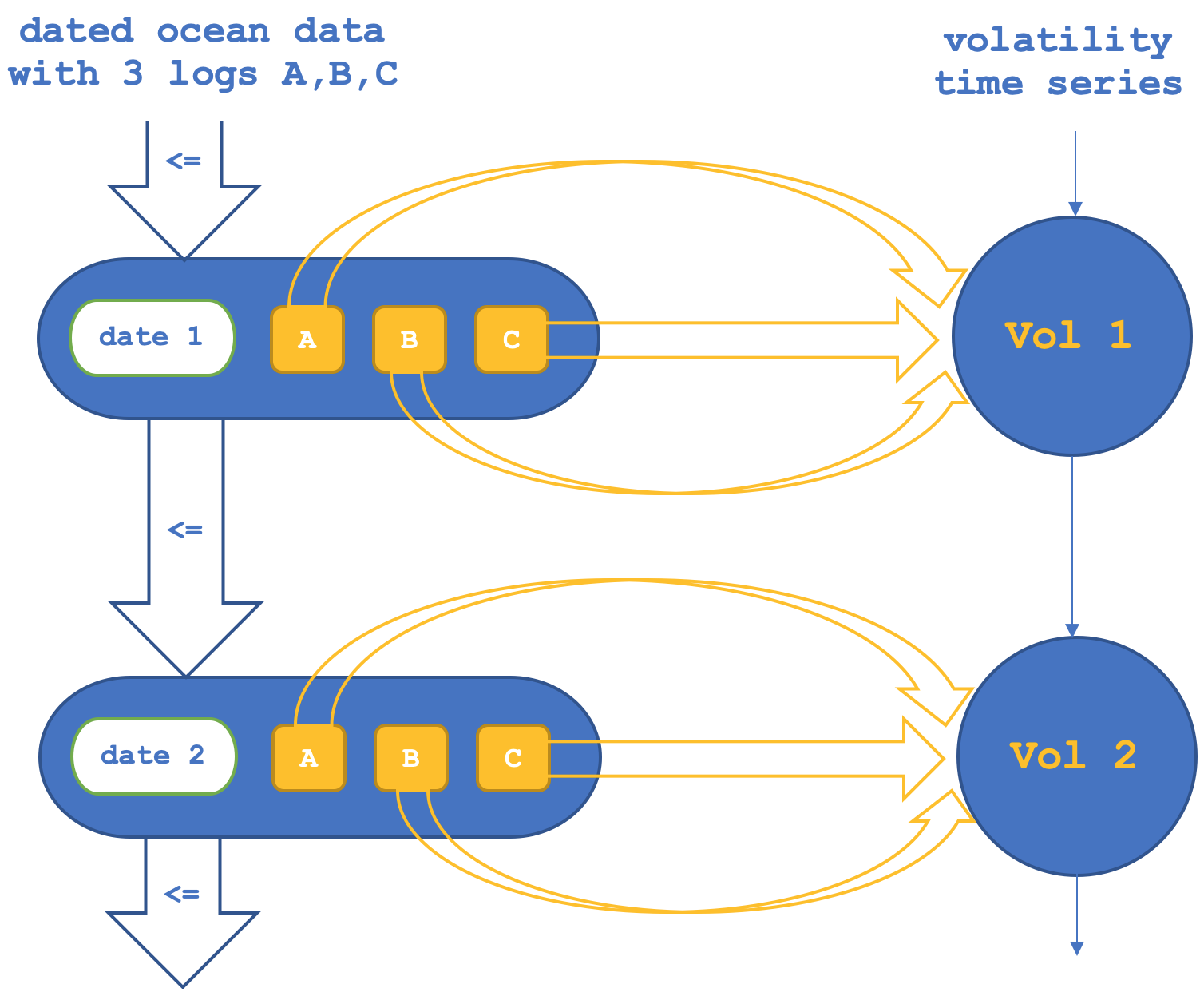
オブジェクト関手のみに基づいてNASDAQのボラティリティを予測するテストを実行すると、以下のようなレポートが得られます（このコードはTraillingCT_14_1aとして添付されています）。

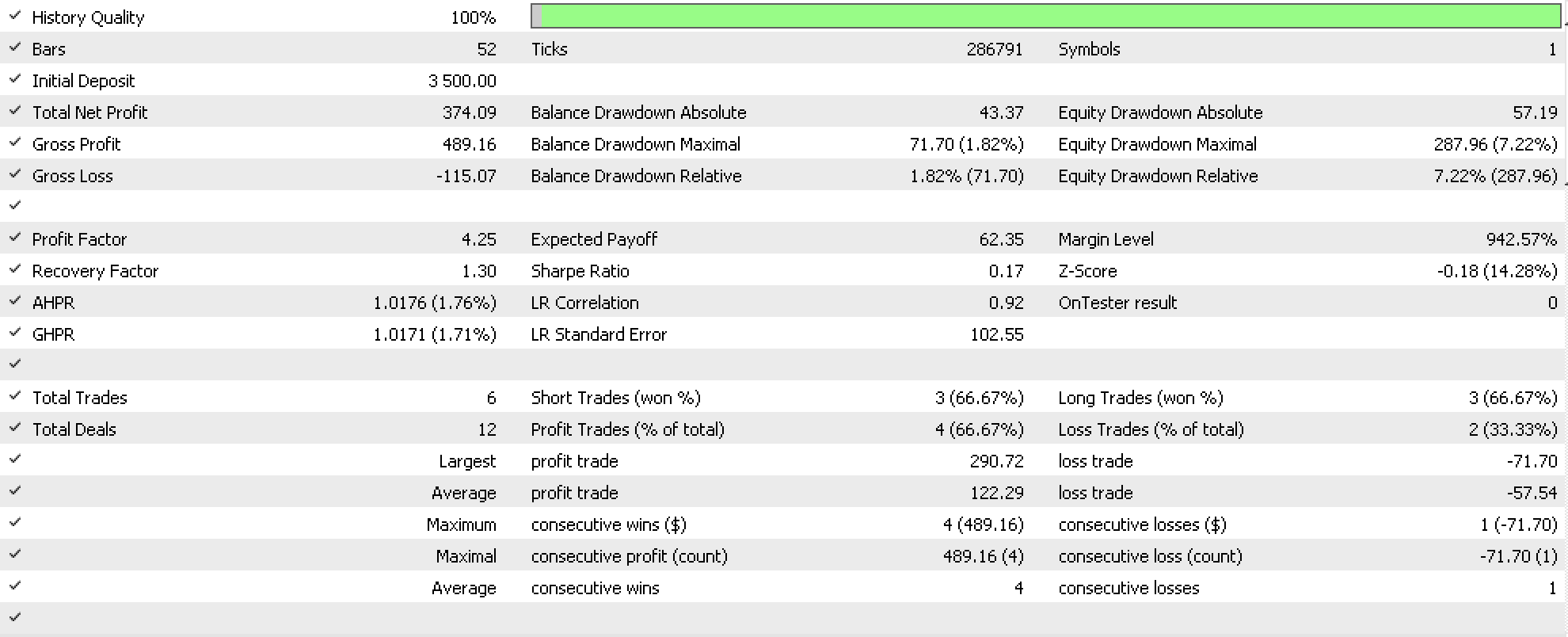
前述したように、射の向こう側にある関手に注目し、その後にオブジェクトを確認するという逆のことも試してみると、これは次のように表すことができます。

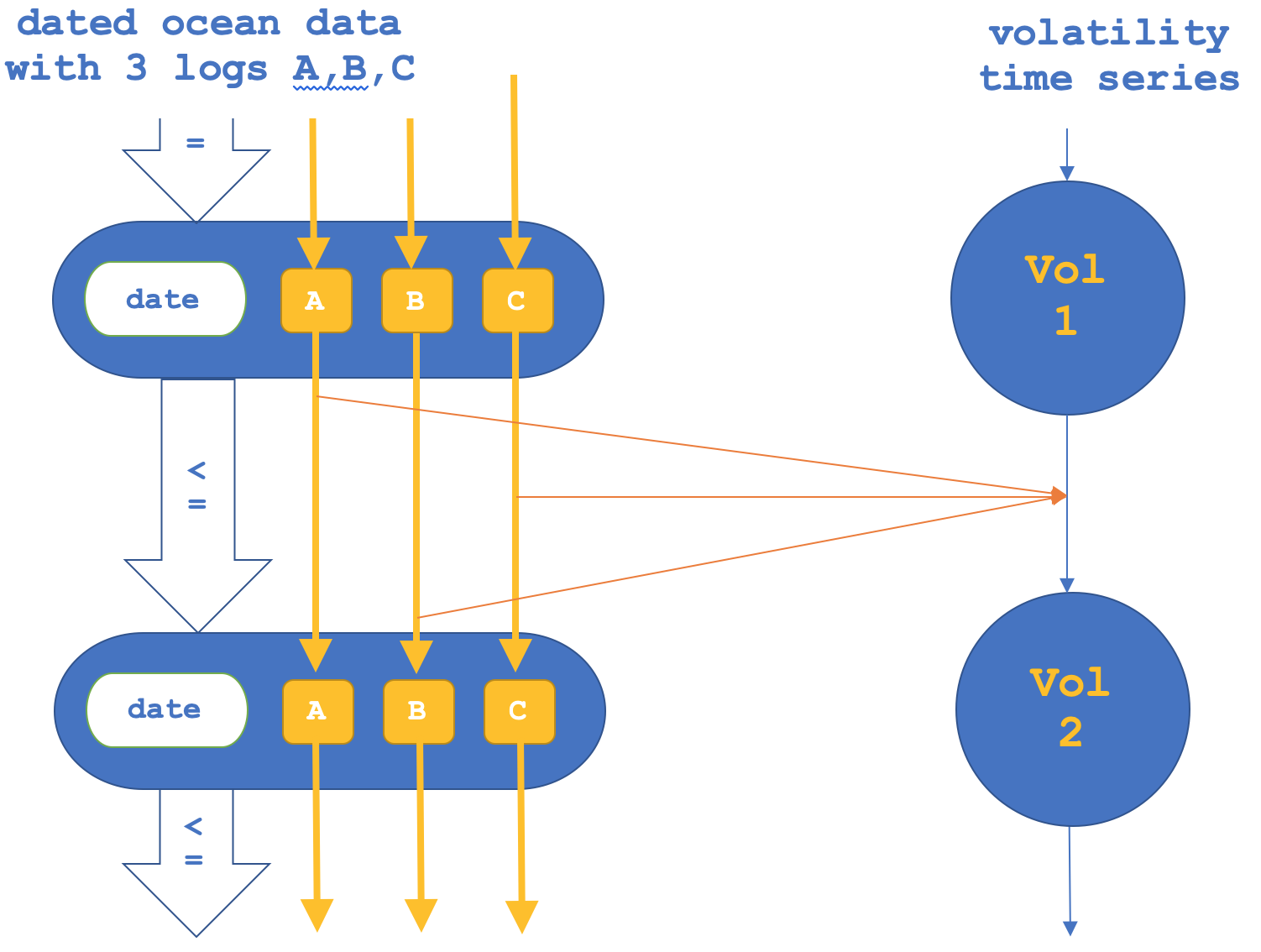
射関手のみのテスターレポートを以下に示します。

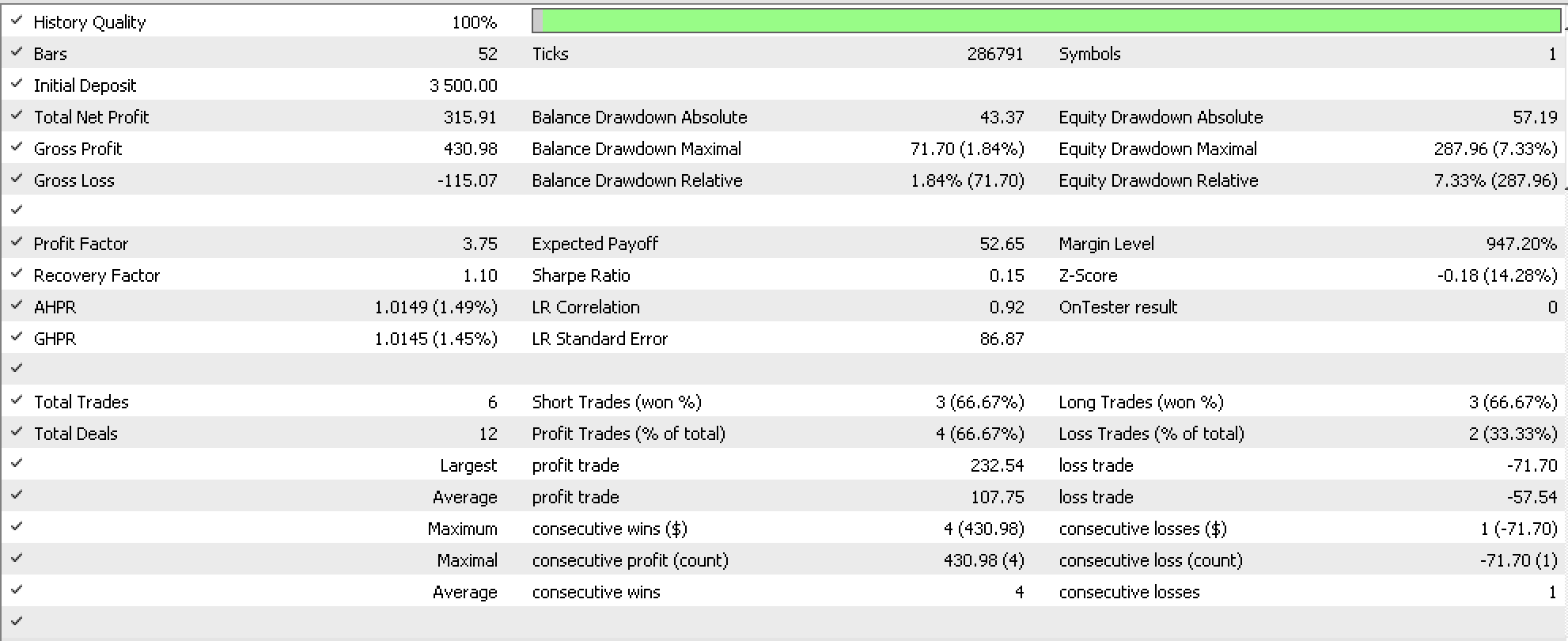
上記の2つのテストオプションから、オブジェクトを写像するのと射を写像するのとでは、2020年1月1日から同年3月15日までという非常に短いテスト期間であっても、1日単位で異なる結果が出ました。この2つのうち、どちらがトレーダーにとって、ボラティリティに限らず、あらゆる種類の予測をする上でより役に立つかは、エントリシグナル、資金管理、今回のようなトレーリングストップなど、テストされる取引システムの特定の側面について、長期間にわたってテストする必要があるでしょう。

このテストに選ばれた期間は非常に短いものでしたが、NASDAQにとって実に重要なもので、指数が史上最高値をつけた後、コロナ発生のさなか、かなり急激に下落した時期でした。したがって、このテストは潮汐データとの相関の可能性を示唆するものではありますが、因果関係を示唆するものではないことは確かです。

この連載で使用されてきたように、エントリシグナルは非常に基本的なもので、今回はそれぞれのシグナルファイルのデフォルト設定で、内蔵の素晴らしいオシレーターを使用しました。ポジションサイジングも通常通り固定証拠金としました。私たちの始域圏のデータは毎日、3つの間隔で収集されていたため、NASDAQを日次の時間枠でテストしました。つまり、これを圏等価の線形順序としてフォーマット化すると、各日は、すでに述べたように、各日の3つのデータポイントである3つの要素を持つ始域（対象）を構成することになります。

ここでの大きな収穫は、一見無関係に見えるバラバラのデータセットを調査し、取引の意思決定に役立つ有用な遅行関係をテストできるということです。私たちのテストではタイムラグは1日でしたが、あなたの場合はもっと長いかもしれません。今回使用したデータセットとは別のデータセットとして、潮汐を選択することもできたでしょう。しかし、上記で使用した潮汐データに代わるデータセットの例をいくつか紹介することは、市場や異質なシステムがいかに相互につながっているかをより深く理解する上で役に立つかもしれません。

代替データセットとしては、商品価格、テクノロジーニュース（例えばAIのような新しいテクノロジートレンドに関する記事数とエンターテインメントのような代替ニュース記事数をラグとともに追跡し、関連性の可能性を探る）、語彙目録に基づいた手法で定量化されたソーシャルメディアへの投稿のトーンに関するソーシャルメディアセンチメントデータも、特にテクノロジー株についてあるいはテクノロジー株に関連するものであれば、NASDAQ（あるいは取引されている証券）のボラティリティとの関連性を調べることができます。これらの例もまた、エッジを築くのに役立つ難解な側面に傾いていますが、他の証券の価格やその指標値のような、より身近なデータセットも考えられます。

結論

要約すると、線形順序形式の圏にあるデータを、関手によってどのように証券価格にリンクさせることができるかを探求してきました。この場合、私たちの始域データはカリフォルニアの海岸沖で計測された潮位というありそうでなかったデータセットであり、これが関手を介して1日遅れでNASDAQのボラティリティにリンクされました。この連結は、オブジェクトからオブジェクトへ、あるいは射から射への2つの形式をとることができます。エントリシグナルとポジションサイジングの方法を同一にしたテストでは、両形式とも短いテストウィンドウで有意に異なる結果を得ました。

圏論の関手は貴重で、さまざまなタイプのデータを写像するのに役立ちます。この記事のために、かなり難しいデータセットを使って分類と構成をおこないました。読者はより好意的な情報源に目を向けることができます。結果は必ずしも優良ではありませんが、テスト目的であれば、より洞察を得られる可能性があります。

トレーダーの視点から線形順序をセットにリンクさせることで、将来的な可能性と拡張性はさまざまな方向に向かう可能性があります。これには以下のようなものがあります。 上で触れた代替データセットなど、他の関心領域に関連する株式市場のトレンドから派生する可能性のある学際的なアプリケーション：この記事でテストしたように、慎重に設定されたタイムラグをまたぐファンクターによる予測モデリングは、金融市場の外でも天気予報などの分野に適用できます。データ統合とナレッジ グラフ：ここで提示された概念により、人工知能などの分野での表現が改善される可能性があります。財務データに関連する関手の線形順序である機械学習と転移学習は、たとえば2つの圏間で得られた関手の重みをテストしたり、異なるドメインに適用したりできれば、さらに開発でき、機械学習モデルとその有効性が向上する可能性があります。

他にも多くの可能性があります。すべてを網羅するわけではありませんが、統計分析とデータ融合、カジュアル推論と相関研究、アルゴリズムファイナンスによるクオンツファイナンス、データ駆動型意思決定などが含まれます。応用の選択は、トレーダーであれば取引に対する考え方やアプローチによって決まります。

自分の専門分野や市場に対するアプローチに関して、この分野を探求することをお勧めします。このテーマは多くの可能性を秘めており、ある意味、学際的なデータ解析のための未開の領域を深く掘り下げるよう、常にあなたを誘っています。

添付ソースのテストに関するノート：

ファイルTrailingCT_14_1a.mqhとTrailingCT_14_1b.mqhを「MQL5\include\Expert\Trailing\」フォルダに入れて、ct_14_1s.mqhをIncludesフォルダに入れます。

ウィザードを使用してエキスパートアドバイザー(EA)を組み立てる方法については、EAの一部としてそれらを組み立てる必要があるため、このガイドに従うとよいでしょう。記事で述べたように、MQL5のライブラリに含まれるAwesome Oscillatorをエントリシグナルとして使い、固定証拠金を資金管理に使いました。いつものように、この記事の目的は聖杯を紹介することではなく、むしろあなた自身の戦略にカスタマイズできるアイデアを紹介することです。添付されているMQL5ファイルは、ウィザードによって組み立てられたものです。