MQL5でのARIMAトレーニングアルゴリズムの実装

はじめに

短期的な動きを利用しようとするほとんどの外国為替および仮想通貨トレーダーは、その取り組みに役立つ基本的な情報の欠如に悩まされています。ここで役に立つのは、標準的な時系列手法です。ジョージ・ボックスとグウィリム・ジェンキンス は、おそらく最も尊敬されている時系列予測方法を開発しました。元の方法を改善するために多くの進歩がもたらされましたが、基礎となる原則は今日でも有効です。

彼らの手法から派生したものの1つは、時系列予測の一般的な手法となった自己回帰和分移動平均モデル(ARIMA)です。これは、データ系列の時間的依存関係をキャプチャし、非定常時系列をモデル化するためのフレームワークを提供するモデルのクラスです。この記事では、MQl5プログラミング言語を使用したARIMAトレーニングアルゴリズムの作成の基礎として、Powell法の関数最小化を使用します。

ARIMAの概要

ボックスとジェンキンスは、ほとんどの時系列は2つのフレームワークの一方または両方でモデル化できると述べました。1つは自己回帰(AR)です。これは、系列の値が、一定のオフセットおよび通常イノベーションまたはノイズと呼ばれる小さな差とともに、以前の値との関係で説明できることを意味します。このテキストでは、ノイズまたはエラーコンポーネントをイノベーションと呼ぶことに注意してください。このイノベーションにより、説明できないランダムな変動が考慮されます。

ARIMAモデルの基礎となる2番目のフレームワークは、移動平均(MA)です。このモデルは、系列の値が、特定の数の以前のイノベーション期間、現在のイノベーション、そしてまた一定のオフセットの比例和であると述べています。これらのモデルを定義する統計的条件は他にも多数ありますが、詳細については説明しません。より詳しい情報は多数のオンラインリソースにあります。私たちがより興味があるのはそれらの応用です。

純粋なMAモデルとARモデルのみに限定されるわけではなく、それらを組み合わせて自己回帰移動平均モデル(ARMA)と呼ばれる混合モデルを作成することもできます。ARMAモデルでは、一定のオフセットと現在のイノベーション項に加えて、有限数のラグ系列とノイズ項を指定します。

これらすべてのフレームワークの適用に影響を与える基本的な要件の1つは、モデル化される系列が静的である必要があることです。定常性の定義がどの程度厳密であるかに応じて、これまで説明したモデルは技術的に金融時系列への適用には適していません。ここでARIMAの登場です。数学的積分は微分の逆です。非定常時系列が1回以上微分されると、通常、結果の系列の定常性が向上します。最初に系列を微分することで、結果の系列にこれらのモデルを適用することが可能になります。ARIMAの「I」は、モデル化された系列を元の領域に戻すために適用された微分を逆にする（積分する）要件を指します。

自己回帰モデルの表記法

モデルの説明を管理する標準表記法があります。AR項の数（定数項は含まない）は通常pと呼ばれます。MA項はqで示され、dは元の系列が微分された回数を表します。これらの項を使用すると、ARIMAモデルはARIMA(p,d,q)として指定されます。純粋なプロセスはMA(q)およびAR(p)として表すことができます。微分のない混合モデルはARMA(p,q)と書かれます。この表記は、項が連続していることを前提としています。たとえば、ARMA(4,2)は、系列が4つの連続するAR項と、前の2つの連続するイノベーション項によって記述できることを意味します。ARIMAを使用すると、p、q、dのいずれかをゼロとして指定することで純粋なプロセスを表現できます。たとえば、ARIMA(1,0,0)は純粋なAR(1)モデルに変換されます。

ほとんどの自己回帰モデルでは、それぞれの項が、AR項とMA項のラグ1からラグpおよびラグqまで連続していることを指定します。実証されるアルゴリズムでは、MAやAR項の非連続ラグの指定が可能になります。このアルゴリズムが導入するもう1つの柔軟性は、定数オフセットの有無にかかわらずモデルを指定できることです。

たとえば、以下の関数で定義されたモデルを構築できます。
                                 

                                                        y(t) = AR1* y(t-4) + AR2*y(t-6) + E(t)         (1)

上記の関数は、4つおよび6つ前のタイムスロット前の系列値によって定義された現在値との定数オフセットのない純粋なAR(2)プロセスを記述しています。標準表記ではそのようなモデルを指定する方法は提供されていませんが、そのような制限に囚われる必要はありません。
 

モデル係数と定数オフセットの計算

モデルはp+q係数を持つことがあり、これらは計算する必要があります。そのために、モデルの仕様を使用して既知の系列値を予測し、その予測値を既知の値と比較し、二乗誤差の合計を計算します。最適な係数は、二乗誤差の合計が最小になる係数です。

無限に広がるデータが利用できないことによる制限があるため、予測する場合は注意が必要です。モデル仕様にAR項がある場合は、すべてのAR項の最大ラグに対応する値の数が経過した後でのみ予測を開始できます。

上記の(1)で指定した例を使用すると、タイムスロット7からのみ予測を開始できます。以前の予測では、系列の開始前に未知の値が参照されるためです。

(1)にMA項がある場合、まだイノベーション系列がないため、この時点ではモデルは純粋に自己回帰として扱われます。一連のイノベーション値は、今後の予測とともに構築されます。例に戻ると、7番目のタイムスロットでの最初の予測は、任意の初期AR係数を使用して計算されます。

 計算された予測と7番目のタイムスロットでの既知の値の差が、そのスロットのイノベーションとなります。指定されたMA条件がある場合、対応するイノベーションの遅れた値が判明した時点で、それらの条件が予測の計算に含まれます。それ以外の場合、MA項は単にゼロに設定されます。純粋なMAモデルの場合、今回を除いて同様の手順に従います。定数オフセットを含める必要がある場合は、系列の平均として初期化されます。

ここで説明した方法には明らかな制限が1つだけあります。既知の系列には、適用されるモデルの次数に応じた数の値が含まれている必要があるということです。項が多いほど、および/またはそれらの項のラグが大きいほど、モデルを効果的に適合させるためにより多くの値が必要になります。その後、適切な大域最小化アルゴリズムを適用して係数を最適化することで、トレーニングプロセスが丸められます。予測誤差を最小限に抑えるために使用するアルゴリズムは、Powell法です。ここで適用される実装の詳細は、「指数平滑法を使用した時系列予測」項に記載されています。

CArimaクラス

ARIMAトレーニングアルゴリズムは、Arima.mqhで定義されたCArimaクラスに含まれます。このクラスには2つのコンストラクタがあり、それぞれが自己回帰モデルを初期化します。デフォルトのコンストラクタは、一定のオフセットを持つ純粋なAR(1)モデルを作成します。

CArima::CArima(void)
  {
   m_ar_order=1;
//---
   ArrayResize(m_arlags,m_ar_order);
   for(uint i=0; i<m_ar_order; i++)
      m_arlags[i]=i+1;
//---
   m_ma_order=m_diff_order=0;
   m_istrained=false;
   m_const=true;

   ArrayResize(m_model,m_ar_order+m_ma_order+m_const);
   ArrayInitialize(m_model,0);
  }

パラメータ化されたコンストラクタを使用すると、モデルの指定をより詳細に制御できます。以下に示す4つの引数を受け取ります。

パラメータ	パラメータの種類	パラメータの説明
p	unsigned integer	モデルのAR項の数
d	unsigned integer	モデル化されている系列に適用される微分の回数
q	unsigned integer	モデルに含める必要があるMA項の数
use_const_term	bool	モデル内での定数オフセットの使用

CArima::CArima(const uint p,const uint d,const uint q,bool use_const_term=true)
  {
   m_ar_order=m_ma_order=m_diff_order=0;

   if(d)
      m_diff_order=d;
   if(p)
     {
      m_ar_order=p;
      ArrayResize(m_arlags,p);
      for(uint i=0; i<m_ar_order; i++)
         m_arlags[i]=i+1;
     }
   if(q)
     {
      m_ma_order=q;
      ArrayResize(m_malags,q);
      for(uint i=0; i<m_ma_order; i++)
         m_malags[i]=i+1;
     }


   m_istrained=false;
   m_const=use_const_term;

   ArrayResize(m_model,m_ar_order+m_ma_order+m_const);
   ArrayInitialize(m_model,0);
  }

提供されている2つのコンストラクタに加えて、オーバーロードされたFit()メソッドの1つを使用してモデルを指定することもできます。どちらのメソッドも、モデル化するデータ系列を最初の引数として受け取ります。1つのFit()メソッドには引数が1つだけありますが、2つ目のメソッドにはさらに4つの引数が必要です。これらの引数はすべて、上の表にすでに記載されているものと同じです。

bool CArima::Fit(double &input_series[])
  {

   uint input_size=ArraySize(input_series);

   uint in = m_ar_order+ (m_ma_order*2);

   if(input_size<=0 || input_size<in)
      return false;

   if(m_diff_order)
      difference(m_diff_order,input_series,m_differenced,m_leads);
   else
      ArrayCopy(m_differenced,input_series);

   ArrayResize(m_innovation,ArraySize(m_differenced));

   double parameters[];
   ArrayResize(parameters,(m_const)?m_ar_order+m_ma_order+1:m_ar_order+m_ma_order);
   ArrayInitialize(parameters,0.0);

   int iterations = Optimize(parameters);

   if(iterations>0)
      m_istrained=true;
   else
      return false;

   m_sse=PowellsMethod::GetFret();

   ArrayCopy(m_model,parameters);

   return true;

  }

より多くのパラメータを指定してこのメ​​ソッドを使用すると、以前に指定されたモデルが上書きされ、項のラグが互いに隣接していると仮定されます。どちらも、最初のパラメータとして指定されたデータ系列が微分されないことを前提としています。したがって、モデルパラメータで指定されている場合、微分が適用されます。どちらのメソッドも、モデルトレーニングプロセスの成功または失敗を示すブール値を返します。

bool CArima::Fit(double&input_series[],const uint p,const uint d,const uint q,bool use_const_term=true)
  {
   m_ar_order=m_ma_order=m_diff_order=0;

   if(d)
      m_diff_order=d;
   if(p)
     {
      m_ar_order=p;
      ArrayResize(m_arlags,p);
      for(uint i=0; i<m_ar_order; i++)
         m_arlags[i]=i+1;
     }
   if(q)
     {
      m_ma_order=q;
      ArrayResize(m_malags,q);
      for(uint i=0; i<m_ma_order; i++)
         m_malags[i]=i+1;
     }

   m_istrained=false;
   m_const=use_const_term;

   ZeroMemory(m_innovation);
   ZeroMemory(m_model);
   ZeroMemory(m_differenced);

   ArrayResize(m_model,m_ar_order+m_ma_order+m_const);
   ArrayInitialize(m_model,0);

   return Fit(input_series);

  }

このクラスにはそれぞれAR項とMA項のラグを設定するSetARLags()メソッドとSetMALags()メソッドがあります。どちらも、コンストラクタのいずれかですでに指定されているモデルの対応するラグを要素とする単一の配列引数を取ることにより、同様に機能します。配列のサイズは、ARまたはMA項の対応する階と一致する必要があります。配列内の要素には、1以上の任意の値を含めることができます。  隣接しないARラグとMAラグを持つモデルを指定する例を見てみましょう。

以下の関数で構築するモデルを指定します。
         

                                        y(t) = AR1*y(t-2) + AR2*y(t-5) + MA1*E(t-1) + MA2*E(t-3) + E(t)                 (2)

このモデルは、ARラグ2および5を使用するARMA(2,2)プロセスによって定義されます。MAラグは1と3です。
以下のコードは、そのようなモデルを指定する方法を示しています。

CArima arima(2,0,2);

uint alags [2]= {2,5};
uint mlags [2]= {1,3};

if(arima.SetARLags(alags) && arima.SetMALags(mlags))
   Print(arima.Summary());

Fit()メソッドのいずれかを使用してモデルをデータ系列に正常にフィッティングすると、GetModelParameters()メソッドを呼び出すことで最適な係数と定数オフセットを取得できます。モデルの最適化されたすべてのパラメータを書き込む配列引数が必要です。最初に定数オフセットの後にAR項が続き、MA項は常に最後にリストされます。

class CArima:public PowellsMethod
  {
private:
   bool              m_const,m_istrained;
   uint              m_diff_order,m_ar_order,m_ma_order;
   uint              m_arlags[],m_malags[];
   double            m_model[],m_sse;
   double            m_differenced[],m_innovation[],m_leads[];

   void              difference(const uint difference_degree, double &data[], double &differenced[], double &leads[]);
   void              integrate(double &differenced[], double &leads[], double &integrated[]);
   virtual double    func(const double &p[]);


public :
                     CArima(void);
                     CArima(const uint p,const uint d, const uint q,bool use_const_term=true);
                    ~CArima(void);

   uint              GetMaxArLag(void)    { if(m_ar_order) return m_arlags[ArrayMaximum(m_arlags)]; else return 0;}
   uint              GetMinArLag(void)    { if(m_ar_order) return m_arlags[ArrayMinimum(m_arlags)]; else return 0;}
   uint              GetMaxMaLag(void)    { if(m_ma_order) return m_malags[ArrayMaximum(m_malags)]; else return 0;}
   uint              GetMinMaLag(void)    { if(m_ma_order) return m_malags[ArrayMinimum(m_malags)]; else return 0;}
   uint              GetArOrder(void)     { return m_ar_order;  }
   uint              GetMaOrder(void)     { return m_ma_order;  }
   uint              GetDiffOrder(void)   { return m_diff_order;}
   bool              IsTrained(void)      { return m_istrained; }
   double            GetSSE(void)         { return m_sse;      }
   uint              GetArLagAt(const uint shift);
   uint              GetMaLagAt(const uint shift);


   bool              SetARLags(uint &ar_lags[]);
   bool              SetMALags(uint &ma_lags[]);
   bool              Fit(double &input_series[]);
   bool              Fit(double &input_series[],const uint p,const uint d, const uint q,bool use_const_term=true);
   string            Summary(void);
   void              GetModelParameters(double &out_array[]) { ArrayCopy(out_array,m_model);      }
   void              GetModelInnovation(double &out_array[]) { ArrayCopy(out_array,m_innovation); }

  };

GetModelInnovation()は、モデルのフィッティング後に最適化された係数を使用して計算された誤差値を単一の配列引数に書き込みます。Summary()関数はモデル全体の詳細を示す文字列の説明を返します。GetArOrder()、GetMaOrder()、GetDiffOrder()は、それぞれモデルのAR項、MA項の数、微分の階を返します。

GetArLagAt()とGetMaLagAt()はそれぞれ、ARまたはMA項の序数位置に対応する符号なし整数の引数を受け取ります。ゼロシフトは最初の項を参照します。GetSSE()は、トレーニングされたモデルの二乗誤差の合計を返します。IsTrained()は、指定されたモデルがトレーニングされているかどうかに応じてtrueまたはfalseを返します。

CArimaはPowellsMethodを継承しているため、Powellのアルゴリズムのさまざまなパラメータを調整できます。PowellsMethodの詳細についてはこちらを参照してください。

CArimaクラスの使用

以下のスクリプトのコードは、モデルを構築する方法と、決定論的系列のパラメータを推定する方法を示しています。スクリプトで示されているデモンストレーションでは、定数オフセット値を指定するオプションと、ノイズを模倣するランダムコンポーネントの追加を使用して、決定的系列が生成されます。

このスクリプトにはArima.mqhが含まれており、決定論的でランダムなコンポーネントから構築された系列を入力配列に入力します。

#include<Arima.mqh>

input bool Add_Noise=false;
input double Const_Offset=0.625;

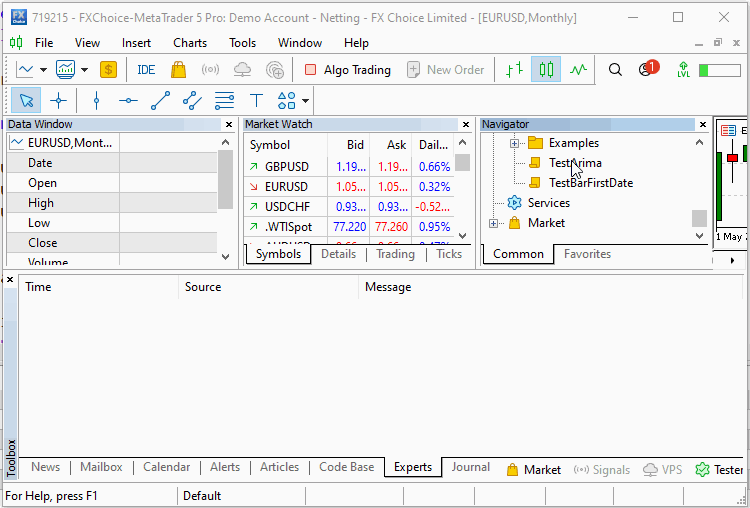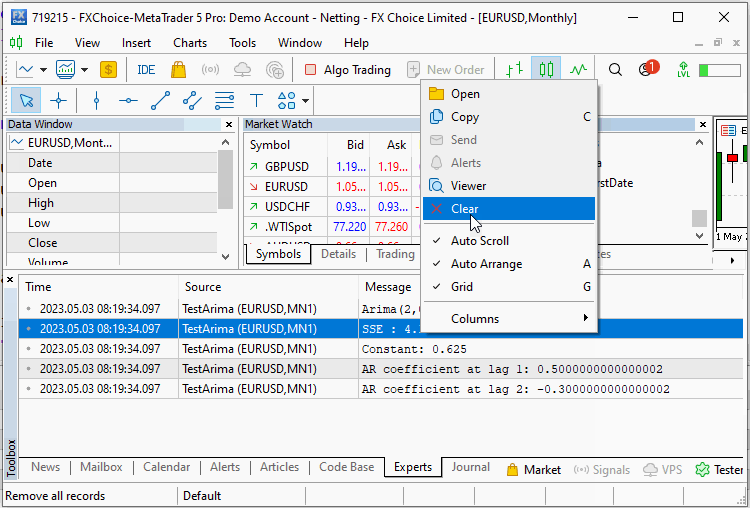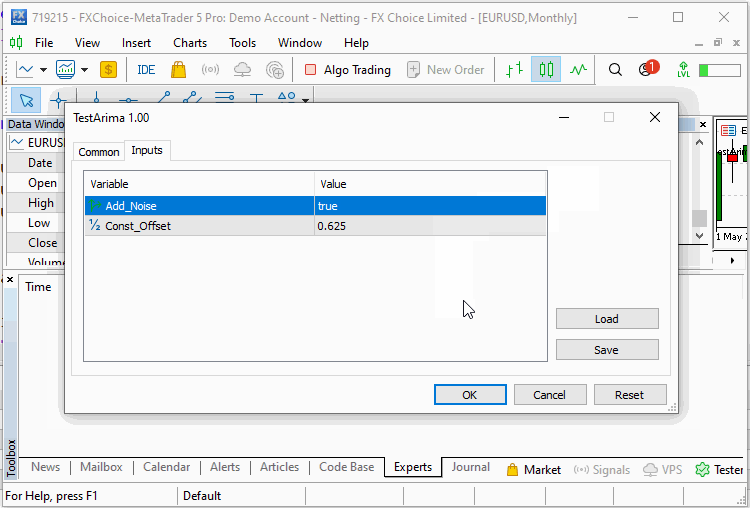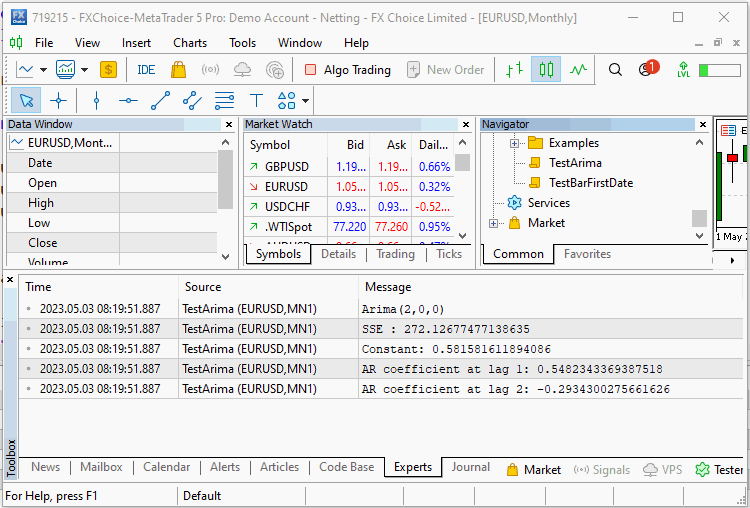
純粋なAR(2)モデルを指定するCArimaオブジェクトを宣言します。入力配列を使用してFit()メソッドが呼び出され、トレーニングの結果がSummary()関数を使用して表示されます。スクリプトの出力を以下に示します。

double inputs[300];
   ArrayInitialize(inputs,0);

   int error_code;

   for(int i=2; i<ArraySize(inputs); i++)
     {
      inputs[i]= Const_Offset;
      inputs[i]+= 0.5*inputs[i-1] - 0.3*inputs[i-2];
      inputs[i]+=(Add_Noise)?MathRandomNormal(0,1,error_code):0;
     }

   CArima arima(2,0,0,Const_Offset!=0);

   if(arima.Fit(inputs))
      Print(arima.Summary());

スクリプトは、ノイズコンポーネントを使用した場合と使用しない場合で2回実行されます。最初の実行では、アルゴリズムが系列の正確な係数を推定できたことがわかります。2回目の実行では、ノイズを追加して、アルゴリズムは系列を定義した真の定数オフセットと係数を再現できました。

ここで示した例は、明らかに、現実世界で遭遇する分析の種類を表したものではありません。この系列に追加されたノイズは、金融時系列に含まれるノイズと比べて中程度でした。

ARIMAモデルの設計

これまで、モデルの適切な次数を導出または選択する方法を示さずに、自己回帰トレーニングアルゴリズムの実装について説明してきました。適切なモデルを決定するのとは対照的に、モデルのトレーニングはおそらく簡単な部分です。

適切なモデルを導出する2つの便利なツールは、研究対象の系列の自己相関と部分自己相関を計算することです。読者が自己相関および部分自己相関プロットを解釈する際に役立つガイドとして、4つの仮説系列を検討します。
                                                                  y(t)=AR1*y(t-1)+E(t)     (3) 

                 
                                                                  y(t)=E(t)-AR1*y(t-1)     (4) 

            
                                                                  y(t)=MA1*E(t-1)+E(t)    (5) 

                
                                                                   y(t)=E(t)-MA1*E(t-1)   (6) 

    
(3)と(4)は、それぞれ正と負の係数を持つ純粋なAR(1)プロセスです。(5)と(6)は、それぞれ正と負の係数を持つ純粋なMA(1)プロセスです。 

上図はそれぞれ(3)と(4)の自己相関です。どちらのプロットでも、ラグが増加するにつれて相関値は小さくなります。系列がさらに上に進むにつれて、以前の値の電流への影響が減少するため、これは理にかなっています。

次の図は、同じ系列ペアの偏自己相関のプロットを示しています。相関値が最初のラグの後に途切れていることがわかります。これらの観察は、ARモデルに関する一般規則の基礎を提供します。一般に、部分自己相関が特定のラグを超えてカットオフし、同時に自己相関が同じラグを超えて減衰し始める場合、部分自己相関プロット上で観測されたカットオフラグまで純粋なARモデルによって系列をモデル化できます。

 MA系列の自己相関プロットを調べると、プロットがAR(1)の部分自己相関と同一であることがわかります。

一般に、特定のピークまたは谷を超えるすべての自己相関がゼロであり、より多くのラグがサンプリングされるにつれて部分的な自己相関がさらに小さくなる場合、系列は自己相関プロット上で観察されたカットオフラグでのMA項によって定義できます。

 
モデルのpパラメータとqパラメータを決定する他の方法には、次のようなものがあります。

• 情報基準：赤池情報量基準(AIC)やベイジアン情報量基準(BIC)など、いくつかの情報基準があります。さまざまなARIMAモデルを比較し、最適なモデルを選択するために使用されます。

• グリッド検索：これには、同じデータセット上で異なる次数で異なるARIMAモデルをフィッティングし、それらのパフォーマンスを比較することが含まれます。最良の結果が得られる順序が、最適なARIMA次数として選択されます。

• 時系列相互検証：これには、時系列データをトレーニングセットとテストセットに分割し、トレーニングセットでさまざまなARIMAモデルをフィッティングし、テストセットでそのパフォーマンスを評価することが含まれます。最良のテスト誤差をもたらすARIMA次数が最適な次数として選択されます。

ARIMAの次数を選択するための万能のアプローチはなく、特定の時系列に最適な次数を決定するには、ある程度の試行錯誤とドメインの知識が必要になる場合があることに注意することが重要です。

結論

Powellの関数最小化法（英語）を使用して自己回帰トレーニングアルゴリズムをカプセル化するCArimaクラスをデモしました。完全なクラスのコードは、その使用法を示すスクリプトとともに、以下に添付されたzipファイルに含まれています。

ファイル	詳細
Arima.mqh	CArimaクラスの定義を含むインクルードファイル
PowellsMethod.mqh	PowellsMethodクラスの定義を含むインクルードファイル
TestArima	CArimaクラスを使用して部分的に決定的な系列を分析するスクリプト