
第三世代ニューラルネットワーク:深層ネットワーク
コンテンツ
- 第二世代ニューラルネットワーク
- 深層学習
- 実践的実験
- 3.1. R 言語
- 3.2. 実装のバリエーションと解決された問題
- 3.3. 実験へのデータ準備
- 3.3.1. ソースデータ
- 3.3.2. 入力データ(予測因子)
- 3.3.2.1. ウェルズ・ワイルダーの方向性指数-ADX(HLC、n)
- 3.3.2.2. アルーン(HL、n)
- 3.3.2.3. コモディティチャンネル指数-CCI(HLC, n)
- 3.3.2.4. chaikinVolatility(HLC、n)
- 3.3.2.5. シャンデモメンタムオシレーター-CMO(Med、n)
- 3.3.2.6. MACD オシレーター
- 3.3.2.7. OsMA(Med,nFast, nSlow, nSig)
- 3.3.2.8. 相対力指数-RSI(Med,n)
- 3.3.2.9. ストキャスティクス- stoch(HLC, nFastK=14, nFastD=3, nSlowD=3)
- 3.3.2.10. 確率的モメンタムインデックス-SMI(HLC, n = 13, nFast = 2, nSlow = 25, nSig = 9)
- 3.3.2.11. 予想変動率(ヤンと張)-volatility(OHLC, n, calc="yang.zhang", N=96)
- 3.3.3. アウトプットデータ(目標)
- 3.3.4. データ消去
- 3.3.5. トレーニングとテストサンプル形成
- 3.3.6. クラス・バランシング
- 3.3.7. 処理
- 3.4. モデルの構築、トレーニング、検証
- 実装(インディケータおよび Expert Advisor)
はじめに
本稿では「深層学習」、「深層ネットワーク」といったテーマの主要な考え方について、平たく言えば複雑な計算なしで考察していこうと思います。
実データでの一件は行列定義と比較(行列定義と比較にすいては明確ではありません)により深層ニューラルネットワークの浅いネットワークにまさる理論的メリットの裏付けをします(またはしません)。取り掛かるタスクは分類です。深層ニューラルネットワークモデルを基にクライアント/さーばーのスキームと共に動作するインディケータと Expert Advisor を作成しそれらの検証を行います。
読者の方はニューラルネットワークで使用される基本コンセプトの正しい考えを持たれていると思います。
1. 第二世代ニューラルネットワーク
ニューラルネットワークは画像処理に関わる広範な課題に対処するために作成されます。
下はニューラルネットワークによって解決される典型的な課題です。
- ポイントセットによる関数の近似化(回帰)
- 指定のクラスセットによるデータ分類
- 以前に道であったプトロタイプクラスの特定を伴うデータのクラスター化
- 情報圧縮
- 損失データの回復
- 連想メモリ
- 最適化、最適制御、その他
上記リストからは『分類』のみ本稿で取り上げます。
1.1. 連携のアーキテクチャ
情報処理方法はネットワーク内のフィードバックループの有無に大きく影響されます。ニューロン間にフィードバックがなければ(すなわちネットワークが各ニューロンが前の層からのみ情報を受け取る連続層を持つ)、ネットワーク内の情報処理は一方向です。入力シグナルは層のシーケンスによって処理され、応答は層数に等しいタクトの数で受信されます。
フィードバックループがあることで予測できないニューラルネットワークの変動(この場合リカレントと呼ばれます)ができます。実際ネットワークは『永久にループし』応答をすることはありません。同時に「チューリング」によると、エレメントが平衡になると( 停止問題)特定する任意のリカレントなネットワークについてのアルゴリズムはありません。
一般的には、リカレントネットワーク内のニューロンは情報を何度も処理することに参加することが、そのようなネットワークが異なる方法でより深いレベルで情報処理が行えるようにするのです。この場合、特殊な手段が撮られネットワークが永遠にループしなくてすみます。たとえばホップフィールドネットワーク内のように対称的な接続を行う、または強制的に反復回数を制限するなどです。
| トレーニングタイプ 接続タイプ |
『教師』あり | 『教師』なし |
|---|---|---|
| フィードバックループなし | 多層パーセプトロン(関数近似化、分類) |
競合ネットワーク、自己組織化マップ(データ圧縮、機能分離) |
| フィードバックループあり | リカレントパーセプトロン(時系列予測、オンライントレーニング) |
ホップフィールドネットワーク(連想メモリ、データクラスター化、最適化) |
表1 接続タイプおよびトレーニングタイプによるニューラルネットワークの分類
1.2. ニューラルネットワークの主なタイプ
パーセプトロンから始まり、ニューラルネットワークは進化への長い道のりをたどりました。今日、ストラクチャやトレーニング方法の異なる大量のニューラルネットワークが利用されています。
以下がもっとも知られるものです。
1.2.1. 多層完全結合型フィードフォワードネットワークM MLP (多層パーセプトロン)
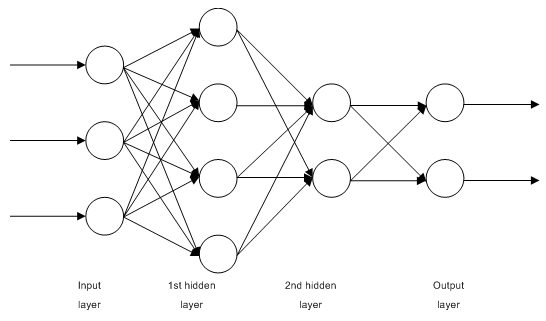
図1 多層ニューラルネットワークのストラクチャ
1.2.2. ジョーダン型ネットワークは部分的にリカレントなネットワークでエルマン型ネットワークに似ています。
それはインプット層に追加のコンテクストのニューロンを持つフィードフォワードネットワークとして扱われます。
こういったコンテキストニューロンはそれ自体がフィードし(直接フィードバック)、入力ニューロンからのものです。コンテキストニューロンは下ネットワークの現状を維持します。ジョーダン型ネットワークではコンテキスト数と入力ニューロン数は等しくなる必要があります。
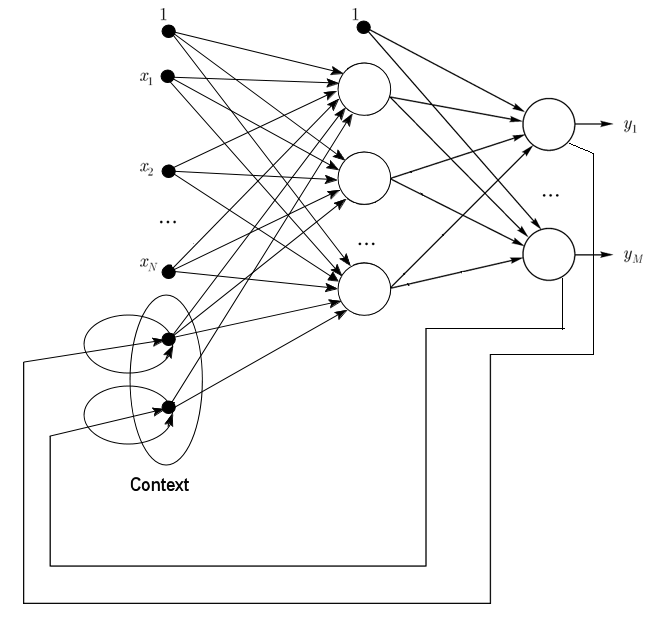
図2 ジョーダン型ネットワークのストラクチャ
1.2.3. エルマン型ネットワークは部分的にリカレントなネットワークでジョーダン型ネットワークに似ています。 エルマン型ネットワークとジョーダン型ネットワークの違いは、エルマン型ではコンテキストニューロンは隠れニューロンではなく出力ニューロンによってフィードされる点です。またコンテキストニューロンに直接フィードバックはありません。
エルマン型ネットワークではコンテキストと隠れニューロン数が一致する必要があります。エルマン型ネットワークの主要なメリットは、コンテキストニューロンの数がジョーダン型のようにアウトプット数で決まるのではなく、隠れニューロン数で決定されることです。それによりネットワークがより柔軟なものとなります。隠れニューロンはアウトプット数とは異なり簡単に追加したり取り去ったりすることができます。
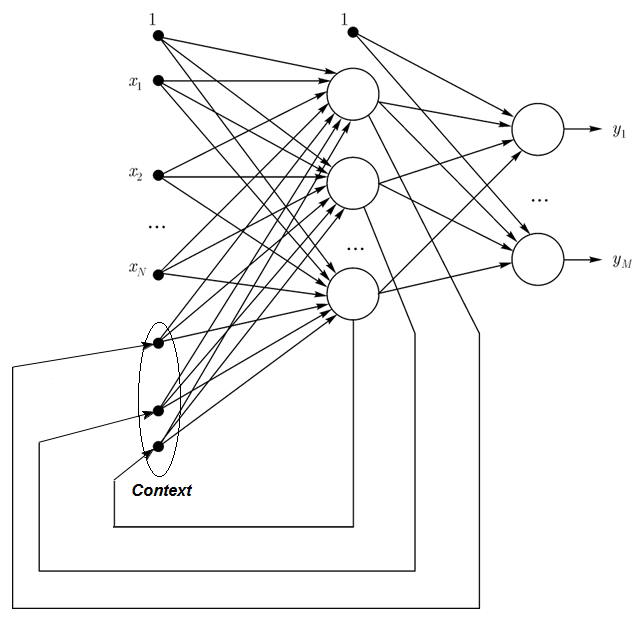
図3 エルマン型ネットワークのストラクチャ
1.2.4. 動径基底関数ネットワーク(RBF)は対称放射性ニューロンの中間(隠れ)層を持つフィードフォワードニューラルネットワークです。そのようなニューロンは指定の入力ベクトルからそれに対応するセンターまでの距離を一般的にガウス分布と理解されるいくつかの非線形法によって変換します。
RBF ネットワークには数多くのメリットがあります。それは多層フィードフォワードネットワークをしのぐものです。まず、それらは中間層1つだけで任意の非線形関数をエミュレートします(語に関しては定かではありません)。それにより開発者は層の数を決定する必要がなくなります。それから、広く知られる線形最適化方法を利用して出力層の線形結合のパラメータを最適化することが可能です。後者は速く動作し、逆伝搬において大きく干渉する極小に関する問題がありません。RBF ネットワークが逆伝搬をする際ずっと速く学習するのはその理由によります。
RBF のデメリット:これらネットワークには 弱い外挿特性があり、入力ベクトルが大きいと面倒なことが判明します。
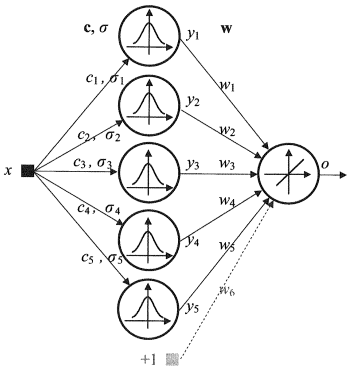
図4 RBF のストラクチャ
1.2.5. 動的学習ベクトル量子化、DLVQ ネットワークは自己組織化マップ(SOM)と酷似しています。 SOM とは異なり、DLVO は教師あり学習が可能で、プロトタイプ間の近隣関係に欠けます。ベクトル量子化にはクラスター化よりも幅広い用途があります。
1.2.6. ホップフィールド型ネットワークは対称接続行列に完全に連携するネットワークです。 処理中はそのようなネットワークのダイナミクスが平衡状態のいずれかに収束します。こういった平衡状態はネットワークのエネルギーとして知られる機能性の極小です。そのようなネットワークは内容アドレス連想記憶システム、フィルターとして最適化の課題に対処するために使用することができます。
特定のタクト数で応答を受け取りまで動作する数多くのニューラルネットワークとは異なり、ホップフィールドネットワークは次のネットワーク状態が前回の状態と正確に一致する平衡状態に淘汰すするまで動作します。この場合、初期状態は入力パターンで、平衡状態では出力画像が受信されます。ホップフィールドネットワークをトレーニングするには、入力層と出力層で同時に存在するトレーニングパターンが必要とされます。
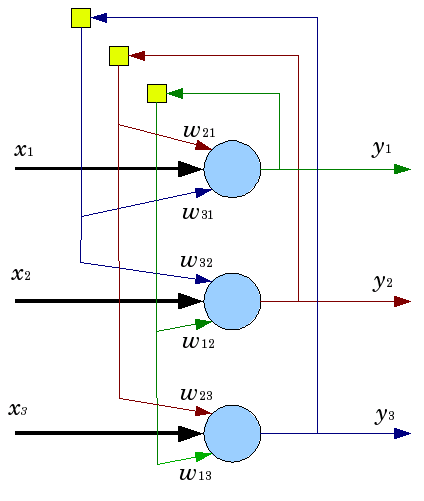
図5 3個のニューロンを持つホップフィールド型ネットワークのストラクチャ
魅力的な特性にもかかわらず、古典的なホップフィールド型ネットワークは理想的とは程遠いものです。それは、ネットワーク N のニューロンの約 15% という限られたメモリを持ち、そのためアドレス指定されたメモリのシステムは N ビットを使用して異なる画像を 2N まで格納することができます。
また、ホップフィールド型ネットワークは画像が表示されているか最初に格納された位置に対する関係に変化しているかを認識することができません。これらおよびその他の欠点により、ホップフィールド型ネットワークは日常使い用の実践的インスツルメントというよりは研究に便利な理論モデルとみなされています。
その他の多く(ヘミングリカレントネットワーク、グロスバーグネットワーク、適応共鳴理論ネットワーク(ART-1、ART-2)他)については本稿では説明しません。それはわれわれの関心対象ではないためです。
1.3. トレーニング方法
新しい事柄を学ぶ能力は人間の脳の主要な特性です。人口ニューラルネットワークの場合、学習は手持ちのタスクに対する効果的なソリューションを取得するためのネットワーク構造体(ニューロン間の結合構成)とシナプスリンクのウェイト(係数信号に影響する)を構成する過程です。通常、ニューラルネットワークのトレーニングはデータサンプル上で行われます。トレーニング過程は特定のアルゴリズムに従い、進むにつれ、入力信号に対するネットワークの反応が良くなっていきます。
学習パラダイムには主なものが3とおりあります。:教師あり、教師なし、複合タイプです。1番目では、入力例ごとに正しい答え が解りウェイトはエラーを最小限に抑えようとします。教師なし学習は、内部ストラクチャの説明とデータの性質によってサンプルを分類することができます。複合タイプではw、上記の両方の方法がとられます。
1.3.1. ニューラルネットワーク学習の主なルール
接続するネットワーク構造体を基にした主要な学習ルールが4つあります。:エラー修正、ボルツマンの法則、ヘップの法則、競合学習です。
1.3.1.1. エラー修正
入力例はそれぞれ指定の望む出力値(目標値)を持ちます。それは実際の値(予測値)とは一致しないかもしれません。エラー修正学習ルールは、エラーを減らすためにウェイトを直接調整するために目標値と予測値の差を利用します。トレーニングは誤った出力がある場合にのみ実行されます。この学習ルールは数多くの改変を有します。
1.3.1.2. ボルツマンの法則
ボルツマンの法則は熱力学の原理と同様で確率的学習です。これは目的の確率分布に応じてニューロンの重み係数を調整することにつながります。ボルツマンの法則学習はエラーが2種類のモード状況の相関の不一致を意味する場合、エラーによる修正の孤立したケースとみなされます。
1.3.1.3. ヘップの法則
ヘップの法則はもっともよく知られるニューラルネットワークの学習アルゴリズムです。この方法の考えはシナプスの両側にあるニューロンが同時に定期的にアクティブ化すると、シナプス結合は強くなる、というものです。ここで重要な特殊性はシナプスのウェイトがこのシナプスに結合されているニューロンの活動のにに応じて変化するということです。シナプス荷重修正における特殊性が異なるこのルールには数多くのバリエーションがあります。
1.3.1.4. 競合学習
数多くの出力ニューロンが同時にアクティブになることのできるヘップの学習法則とは異なり、ここでは出力ニューロンはお互い競合します。加重和の最大値を持つ出力ニューロンが『勝者』となり『勝者が全てを手に入れる』のです。その他の出力ニューロンは非アクティブに設定されます。学習時、現在の入力インスタンスに対して近接性の増加を目標に『勝者』のウェイトのみ修正されます。
異なる課題に対処する学習アルゴリズムは数多く存在します。もっとも効率的な最新アルゴリズムの一つである逆伝搬は、そのうちの一つです。背後にある原理はシナプス重量変化は誤差関数の局所的な勾配を考慮して行われる、というものです。
出力層で評価されるニューラルネットワークの現実の応答と正しい応答の間の差は、逆伝搬的です。-シグナルの流れに逆らっています(図5)。このようにニューロンはすべてネットワークの累積エラーに対するウェイトの寄与を決定することができます。もっともシンプルな学習ルールは最急降下法で、それは累積エラーに対する寄与に比例したシナプスのウェイト変化です。
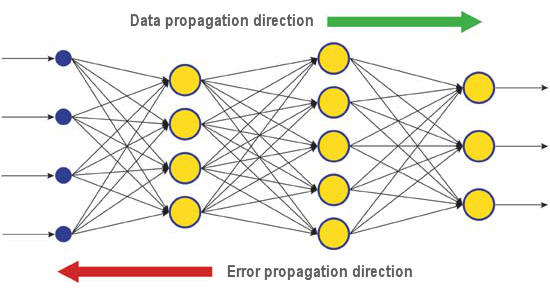
図6 逆伝搬による学習時のネットワークにおけるデータパターンとエラー拡散
確実にこのタイプのニューラルネットワーク学習は最良の学習結果を保証しません。なぜならつねにアルゴリズムが極小になる可能性があるためです。極小ポイントから見出した解決法を打ち負かす特殊な技術があります。この技術のアプリケーションいくつかの後に、ニューラルネットワークが同じ決定をすると、それは見出された解決策がもっとも最適であろうと結論づけることができそうです。
1.4. 欠点
- ニューラスネットワークを使用する際の主な問題はいわゆる『次元の呪い』です。次元を入力し層数が増加すると、ネットワークはより複雑になり、学習時間が指数的に増え、受信結果はつねに最適とは限りません。
- ニューラスネットワークを使用する際のもうひとつ別の問題は従来のニューラルネットワークはタスクを遂行する方法を説明できないことです。アプリケーションフィールドの中には、薬のように結果そのものよりもこの説明の方が重要なものがあります。内部結果の表示は複雑なことが多いため、通常関心を払うことのないもっともシンプルな場合以外は解析が不可能です。
2. 深層学習
今日、マシン学習の理論と実践は『深い革命』を経験しています。それは、深層学習方法の実装が成功したからで、それは第三世代のニューラルネットワークを示しています。前世紀80年代~90年代に利用されていたかつての第二世代ネットワークとは異なり、新たな学習パラダイムは拡張および従来のニューラルネットワークを正常に実装するのを妨げる数多くの問題を解決します。
深層学習アルゴリズムでトレーニングされたネットワークは精度において最良の代替え方法として優れてはいるだけでなく、入力情報を理解する基礎を明らかにする場合もありました。画像任氏kとテキスト情報分析はもっともすぐれた例です。
今日ではコンピュータビジョンと音声認識のもっとも先進的な工業的手法は深層ネットワークを基にしています。Apple、Google、Facebook のような IT 産業の巨大企業は深層ニューラルネットワークの研究者を採用しています。
2.1. 背景
Geoffrey E. Hinton 博士の率いるトロント大学で学んでいる大学院生のチームが Merck が主催したコンテストで一位を獲得しました。限られたデータセットを用いて15分子の化学構造を記述し、G. Hinton 博士のグループはそのうちどの分子が効果的な薬品である可能性が高いか決定する特殊なプログラムシステムを作成し応募しました。
それが特殊だった点は開発者が深層学習に基づく人口ニューラルネットワークを使用していたことでした。ニューラルネットワークをふつうにトレーニングすることは、このシステムにかなりの情報量を入れることが必要ですが、結果そのシステムはひじょうに限られたソースデータセットを基に計算を行い検索をしました。
Hinton 博士のチームの達成は特に印象深く、それはチームが直前にコンテストへの参加を決めたためです。その上、深層学習システムは分子が標的に結合する仕組みについて特に知識なく開発されました。ただし深層学習の実装が成功したのは波乱に満ちた2012年の人工知能開発における別の成果におけるものでした。
2012年夏、Google の Jeff Dean と Andrew Y. Ng は、正解率15.8%の新しい画像認識システムを提示しました。彼らは16,000 ノードのクラスターシステムをトレーニングするのに異なる 20,000 のオブジェクトの1,400万枚の描画のライブラリを持つImageNet ネットワークを使用しました。去年スイス人科学者によって作成されたプログラムは交通標識の画像を認識するのに人間を越えました。勝利したプログラムは50,000 セット中 99.46 パーセントの画像を正確に特定しました。ちなみに人間の参加者32人中最高スコア 99.22 パーセントで、人間の平均は 98.84 パーセントでした。2012年10月、Microsoft の科学プログラムのコーディネータである Richard F. Rashid 氏は中国、天津の学会で自身の声による英語から北京語への同時通訳技術を披露しました。
人工知能分野におけるブレークスルーを示すこういった技術はすべて、特定の範囲への深層学習手法に基づいています。深層学習理論への主な貢献は英国の科学者、近代コンピュータの基礎となるブール代数の始祖である George Boole の孫の孫、、Hinton 博士によるものです。
深層学習理論は、一般的なマシン学習の手法を複数のプレゼンテーションレベルで入力される情報分析のための特殊なアルゴリズムで補うものです。新しい方法が特別なのは、深層学習が、問題のオブジェクトのパラメータに英k表を与えるすべての要因の説明となる十分な情報を提供するプレゼンテーションレベルを検出するまで対象を研究する点です。
そのような方法に基づくニューラルネットワークには、学習のための入力情報は少なくてすみ、トレーニングされたネットワークは通常のニューラル根とワークよりも高いレベルの精度の情報分析が可能です。Hinton 博士と共同研究者の方々は彼らの技術は多次元で情報がよく構造化された配列における特殊性を検索するのに特にすぐれている、と語ります。
人工知能技術(AI)、特に深層学習は異なるシステムで幅広く利用されています。「ニュアンスコミュニケーション」技術に基づく知的パーソナル アシスタント、Apple Siri やGoogle の「ストリートビュー」での住所認識もその例です。それでも科学者によるこの分野での成功はひじょうに注意深く予想されるものです。というのも人工知能作成の歴史が楽観的な期待と失望に満ちているからです。
1960年代、科学者は10年後には完全な機能を備えた人工知能を作り出していると信じていました。そののち1980年代、『既製人工知能』を提供する若い企業の波があり、それに続いてこの分野の『氷河期』が訪れ、それは最近まで続きました。今日、クラウドサービスで利用可能な広い計算能力により新しい理論ベース、アルゴリズムベースによる力強いニューラルネットワーク実装の新しい段階がやってきています。
ニューラルネットワーク、畳み込みニューラルネットワーク、オートアソシエータ、ボルツマンマシンといった第三世代でさえ名前以外は生物的ニューロンとはなにも関わりがないことに注意が必要です。
新しい学習パラダイムは学習の考えを二段階で取り入れます。第一段階では、入力データの内部構造に関する情報は教師なしでトレー二ングされる層ひとつひとつでのオートアソシエータを持つフォーマット化されていないデータの大きな配列から抽出されます。そして多層ニューラルネットワークで、フォーマット化されたデータによってこの情報を用いて教師ありトレーニングを通過します。同時にフォーマット化されていないデータ量はできるだけ大きい必要があります。フォーマット化されたデータはひじょうに小さいサイズです。われわれの場合、それは特に重要ではありません。
2.2. オートエンコーダオートエンコーダと制限付きボルツマン マシン違いと特殊性
2.2.1. オートエンコーダ
最初のオートアソシエータ(АА) は福島ネオコグニトロンでした。
そのストラクチャは図7に示されています。

図7 福島ネオコグニトロン
オートアソシエータ(АА) はアウトプットで可能な限り正確な画像としてインプット画像を受け取るためのものです。
АА には2タイプあります。— 生成と合成です。制限あるボルツマンマシンは最初のタイプのひとつで、オードエンコーダは二番目のタイプを代表します。
オードエンコーダはオープンレイヤを1つ持つニューラルネットワークです。教師なしの学習アルゴリズムとバックプロパゲーションを用い、それは入力ベクトル、すなわちy = xに等しい目標値を設定します。
図8にオードエンコーダ例を示します。
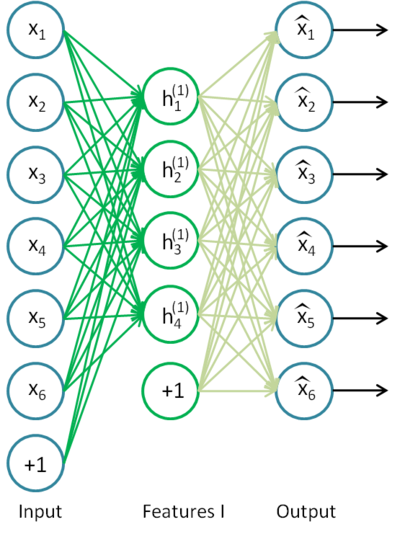
図8 オードエンコーダのストラクチャw
オードエンコーダは関数 h(x)=x を構成しようとしています。言い換えると、ニューラルネットワークのフィードバックがおおよそ入力パラメータに等しくなることを保証する関数の近似を検索しようとしています。問題の解決策が非自明となるため、オープンレイヤのニューロン数は入力データの次元よりも低い必要があります(図のように)。
それにより入力シグナルがネットワークの出力に渡されるときデータを圧縮することができます。たとえば入力ベクトルがサイズ 10х10 ピクセル(指標100)の画像の輝度レベル設定であれば、隠れ層のニューロン数は50で、ネットワークは画像を圧縮する学習を余儀なくされます。要件 h(x)=x は隠れ層の50ニューロンのアクティブ化レベルに応じ、出力層は最初の画像の100ピクセルを格納しなおすことを意味します。隠された相互接続、特性相関関係、なんらかのストラクチャがあれば、そのようは圧縮は可能です。このようにオートエンコーダ処理は入力データが減少するという意味で主成分分析法(PCA)を思い出させます。
驚くべきことに、Bengio ら(2007)が行った実験の数々が確率的勾配降下によるトレーニングをすると、入力数よりも大きい隠れニューロン数を持つ非線形自動ネットワークは、入力からププレゼンテーションを取ったネットワークの適合エラーの観点からすると有益なプレゼンテーションを持つことを示しました。
その後、スパースの考え方が登場すると、スパース オートエンコーダが広く使用されました。
スパース オートエンコーダは入力次元よりもかなり大きな隠れニューロン数を持つオートエンコーダですが、スパースのアクティブ化を行うものです。スパースのアクティブ化は隠れ層の非アクティブなニューロン数がアクティブなニューロン数を大きく上回る場合行われます。非公式にクティブであるとみなされます。シグモイド関数が使用されていれば、非アクティブなニューロンに対するその値は 0 に近くなります(双曲線正弦関数に対しては値は -1 に近くなりま)。
オートエンコーダにはノイズ除去のオートエンコーダ(Vincent その他、2008)と呼ばれるバリエーションがあります。これは同じオートエンコーダですが、トレーニングがいくらか特殊なものです。このネットワークをトレーニングするとき、『破損した』データが入力されます(値のいくつかは 0 で代用されます)。小津時に、出力データと比較する『正確な』データがあります。このようにオートエンコーダは破損したデータを復元することができます。
2.2.2. 制限付きボルツマン マシン、RBM
制限付きボルツマン マシン(RBM)の履歴については着目しません。トレーニングがひじょうに困難なフィードバックを伴うリカレントニューラルネットワークから始まったことを知っていれば十分です。この学習のむつかしさゆえに、シンプルな学習アルゴリズムを取り入れることができるよう、より制限のあるリカレントモデルが出現しました。そのようなモデルの一つがホップフィールド型ニューラルネットワークです。John Hopfield はニューラルネットワーク力学を熱力学と比較したネットワークエネルギーのコンセプトを取り入れた人物です。
RBM への次のステップはひゅじゅん的なボルツマン マシンでした。ホップフィールド型ネットワークとの違いは、確率的性質を有することで、そのニューロンは可視的状態と非表示状態(隠れマルコフモデルに似ています)を述べる2つのグループに分けられます。制限付きボルツマン マシンは一層内のニューロン間に結合がない点で標準的なボルツマン マシンとは異なります。
図9がRBM のストラクチャを示しています。
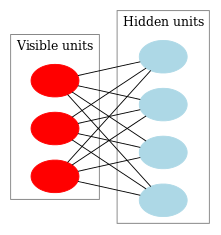
図9 RBM ストラクチャ
このモデルの特殊な点は、あるグループのニューロンの現在状態において、別のグループのニューロン状態がお互い独立しようとすることです。この性質が主要な役割を担ういくつかの理論に進みます。
解釈と目的
RBM は隠れマルコフモデルに似ていると解釈されます。観測できる数多くの状態(可視的ニューロン)があり、直接確認できない隠れた状態(隠れニューロン)が数多くあります。観察できる状態に依存する隠れ状態について可能性に基づく結論に至ることができます。そのようなモデルがトレーニングされたあと、隠れ状態がベイズの定理に従うと知る可視状態に関する結論を導くチャンスを得ます。これによりモデルをトレーニングするのに使用される確率分布からデータを生成することができます。
このようにモデルトレーニングの目標を作成することができます。初期状態から回復されたベクトルが元の状態に近づくようモデルパラメータを調整する、というものです。回復されたベクトルは隠れ状態からの確率的推論により受け取られるベクトルで、それは次に可視状態からの確率的推論、すなわち元のベクトル、により受け取られました。
トレーニングアルゴリズムは Contrastive Divergence CD-k です。
そのようなヘッジを信頼して行うアルゴリズムは解りやすい言葉で、またシンプルなグラフと図で説明されています。主な考えは数学的期待値は定義された値で痴漢されている、というものです。導入されているのはギブスサンプリングの考え方です。
CD-k は以下のようなものです。
- 可視的ニューロン状態は入力パターンに等しく設定される。
- 隠れ層状態の確立が描かれる。
- 隠れ層のニューロンすべてが、現在状態に等しい確率を持つ "1" 状態を割り当てる。
- 可視層の状態の確率は隠れ層を基に描かれる。
- 現在の反復が k 未満であれば、ステップ 2 に戻る。
- 隠れ層状態の確立が描かれる。
Hinton 氏のレクチャーではそれは次のようなものです。
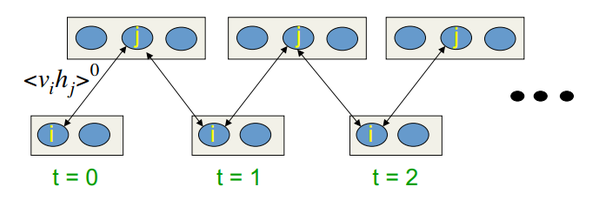
図10 CD-k 学習のアルゴリズム
すなわち、サプリングを長く行うほど、勾配はより正確になるのです。博士はProfessor CD-1、すなわちサンプリング反復1度のみの場合、に対する結果はすでに良好なものです。
2.3. 積み上げオートアソシエータ ネットワーク積み上げオートエンコーダ SAE、積み上げ制限付きボルツマンマシン(積み上げRBM)
入力データセットから高いレベルの抽象性を抽出するためには、オートアソシエータはネットワークに統合されます。
図11は積み上げられたオートエンコーダのストラクチャとニューラルネットワークを示しています。それらはともに積み上げオートエンコーダにより初期化されたウェイトを持つ深層ニューラルネットワークを表しています。
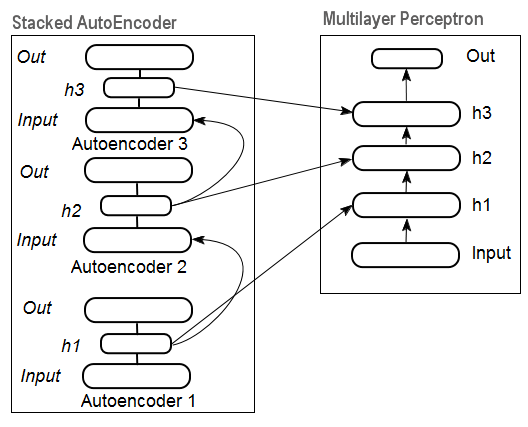
図11 DN SAE のストラクチャ
図12には、積み上げられた RBM (SRBM)のパターンとニューラルネットワークがあります。それはともにSRBM により初期化されたウェイトを持つ深層ニューラルネットワークを表しています。
これら深層ネットワークストラクチャの説明は情報が下から上に抽出されることを強調しています。
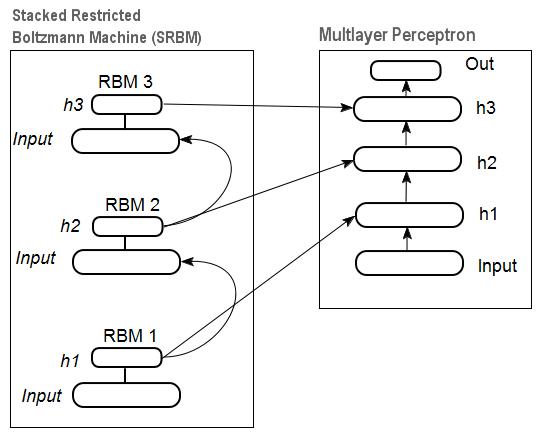
図12 DN SRBM のストラクチャ
2.4. 深層ネットワーク(DN)のトレーニング 段階特殊性
深層ネットワークのトレーニングは二段階です。第一段階では、オートアソシエータネットワーク(DN タイプによりSAE または SRBMtype)はフォーマット化されていないデータ配列上で教師なしのトレーニングを受けます。その後、通常の MLP の隠れ層ニューロンがトレーニング後受け取られる隠れ層のウェイトによって初期化されます。図11および図12は学習と転送過程を示しています。最初の АЕ/RBM トレーニング後、隠れ層のニューロンウェイトは二番目等のインプットとなります。このように、ストラクチャに関する一般的情報(ライン、コンター、パター等)がデータから抽出されます。
第二段階はよく知られるメソッドによって設定されるフォーマット化されたデータ上で MLP (教師ありトレーニング)を微調整します。実践によりそのような初期化が MLP の隠れ層のニューロンウェイトをグローバルな最小値に設定し、続く微調整はひじょうに短い時間で行われることをh聡明しました。
その上、3 より大きい層数の深層ネットワークに対して、D. Hinton は微調整は二段階で行うべきだと提案しました。第一段階では、上部2層のみトレーニングし、第二段階でネットワークの残りの層をトレーニングするのです。
SRBM の教師なしのトレーニング結果は SAE よりも不安定なものであることを述べておきます。
注意:これら用語はよく混乱します。SRBM は深い信念ネットワーク DBN で識別されます。RBM が DBN から派生しているにもかかわらず、これらは全くことなるストラクチャをしています。DBN は多層ニューラルネットワークで、バイナリパターンでランダムに初期化された隠れ層のニューロンウェイトを持ちます。
3. 実践的実験
深層ネットワークは R 言語で操作されます。
3.1. R 言語
歴史R 言語はプログラム言語で、統計的計算とチャート化のための環境です。1996 年にニュージーランドの科学者、Ross Ihaka と Robert Gentlemanによってオークランド大学で作成されました。
R 言語は、フリーソフトウェアでその哲学は以下の原則に及ぶGNU プロジェクトです。
- どんな目的に対してもプログラムを起動する自由(自由0)
- プログラムの動作方法を学び個人の必要に応じて取り入れる自由(自由1)
- 他者に役立つようコピーを配布する自由(自由2)
- プログラムを改善しそこから社会に恩恵をもたらす自由
歴史的観点では、R は S を実装するための代替手段です。S は1976年にベル研究所で John Chambers とその同僚によって作成されました。今日、R はまだ John Chambers を含む R 開発コアチームによって改善されつつあります。
実験を繰り返すためには R および Rstudio をインストールする必要があります。ダウンロード先とダウンロード方法に関する情報はインターネットを参照ください。質問があれば、本稿に対するコメントで話し合うことができます。 the article.
R 言語のメリット
- 今日、R は統計的計算では標準です。
- それは世界的な大学の科学コミュニティによって開発されサポートされています。
- データ毎にングの高度な分野に対する幅広いパッケージセットです。この考えの発表と R パッケージへの導入の間の時間は通常2週間もかかりません。
- そして少なくともそれは完全無料です。無料 OS の著名は開発者がかつてこう言いました。「プログラムはセックスのようなものだ。タダが一番だ。」
3.2. 実装のバリエーションと解決された問題
実装には2とおりの方法があります。
第一の方法は Matlab のためにJohn Hinton が開発したユニークなプログラムを使用することです。そのためには "R.matlab" が必須です。このパッケージには MAT ファイルを読み書きするためのメソッド writeMat() および readMat() が入っています。それにより、ローカルであるいはクライアントサーバーリンクにてリモートホストで起動される Matlab v6 以上からの通信(コード実装、オブジェクトの送信および受信等)が可能となります。詳細はパッケージの説明にあります。これは Matlab を使い慣れているかたむけの方法です。私はこの方法を試してみたことはありませんが、このようにして Matlab と MQL をリンクできる可能性があります。
実装の第二の方法は本トピックの R 言語パッケージを使用することです。その方法を見ていきます。
本稿のトピックに関連して私の知るパッケージは3個あります。
"deepnet" は DN SAE および DN SRBM モデルを取り入れているシンプルなパッケージです。教師あり、教師なし学習に設定されている入力データの長さは同じです。二段階でシステムの微調整を行う必要はありません。最初にモデルに対する調査と検証を行います。
"darh" は DN SRBM をモデル化するための高度な広範なパッケージです。DN SAE 用モデルがありますが、それは起動に失敗しました。パッケージは経験あるユーザー用で、それを用いることであらゆる複雑なレベルのモデルも作成、調整することができます。それは MatLab 用言語で Hinton によって開発されたユニークなプログラムを基にしています。
"H2O" は csv ファイルに書かれた大きなデータセット(>1 Гб)について深層ネットワークをトレーニングするための幅広いパッケージです。
下記の実験では "deepnet" パッケージを使用していきます。
3.3. 実験用入力データ、目標データの準備
今日データ毎にングには特定の作業順序があります。
- 入力データの選定(調査、分析、事前準備、評価)トレーニング、検証、テストセット(サンプル)にデータ分割
- トレーニングデータセットにてモデルとトレーニングし、検証データセットでモデルを選択
- テストサンプルにてモデルのクオリティー評価、および特定の計測によりセットから最適モデルパラメータまたは最良モデルの決定
- モデルの動作開始
第一段階はもっとも時間が取られる部分で最終結果にとってひじょうに重要です。公正を期して、この段階は形式化されたおらず、一般的に言えば芸術形式に近いものです。研究者の経験に追うところが多いのです。ただし!もっともセットを選択するために入力データセットの定量評価を取得することはひじょうに重要です。この場合には、特定モデルについてベストな変数を自動で選択することのほうが適していると言えます。R は全段階における課題を満たすための広範な機能性を提供してくれます。
ソースデータは重要なだけではなく、それには考慮すべき面が数多くあります。それは1件の記事に相当するものです。本稿の目的は複雑な事柄をシンプルにお話することですので、重要なポイントは取り上げますがあまり細かい部分には踏み込みません。
3.3.1. ソースデータ
われわれの分類のためには一組の独立した(入力)変数と目標変数が必要です。深層ネットワークの主に顕著なメリットは大きな入力サンプルを迅速に学習する能力であるため、プレディクター17(11インディケータ)の入力データセットを作成します。ZigZag は目標変数の役割をします。4000 バーの深さのオープン、高、低、クローズのクオートのベクトルを R 環境にダウンロードします。方法はインディケータを書く以下の説明でお伝えします。この段階では重要ではありません。それ以上の計算は R で行います。
4 ベクトル、平均価格、バー本体サイズから行列を構成します。それを関数に変えます。
pr.OHLC <- function (o, h, l, c)
{
#Unite quote vectors into a matrix having previously expanded them
#Indexing of time series of vectors in R starts with 1.
#Direction of indexing is from old to new ones.
price <- cbind(Open = rev(o), High = rev(h), Low = rev(l), Close = rev(c))
Med <- (price[, 2] + price[, 3])/2
CO <- price[, 4] - price[, 1]
#add Med and CO to the matrix
price <- cbind(price, Med, CO)
}
結果を見ます(2014年10月8日12:00 の状態)
> head(price)
Open High Low Close Med CO
[1,] 1.33848 1.33851 1.33824 1.33844 1.338375 -4e-05
[2,] 1.33843 1.33868 1.33842 1.33851 1.338550 8e-05
[3,] 1.33849 1.33862 1.33846 1.33859 1.338540 1e-04
[4,] 1.33858 1.33861 1.33856 1.33859 1.338585 1e-05
[5,] 1.33862 1.33868 1.33855 1.33855 1.338615 -7e-05
[6,] 1.33853 1.33856 1.33846 1.33855 1.338510 2e-05
3.3.2. 入力データ(予測因子)
インディケータをリストアップします。インディケータはランダムに選択され、入力サイズの行列差を取得することに優先はついていません。
インディケータすべての計算は数多くのインディケータを持つ "TTR" パッケージによって行われます。
3.3.2.1. ウェルズ・ワイルダーの方向性指数-ADX(HLC, n) -4 アウト (Dip, Din,DX, ADX)
計算し、最初の 200 バーでそれがどのように見えるか確認します。
> library(TTR)
> adx<-ADX(price, n = 16)
> plot.ts(head(adx, 200))
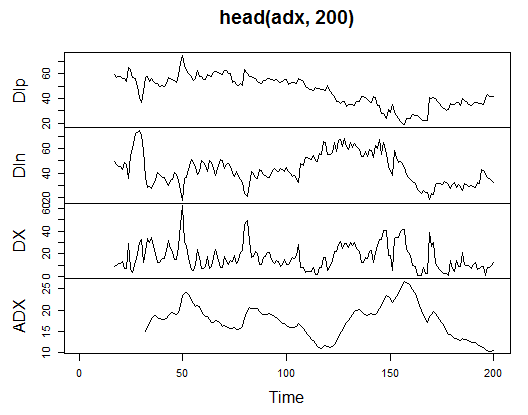
図13 ウェルズ・ワイルダーの方向性指数インディケータ-ADX(HLC, n)
> summary(adx) DIp DIn DX ADX Min. :15.90 Min. : 5.468 Min. : 0.00831 Min. : 5.482 1st Qu.:41.21 1st Qu.: 33.599 1st Qu.: 8.05849 1st Qu.:14.046 Median :47.36 Median : 43.216 Median :16.95423 Median :18.099 Mean :47.14 Mean : 46.170 Mean :19.73032 Mean :19.609 3rd Qu.:53.31 3rd Qu.: 55.315 3rd Qu.:27.97471 3rd Qu.:23.961 Max. :80.12 Max. :199.251 Max. :81.08751 Max. :52.413 NA's :16 NA's :16 NA's :16 NA's :31
行列の冒頭には31個定義されていない値(NA)があります。それから詳細説明なしですべてのインディケータを同様に計算します。
3.3.2.2. アルーン(HL, n)-1 アウト (oscillator)
ただひとつの変数"oscillator" の最初の 200 バーを計算し確認します。
> ar<-aroon(price[ , c('High', 'Low')], n = 16)[ ,'oscillator']
> plot(head(ar, 200), t = "l")
> abline(h = 0)
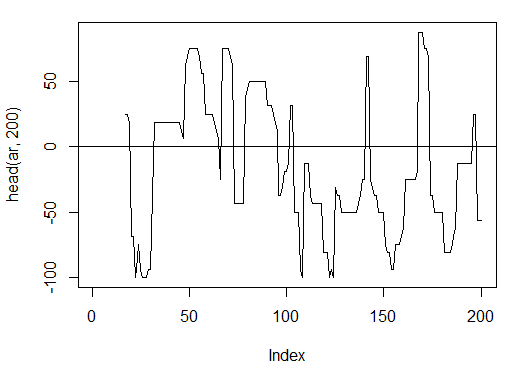
図14 アルーンインディケータ(HL, n)
> summary(ar) Min. 1st Qu. Median Mean 3rd Qu. Max. NA's -100.00 -56.25 -18.75 -7.67 43.75 100.00 16
3.3.2.3. コモディティチャンネル指数-CCI(HLC, n) -1 アウト
> cci<-CCI(price[ ,2:4], n = 16)
> plot.ts(head(cci, 200))
> abline(h = 0)
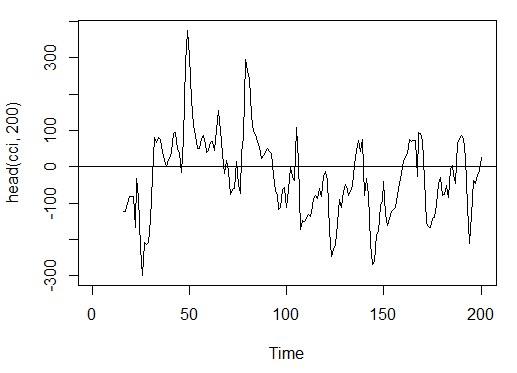
図15 コモディティチャンネル指数インディケータ-CCI(HLC, n)
> summary(cci) Min. 1st Qu. Median Mean 3rd Qu. Max. NA's -469.10 -90.95 -18.74 -14.03 66.91 388.20 15
3.3.2.4. チェイキンのボラティリティ- chaikinVolatility (HLC, n) -1 アウト
> chv<-chaikinVolatility(price[ , 2:4], n = 16)
> summary(chv)
Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
-0.67570 -0.29940 0.02085 0.12890 0.41580 5.15700 31
> plot(head(chv, 200), t = "l")
> abline(h = 0)
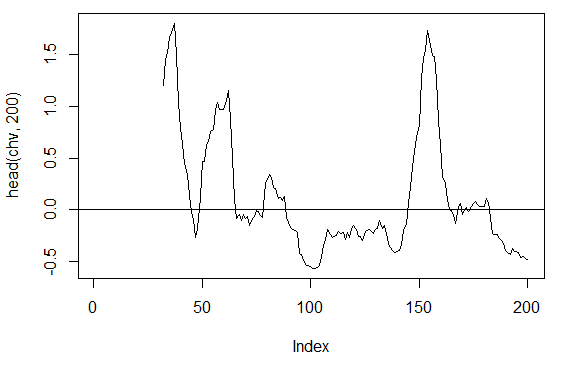
図16 チェイキンのボラティリティインディケータ (HLC, n)
3.3.2.5. シャンデモメンタムオシレーター- CMO(Med, n)-1 アウト
> cmo<-CMO(price[ ,'Med'], n = 16)
> plot(head(cmo, 200), t = "l")
> abline(h = 0)
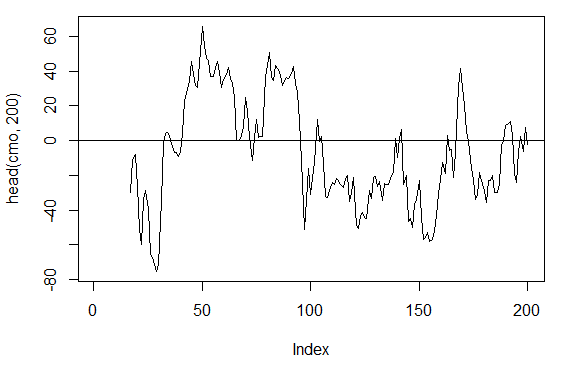
図17 シャンデモメンタムオシレーターインディケータ-CMO(Med, n)
> summary(cmo) Min. 1st Qu. Median Mean 3rd Qu. Max. NA's -97.670 -32.650 -5.400 -6.075 19.530 93.080 16
3.3.2.6. MACD オシレータ-MACD(Med, nFast, nSlow, nSig) 1 アウトが使用されます (macd)
> macd<-MACD(price[ ,'Med'], 12, 26, 9)[ ,'macd'] > plot(head(macd, 200), t = "l") > abline(h = 0)
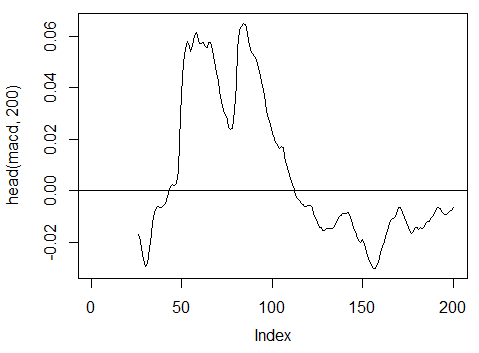
図18 MACDオシレーターインディケータ
> summary(macd) Min. 1st Qu. Median Mean 3rd Qu. Max. NA's -0.346900 -0.025150 -0.005716 -0.011370 0.013790 0.088880 25
3.3.2.7. OsMA(Med,nFast, nSlow, nSig) -1 アウト
> osma<-macd - MACD(price[ ,'Med'],12, 26, 9)[ ,'signal'] > plot(head(osma, 200), t = "l") > abline(h = 0)
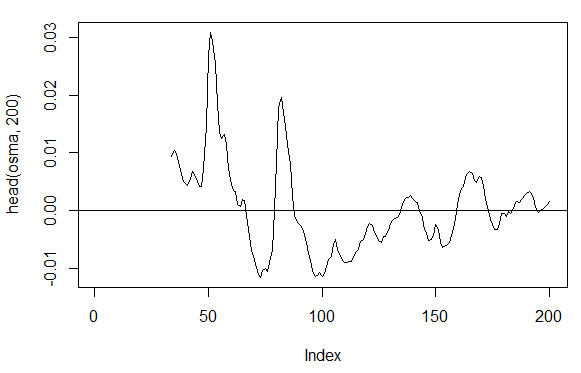
図19 OsMA インディケータ(Med,nFast, nSlow, nSig)
> summary(osma) Min. 1st Qu. Median Mean 3rd Qu. Max. NA's -0.10560 -0.00526 0.00034 0.00007 0.00646 0.05922 33
3.3.2.8. 相対力指数-RSI(Med,n) -1 アウト
> rsi<-RSI(price[ ,'Med'], n = 16)
> plot(head(rsi, 200), t = "l")
> abline(h = 50)

図20 相対力指数インディケータ-RSI(Med,n)
> summary(rsi) Min. 1st Qu. Median Mean 3rd Qu. Max. NA's 5.32 37.33 47.15 46.53 55.71 84.82 16
3.3.2.9. ストキャスティクス-stoch(HLC, nFastK=14, nFastD=3, nSlowD=3) -3 アウト
> stoh<-stoch(price[ ,2:4], 14, 3, 3) > plot.ts(head(stoh, 200))
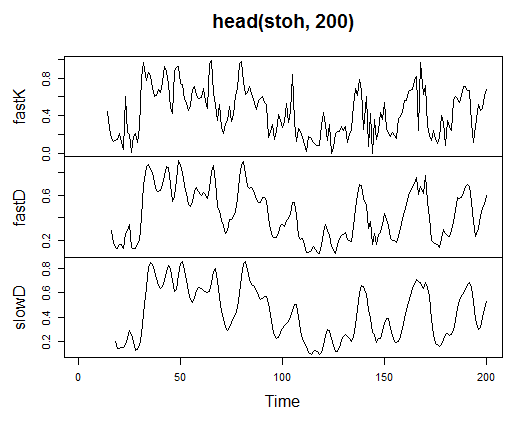
図21 ストキャスティクスインディケータ-stoch(HLC, nFastK=14, nFastD=3, nSlowD=3)
> summary(stoh) fastK fastD slowD Min. :0.0000 Min. :0.01782 Min. :0.02388 1st Qu.:0.2250 1st Qu.:0.23948 1st Qu.:0.24873 Median :0.4450 Median :0.44205 Median :0.44113 Mean :0.4622 Mean :0.46212 Mean :0.46207 3rd Qu.:0.6842 3rd Qu.:0.67088 3rd Qu.:0.66709 Max. :1.0000 Max. :0.99074 Max. :0.97626 NA's :13 NA's :15 NA's :17
3.3.2.10. 確率的モメンタムインデックス-SMI(HLC, n = 13, nFast = 2, nSlow = 25, nSig = 9) — 2 アウト
> smi<-SMI(price[ ,2:4],n = 13, nFast = 2, nSlow = 25, nSig = 9) > plot.ts(head(smi, 200))

図22 確率的モメンタムインデックスインディケータ-SMI(HLC, n = 13, nFast = 2, nSlow = 25, nSig = 9)
> summary(smi) SMI signal Min. :-82.185 Min. :-78.470 1st Qu.:-33.392 1st Qu.:-31.307 Median : -9.320 Median : -8.839 Mean : -8.942 Mean : -8.985 3rd Qu.: 15.664 3rd Qu.: 14.069 Max. : 71.878 Max. : 63.865 NA's :25 NA's :33
3.3.2.11. Volatility (Yang and Zhang) - volatility(OHLC, n, calc="yang.zhang", N=96)- 1 out
> vol<-volatility(price[ ,1:4],n = 16,calc = "yang.zhang", N =96) > plot.ts(head(vol, 200))
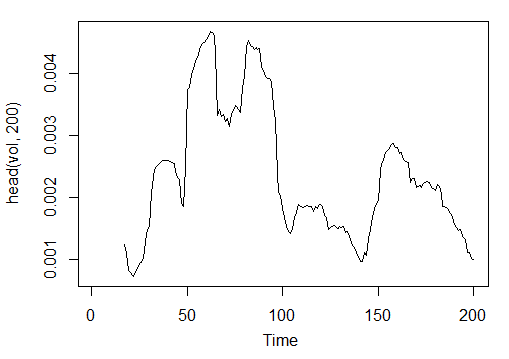
図23 予想変動率(ヤンと張)インディケータ-volatility(OHLC, n, calc="yang.zhang", N=96)
> summary(vol) Min. 1st Qu. Median Mean 3rd Qu. Max. NA's 0.000599 0.001858 0.002638 0.003127 0.004015 0.012840 16
これで 4000 バー深さの OHLC サンプルに対しタイムフレームМ15 で EURUSD に対する11インディケータから 17 の変数を取得しました。
それらを用いて行列を形成し、上記パラメータを1個の仮パラメータ рを使って1つの関数に書き込みます。それは最適化を必要とします。
式を用いて入力パラメータの行列を計算します。
In<-function(p = 16){
adx<-ADX(price, n = p);
ar<-aroon(price[ ,c('High', 'Low')], n=p)[ ,'oscillator'];
cci<-CCI(price[ ,2:4], n = p);
chv<-chaikinVolatility(price[ ,2:4], n = p);
cmo<-CMO(price[ ,'Med'], n = p);
macd<-MACD(price[ ,'Med'], 12, 26, 9)[ ,'macd'];
osma<-macd - MACD(price[ ,'Med'],12, 26, 9)[ ,'signal'];
rsi<-RSI(price[ ,'Med'], n = p);
stoh<-stoch(price[ ,2:4],14, 3, 3);
smi<-SMI(price[ ,2:4],n = p, nFast = 2, nSlow = 25, nSig = 9);
vol<-volatility(price[ ,1:4],n = p,calc="yang.zhang", N=96);
In<-cbind(adx, ar, cci, chv, cmo, macd, osma, rsi, stoh, smi, vol);
return(In)
}
> X<-In()
> tail(X)
DIp DIn DX ADX ar cci chv
[3995,] 46.49620 36.32411 12.28212 18.17544 25.0 168.0407 0.1835102
[3996,] 52.99009 31.61164 25.26952 18.61882 37.5 227.7030 0.3189822
[3997,] 58.11948 28.16241 34.72000 19.62515 37.5 145.2337 0.3448520
[3998,] 56.00323 30.48687 29.50206 20.24245 37.5 118.5831 0.3068059
[3999,] 55.96197 28.78737 32.06467 20.98134 37.5 116.5376 0.3517668
[4000,] 54.97777 26.85440 34.36713 21.81795 62.5 160.0767 0.6169701
cmo macd osma rsi fastK
[3995,] 29.71342 -0.020870825 0.01666593 52.91932 0.8832685
[3996,] 41.89526 -0.009654368 0.02230591 61.49793 0.8833819
[3997,] 30.98237 -0.002051532 0.02392699 58.94513 0.7259475
[3998,] 33.84813 0.003454534 0.02354645 58.00549 0.7930029
[3999,] 38.84892 0.009590136 0.02374564 60.63806 0.8367347
[4000,] 54.71698 0.019303110 0.02676689 66.64815 0.9354120
fastD slowD SMI signal vol
[3995,] 0.7773581 0.7735064 -35.095406 -47.27712 0.003643196
[3996,] 0.7691688 0.7761507 -26.482951 -43.11828 0.003858942
[3997,] 0.8308660 0.7924643 -19.699762 -38.43458 0.003920541
[3998,] 0.8007775 0.8002707 -13.141932 -33.37605 0.003916109
[3999,] 0.7852284 0.8056239 -6.569699 -28.01478 0.003999789
[4000,] 0.8550499 0.8136852 2.197810 -21.97226 0.004293766
生の入力データが準備できました。
3.3.3. アウトプットデータ(目標)
ここで出力(目標データ)を作成します。前にお話ししたとおり、ZigZag を利用します。
37 大ポイントのチャネル幅を持つ ZigZag を使用していきます。ZigZag は平均価格によって計算されます。インディケータは HL 価格で計算されますが、平均価格のほうが適しています。というのもこの場合、インディケータが安定しているからです。シグナル(0-買い、1-売り)を抽出したら、それとインプット行列に変換します。それはネットワークモデル想定しています。
関数を書きます。
Out<-function(ch=0.0037){ # ZigZag has values on each bar and not only in the points zz<-ZigZag(price[ ,'Med'], change = ch, percent = F, retrace = F, lastExtreme = T); n<-1:length(zz); # On the last bars substitute the undefined values for the last known ones for(i in n) { if(is.na(zz[i])) zz[i] = zz[i-1];} #Define the speed of ZigZag changes and move one bar forward dz<-c(diff(zz), NA); #If the speed >0 - signal = 0(Buy), if <0, signal = 1 (Sell) otherwise NA sig<-ifelse(dz>0, 0, if else(dz<0, 1, NA)); return(sig); }
Calculate signals.
> Y<-Out() > table(Y) Y 0 1 1567 2423
クラス比はアンバランスです。1クラスの例の数はもう一つのものより大きくなっています。分類のモデルが必ずしもそのセットに対して不都合があるわけではありません。
この状況はデータとトレーニングとテストサンプルに分けるときに修正します。
3.3.4. データ消去
定義されていないデータからデータセットを消去します。この場合の消去とはタスクの幅広い四捨五入を意味します。それには『仮想的ゼロ変数』の消去、高い相関関係のあるもの、ここではあえてお話しないその他タスクが含まれます。
関数を書き、データを消去します。
Clearing<-function(x, y){
dt<-cbind(x,y);
n<-ncol(dt)
dt<-na.omit(dt)
return(dt);
}
> dt<-Clearing(X,Y); nrow(dt)
[1] 3957
行列は 43 バー分短くなりました。
3.3.5. トレーニングとテストサンプル形成
ソースデータをトレーニングとテストサンプルに分ける方法は複数あります。8:10 の割合でソースデータをトレーニングとテスト用データに分ける通常のランダムな分け方を採用しようと思います。重要なのはサンプルが層状になっていることです。それはトレーニング用とテスト用サンプルでクラスインスタンスの割合がソースデータセットのクラス割合に対応している、ということです。またソースデータセット内のクラスの不均衡を修正することも有益だと思われます。それには方法が2とおりあります。大きい方のクラスで平滑化するか、小さい方のクラスで平滑化するかです。より多くの例が必要なので、大きい方のクラス "1" で平滑化します。この場合には『キャレット』パッケージを使います。
どちらのクラスのインスタンスも同じで大きいクラスに等しい、バランスのとれた新しいセットを作成します。
3.3.6. クラス・バランシング
以下が大きい側にクラス数を平滑化し(分散が15%以上の場合)、バランスのとれた行列を返す関数です。
Balancing<-function(DT){
#Calculate a table with a number of classes
cl<-table(DT[ ,ncol(DT)]);
#If the divergence is less than 15%, return the initial matrix
if(max(cl)/min(cl)<= 1.15) return(DT)
#Otherwise level by the greater side
DT<-if(max(cl)/min(cl)> 1.15){
upSample(x = DT[ ,-ncol(DT)],y = as.factor(DT[ , ncol(DT)]), yname = "Y")
}
#Convert у (factor) into a number
DT$Y<-as.numeric(DT$Y)
#Recode у from 1,2 into 0,1
DT$Y<-ifelse(DT$Y == 1, 0, 1)
#Convert dataframe to matrix
DT<-as.matrix(DT)
return(DT);
}
説明1番目の文字列では、各クラスのインスタンス数を計算します(クラス数に等しい次元を持つベクトル)。
大きいベクトルの小さいベクトルに対する割合を見つけ、設定された閾値よりも小さければ終了します。割合が閾値よりも大きければ、 х とy wを別々に入れて関数を計算します。Y は事前にファクターに変換します。
これは upSample() 関数の仮パラメータに対して必要です。ファクターとして目標変数は必要ないため、それを値 0 および 1 で数字に変換しなおします。数値(0、1)をファクターに変換する際、テキスト変数 "0" および "1" を受け取ることに注意が必要です。数字変数に変換しなおすときには、1 および 2 (!)を受け取ります。そしてそれらを 0 と 1 に置き換えます。われわれのデータセットは『データフレーム』から "matrix" クラスに変換されます。それを計算します。
dt.b<-Balancing(dt) x<-dt.b[ ,-ncol(dt.b)] y<-dt.b[ , ncol(dt.b)]
このようにしてソースの dt データセット(入力および出力)とバランスのとれたセットdt.b を取得します。
それをトレーニングサンプルとテストサンプルに分けます。
holdout()関数によって"rminer" パッケージからトレーニングサンプルとテストサンプルのインデックスを取得します。
> library('rminer')
> t<-holdout(y, ratio = 8/10, mode = "random")
オブジェクトはトレーニング (t$tr) およびテスト (t$ts) データセットを持つリストです。受け取ったセットは層状になっています。
3.3.7. 処理
入力データソースには異なる値範囲の変数が入っています。基本的に深層ネットワークはウェイトを初期化する特殊な方法を持つ通常のネットワークです。
ニューラルネットワークは (-1; 1) または (0, 1) の範囲で入力変数を受け取ります。入力変数を範囲 [-1, 1] に正規化します。
それには 『キャレット』 パッケージの preProcess()関数を使用します。処理パラメータはトレーニングデータセット上で計算し、テストデータセットおよび新らしい入力データの後の処理のために保存することに留意ください。
> spSign<-preProcess(x[t$tr, ], method = "spatialSign")
> x.tr<-predict(spSign, x[t$tr, ])
> x.ts<-predict(spSign, x[t$ts, ])
これで深層ニューラルネットワークの構築、トレーニング、検証に必要なすべてがそろいました。
3.4. モデルの構築、トレーニング、検証
DN SAE モデルを構築しトレーニングしていきます。以下がモデルの式と変数の記述です。
sae.dnn.train(x, y, hidden = c(10), activationfun = "sigm", learningrate = 0.8, momentum = 0.5, learningrate_scale = 1, output = "sigm", sae_output = "linear", numepochs = 3, batchsize = 100, hidden_dropout = 0, visible_dropout = 0)
ここで
- х は入力データの行列
- y は目標変数のベクトルまたは行列
- hidden は各隠れ層のニューロン数を持つベクトルデフォルト с(10)では
- activationfun は隠れニューロンをアクティブ化する関数は "sigm"、"linear"、"tanh" です。デフォルト "sigm"では
- learningrate が傾斜降下に対するトレーにングレベルデフォルト = 0.8 では
- momentum は傾斜降下に対するモメンタムデフォルト = 0.5 では
- learningrate_scale トレーニングレベルは反復ごとにこの値を乗算されます。デフォルト = 1.0 では
- numepochs はトレーニング用反復回数デフォルト = 3 では
- batchsize はトレーニングされる小さい量のサイズデフォルト = 100 では
- output は出力ニューロンが "sigm"、"linear"、"softmax"であるアクティブ化関数デフォルト "sigm"では
- output は SAE の出力ニューロンが "sigm"、"linear"、"softmax"であるアクティブ化関数デフォルト "linear"では
- hidden_dropout は隠れ層について削除可能な部分デフォルト = 0 では
- visible_dropout は可視的(入力)層の削除可能部分デフォルト = 0 では
以下の次元(17, 100, 100, 100, 1)を持つモデルを作成し、トレーニングし、学習時間を記録し予測を観察します。
> system.time(SAE<-sae.dnn.train(x= x.tr, y= y[t$tr], hidden=c(100,100,100), activationfun = "tanh", learningrate = 0.6, momentum = 0.5, learningrate_scale = 1.0, output = "sigm", sae_output = "linear", numepochs = 10, batchsize = 100, hidden_dropout = 0, visible_dropout = 0)) begin to train sae ...... training layer 1 autoencoder ... training layer 2 autoencoder ... training layer 3 autoencoder ... sae has been trained. begin to train deep nn ...... deep nn has been trained. user system elapsed 12.92 0.00 13.09
見てのとおり、それは二段階で起こります。第一段階では、オートエンコーダがトレーニングされた層を層ごとに取得し、それからニューラルネットワークを取得します。
トレーニング時間の短い数と3層内の膨大な隠れニューロンは故意に設定されました。処理は全体で13秒かかりました。
プレディクターのテストセットで予測値を評価します。
> pr.sae<-nn.predict(SAE, x.ts); > summary(pr.sae) V1 Min. :0.2649 1st Qu.:0.2649 Median :0.5881 Mean :0.5116 3rd Qu.:0.7410 Max. :0.7410
レベル 0、1 に変換し測定値を計算します。
> pr<-ifelse(pr.sae>mean(pr.sae), 1, 0) > confusionMatrix(y[t$ts], pr) Confusion Matrix and Statistics Reference Prediction 0 1 0 316 128 1 134 378 Accuracy : 0.7259 95% CI : (0.6965, 0.754) No Information Rate : 0.5293 P-Value [Acc > NIR] : <2e-16 Kappa : 0.4496 Mcnemar's Test P-Value : 0.7574 Sensitivity : 0.7022 Specificity : 0.7470 Pos Pred Value : 0.7117 Neg Pred Value : 0.7383 Prevalence : 0.4707 Detection Rate : 0.3305 Detection Prevalence : 0.4644 Balanced Accuracy : 0.7246 'Positive' Class : 0
これはすぐれた係数ではありません。われわれはこれらシグナルを使用して出す収益に対してもっと関心があるのであって、係数にではありません。それを最後の 500 バー(およそ1週間)で確認します。トレーニングしたネットワークの最後の連続した500 本のバーでシグナルを受信しようと思います。
入力データの最後の500バーを正規化し、トレーニングしたニューラルネットワークから予測値を受け取り、それはシグナル -1= (売り) および 1 = (買い)に変換します。
> new.x<-predict(spSign,tail(dt[ ,-ncol(dt)], 500)) > pr.sae1<-nn.predict(SAE, new.x) > pr.sig<-ifelse(pr.sae1>mean(pr.sae1), -1, 1) > table(pr.sig) pr.sig -1 1 235 265 > new.y<-ifelse(tail(dt[ , ncol(dt)], 500) == 0, 1, -1) > table(new.y) new.y -1 1 201 299 > cm1<-confusionMatrix(new.y, pr.sig) > cm1 Confusion Matrix and Statistics Reference Prediction -1 1 -1 160 41 1 75 224 Accuracy : 0.768 95% CI : (0.7285, 0.8043) No Information Rate : 0.53 P-Value [Acc > NIR] : < 2.2e-16 Kappa : 0.5305 Mcnemar's Test P-Value : 0.002184 Sensitivity : 0.6809 Specificity : 0.8453 Pos Pred Value : 0.7960 Neg Pred Value : 0.7492 Prevalence : 0.4700 Detection Rate : 0.3200 Detection Prevalence : 0.4020 Balanced Accuracy : 0.7631 'Positive' Class : -1
われわれは係数にではなく収益に対してもっと関心があるとしても、係数の精度は悪くありません。
予測シグナルを用いて最終 500 バーに対する収益を検証しバランス曲線を出します。
> bal<-cumsum(tail(price[ , 'CO'], 500) * pr.sig) > plot(bal, t = "l") > abline(h = 0)
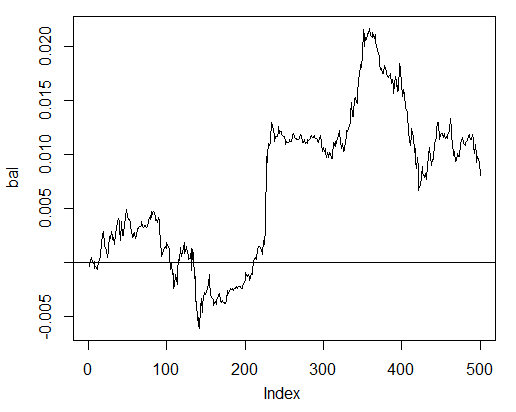
図24 ニューラルネットワークシグナルによる最終500 バーのバランス
バランスはスプレッド、スリッページ、その他実際のマーケットの現実は考慮せず計算されました。
ここで ZZ の理想的なシグナルから取得されたバランスと比較します。赤線はニューラルネットワークシグナルによるバランスです。
> bal.zz<-cumsum(tail(price[ , 'CO'], 500) * new.y) > plot(bal.zz, t = "l") > lines(bal, col = 2)
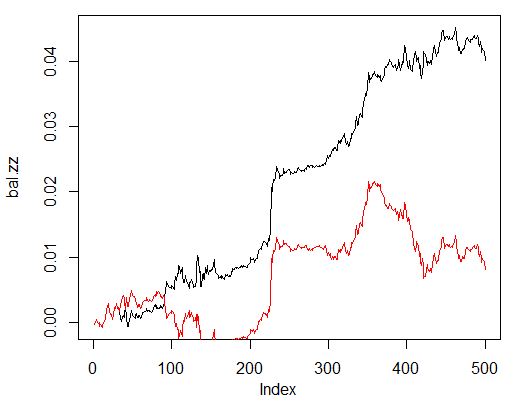
図25 ニューラルネットワークシグナルおよび ZigZag シグナルによる最終500 バーのバランス
改善の可能性はあります。
2つのヘルパー関数 Estimation() および Testing()をアシストする関数を2つ書きます。最初の関数は係数 Accuracy/Err を、二番目の関数はバランス Bal/BalZZ.を生成します。
それによりすぐにネットワークパラメータをいくつか変更する結果と取得し、ネットワークのクオリティーに影響を及ぼすパラメータがどれであるか確認することができます。
フィットネス関数を書いたので、トレード処理に混乱をきたすことなく進化(遺伝的)アルゴリズムによって最適なネットワークパラメータが見つけ出せます。本稿ではそれに時間を遣う気はないので、それについてはまたの機会に詳しく考察することとします。
以下は係数 Err/Accuracy を計算するEstimation() 関数です。
Estimation<-function(X, Y, r = 8/10, m = "random", norm = "spatialSign", h = c(10), act = "tanh", LR = 0.8, Mom = 0.5, out = "sigm", sae = "linear", Ep = 10, Bs = 50, CM=F){ #Indices of the training and test data set t<-holdout(Y, ratio = r, mode = m) #Parameters of preprocessing prepr<-preProcess(X[t$tr, ], method = norm) #Divide into train and test data sets with preprocessing x.tr<-predict(prepr, X[t$tr, ]) x.ts<-predict(prepr, X[t$ts, ]) y.tr<- Y[t$tr]; y.ts<- Y[t$ts] #Train the model SAE<-sae.dnn.train(x = x.tr , y = y.tr , hidden = h, activationfun = act, learningrate = LR, momentum = Mom, output = out, sae_output = sae, numepochs = Ep, batchsize = Bs) #Obtain a forecast on the test data set pr.sae<-nn.predict(SAE, x.ts) #Recode it into signals 1,0 pr<-ifelse(pr.sae>mean(pr.sae), 1, 0) #Calculate the Accuracy coefficient or classification error if(CM) err<-unname(confusionMatrix(y.ts, pr)$overall[1]) if(!CM) err<-nn.test(SAE, x.ts, y.ts, mean(pr.sae)) return(err) }
以下は仮パラメータです。
- X -入力原プレディクタの行列
- Y -目標変数のベクトル
- r -トレーニング:テスト割合
- m -サンプル形成モード(ランダムまたはコンセクエント)
- norm -入力パラメータ正規化モード([ -1, 1]= "spatialSign";[0, 1]="range")
- h -隠れ層内のニューロン数と持つベクトル
- act -隠れニューロンのアクティブ化関数
- LR -トレーニングレベル
- Мом — モメンタム
- out -出力層のアクティブ化関数
- sae -オートエンコーダののアクティブ化関数
- Ep -トレーニングエポック数
- Bs -小サンプルサイズ
- СM-ブール変数、真であれば Accuracy を表示それ以外は Err を表示
例としてバランスの取れていないデータセット dt で各30ニューロンを持つ3つの隠れ層のあるネットワークにより分類エラーを計算します。
> Err<-Estimation(X = dt[ ,-ncol(dt)], Y = dt[ ,ncol(dt)], h=c(30, 30, 30), LR= 0.7) begin to train sae ...... training layer 1 autoencoder ... training layer 2 autoencoder ... training layer 3 autoencoder ... sae has been trained. begin to train deep nn ...... deep nn has been trained. > Err [1] 0.1376263
関数 Testing() は予測シグナルまたは理想シグナル(ZigZag)ごとにバランスを計算します。
Testing<-function(dt1, dt2, r=8/10, m = "random", norm = "spatialSign", h = c(10), act = "tanh", LR = 0.8, Mom = 0.5, out = "sigm", sae = "linear", Ep = 10, Bs=50, pr = T, bar = 500){ X<-dt1[ ,-ncol(dt1)] Y<-dt1[ ,ncol(dt1)] t<-holdout(Y, ratio = r, mode = m) prepr<-preProcess(X[t$tr, ], method = norm) x.tr<-predict(prepr, X[t$tr, ]) y.tr<- Y[t$tr]; SAE<-sae.dnn.train(x = x.tr , y = y.tr , hidden = h, activationfun = act, learningrate = LR, momentum = Mom, output = out, sae_output = sae, numepochs = Ep, batchsize = Bs) X<-dt2[ ,-ncol(dt2)] Y<-dt2[ ,ncol(dt2)] x.ts<-predict(prepr, tail(X, bar)) y.ts<-tail(Y, bar) pr.sae<-nn.predict(SAE, x.ts) sig<-ifelse(pr.sae>mean(pr.sae), -1, 1) sig.zz<-ifelse(y.ts == 0, 1,-1 ) bal<-cumsum(tail(price[ ,'CO'], bar) * sig) bal.zz<-cumsum(tail(price[ ,'CO'], bar) * sig.zz) if(pr) return(bal) if(!pr) return(bal.zz) }
以下は仮パラメータです。
- dt1 -ネットワークのトレーニングに利用される入力変数または目標変数の行列
- dt2 -ネットワークの検証に利用される入力変数または目標変数の行列
- pr -ブール変数。真であれば予測シグナルによるバランスを表示、それ以外は ZigZag シグナルによるバランスを表示
- bar -バランス計算に使用する最終バー数
上記と同じパラメータを持つニューラルネットワークによりバランスのとれたデータセット dt.b のトレーニングを行うとき、データセット dt の最終500バーについてバランスを計算します。
> Bal<-Testing(dt.b, dt, h=c(30, 30, 30), LR= 0.7) begin to train sae ...... training layer 1 autoencoder ... training layer 2 autoencoder ... training layer 3 autoencoder ... sae has been trained. begin to train deep nn ...... deep nn has been trained. > plot(Bal, t = "l") > abline(h = 0)
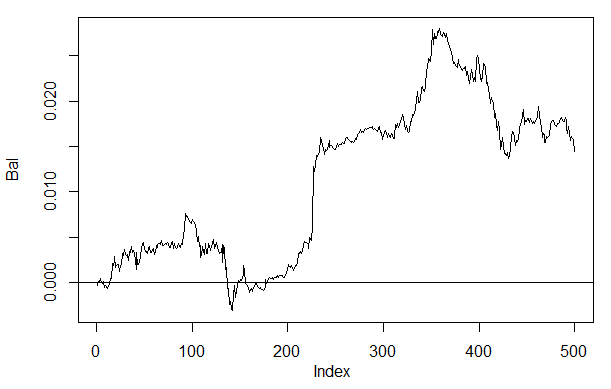
図26 ニューラルネットワークシグナル h(30,30,30) による最終500 バーのバランス
結果を前回取得したバランスと比較すれば、著しい改善が見られます。ただこれはここでの最大の関心事ではありません。
最終500バーにおける価格プロットを見れば、どの場所のどの部分がわれわれのネットワーク(150~350バー)によりもっとも受け入れられているか確認することができます。
> plot(tail(price[ ,'Close'], 500), t = "l") > abline(v = c(150,350), col=2)
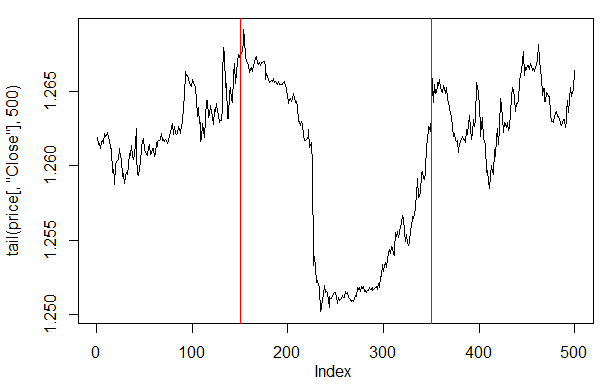
図27 最終 500 バーにおける終値のプロット
注意:予測出力値をデコードする際、別のバージョンも使用できるところ、平均よりも大きい/小さいシンプル化したバージョンを使用 しました。
値が 0.6 より大きい、または 0.4 より小さければ、0.4~0.6 の不安的なセグメントは切り捨てられます。より正確なクラス境界はキャリブレーションによって取得可能です。この件については後程お話します。
われわれの関数 Testing() は、追加のパラメータ dec が取り入れられれば若干変更されます。これによりデコード方法("mean" or "60/40")を選択し、予測値についてバランスに関しどんな影響を受けるか確認することができます。
Testing.1<-function(dt1, dt2, r = 8/10, m = "random", norm = "spatialSign", h = c(10), act = "tanh", LR = 0.8, Mom = 0.5, out = "sigm", sae = "linear", Ep = 10, Bs = 50, pr = T, bar = 500, dec=1){ X<-dt1[ ,-ncol(dt1)] Y<-dt1[ ,ncol(dt1)] t<-holdout(Y, ratio = r, mode = m) prepr<-preProcess(X[t$tr, ], method = norm) x.tr<-predict(prepr, X[t$tr, ]) y.tr<- Y[t$tr]; SAE<-sae.dnn.train(x = x.tr , y = y.tr , hidden = h, activationfun = act, learningrate = LR, momentum = Mom, output = out, sae_output = sae, numepochs = Ep, batchsize = Bs) X<-dt2[ ,-ncol(dt2)] Y<-dt2[ ,ncol(dt2)] x.ts<-predict(prepr, tail(X, bar)) y.ts<-tail(Y, bar) pr.sae<-nn.predict(SAE, x.ts) #Вариант +/- mean if(dec == 1) sig<-ifelse(pr.sae>mean(pr.sae), -1, 1) #Вариант 60/40 if(dec == 2) sig<-ifelse(pr.sae>0.6, -1, ifelse(pr.sae<0.4, 1, 0)) sig.zz<-ifelse(y.ts == 0, 1,-1 ) bal<-cumsum(tail(price[ ,'CO'], bar) * sig) bal.zz<-cumsum(tail(price[ ,'CO'], bar) * sig.zz) if(pr) return(bal) if(!pr) return(bal.zz) }
デコードの1番目と2番目の方法でバランスを計算し評価します。
結果が繰り返すように同じ位置に疑似乱数ジェネレータを設定します。
> set.seed<-1245 > Bal1<-Testing.1(dt.b, dt, h = c(30, 30, 30), LR = 0.7, dec = 1) begin to train sae ...... training layer 1 autoencoder ... training layer 2 autoencoder ... training layer 3 autoencoder ... sae has been trained. begin to train deep nn ...... deep nn has been trained. > set.seed<-1245 > Bal2<-Testing.1(dt.b, dt, h = c(30, 30, 30), LR = 0.7, dec = 2) begin to train sae ...... training layer 1 autoencoder ... training layer 2 autoencoder ... training layer 3 autoencoder ... sae has been trained. begin to train deep nn ...... deep nn has been trained. > plot(Bal2, t = "l") > lines(Bal1, col = 2)
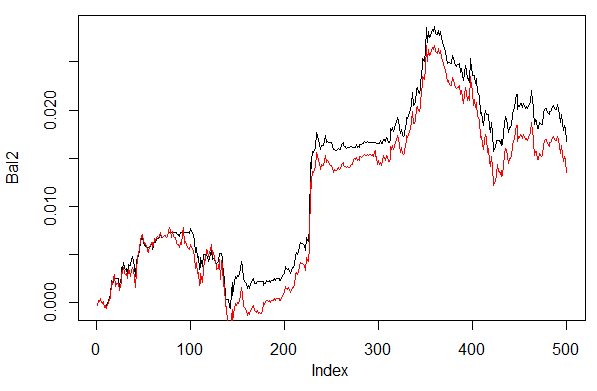
図28 異なるデコード予測方法を持つニューラルネットワークシグナルによる最終500バーに対するバランス
あきらかに2番目の方法 60/40 によるバランスがよりよく見えます。この点にも改善の可能性はあります。
最終確認事項です。理論では、複数のニューラスネットワークの集合体はより良い、より安定した結果を出します。複数のネットワークで構成される集合体を検証します。独立したサンプルでトレーニングすることは可能ですが、同じサンプルでトレーニングします。集合体予測結果は全ネットワークの予測の単純な平均値です。平均化するのにより複雑な方法も他にあります。
もう一つパラメータを追加してわれわれの関数 Testing() を改良します。そのパラメータというのは ans=1 で、集合体におけるネットワーク数を指定します。
3.4.1. 並列計算
複数の独立したモデルによる計算は簡単に並列化できるため、R 言語が提供してくれる機会を利用して、複数のプロセッサコアまたはどのオペレーションシステムを持っているかにかかわらずローカルネットワークのコンピュータで構成されるクラスターを作成します。
それにはパッケージ "foreach" および "doParallel" が必要です。以下はわれわれのプロセッサのコアすべてに対してクラスターを起動するひじょうにシンプルな関数です。
library(doParallel) library(foreach) puskCluster<-function(){ cores<-detectCores() cl<-makePSOCKcluster(cores) registerDoParallel(cl) clusterSetRNGStream(cl) return(cl) }
以下で何点か明確にします。最初の2つの文字列では必要なライブラリをロードします。それらは事前にコンピュータにインストールする必要があります。それからプロセッサにコアがいくつあるか明確にし、クラスターを作成、並列計算用パッケージを登録、独立した疑似乱数ジェネレータを計算のストリームすべてにインストールし、クラスターハンドルを返します。各モデルの計算用疑似乱数ジェネレータのクオリティーはひじょうに重要ですが、これは今回のトピックには含まれません。
クラスターが起動し、必要な計算が行われたら、それを停止することを忘れてはいけません。
cl<-puskCluster() stopCluster(cl)
並列計算は "foreach" パッケージの以下の式によって行われます。
SAE<-foreach(times(ans), .packages = "deepnet") %dopar% sae.dnn.train(x = x.tr , y = y.tr , hidden = h, activationfun = act, learningrate = LR, momentum = Mom, output = out, sae_output = sae, numepochs = Ep, batchsize = Bs)
ここで times(ans) は取得したいネットワーク数、.packages は計算された関数を取るパッケージを示します。
結果はリスト形式でわれわれが必要とするトレーニングされたネットワークが入っています。
それからネットワークすべてからの予測値が必要で、平均を計算します。
pr.sae<-(foreach(i = 1:ans, .combine = "+") %do% nn.predict(SAE[[i]], x.ts))/ans
ここで i はトレーニングされた根とワークのインデックスのベクトルで、combine="+" はすべてのニューラルネットワークが返される予測値形式を指定します。この場合、合計を返し、並列(オペレー タ%do%)ではなくこれら計算を連続して行う必要があります。取得した合計はニューラスネットワーク数で割り、それは結果の最終です。これはすばらしく、そしてシンプルです。
上記と同じパラメータでデコード方法 60/40 を用いた3つおよび4つのニューラルネットワークで構成される集合体から取得したバランスを計算します。この結果をニューラルネットワークの結果と比較します。並列計算の効率を評価するには、エポック数を300まで増やし予測値を取得する処理時間を増やします。
1. ニューラルネットワーク
> system.time(Bal21<-Testing.1(dt.b, dt, h = c(30, 30, 30), LR = 0.7, dec = 2, Ep=300)) begin to train sae ...... training layer 1 autoencoder ... ####loss on step 10000 is : 0.000057 ####loss on step 20000 is : 0.000043 training layer 2 autoencoder ... ####loss on step 10000 is : 0.000081 ####loss on step 20000 is : 0.000086 training layer 3 autoencoder ... ####loss on step 10000 is : 0.000072 ####loss on step 20000 is : 0.000066 sae has been trained. begin to train deep nn ...... ####loss on step 10000 is : 0.069451 ####loss on step 20000 is : 0.079629 deep nn has been trained. user system elapsed 115.78 0.00 116.96 > plot(Bal21, t = "l") > abline(h = 0)
2. ニューラルネットワーク3つの集合体
> system.time(Bal41<-Testing.2(dt.b, dt, h = c(30, 30, 30), LR = 0.7, Ep=300, dec = 2, ans=3)) user system elapsed 0.22 0.06 233.64 > lines(Bal41, col=4)
3. ニューラルネットワーク4つの集合体
> system.time(Bal44<-Testing.2(dt.b, dt, h = c(30, 30, 30), LR = 0.7, Ep=300, dec = 2, ans=4)) user system elapsed 0.13 0.03 247.86 > lines(Bal44, col=2)
ストリーム数がコア数の倍数であれば、並列計算における実行時間は最適です。私はコアを2個使用しました。
だからと言って、バランスにおいては著しいメリットはありません。下のチャート上ではブルーのプロットがネットワーク3つ、赤のプロットが4つ、黒が1つを表します。
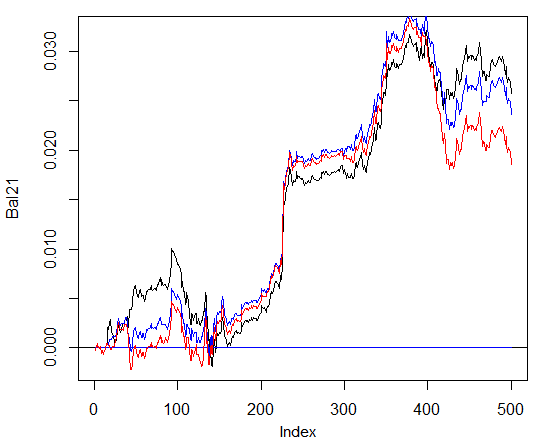
図29 ニューラルネットワーク3、4の集合体とネットワーク1つのシグナルによる最終500バーのバランス
一般に結果は多くのパラメータに依存します。それらは入力および出力データに始まり、正規化方法、隠れ層数、隠れ層内のニューロン数、トレーニングレベル、トレーニングエポック数、その他多数です。
最後の3例です。3つの隠れ層に異なる隠れニューロン数を持つニューラルネットワーク3つの最終1000バーにおけるバランスを計算します。
> system.time(Bal0<-Testing.1(dt.b, dt, h = c(30, 30, 30), LR = 0.7, dec = 2, Ep=300, bar=1000)) begin to train sae ...... training layer 1 autoencoder ... ####loss on step 10000 is : 0.000054 ####loss on step 20000 is : 0.000044 training layer 2 autoencoder ... ####loss on step 10000 is : 0.000078 ####loss on step 20000 is : 0.000079 training layer 3 autoencoder ... ####loss on step 10000 is : 0.000090 ####loss on step 20000 is : 0.000072 sae has been trained. begin to train deep nn ...... ####loss on step 10000 is : 0.072633 ####loss on step 20000 is : 0.057917 deep nn has been trained. user system elapsed 116.09 0.02 116.26 > max(Bal0) [1] 0.04725 > plot(Bal0, t="l") > tail(Bal0,1) [1] 0.03514
最大収益は 472 ポイント。最終バーでは 351 ポイントです。チャート上では黒で示されています。
> system.time(Bal0<-Testing.1(dt.b, dt, h = c(13, 8, 5), LR = 0.7, dec = 2, Ep=300, bar=1000)) begin to train sae ...... training layer 1 autoencoder ... ####loss on step 10000 is : 0.005217 ####loss on step 20000 is : 0.004846 training layer 2 autoencoder ... ####loss on step 10000 is : 0.051324 ####loss on step 20000 is : 0.046230 training layer 3 autoencoder ... ####loss on step 10000 is : 0.023292 ####loss on step 20000 is : 0.026113 sae has been trained. begin to train deep nn ...... ####loss on step 10000 is : 0.057788 ####loss on step 20000 is : 0.056932 deep nn has been trained. user system elapsed 64.04 0.01 64.24 Warning message: In sae$encoder[[i - 1]]$W[[1]] %*% t(train_x) + sae$encoder[[i - : longer object length is not a multiple of shorter object length > lines(Bal0, col="blue")
これは明らかに非効率的なバリエーションです。
三番目のバリエーション
> system.time(Bal0<-Testing.1(dt.b, dt, h = c(50, 50, 50), LR = 0.7, dec = 2, Ep=300, bar=1000)) begin to train sae ...... training layer 1 autoencoder ... ####loss on step 10000 is : 0.000018 ####loss on step 20000 is : 0.000013 training layer 2 autoencoder ... ####loss on step 10000 is : 0.000062 ####loss on step 20000 is : 0.000048 training layer 3 autoencoder ... ####loss on step 10000 is : 0.000053 ####loss on step 20000 is : 0.000055 sae has been trained. begin to train deep nn ...... ####loss on step 10000 is : 0.096490 ####loss on step 20000 is : 0.084860 deep nn has been trained. user system elapsed 186.18 0.00 186.39 > lines(Bal0, col="red") > max(Bal0) [1] 0.0543
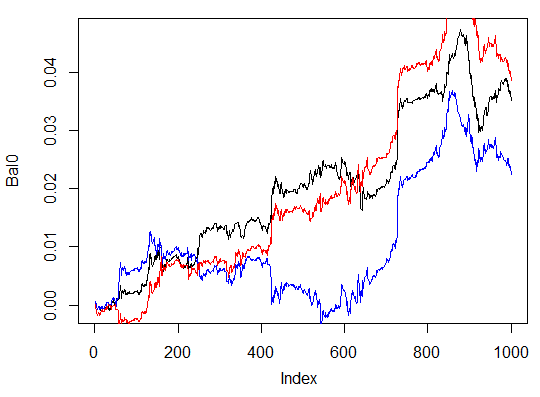
図30 異なる隠れニューロン数を持つニューラルネットワーク3つのシグナルによる最終1000バーにおけるバランス
結果は三番目のバリアントは最大収益 543 ポイントで3つの中でもっともすぐれています。隠れニューロン数を変更しただけで、著しい改善につながりました。最適パラメータの検索は進化的アルゴリズムによって行います。この探索は読者のみなさんにゆだねます。
著者のアルゴリズムはこのパッケージに完全に実装されていないことを念頭におく必要があります。
4. 実装(インディケータおよび Expert Advisor)
トレードシグナルを受信するための深層ネットワークを用いたインディケータおよび Expert Advisor のプログラムを書いていきます。
その実装方法は2とおりあります。
- 第一番目の方法 ニューラルネットワークのトレーニングはRstudio でマニュアルで行われます。受け入れ可能な結果を取得したら、ネットワークを適切なカタログに保存します。それからチャート上で EA とインディケータを起動します。EA はトレーニング済みネットワークをロードします。インディケータは新規バーすべてに新規入力データを準備し、それを EA に渡します。EA はネットワークデータを提示し、シグナルを受信するとそれを処理します。EA はそれについてオーダーのオープン、クローズ、トレーリングなどのような通常の処理を行います。インディケータの目的は新規バーすべての新規入力データを準備し EA に渡すことで、もっとも重要なのはチャート上でネットワークによるシグナル予測を表示することです実践により、ニューラルネットを評価するにはワークビジュアル制御がもっとも効率的な方法であることが示されています。
- 第二の方法 チャート上で EA とインディケータを起動します。初期起動時にはインディケータは、 EA に準備済みの大きな入力および出力データセットを渡します。EA はトレーニング、検証、最良のニューラルネットワーク選択を始めます。その後、第一の方法と同じように処理が進みます。
最初のアルゴリズムに従い、リンクインディケータ-EA を書きます。最小のボウとフリルを持つEA。
それはなぜそんなに難しいのでしょうか?この実装方法により、異なるシンボル/タイムフレームに位置する複数のインディケータを1件の EA に接続し、結果、共に動作することができます。そのために EA にはわずかな変更が必要です。それについては後にお話しします。
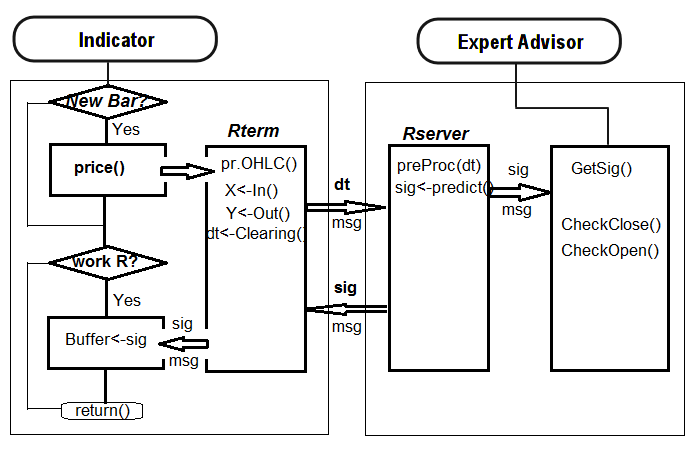
以下はインディケータと EA の連携ストラクチャです。
4.1. モデルのトレーニングと保存
われわれの関心のチャートに入れたインディケータを使い、必要なソースデータを取得します。それには、インディケータをチャート上に置きます。入力変数send=false を設定します。すなわち視覚的表現はサーバーに送信されるよう想定されていません。このシンボルまたはタイムフレームについての初期起動時、インディケータはターミナルのデータファイル(/MQL4/Files)にディレクトリ /Symbol/TF/Test_Data/ を作成します。
そのようなディレクトリの構成により、実験結果をモデルの事前トレーニングと一緒に入れ、古いデータを新しいデータで上書きすることにはなりません。中間結果は /Symbol/TF/Test_Data/ ディレクトリに格納され、EA が処理に使用することになっているモデルは /Symbol/TF/ に入れられます(マニュアルでそこに入れる必要があります)。新規シンボルや EA の新しいタイムフレームについての初期起時、動同じ結果となります。
2014年10月14日、シンボル EURUSD、タイムフレーム М30に対しては4000 バーあります。われわれは dt[] データフレームを要求します。
バランスクラス
> dt.b<-Balancing(dt) > table(dt.b[ ,ncol(dt.b)]) 0 1 2288 2288
ここで、以前に書かれた関数 Testing.1() によって500および300エポックの深層ニューラルネットワークをトレーニングし、ニューラルネットワークによるシグナル予測の最終500バーで取得されるバランスを評価します。
> system.time(bal<-Testing.1(dt.b, dt, h = c(50, 50, 50), LR = 0.7, dec = 2, Ep=500, bar=500)) begin to train sae ...... training layer 1 autoencoder ... ####loss on step 10000 is : 0.000017 ####loss on step 20000 is : 0.000015 ####loss on step 30000 is : 0.000015 training layer 2 autoencoder ... ####loss on step 10000 is : 0.000044 ####loss on step 20000 is : 0.000041 ####loss on step 30000 is : 0.000039 training layer 3 autoencoder ... ####loss on step 10000 is : 0.000042 ####loss on step 20000 is : 0.000042 ####loss on step 30000 is : 0.000036 sae has been trained. begin to train deep nn ...... ####loss on step 10000 is : 0.089417 ####loss on step 20000 is : 0.043276 ####loss on step 30000 is : 0.069399 deep nn has been trained. user system elapsed 267.59 0.08 269.37 > plot(bal, t="l")
別の名前でニューラルネットワークを保存し、別のニューラルネットワークをトレーニングします。
> SAE1<-SAE > system.time(bal<-Testing.1(dt.b, dt, h = c(50, 50, 50), LR = 0.7, dec = 2, Ep=300, bar=500)) begin to train sae ...... training layer 1 autoencoder ... ####loss on step 10000 is : 0.000020 ####loss on step 20000 is : 0.000016 training layer 2 autoencoder ... ####loss on step 10000 is : 0.000050 ####loss on step 20000 is : 0.000050 training layer 3 autoencoder ... ####loss on step 10000 is : 0.000051 ####loss on step 20000 is : 0.000043 sae has been trained. begin to train deep nn ...... ####loss on step 10000 is : 0.083888 ####loss on step 20000 is : 0.083941 deep nn has been trained. user system elapsed 155.32 0.02 156.25 > lines(bal, col=2)
バランスチャートを見ます(赤で表示されている最終結果)。
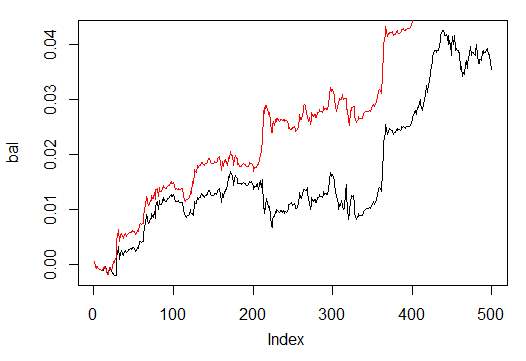
図32 500と300エポックでトレーニングされたニューラルネットワークシグナルによる最終500バーのバランス
見てのとおり、300エポックでトレーニングされたニューラルネットワークは300エポックでトレーニングされたニューラルネットワークより良い結果を示しています。
後者のトレーニング時間はこのタイムフレームでトレーディング中にすばやくトレーニングし直すには適しています。
実チャート上でこれ以上に処理するにはオブジェクトが2つ必要です。トレーニング済みモデル "SAE" と入力データに対する正規化パラメータ"prepr" です。それらは適切なディレクトリに保存します。私の場合は "D:/Alpari Limited MT4/MQL4/Files/EURUSD/M30/Test_2014-10-14"に保存しています。Rstudio の "i_SAE_EURUSD_30.Rdata"インディケータによって保存されるワーキング領域で開くなら、これは定義され、動作中のものとして処理します。
save(SAE, prepr, file="SAE.model")
"SAE.model" ファイル内にモデル自体と正規化パラメータを保存します。それなしでモデルを使用することに意味はありません。毎日のように実験をしてモデルを保存することができます。それらはフォルダ "/File/Symbol/TF/Test_Data"に保存されます。EA がモデルを使用するには、"SAE.model" ファイルをマニュアルで "File/Symbol/TF/" フォルダに入れます。このフォルダはモデル一つだけを保持することができ、EA は処理のためにそれを使用します。
"SAE.model" ファイルをロードしているので、EA はこれらオブジェクトを処理に使用するためワーキング領域にロードします。この時点では作業のマニュアル部分は終了し、インディケータ-EA をチャートに入れ、リアルタイムでそれを検証することができます。
EA の動作の効率性を評価するには、定量的基準が必要となります。精度係数はこのためには適しているとは言えません。
バランス予測率の平均とバー数に対する最終バーのバランス率がZigZag によって受け取りました。われわれの場合、これは ZigZag によるバランスです。
sig.zz<-ifelse(tail(dt[ , ncol(dt)], 500) == 0, 1, -1) bal.zz<-cumsum(tail(price[ , 'CO'], 500) * sig.zz) Kzz<-mean(bal.zz / bal) > Kzz [1] 0.9173312
これはひじょうに高いスコアですが相対的なものです。
時間の経過とともにそれがどのように見えるか確認すれば、のちにそれがほぼ一定となるとしても、最初の 50~100 バーに対してこれは不適切な指標であることがわかります。統計は以下のようなものです。
> plot(bal/bal.zz, t="l") > summary(bal/bal.zz) Min. 1st Qu. Median Mean 3rd Qu. Max. -15.2500 0.7341 0.7844 0.9173 0.8833 55.0000
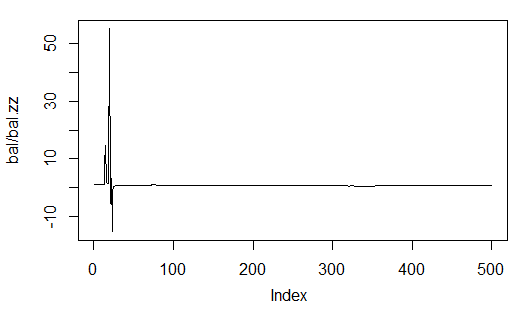
図33 ZigZag によって取得されるバランスに対する予測バランス率
二番目のものはより正確です。というのも N 個の長さのバー1本に対してくらのポイントの収益があるか示しているためです。
たとえば、500バーの範囲のニューラルネットワーク予測に対しては以下です。
> Kb<-tail(bal,1)/length(bal)*10^Dig > Kb [1] 11.508
ZigZag シグナルでは以下です。
> Kbz<-tail(bal.zz,1)/length(bal)*10^Dig > Kbz [1] 13.784
パラメータの一つについて効率の低い方の限度が決まっていると、ニューラルネットワークを保持するとき、またはそのパラメータを最適化するときがわかります。
EA はチャート上で次のパラメータを表示します。:OP -実行済み処理、Acc -精度、K -前に定義された Kb と同じパラメータであるが、高バランスに定義されこのパラメータが最終バーからの最大バランスとどれだけ差があるかという考えを提供します。
4.2. インストールと起動順序
添付されているアーカイブ SAE.zip に以下があります。
- i_SAE.mq4 インディケータ、~/MQL4/Indicators/ フォルダに入れられています。
- e_SAE.mq4 EA、 ~/MQL4/Experts/フォルダに入れられています。
- mt4Rb7.dll ライブラリ、~/MQL4/Libraries/ フォルダに入れられています。
- mt4Rb7.mqhヘッダファイル、~/MQL4/Include/ フォルダに入れられています。ライブラリおよびヘッダファイルは Bernd Kreuss 氏により作成され、氏のご厚意により提供されています。その名前は最終変更のインデックス(b7)もインクルードしています。同じ名前で数多くのバージョンがある場合、修正に多くの時間がかかる混乱があります。
- R でのスクリプト: i_SAE.r (メインのインディケータスクリプト)、i_SAE_fun.r (インディケータスクリプトの関数)、e_SAE.r (EA スクリプト)、e_SAE_init.r (EA 初期化スクリプト)、 SAE_SetDir.r (期限のスクリプトと必要なディレクトリの作成)。スクリプトはシンボルにもタイムフレームにも従属しないため、それらは個別のディレクトリに入れることができます。私の場合、それは "C:Rdata/SAE/"です。"C:Rdata/" ディレクトリには特定のプロジェクトにアタッチされていない異なるスクリプトがあります。スクリプトを渡しのフォルダとは違うフォルダに入れるなら、スクリプトの方法を修正するインディケータや EA に適切な修正を加えてください。
- SAE.model は"SAE" モデルと正常化パラメータ "prepr"を持つファイルです。このモデルは最終日92014年10月14日のシンボル EURUSD (M30), でトレーニングされています。トレーニング過程は上で説明しています。
また、R 言語がお手持ちのコンピュータで格納されるディレクトリへの道を忘れないでください。
次の順序は作業を始めるにあたり従うのが望ましいものです。チャート上に EA を配置します。EA を別のシンボルについて配置しようと思ったら、前回起動したサーバーとは異なるポートを指定します。たとえばポート8886 (デフォルトではポート 8888)です。
注意: これはまったく非効率的な方法です。サーバサイズはすべて 120~130 Mb です。これは今物事がある姿です。
通常の EA 初期化後、警告『計算された結果がありません!記号』が表示されます。そして外部パラメータ send = true と共にインディケータをインストールし、インディケータが接続される先のサーバーポート(上記参照)を指定します。すべてが正しく動作すれば、実データ『処理』、精度、K および Kmax が出力文字列に表示され、トレードが開始されます。
処理の効率的な制御はウィンドウズのタスクマネジャーからもっとも促進されます。EA またはインディケータが起動されたあとに Rterm が表示されなければ、R 処理は混乱したということです。その混乱の主な理由はスクリプト内の構文エラー、受信される MQL ベクトル Rterm から抽出されるベクトルの長さの不一致です。
スクリプトは一行ずつ最初から最後まで開始されることで Rstudio 内でデバッグされます。
残念ながら、私はテスタで EA を起動することができず、そのためデモアカウントで検証しなければなりませんでした。
4.3. 質的特性を改善する方法と手段
- 入力で使用されるインディケータの設定を変更します。
- 入力データ正常化方法を変更します。
- 『教師』のパラメータと入力時インディケータを最適化します。
- 2列の行列用入力変数のコードを変更します。予測シグナルをキャリブレートします。
- ネットワークパラメータ(隠れ層のニューロン数、層数、学習レベル、エポック数)を最適化します。
おわりに
SAE からの隠れ層にあるニューロンウェイトの初期化を伴う深層ネットワークモデルを作成、トレーニング、検証をしました。ネットワークはひじょうに迅速に再トレーニングし、トレード処理を混乱させることなく再トレーニングすることを可能にします。
ニューラルネットワークにより示される結果は行列の観点からは平均です。理想的な結果は第一の目標ではありませんでした。
そのようなモデルと効率係数のパラメータ評価を使用することで、モデルはトレード処理を混乱させることなく再トレーニングされ最適化されることが可能です。
添付資料
- SAE.zip -インディケータ、EA と添付ファイル
- R_intro.zip -R 言語および Rstudio についてのロシア語文献
- DeepLearning.zip -深層学習についての文献
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/1103
 MQL5 クックブック:トレードトランザクションイベントの処理
MQL5 クックブック:トレードトランザクションイベントの処理
 貨幣価格変動に対するマクロ経済データの影響の回帰分析
貨幣価格変動に対するマクロ経済データの影響の回帰分析
 MetaTrader マーケットの概要(インフォグラフィック)
MetaTrader マーケットの概要(インフォグラフィック)
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索