ディープニューラルネットワーク(その2)予測変数の変換と選択
内容
はじめに
前稿では、入力データと目標変数の取得と準備のさまざまな側面について検討しました。本稿のスクリプトを実行するには、前稿のスクリプトをすべて実行するか、前稿のRStudioアプリケーションの計算結果を読み込む必要があります。
1. 特徴の生成
特徴の生成とは、手元のデータから追加情報を取得する科学(及び技術)です。ここでの目標は、新しいデータを追加することではなく、すでに持っているものを活用することです。新能力によって、データサンプルの新しい特徴を得ることができ、これらの特徴によって、訓練データセットのより正確なラベル化、特性評価、及び分割が可能になります。これにより、より高い精度が得られます。
この過程は次の2つの段階に分けることができます。
- 変換 - これはシナリオによって、データの正規化、変数の歪みの除去、外れ値の除去、離散化の4種類の変換のいずれかになります。
- 特徴の生成 - 新しい特徴の生成とは既存の変数から新しい変数を抽出することです。これにより、データセット内の隠れた関係が明らかになります。
1.1. 特徴の変換
1.1.1. 変換
変数の変換とは?
データモデリングにおける変換とは変数のその関数による置き換えです。例えば、変数xはxの平方根、立方根または対数に変更できます。言い換えれば、変換とは変数の分布や変数間の関係を変える過程です。
変数の変換がいつ有用であるかを思い出してみましょう。
- より良い理解のために、変数のスケールを変更したりその値を標準化したい場合 - この変換は、異なるデータのスケールが異なる場合に必要で、分布形状の変化をもたらしません。
- 変数間の複雑な非直線関係や曲線関係を直線関係に変換する必要がある場合 - これはより鮮明で、より良い予測機能を提供し、そのような場合、散布図を使用して2つの連続変数間の関係を見つけることができます。このような状況では、通常、対数変換が使用されます。
- より単純な解釈と分析のために、非対称分布を対称分布に変更する必要がある場合 - いくつかのモデル化手法では、変数の正規分布が必要なため、非一様分布に対処する場合には歪度を低減する変換を使用することができます。分布が右への歪みに対しては変数の平方根、立方根または対数をとりますが、左への歪みに対しては二乗/三乗または指数関数を使用して平滑化します。
- 連続変数を離散変数に変換する必要がある場合 - このような変換の方法は、離散化です。
一般的な変換法は?
変数の変換にはさまざまな方法があります。そのうち平方根、立方根、対数、三角関数とセグメンテーションはすでに言及されました。方法のいくつかを詳しく見て、その利点と欠点を特定しましょう。
- 対数 - これは、変数の分布の形状を変更するために使用される一般的な変換法です。これは、通常、右への歪みを減らすために使用されます。この関数は、ゼロと負の値には適用されません。
- 平方根/立方根 - この関数は、対数をとるほど強力ではないものの、変数の分布に大きな影響を与えます。立方根の利点は、ゼロと負の値に使用できることです。平方根は正の値とゼロのみに使用できます。
- 離散化/ビニング - これは値の分類に使用されます。離散化は、元のデータ、百分位数及び頻度に適しています。分類方法の選択は、データの性質に基づいています。相互依存変数のジョイントセグメンテーションを実行することができます。
データのあらゆる変換は、分布の変化につながります。これを説明するために、2つの変換法の例を使用します。
初期データセットの2つの問題は、外れ値と右への歪みです。アウトライアを削除する方法は既に考察されました。さて、非対称性を最初に除去/減少させてから、外れ値の除去を試みましょう。
手法1
xデータセットの右への強い歪みを取り除くためには、底を2とする対数を取って外れ値を取り除きます。初期データセットの変数の値が1よりもずっと小さく、その中に負の値があるので、精度を高めるために、それぞれに1を加えた変数の対数を取ります。曲線に何が起こるかを見てみましょう。
evalq({x.ln <- apply(x, 2, function(x) log2(x + 1))
sk.ln <- skewness(x.ln)},
env)
> env$sk.ln
ftlm stlm rbci pcci v.fatl
Skewness -0.2715663 -2.660613 -4.484301 0.4267873 1.253008
v.satl v.rftl v.rstl v.ftlm v.stlm
Skewness 1.83489 2.065224 -0.0343451 -15.62414 0.01529019
v.pcci
Skewness 0.1811206
stlm、rbci及び v.ftlmの3つの変数では左への歪みが顕著です。v.fatl、v.satl及びv.rftl変数は、依然として右に歪んでいます。他の変数の歪度は均等になっています。このデータセットから外れ値を除去して代入し、変数の歪度と分布を見てみましょう。
evalq({
foreach(i = 1:ncol(x.ln), .combine = "cbind") %do% {
remove_outliers(x.ln[ ,i])
} -> x.ln.out
colnames(x.ln.out) <- colnames(x.ln)
},
env)
evalq({
foreach(i = 1:ncol(x.ln), .combine = "cbind") %do% {
capping_outliers(x.ln[ ,i])
} -> x.ln.cap
colnames(x.ln.cap) <- colnames(x.ln)
},
env)
evalq({
sk.ln.out <- skewness(x.ln.out)
sk.ln.cap <- skewness(x.ln.cap)
},
env)
> env$sk.ln.out
ftlm stlm rbci pcci
Skewness -0.119055 -0.3549119 -0.1099921 -0.01476384
v.fatl v.satl v.rftl v.rstl
Skewness -0.02896319 -0.03634833 -0.06259749 -0.2120127
v.ftlm v.stlm v.pcci
Skewness -0.05819699 -0.01661317 -0.05420077
> env$sk.ln.cap
ftlm stlm rbci pcci
Skewness -0.1814781 -0.4582045 -0.1658855 -0.02849945
v.fatl v.satl v.rftl v.rstl
Skewness -0.04336238 -0.04400781 -0.0692754 -0.2269408
v.ftlm v.stlm v.pcci
Skewness -0.06184128 -0.02856397 -0.06258243
両方のデータセット(x.out及びx.cap)のデータはほぼ対称的です。分布は下の図に示されています。
par(mfrow = c(2,2)) boxplot(env$x.ln, main = "x.ln with outliers", xlab = "") boxplot(env$x.ln.out, main = "x.ln.out without outliers", xlab = "") boxplot(env$x.ln.cap, main = "x.ln.cap with imputed outliers", xlab = "") par(mfrow = c(1,1))
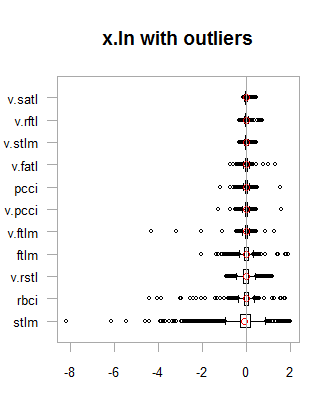

図1 外れ値を含む/含まないログ変換データ
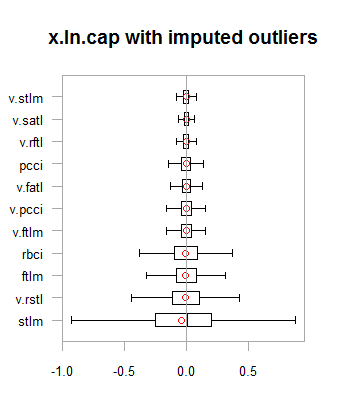
図2 外れ値が補完されたログ変換データ
結果は、1つの例外を除いて、前の変換と非常に似ており、変数の変化の幅が広がっています。
x.ln.capデータフレームを変換してセットの変動と共分散を見てみましょう。
evalq(x.ln.cap %>% tbl_df() %>% cbind(Data = dataSetClean$Data, ., Class = dataSetClean$Class) -> dataSetLnCap, env)
チャートをプロットします。
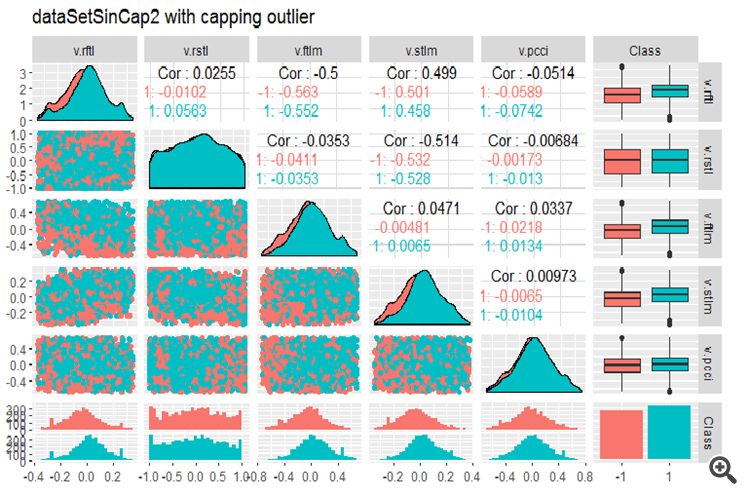
require(GGally) evalq(ggpairs(dataSetLnCap, columns = 2:7, mapping = aes(color = Class), title = "PredLnCap1"), env) evalq(ggpairs(dataSetLnCap, columns = 8:13, mapping = aes(color = Class), title = "PredLnCap2"), env)
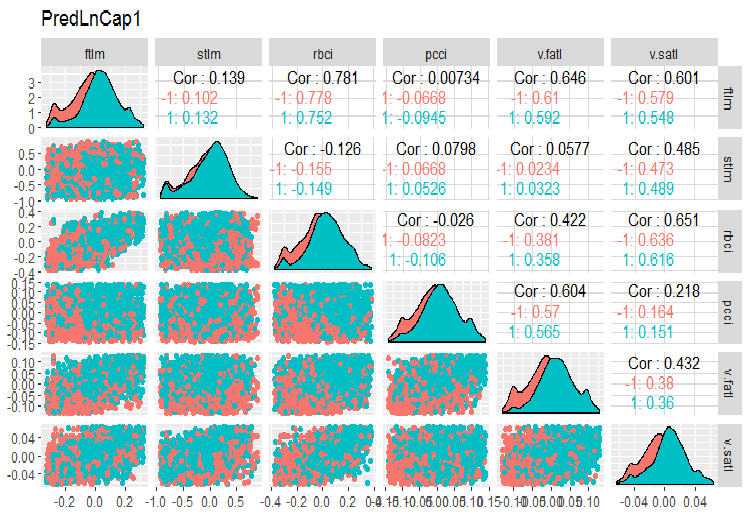
図3 ログ変換されたデータのパラメータ(その1)
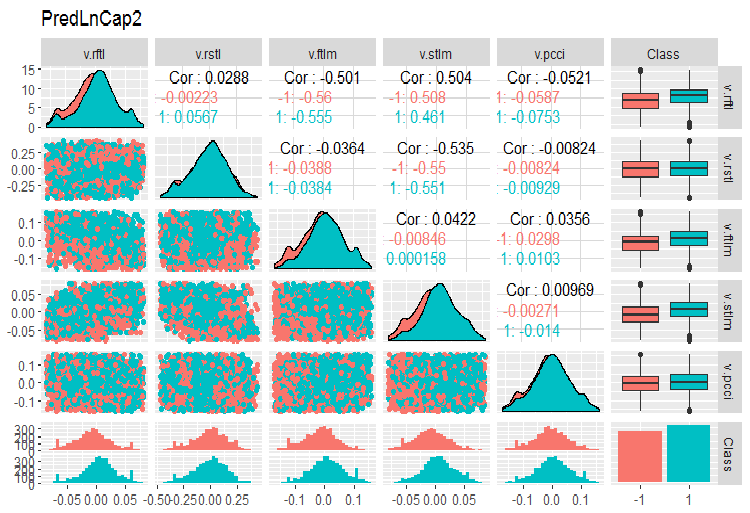
図4 ログ変換されたデータのパラメータ(その2)
手法2
sin(2*pi*x)関数を使用してデータを変換し、外れ値を除去して補完し、歪度、外れ値の分布、及び変換された変数の共変をグラフで評価します。
evalq({x.sin <- apply(x, 2, function(x) sin(2*pi*x))
sk.sin <- skewness(x.sin)
},
env)
#----------
evalq({
foreach(i = 1:ncol(x.sin), .combine = "cbind") %do% {
remove_outliers(x.sin[ ,i])
} -> x.sin.out
colnames(x.sin.out) <- colnames(x.sin)
},
env)
#-----------------
evalq({
foreach(i = 1:ncol(x.sin), .combine = "cbind") %do% {
capping_outliers(x.sin[ ,i])
} -> x.sin.cap
colnames(x.sin.cap) <- colnames(x.sin)
},
env)
#-----------
evalq({
sk.sin.out <- skewness(x.sin.out)
sk.sin.cap <- skewness(x.sin.cap)
},
env)
これらの変換されたデータセットの歪度はどのくらいでしょうか?
env$sk.sin ftlm stlm rbci pcci Skewness -0.02536085 -0.04234074 -0.00587189 0.0009679463 v.fatl v.satl v.rftl v.rstl Skewness 0.03280465 0.5217757 0.05611136 -0.02825112 v.ftlm v.stlm v.pcci Skewness 0.04923953 -0.2123434 0.01738377 > env$sk.sin.out ftlm stlm rbci pcci Skewness -0.02536085 -0.04234074 -0.00587189 0.03532892 v.fatl v.satl v.rftl v.rstl Skewness 0.00360966 -0.02380975 -0.05336561 -0.02825112 v.ftlm v.stlm v.pcci Skewness 0.0009366441 0.01835948 0.0008843329 > env$sk.sin.cap ftlm stlm rbci pcci Skewness -0.02536085 -0.04234074 -0.00587189 0.03283132 v.fatl v.satl v.rftl v.rstl Skewness 0.007588308 -0.02424707 -0.04106469 -0.02825112 v.ftlm v.stlm v.pcci Skewness 0.007003051 0.009237835 0.002101687
ご覧のように、この変換によってすべてのデータセットが対称になりました。これらのセットがどのように見えるかを見てみましょう。
par(mfrow = c(2, 2)) boxplot(env$x.sin, main = "x.sin with outlier") abline(h = 0, col = 2) boxplot(env$x.sin.out, main = "x.sin.out without outlier") abline(h = 0, col = 2) boxplot(env$x.sin.cap, main = "x.sin.cap with capping outlier") abline(h = 0, col = 2) par(mfrow = c(1, 1))
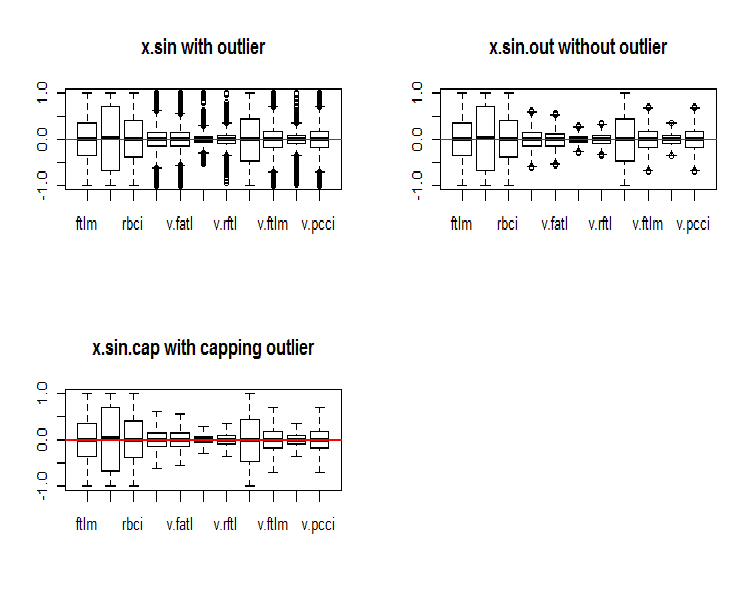
図5 sin()関数で変換されたデータセット
一見すると、これらのデータセットは以前のもの(初期のものと変換されたもの)よりも見栄えがよくなります。
さて、外れ値が取り除かれた後の変数におけるNAの分布を見たいと思います。
require(VIM)
evalq(a <- aggr(x.sin.out), env)
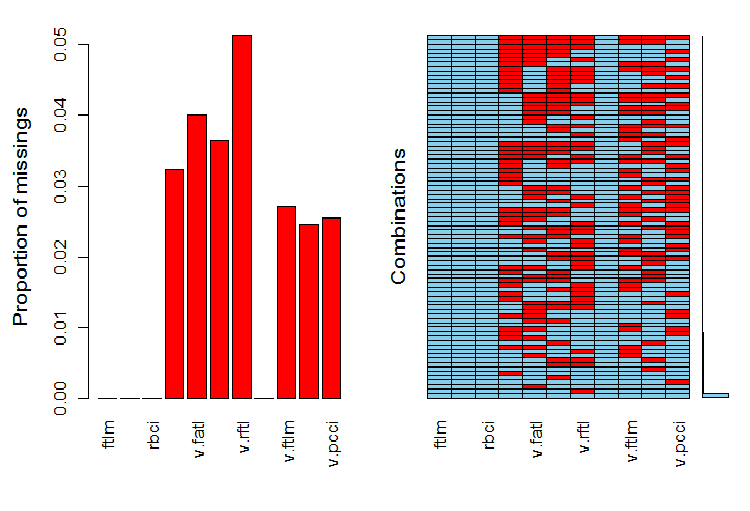
図6 データセットにおけるNAの分布
左のグラフは各変数の未定義データの相対的な数を示しています。右には異なる数のNA(下から上へ)の例の組み合わせが示されています。値は次のとおりです。
> print(env$a) Missings in variables: Variable Count pcci 256 v.fatl 317 v.satl 289 v.rftl 406 v.ftlm 215 v.stlm 194 v.pcci 201
変数でのNAの分布はどうでしょうか?
par(mfrow = c(3, 4)) evalq( foreach(i = 1:ncol(x.sin.out)) %do% { barMiss(x.sin.out, pos = i, only.miss = TRUE, main = "x.sin.out without outlier") }, env ) par(mfrow = c(1, 1))
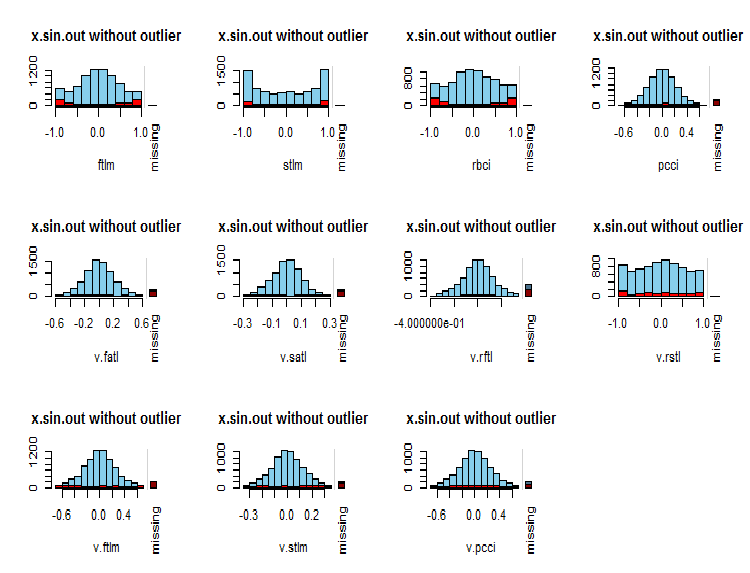
図7 変数でのNAの分布
観測された変数の値は青、現在の変数の値の異なる範囲内の他の変数のNAの数は赤で示されます。右側のバーは、現在の変数がすべての変数のNAの総数に占める割合を表します。
最後に、補完された外れ値を持つ変換されたデータセットの変動と共分散を見てみましょう。
#--------------- evalq(x.sin.cap %>% tbl_df() %>% cbind(Data = dataSetClean$Data, ., Class = dataSetClean$Class) -> dataSetSinCap, env) require(GGally) evalq(ggpairs(dataSetSinCap, columns = 2:7, mapping = aes(color = Class), title = "dataSetSinCap1 with capping outlier "), env) evalq(ggpairs(dataSetSinCap, columns = 8:13, mapping = aes(color = Class), title = "dataSetSinCap2 with capping outlier"), env) #---------------------------
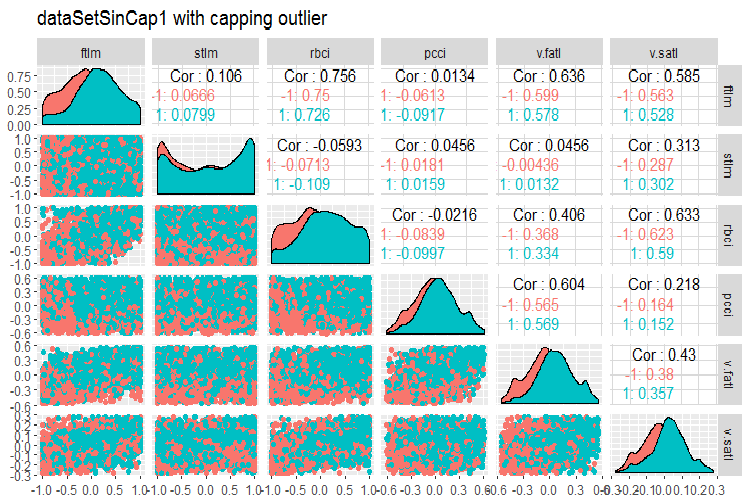
図8 sin()で変換されたデータのパラメータ(その1)
図9 sin()で変換されたデータのパラメータ(その2)
1.1.2. 正規化
ここではニューラルネットワークのためのデータを準備しているので、変数は{-1 .. + 1}の範囲内に収める必要があります。これにはpreProcess()::caret関数がmethod = “spatialSign”で使用されます。あるいは、データは正規化される前に中心に置くかスケーリングすることができます。この過程は非常に単純であり、本稿では考慮しません。
しかし、心に留めておくべきことが1つあります。訓練データセットから得られた正規化のパラメータは、テストセットと検証セットに使用されます。
前回の計算で得られたデータセット(相関性の高い値を削除しないdataSet)をさらに活用するために、 訓練/テスト/検証に分割して標準化せずに (-1,+1) の範囲に収めましょう。
標準化による正規化を実行する際には、正規化パラメータ(平均/中央値、sd/mad)が定義されている場合、補完された外れ値のパラメータも定義する必要があることに留意してください。それらは今後は訓練/テスト/検証に使用されます。本稿前半ではprep.outlier()とtreatOutlier()の2つの関数を記述しました。それらはこの目的のために設計されています。
操作の順序は下記の通りです。
- 訓練で外れ値パラメータを定義する
- 訓練で外れ値を除去する
- 訓練で標準化パラメータを定義する
- 訓練/テスト/検証で外れ値を補完する
- 訓練/テスト/検証を正規化する
ここではこのバリアントは考慮されないので、各自でお勉強ください。
データを訓練/テスト/検証に分けます。
evalq(
{
train = 1:2000
val = 2001:3000
test = 3001:4000
DT <- list()
list(clean = data.frame(dataSet) %>% na.omit(),
train = clean[train, ],
val = clean[val, ],
test = clean[test, ]) -> DT
}, env)
訓練セットの正規化パラメータを定義して訓練/テスト/検証で外れ値を正規化します。
require(foreach)
evalq(
{
preProcess(DT$train, method = "spatialSign") -> preproc
list(train = predict(preproc, DT$train),
val = predict(preproc, DT$val),
test = predict(preproc, DT$test)
) -> DTn
},
env)
下記で訓練セットの総統計を見てみましょう。
> table.Stats(env$DTn$train %>% tk_xts()) Using column `Data` for date_var. ftlm stlm rbci pcci Observations 2000.0000 2000.0000 2000.0000 2000.0000 NAs 0.0000 0.0000 0.0000 0.0000 Minimum -0.5909 -0.7624 -0.6114 -0.8086 Quartile 1 -0.2054 -0.2157 -0.2203 -0.2110 Median 0.0145 0.0246 0.0147 0.0068 Arithmetic Mean 0.0070 0.0190 0.0085 0.0028 Geometric Mean -0.0316 -0.0396 -0.0332 -0.0438 Quartile 3 0.2139 0.2462 0.2341 0.2277 Maximum 0.6314 0.8047 0.7573 0.7539 SE Mean 0.0060 0.0073 0.0063 0.0065 LCL Mean (0.95) -0.0047 0.0047 -0.0037 -0.0100 UCL Mean (0.95) 0.0188 0.0333 0.0208 0.0155 Variance 0.0719 0.1058 0.0784 0.0848 Stdev 0.2682 0.3252 0.2800 0.2912 Skewness -0.0762 -0.0221 -0.0169 -0.0272 Kurtosis -0.8759 -0.6688 -0.8782 -0.7090 v.fatl v.satl v.rftl v.rstl Observations 2000.0000 2000.0000 2000.0000 2000.0000 NAs 0.0000 0.0000 0.0000 0.0000 Minimum -0.5160 -0.5943 -0.6037 -0.7591 Quartile 1 -0.2134 -0.2195 -0.1988 -0.2321 Median 0.0015 0.0301 0.0230 0.0277 Arithmetic Mean 0.0032 0.0151 0.0118 0.0177 Geometric Mean -0.0323 -0.0267 -0.0289 -0.0429 Quartile 3 0.2210 0.2467 0.2233 0.2657 Maximum 0.5093 0.5893 0.6714 0.7346 SE Mean 0.0058 0.0063 0.0062 0.0074 LCL Mean (0.95) -0.0082 0.0028 -0.0003 0.0033 UCL Mean (0.95) 0.0146 0.0274 0.0238 0.0321 Variance 0.0675 0.0783 0.0757 0.1083 Stdev 0.2599 0.2798 0.2751 0.3291 Skewness -0.0119 -0.0956 -0.0648 -0.0562 Kurtosis -1.0788 -1.0359 -0.7957 -0.7275 v.ftlm v.stlm v.rbci v.pcci Observations 2000.0000 2000.0000 2000.0000 2000.0000 NAs 0.0000 0.0000 0.0000 0.0000 Minimum -0.5627 -0.6279 -0.5925 -0.7860 Quartile 1 -0.2215 -0.2363 -0.2245 -0.2256 Median -0.0018 0.0092 -0.0015 -0.0054 Arithmetic Mean -0.0037 0.0036 -0.0037 0.0013 Geometric Mean -0.0426 -0.0411 -0.0433 -0.0537 Quartile 3 0.2165 0.2372 0.2180 0.2276 Maximum 0.5577 0.6322 0.5740 0.9051 SE Mean 0.0061 0.0065 0.0061 0.0070 LCL Mean (0.95) -0.0155 -0.0091 -0.0157 -0.0124 UCL Mean (0.95) 0.0082 0.0163 0.0082 0.0150 Variance 0.0732 0.0836 0.0742 0.0975 Stdev 0.2706 0.2892 0.2724 0.3123 Skewness 0.0106 -0.0004 -0.0014 0.0232 Kurtosis -1.0040 -1.0083 -1.0043 -0.4159
この表によって、変数が対称で、非常に近いパラメータを持っていることがわかります。
次に訓練/テスト/検証セットの変数の分布を見てみましょう。
boxplot(env$DTn$train %>% dplyr::select(-c(Data, Class)), horizontal = T, main = "Train") abline(v = 0, col = 2) boxplot(env$DTn$test %>% dplyr::select(-c(Data, Class)), horizontal = T, main = "Test") abline(v = 0, col = 2) boxplot(env$DTn$val %>% dplyr::select(-c(Data, Class)), horizontal = T, main = "Val") abline(v = 0, col = 2)
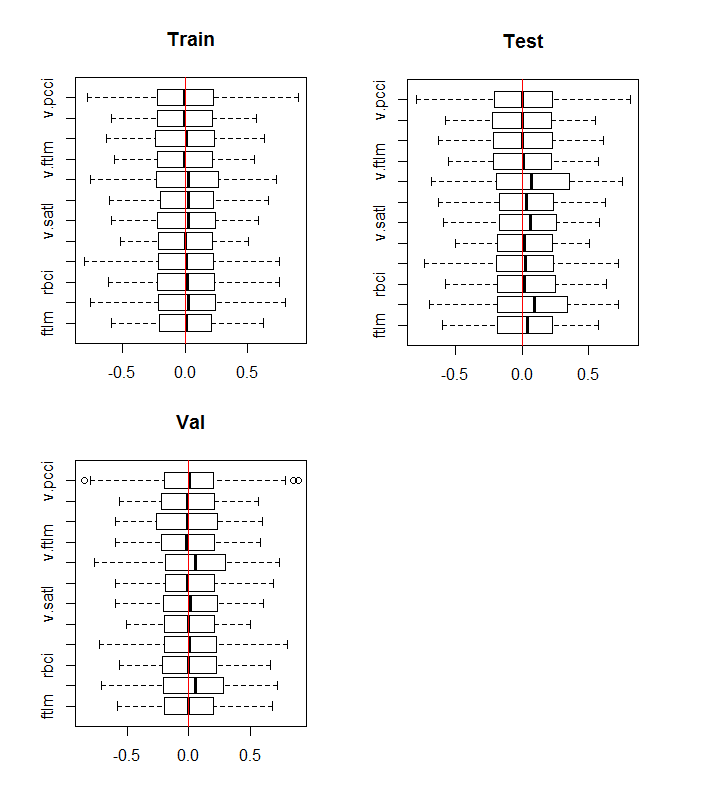
図10 正規化後の訓練/テスト/検証セットの変数の分布
分布はすべてのセットでほぼ同じです。ここでは訓練セットの変数の相関と共分散を考慮する必要もあります。
require(GGally) evalq(ggpairs(DTn$train, columns = 2:7, mapping = aes(color = Class), title = "DTn$train1 "), env) evalq(ggpairs(DTn$train, columns = 8:14, mapping = aes(color = Class), title = "DTn$train2"), env)
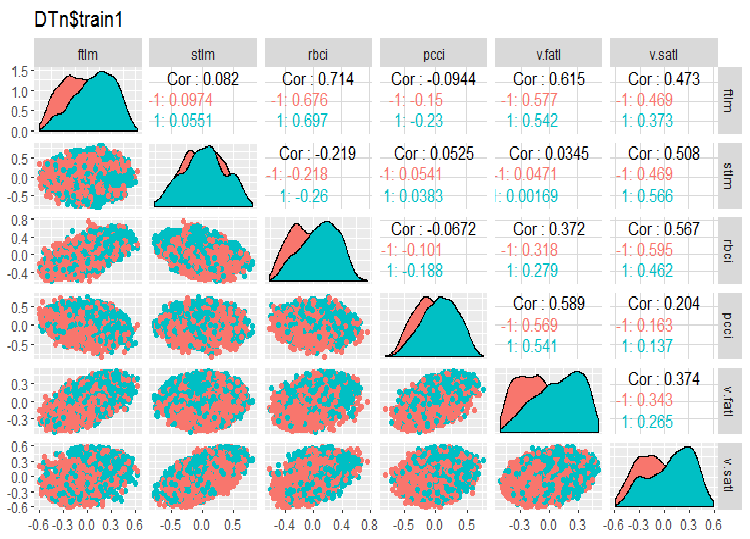
図11 訓練セット1の変動と共分散
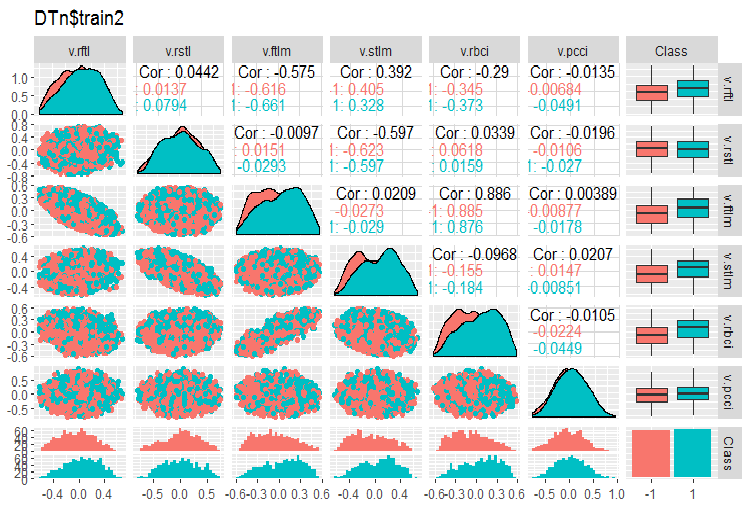
図12 訓練セット2の変動と共分散
相関の高いデータはなく、分布は詰まっており、外れ値もありません。データはうまく分割できます。stlm変数とv.rstl変数には問題がありますがそれだけです。これについては、予測変数の関連性を評価する際に後で確認します。ここで、これらの予測変数と目標変数の相関関係を見ることができます。
> funModeling::correlation_table(env$DTn$train %>% tbl_df %>% + select(-Data), str_target = 'Class') Variable Class 1 Class 1.00 2 v.fatl 0.38 3 ftlm 0.34 4 rbci 0.28 5 v.rbci 0.28 6 v.satl 0.27 7 pcci 0.24 8 v.ftlm 0.22 9 v.stlm 0.22 10 v.rftl 0.18 11 v.pcci 0.08 12 stlm 0.03 13 v.rstl -0.01名前付き変数はテーブルの最下部にあり、相関係数は非常に小さいです。v.pcci.変数の関連性も検証する必要があります。訓練/テスト/検証セットのv.fatl変数を確認しましょう。
require(ggvis) evalq( DTn$train %>% ggvis(~v.fatl, fill = ~Class) %>% group_by(Class) %>% layer_densities() %>% add_legend("fill", title = "DTn$train$v.fatl"), env) evalq( DTn$val %>% ggvis(~v.fatl, fill = ~Class) %>% group_by(Class) %>% layer_densities() %>% add_legend("fill", title = "DTn$val$v.fatl"), env) evalq( DTn$test %>% ggvis(~v.fatl, fill = ~Class) %>% group_by(Class) %>% layer_densities() %>% add_legend("fill", title = "DTn$test$v.fatl"), env)
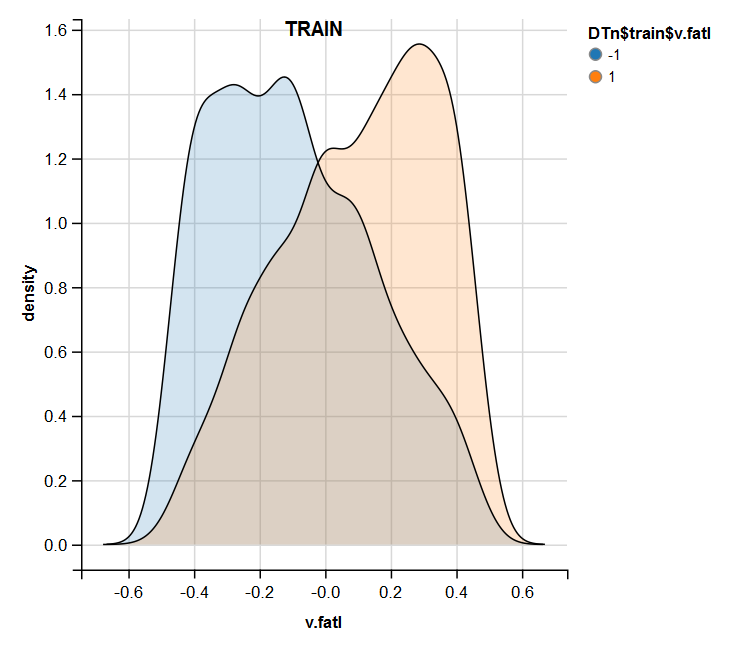
図13 正規化後の訓練セットにおけるv.fatal変数の分布
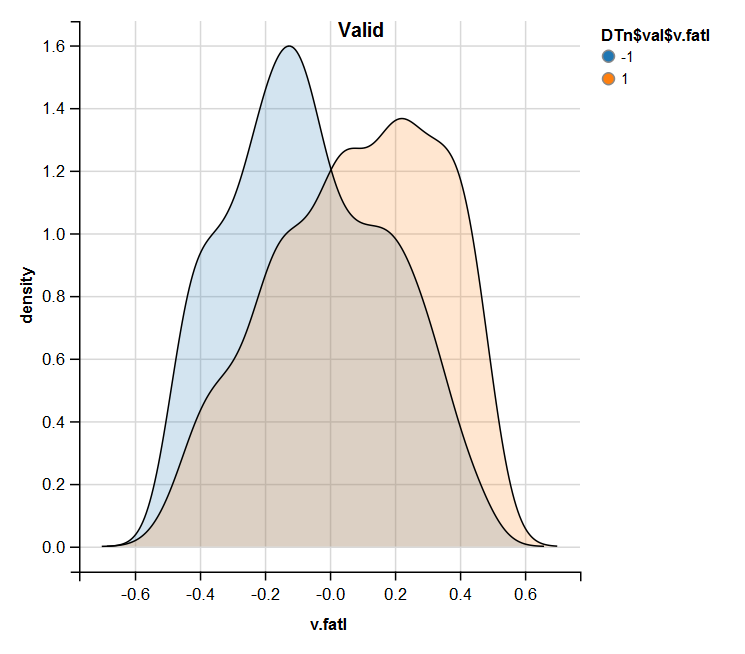
図14 正規化後の有効なセットにおけるv.fatal変数の分布
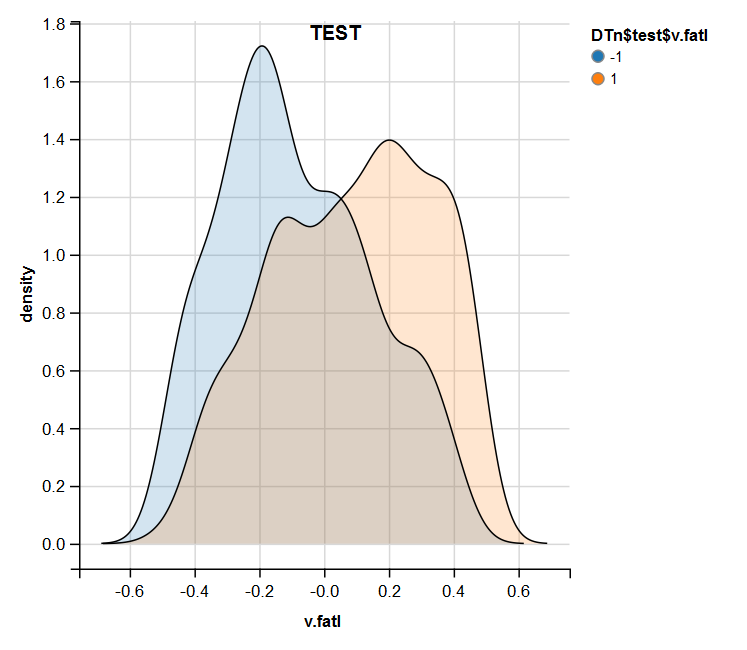
図15 正規化後のテストセットにおけるv.fatal変数の分布
正規化では外れ値や相関の高いデータがない予測変数がよく生成されることは分析によってわかります。大きくは、これは生データの特徴に依存します。
1.1.3. 離散化
離散化とは連続変数値を領域に分割して離散変数に変換する過程を指します。これらの領域の境界はさまざまな方法で設定できます。
分離方法は、目標変数との関係を含まない定量的方法と目標変数の範囲を考慮する方法の2つのグループに分けることができます。
最初のメソッド群はcut2()::Hmisc関数によってほぼ完全にカバーされています。サンプルは、指定された境界線を有する予め設定された数の領域、四分位数、それぞれについて最小限の数の例を有する領域、及び等価な領域に分割することができます。
第2の方法群は、変数を目標変数のレベルと関連する領域に分割するので、より興味深いものです。これらの方法を実現するいくつかのパッケージについて考察してみましょう。
離散化。このパッケージは、トレーナー付きの離散化アルゴリズムのセットです。これは「上から下へ」及び「下から上へ」でグループ化することも可能で離散化のアルゴリズムを実装します。dataSetの例についていくつか考えてみましょう。
最初は、(相関の高い変数を削除せずに)セットを消去し、それを2000/1000/1000の比率で訓練/テスト/検証セットに分割します。
require(discretization)
require(caret)
require(pipeR)
evalq(
{
dataSet %>%
preProcess(.,
method = c("zv", "nzv", "conditionalX")) %>%
predict(., dataSet) %>%
na.omit -> dataSetClean
train = 1:2000
val = 2001:3000
test = 3001:4000
DT <- list()
list(train = dataSetClean[train, ],
val = dataSetClean[val, ],
test = dataSetClean[test, ]) -> DT
},
env)
最小記述長を使用して離散化を記述するmdlp()::discretization関数を使用します。この関数は、最小記述長を停止規則として、エントロピー基準によって行列の連続属性を離散化します。
evalq(
pipeline({
DT$train
select(-Data)
as.data.frame()
mdlp()}) -> mdlp.train, envir = env)
この関数は、2つのスロットを持つリストを返します。それらはcutp(各変数の分割点を持つデータフレーム)とDisc.data(ラベル付き変数を持つデータフレーム)です。
> env$mdlp.train%>%str() List of 2 $ cutp :List of 12 ..$ : num [1:2] -0.0534 0.0278 ..$ : chr "All" ..$ : num -0.0166 ..$ : num [1:2] -0.0205 0.0493 ..$ : num [1:3] -0.0519 -0.0055 0.019 ..$ : num 0.000865 ..$ : num -0.00909 ..$ : chr "All" ..$ : num 0.0176 ..$ : num [1:2] -0.011 0.0257 ..$ : num [1:3] -0.03612 0.00385 0.03988 ..$ : chr "All" $ Disc.data:'data.frame': 2000 obs. of 13 variables: ..$ ftlm : int [1:2000] 3 3 3 3 3 2 1 1 1 1 ... ..$ stlm : int [1:2000] 1 1 1 1 1 1 1 1 1 1 ... ..$ rbci : int [1:2000] 2 2 2 2 2 2 1 1 1 1 ... ..$ pcci : int [1:2000] 2 2 1 2 2 1 1 2 3 2 ... ..$ v.fatl: int [1:2000] 4 4 3 4 3 1 1 2 3 2 ... ..$ v.satl: int [1:2000] 1 1 1 2 2 1 1 1 1 1 ... ..$ v.rftl: int [1:2000] 1 2 2 2 2 2 2 2 1 1 ... ..$ v.rstl: int [1:2000] 1 1 1 1 1 1 1 1 1 1 ... ..$ v.ftlm: int [1:2000] 2 2 1 1 1 1 1 1 2 1 ... ..$ v.stlm: int [1:2000] 1 1 1 2 2 1 1 1 1 1 ... ..$ v.rbci: int [1:2000] 4 4 3 3 2 1 1 2 3 2 ... ..$ v.pcci: int [1:2000] 1 1 1 1 1 1 1 1 1 1 ... ..$ Class : Factor w/ 2 levels "-1","1": 2 2 2 2 2 1 1 1 1 1 ...
最初のスロットでは何がわかるでしょうか?
目標変数に接続されていない値を持つ3つのラベルなしの変数があります。これらは2、8及び12 (stlm、v.rstl、v.pcci)で、データセットの品質を損なうことなく削除できます。これらの変数は以前は不適切だと定義されていました。
4つの変数を2つのクラスに分け、3つの変数を3つのクラスに分け、2つの変数を4つのクラスに分けます。
訓練セットから得られた分割点を使用して検証/テストセットを分割します。そのためには、訓練セットからラベルのない変数を削除してtrain.dデータフレームに保存します。その後findInterval()関数を使って、以前に得られた分割点を使用して検証/テストセットにラベルをつけます。
evalq(
{
mdlp.train$cutp %>%
lapply(., function(x) is.numeric(x)) %>%
unlist -> idx # bool
#----train-----------------
mdlp.train$Disc.data[ ,idx] -> train.d
#---test------------
DT$test %>%
select(-c(Data, Class)) %>%
as.data.frame() -> test.d
foreach(i = 1:length(idx), .combine = 'cbind') %do% {
if (idx[i]) {findInterval(test.d[ ,i],
vec = mdlp.train$cutp[[i]],
rightmost.closed = FALSE,
all.inside = F,
left.open = F)}
} %>% as.data.frame() %>% add(1) %>%
cbind(., DT$test$Class) -> test.d
colnames(test.d) <- colnames(train.d)
#-----val-----------------
DT$val %>%
select(-c(Data, Class)) %>%
as.data.frame() -> val.d
foreach(i = 1:length(idx), .combine = 'cbind') %do% {
if (idx[i]) {findInterval(val.d[ ,i],
vec = mdlp.train$cutp[[i]],
rightmost.closed = FALSE,
all.inside = F,
left.open = F)}
} %>% as.data.frame() %>% add(1) %>%
cbind(., DT$val$Class) -> val.d
colnames(val.d) <- colnames(train.d)
},env
)
これらのセットはどのように見えるでしょうか?
> env$train.d %>% head() ftlm rbci pcci v.fatl v.satl v.rftl v.ftlm v.stlm v.rbci Class 1 3 2 2 4 1 1 2 1 4 1 2 3 2 2 4 1 2 2 1 4 1 3 3 2 1 3 1 2 1 1 3 1 4 3 2 2 4 2 2 1 2 3 1 5 3 2 2 3 2 2 1 2 2 1 6 2 2 1 1 1 2 1 1 1 -1 > env$test.d %>% head() ftlm rbci pcci v.fatl v.satl v.rftl v.ftlm v.stlm v.rbci Class 1 1 1 1 2 1 1 1 1 2 -1 2 1 1 3 3 1 1 2 2 3 -1 3 1 1 2 2 1 1 1 2 2 -1 4 2 1 2 3 1 1 2 2 3 1 5 2 2 2 3 1 1 1 2 3 1 6 2 2 2 4 1 1 2 2 3 1 > env$val.d %>% head() ftlm rbci pcci v.fatl v.satl v.rftl v.ftlm v.stlm v.rbci Class 1 2 2 2 2 2 2 1 2 2 1 2 2 2 2 2 2 2 1 2 2 1 3 2 2 2 3 2 2 1 2 2 1 4 2 2 2 4 2 2 2 2 3 1 5 2 2 2 3 2 2 1 2 2 1 6 2 2 2 3 2 2 2 2 2 1 > env$train.d$v.fatl %>% table() . 1 2 3 4 211 693 519 577 > env$test.d$v.fatl %>% table() . 1 2 3 4 49 376 313 262 > env$val.d$v.fatl %>% table() . 1 2 3 4 68 379 295 258
離散データを含むセットの使用は、使用するモデルによって異なります。これがニューラルネットワークである場合、予測変数はダミー変数に変換する必要があります。これらのクラスはこれらの変数でどれだけうまく分けられるでしょうか?それらはどのように目標変数と相関してるのでしょうか?これらの関係を cross-plot()::funModelingで視覚化しましょう。Cross_plotは、入力変数が各入力の各範囲の尤度係数を受け取る目標変数とどのように相関するかを示します。
v.fatl、ftlm及びv.satlの3つの変数をそれぞれ4、3及び2の範囲に分けて考えてみましょう。チャートをプロットします。
evalq(
cross_plot(data = train.d,
str_input = c("v.fatl", "ftlm", "v.satl"),
str_target = "Class",
auto_binning = F,
plot_type = "both"), #'quantity' 'percentual'
env
)
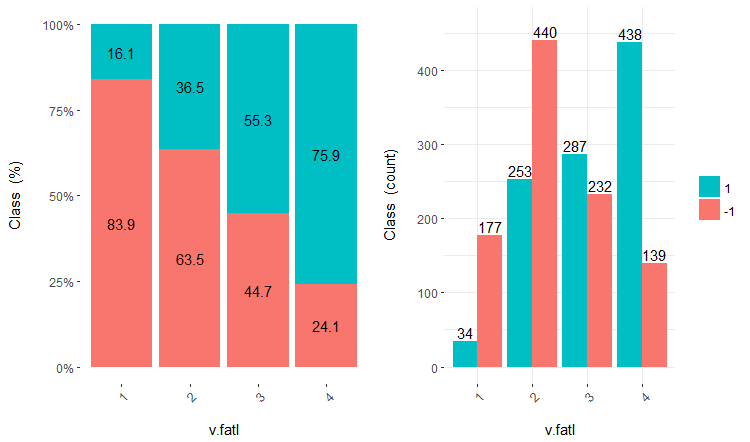
図16 v.fatl/クラス変数のクロスプロット
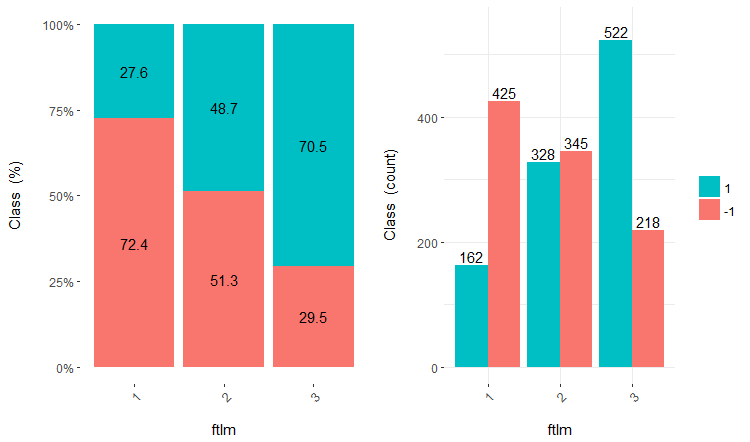
図17 ftlm/クラス変数のクロスプロット
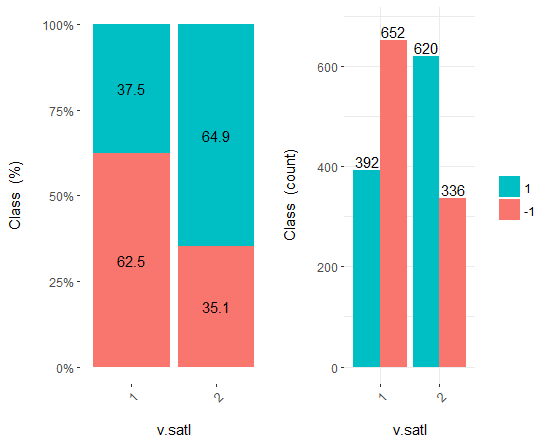
図18 v.satl/クラス変数のクロスプロット
予測変数は目標変数のレベルとよく相関しており、クラス変数のレベルを分ける明確な閾値があることがわかります。
予測変数がどのような場合に目標変数と相関するかを見るために、(最適ではない方法で)等しい領域に単純に分割することができます。前の3つの変数と2つの悪い変数(stlm、v.rstl) を訓練セットから10の平等なエリアに分け、それらのクロスプロットを目標変数とで見てみましょう。
evalq(
cross_plot(
DT$train %>% select(-Data) %>%
select(c(v.satl, ftlm, v.fatl, stlm, v.rstl, Class)) %>%
as.data.frame(),
str_input = Cs(v.satl, ftlm, v.fatl, stlm, v.rstl),
str_target = "Class",
auto_binning = T,
plot_type = "both"), #'quantity' 'percentual'
env
)
これらの変数の5つのグラフをプロットします。
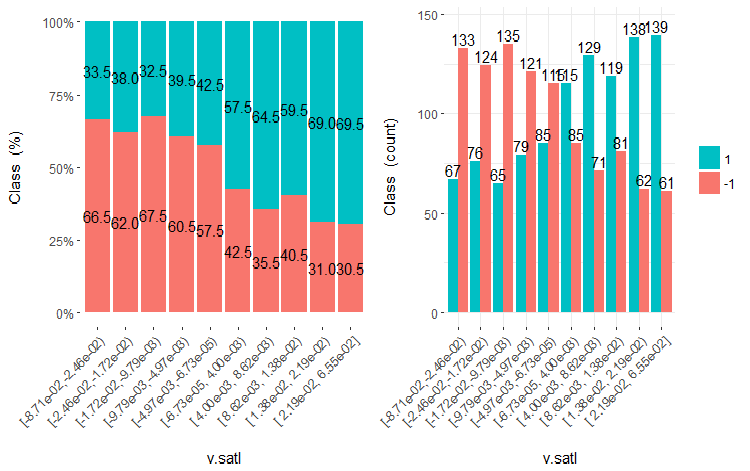
図19 v.satl変数vsクラスのクロスプロット(10領域)
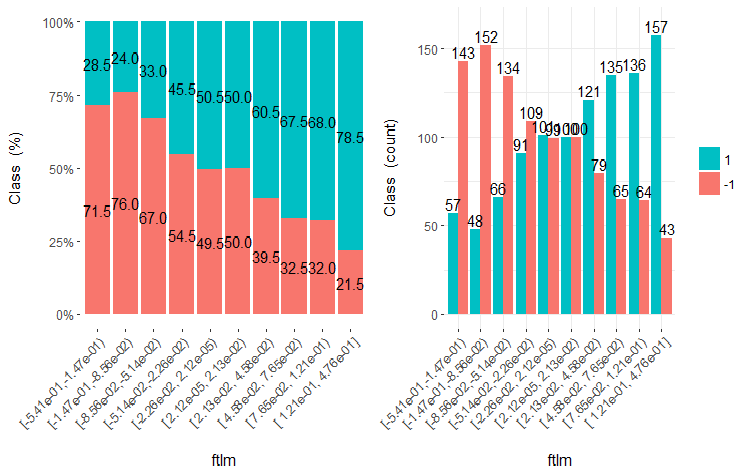
図20 ftlml変数vsクラスのクロスプロット(10領域)
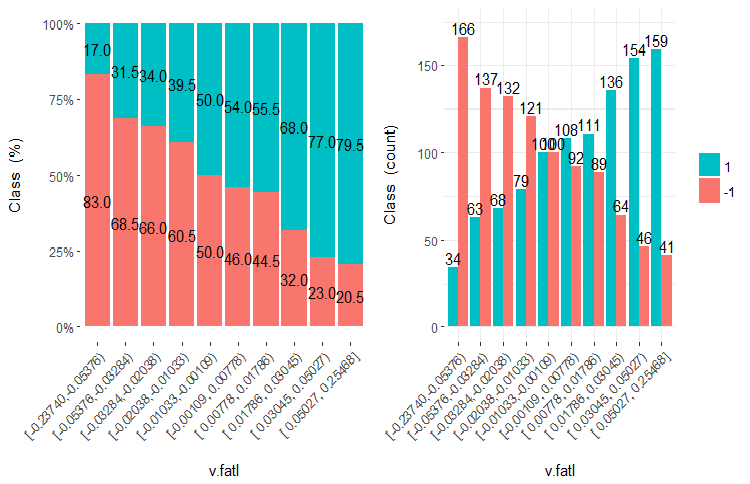
図21 v.fatl変数vsクラスのクロスプロット(10領域)
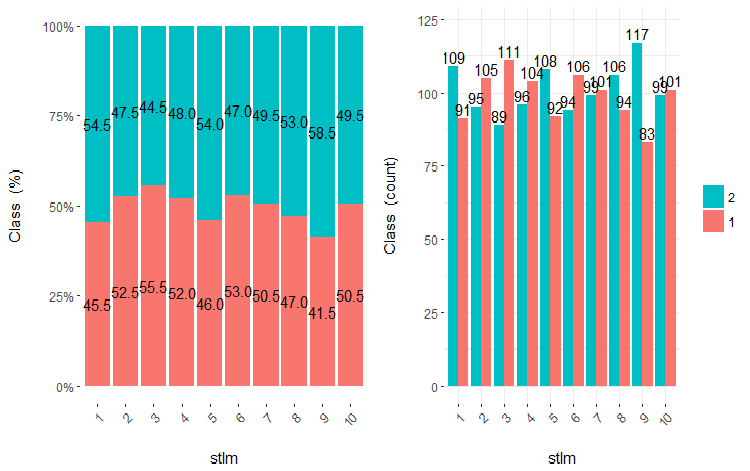
図22 stlm変数vsクラスのクロスプロット(10領域)
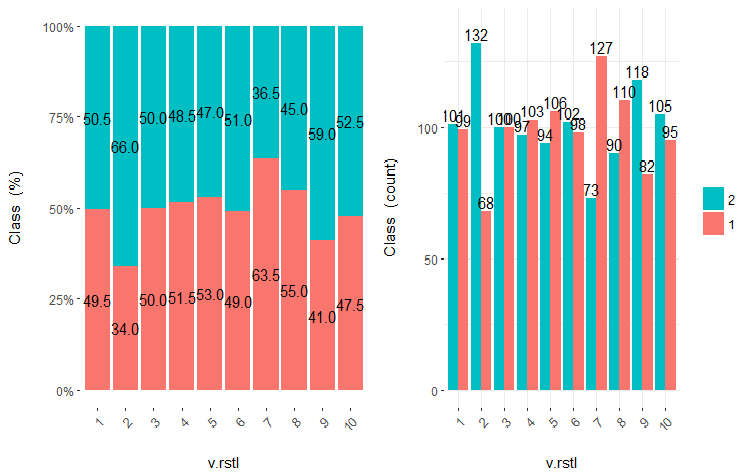
図23 v.rstl変数vsクラスのクロスプロット(10領域)
この図から明らかなように、変数を10個の別々の等価領域に分割しても、v.fatl、ftlm及びv.satl変数には、変数のレベルを分割する際の明確な閾値があります。他の2つの変数 (stlm、v.rstl) が何故不適切なのかは明らかです。これは、予測変数の重要性を識別する効率的な方法です。これには本稿の後半で戻ってきます。
さて、入力変数が目標変数とどのように相関するかをベイズ法事後変換率を使用して比較してみましょう。内部の順序を持たないカテゴリ値を比較すると便利です。このためにはbayes_plot::funModeling関数を使用します。v.fatl、ftlm及びv.satl変数をtrain.d、val.d、test.dの各セットから取得します。
#------BayesTrain------------------- evalq( { bayesian_plot(train.d, input = "v.fatl", target = "Class", title = "Bayesian comparison train$v.fatl/Class", plot_all = F, extra_above = 5, extra_under = 5) },env ) evalq( { bayesian_plot(train.d, input = "ftlm", target = "Class", title = "Bayesian comparison train$ftlm/Class", plot_all = F, extra_above = 5, extra_under = 5) },env ) evalq( { bayesian_plot(train.d, input = "v.satl", target = "Class", title = "Bayesian comparison train$v.satl/Class", plot_all = F, extra_above = 5, extra_under = 5) },env ) #------------Bayesテスト------------------------ evalq( { bayesian_plot(test.d, input = "v.fatl", target = "Class", title = "Bayesian comparison test$v.fatl/Class", plot_all = F, extra_above = 5, extra_under = 5) },env ) evalq( { bayesian_plot(test.d, input = "ftlm", target = "Class", title = "Bayesian comparison test$ftlm/Class", plot_all = F, extra_above = 5, extra_under = 5) },env ) evalq( { bayesian_plot(test.d, input = "v.satl", target = "Class", title = "Bayesian comparison test$v.satl/Class", plot_all = F, extra_above = 5, extra_under = 5) },env ) #-------------BayesVal--------------------------------- evalq( { bayesian_plot(val.d, input = "v.fatl", target = "Class", title = "Bayesian comparison val$v.fatl/Class", plot_all = F, extra_above = 5, extra_under = 5) },env ) evalq( { bayesian_plot(val.d, input = "ftlm", target = "Class", title = "Bayesian comparison val$ftlm/Class", plot_all = F, extra_above = 5, extra_under = 5) },env ) evalq( { bayesian_plot(val.d, input = "v.satl", target = "Class", title = "Bayesian comparison val$v.satl/Class", plot_all = F, extra_above = 5, extra_under = 5) },env ) #------------------------------------------
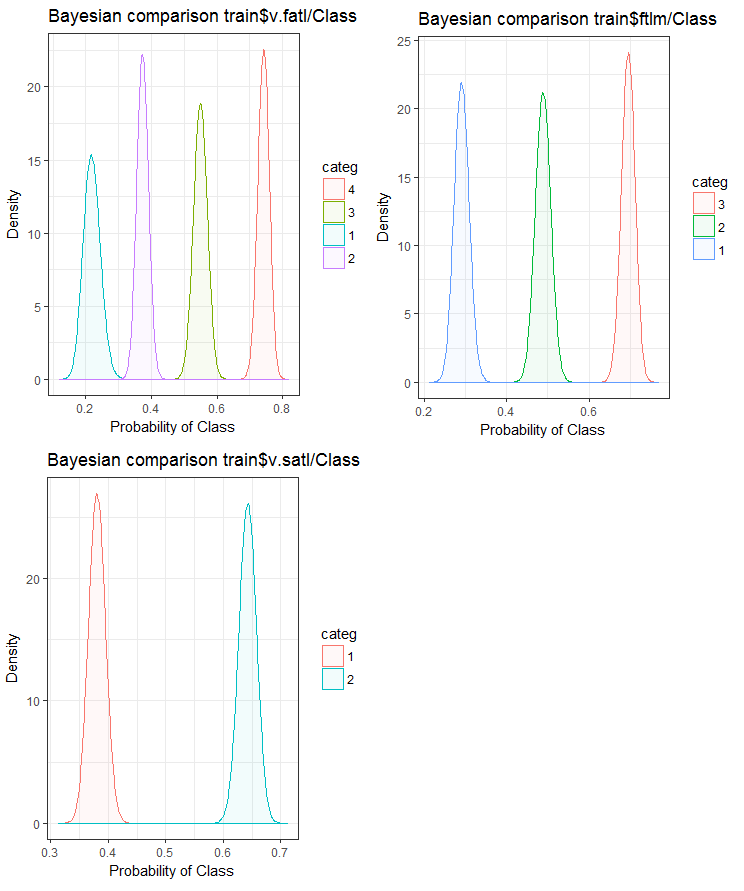
図24 訓練セットにおける目標変数と変数のベイジアン比較
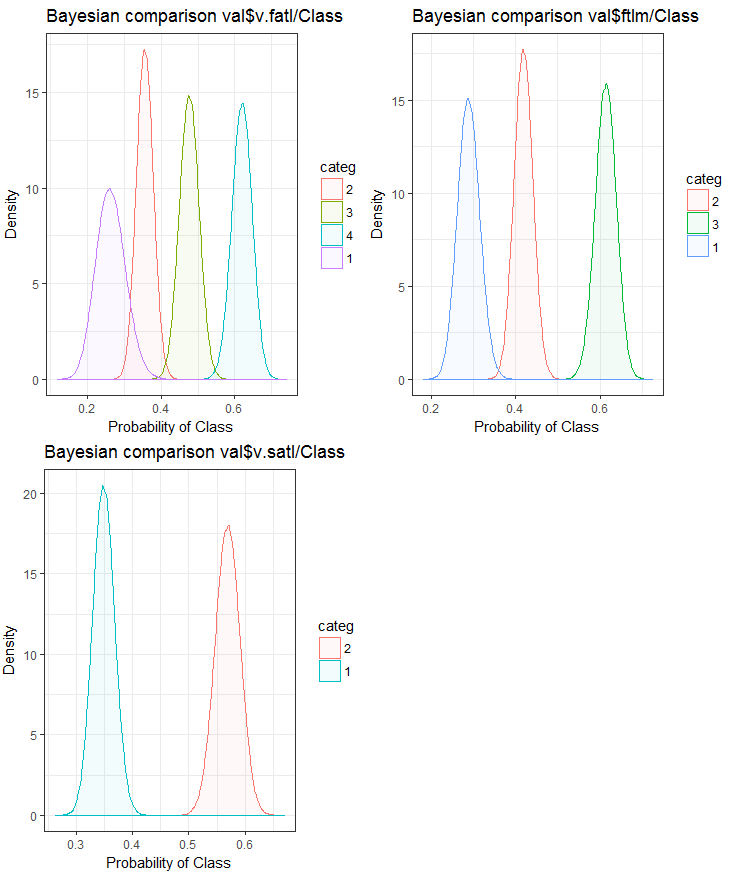
図25 検証セットにおける目標変数と変数のベイジアン比較
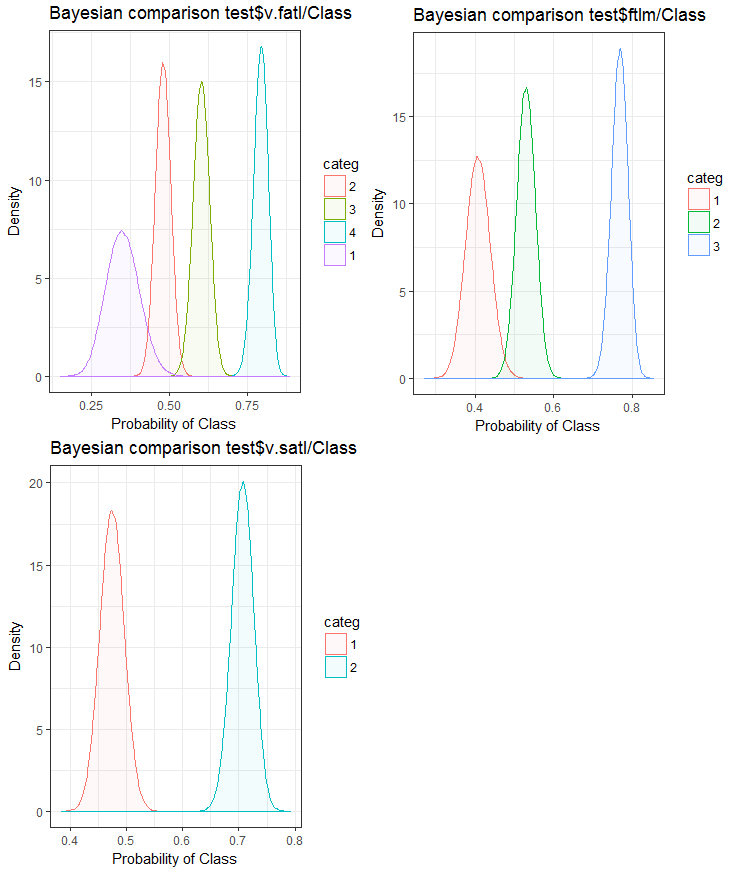
図26 テストセットにおける目標変数と変数のベイジアン比較
予測変数と目標変数との相関関係は、4つ以上のレベルの変数でより多く横滑りしていることがわかります。この動向は、2つのグループを持つ変数においてはより小さいものです。今後は、2範囲の予測変数のみを使用することによって、モデルの精度がどのように影響を受けるかを調べることが役立ちます。
変数を目標変数のレベルに近似した領域に分割するという同じタスクはsmbinningパッケージを使うことで別の方法で解決できます。ご自身でお確かめください。前稿は、別の興味深い離散化方法を検討しています。これは"RoughSets"パッケージを使って実装できます。
離散化は、予測変数を変換する効率的な方法です。残念ながら、すべてのモデルが因子予測変数で作業できるわけではありません。
1.2. 新しい特徴の生成
変数の作成とは、既存の変数に基づいて新しい変数を作成する過程です。日付(dd-mm-yy)が入力変数であるデータセットを見てみましょう。日、月、年、曜日のように、目標変数とよりよく関連する新しい変数の作成が可能です。このステップは、変数内の隠れた関係を明らかにするために使用されます。
派生変数の作成とは、関数のセットとさまざまな手法を使用して既存の変数から新しい変数を作成する過程を指します。どのような変数を作成するかは、ビジネスアナリストの好奇心、仮説セット、及び理論的知識に依存します。方法の選択は多数です。対数を取る、セグメンテーション、n乗するといったものは、変換方法のほんの一例に過ぎません。
ダミー変数の作成は、変数を扱うもう一つの一般的な方法です。ダミー変数は通常、カテゴリ変数を数値変数に変換する際に使用されます。カテゴリ変数は0と1の値をとることができます。ダミー変数はNとN-1変数を持つカテゴリ変数の2つ以上のクラスに対して作成できます。
本稿では、アナリストとして毎日遭遇する状況について説明します。以下に、データセットから最大の情報を抽出するいくつかの方法を示します。
- 変数としてデータと時刻の値を使用します。新しい変数は、日付と時刻の違いを考慮して作成できます。
- 新しい比率と比率を作成します。過去の入力と出力をデータセットに格納するのではなく、その比率を含めることができます。これはより重要な意味を持つかもしれません。
- 標準的な変換を使用します。変数の変動と領域を出力とともに見ると、基本的な変換の後に相関が改善するかどうかを見ることができます。最も頻繁に使用される変換は、対数、指数、二乗、及び三角関数のバリエーションです。
- 季節性の変数をチェックし、必要な期間(週、月、セッションなど)のモデルを作成します。
月曜日の市場の動きが水曜日と木曜日の動きとは異なっていることは直感的です。つまり、曜日は重要な機能です。時間は、市場にとって同じくらい重要です。これは、このセッションがアジア、ヨーロッパ、アメリカのものであるかを定義します。これらの特徴はどのように定義できるでしょうか?
これにはtimekitパッケージを使います。tk_augment_timeseries_signature()はパッケージの中心的な関数です。これは、初期データセットprの時間ラベルに時間データの行全体を追加して、グループの追加機能とパラメータの両方として役立ちます。これらは何でしょうか?
| Index | 解決されたインデックスの値 |
| Index.num | インデックスの“1970-01-01 00:00:00”からの秒単位の数値 |
| diff | 指標の以前の数値との秒差 |
| Year | 年、インデックスコンポーネント |
| half | 半分、インデックスコンポーネント |
| quarter | 4分の1、インデックスコンポーネント< |
| month | 月、インデックスコンポーネント(1ベース) |
| month.xts | 月、xtsで実装されているのと同じ0ベースのインデックスコンポーネント |
| month.lbl | 順序付けられた要素としての月ラベル(1月に始まり12月に終わる) |
| day | 日、インデックスコンポーネント |
| hour | 時間、インデックスコンポーネント |
| minute | 分、インデックスコンポーネント |
| second | 秒、インデックスコンポーネント |
| hour12 | 12時間スケールの1時間コンポーネント |
| am.pm | 午前 (am) = 1、午後 (pm) = 2 |
| wday | 曜日(日曜 = 1、...土曜 = 7) |
| wday.xts | 日、xtsで実装されているのと同じ(日曜 = 0, 土曜 = 6) |
| wday.lbl | 順序付けられた因子としての曜日のラベル(日曜日で始まり土曜日に終わる) |
| mday | 月の日 |
| qday | 四半期の日 |
| yday | 年の日 |
| mweek | 月の週 |
| week | 1年の週の番号(日曜日から始まる) |
| week.iso | ISOによる1年間の週数(月曜日から始まる) |
| week2 | 2週間の頻度のモジュール |
| week3 | 3週間の頻度のモジュール |
| week4 | 4週間の頻度のモジュール |
最初のデータセットprを取得してtk_augment_timeseries_signature()関数で強化し、mday、wday.lbl、hour変数を初期データセットに追加し、未定義変数(NA)を削除し、曜日別にグループ化します。
evalq(
{
tk_augment_timeseries_signature(pr) %>%
select(c(mday, wday.lbl, hour)) %>%
cbind(pr, .) -> pr.augm
pr.compl <- pr.augm[complete.cases(pr.augm), ]
pr.nest <- pr.compl %>% group_by(wday.lbl) %>% nest()
},
env)
> str(env$pr.augm)
'data.frame': 8000 obs. of 33 variables:
$ Data : POSIXct, format: "2017-01-10 11:00:00" ...
$ Open : num 123 123 123 123 123 ...
$ High : num 123 123 123 123 123 ...
$ Low : num 123 123 123 123 123 ...
$ Close : num 123 123 123 123 123 ...
$ Vol : num 3830 3360 3220 3241 3071 ...
..................................................
$ zigz : num 123 123 123 123 123 ...
$ dz : num NA -0.0162 -0.0162 -0.0162 -0.0162 ...
$ sig : num NA -1 -1 -1 -1 -1 -1 -1 -1 -1 ...
$ mday : int 10 10 10 10 10 10 10 10 10 10 ...
$ wday.lbl: Ord.factor w/ 7 levels "Sunday"<"Monday"<..: 3 3 3 3 3 3 3 3 3 3 ...
$ hour : int 11 11 11 11 12 12 12 12 13 13 ...
土曜日のデータを削除して lubridateライブラリを使用しても同じ結果が得られます。
require(lubridate)
evalq({pr %>% mutate(.,
wday = wday(Data), #label = TRUE, abbr = TRUE),
day = day(Data),
hour = hour(Data)) %>%
filter(wday != "Sat") -> pr1
pr1.nest <- pr1 %>% na.omit %>%
group_by(wday) %>% nest()},
env
)
#-------
str(env$pr1)
'data.frame': 7924 obs. of 33 variables:
$ Data : POSIXct, format: "2017-01-10 11:00:00" ...
$ Open : num 123 123 123 123 123 ...
$ High : num 123 123 123 123 123 ...
$ Low : num 123 123 123 123 123 ...
$ Close : num 123 123 123 123 123 ...
$ Vol : num 3830 3360 3220 3241 3071 ...
..........................................
$ zigz : num 123 123 123 123 123 ...
$ dz : num NA -0.0162 -0.0162 -0.0162 -0.0162 ...
$ sig : num NA -1 -1 -1 -1 -1 -1 -1 -1 -1 ...
$ wday : int 3 3 3 3 3 3 3 3 3 3 ...
$ day : int 10 10 10 10 10 10 10 10 10 10 ...
$ hour : int 11 11 11 11 12 12 12 12 13 13 ...
曜日別にグループ化されたデータは、次のようになります(日曜日= 1、月曜日= 2など)。
> env$pr1.nest # A tibble: 5 × 2 wday data <int> <list> 1 4 <tibble [1,593 Ч 32]> 2 5 <tibble [1,632 Ч 32]> 3 6 <tibble [1,624 Ч 32]> 4 2 <tibble [1,448 Ч 32]> 5 3 <tibble [1,536 Ч 32]>
さらに、prデータセットからのdL変数とdH変数は、最後の3つのバーで使用することができます。
2. 予測変数の選択
予測変数の重要性を評価する方法と基準は数多くあり、それらのいくつかは前稿で考慮されました。本稿では視覚化に重点を置いているので、予測変数の重要性を高める視覚的方法と分析的方法を比較してみましょう。
2.1. 視覚評価
ここでは smbinningパッケージを使用します。.以前は、funModelingパッケージを使用して予測変数を評価し、関係の視覚が予測変数の関連性を識別する簡単で信頼性の高い方法であることを結論づけました。ここではsmbinning パッケージが正規化され変換されたデータをどのように処理するかをテストし、予測変数の変換がその重要性にどのように影響を与えるかについても説明します。
対数変換、sin変換、tanh変換、正規化されたデータのセットを収集し、これらのセットにおける目標変数と予測変数の依存性を評価します。
データセットの未加工データを(相関性の高いデータを削除することなく)消去してデータセットを訓練/検証/テストに分割してDTセットを設定、取得するというのがプライマリセットの処理のシーケンスです(以下の図を参照)。この後、以下のブロック図に従って、各種の変換のアクションを実行します。すべてを1つのスクリプトにまとめましょう。
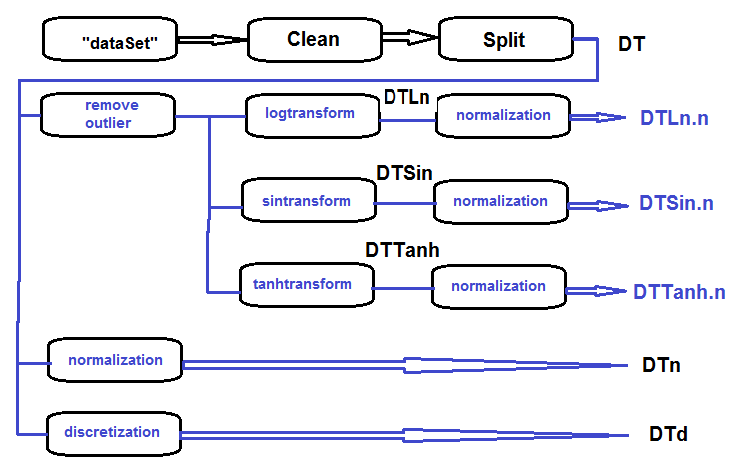
図27 予備処理ブロック図
セットをクリーンして訓練/テスト/検証セットに分割し、不要なデータを削除します。
#----クリーン--------------------- require(caret) require(pipeR) evalq( { train = 1:2000 val = 2001:3000 test = 3001:4000 DT <- list() dataSet %>% preProcess(., method = c("zv", "nzv", "conditionalX")) %>% predict(., dataSet) %>% na.omit -> dataSetClean list(train = dataSetClean[train, ], val = dataSetClean[val, ], test = dataSetClean[test, ]) -> DT rm(dataSetClean, train, val, test) }, env)
外れ値を全て処理します。
#------外れ値-------------
evalq({
# 結果の新しいリストを定義する
DTcap <- list()
# 3つのセットを処理する
foreach(i = 1:3) %do% {
DT[[i]] %>%
# (データ、クラス)の列を削除する
select(-c(Data, Class)) %>%
# data.frameに変換して一時変数xに格納する
as.data.frame() -> x
if (i == 1) {
# 最初の入力に外れ値のパラメータを定義する
foreach(i = 1:ncol(x), .combine = "cbind") %do% {
prep.outlier(x[ ,i]) %>% unlist()
} -> pre.outl
colnames(pre.outl) <- colnames(x)
}
# 5/95 % の代わりに外れ値を代入し、その結果をx.capに格納する
foreach(i = 1:ncol(x), .combine = "cbind") %do% {
stopifnot(exists("pre.outl", envir = env))
lower = pre.outl['lower.25%', i]
upper = pre.outl['upper.75%', i]
med = pre.outl['med', i]
cap1 = pre.outl['cap1.5%', i]
cap2 = pre.outl['cap2.95%', i]
treatOutlier(x = x[ ,i], impute = T, fill = T,
lower = lower, upper = upper,
med = med, cap1 = cap1, cap2 = cap2)
} %>% as.data.frame() -> x.cap
colnames(x.cap) <- colnames(x)
return(x.cap)
} -> Dtcap
# 不要な変数を削除する
rm(lower, upper, med, cap1, cap2, x.cap, x)
}, env)
外れ値のないすべてのDtcapセットの変数をlog(x+1)関数で変換します。DTLnリストを、3セットの対数変換された変数で取得します。
#------logtrans------------
evalq({
DTLn <- list()
foreach(i = 1:3) %do% {
DTcap[[i]] %>%
apply(., 2, function(x) log2(x + 1)) %>%
as.data.frame() %>%
cbind(., Class = DT[[i]]$Class)
} -> DTLn
},
env)
外れ値のないすべてのDtcapセットの変数をsin(2*pi*x)関数で変換します。DTSinリストを、3セットのsin変換された変数で取得します。
#------sintrans--------------
evalq({
DTSin <- list()
foreach(i = 1:3) %do% {
DTcap[[i]] %>%
apply(., 2, function(x) sin(2*pi*x)) %>%
as.data.frame() %>%
cbind(., Class = DT[[i]]$Class)
} -> DTSin
},
env)
外れ値のないすべてのDtcapセットの変数をtanh(x)関数で変換します。DTTanhリストを、3セットのtanh変換された変数で取得します。
#------tanhTrans----------
evalq({
DTTanh <- list()
foreach(i = 1:3) %do% {
DTcap[[i]] %>%
apply(., 2, function(x) tanh(x)) %>%
as.data.frame() %>%
cbind(., Class = DT[[i]]$Class)
} -> DTTanh
},
env)
DT、DTLn、DTSin、DTTanhのセットを正規化します。
#------正規化----------- evalq( { # 正規化のパラメータを定義する preProcess(DT$train, method = "spatialSign") -> preproc list(train = predict(preproc, DT$train), val = predict(preproc, DT$val), test = predict(preproc, DT$test) ) -> DTn }, env) #--ln--- evalq( { preProcess(DTLn[[1]], method = "spatialSign") -> preprocLn list(train = predict(preprocLn, DTLn[[1]]), val = predict(preprocLn, DTLn[[2]]), test = predict(preprocLn, DTLn[[3]]) ) -> DTLn.n }, env) #---sin--- evalq( { preProcess(DTSin[[1]], method = "spatialSign") -> preprocSin list(train = predict(preprocSin, DTSin[[1]]), val = predict(preprocSin, DTSin[[2]]), test = predict(preprocSin, DTSin[[3]]) ) -> DTSin.n }, env) #-----tanh----------------- evalq( { preProcess(DTTanh[[1]], method = "spatialSign") -> preprocTanh list(train = predict(preprocTanh, DTTanh[[1]]), val = predict(preprocTanh, DTTanh[[2]]), test = predict(preprocTanh, DTTanh[[3]]) ) -> DTTanh.n }, env)
mdlp::discretization関数を使用して、DTセットを離散化します。
##------離散化----------
#--------preCut---------------------
# カットポイントを定義する
require(pipeR)
require(discretization)
evalq(
#require(pipeR)
# 時間がかかる
pipeline({
DT$train
select(-Data)
as.data.frame()
mdlp()
}) -> mdlp.train,
env)
#-------cut_opt----------
evalq(
{
DTd <- list()
mdlp.train$cutp %>%
# 離散化しなければならない列を定義する
lapply(., function(x) is.numeric(x)) %>%
unlist -> idx # bool
#----train-----------------
mdlp.train$Disc.data[ ,idx] -> DTd$train
#---test------------
DT$test %>%
select(-c(Data, Class)) %>%
as.data.frame() -> test.d
# 計算された範囲に従ってデータを再配置する
foreach(i = 1:length(idx), .combine = 'cbind') %do% {
if (idx[i]) {
findInterval(test.d[ ,i],
vec = mdlp.train$cutp[[i]],
rightmost.closed = FALSE,
all.inside = F,
left.open = F)
}
} %>% as.data.frame() %>% add(1) %>%
cbind(., DT$test$Class) -> DTd$test
colnames(DTd$test) <- colnames(DTd$train)
#-----val-----------------
DT$val %>%
select(-c(Data, Class)) %>%
as.data.frame() -> val.d
# 計算された範囲に従ってデータを再配置する
foreach(i = 1:length(idx), .combine = 'cbind') %do% {
if (idx[i]) {
findInterval(val.d[ ,i],
vec = mdlp.train$cutp[[i]],
rightmost.closed = FALSE,
all.inside = F,
left.open = F)
}
} %>% as.data.frame() %>% add(1) %>%
cbind(., DT$val$Class) -> DTd$val
colnames(DTd$val) <- colnames(DTd$train)
# 片付ける
rm(test.d, val.d)
},
env
)
元のDT$trainデータセットに含まれる変数を思い出してみましょう。
require(funModeling)
plot_num(env$DT$train %>% select(-Data), bins = 20)
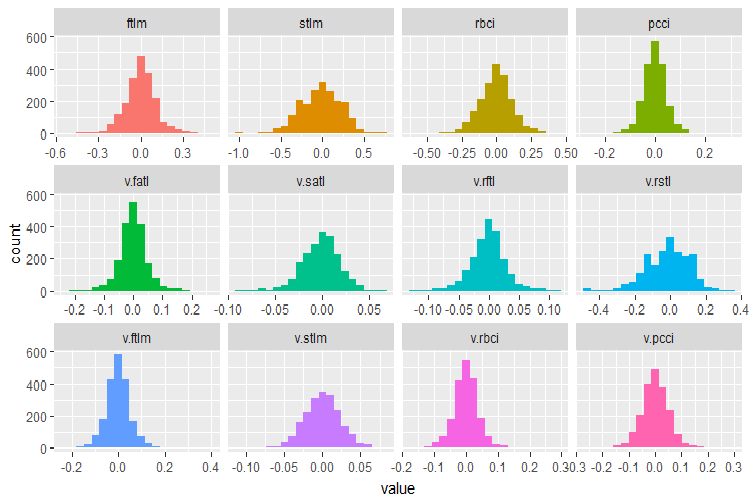
図28 DT$trainデータセットにおける変数の分布
前に取得したすべての正規化されたデータセット (Dtn、DTLn.n、DTSin.n、DTTanh.n)の訓練サブセットで関連する予測変数を識別するには、smbinningパッケージの機能を使用します。このパッケージの目標変数は数値でなければならず、値は (0, 1)でなければなりません。必要な変換のための関数を記述しましょう。
#-------------------------------- require(smbinning) targ.int <- function(x){ x %>% tbl_df() %>% mutate(Cl = (as.numeric(Class) - 1) %>% as.integer()) %>% select(-Class) %>% as.data.frame() }
さらに、このパッケージでは、名前にドットを含む変数は受け入れられません。以下の関数は、すべての変数の名前のドットをアンダースコアに変更します。
renamepr <- function(X){
X %<>% rename(v_fatl = v.fatl,
v_satl = v.satl,
v_rftl = v.rftl,
v_rstl = v.rstl,
v_ftlm = v.ftlm,
v_stlm = v.stlm,
v_rbci = v.rbci,
v_pcci = v.pcci)
return(X)
}
関連する予測変数を使ってチャートを計算し、プロットします。
par(mfrow = c(2,2)) #--Ln-------------- evalq({ df <- renamepr(DTLn.n[[1]]) %>% targ.int sumivt.ln.n = smbinning.sumiv(df = df, y = 'Cl') smbinning.sumiv.plot(sumivt.ln.n, cex = 0.7) rm(df) }, env) #---Sin----------------- evalq({ df <- renamepr(DTSin.n[[1]]) %>% targ.int sumivt.sin.n = smbinning.sumiv(df = df, y = 'Cl') smbinning.sumiv.plot(sumivt.sin.n, cex = 0.7) rm(df) }, env) #---norm------------- evalq({ df <- renamepr(DTn[[1]]) %>% targ.int sumivt.n = smbinning.sumiv(df = df, y = 'Cl') smbinning.sumiv.plot(sumivt.n, cex = 0.7) rm(df) }, env) #-----Tanh---------------- evalq({ df <- renamepr(DTTanh.n[[1]]) %>% targ.int sumivt.tanh.n = smbinning.sumiv(df = df, y = 'Cl') smbinning.sumiv.plot(sumivt.tanh.n, cex = 0.7) rm(df) }, env) par(mfrow = c(1,1))
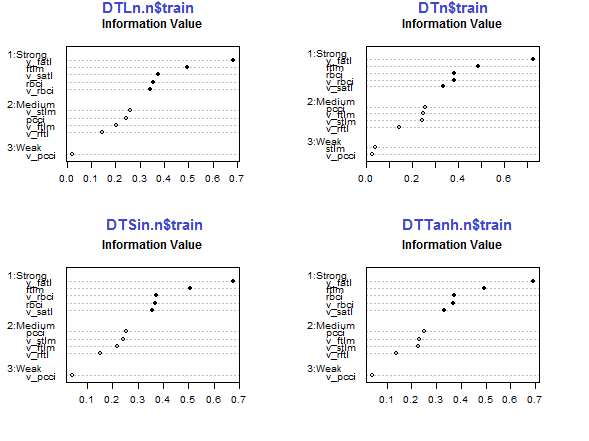
図29 正規化されたセットの訓練サブセットの予測変数の重要性
v_fatl、ftlm、v_satl、rbci、v_rbciの5つの予測変数はすべてのセットで強いですが、その順序は異なります。pcci、v_ftlm、v_stlm、v_rftlの4つの予測変数の強さは平均的です。v_pcci及びstlm予測変数は弱いです。変数の分布は各セットで、重要度の順に見ることができます。
env$sumivt.ln.n Char IV Process 5 v_fatl 0.6823 Numeric binning OK 1 ftlm 0.4926 Numeric binning OK 6 v_satl 0.3737 Numeric binning OK 3 rbci 0.3551 Numeric binning OK 11 v_rbci 0.3424 Numeric binning OK 10 v_stlm 0.2591 Numeric binning OK 4 pcci 0.2440 Numeric binning OK 9 v_ftlm 0.2023 Numeric binning OK 7 v_rftl 0.1442 Numeric binning OK 12 v_pcci 0.0222 Numeric binning OK 2 stlm NA No significant splits 8 v_rstl NA No significant splits
最後の3つの変数は破棄できます。このようにして、5つの最も強いものと4つの平均的なものが残されます。最良の変数(IV> 0.1)の名前を定義しましょう。
evalq(sumivt.sin.n$Char[sumivt.sin.n$IV > 0.1] %>% na.omit %>% as.character() -> best.sin.n, env) > env$best.sin.n [1] "v_fatl" "ftlm" "rbci" "v_rbci" "v_satl" "pcci" [7] "v_ftlm" "v_stlm" "v_rftl"
v_fatl及びftlm変数をもっと詳しくみてみましょう。
evalq({
df <- renamepr(DTTanh.n[[1]]) %>% targ.int
x = 'v_fatl'
y = 'Cl'
res <- smbinning(df = df,
y = y,
x = x)
#res$ivtable # 集計及び情報値
#res$iv # 情報値
#res$bands # ビンまたはバンド
#res$ctree # partykitの決定木
par(mfrow = c(2,2))
sub = paste0(x, " vs ", y) #rbci vs Cl"
boxplot(df[[x]]~df[[y]],
horizontal = TRUE,
frame = FALSE, col = "lightblue",
main = "Distribution")
mtext(sub,3) #ftlm
smbinning.plot(res, option = "dist",
sub = sub) #"pcci vs Cl")
smbinning.plot(res, option = "goodrate", #"badrate"
sub = sub) #"pcci vs Cl")
smbinning.plot(res, option = "WoE",
sub = sub) #"pcci vs Cl")
par(mfrow = c(1, 1))
}, env)
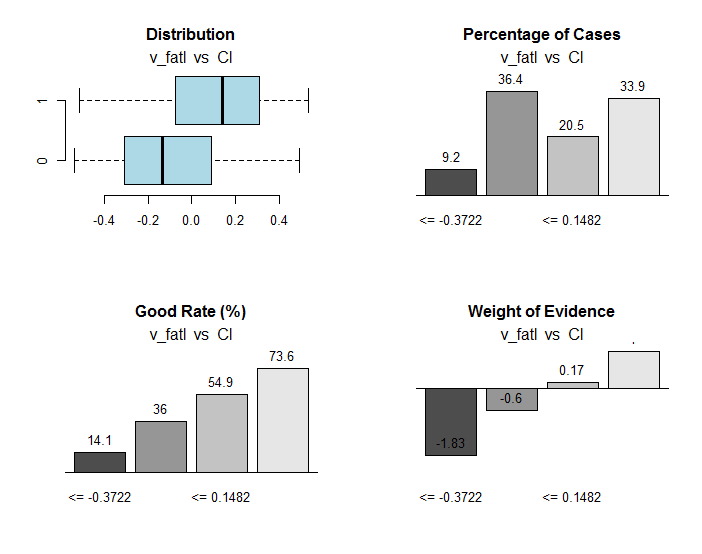
図30 v_fatl変数の範囲とCl目標変数の関係
resオブジェクトには、有用な情報とともに、目標変数に最適に接続された範囲に変数を分割する点が含まれています。ここでの場合、4つの範囲があります。
> env$res$cuts [1] -0.3722 -0.0433 0.1482
ftlm変数にも同じ計算をしてチャートをプロットします。
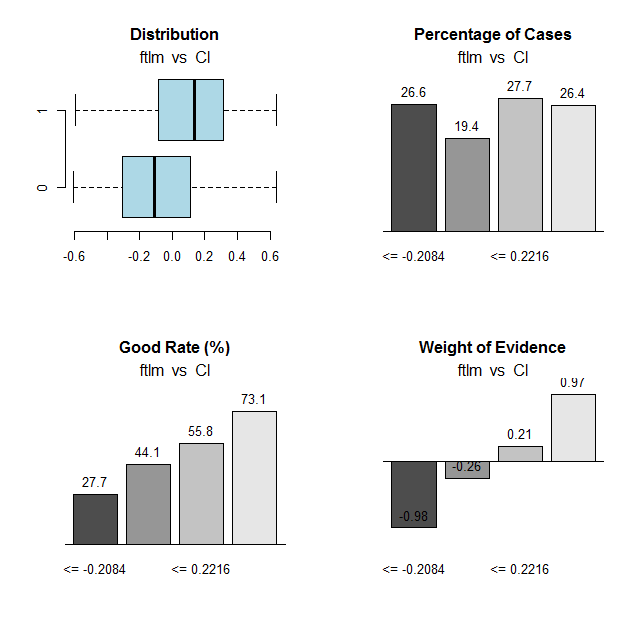
図31 ftlm変数とCl目標変数の接続範囲
範囲の分割点は下記です。
> env$res$cuts [1] -0.2084 -0.0150 0.2216
分割点によって、セット内の変数を離散化し、次の項目がどれだけ異なるかを見ることができます。
- smbinning::smbinning f関数を使用して定義された変数とmdlp::discretization関数を使用して定義された重要な変数
- 変数の範囲への分割
mdlp::discretization DTd関数で離散化されたデータセットはすでに1つあります。同じことを試みるのですが、今回はsmbinning::smbinning関数を訓練サブセットに対してのみ使用します。
分割点を定義します。
evalq({
res <- list()
DT$train %>% renamepr() %>% targ.int() -> df
x <- colnames(df)
y <- "Cl"
foreach(i = 1:(ncol(df) - 1)) %do% {
smbinning(df, y = y, x = x[i])
} -> res
res %>% lapply(., function(x) x[1] %>% is.list) %>%
unlist -> idx
}, env)
DT$train:サブセットを離散化します。
evalq({
DT1.d <- list()
DT$train %>% renamepr() %>%
targ.int() %>% select(-Cl) -> train
foreach(i = 1:length(idx), .combine = 'cbind') %do% {
if (idx[i]) {
findInterval(train[ ,i],
vec = res[[i]]$cuts,
rightmost.closed = FALSE,
all.inside = F,
left.open = F)
}
} %>% as.data.frame() %>% add(1) %>%
cbind(., DT$train$Class) -> DT1.d$train
colnames(DT1.d$train) <- colnames(train)[idx] %>%
c(., 'Class')
},
env)
重要度が0.1より大きい最良の変数を昇順に特定します。
evalq({
DT$train %>% renamepr() %>% targ.int() -> df
sumivt.dt1.d = smbinning.sumiv(df = df, y = 'Cl')
sumivt.dt1.d$Char[sumivt.dt1.d$IV > 0.1] %>%
na.omit %>% as.character() -> best.dt1.d
rm(df)
},
env)
DTd$train:セットの分割変数のチャートをプロットします。
require(funModeling) plot_num(env$DTd$train)
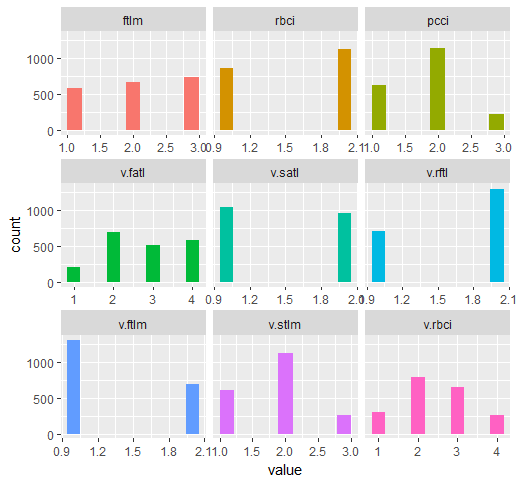
図32 mdlp関数で離散化されたDT$trainセットの変数
DT1.dのすべての変数のグラフとDT1.dの最良の変数のグラフを以下に示します。
plot_num(env$DT1.d$train)
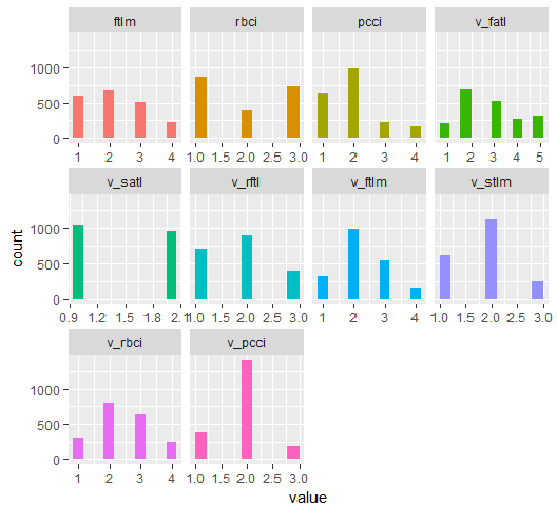
図33 smbinning関数で離散化されたDT1.d$trainセットの変数
plot_num(env$DT1.d$train[ ,env$best.dt1.d])
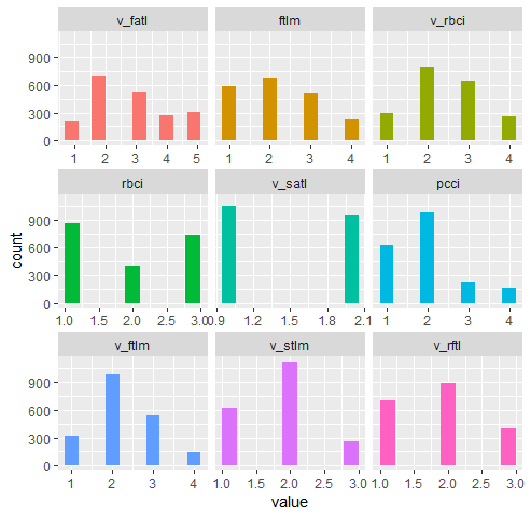
図34 smbinning関数で離散化されたDT1.d$trainセットの変数
グラフから何がわかるでしょうか?重要と定義された変数はどちらの場合も同じですが、範囲に分割するのは異なります。どのモデルがモデルに対してより良い予測を与えるかをテストしなければなりません。
2.2. 分析的評価
さまざまな基準による予測変数の重要性を特定するための分析手法は数多くあります。そのうちのいくつかは以前に考えました。さて、ここで予測変数の選択に対する珍しいアプローチをテストしたいと思います。
使うのはvarbvsパッケージです。varbvs関数には、変数を選択するベイジアンモデルをインストールするための高速アルゴリズムと、結果(または目標変数)が線形回帰またはロジスティック回帰でモデル化されるベイジアン係数の計算の実装が含まれます。これらのアルゴリズムは、"Scalable variational inference for Bayesian variable selection in regression, and its accuracy in genetic association studies"(回帰におけるベイジアン変数選択のためのスケーラブルな変分推論と遺伝的関連研究におけるその精度)(P. CarbonettoとM. Stephens、Bayesian Analysis 7、2012、ページ73-108)で説明されている変分近似に基づいています。このソフトウェアは、100万を超える変数と数千のサンプルを持つ大規模なデータセットでの作業に使用されました。
varbvs()関数は行列を受け取り、目標変数は入力データとして数値ベクトル(0,1)を受け取ります。この方法を使用して、正規化されたデータ DTTanh.n$trainを使用して、どの予測変数が重要であると定義するかをテストしてみましょう。
require(varbvs)
evalq({
train <- DTTanh.n$train %>% targ.int() %>% as.matrix()
fit <- varbvs(X = train[ ,-ncol(train)] ,
Z = NULL,
y = train[ ,ncol(train)] %>% as.vector(),
"binomial",
logodds = seq(-2,-0.5,0.1),
optimize.eta = T,
initialize.params = T,
verbose = T, nr = 100
)
print(summary(fit))
}, env)
Welcome to -- * *
VARBVS version 2.0.3 -- | | |
large-scale Bayesian -- || | | | || | | |
variable selection -- | || | | | | || || |||| || | ||
****************************************************************************
Copyright (C) 2012-2017 Peter Carbonetto.
See http://www.gnu.org/licenses/gpl.html for the full license.
Fitting variational approximation for Bayesian variable selection model.
family: binomial num. hyperparameter settings: 16
samples: 2000 convergence tolerance 1.0e-04
variables: 12 iid variable selection prior: yes
covariates: 0 fit prior var. of coefs (sa): yes
intercept: yes fit approx. factors (eta): yes
Finding best initialization for 16 combinations of hyperparameters.
-iteration- variational max. incl variance params
outer inner lower bound change vars sigma sa
0016 00018 -1.204193e+03 6.1e-05 0003.3 NA 3.3e+00
Computing marginal likelihood for 16 combinations of hyperparameters.
-iteration- variational max. incl variance params
outer inner lower bound change vars sigma sa
0016 00002 -1.204193e+03 3.2e-05 0003.3 NA 3.3e+00
Summary of fitted Bayesian variable selection model:
family: binomial num. hyperparameter settings: 16
samples: 2000 iid variable selection prior: yes
variables: 12 fit prior var. of coefs (sa): yes
covariates: 1 fit approx. factors (eta): yes
maximum log-likelihood lower bound: -1204.1931
Hyperparameters:
estimate Pr>0.95 candidate values
sa 3.49 [3.25,3.6] NA--NA
logodds -0.75 [-1.30,-0.50] (-2.00)--(-0.50)
Selected variables by probability cutoff:
>0.10 >0.25 >0.50 >0.75 >0.90 >0.95
3 3 3 3 3 3
Top 5 variables by inclusion probability:
index variable prob PVE coef* Pr(coef.>0.95)
1 1 ftlm 1.0000 NA 2.442 [+2.104,+2.900]
2 4 pcci 1.0000 NA 2.088 [+1.763,+2.391]
3 3 rbci 0.9558 NA 0.709 [+0.369,+1.051]
4 10 v.stlm 0.0356 NA 0.197 [-0.137,+0.529]
5 6 v.satl 0.0325 NA 0.185 [-0.136,+0.501]
*See help(varbvs) about interpreting coefficients in logistic regression.
ご覧のように、5つの最良の予測変数(ftlm、pcci、rbci、v.stlm、v.satl)が特定されています。これらは、異なる順序で他の重要度の重みを持つ、以前に識別されたトップ10に入っています。すでにモデルがあるので、検証セットとテストセットでどのような結果が得られるかを確認します。
下記は検証セットです。
#-----------------
evalq({
val <- DTTanh.n$val %>% targ.int() %>%
as.matrix()
y = val[ ,ncol(val)] %>% as.vector()
pr <- predict(fit, X = val[ ,-ncol(val)] ,
Z = NULL)
}, env)
cm.val <- confusionMatrix(table(env$y, env$pr))
> cm.val
Confusion Matrix and Statistics
0 1
0 347 204
1 137 312
Accuracy : 0.659
95% CI : (0.6287, 0.6884)
No Information Rate : 0.516
P-Value [Acc > NIR] : < 2.2e-16
Kappa : 0.3202
Mcnemar's Test P-Value : 0.0003514
Sensitivity : 0.7169
Specificity : 0.6047
Pos Pred Value : 0.6298
Neg Pred Value : 0.6949
Prevalence : 0.4840
Detection Rate : 0.3470
Detection Prevalence : 0.5510
Balanced Accuracy : 0.6608
'Positive' Class : 0
結果は全く印象的ではありません。下記はテストセットです。
evalq({
test <- DTTanh.n$test %>% targ.int() %>%
as.matrix()
y = test[ ,ncol(test)] %>% as.vector()
pr <- predict(fit, X = test[ ,-ncol(test)] ,
Z = NULL)
}, env)
cm.test <- confusionMatrix(table(env$y, env$pr))
> cm.test
Confusion Matrix and Statistics
0 1
0 270 140
1 186 404
Accuracy : 0.674
95% CI : (0.644, 0.703)
No Information Rate : 0.544
P-Value [Acc > NIR] : < 2e-16
Kappa : 0.3375
Mcnemar's Test P-Value : 0.01269
Sensitivity : 0.5921
Specificity : 0.7426
Pos Pred Value : 0.6585
Neg Pred Value : 0.6847
Prevalence : 0.4560
Detection Rate : 0.2700
Detection Prevalence : 0.4100
Balanced Accuracy : 0.6674
'Positive' Class : 0
結果はほぼ同じです。これは、モデルが再訓練されておらず、データが一般化していることを意味します。
よって、varbvsによるとftlm、pcci、rbci、v.stlm、v.satlが最高となります。
2.3. ニューラルネットワーク
ここではニューラルネットワークを研究しているので、ニューラルネットワークがどの予測変数を最も重要なものとして選択するかをテストしましょう。
これにはFCNN C ++ライブラリのコアプログラムのインターフェイスを提供するFCNN4Rパッケージを使用します。FCNNはニューラルネットワークの全く新しい表現に基づいており、効率、モジュール性、拡張性を意味します。FCNN4Rは、標準学習(誤差逆伝播法、Rprop、シミュレーテッドアニーリング、確率的勾配)と刈り込みアルゴリズム(最小マグニチュード、Optimal Brain Surgeon)を可能にしますが、私はこのパッケージがとりわけ効率的な計算エンジンであると考えています。
ユーザは、ネットワークを復元する機能(重みや過剰なニューロンの削除、入力データの並べ替え、ネットワークの統合)と共に、クイックグラジエントメソッドを使用してアルゴリズムを簡単に実装できます。
ネットワークは、どのようなプログラムソリューションにも統合できるように、C関数にエクスポートできます。
2つの隠れ層を持つ完全接続ネットワークを作成します。各層のニューロンの数は入力= 12(予測変数の数)、出力= 1です。+/- 0.17の範囲のランダムな重みでニューロンを動かします。ニューラルネットワークの各層(入力層を除く)の活性化関数を c( "tanh"、 "tanh"、 "sigmoid")に設定します。訓練/テスト/検証セットを準備します。
以下のスクリプトは、この一連の操作を実行します。
require(FCNN4R)
evalq({
mlp_net(layers = c(12, 8, 5, 1), name = "n.tanh") %>%
mlp_rnd_weights(a = 0.17) %>%
mlp_set_activation(layer = c(2, 3, 4),
activation = c("tanh", "tanh", "sigmoid"), #"threshold", "sym_threshold",
#"linear", "sigmoid", "sym_sigmoid",
#"tanh", "sigmoid_approx",
#"sym_sigmoid_approx"),
slope = 0) -> Ntanh #show()
#-------
train <- DTTanh.n$train %>% targ.int() %>% as.matrix()
test <- DTTanh.n$test %>% targ.int() %>% as.matrix()
val <- DTTanh.n$val %>% targ.int() %>% as.matrix()
}, env)
rprop訓練メソッドを使用します。tol - 訓練の最高レベル(達した場合訓練を停止してエラーとする)、max_ep - 訓練の最大エポック数(越された場合訓練を停止する)、l2reg - 正則化係数の定数を設定します。これらのパラメータを使用してネットワークを訓練し、どのネットワーク及び訓練エラーが発生しているかを視覚的に評価します。
evalq({
tol <- 1e-1
max_ep = 1000
l2reg = 0.0001
net_rp <- mlp_teach_rprop(Ntanh,
input = train[ ,-ncol(train)],
output = train[ ,ncol(train)] %>% as.matrix(),
tol_level = tol,
max_epochs = max_ep,
l2reg = l2reg,
u = 1.2, d = 0.5,
gmax = 50, gmin = 1e-06,
report_freq = 100)
}, env)
plot(env$net_rp$mse, t = "l",
main = paste0("max_epochs =", env$max_ep, " l2reg = ", env$l2reg))
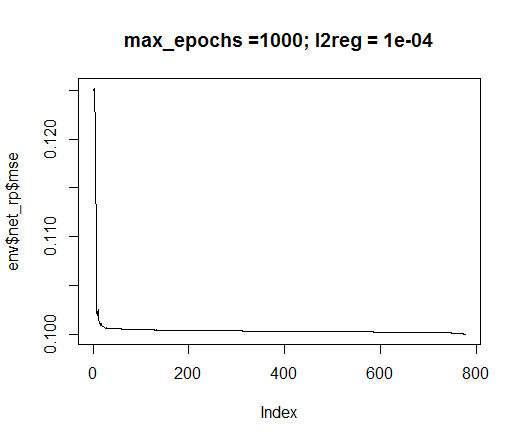
図35 ニューラルネットワーク訓練におけるエラー
evalq(mlp_plot(net_rp$net, FALSE), envir = env)
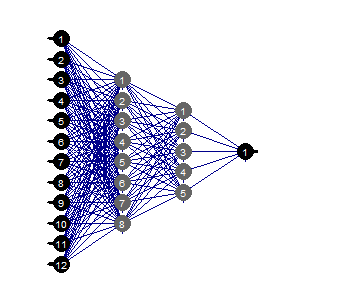
図36 ニューラルネットワークの構造
刈り込み
最小値の刈り込みは、使いやすいアルゴリズムです。ここでは、絶対値が最小である重みが各ステップでオフになります。このアルゴリズムは、各ステップでネットワークリレーをほぼ必要とし、最適ではない結果をもたらします。
evalq({
tol <- 1e-1
max_ep = 1000
l2reg = 0.0001
mlp_prune_mag(net_rp$net,
input = train[ ,-ncol(train)],
output = train[ ,ncol(train)] %>% as.matrix(),
tol_level = tol,
max_reteach_epochs = max_ep,
report = FALSE,
plots = TRUE) -> net_rp_prune
}, env)
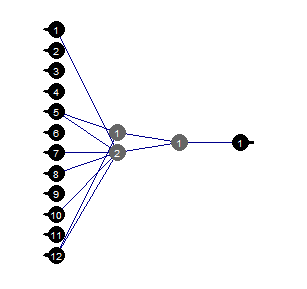
図37 刈り込みされたニューラルネットワーク
ニューラルネットワークの特定の構造、初期設定、活性化関数、学習誤差では、構造(12,2,1,1 )で十分なことがわかります。ニューラルネットワークはどの予測変数を選択したのでしょうか?
evalq( best <- train %>% tbl_df %>% select(c(1,5,7,8,10,12)) %>% colnames(), env) env$best [1] "ftlm" "v.fatl" "v.rftl" "v.rstl" "v.stlm" [6] "v.pcci"
v.rstl及びv.pcci変数は前に定義した最良の9変数中には存在しません。
ここでは、ニューラルネットワークが独立して自動的に重要な予測変数を選択できることを示したということを強調したいと思います。この選択は、予測変数だけでなく、ネットワークの構造及びパラメータによっても左右されます。
頑張って実験してください。
終わりに
次の部分では、セットからノイズの例を削除する方法、入力のサイズを小さくする方法、及び元のデータを訓練/検証/テスト
に分割する方法について説明します。
適用
1. FeatureTransformation.R、FeatureSelect.R、FeatureSelect_analitic.R、FeatureSelect_NN.Rスクリプトと本稿Part_1のRDataスクリプトの作業を示す図はGit /Part_IIからダウンロードできます。
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/3507
 ターミナル間のデータ交換にクラウドストレージサービスを使用
ターミナル間のデータ交換にクラウドストレージサービスを使用
 ディープニューラルネットワーク(その3)サンプル選択と次元削減
ディープニューラルネットワーク(その3)サンプル選択と次元削減
 MetaTrader5の任意のシンボルでトレーディングアイデアをテスト!
MetaTrader5の任意のシンボルでトレーディングアイデアをテスト!
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索