[Matematica pura, fisica, chimica, ecc.: problemi di allenamento del cervello non legati in alcun modo al commercio - pagina 14
Ti stai perdendo delle opportunità di trading:
- App di trading gratuite
- Oltre 8.000 segnali per il copy trading
- Notizie economiche per esplorare i mercati finanziari
Registrazione
Accedi
Accetti la politica del sito e le condizioni d’uso
Se non hai un account, registrati
Какие это такие запросы? Вы свой запрос перечитайте, запрос так запрос, - я на первом предложении то застрял, а развитие мысли "какие после каких бывают" добил меня окончательно.
PS: Жаль, что у Вас нет компаса. Хорошая штука - стороны света разные там показывает, направления всякие ...
Beh, non ho niente da dire, ahimè. :(
Ну мне сказать тут нечего, увы. :(
sulla bussola? - È uno scherzo, ho pensato che si adattasse al tuo "psicotipo". :о)
Алексей, тебя мое решение устраивает ?
Думаешь для 7-го это слишком круто (не общий, а частный случай 25 одноклассников) ?
Sì, è un po' caro per un 7. Ma è elementare, il che è bello.
Yurixx ha scritto(a) >> Due elementi devono avere gli stessi valori.
Non è difficile verificare che con N=26 (cioè non c'è nessuno studente con zero connessioni nella classe), questo numero ripetuto = 13.
L'unica cosa che non capisco è perché 13 e non 14 o 2. Tu e la tua procedura di partizionamento sequenziale mi avete fatto ammorbidire il cervello - ma forse è lì che dovresti cercare una spiegazione del perché è 13 :)
A proposito, hai usato il principio di Dirichlet senza nominarlo.
А почему так?
buona domanda)
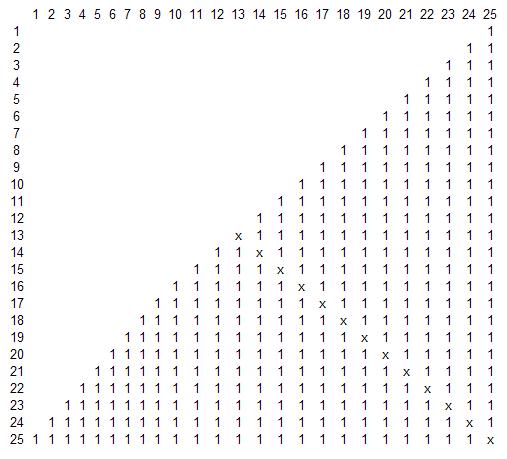
l'immagine è (da 1 a 25)
diagonale xxx, nessuno è amico di se stesso, è necessario farlo Petya e così è visibile tredici volte)))
nel caso di zero a 24, si può ignorare un compagno di classe e ottenere un quadrato di 24*24 e 12 X.
Nel caso di un quadrato dispari, la diagonale = (N+1)/2, nel caso di uno pari N/2.
Potete pensarla come la differenza di amicizie) nella classe con e senza Petya.
Non sembra una prova rigorosa. È più che altro un'illustrazione che punta il dito senza una chiara ragione per cui esattamente 12 o 13. Ok, pensiamoci.
L'unica cosa che non capisco è perché 13 e non 14 o 2. Tu e la tua procedura di partizionamento sequenziale mi avete ammorbidito la mente - ma forse è lì che dovresti cercare una spiegazione del perché è 13 :)
A proposito, hai usato il principio di Dirichlet, senza nominarlo.
Il punto è che sotto questo partizionamento (e obbedisce a un solo principio - ognuno ha un numero diverso di amici, e quindi è abbastanza generale) Petya non partecipa affatto. È uno dei 26 studenti, assolutamente uguale agli altri. Come risultato, si scopre che ognuno non può avere un numero diverso di amici - la serie da 1 a N-1 non può essere numerata consecutivamente N numeri diversi (è nella prova finale). Pertanto, due studenti devono avere lo stesso numero di amici. E questi due studenti sono uno accanto all'altro nel centro della fila. Così si scopre che Petya deve essere uno di questi due. Solo che in questo caso tutti gli altri hanno un numero diverso di amici. Qualsiasi altra marcatura non può soddisfare questa condizione.
Se provate a dividere a mano il centro, ve ne accorgerete da soli.
La tabella di Swan lo illustra.
Spero di aver capito bene la sua domanda.
Credo di non aver usato il principio di Dirichlet, ma di aver offerto una prova elementare del suo caso speciale.
Personalmente l'ho amato.
È elegante.
Mi ha ricordato la favola dell'agile piccolo Gauss e dell'insegnante che dava alla classe il compito di sommare i numeri da 1 a 99 e se ne andava per un po' - mentre i bambini aggiungevano.
Sapevano già la moltiplicazione, ma la ripetizione è la madre dell'apprendimento...
Gauss ingannò l'insegnante - la risposta arrivò subito.
;)
Swetten у нас самая дружелюбная.
:)
В коллективе из N сотрудников не может быть ситуации когда у каждого разное количество друзей
А вот если добавить - "у двух возможно одинаковое количество друзей" тогда нет проблем
Остается обозвать Петей одного из этих двух
Sì, è quasi giusto.
Se leggete il problema legalmente, allora Peter POTREBBE avere lo stesso numero di amici di uno degli altri.
Te l'ho detto - questo problema non è corretto - da QUALSIASI lettura delle condizioni. Probabilmente posso provarlo, e in vari modi. Ma non lo farò..... ancora.