
Sorting methods and their visualization using MQL5
Contents
- Introduction
- Applying the Graphics\Graphic.mqh library
- Exchange, comparison and boundary functions
- Sorting methods
- Selection Sort
- Insertion Sort
- Bubble Sort
- Quick Sort
- Merge Sort
- Heap Sort
- Radix MSD and LSD Sorts
- Other sorts
- Methods speed summary table
- All methods on a single screen
- Testing multi-threading
- Editor's note
Introduction
On the web, you can find a number of videos showing various sorting types. For example, here you can find visualization of 24 sorting algorithms. I have taken this video as a basis along with a list of sorting algorithms.
The Graphic.mqh library is responsible for working with graphics in MQL5. It has already been described in a number of articles. For example, the library features are shown in details here. My objective is to describe its application areas and consider the process of sorting in details. The general concept of sorting is described here since each type of sorting already has at least one separate article, while some of sorting types are objects of detailed studies.
Applying the Graphics\Graphic.mqh library
First, we need to include the library.
#include <Graphics\Graphic.mqh>
We will sort the histogram columns by applying the Gswap() and GBool() exchange and comparison functions. The elements to be processed (compared, replaced, etc.) are highlighted in color. To achieve this, a separate CCurve type object is assigned to each color. Make them global in order not to compartmentalize these objects by the Gswap functions (int i, int j, CGraphic &G, CCurve &A, CCurve &B and CCurve &C). The CCurve class has no default constructor, so it cannot be simply declared global. Therefore, declare global CCurve type pointers — *CMain.
The color can be set in three different ways. The most visible of them is C'0x00,0x00,0xFF' or C'Blue, Green, Red'. The curve is created using the CurveAdd() of the CGraphic class that has several implementations. For the majority of elements, it is convenient to select CurveAdd(arr, CURVE_HISTOGRAM, "Main") with a single array of values, while for auxiliary ones — CurveAdd(X, Y, CURVE_HISTOGRAM, "Swap") with the X array of arguments and Y array of values, since there will be only two elements. It is convenient to make arrays for auxiliary lines global.
#include <Graphics\Graphic.mqh> #property script_show_inputs input int N =42; CGraphic Graphic; CCurve *CMain; CCurve *CGreen; CCurve *CBlue; CCurve *CRed; CCurve *CViolet; double X[2],Y[2],XZ[2],YZ[2]; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //arrays------------------------------ double arr[]; FillArr(arr,N); X[0]=0;X[1]=0; Y[0] =0;Y[1]=0; //------------------------------------- Graphic.Create(0,"G",0,30,30,780,380); CMain =Graphic.CurveAdd(arr,CURVE_HISTOGRAM,"Main"); //index 0 CMain.HistogramWidth(4*50/N); CBlue =Graphic.CurveAdd(X,Y,CURVE_HISTOGRAM,"Pivot"); //index 1 CBlue.Color(C'0xFF,0x00,0x00'); CBlue.HistogramWidth(4*50/N); CRed =Graphic.CurveAdd(X,Y,CURVE_HISTOGRAM,"Swap"); //index 2 CRed.Color(C'0x00,0x00,0xFF'); CRed.HistogramWidth(4*50/N); CGreen =Graphic.CurveAdd(X,Y,CURVE_HISTOGRAM,"Borders"); //index 3 CGreen.Color(C'0x00,0xFF,0x00'); CGreen.HistogramWidth(4*50/N); CViolet =Graphic.CurveAdd(X,Y,CURVE_HISTOGRAM,"Compare"); //index 4 CViolet.Color(C'0xFF,0x00,0xFF'); CViolet.HistogramWidth(4*50/N); Graphic.XAxis().Min(-0.5); Graphic.CurvePlot(4); Graphic.CurvePlot(2); Graphic.CurvePlot(0); //Graphic.CurvePlotAll(); simply display all available curves Graphic.Update(); Sleep(5000); int f =ObjectsDeleteAll(0); } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void FillArr(double &arr[],int num) { int x =ArrayResize(arr,num); for(int i=0;i<num;i++) arr[i]=rand()/328+10; }
Graphic.XAxis().Min(-5) set the indent from the Y axis, so that the zero element does not merge with it. Histogramwidth() is a column width.
The FillArr() function fills the array with random numbers from 10 (not to merge with the X axis) to 110. The 'arr' array is made local so that exchange functions have the standard look swap(arr, i, j). The last command ObjectDeleteAll erases what we have plotted. Otherwise, we would have to delete the object via the Menu's Object List Ctrl+B.
Our preparations are complete. It is time to start sorting.
Exchange, comparison and boundary functions
Let's write the functions for visualizing the exchange, comparisons, and allocation of boundaries for sorting by division. The first exchange function void Gswap() is standard, although it features the CRed curve for allocating compared elements
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void Gswap(double &arr[],int i, int j) { X[0]=i;X[1]=j; Y[0] =arr[i];Y[1] =arr[j]; CRed.Update(X,Y); Graphic.Redraw(); Graphic.Update(); Sleep(TmS); double sw = arr[i]; arr[i]=arr[j]; arr[j]=sw; //------------------------- Y[0] =0; Y[1] =0; CRed.Update(X,Y); CMain.Update(arr); Graphic.Redraw(); Graphic.Update(); //------------------------- }
First, allocate the columns. Then return to the initial state after Sleep(TmS) time defining the demonstration speed. Write the comparison functions for "<" and "<=" as bool GBool(double arr, int i, int j) and GBoolEq(double arr, int i, int j) in similar way. Add the columns of another color CViole to them.
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ bool GBool(double &arr[], int i, int j) { X[0]=i;X[1]=j; Y[0] =arr[i];Y[1] =arr[j]; CViolet.Update(X,Y); Graphic.Redraw(); Graphic.Update(); Sleep(TmC); Y[0]=0; Y[1]=0; CViolet.Update(X,Y); Graphic.Redraw(); Graphic.Update(); return arr[i]<arr[j]; }
The function for allocating borders, the columns of which should not be erased.
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void GBorders(double &a[],int i,int j) { XZ[0]=i;XZ[1]=j; YZ[0]=a[i];YZ[1]=a[j]; CGreen.Update(XZ,YZ); Graphic.Redraw(); Graphic.Update(); }
Now, let's focus our attention on sorting.
Sorting methods
Before proceeding to analyzing the methods, I recommend to launching the VisualSort application attached below (VisualSort.ex5). It allows you to visually see how each sort works separately. The complete sort code is in the GSort.mqh include file. The file is quite big, therefore I have outlined only the main ideas here.
- The first sorting, which usually opens the study is Selection sort. First, we find the number of the minimum value in the current list and replace it with the value of the first unsorted position.
template <typename T> void Select(T &arr[]) { int n = ArraySize(arr); for(int j=0;j<n;j++) { int mid=j; for(int i=j+1;i<n;i++) { if(arr[i]<arr[mid]) { mid=i; } } if(arr[j]>arr[mid]){swap(arr,j,mid);} } }
Here and further below, the exchange function is a previously described Gswap(), while comparing the array elements is then replaced with GBool(). For example, if(arr[i]<arr[mid]) => if(GBool(arr,i,mid).
- The next sorting type (often used when playing cards) is insertion sort. In this method, the elements of the input sequence are analyzed one at a time. Each newly arrived element is placed in a suitable location among the previously arranged ones. Basic method:
template<typename T> void Insert(T &arr[]) { int n= ArraySize(arr); for(int i=1;i<n;i++) { int j=i; while(j>0) { if(arr[j]<arr[j-1]) { swap(arr,j,j-1); j--; } else j=0; } } }
The derivatives of the method are Shell Sort and Binary Insertion Sort. The first one compares not only the adjacent elements but also the ones located at a certain distance from each other. In other words, this is the Insertion Sort with preliminary "rough" passes. Binary Insertion applies binary search to find the insertion location. On the above mentioned demonstration (VisualSort.ex5), we can clearly see that Shell searches the array using a gradually decreasing "comb". In this regard, it has much in common with the Comb method described below.
- Bubble Sort and its derivatives — Shake, Gnom, Comb and Odd-Even Sort. The idea behind the Bubble Sort is simple: we go through the entire array from the beginning to the end comparing two neighboring elements. If they are not sorted, we interchange their positions. As a result of each iteration, the largest element will be located at the end of the array. The process is then repeated. In the end, we receive a sorted array. The basic Bubble Sort algorithm:
template<typename T> void BubbleSort(T &a[]) { int n =ArraySize(a); for (int i = 0; i < n - 1; i++) { bool swapped = false; for (int j = 0; j < n - i - 1; j++) { if (a[j] > a[j + 1]) { swap(a,j,j+1); swapped = true; } } if (!swapped) break; } }
In Shake Sort, passes are made in both directions allowing us to detect both large and small elements. Gnome Sort is interesting in that it is implemented in a single cycle. Let's have a look at its code:
void GGnomeSort(double &a[]) { int n =ArraySize(a); int i=0; while(i<n) { if(i==0||GBoolEq(a,i-1,i)) i++; //if(i==0||a[i-1]<a[i]) else { Gswap(a,i,i-1); //Exchange a[i] and a[i-1] i--; } } }
If we mark the place of the already sorted elements, we will get the Insertion Sort. Comb uses the same idea as Shell: it goes along the array with combs having different steps. The optimal reduction factor = 1.247 ≈ ( 1 / ( 1-е^(-φ) ) ), where е is an exponent and φ is a "golden" number. When applied to small arrays, Comb and Shell Sorts are similar to fast sorting methods in terms of speed. Odd-Even Sort passes odd/even elements in turns. Since it has been developed for multi-threaded implementation, it is of no use in our case.
- More complex methods are based on "divide and conquer" principle. The standard examples are Hoare Sort or Quick Sort
The general idea of the algorithm is as follows: we select the pivot element from the array. Any array element can be selected as a pivot one. All other elements are compared with the pivot one and re-arranged within the array so that the array is divided into two continuous segments: "less" than the pivot one and "exceeding" it. If the segment length is greater than one, the same sequence of operations is performed for "less" and "exceeding" segments recursively. The basic idea can be found in the pseudocode:
algorithm quicksort(A, lo, hi) is if (lo < hi) { p = partition(A, lo, hi); quicksort(A, lo, p – 1); quicksort(A, p, hi);}
The difference in sorting options in this case is reduced to different ways of partitioning the array. In the original version, the pointers move towards each other from the opposite sides. The left pointer finds the element exceeding the pivot one, while the right one looks for the lesser one, and they are interchanged. In another version, both pointers move from left to right. When the first pointer finds the "lesser" element, it moves that element to the second pointer's location. If the array contains many identical elements, the partitioning allocates space for elements equal to the pivot one. Such an arrangement is applied, for example, when it is necessary to categorize employees only by two keys — "M" (male) and "F" (female). The appropriate partitioning is displayed below:
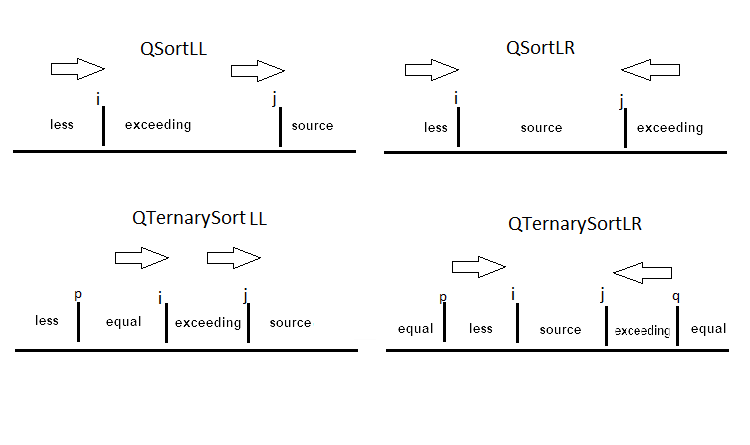
Let's have a look at QSortLR with Hoare partitioning as an example:
//----------------------QsortLR----------------------------------------+ void GQsortLR(double &arr[],int l,int r) { if(l<r) { GBorders(arr,l,r); int mid =PartitionLR(arr,l,r); GQsortLR(arr,l,mid-1); GQsortLR(arr,mid+1,r); } } int PartitionLR(double &arr[],int l,int r) { int i =l-1; int j =r; for(;;) { while(GBool(arr,++i,r)); j--; while(GBool(arr,r,j)){if(j==l) break;j--;} if(i>=j) break; Gswap(arr,i,j); } //--------------------------------------------- Gswap(arr,i,r); YZ[0]=0;YZ[1]=0; CGreen.Update(XZ,YZ); Graphic.Redraw(); Graphic.Update(); return i; }
The array can be divided into 3, 4, 5... parts with several pivot elements. The DualPivot sorting with two pivot elements can also be used.
- Other methods based on "divide and conquer" principle use the merging of the already sorted array parts. They divide the array until its length becomes equal to 1 (sorted), then they apply the merging function that also sorts the elements along the way. General principle:
void GMergesort (double &a[], int l, int r) { int m = (r+l)/2; GMergesort(a, l, m); GMergesort(a, m+1, r) ; Merge(a, l, m, r); }
BitonicSort() makes one half of the array ascending, while the other one descending combining them afterwards.
- Heap Sort
The general principle is as follows. Form a "heap" by "sifting" the array. Remove the older element at the top of the "heap". Move it to the end of the source array as the oldest one replacing it with the last element from the unsorted part. Build the new "heap" having the size of n-1, etc. The "heaps" can be based on different principles. For example, Smooth() sorting applies "heaps" having the number of elements equal to Leonardo numbers L(x+2) = L(x+1) +L(x) +1.
- Radix Sorts. Counting Sort and Radix MSD/LSD Sorts
Counting Sort is a sorting algorithm applying the range of numbers of the sorted array (list) for calculating matching elements. Applying the Counting Sort is reasonable only when sorted numbers have a range of possible values that is small enough compared to the sorted set, for example, a million natural numbers less than 1000. Its principle is applied in Radix Sorts as well. Here is the algorithm:
void CountSort(double &a[]) { int count[]; double aux[]; int k =int(a[int(ArrayMaximum(a))]+1); int n =ArraySize(a); ArrayResize(count,k); ArrayResize(aux,n); for (int i=0;i<k;i++) count[i] = 0; for (int i=0;i<n;i++) count[int(a[i])]++; // number of elements equal to i for (int i=1;i<k;i++) count[i] = count[i]+count[i-1]; // number of elements not exceeding i for(int j=n-1;j>=0;j--) aux[--count[int(a[j])]]=a[j]; // fill the intermediary array for(int i=0;i<n;i++)a[i]=aux[i]; }
The Counting Sort ideas are applied in MSD and LSD Sorts in linear time. This is the N*R time, where N is a number of elements, while R is a number of digits in the number representation within the selected number system. MSD (most significant digit) sorts by the top digit, while LSD (least significant digit) — by the lowest one. For example, in the binary system, LSD calculates how many numbers end in 0 and 1 placing even numbers (0) to the first half and odd numbers (1) to the second half afterwards. MSD, on the contrary, starts with the top digit. In the decimal system, it places the numbers < 100 in the beginning and the numbers >100 further on. Then, the array is again sorted into segments 0-19, 10-19,..., 100-109 etc. This sorting method is applied to integers. However, the quote 1.12307 can be made integer 1.12307*100 000.
The QuicksortB() binary quick sort is obtained by combining the Quick and Radix Sorts. QSortLR sorting is applied here, although selection is performed by the top digit rather than the pivot array element. To do this, the function of searching for the n th digit number is applied here and in LSD/MSD:
int digit(double x,int rdx,int pos) // Here x number, rdx number system { // in our case 2, pos digit index int mid =int(x/pow(rdx,pos)); return mid%rdx; }First, the sorting by the top digit is performed int d =int(log(a[ArrayMaximum(a)])/log(2)), then the parts are sorted by lower digits recursively. Visually, it look similar to QuickSortLR.
- Some specific sorts
Cycle Sort is intended for systems where data overwriting leads to resource wear. Therefore, the task here is to find the sort with the least amount of exchanges (Gswap). Cycle Sorts are used for that. Roughly speaking, 1 is rearranged to 3, 3 to 2, 2 to 1. Each element is re-arranged either 0 or 1 time. All this takes much time: O(n^2). The details on the idea and the method can be found here.
Stooge sort. This is yet another example of a far-fetched and very slow sorting. The algorithm is as follows. If the element value at the end of the list is less than the element value at the beginning, they should exchange their places. If the current subset of the list contains 3 or more elements, then: call Stoodge() recursively for the first 2/3 of the list, recursively call Stoodge() for the last 2/3, call Stoodge() recursively for the first 2/3 again, etc.
Methods speed summary table
| Sorting methods | Average time |
|---|---|
| Selection Sort | O(n^2) |
| Insertion Sort | O(n^2) |
| Binary Selection Sort | O(n^2) |
| Shell Sort | O(n*log(n)) |
| Bubble Sort | O(n^2) |
| Shaker/Cocktail Sort | O(n^2) |
| Gnom Sort | O(n^2) |
| Comb Sort | O(n*log(n)) |
| Merge Sort | O(n*log(n)) |
| Bitonic Sort | O(n*log(n)) |
| Heap Sort | O(n*log(n)) |
| Smooth Sort | O(n*log(n)) |
| Quick Sort LR | O(n*log(n)) |
| Quick Sort LL | O(n*log(n)) |
| Quick Sort (ternary, LR ptrs) | O(n*log(n)) |
| Quick Sort (ternary, LL ptrs) | O(n*log(n)) |
| Quick Sort (dual pivot) | O(n*log(n)) |
| Counting Sort | O(n+k) |
| Radix LSD | O(n*k) |
| Radix MSD | O(n*k) |
| Quick Binary Sort | O(n*log(n)) |
| Cycle Sort | O(n^2) |
| Stoodge Sort | O(n^2.7) |
All methods on a single screen
Let's plot all described sorts on a single screen simultaneously. On the source video, described sorts are launched one by one. The results then have been edited in the video editor. The trading platform has no built-in video editing features. There are several solutions.
Option 1
Simulate multi-threading. Parallelize the sorts so that it is possible to exit function after each comparison and exchange passing the queue to other sort and then re-enter it again in the same place. The absence of the GOTO operator complicates the task. For example, this is how the simplest Selection Sort described at the very beginning looks like in that case:
void CSelect(double &arr[]) { static bool ch; static int i,j,mid; int n =ArraySize(arr); switch(mark) { case 0: j=0; mid=j; i=j+1; ch =arr[i]<arr[mid]; if(ch) mid =i; mark =1; return; break; case 1: for(i++;i<n;i++) { ch =arr[i]<arr[mid]; mark =1; if(ch) mid=i; return; } ch =arr[j]>arr[mid]; mark=2; return; break; case 2: if(ch) { swap(arr,j,mid); mark=3; return; } for(j++;j<n;j++) { mid=j; for(i=j;i<n;i++) { ch =arr[i]<arr[mid]; if(ch) mid=i; mark =1; return; } ch =arr[j]>arr[mid]; mark =2; return; } break; case 3: for(j++;j<n;j++) { mid=j; for(i=j;i<n;i++) { ch =arr[i]<arr[mid]; if(ch) mid=i; mark =1; return; } ch =arr[j]>arr[mid]; mark=2; return; } break; } mark=10; }
The solution is quite viable. At such a launch, the array is sorted:
while(mark !=10) { CSelectSort(arr); count++; }
The 'count' variable shows the total number of comparisons and exchanges. At the same time, the code has become bigger three to four times, and this is the simplest sorting. There are also sorts consisting of several functions, recursive ones, etc.
Option 2
There is a simpler solution. The MQL5 terminal supports the concept of multi-threading. To implement it, a custom indicator should be called for each sort. The indicator should belong to a separate currency pair for each thread. The Market Watch window should have enough tools for each sort.
n = iCustom(SymbolName(n,0),0,"IndcatorSort",...,SymbolName(n,0),Sort1,N);
Here, SymbolName (n,0) is a separate tool for each created flow and the parameters passed to the indicator. The graphical object name can be conveniently assigned by SymbolName (n,0). One chart can only have one CGraphic class object with the given name. Sort method, number of elements in the array and the size of the CGraphic itself are not displayed here.
The sorting function selection and other additional actions related to visual display (for example, adding the sort name to the axes) take place in the indicator itself.
switch(SortName) { case 0: Graphic.XAxis().Name("Selection"); CMain.Name("Selection");Select(arr); break; case 1: Graphic.XAxis().Name("Insertion"); CMain.Name("Insertion");Insert(arr);break; etc............................................. }
The creation of graphical objects takes a certain amount of time. Therefore, the global variables have been added to make sorts work simultaneously. NAME is a global variable with the instrument name with an initial value of 0. After creating all the necessary objects, it gets the value of 1, while the value of 2 is assigned after the sorting is complete. In this way, you are able to track the sort start and end. To do this, the timer is launched in the EA:
void OnTimer() { double x =1.0; double y=0.0; static int start =0; for(int i=0;i<4;i++) { string str; str = SymbolName(i,0); x =x*GlobalVariableGet(str); y=y+GlobalVariableGet(str); } if(x&&start==0) { start=1; GlobalVariableSet("ALL",1); PlaySound("Sort.wav"); } if(y==8) {PlaySound("success.wav"); EventKillTimer();} }
Here the variable of х catches the beginning, while у — the end of the process.
At the beginning of the process, the sound from the original video is played. To work with the source files, it should be located in the MetaTrader/Sound folder together with other *.wav system sounds. If it is located elsewhere, specify the path from the MQL5 folder. For completion, the success.wav file is used.
So, let's create the EA and the indicator of the following type. EA:
enum SortMethod { Selection, Insertion, ..........Sorting methods......... }; input int Xscale =475; //Chart scale input int N=64; //Number of elements input SortMethod Sort1; //Method ..........Various inputs................. int OnInit() { //--- Set the global variables, launch the timer, etc. for(int i=0;i<4;i++) { SymbolSelect(SymbolName(i,0),1); GlobalVariableSet(SymbolName(i,0),0);} ChartSetInteger(0,CHART_SHOW,0); EventSetTimer(1); GlobalVariableSet("ALL",0); //.......................Open a separate indicator thread for each sort......... x=0*Xscale-Xscale*2*(0/2);//row with the length of 2 y=(0/2)*Yscale+1; SymbolSelect(SymbolName(0,0),1); // Without it, an error may occur on some instruments S1 = iCustom(SymbolName(0,0),0,"Sort1",0,0,x,y,x+Xscale,y+Yscale,SymbolName(0,0),Sort1,N); return(0); } //+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { ChartSetInteger(0,CHART_SHOW,1); EventKillTimer(); int i =ObjectsDeleteAll(0); PlaySound("ok.wav"); GlobalVariableSet("ALL",0); IndicatorRelease(Sort1); .......All that is to be removed...... //+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { ...Empty... } //+------------------------------------------------------------------+ void OnTimer() { ....Described above.... }
The appropriate indicator:
#include <GSort.mqh> //Include all previously written sorts //+------------------------------------------------------------------+ //| Custom indicator initialization function | //+------------------------------------------------------------------+ ..........Inputs block..................................... input int SortName; //method int N=30; //number ...................................................................... int OnInit() { double arr[]; FillArr(arr,N); //fill the array with random numbers GlobalVariableSet(NAME,0); //set the global variables Graphic.Create(0,NAME,0,XX1,YY1,XX2,YY2); //NAME — currency pair Graphic.IndentLeft(-30); Graphic.HistoryNameWidth(0); CMain =Graphic.CurveAdd(arr,CURVE_HISTOGRAM,"Main"); //index 0 CMain.HistogramWidth(2); CRed =Graphic.CurveAdd(X,Y,CURVE_HISTOGRAM,"Swap"); //index 1 CRed.Color(C'0x00,0x00,0xFF'); CRed.HistogramWidth(width); ......Various graphical parametes.......................... Graphic.CurvePlotAll(); Graphic.Update(); GlobalVariableSet(NAME,1); while(!GlobalVariableGet("ALL")); //Wait till all graphic objects are created switch(SortName) { case 0: Graphic.XAxis().Name("Selection"); CMain.Name("Selection");GSelect(arr); break; .....List of sorts.............................................. } GlobalVariableSet(NAME,2); return INIT_SUCCEEDED; } //+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(...) { ..............Empty........................ } //+------------------------------------------------------------------+ void OnDeinit(const int reason) { Graphic.Destroy(); delete CMain; delete CRed; delete CViolet; delete CGreen; ObjectDelete(0,NAME); }
Testing multi-threading
Light.ex5 and Sort24.ex5 are ready-to-use programs. They have been copied via the resources and do not require anything else. When working with source codes, they should be installed in the corresponding folders of indicators and sounds.
Sort24.ex5 with 24 sorts is unstable and works unevenly on my common single-core PC. Therefore, I should close all unnecessary programs and do not touch anything. Each sort contains five graphical objects — four curves and a canvas. All of them are continuously redrawn. Twenty four threads create 120 (!) individual continuously changing graphical objects in 24 threads. This is a mere demonstration. I have not worked with it anymore.
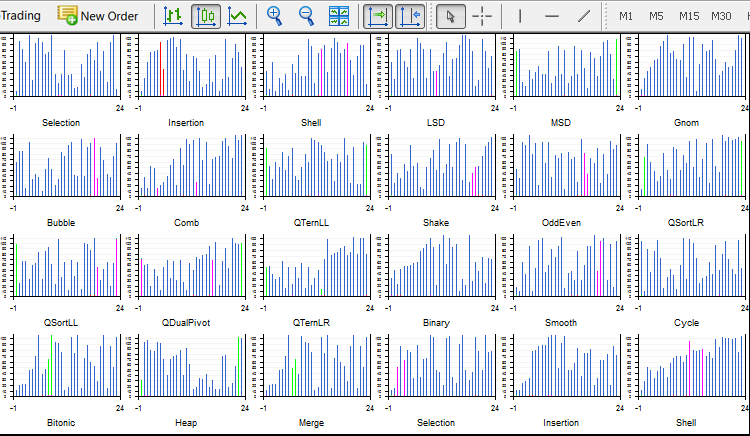
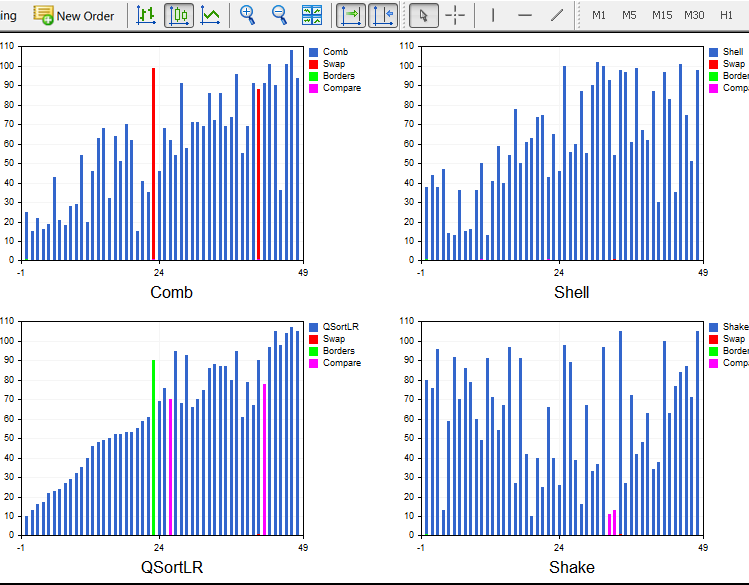
The working and quite stable version of Light.ex5 displays 4 sorts simultaneously. Here you can select the number of elements and sorting methods in each window. Besides, it is possible to select the method of shuffling the array: random, upward (already sorted), downward (sorted in reverse order) and an array with many identical elements (step array). For example, Quick Sort degrades down to O(n^2) on an array sorted in reverse order, while the Heap one always sorts for n*log(n). Unfortunately, the Sleep() function is not supported in the indicators, therefore the speed depends only on the system. Besides, the amount of resources allocated for each thread is also arbitrary. If the same sorting is launched in each window, they all make the finish in different ways.
Summary:
- Single-threaded VisualSort is 100% working
- Four-threaded Light is stable
- Twenty four-threaded Sort24 is unstable
We could follow the first option simulating multi-threading. In that case, we would be able to control the process. The Sleep() functions would work, each sorting would receive a strictly equal time, etc. But the very concept of MQL5 multi-threaded programming would be lost in that case.
Final version:
....................................................................................................................................................................
The list of attached files
- VisaulSort.ex5 - each sort presented individually
- Programs(Sort24.ex5, Light.ex5) - ready-made applications
- Audio files
- Codes. Program source codes - sorts, indicators, include files, EAs.
Editor's note
The author of the article implemented an interesting version of multi-threaded sorting using simultaneous launch of multiple indicators. This architecture loads the PC heavily, so we have slightly modified the author's source codes, namely:
- disabled calling for chart re-drawing from each indicator in the auxiliary.mq file
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void GBorders(double &a[],int i,int j) { XZ[0]=i;XZ[1]=j; YZ[0]=a[i]+2;YZ[1]=a[j]+5; CGreen.Update(XZ,YZ); Graphic.Redraw(false); Graphic.Update(false); }
- added the randomize() function that prepares the same random data in the array for all indicators
- added the external parameters to the IndSort2.mq5 file for defining the array size with random values (it has been rigidly equal to 24 in the author's version) and the initializing 'sid' number for data generation
input uint sid=0; //initialization of randomizer int N=64; //number of bars on histogramm
- added the timer for drawing the chart using ChartRedraw() to the Sort24.mq5 file
//+------------------------------------------------------------------+ //| Timer function | //+------------------------------------------------------------------+ void OnTimer() { double x=1.0; double y=0.0; static int start=0; //--- check each indicator's initialization flag in the loop for(int i=0;i<methods;i++) { string str; str=SymbolName(i,0); x=x*GlobalVariableGet(str); y=y+GlobalVariableGet(str); } //--- all indicators are successfully initialized if(x && start==0) { start=1; GlobalVariableSet("ALL",1); PlaySound("Sort.wav"); } //--- all sorts are over if(y==methods*2) { PlaySound("success.wav"); EventKillTimer(); } //--- update the sort charts ChartRedraw(); }
- moved the audio files to the <>\MQL5\Sounds folders, so that they can be included as a resource
#resource "\\Sounds\\Sort.wav"; #resource "\\Sounds\\success.wav"; #resource "\\Indicators\\Sort\\IndSort2.ex5"
The compilation-ready structure is attached in the moderators_edition.zip archive. Simply unpack it and copy to your terminal. If your PC is not too powerful, we recommend setting methods=6 or methods=12 in the inputs.
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/3118
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
 Creating Documentation Based on MQL5 Source Code
Creating Documentation Based on MQL5 Source Code
 Patterns available when trading currency baskets. Part III
Patterns available when trading currency baskets. Part III
 Custom indicators and infographics in CCanvas
Custom indicators and infographics in CCanvas
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
By the way, in the original youtube, all the sorting is done individually and then edited in a video editor. There is a link to a C++ programme there. But they are also written one at a time in C++, although C++ has more possibilities.
I read about it in the article. And by no means I wanted to reproach you for unfair work.
But it would be interesting to figure it out.
I read about it in the article. And by no means did I want to reproach you for unfair work.
But it would be interesting to look into it.
I know what the problem is. MQL5 is written for Windows, and we can't control threads...The indicators have multi-threading, but without interruptions.We should have written through the Expert Advisor...
Will you join the discussion?