Analisi Tecnica: Come analizziamo?

Introduzione

Sfogliando varie pubblicazioni, in qualche modo legate all'uso dell'analisi tecnica, ci imbattiamo in informazioni che a volte ti lasciano indifferente e talvolta appare il desiderio di commentare le informazioni lette. È questo desiderio che ha portato alla stesura di questo articolo, che prima di tutto è puntato a un tentativo di analizzare ancora una volta le nostre azioni e risultati utilizzando un particolare metodo di analisi.

Ridisegno

Se guardi i commenti sugli indicatori pubblicati su https://www.mql5.com/it/code, noterai che la stragrande maggioranza degli utenti ha un atteggiamento estremamente negativo nei confronti di quelli i cui valori precedentemente calcolati cambiano e vengono ridisegnati durante la formazione della barra successiva.

Una volta che diventa chiaro che l'indicatore viene ridisegnato non è più interessante per nessuno. Un tale atteggiamento nei confronti del ridisegno degli indicatori è spesso abbastanza ragionevole, ma in alcuni casi il ridisegno potrebbe non essere così terribile come sembra a prima vista. Per dimostrarlo, analizzeremo il più semplice indicatore SMA.

Nella Figura 1 il colore blu mostra la caratteristica di impulso del filtro a bassa velocità, che corrisponde all'indicatore SMA (15). Per il caso mostrato nella figura, l’SMA (15) è una somma degli ultimi 15 conteggi della sequenza di input in cui ciascuno dei conteggi di input viene moltiplicato per 1/15 corrispondente alla caratteristica dell'impulso presentata. Ora, avendo il valore SMA (15) calcolato sull'intervallo di 15 conteggi, dobbiamo decidere a quale punto di tempo assegnare questo valore. 

Accettando l’SMA (15) come media dei precedenti 15 conteggi di input, questo valore deve apparire come mostrato nel grafico superiore, quindi deve corrispondere a una barra zero. In caso di accettazione di SMA (15) come filtro a bassa velocità con la caratteristica di impulso di una lunghezza finita, il valore calcolato, tenendo conto del ritardo nel filtro, deve corrispondere alla barra numero sette, come mostrato nel grafico in basso.

Quindi, con il semplice spostamento, trasformiamo il grafico di una media mobile nel grafico di un filtro a bassa velocità con latenza zero.

Da notare che, in caso di utilizzo di grafici a latenza zero, alcuni metodi di analisi tradizionali cambiano leggermente il loro significato. Ad esempio, l'intersezione di due grafici MA con periodi diversi e l'intersezione degli stessi grafici con ritardo compensato si verificheranno in momenti diversi. Nel secondo caso otterremo momenti di intersezione che saranno determinati solo dai periodi MA, ma non dalla loro latenza.

Tornando alla figura 1 è facile vedere nel grafico in basso che la curva SMA (15) non raggiunge i conteggi più recenti del segnale di ingresso per il valore pari alla metà del periodo di media. Si sta formando un'area dei sette conteggi, in cui il valore SMA (15) non è definito. Possiamo presumere che, dopo aver compensato il ritardo, abbiamo perso alcune informazioni a causa di un'area di ambiguità, ma questo è fondamentalmente sbagliato.

La stessa ambiguità è sul grafico in alto (figura 1), ma a causa dello spostamento è nascosto nella parte destra dove non ci sono conteggi di input. Il grafico MA perde il suo legame temporale alla sequenza di input e la dimensione del ritardo dipende dal periodo di smoothing MA a causa dello spostamento.

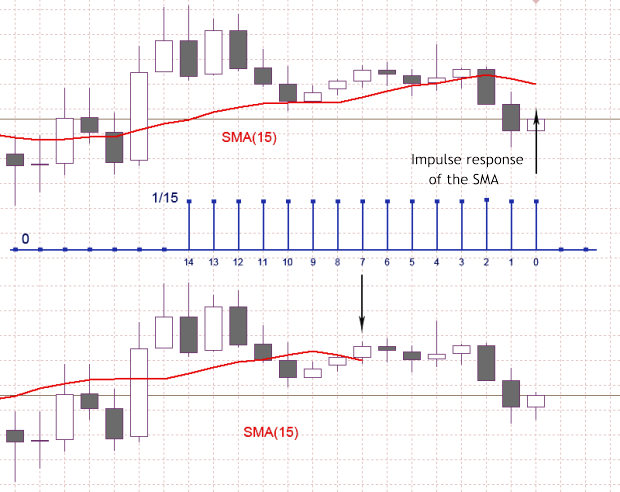
 Figura 1. Risposta all'impulso dell’SMA (15)

Se tutti i ritardi verificatisi vengono sempre compensati quando si utilizza MA con periodi diversi, ciò si tradurrà in grafici con un certo legame temporale alla sequenza di input e tra loro. Ma oltre ai vantaggi inconfutabili, questo approccio assume aree di ambiguità. La ragione del loro verificarsi sono le caratteristiche ben note dell'elaborazione delle sequenze a lunghezza finita nel tempo, ma non i nostri errori di ragionamento.

Stiamo affrontando i problemi che si verificano ai bordi di tali sequenze utilizzando algoritmi di interpolazione, varie filtrazioni, smoothing, ecc. E nessuno ha il pensiero di nascondere la parte del risultato con il suo spostamento.

Devo ammettere che i grafici MA con una certa parte non disegnata sono una rappresentazione più corretta di un filtro, ma sembrano molto insoliti. Dal punto di vista formale, non possiamo calcolare il valore del filtro SMA (15), Shift=-7 per i conteggi di output con l'indice inferiore a 7. Quindi c'è un altro modo per smussare il conteggio sul bordo nel caso della sequenza di input?

Proviamo a filtrare questi conteggi usando lo stesso algoritmo SMA, ma diminuendo il suo periodo di smoothing con ogni barra che si avvicina allo zero. Inoltre, non dobbiamo dimenticare la compensazione del ritardo del filtro utilizzato.

 

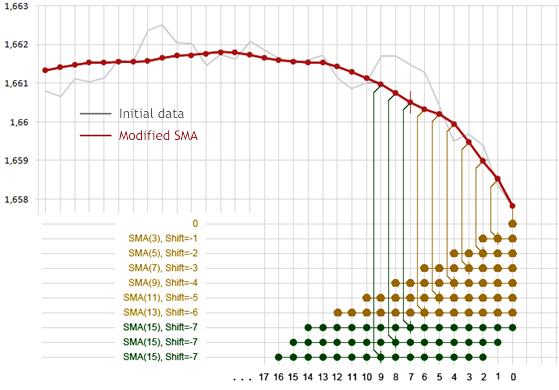
Figura 2. SMA modificato

La Figura 2 mostra come verranno formati i conteggi di output con indici da 0 a 6. I conteggi che prenderanno parte al calcolo del valore medio sono convenzionalmente contrassegnati con punti colorati nella parte inferiore della figura e le linee verticali mostrano a quale conteggio di output verrà assegnata questa media. Sulla barra zero non viene effettuata alcuna elaborazione, il valore della sequenza di input viene assegnato a quello di output. Per la sequenza di output con indici vengono effettuati sette o più calcoli con il solito SMA (15) Shift =- 7.

È ovvio che quando si utilizza un tale approccio il grafico di output sull'intervallo dell'indice da 0 a 6 verrà ridisegnato ad ogni nuova occorrenza di barra e l'intensità del ridisegno aumenterà con una diminuzione dell'indice. Allo stesso tempo viene compensato un ritardo per qualsiasi conteggio della sequenza di output.

Nell'esempio analizzato, abbiamo un indicatore di ridisegno che è un analogo dello standard SMA (15), ma con un ritardo zero e informazioni extra sul bordo della sequenza di input, assente nella SMA standard (15). Anche accettando zero ritardi e informazioni extra come vantaggio, tuttavia abbiamo un indicatore di ridisegno, ma più informativo dell'indicatore SMA standard.

Va sottolineato che il ridisegno in questo esempio non porta a conseguenze catastrofiche. Sul grafico risultante ci sono le stesse informazioni dell’SMA standard, con i suoi conteggi spostati a sinistra.

Nell'esempio considerato è stato scelto il periodo SMA dispari, che ha completamente compensato il ritardo nel tempo per SMA:

t = (N-1)/2,

dove N è un periodo di smoothing.

A causa del fatto che per i valori pari di N il ritardo non può essere completamente compensato utilizzando questo approccio e il metodo offerto di conteggio dello smoothing sul bordo della sequenza non è l'unico possibile, la variante della costruzione dell'indicatore è considerata solo come un esempio qui, ma non come un indicatore completo.

Multi-timeframe

Sui siti web MQL4 e MQL5 è possibile visualizzare i cosiddetti indicatori multi-timeframe. Proviamo a capire cosa ci dà il multi-timeframe con un esempio di indicatore "iUniMA MTF ".

Supponiamo di trovarci nella finestra temporale M1 più bassa e di mostrare lo smoothing di Open o Close del valore dell'intervallo di tempo M30 nella stessa finestra, applicando SMA (3) per lo smoothing. È noto che la sequenza temporale M30 si forma dalla sequenza temporale M1 campionando ogni trentesimo valore e scartando i restanti 29 valori. I dubbi sembrano essere ragionevoli nell'utilizzare la sequenza temporale M30. 

Se abbiamo accesso a una certa quantità di informazioni sul periodo di tempo M1, allora qual è il punto di contatto con il periodo di tempo M30, che contiene solo la trentesima parte di tali informazioni? Nel caso considerato, eliminiamo intenzionalmente la maggior parte delle informazioni disponibili ed elaboriamo ciò che rimane dell’SMA (3) e visualizziamo il risultato nella finestra di origine del timeframe M1.

È ovvio che le azioni descritte sembrano piuttosto strane. Non è più semplice applicare SMA (90) alla sequenza completa dell'intervallo di tempo M1? La frequenza della sezione di filtro SMA (90) sull'intervallo di tempo M1 è uguale alla frequenza della sezione di filtro SMA (3) sull'intervallo di tempo M30.

Nella figura 3 viene mostrato un esempio di utilizzo dell'indicatore multi-timeframe "iUniMA MTF" sul grafico della coppia di valute EURUSD M1. La curva blu è il risultato dell'applicazione di SMA (3) alla sequenza temporale M30. Nella stessa figura, la curva di colore rosso è il risultato ottenuto con il normale indicatore "Media Mobile". Quindi il risultato dell'applicazione dell'indicatore SMA standard (90) è più naturale.

E non sono richieste tecniche speciali.

 

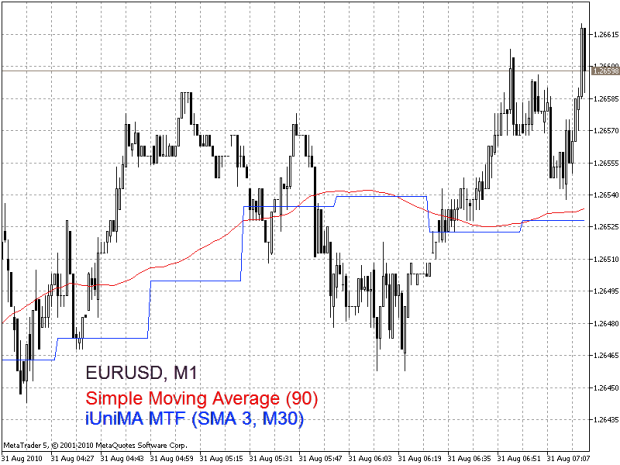
Figura 3. Utilizzo dell'indicatore multi-timeframe

Un'altra variante dell'utilizzo di indicatori multi-timeframe è possibile quando un'informazione dall'intervallo di tempo più basso, in base a quello corrente, viene mostrata su un terminale. Questa variante può essere utile se è necessario comprimere la scala di quotazione visualizzando anche più di quanto consentito dal terminale nel periodo di tempo più basso. Ma anche in questo caso, non è possibile ottenere ulteriori informazioni sulle quotazioni.

È più facile passare al timeframe più basso e gestire tutta l'elaborazione dei dati con indicatori regolari, ma non con quelli multi-timeframe.

Quando si sviluppano indicatori personalizzati o Expert Advisor, possono verificarsi situazioni particolari nel momento in cui un'organizzazione di accesso a varie sequenze temporali è ragionevole ed è l'unica soluzione possibile, ma, anche in questo caso, dobbiamo ricordare che le sequenze temporali più elevate sono formate da quelle inferiori e non portano alcuna informazione univoca aggiuntiva.

Grafico a candele

Nelle pubblicazioni di analisi tecnica possiamo spesso incontrare relazioni eccitate con tutto ciò che è collegato ai grafici a candele. Ad esempio, nell'articolo "Analysing Candlestick Patterns" viene detto che: "Il vantaggio delle candele è che rappresentano i dati in un modo in cui è possibile vedere lo slancio all'interno dei dati". I grafici a candele giapponesi possono aiutarti a penetrare "all'interno" dei mercati finanziari, il che è molto difficile da fare con altri metodi grafici.

E questa non è l'unica fonte di tali affermazioni. Proviamo a capire se i grafici a candele ci permettono di entrare nei mercati finanziari.

Le sequenze di valori "Low", "High", "Open" e "Close" vengono utilizzate per la rappresentazione dei tassi sotto forma di grafici a candele. Ricordiamoci che tipo di valori sono. I valori "Low" e "High" sono uguali ai valori minimi e massimi sul periodo di tempo scelto. Il valore "Open" è uguale al primo valore noto dei tassi nel periodo analizzato. Il valore "Close" è uguale all'ultimo valore noto dei tassi nel periodo analizzato. Che cosa potrebbe significare?

Ciò significa principalmente che da qualche parte ci sono tassi di mercato da cui si formano i valori "Low", "High", "Open" e "Close". I valori «Low», «High», «Open» e «Close» non sono strettamente legati al tempo con questo metodo di formazione. Inoltre, non c'è modo di ripristinare i tassi iniziali da queste sequenze. La cosa più interessante è che la stessa combinazione di valori «Low», «High», «Open» e «Close» su qualsiasi barra di qualsiasi intervallo di tempo può essere formata da un numero infinito di varianti della sequenza di tassi originale. Queste conclusioni sono banali e basate su fatti ben noti.

Pertanto, le informazioni originali sono irreversibilmente distorte se si utilizzano i tassi di mercato sotto forma di grafici a candele. Utilizzando rigorosi metodi matematici di analisi per la valutazione del comportamento dei tassi da parte di una qualsiasi delle sequenze «Low», «High», «Open» o «Close», i risultati sono collegati non ai tassi di mercato, ma alla loro rappresentazione distorta. Tuttavia, dobbiamo ammettere che l'analisi dei grafici a candele ha molti sostenitori.

Come si potrebbe spiegare? Forse il segreto è che, inizialmente, l'obiettivo della rappresentazione dei tassi sotto forma di grafici a candele era un'analisi di mercato rapida, intuitiva e visiva, ma non applicando metodi di analisi matematica ai grafici a candele.

Quindi, per capire come la rappresentazione dei tassi sotto forma di grafici a candele può essere utilizzata con l'analisi tecnica, passiamo alla teoria del riconoscimento dei modelli, la quale è più vicina ai soliti metodi decisionali umani rispetto ai metodi di analisi matematica formale.

Nella figura 4, secondo la teoria del riconoscimento dei modelli, viene disegnato uno schema semplificato del processo decisionale. Una decisione, in questo caso, può essere una definizione di momento di inizio o fine della tendenza e il rilevamento di momenti ottimali per l'apertura di una posizione di momenti temporali, ecc.

 

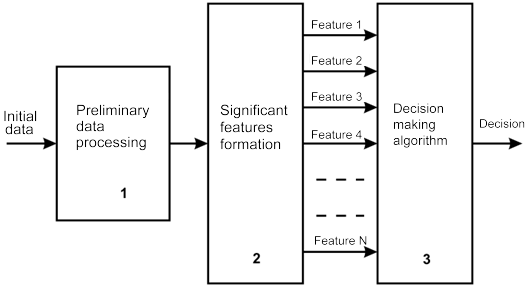
Figura 4. Schema decisionale

Come mostrato nella figura 4, i dati iniziali (tassi) sono trattati in via preliminare e da essi si formano caratteristiche significative nel blocco 2. Nel nostro caso questi valori sono «Low», «High», «Open» e «Close». Non possiamo influire sui processi nei blocchi 1 e 2. Sul lato terminale sono disponibili solo le funzionalità che sono già dedicate a noi. Queste funzionalità arrivano al blocco 3, dove le decisioni vengono prese sulla loro base.

L'algoritmo decisionale può essere implementato nel software o manualmente nel rigoroso rispetto delle specifiche. Possiamo sviluppare e in qualche modo implementare gli algoritmi decisionali, ma non possiamo scegliere caratteristiche significative dalla sequenza dei tassi analizzati perché questa sequenza non è disponibile per noi.

Nell’aumentare la probabilità di prendere la decisione giusta, la cosa più cruciale è la scelta delle caratteristiche significative e della loro quantità essenziale, ma non abbiamo questa importante possibilità. In questo caso, impattare sull'affidabilità di questo o quel riconoscimento della situazione di mercato è tranquillamente difficile, poiché anche l'algoritmo decisionale più avanzato non è in grado di compensare gli svantaggi connessi alla scelta non ottimale delle funzionalità.

Cos'è un algoritmo decisionale secondo questo schema? Nel nostro caso, questo è un insieme di regole pubblicate nella ricerca di analisi dei grafici a candele. Ad esempio, la definizione dei tipi di grafici a candele, la divulgazione del loro significato di varie combinazioni, ecc.

Facendo riferimento alla teoria del riconoscimento dei modelli, arriviamo alla conclusione che l'analisi dei grafici a candele si adatta allo schema di questa teoria, ma non abbiamo alcun motivo per affermare che la scelta dei valori «Low», «High», «Open» e «Close» come caratteristiche significative sia la migliore. Inoltre, una scelta non ottimale di funzionalità può ridurre drasticamente la probabilità di prendere decisioni corrette in un processo di analisi delle tariffe.

Tornando all'inizio, possiamo dire con sicurezza che l'analisi del grafico a candele difficilmente "penetrerebbe "all'interno" dei mercati finanziari" o "vedrebbe lo slancio all'interno dei dati". Inoltre, la sua efficienza rispetto ad altri metodi di analisi tecnica può causare seri dubbi.

Conclusione

L'analisi tecnica è un'area abbastanza conservativa. La formazione dei postulati di base dell'analisi tecnica ha preso campo nei secoli 18^-19^ e questa base ha raggiunto i giorni nostri quasi invariata. Allo stesso tempo, nell'ultimo decennio la struttura del mercato globale è cambiata radicalmente durante il suo sviluppo. Lo sviluppo del trading online ha contribuito alla natura del comportamento del mercato.

In questa situazione, anche l'uso delle teorie e dei metodi più popolari dell'analisi tecnica classica non sempre ci fornisce una sufficiente efficienza di trading.

Tuttavia, la disponibilità di computer e l'interesse per il trading sui mercati mostrati da persone di varie professioni possono stimolare lo sviluppo di metodi di analisi tecnica. È ovvio che oggi l'analisi di mercato ha bisogno di uno sviluppo di strumenti analitici più accurati e sensibili.