
Analisi delle principali caratteristiche delle serie temporali
Introduzione
L'analisi dei processi rappresentati da serie di prezzi è un compito piuttosto impegnativo che spesso richiede una notevole quantità di tempo e sforzi. Ha a che fare con le peculiarità delle sequenze in studio e con il fatto che, nonostante un gran numero di pubblicazioni varie, a volte è difficile trovare una soluzione di programmazione adeguata per un determinato problema.
Anche se è stato trovato uno script o un indicatore adatto, ciò non significa che il suo codice sorgente non debba essere adattato all'attività da svolgere.
Inoltre, anche per la soluzione di problemi semplici, questi programmi possono richiedere l'uso di parametri di input il cui punto è ben noto agli sviluppatori ma non è sempre completamente chiaro ad un utente.
Queste difficoltà non possono certamente diventare un ostacolo insormontabile nella ricerca seria, ma quando si vuole dimostrare un'ipotesi o semplicemente soddisfare la propria curiosità, tale curiosità rimarrà il più delle volte insoddisfatta. Ecco perché ho avuto l'idea di creare uno strumento di programmazione universale che consenta una facile analisi preliminare delle principali caratteristiche e parametri di una sequenza di input.
Tale strumento deve essere assolutamente semplice nella sua installazione, senza richiedere alcun parametro di input per semplificarne al massimo l'uso. Allo stesso tempo, i parametri e le caratteristiche stimati devono riflettere adeguatamente e chiaramente la natura della sequenza in esame.
La stima preliminare delle caratteristiche potrebbe aiutare a determinare i modi per ulteriori studi approfonditi o rifiutare qualsiasi ipotesi data in una fase iniziale ed evitare la perdita di tempo per quanto riguarda ulteriori studi.
È noto che il software universale è spesso scarsamente paragonato al software personalizzato in termini di caratteristiche. Si tratta di un prezzo regolare per l'universalità che viene quasi sempre raggiunto attraverso l'intero sistema di compromessi. Questo articolo rappresenta comunque uno sforzo per creare uno strumento universale che permetta di facilitare al massimo l'analisi preliminare delle caratteristiche delle sequenze.
Installazione e capacità
Il file TSAnalysis.zip, che si trova alla fine dell'articolo, include la directory \TSAnalysis contenente tutti i file necessari per il lavoro. Dopo la decompressione, la directory con tutto il suo contenuto (senza rinominarla) deve essere copiata nella directory \MQL5\Scripts. La directory copiata \TSAnalysis contiene uno script di test TSAexample.mq5, il quale può essere eseguito dopo la compilazione.
Questo script deve preparare i dati e chiamare il browser predefinito per visualizzarli utilizzando la classe TSAnalysis. Va notato che l'uso di DLL esterne deve essere abilitato nel Terminale per il normale funzionamento della classe TSAnalysis. Per disinstallare, è sufficiente eliminare semplicemente la directory \TSAnalysis.
L'intero codice sorgente utilizzato per l'analisi delle sequenze è rappresentato dalla classe TSAnalysis e può essere trovato solo nel file TSAnalysis.mqh.
Quando si utilizza questa classe per una sequenza di input,stima e può visualizzare le seguenti informazioni:
- Numero di elementi nella sequenza;
- Valore massimo e minimo della sequenza (max, min);
- Mediana;
- Mezzo;
- Varianza;
- Deviazione standard;
- Varianza imparziale;
- Deviazione standard imparziale;
- Asimmetria;
- Curtosi;
- Curtosi in eccesso;
- Test Jarque-Bera;
- Test Jarque-Bera del valore p;
- Test Jarque-Bera regolato;
- Valori p del test Jarque-Bera regolati;
- Limiti per valori non appartenenti alla sequenza data (outlier);
- Dati dell'istogramma;
- Dati del grafico di probabilità normale;
- Dati del correlogramma;
- Bande di confidenza al 95% per la funzione di autocorrelazione;
- Dati del grafico spettrale calcolati tramite la funzione di autocorrelazione;
- Dati del grafico della funzione di autocorrelazione parziale;
- Dati del grafico di stima spettrale calcolati utilizzando il metodo dell'entropia massima.
Per visualizzare visivamente i risultati ottenuti nella classe TSAnalysis in esame, viene utilizzato un metodo show virtuale che è responsabile solo di un metodo di visualizzazione delle informazioni pre-preparato.
Pertanto, ridefinendo questo metodo nei discendenti della classe TSAnalysis, è possibile organizzare l'output dei risultati in qualsiasi modo possibile, non solo utilizzando un file HTML come nella classe base dove, al momento della generazione di un file di dati per la visualizzazione dei grafici, viene chiamato un browser Web.
Prima di procedere alla revisione della classe TSAnalysis, illustreremo il risultato del suo utilizzo attraverso una sequenza di test di dati. La figura seguente mostra il risultato operativo dello script TSAexample.mq5.
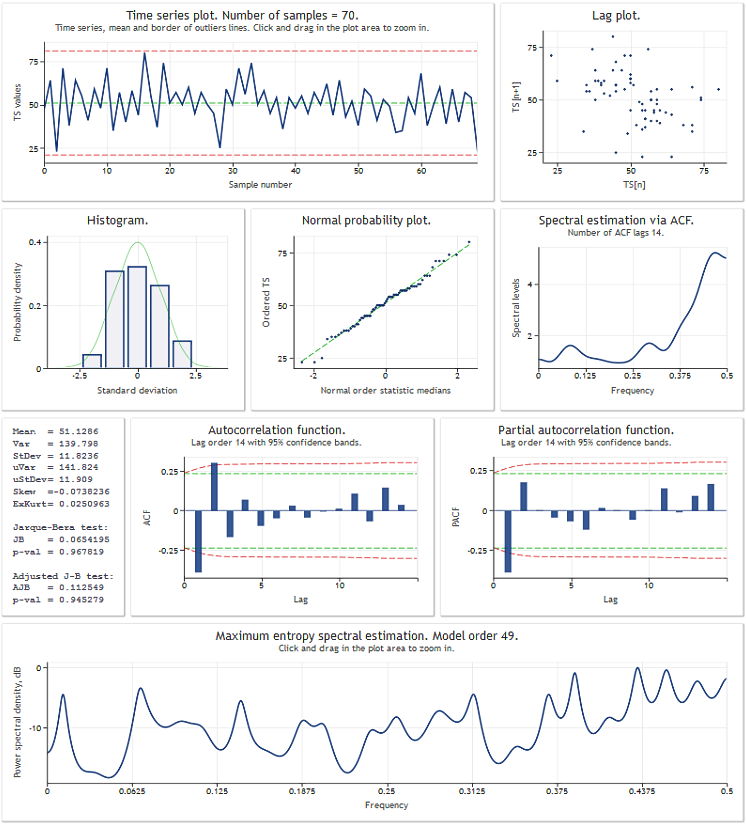
Figura 1. Risultato operativo dello script TSAexample.mq5
Dopo una breve familiarizzazione con la capacità della classe TSAnalysis, passeremo ora a una considerazione più dettagliata della classe stessa.
Classe TSAnalysis
La classe TSAnalysis (vedi TSAnalysis.mqh) include un solo metodo disponibile (pubblico) Calc, il quale è responsabile di tutti i calcoli necessari a seguito dei quali viene chiamato lo spettacolo del metodo virtuale. Il metodo show verrà brevemente rivisto in seguito e ora procederemo a un chiarimento passo-passo del punto principale dei calcoli effettuati.
Quando si utilizza la classe TSAnalysis, vengono imposti alcuni vincoli alla sequenza di input in studio.
In primo luogo, la sequenza deve essere composta da almeno otto elementi. Tale vincolo, probabilmente, non è molto rigido in quanto difficilmente sarà necessario studiare sequenze così brevi per scopi pratici.
Oltre al vincolo di lunghezza minima della sequenza, il valore di varianza della sequenza di input deve essere diverso da quello vicino allo zero. Questo requisito è dovuto al fatto che il valore di varianza viene utilizzato in ulteriori calcoli e non può essere inferiore a un certo valore per un risultato stabile.
Le sequenze con un valore di varianza molto basso non sono così comuni, quindi anche questo vincolo probabilmente non sarà un grave svantaggio. Se la sequenza è troppo breve e c'è un valore di varianza vicino allo zero, i calcoli verranno interrotti e nel registro verrà visualizzato un messaggio di errore pertinente.
C'è ancora un altro vincolo implicito per quanto riguarda la lunghezza massima consentita di una sequenza di input. Questo vincolo non è impostato esplicitamente, dipende dalle prestazioni di un computer in uso e dalla sua capacità di memoria ed è determinato in modo puramente soggettivo dal tempo necessario per l'esecuzione dello script e dalla velocità di disegno dei risultati in un browser web. Si presume che l'elaborazione di sequenze costituite da 2-3 mila elementi non dovrebbe causare gravi difficoltà.
Il calcolo dei parametri statistici della sequenza si baserà sul frammento sottostante del codice sorgente del metodo Calc (vedi TSAnalysis.mqh).
La descrizione dell'algoritmo impiegato può essere trovata a questo link "Algorithms for Calculating Variance".
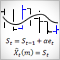
. . . Mean=0; sum2=0; sum3=0; sum4=0; for(i=0;i<NumTS;i++) { n=i+1; delta=TS[i]-Mean; a=delta/n; Mean+=a; // Mean (average) sum4+=a*(a*a*delta*i*(n*(n-3.0)+3.0)+6.0*a*sum2-4.0*sum3); // sum of fourth degree b=TS[i]-Mean; sum3+=a*(b*delta*(n-2.0)-3.0*sum2); // sum of third degree sum2+=delta*b; // sum of second degree } . . .
Come risultato dell'esecuzione di questo frammento, vengono calcolati i seguenti valori
![]()
dove n = NumTS è il numero di elementi nella sequenza.
Utilizzando i valori ottenuti, calcoliamo i seguenti parametri.
Varianza e deviazione standard:
![]()
Varianza imparziale e deviazione standard:
![]()
Asimmetria:
![]()
Curtosi. La curtosi minima è 1, la curtosi della sequenza normalmente distribuita sarà 3.
![]()
Curtosi in eccesso:
![]()
In questo caso, la curtosi minima è -2 e la curtosi della sequenza normalmente distribuita sarà 0.
Convenzionalmente, quando si esegue il primo test preliminare di bontà di adattamento su una sequenza, viene utilizzata la statistica di Jarque-Bera, la quale viene facilmente calcolata utilizzando i valori noti di asimmetria e curtosi. La significatività statistica (valore p) per la statistica di Jarque-Bera, all'aumentare della lunghezza della sequenza, tende asintoticamente alla funzione di distribuzione del chi quadrato inverso con due gradi di libertà.
Quindi,
![]()
Quando la sequenza è breve, il valore p ottenuto in questo modo è destinato ad avere un errore apprezzabile. Questa stessa opzione di calcolo è tuttavia molto spesso utilizzata. È difficile dire perché. Forse ha a che fare con formule semplici e chiare utilizzate o potrebbe essere il fatto che la statistica di Jarque-Bera di per sé non rappresenta un test di bontà ideale e quindi non ha senso calcoli più accurati.
Nel nostro caso, la statistica di Jarque-Bera e il relativo valore p sono calcolati nel metodo Calc (TSAnalysis.mqh) in conformità con le formule di cui sopra.
Inoltre, viene calcolato anche un test Jarque-Bera regolato:
![]()
dove
![]()
La versione regolata del test Jarque-Bera per brevi sequenze riduce l'errore del valore p calcolato nel modo specificato, ma non lo elimina completamente.
Il risultato finale dell'analisi deve includere un grafico di sequenza di input che mostra la linea corrispondente alla media e le linee che definiscono i limiti al di fuori dei quali i valori possono essere considerati non validi e non appartenenti alla sequenza data (outlier).
Questi limiti sono, in questo caso, calcolati come segue:
![]()
![]()
Questa formula è fornita nel libro di S. V. Bulashev "Statistics for Traders" con un riferimento al libro di P. V. Novitsky e I.A. Zograf "Estimation of Error in Measurement Results". Dopo aver determinato i limiti, non è prevista alcuna elaborazione della sequenza di input; i limiti devono essere visualizzati solo a fini informativi.
Oltre al grafico della sequenza di input, è previsto un istogramma che riflette una stima empirica della distribuzione della sequenza di input. Il numero di intervalli per l'istogramma è definito come segue (S. V. Bulashev "Statistics for Traders"):
![]()
Il risultato viene arrotondato al valore intero dispari più vicino. Se il valore ottenuto è inferiore a cinque, viene utilizzato il valore di 5.
Il numero di elementi negli array di dati per l'asse X e l'asse Y dell'istogramma corrisponde al numero ottenuto di intervalli più due, poiché una colonna di valore zero viene aggiunta a sinistra e a destra dell'istogramma.
Di seguito è riportato un frammento del codice (vedi TSAnalysis.mqh) che prepara i dati per la costruzione di un istogramma.
. . . n=(int)MathRound((Kurt+1.5)*MathPow(NumTS,0.4)/6.0); if((n&0x01)==0)n--; if(n<5)n=5; // Number of bins ArrayResize(XHist,n); ArrayResize(YHist,n); ArrayInitialize(YHist,0.0); a=MathAbs(TSort[0]-Mean); b=MathAbs(TSort[NumTS-1]-Mean); if(a<b)a=b; v=Mean-a; delta=2.0*a/n; for(i=0;i<n;i++)XHist[i]=(v+(i+0.5)*delta-Mean)/StDev; // Histogram. X-axis for(i=0;i<NumTS;i++) { k=(int)((TS[i]-v)/delta); if(k>(n-1))k=n-1; YHist[k]++; } for(i=0;i<n;i++)YHist[i]=YHist[i]/NumTS/delta*StDev; // Histogram. Y-axis . . .
Nel codice sopra:
- NumTS è il numero di elementi nella sequenza,
- XHist[] e YHist[] sono array contenenti valori rispettivamente per gli assi X e Y,
- TSort[] è l'array contenente una sequenza di input ordinata.
Utilizzando questo metodo di calcolo, i valori dell'asse X saranno espressi in unità di deviazione standard e i valori dell'asse Y corrisponderanno alla densità di probabilità.
Ai fini della creazione di un grafico con l'asse di distribuzione normale, la sequenza di input ordinata in ordine crescente viene utilizzata come valori dell'asse Y. Il numero di valori degli assi Y e X dovrebbe essere uguale. Per calcolare i valori dell'asse X, bisogna prima trovare i valori mediani come nella legge di distribuzione uniforme:
![]()
![]()
![]()
Sono inoltre utilizzati per calcolare i valori dell'asse X mediante la funzione di distribuzione normale inversa (vedi metodo ndtri).
Per creare un grafico della funzione di autocorrelazione (ACF), si deve tracciare la funzione di autocorrelazione parziale (PACF) e calcolare la stima spettrale utilizzando il metodo dell'entropia massima, Occorre trovare i valori della funzione di autocorrelazione per la sequenza di input.
Definiremo il numero di valori che devono essere visualizzati sui grafici ACF e PACF come segue:
![]()
![]()
![]()
Il numero di valori determinati nel modo specificato sarà abbastanza sufficiente per la visualizzazione della funzione di autocorrelazione sul grafico, ma per un ulteriore calcolo della stima spettrale è consigliabile avere un numero maggiore di valori ACF calcolati e che nel nostro caso saranno uguali all'ordine del modello autoregressivo impiegato.
L'ordine del modello IP sarà definito dal valore NLags ottenuto:
![]()
![]()
È abbastanza difficile formalizzare il processo di determinazione dell'ordine ottimale del modello per la stima spettrale. Un modello di ordine basso porterà risultati estremamente uniformi, mentre un modello di ordine elevato porterà molto probabilmente a una stima spettrale instabile con un ampio intervallo di valori.
Inoltre, l'ordine del modello è influenzato anche dalla natura della sequenza di input, pertanto l'ordine IP determinato utilizzando la formula di cui sopra sarà in alcuni casi troppo alto e in altri casi troppo basso. Sfortunatamente, non è stato trovato un approccio efficace per determinare l'ordine del modello richiesto.
Pertanto, per la sequenza di input si dovrà determinare il numero dei valori ACF pari all'ordine del modello IP che viene utilizzato per la stima spettrale della sequenza.
. . . ArrayResize(cor,IP); a=0; for(i=0;i<NumTS;i++)a+=TSCenter[i]*TSCenter[i]; for(i=1;i<=IP;i++) { c=0; for(k=i;k<NumTS;k++)c+=TSCenter[k]*TSCenter[k-i]; cor[i-1]=c/a; // Autocorrelation } . . .
Questo frammento del codice sorgente (vedi TSAnalysis.mqh) illustra il processo di calcolo della funzione di autocorrelazione (ACF). Il risultato del calcolo viene inserito nell’array cor[]. Come si può vedere, viene calcolato prima un coefficiente di autocorrelazione zero, seguito dal calcolo e dalla normalizzazione dei coefficienti rimanenti nel ciclo. A tale normalizzazione, il coefficiente zero sarà sempre uguale a uno, quindi non è necessario salvarlo nell’array cor[].
Questo array contiene il numero di coefficienti uguali a IP a partire dal primo. Quando si calcola l'ACF, viene utilizzato l'array TSCenter[]; contiene la sequenza di input degli elementi da cui è stato sottratto il valore medio.
Al fine di ridurre il tempo necessario per il calcolo dell'ACF, è possibile utilizzare i metodi che impiegano algoritmi di trasformazione rapida, ad esempio FFT. Ma, in questo caso, il tempo necessario per calcolare l'ACF è abbastanza accettabile, quindi, probabilmente, non c'è bisogno di complicare il codice di programmazione.
Un grafico ACF (correlogramma) può essere facilmente costruito utilizzando i valori ottenuti dei coefficienti di correlazione. Per poter visualizzare le bande di confidenza del 95% su questo grafico, i loro valori possono essere calcolati utilizzando le formule seguenti.
Per le bande utilizzate per testare la casualità:
![]()
Per le bande utilizzate per determinare l'ordine del modello ARIMA:
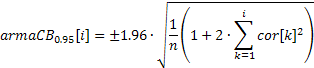
Il valore della banda di confidenza nel primo caso sarà costante e aumenterà con l'aumento del coefficiente di autocorrelazione nel secondo caso.
Una risposta in frequenza molto fluida della sequenza di ingresso che riflette solo l'andamento generale della distribuzione della frequenza può talvolta essere interessante. Ad esempio, aumenti considerevoli della gamma di basse o alte frequenze, predominanza di frequenze di fascia media, ecc.
Si consiglia di visualizzare tale risposta in frequenza in scala lineare per enfatizzare fortemente le gamme di frequenza dominanti. Tale risposta in ampiezza-frequenza (AFR) può essere tracciata in base ai coefficienti di autocorrelazione ottenuti in precedenza. Per il calcolo dell'AFR useremo il numero di coefficienti pari al numero visualizzato sul grafico ACF.
Dato che questo numero non è grande, le stime spettrali ottenute come risultato dovrebbero essere abbastanza fluide.
La risposta in frequenza della sequenza, in questo caso, può essere espressa per mezzo di coefficienti di autocorrelazione come segue:
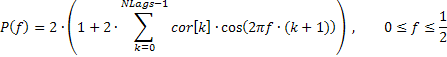
Un frammento del codice (vedi TSAnalysis.mqh) che viene utilizzato per calcolare l'AFR in base alla formula fornita, è riportato di seguito
. . . n=320; // Number of X-points ArrayResize(Spect,n); v=M_PI/n; for(i=0;i<n;i++) { a=i*v; b=0; for(k=0;k<NLags;k++)b+=((double)NLags-k)/(NLags+1.0)*ACF[k]*MathCos(a*(k+1)); Spect[i]=2.0*(1+2*b); // Spectrum Y-axis } . . .
Va notato che i valori del coefficiente di correlazione nel codice sopra sono, per un ulteriore livellamento, moltiplicati per la funzione di finestra triangolare.
Per un'analisi spettrale più dettagliata, il metodo dell'entropia massima è stato selezionato come un altro compromesso. La selezione di un metodo di stima spettrale universale è piuttosto difficile. Gli svantaggi associati ai metodi classici non parametrici di analisi spettrale sono ben noti.
I metodi di periodogramma e correlogramma possono servire come esempi di tali metodi, i quali sono facilmente implementati utilizzando algoritmi di trasformata di Fourier veloci. Ma nonostante l'elevata stabilità dei risultati, questi metodi richiedono sequenze di input molto lunghe per ottenere una potenza di risoluzione adeguata. Al contrario, i metodi parametrici di stima spettrale (ad esempio i metodi autoregressivi) possono garantire una risoluzione molto più elevata per brevi sequenze.
Sfortunatamente, quando li si utilizza, si deve prendere in considerazione non solo le peculiarità di una certa implementazione di questi metodi, ma anche la natura della sequenza di input. Allo stesso tempo, è abbastanza difficile determinare l'ordine ottimale del modello AR il cui aumento porta ad aumentare la potenza di risoluzione ma i risultati sparsi ottenuti. Se vengono utilizzati modelli di ordine molto elevato, questi metodi iniziano a dare risultati instabili.
Le caratteristiche comparative di diversi algoritmi di stima spettrale possono essere trovate nel libro di S. L. Marple "Digital Spectral Analysis with Applications". Come già accennato, in questo caso è stato selezionato il metodo dell'entropia massima. Questo metodo si traduce probabilmente nella potenza di risoluzione più bassa rispetto ad altri metodi autoregressivi, ma è stato selezionato al fine di ottenere stime spettrali più stabili.
Diamo un'occhiata all'ordine dei calcoli autoregressivi delle stime spettrali. La scelta dell'ordine del modello è stata toccata in precedenza, quindi assumeremo che l'ordine del modello sia già stato selezionato essendo uguale a IP e che siano stati calcolati i coefficienti di autocorrelazione IP cor[].
Al fine di ottenere i coefficienti autoregressivi utilizzando i noti coefficienti di autocorrelazione, l'algoritmo Levinson-Durbin viene utilizzato implementato come metodo LevinsonRecursion.
//----------------------------------------------------------------------------------- // Calculate the Levinson-Durbin recursion for the autocorrelation sequence R[] // and return the autoregression coefficients A[] and partial autocorrelation // coefficients K[] //----------------------------------------------------------------------------------- void TSAnalysis::LevinsonRecursion(const double &R[],double &A[],double &K[]) { int p,i,m; double km,Em,Am1[],err; p=ArraySize(R); ArrayResize(Am1,p); ArrayInitialize(Am1,0); ArrayInitialize(A,0); ArrayInitialize(K,0); km=0; Em=1; for(m=0;m<p;m++) { err=0; for(i=0;i<m;i++)err+=Am1[i]*R[m-i-1]; km=(R[m]-err)/Em; K[m]=km; A[m]=km; for(i=0;i<m;i++)A[i]=(Am1[i]-km*Am1[m-i-1]); Em=(1-km*km)*Em; ArrayCopy(Am1,A); } return; }
Il metodo ha tre parametri di input. Tutti e tre i parametri sono riferimenti a array. Quando si chiama questo metodo, i coefficienti di autocorrelazione di input devono essere posizionati nel primo array R[]. Nel corso dei calcoli questi valori rimangono invariati.
I coefficienti di autocorrelazione ottenuti saranno collocati nell’array A[]. Oltre a ciò, la matrice K[] conterrà valori della funzione di autocorrelazione parziale uguali ai coefficienti di riflessione del modello autoregressivo, presi con segno opposto. L'ordine del modello non viene passato come parametro di input; si presume che sia uguale al numero di elementi nell’array di input R[].
Le dimensioni dell'array di output devono quindi essere non inferiori alla dimensione dell'array di input; l'adempimento a questo requisito non viene controllato all'interno della funzione. Al termine dei calcoli, il coefficiente autoregressivo zero e il coefficiente zero della funzione di autocorrelazione parziale non vengono salvati negli array A[] e K[].
Si presume che siano sempre uguali a uno. Pertanto, gli array di output, come nella sequenza di input, conterranno coefficienti con indici da 1 a IP (da non confondere con gli indici di array che partono da 0).
I valori ottenuti della funzione di autocorrelazione parziale sono ulteriormente utilizzati solo per la visualizzazione su un rispettivo grafico e i coefficienti autoregressivi servono come base per il calcolo della stima della risposta in frequenza che è definita dalla seguente formula:
![]()
La risposta in frequenza viene calcolata per 4096 valori di frequenza normalizzati nell'intervallo da 0 a 0,5. Il calcolo diretto dei valori AFR utilizzando la formula di cui sopra richiede troppo tempo che può essere sostanzialmente ridotto utilizzando l'algoritmo di trasformata di Fourier veloce per calcolare la somma di esponenziali complessi.
A tale scopo, il metodo Calc utilizza la trasformata di Hartley veloce (FHT) invece della trasformata di Fourier veloce.
La trasformata di Hartley non comporta operazioni complesse e sia le sequenze di input che di output sono valide. La trasformata di Hartley inversa viene calcolata usando la stessa formula che richiede solo un fattore aggiuntivo 1/N.
In una sequenza di input valida, esiste una semplice connessione tra i coefficienti di questa trasformata e i coefficienti della trasformata di Fourier
![]()
Informazioni sugli algoritmi di trasformazione di Hartley veloce possono essere trovate qui "FXT algorithm library" e "Discrete Fourier and Hartley Transforms".
Nell'implementazione data, la funzione di trasformazione di Hartley veloce è rappresentata dal metodo fht.
//----------------------------------------------------------------------------------- // Radix-2 decimation in frequency (DIF) fast Hartley transform (FHT). // Length is N = 2 ** ldn //----------------------------------------------------------------------------------- void TSAnalysis::fht(double &f[], ulong ldn) { const ulong n = ((ulong)1<<ldn); for (ulong ldm=ldn; ldm>=1; --ldm) { const ulong m = ((ulong)1<<ldm); const ulong mh = (m>>1); const ulong m4 = (mh>>1); const double phi0 = M_PI / (double)mh; for (ulong r=0; r<n; r+=m) { for (ulong j=0; j<mh; ++j) { ulong t1 = r+j; ulong t2 = t1+mh; double u = f[t1]; double v = f[t2]; f[t1] = u + v; f[t2] = u - v; } double ph = 0.0; for (ulong j=1; j<m4; ++j) { ulong k = mh-j; ph += phi0; double s=MathSin(ph); double c=MathCos(ph); ulong t1 = r+mh+j; ulong t2 = r+mh+k; double pj = f[t1]; double pk = f[t2]; f[t1] = pj * c + pk * s; f[t2] = pj * s - pk * c; } } } if(n>2) { ulong r = 0; for (ulong i=1; i<n; i++) { ulong k = n; do {k = k>>1; r = r^k;} while ((r & k)==0); if (r>i) {double tmp = f[i]; f[i] = f[r]; f[r] = tmp;} } } }
Quando si chiama questo metodo, un riferimento all'array di dati di input f[] e l'intero senza segno ldn che definisce la lunghezza della trasformazione N = 2 ** ldn vengono passati in input. La dimensione dell’array f[] non deve essere inferiore alla lunghezza della trasformazione N. Tieni presente che non ci sono controlli all'interno della funzione. Tieni inoltre presente che il risultato della trasformazione viene memorizzato nell’array in cui sono stati posizionati i dati di input.
Dopo la trasformazione, i dati di input stessi non vengono memorizzati. Nel metodo Calc in esame viene utilizzata una trasformazione di lunghezza N=8192 per calcolare i valori AFR di 4096. Seguendo il calcolo della magnitudine quadrata della trasformata e prendendo il reciproco, il risultato ottenuto viene normalizzato al suo valore massimo e scalato logaritmicamente.
A parte questo, non ci sono grandi peculiarità del metodo Calc; se necessario, si può dare un'occhiata più da vicino alla sua implementazione facendo riferimento a TSAnalysis.mqh.
Tutti i valori ottenuti e preparati per la visualizzazione come risultato dei calcoli vengono salvati in variabili che sono i membri della classe TSAnalysis. Pertanto, non è necessario passare come argomenti quando si chiama il metodo virtuale per visualizzare i risultati.
Visualizzazione
Come già accennato, il metodo show è dichiarato virtuale. Quindi, ridefinendolo, è possibile implementare il metodo richiesto per visualizzare i risultati del calcolo che sarebbero diversi da quello proposto. La visualizzazione nella classe TSAnalysis proposta viene effettuata mediante la preparazione di file di dati e la chiamata di un browser Web per la visualizzazione dei dati.
Affinché un browser Web sia in grado di visualizzare tali dati, il file TSA.htm viene utilizzato nella stessa directory del resto dei file di progetto. Questo metodo per la visualizzazione di informazioni grafiche è stato descritto in precedenza nell'articolo "Graphs and Diagrams in HTML".
La classe TSAnalysis del metodo show è responsabile della formattazione e del salvataggio di tutti i risultati del calcolo destinati alla visualizzazione in una variabile di tipo stringa (vedi TSAnalysis.mqh). Una lunga linea generata in questo modo viene salvata in TSDat.txt in un unico passaggio. La creazione di questo file e il salvataggio dei dati in esso viene effettuato utilizzando gli strumenti standard MQL5, pertanto il file viene creato nella directory \MQL5\Files.
Questo file viene quindi spostato nella directory di questo progetto chiamando le funzioni di sistema esterne. A questo segue una chiamata di un browser Web che visualizza TSA.htm, la quale utilizza i dati di TSDat.txt. Poiché le funzioni di sistema sono chiamate nel metodo show, l'uso di DLL esterne deve essere abilitato nel Terminale per lavorare con la classe TSAnalysis.
Esempi
TSAexample.mq5, incluso nell’archivio TSAnalysis.zip, è un esempio di utilizzo della classe TSAnalysis.
//----------------------------------------------------------------------------------- // TSAexample.mqh // 2011, victorg // https://www.mql5.com //----------------------------------------------------------------------------------- #property copyright "2011, victorg" #property link "https://www.mql5.com" #include "TSAnalysis.mqh" //----------------------------------------------------------------------------------- // Script program start function //----------------------------------------------------------------------------------- void OnStart() { double bd[]={47,64,23,71,38,64,55,41,59,48,71,35,57,40,58,44,80,55,37,74,51,57,50, 60,45,57,50,45,25,59,50,71,56,74,50,58,45,54,36,54,48,55,45,57,50,62,44,64,43,52, 38,59,55,41,53,49,34,35,54,45,68,38,50,60,39,59,40,57,54,23}; TSAnalysis *tsa=new TSAnalysis; tsa.Calc(bd); delete tsa; }
Come si può vedere, il riferimento alla classe è abbastanza semplice; se è presente un array preparato contenente la sequenza di input, non ci vorrà molto sforzo per passarlo al metodo Calc per l'analisi. Inoltre, dovresti ricordarti di liberare la memoria chiamando delete. Il risultato dell'esecuzione di questo script è già stato fornito all'inizio dell'articolo.
Per dimostrare l'efficienza delle stime spettrali prodotte, passiamo ad ulteriori esempi in cui verranno utilizzate sequenze generate.
Per cominciare, useremo una sequenza composta da due sinusoidi.
int i,n; double a,x[]; n=400; ArrayResize(x,n); a=2*M_PI; for(i=0;i<n;i++)x[i]=MathSin(0.064*a*i)+MathSin(0.071*a*i);
La figura seguente mostra la stima della risposta in frequenza di questa sequenza.
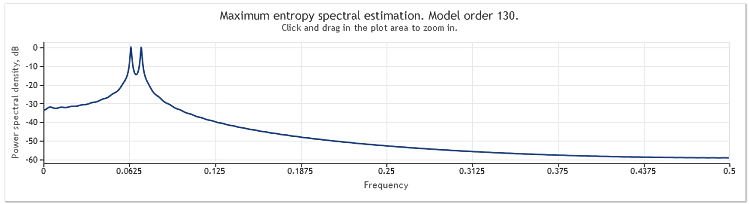
Figura 2. Stima spettrale. Due sinusoidi
Sebbene entrambe le sinusoidi siano ben osservabili, lo zoom sull'area del grafico di interesse ci ha permesso di scoprire che i picchi si trovano a frequenze di 0,0637 e 0,0712. In altre parole, sono in qualche modo diversi dai veri valori. Quando una sequenza è costituita da una singola sinusoide, tale distorsione di una stima non viene osservata. Consideriamo questo evento come l'effetto del metodo selezionato di analisi spettrale.
Complicheremo ulteriormente il compito aggiungendo un componente casuale alla nostra sequenza. A tale scopo, verrà utilizzato un generatore di sequenze pseudo-casuali rappresentato dalla classe RNDXor128, che può essere trovata nell'archivio RNDXor128.zip alla fine dell'articolo.
Il frammento di codice riportato di seguito è stato utilizzato per generare un segnale di test.
int i,n; double a,x[]; RNDXor128 *rnd=new RNDXor128; n=800; ArrayResize(x,n); a=2*M_PI; for(i=0;i<n;i++)x[i]=MathSin(0.064*a*i)+MathSin(0.071*a*i)+rnd.Rand_Norm(); delete rnd;
In questo esempio, un segnale casuale con distribuzione normale e varianza unitaria è stato aggiunto a due sinusoidi.
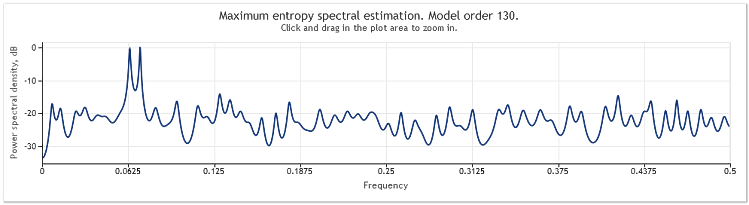
Figura 3. Stima spettrale. Due sinusoidi più un segnale casuale
In questo caso, le componenti sinusoidali rimangono ben distinguibili.
Un aumento di cinque volte dell'ampiezza della componente casuale si traduce in sinusoidi sostanzialmente mascherate.
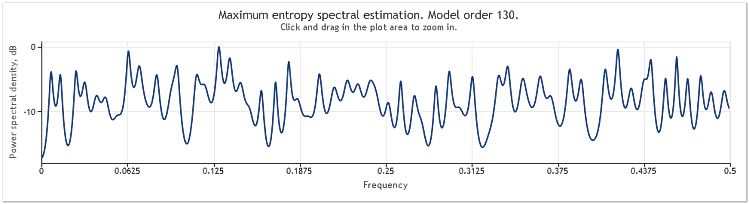
Figura 4. Stima spettrale. Due sinusoidi più un segnale casuale con ampiezza maggiore
Quando la lunghezza della sequenza viene aumentata da 400 a 800 elementi, le sinusoidi diventano di nuovo ben osservabili.
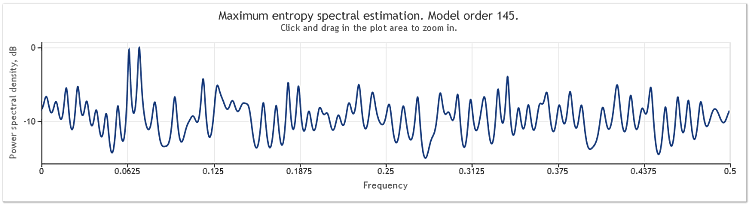
Figura 5. Due sinusoidi più un segnale casuale con ampiezza maggiore. N=800
L'ordine del modello autoregressivo è quindi aumentato da 130 a 145. L'aumento della lunghezza della sequenza ha portato a un ordine più elevato del modello e, di conseguenza, la potenza di risoluzione della stima spettrale è aumentata: i picchi del grafico sono diventati marcatamente più nitidi.
La stima spettrale delle quotazioni per EURUSD, D1 su due anni (2009 e 2010) può essere mostrata come segue.

Figura 6. Quotazioni EURUSD. 2009-2010. Period D1
La sequenza di input consisteva di 519 valori e l'ordine del modello, come si vede dalla figura, sembrava essere 135.
Come si può vedere, questa stima spettrale contiene un numero di picchi distinti. Ma questa stima da sola non è sufficiente per determinare se questi picchi sono componenti periodiche delle quotazioni.
Il verificarsi di picchi nella risposta in frequenza può essere causato da una componente casuale di alto livello presente nelle virgolette o da un'esplicita non stazionarietà della sequenza in questione.
È quindi sempre consigliabile verificare il risultato ottenuto utilizzando i dati di un'altra frazione della sequenza o di un altro lasso di tempo prima di trarre una conclusione finale in merito alla presenza della componente periodica. Inoltre, quando si studia la ricorrenza ciclica, si può provare a utilizzare le differenze di sequenza invece della sequenza stessa.
Conclusione
Poiché il metodo di stima spettrale impiegato nell'articolo si basa sui coefficienti di autocorrelazione, la media della sequenza di input sembra sempre essere eliminata dalla sequenza al momento dell'applicazione del metodo. Spesso è assolutamente necessario eliminare un componente costante dalla sequenza di input ma, quando si utilizzano metodi autoregressivi, tale delezione può, in alcuni casi, causare distorsione della stima spettrale nella gamma di basse frequenze.
Un esempio di tali distorsioni è riportato alla fine del capitolo "Summary of Results Regarding Spectral Estimatesi" nel libro di S. L. Marple "Digital Spectral Analysis with Applications". Nel nostro caso, il metodo di analisi spettrale impiegato non ci lascia altra scelta, quindi tieni semplicemente presente che la stima spettrale viene sempre eseguita rispetto a una sequenza con una media cancellata.
Fonti
- Wuertz, Diethelm and Katzgraber, Helmut (2009): Precise finite-sample quantiles of the Jarque-Bera adjusted Lagrange multiplier test, Swiss Federal Institute of Technology, Zurich,2009.
- Tanweer-ul-Islam, Asad Zaman, Normality Testing - A new Direction, IIE, International Islamic University, Islamabad, Pakistan, 2008.
- Carlos M. Urzua, Portable and powerful tests for normality, Tecnologico de Monterrey, Campus Ciudad de Mexico, 2007.
- Comparison of Common Tests for Normality
- S. V. Bulashev. Statistics for Traders. - М.: Kompania Sputnik +, 2003. - 245 pp.
- P. V. Novitsky, I. A. Zograf. Estimation of Error in Measurement Results. Energoatomizdat, 1991.
- S. L. Marple, Jr. Digital Spectral Analysis with Applications. Moscow: Mir, 1990.
- David J. Sheskin, Handbook of Parametric and Nonparametric Statistical Procedures, Chapman and Hall/CRC.
Tradotto dal russo da MetaQuotes Ltd.
Articolo originale: https://www.mql5.com/ru/articles/292
 Previsione di serie temporali mediante livellamento esponenziale
Previsione di serie temporali mediante livellamento esponenziale
 Teoria e implementazione di indicatori adattivi avanzati con MQL5
Teoria e implementazione di indicatori adattivi avanzati con MQL5
 Analisi dei parametri statistici degli indicatori
Analisi dei parametri statistici degli indicatori
 Il Wizard MQL5 per principianti
Il Wizard MQL5 per principianti
- App di trading gratuite
- Oltre 8.000 segnali per il copy trading
- Notizie economiche per esplorare i mercati finanziari
Accetti la politica del sito e le condizioni d’uso
È stato pubblicato l'articolo Analizzare le principali caratteristiche delle serie temporali:
Autore: Victor
Viktor, buon pomeriggio.
Purtroppo non sono in grado di ottenere le informazioni finali. Vengono visualizzate le caratteristiche che compaiono nella forma originale: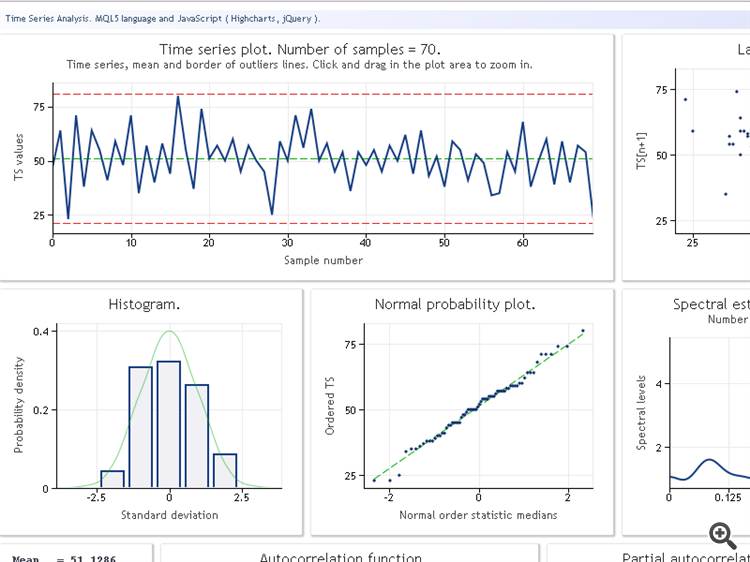
Osservate il testo dello script TSAexample.mq5 .
In esso, l'array bd[] viene riempito con i valori della sequenza analizzata e poi utilizzato come argomento quando si chiama il metodo Calc della classe TSAnalysis.
Scrivete il vostro script (o indicatore), formate un array contenente la vostra sequenza con qualsiasi metodo disponibile e passatelo come argomento al metodo Calc, per analogia con l'esempio fornito nell'articolo.
Mi sembra che dovreste essere in grado di farlo.
Victor.
Cosa significa l'acronimo "IP"?
Osservate il testo dello script TSAexample.mq5 .
In esso, l'array bd[] viene riempito con i valori della sequenza analizzata e poi utilizzato come argomento quando si chiama il metodo Calc della classe TSAnalysis.
Scrivete il vostro script (o indicatore), formate un array contenente la vostra sequenza con qualsiasi metodo disponibile e passatelo come argomento al metodo Calc, per analogia con l'esempio fornito nell'articolo.
Mi sembra che dovreste essere in grado di farlo.
Victor.
Funziona tutto bene! Uno strumento molto utile! Grazie!