Vous manquez des opportunités de trading :
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Inscription
Se connecter
Vous acceptez la politique du site Web et les conditions d'utilisation
Si vous n'avez pas de compte, veuillez vous inscrire
Oui, mais seulement à un niveau associatif. Les graphiques sont fortement compressés. Jeu de devinettes))))
Supposition ou pas, Nova le dira...
Je vais torturer tout le monde pour le moment))
C'est quand même joli !
Oh, aussi bien que je puisse, je connais la gauche et la droite)).
Ici,danminin écrit que la différence n'est que dans le kurtosis, c'est-à-dire dans l'insularité, d'où il découle qu'un grand nombre de petits incréments, pourquoi est-ce le cas et la PST n'est pas remplie ?
il y a plus d'incréments que sur qqn.
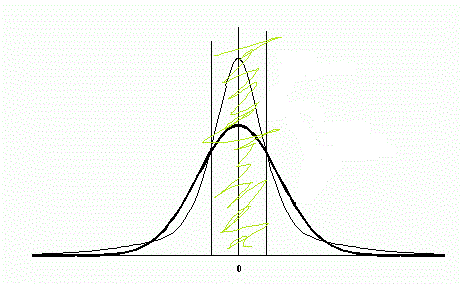
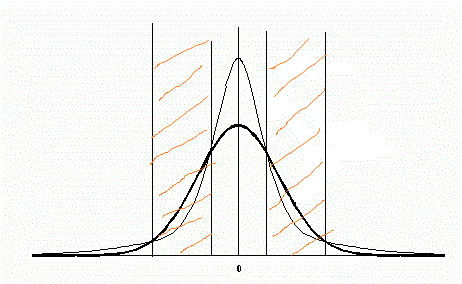
Ceux-ci sont moins nombreux.
il y en a encore d'autres.
Où est la réfutation que les citations sont aléatoires ? Et où est la preuve que l'ensemble du processus de vie des citations ne finira pas par converger vers la normale ? Et dans quelle dimension l'avez-vous mesurée en premier lieu ?)
Et qui dit que nous avons un processus aléatoire infini qui va nécessairement converger vers la normale.J'ai traversé cette étape il y a longtemps. J'ai essayé de "normaliser" le marché. J'ai calculé toutes sortes de mesures, conduit des tests d'hypothèse... J'ai toujours tiré une conclusion au niveau de signification de 0,9 ou plus - que le mouvement des prix n'était pas normal, où que ce soit.
Le théorème limite de Gauss dit que si une variable aléatoire dépend d'un grand nombre de variables indépendantes - sa valeur est décrite par la loi normale dans la limite.
C'est le point que notre processus aléatoire - ne convergera jamais vers la normale. Tout au plus - elle ne peut coïncider avec une distribution normale que pendant un certain temps.
Disons que nous jouons à pile ou face, si face est en haut, si pile est en bas. Cinq autres pièces sont lancées, si elles sont toutes face, on ajoutera 5 points à partir de la première pièce - une sorte de simulation de nouvelles, jusqu'à ce que trois aigles sortent. Il y aura un pic de volatilité. Où est l'anomalie ici ? Pourquoi un tel processus est-il anormal sur le marché réel ?
Eh bien, vous modélisez simplement un processus aléatoire normal, car le tirage d'une pièce de monnaie dépend d'un grand nombre de facteurs indépendants. En vérifiant l'hypothèse de l'uniformité de la distribution, vous confirmerez sûrement, avec un niveau de signification élevé, que le tirage d'une pièce de monnaie est un processus uniformément aléatoire.
Le mouvement réel des prix, en revanche, est un processus entièrement différent. Et il ne peut être décrit en termes de distribution uniforme, ni en termes de distribution normale - encore une fois, parce que le prix n'est pas influencé par des facteurs indépendants.
C'est ça le truc - notre processus aléatoire - ne convergera jamais vers un processus normal. Tout au plus, elle ne peut coïncider avec une distribution normale que pendant un certain temps.
Quelqu'un a comparé le mouvement d'un prix à la vitesse d'une voiture, un bon exemple - à certains moments, la vitesse d'une voiture obéit aux lois de l'accélération, puis elle peut s'arrêter, puis elle peut tourner...
Vous avez beau essayer, la loi qui régit la vitesse d'une voiture ne peut être décrite par une formule mathématique.
il y avait la déclaration de @Maxim Dmitrievsky selon laquelle un processus non aléatoire doit être périodique, eh bien, ce n'est pas une "condition nécessaire" pour le caractère non aléatoire... Le même graphique d'un exposant n'est pas périodique, mais il ne sera pas non plus aléatoire.
un dans les bois et un hors des bois...
Je recommande vivement de le lire :
Ventzel E.S., Ovcharov L.A.
Théorie des probabilités et ses applications en ingénierie
Moscou : Nauka. 1988 (Bibliothèque de Physique et de Mathématiques pour l'Ingénieur). - 480 с.
Exposé systématique des fondements de la théorie des probabilités du point de vue des applications pratiques dans les spécialités : cybernétique, mathématiques appliquées, informatique, systèmes de contrôle automatisé, théorie des mécanismes, radiotechnique, théorie de la fiabilité, transports, communications, etc. Malgré la variété des domaines auxquels les applications se rapportent, elles sont toutes imprégnées d'un cadre méthodologique commun.
Pour un large éventail d'ingénieurs et de scientifiques de différents profils, qui, dans leurs activités pratiques, sont confrontés à la nécessité de poser et de résoudre des problèmes liés à des phénomènes aléatoires. Il peut également être utilisé par les étudiants universitaires et les enseignants des spécialités concernées.
.
Et commencez à lire depuis le début.
Oh, aussi bien que je puisse, je connais la gauche de la droite)).
Je parlais des photos de Vizard_.
Vous modélisez donc un processus aléatoire normal, car le tirage d'une pièce de monnaie dépend d'un grand nombre de facteurs indépendants. Test de l'hypothèse d'uniformité de la distribution - vous pouvez probablement confirmer, avec un niveau de signification élevé, que le tirage d'une pièce de monnaie est un processus uniformément aléatoire.
Le mouvement réel des prix, en revanche, est un processus entièrement différent. Et il ne peut être décrit ni dans le cadre d'une distribution uniforme ni dans le cadre d'une distribution normale - là encore, parce que le prix est influencé par des facteurs loin d'être indépendants.
Comment déterminez-vous qu'il s'agit d'un processus entièrement différent ?
quelqu'un a comparé le mouvement d'un prix à la vitesse d'une voiture, à mon avis, bon exemple - à certains moments, la vitesse d'une voiture obéit aux lois de l'accélération, puis elle peut s'arrêter, puis il peut y avoir un virage
On a beau essayer, la loi qui régit la vitesse d'une voiture ne peut être décrite par une formule mathématique.
il y avait la déclaration de @Maxim Dmitrievsky selon laquelle un processus non aléatoire doit être périodique, eh bien, ce n'est pas une "condition nécessaire" pour le caractère non aléatoire... Le même graphique d'un exposant n'est pas périodique mais il ne sera pas non plus aléatoire.
Un processus non aléatoire peut avoir une tendance linéaire ou une tendance cyclique. Mais encore faut-il qu'il y ait quelque chose qui caractérise le processus comme non aléatoire, sinon c'est un SB avec une densité de distribution quelconque
Si aucune composante constante ne peut être distinguée, alors le processus est bien sûr aléatoire, qu'y a-t-il à réfléchir ?
Un processus aléatoire peut prétendre être non aléatoire, par hasard. C'est pourquoi, sur le marché, il y a souvent l'illusion qu'il est prévisible, mais ensuite cette période passe et tous les signaux se confondent