L'étiquette du marché ou les bonnes manières dans un champ de mines - page 57
Vous manquez des opportunités de trading :
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Inscription
Se connecter
Vous acceptez la politique du site Web et les conditions d'utilisation
Si vous n'avez pas de compte, veuillez vous inscrire
C'est reparti avec l'OTO du marché. Le fait est qu'il y a un retard, bien sûr, car le milieu de la barre arrive immédiatement après son ouverture, mais, d'un autre côté, il n'existe pas, car lorsque la barre est déjà formée, nous ne nous soucions pas de savoir quand exactement à l'intérieur de la barre ce juste milieu est arrivé. J'ai vu des bars qui commencent et finissent au milieu. L'essentiel de votre argumentation avec Neutron ne vaut pas un seul mot. C'est parce que les barres ne sont pas des barres pour Neutron, parce qu'un quotient n'est pas quantifié par le temps, alors qu'une barre est une BAR pour vous.
Vous avez des "cadres de référence" différents - c'est tout ce qu'il y a à faire.
Non, pas vieux... >> oh, Superstar !
Tu es toujours aussi stupide, ma chère ? La vieillesse n'est vraiment pas drôle.
C'est reparti avec l'OTO du marché. Le fait est qu'il y a un retard, bien sûr, parce que le milieu de la barre arrive immédiatement après son ouverture, mais, d'un autre côté, il n'existe pas, parce que lorsque la barre est déjà formée, personne ne se soucie de savoir quand ce juste milieu de la barre est arrivé. J'ai vu des bars qui commencent et finissent par le milieu. L'essentiel de votre argumentation avec Neutron ne vaut pas un seul mot. C'est parce que les barres ne sont pas des barres pour Neutron, parce qu'un quotient n'est pas quantifié par le temps, alors qu'une barre est une BAR pour vous.
Vous avez des "cadres de référence" différents - c'est tout ce qu'il y a à faire.
L'argument porte sur de nombreuses choses, dont celle-ci en particulier. Sergei en a fait un argument "convaincant". Mais il semble que je ne sois pas capable d'expliquer une chose simple. Il n'y a pas de retard, il n'y a pas de retard du tout. Il ne peut pas être là par définition. Les données sur lesquelles reposent ces chiffres ne se recoupent pas. Il n'y a pas de phase, les chiffres sont complètement égaux.
Addendum : C'est comme prendre deux points sur une onde sinusoïdale et dire qu'à x par incréments de 0,1 et à x par incréments de 10,0, il y a un retard.
Ce n'est pas grave - nous nous en tiendrons à notre opinion...
Essayez-le.
Alors bonne chance :). La décomposition en série de Taylor est encore pire qu'en harmoniques car un polynôme de degré non nul n'a pas de plage de valeurs limitée.
D'ailleurs d'après vos propos, il s'avère qu'il ne s'agit pas du tout d'un polynôme, mais d'une machine à onduler SMA ordinaire.
Très bien, alors. Voici l'idée elle-même. Si vous réfléchissez bien, aucune force du marché ne sous-estimerait l'importance des 2e, 4e et 11e mesures par rapport aux mesures voisines. Autrement dit, il faut s'attendre à ce que des barres voisines aient des valeurs très proches. Ce qui s'est passé il y a 11 heures est tout aussi important que ce qui s'est passé il y a 12 heures. Nous devons donc nous attendre à une transition en douceur des poids d'un bar à ses voisins. Ainsi, la courbe décrivant le poids en fonction du numéro de barre (retard) devrait être lisse. Si cela est vrai, cette courbe w[n] peut être approximée par une série de Taylor, c'est-à-dire par un polynôme. Vous pouvez, par exemple, adapter un polynôme de 3e ou 4e degré à vos poids. L'hypothèse suivante de mon idée est la suivante. Au lieu d'optimiser les poids eux-mêmes (vous en avez 16), optimisez les coefficients polynomiaux (a0+a1*n+a2*n^2+a3*n^3, vous optimisez a0...a3, vous obtenez 4 paramètres au total), et utilisez la formule a0+a1*n+a2*n^2+a3*n^3 pour la n-ième barre. Beaucoup moins de calculs. Essayez-le.
Je vous suis sincèrement reconnaissant pour cette idée, cependant, une fois dans mon enfance, j'ai entendu (par les garçons dans le hall d'entrée), que si une erreur est trouvée dans la fondation du concept, toutes les constructions ultérieures peuvent être ignorées, indépendamment de leur attrait scientifique. Vous avez une erreur dans l'idée de la fluidité comme fonction nécessaire pour la transition d'un état (de marché) à un autre. Hélas. Je dois vous décevoir. Le marché passe de A à Z sans révérence intermédiaire. S'il en était autrement, ce ne serait pas un forum, mais une réunion de Soros.
Peu importe... Je vais vous donner une nouvelle idée (concept de marché), elle est certainement plus fructueuse que celle que vous avez eue jusqu'à présent :
C'est assez simple à première vue :
La régularité est un moyen pour le hasard d'exister. Le contraire n'est pas vrai.
à Neutron
Le produit ne fonctionnera pas sur ce système d'exploitation
Je suis allé chercher du savon...
Je peux prédire comme ça aussi, d'ailleurs. Même sans un AR. :) Mais ça ne m'a rien donné. Je peux deviner "où" le prix va aller avec une précision de 80% mais je n'ai aucun PROFIT. C'est triste. ;)
La série (H+L)/2. Je le désigne par Mu par souci de concision. Supposons que nous ne puissions pas prédire avec précision cette valeur, mais que nous puissions prédire avec précision le signe de la différence Mu(n)- Mu(n+1). Par exemple, pour la barre actuelle, nous savons que le prochain delta Mu(n) - Mu(n+1) sera positif. Ensuite, nous devons estimer statistiquement le nouvel incrément et, à partir de là, passer à Mu(n+1). Ajoutons à ce niveau l'estimation RMS de l'écart entre les barres. Nous obtenons le niveau du métier et j'ai même fait un dessin pour renforcer l'expression artistique :
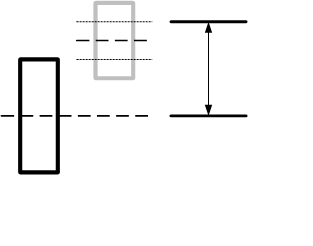
Si les fréquences d'apparition de ces niveaux sont importantes et proportionnelles à l'écart, nous pouvons réussir. Prévoyez-vous vraiment ce delta à 80% ?
PS : Personnellement, je ne travaille pas aussi étroitement avec le prix. Il n'y a pas beaucoup de chance, ou plutôt aucune chance du tout. Je viens d'avoir l'idée qu'il est en effet possible de prévoir non pas précisément, mais seulement dans la direction. J'ai fait mes propres prévisions avec cette "technologie" : "Avez-vous vu cette image ?" au moins pour 24 heures sur des barres de 15 min, voici des exemples de prévisions réelles, je vais terminer le prochain test - il y en aura d'autres (juste du débogage, tout l'astrolabe n'a pas encore été construit) :
Test des systèmes de prédiction en temps réel
à gpwr
Oui, j'ai en quelque sorte manqué votre avant-dernier message. Il y a là une question intéressante : qu'est-ce qui vous fait penser que le poids (en principe) peut être une fonction de son propre indice par rapport au temps ? Je pense avoir compris l'origine de votre idée - vous regardez des graphiques de poids. Il y a une subtilité : dans deux expériences différentes (résultats d'entraînement sur le même vecteur d'entraînement), ces graphiques (visuellement et topologiquement) peuvent être sensiblement différents, alors que les résultats de la grille (statistiquement) sont sensiblement les mêmes. Si vous parvenez même à trouver une fonction satisfaisante pour former le réseau par la méthode proposée, les résultats de la formation (deux expériences consécutives sur le même vecteur) seront totalement identiques - c'est-à-dire qu'il ne s'agira pas d'un réseau neuronal, mais de quelque chose de totalement déterministe. Comme le dirait Neutron, qui est déjà endormi, un tel réseau sera exactement entraîné pour un vecteur, mais ne sera pas capable de composer des poèmes. Par conséquent, il n'est d'aucune utilité pour le commerce. Chaque comptage successif n'est pas similaire au précédent (et aux nouveaux), et une grille normale ne compte même pas là-dessus. Il ressemble grossièrement à une certaine image qu'il a apprise. Si on remplace approximativement par exactement, l'entropie d'un tel réseau sera égale à zéro (c'est-à-dire un pas à gauche, un pas à droite - peloton d'exécution, un saut sur place - provocation).
Entre autres choses, je ne vois pas de différence particulière dans la vitesse d'entraînement avec la méthode que vous suggérez, car pour changer un coefficient du polynôme, j'aurai besoin exactement des mêmes ressources que pour corriger un poids, et il y a n coefficients (pour chaque poids), alors quel est le gain ?
La série (H+L)/2. Je le désigne par Mu par souci de concision. Supposons que nous ne puissions pas prédire avec précision cette valeur, mais que nous puissions prédire avec précision le signe de la différence Mu(n) - Mu(n+1). Par exemple, pour la barre actuelle, nous savons que le prochain delta Mu(n) - Mu(n+1) sera positif. Ensuite, nous devons estimer statistiquement le nouvel incrément et, à partir de là, passer à Mu(n+1). Ajoutons à ce niveau l'estimation RMS de l'écart entre les barres. Nous obtenons le niveau du métier et j'ai même fait un dessin pour renforcer l'expression artistique :
Si les fréquences d'apparition de ces niveaux sont importantes et proportionnelles à l'écart, nous pouvons réussir. Prévoyez-vous vraiment ce delta de 80% ?
Surpris de voir l'algorithme qui le démontre à 80%. Je cherche une erreur. Cela semble très simple. Cela ne fonctionne pas de cette façon.
а-а-а-а-а-а-а-а-а-а-а-!!!!! Nous devons voir où est la lune, c'est peut-être la raison. Je comprends maintenant l'expression - "les mots manquent" C'est là que se situe le retard ? ??
Nous l'avons construit spécialement pour vous :
Vous pouvez clairement voir que le FZ est toujours là et qu'il est visuellement bien visible sur les mouvements brusques du kotir.
Vous pouvez voir que le retard est toujours présent, et il est facile de le repérer visuellement sur les mouvements brusques du kotir. Apprenez les mathématiques, et la prochaine fois que vous aurez une idée super brillante, pour la mise en œuvre de laquelle vous pensez avoir besoin d'un ou deux instituts de recherche et d'un groupe de PC, vous réfléchirez une minute - peut-être ne savez-vous pas ou ne comprenez-vous pas. Après tout, c'est plus probable qu'une "découverte marquante", dans un domaine où tout a été piétiné avant vous.
Je propose un moyen raccourci de décrire toutes les échelles, dans ce cas un polynôme. Je vais vous le montrer avec votre exemple. Vous avez appris votre réseau sur un certain vecteur d'entrée et obtenu les valeurs de tous les poids w[n] où n=0...15.
Je crois que paralocus vous fait remarquer à juste titre que votre idée est basée sur l'hypothèse non prouvée de la stationnarité des processus de marché alloués à NS. Ce n'est que dans le cas de sa confirmation que nous pouvons espérer un semblant de stationnarité des poids du NS et par conséquent l'applicabilité de la méthode d'extrapolation pour trouver des poids sans entraînement du réseau. Mais, si c'était le cas, nous ne réentraînerions pas la grille à chaque nouvelle donnée BP, mais nous devons le faire, et ce fait, bien qu'indirect, parle en faveur de la non-stationnarité des poids ! En outre, vous pouvez toujours effectuer une expérience numérique et voir comment les poids de la grille entraînée se comportent d'un échantillon à l'autre. On va voir ?
À cette fin, effectuons 500 expériences en décalant d'une barre à chaque fois et en apprenant à prédire la suivante. Nous allons enseigner le filet à nouveau à chaque bar. Pour éviter d'afficher le vecteur des poids 500 fois sur un seul graphique, nous allons faire la moyenne des valeurs obtenues pour chaque poids et les afficher en montrant la variance (dispersion des valeurs) correspondant à chaque poids sous forme de poignée tracée en fonction du niveau 1/e :
L'axe des abscisses indique le numéro de l'entrée NS, l'axe des ordonnées la valeur moyenne du poids sur cette entrée, pour un réseau entièrement entraîné. Comme on peut le constater, pour les marqueurs horaires (fig. de gauche), les valeurs des poids se situent dans la zone de leur dispersion statistique (intervalle des moustaches), ce qui réfute directement l'hypothèse de stationnarité. Le cas est un peu meilleur sur les minutes ; statistiquement significative est la première entrée de NS (échantillon zéro dans le graphique) qui est responsable de l'antipersistance connue du kotier (coefficient de corrélation négatif dans une série de la première différence entre échantillons voisins) sur les petites TF.
Il est donc prématuré de parler de la nécessité de développer une méthode d'approximation des poids NS par un polynôme.