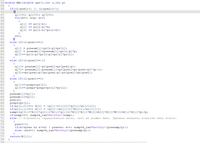
void calcPolynomialRegression(double &PricesArray[],double &RegressionArray[], int power) { ArrayResize(RegressionArray, ArraySize(PricesArray)); ArraySetAsSeries(RegressionArray,ArrayGetAsSeries(PricesArray)); double summ_x_value[21],summ_y_value[11],constant[11],matrix[11][11]; ArrayInitialize(summ_x_value,0); ArrayInitialize(summ_y_value,0); ArrayInitialize(constant,0); ArrayInitialize(matrix,0); double summ=0,summ_x=0,summ_y=0; int pos=ArraySize(PricesArray)-1; summ_x_value[0]=ArraySize(PricesArray); for(int exp_n=1; exp_n<=2*power; exp_n++) { summ_x=0; summ_y=0; for(int k=1; k<=ArraySize(PricesArray); k++) { summ_x+=MathPow(k,exp_n); if(exp_n==1) summ_y+=PricesArray[pos-k+1]; else if(exp_n<=power+1) summ_y+=PricesArray[pos-k+1]*MathPow(k,exp_n-1); } summ_x_value[exp_n]=summ_x; if(summ_y!=0) summ_y_value[exp_n-1]=summ_y; } for(int row=0; row<=power; row++) for(int col=0; col<=power; col++) matrix[row][col]=summ_x_value[row+col]; int initial_row=1; int initial_col=1; for(int i=1; i<=power; i++) { for(int row=initial_row; row<=power; row++) { summ_y_value[row]=summ_y_value[row]-(matrix[row][i-1]/matrix[i-1][i-1])*summ_y_value[i-1]; for(int col=initial_col; col<=power; col++) matrix[row][col]=matrix[row][col]-(matrix[row][i-1]/matrix[i-1][i-1])*matrix[i-1][col]; } initial_col++; initial_row++; } int j=0; for(int i=power; i>=0; i--) { if(j==0) constant[i]=summ_y_value[i]/matrix[i][i]; else { summ=0; for(int k=j; k>=1; k--) summ+=constant[i+k]*matrix[i][i+k]; constant[i]=(summ_y_value[i]-summ)/matrix[i][i]; } j++; } int k=1; for(int i=ArraySize(PricesArray)-1; i>=0; i--) { summ=0; for(int n=0; n<=power; n++) summ+=constant[n]*MathPow(k,n); RegressionArray[i]=summ; k++; } }
He implementado el cálculo de regresión (no sólo lineal) sin ciclos en absoluto. Más concretamente, sólo se necesita un ciclo durante la inicialización.
Como resultado, la velocidad de cálculo es mil veces más rápida.
Y el código es más corto.
Pero lo siento, no voy a publicar el código. Es un secreto.
Sólo digo que es real.
Hay dos artículos que le ayudarán

- www.mql5.com
He implementado el cálculo de la regresión (no sólo lineal) sin ningún tipo de bucle. Para ser más exactos, el bucle sólo se necesita una vez en la inicialización.
Como resultado, la velocidad de cálculo es mil veces más rápida.
Y el código es más corto.
Pero lo siento, no voy a publicar el código. Es un secreto.
Sólo digo que es real.
El código es muy sencillo. Sumamos los cuadrados actuales, restamos los cuadrados fuera del intervalo. Eso es todo. Ese es todo el secreto).
Puede ser aún más interesante, pero siguiendo principios diferentes.
El código es muy sencillo. Sumamos los cuadrados actuales, restamos los cuadrados fuera del intervalo. Eso es todo. Ese es el secreto).
Es gracioso ))
Para hacerlo aún más divertido, podrías contar no sobre el canal, sino sobre cómo hacer una línea de regresión polinómica sin ciclos. Pero definitivamente no voy a hacer eso. No lo necesitas.
He implementado el cálculo de regresión (no sólo lineal) sin ciclos en absoluto. En concreto, el ciclo es necesario sólo una vez en la inicialización.
Como resultado, la velocidad de cálculo es miles de veces más rápida.
Y el código es más corto.
Pero lo siento, no voy a publicar el código. Es un secreto.
Sólo digo que es real.
Miles de veces más rápido, y sin un bucle de valores de entrada...
¡¡¡No me lo creo!!!
Como mínimo, es obligatorio un bucle de parámetros de entrada.
He implementado el cálculo de regresión (no sólo lineal) sin ciclos en absoluto. Más concretamente, el bucle sólo se necesita una vez en la inicialización.
Como resultado, la velocidad de cálculo es mil veces más rápida.
Y el código es más corto.
Pero lo siento, no voy a publicar el código. Es un secreto.
Sólo digo que es real.
E incluso sin un bucle de suma x*y? ¿Y si x e y no son líneas rectas?
Miles de veces más rápido, y sin un bucle de valores de entrada...
¡¡¡No me lo creo!!!
¡Al menos un bucle sobre los parámetros de entrada es obligatorio!
E incluso sin un bucle de suma x*y ? ¿Y si x e y no son líneas rectas?
No te lo creas a pies juntillas.
Rashid dejó caer los artículos. Léalos con atención. Allí hay un enlace a otro artículo:
https://www.mql5.com/ru/articles/270
Si te devanas los sesos al nivel de las matemáticas de 7º-8º grado, puedes obtener la desviación estándar para obtener el canal, no sólo la media deslizante, de forma similar sin un ciclo. Lo tengo implementado para un polinomio de cualquier grado, no sólo del primer grado (regresión lineal). Puedes sentirlo en la versión demo en el mercado.
HH escribí que el bucle es necesario una vez en la inicialización.
Miles de veces más rápido: esto incluye el cálculo de la desviación estándar (es decir, la anchura del canal)- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
Tengo un indicador de regresión lineal.
Cómo construir su cálculo en el EA y obtener datos en 0 bar o en 1.
Intenté hacerlo así:
Pero no da algo...